-
Since the very early stages of nuclear physics, the nuclear interaction (nuclear force) remained as one of the most fundamental topics of the field [1–12]. By adopting normalized nucleon-nucleon interactions in the medium, i.e., the effective nuclear force, self-consistent mean field models have achieved great success in describing not only the ground-state [13-19], but also excited properties [19–24] of almost all nuclei on the nuclear chart. In recent decades, the self-consistent mean field theory has also been referred to as the nuclear density functional theory (DFT), and in the foreseeable future it might be the only efficient self-consistent theory that covers almost the entire nuclear chart [25, 26]. Nowdays, the nuclear DFT contains two main branches, namely the relativistic DFTs [27–30] and nonrelativistic ones [14, 15, 31].
In 1935, the interactions between nucleons were recognized to be propagated by massive bosons (mesons) [1], according to the meson exchange diagram of nuclear force. Adhering to such idea, researchers established the relativistic DFT for nuclear systems, which is also referred to as the covariant density functional theory (CDFT). It contains two branches, i.e., the relativistic mean field (RMF) theory considering only the Hartree terms [16, 17, 19] and the relativistic Hartree-Fock (RHF) theory implemented with the Fock terms [24, 29, 32, 33]. Because of the covariant representation of the mean field, the CDFT has several distinctive advantages: 1) natural strong spin-orbit potential that originates from the explicit consideration of the nucleon spin degree of freedom [34]; 2) natural interpretation on the origin of the pseudo-spin symmetry (PSS) [33, 35-39] and the spin symmetry [39–41] in the nucleon and anti-nucleon spectra, respectively; 3) appropriate saturation mechanism of nuclear matter. Moreover, within RHF, the important ingredient of nuclear force, i.e., the tensor force, can be taken into account naturally via the Fock terms [12,42–45].
In practice, the meson-nucleon coupling strengths in CDFT are determined by fitting to global nuclear observables, such as the saturation properties of nuclear matter, and the binding energies and radii of some selected nuclei. On the mean field approach level, due to the non-perturbative nature of the nuclear force, one has to consider the in-medium effects to provide a reliable description of nuclear systems, either by introducing the nonlinear self-couplings of mesons or the density-dependent coupling strengths. For the former, a large number of effective Lagrangians have been developed, such as the NL series [46–49], TM series [50], PK series [51], PC-PK1 with the point couplings [52], etc. For the RMF models with density-dependent coupling strengths, the popular Lagrangians include TW99 [53], DD-ME1 [54] and DD-ME2 [55], PKDD [51], etc. Implemented with the Fock terms, namely the RHF theory, the quantitative accuracy is remarkably improved by introducing the nonlinear self-couplings of the
$ \sigma $ -meson [56] or scalar field [32], as compared to the earlier RHF model [29]. Considering the density-dependent coupling strengths, such as the density-dependent RHF (DDRHF) theory [30, 42, 57], similar accuracies as the conventional RMF models are achieved in describing nuclear structure properties for the first time with the proposed RHF Lagrangians PKOi ($ i = 1,2,3 $ ) [30, 43] and PKA1 that contains the$ \rho $ -tensor ($ \rho $ -T) coupling [42].At the end of last century, the PSS [58, 59], a near degeneracy of the orbits (
$ n,l,j = l+1/2 $ ) and ($n-1, $ $ l+2, j = l+3/2 $ ), which form the pseudo-spin (PS) doublet ($ l' = l+1, j = l'\pm1/2 $ ), was revealed as a relativistic symmetry [35, 60], and the pseudo orbit$ l' $ only represents the orbital angular momentum of the lower component of the Dirac spinor. Within CDFT, the conservation condition of the PSS is demonstrated as$ S(r) + V(r) = 0 $ [35] or$ {\rm d}[S(r)+V(r)]/{\rm d}r = 0 $ [36, 39], which indicates a delicate balance between the nuclear attractive scalar potential$ S(r) $ and the repulsive vector potential$ V(r) $ [61]. Nevertheless, it is still often found in the RMF calculations [62] as well as RHF calculations with PKOi, it is still often found that the PSS is significantly violated for the high-l PS doublet nearby the Fermi levels, corresponding to the so-called spurious shell closures$ N/Z = 58 $ and 92.Implemented with the
$ \rho $ -T coupling that plays the role almost fully via the Fock terms, the RHF Lagrangian PKA1 eventually cures such common discrepancies [42] due to the delicate in-medium balance between nuclear attraction and repulsions [61]. Nevertheless, one cannot ignore the fact that the explicit treatment of the Fock terms, particularly the$ \rho $ -T coupling, largely increase the theoretical complexity, as well as the numerical cost. For some practical applications of CDFT, e.g., describing the octuple motion of nuclei, it is still quite valuable to develop a new RMF Lagrangian that shares the mentioned advantages of PKA1. In Ref. [61], it has been pointed out that the$ \rho $ -T coupling in PKA1, which contributes a fairly strong attractive potential, changes the in-medium balance between the dominant$ \sigma $ -S and$ \omega $ -V channels, leading to notably different density-dependent behaviors for the coupling strengths$ g_\sigma $ ($ \sigma $ -S) and$ g_\omega $ ($ \omega $ -V). It plays a crucial role in the PSS restoration of high-l PS doublets, as well as the elimination of the so-called spurious shell closures. In fact, this also provides qualitative guidance to constrain the density dependence of$ g_\sigma $ and$ g_\omega $ , which are nearly paralleled with each other for the other density-dependent RMF Lagrangians.In contrast, with the occurrence of spurious shell closures, the nuclear binding energies in relevant regions are largely overestimated, e.g., around
$^{140}_{~\,58}$ Ce and$^{218}_{~\,92}$ U [62]. Notably, the nuclear mass is an elementary quantity of atomic nuclei [63–66], whose accuracy is essential for the reliable description of the half-life of$ \beta $ -decay and for further understanding the origin of heavy elements in the universe [67–69]. Therefore, it is expected that an improved accuracy in describing nuclear mass can be achieved by the newly developed RMF Lagrangian, which may benefit the extensive application of CDFT in nuclear$ \beta $ -decay, nuclear reactions, and astro-nuclear physics. With this aim, we consider the$ \sigma $ -S,$ \omega $ -V,$ \rho $ -vector ($ \rho $ -V) and photon vector (A-V) couplings within the RMF and develop a novel RMF Lagrangian DD-LZ1.This paper is arranged as follows. In Sec. 2, we briefly introduce the RMF theory with the density-dependent meson-nucleon coupling strengths and the parametrization of DD-LZ1. In Sec. 3, we apply the new RMF Lagrangian DD-LZ1 to study the masses of the widely selected nuclei from light to heavy regions, and the structure properties of magic nuclei with special focus on the elimination of spurious shell closures and the PSS restoration. Finally, conclusions and perspectives are presented in Sec. 4.
-
The basic ansatz of the RMF theory [70] is the Lagrangian density that contains the degrees of freedom associated with nucleon (
$ \psi $ ), isoscalar scalar$ \sigma $ - ($ \sigma $ -S) and vector$ \omega $ -mesons ($ \omega $ -V), isovector vector$ \rho $ -meson ($ \rho $ -V), and photon A field (A-V). Starting from the Lagrangian density [16, 17, 19, 22], one can derive the Hamiltonian via the Legendre transformation as$ \begin{split} H =& \int {\rm d}{{r}}\bar{\psi}({{r}})\big[-{\rm i}{{\gamma}} \cdot\nabla +M \big]\psi({{r}})\\ &+\frac{1}{2}\int {\rm d}{{r}} {\rm d}{{r}}'\sum\limits_{\phi}\bar{\psi}({{r}})\bar{\psi}({{r}}')\Gamma_{\phi}D_{\phi}\psi({{r}}')\psi({{r}}), \end{split} $

(1) where M is the mass of nucleon,
$ \phi $ denotes the selected coupling channels, namely$ \phi = {\sigma{\rm{-S}} } $ ,$ {\omega{\rm{-V}} } $ ,$ {\rho {\rm{-V}} } $ , and$ { A {\rm{-V}} } $ , and$ D_{\phi} $ denotes the propagators of Yukawa form. The interaction vertexes$ \Gamma_{\phi} $ in the Hamiltonian read as$ \begin{array}{l} \Gamma_{\sigma{\rm{-S}}}(x,y) = -(g_{\sigma})_{x}(g_{\sigma})_{y}, \end{array} $

(2) $ \begin{array}{l} \Gamma_{\omega{\rm{-V}}}(x,y) = +(g_{\omega}\gamma_{\mu})_{x}(g_{\omega}\gamma^{\mu})_{y}, \end{array} $

(3) $ \begin{array}{l} \Gamma_{\rho{\rm{-V}}}(x,y) = +(g_{\rho}\gamma_{\mu}\vec{\tau})_{x}\cdot(g_{\rho}\gamma^{\mu}\vec{\tau})_{y}, \end{array} $

(4) $ \begin{aligned} \Gamma_{A{\rm{-V}}}(x,y) = +\frac{e^{2}}{4}[\gamma_{\mu}(1-\tau_{3})]_{x}[\gamma^{\mu}(1-\tau_{3})]_{y}, \end{aligned} $

(5) where the meson-nucleon coupling strengths
$ g_{\phi} $ are taken as functions of the nucleon density$ \rho_b $ . Following the standard procedure, the energy functional can be obtained from the expectation of the Hamiltonian with respect to the Hartree-Fock ground state [29]. We restrict ourselves within the RMF scheme in this work. Therefore, the Fock terms of the two-body interactions in the Hamiltonian are dropped.On the level of the mean field approach, the nuclear in-medium effects have to be taken into account for a reliable description of nuclear systems, and such effects are considered phenomenologically via the density dependence of the coupling strengths
$ g_\phi $ . In particular, the density dependencies of the coupling strengths$ g_\sigma $ and$ g_\omega $ in the isoscalar channels$ \sigma $ -S and$ \omega $ -V are adopted as the following form [53],$ \begin{array}{l} g_{\phi}(\rho_{b}) = g_{\phi}(0)f_{\phi}(x), \;\;\;\;\;\; \phi = {\sigma{\rm{-S}} }, {\omega{\rm{-V}} }, \end{array} $

(6) where
$ x = \rho_b/\rho_0 $ ,$ \rho_0 $ being the saturation density. For the function$ f_\phi(x) $ , it has the following explicit form,$ \begin{split} f_{\phi}(x) = a_{\phi}\frac{1+b_{\phi}(x+d_{\phi})^{2}}{1+c_{\phi}(x+d_{\phi})^{2}}. \end{split} $

(7) Thus, there are eight density-dependent parameters to be determined in the isoscalar channels
$ \sigma $ -S and$ \omega $ -V. For the isovector$ {\rho {\rm{-V}} } $ coupling, an exponential density dependence is utilized for$ g_\rho $ as people usually do,$ \begin{array}{l} g_{\rho} = g_{\rho}(0)\exp(-a_{\rho} x), \end{array} $

(8) where
$ a_\rho $ is the density-dependent parameter to be determined. In Eqs. (6) and (8),$ g_{\phi}(0) $ corresponds to the values of coupling strengths at$ \rho_b = 0 $ .In general, the masses of the vector mesons, namely the
$ \omega $ - and$ \rho $ -meson, are fixed as their experimental values. Thus in total, 13 parameters remain to be determined for quantifying the RMF Lagrangian, including the mass of$ \sigma $ -meson$ m_\sigma $ , three coupling strengths$ g_\sigma(0) $ ,$ g_\omega(0) $ and$ g_\rho(0) $ , and nine density-dependent parameters. To reduce the number of free parameters, four constraint conditions are introduced for the functions$ f_\phi(x) $ , namely$ f_{\phi}(0) = 1 $ and$ f_{\phi}''(0) = 0 $ ($ \phi = {\sigma{\rm{-S}} } $ ,$ {\omega{\rm{-V}} } $ ). The condition$ f_{\sigma}''(1) = f_{\omega}''(1) $ is ignored in current parametrization. Therefore, a total of nine free parameters remains to be determined.During the parametrization, the pairing correlations are considered for open-shell nuclei with the BCS method, which is briefly recalled in the following. For even-even nuclei, the BCS ground state is defined as
$ \begin{array}{l} \big|{\rm{BCS}}\big> = \prod\limits_{i>0}(u_{i}+v_{i}c_{i}^†c_{\bar{i}}^†)\big|-\big> ,\end{array} $

(9) where
$ \bar{i} $ denotes the time reversal partner of the state i, and$ u_{i}^{2}+v_{i}^{2} = 1 $ . From the following variation with respect to$ v_{i} $ ,$ \begin{array}{l} \delta\big<{\rm{BCS}}\big|(H-\lambda\hat{N})\big|{\rm{BCS}}\big> = 0, \end{array} $

(10) the gap equations can be derived as,
$ \begin{split} \Delta_{i} = -\frac{1}{2}\sum_{i^{\prime}>0} V_{ii^{\prime}}^{pp}\frac{\Delta_{i^{\prime}}}{\sqrt{(\varepsilon_{i^{\prime}}-\lambda)^{2}+\Delta_{i^{\prime}}^{2}}}, \end{split} $

(11) where
$ \Delta_{i} $ is the pairing gap of state i, the$ \hat{N} $ is the particle number operator, and the chemical potential$ \lambda $ is introduced to preserve the particle number on the average. For the pairing interaction matrix element$ V_{ii'}^{pp} $ in the gap equations, phenomenological pairing force is often utilized, such as the zero-range$ \delta $ -force and finite-range Gogny force. Because of the advantage of smooth convergence [71], we choose the finite-range Gogny interaction D1S [14] as the pairing force,$ \begin{split} V^{pp}({{r}},{{r}}^{\prime}) =& \sum_{\chi = 1,2}{\rm e}^{({{r}}-{{r}}^{\prime})^{2}/\mu_{\chi}^{2}}(W_{\chi}+B_{\chi}P^{\sigma}\\ & -H_{\chi}P^{\tau}-M_{\chi}P^{\sigma}P^{\tau}), \end{split} $

(12) where
$ \mu_{\chi}, W_{\chi}, B_{\chi}, H_{\chi} $ , and$ M_{\chi} $ ($ \chi = 1,2 $ ) are the parameters in the finite range part of the Gogny force, and$ P^{\sigma} $ and$ P^{\tau} $ are the spin and isospin exchange operators, respectively. Imposing the spherical symmetry, the pairing interaction matrix element$ V_{ii^{\prime}}^{pp} $ can be derived as,$ \begin{array}{l} V_{ii^{\prime}}^{pp} = \int {\rm d} r {\rm d} r' \begin{pmatrix} K^{G}_{ii'} & K^{F}_{ii'} \end{pmatrix}_{r}\begin{pmatrix} \bar{Y}^{G}_{ii'} & \bar{Y}^{F}_{ii'} \\[0.5em] \bar{X}^{G}_{ii'} & \bar{X}^{F}_{ii'} \end{pmatrix}_{(r,r^{\prime})} \begin{pmatrix} K^{G}_{ii'} \\[0.5em] K^{F}_{ii'} \end{pmatrix}_{r^{\prime}}, \end{array} $

where G and F are the radial parts of the upper and lower components of the spherical Dirac spinor, respectively, and
$ K_{ii'} $ reads as$ \begin{split} K^{G}_{ii'}(r) = \frac{G_i G_{i'}}{2\pi r^{2}},\;\;\;\;\; K^{F}_{ii'}(r) = \frac{F_i F_{i'}}{2\pi r^{2}}. \end{split} $

(13) The non-local terms
$ \bar{Y}^{G}, \,\bar{Y}^{F}, \,\bar{X}^{G} $ , and$ \bar{X}^{F} $ , they can be expressed in the following compact form,$ \begin{split} \bar Y^G_{ii'} =& \frac{1}{2} \sum_{\chi, L} V_{\chi, L}(r,r') \Big[\big(A_\chi + D_\chi\big)\big(C_{j\frac{1}{2} j'-\frac{1}{2}}^{ L0}\big)^2 \\ & - D_\chi \big(C_{l_u0l_u'0}^{ L0}\big)^2\Big], \end{split} $

(14) $ \begin{split} \bar Y^F_{ii'} = \frac{1}{2} \sum_{\chi, L} V_{\chi, L}(r,r') \big(A_\chi + D_\chi\big)\big(C_{j\frac{1}{2} j'-\frac{1}{2}}^{ L0}\big)^2, \end{split} $

(15) $ \begin{split} \bar X^G_{ii'} = \frac{1}{2} \sum_{\chi, L} V_{\chi, L}(r,r') \big(A_\chi + D_\chi\big)\big(C_{j\frac{1}{2} j'-\frac{1}{2}}^{ L0}\big)^2, \end{split} $

(16) $ \begin{split} \bar X^F_{ii'} =& \frac{1}{2} \sum_{\chi, L} V_{\chi, L}(r,r') \Big[\big(A_\chi + D_\chi\big)\big(C_{j\frac{1}{2} j'-\frac{1}{2}}^{ L0}\big)^2 \\ & - D_\chi \big(C_{l_d0l_d'0}^{ L0}\big)^2\Big]. \end{split} $

(17) where
$ A_\chi = W_\chi - H_\chi P^\tau $ and$ D_\chi = B_\chi - M_\chi P^\tau $ , and the radial part$ V_{\chi, L} $ , given by the decomposition of the Gogny force in spherical coordinate space, reads as$ \begin{split} V_{\chi, L}(r,r') = {\rm e}^{-(r^2+r'^2)/\mu_\chi^2} \sqrt{2\pi \frac{\mu_\chi^2}{2rr'}} I_{ L+1/2}\Big(\frac{2rr'}{\mu_\chi^2}\Big). \end{split} $

(18) In above expressions, j and
$ j' $ are the angular momenta of the orbits i and$ i' $ ,$ l_u $ and$ l_d $ represent the orbital angular momenta of the upper and lower component of the Dirac spinor, respectively, and the sum over L shall fulfill$ L+l_u+l_u' $ to be even. -
The traditional doubly magic nuclei include 16O, 40Ca, 48Ca, 56Ni, 132Sn and 208Pb, which were often selected as the observable nuclei in quantifying the RMF Lagrangians. For the parametrization of DD-LZ1, we considered several isotopes of O and Pb to improve the descriptions of exotic nuclei with extreme neutron to proton ratios. Furthermore, the heavy nuclide 218U is also introduced in the parametrization, aiming at the elimination of the spurious shell closures mentioned before. Eventually, the new RMF Lagrangian DD-LZ1 is obtained by fitting to the saturation properties of nuclear matter, and the binding energies and charge radii of 10 selected nuclei, including 16, 22, 24, 26O, 40, 48Ca, 194,208,214Pb and 218U. The doubly magic 56Ni is not introduced in the parametrization of DD-LZ1.
Numerically in calculating the observable nuclei, the spherical symmetry is imposed and a spherical box of 20 fm is introduced in solving the radial Dirac equations with the radial step 0.1 fm. During the whole procedure of the parametrization, the Levenberg-Marquardt method is adopted in minimizing the
$ \chi^2 $ , the sum of the weighted square deviations of the observables (saturation quantities, binding energies, etc.) from the reference values or experimental data. Coincident with our motivations, we treated specially the density dependent behaviors of$ g_\sigma $ and$ g_\omega $ as referred to PKA1, and also regarding the accuracy in describing the binding energies and charge radii of selected nuclei. Importantly, the reference nuclide 218U essentially advances the parametrization of DD-LZ1. The details of the obtained RMF Lagrangian DD-LZ1 are shown in Table 1.parameter value parameter value M/MeV 938.900000 $a_{\sigma} $ 

1.062748 $m_{\sigma} $ /MeV

538.619216 $b_{\sigma} $ 

1.763627 $m_{\omega} $ /MeV

783.000000 $c_{\sigma} $ 

2.308928 $m_{\rho} $ /MeV

769.000000 $d_{\sigma} $ 

0.379957 $g_{\sigma}(0)$ 

12.001429 $a_{\omega} $ 

1.059181 $g_{\omega}(0)$ 

14.292525 $b_{\omega} $ 

0.418273 $g_{\rho}(0) $ 

7.575467 $c_{\omega} $ 

0.538663 $\rho_{0} $ /fm-3

0.158100 $d_{\omega} $ 

0.786649 $a_{\rho} $ 

0.776095 Table 1. Novel RMF Lagrangian DD-LZ1, including nucleon, σ-, ω- and ρ-mesons masses, i.e., M, mσ, mω, and mρ, the coupling strengths at zero density
$g_\phi(0)$ , and the density-dependent parameters. ρ0 is the saturation density. -
To qualitatively appraise the newly obtained RMF Lagrangian DD-LZ1, we first calculated the bulk properties of the saturation nuclear matter. The results are shown in Table 2, as compared to the RMF Lagrangians DD-ME2 [55] and PK1 [51], and the RHF ones PKA1 [42] and PKO1 [30]. For the saturation properties of nuclear matter, all the selected effective Lagrangians present a reasonable description. Specifically, DD-LZ1 presents a larger saturation density
$ \rho_0 $ than DD-ME2, PK1 and PKO1, close to PKA1. For the incompressibility K, the value predicted by DD-LZ1 is consistent with the constraint$ K = 240\pm 20 $ MeV by the isoscalar giant monopole resonance [72]. Concerning the symmetry energy J and the slope L, DD-LZ1 provides the smallest values among the selected effective Lagrangians, being coincident with a systematic evaluation in Ref. [73] that$ J = 31.7 \pm 3.2 $ MeV and$ L = 58.7 \pm 28.1 $ MeV. Moreover, the scalar mass$ M_S^* $ obtained by DD-LZ1 is only slightly larger than that obtained by PKA1, but smaller than those given by DD-ME2, PK1, and PKO1. As pointed out in Ref. [37], this can be essential for DD-LZ1 to provide appropriate restoration of the pseudo-spin symmetry, as well as reasonable spin-orbit splittings.$\rho_0$ /fm-3

$E/A$ /MeV

$K$ /MeV

$J$ /MeV

$L$ /MeV

$M_S^*$ 

DD-LZ1 0.158 $-$ 16.06

230.7 32.0 42.5 0.56 DD-ME2 0.152 $-$ 16.13

250.8 32.3 51.2 0.57 PK1 0.148 $-$ 16.27

282.7 37.6 115.9 0.61 PKA1 0.160 $-$ 15.83

229.9 36.0 103.5 0.55 PKO1 0.152 $-$ 16.00

250.2 34.4 97.8 0.59 empirical data $0.155\pm0.005$ 

$-15.8\pm0.3$ 

$240\pm 20$ 

$31.7 \pm 3.2$ 

$58.7 \pm 28.1$ 

$0.55\sim 0.6$ 

Table 2. Saturation density
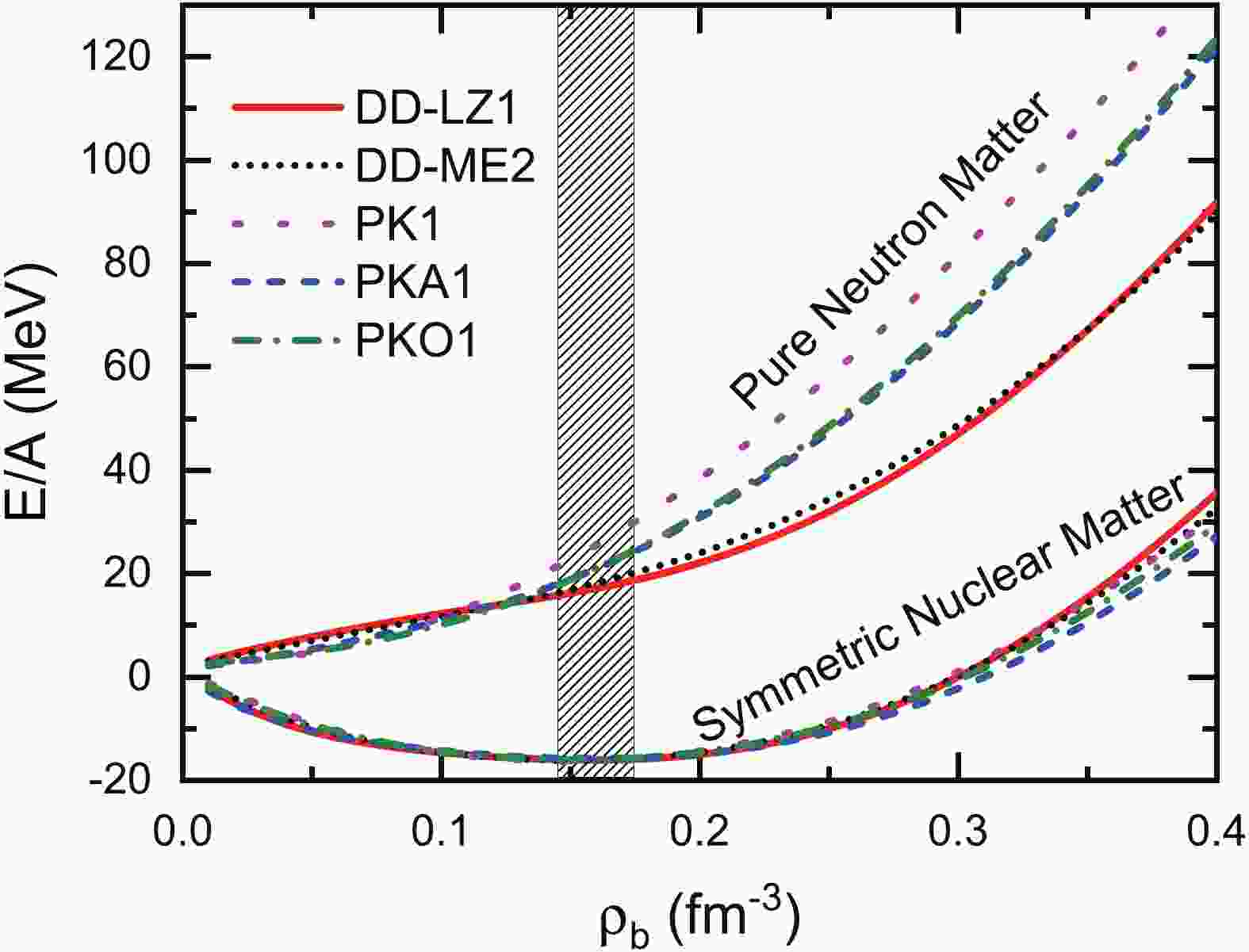
$\rho_{0}\, $ , binding energy per nucleon E/A, compression modulus K, symmetry energy J, slope of symmetry energy L, and scalar mass$M_{S}^{*}$ [30] of the saturated nuclear matter. The results are calculated by DD-LZ1, DD-ME2, PK1, PKA1, and PKO1, as compared to the estimation value [72-74].As another qualitative evaluation, we further calculate the equation of state (EoS) for symmetric nuclear matter and pure neutron matter with the selected RMF and RHF Lagrangians, namely the binding energy
$ E/A $ (MeV) with respect to the density$ \rho_b $ (fm−3), and the results are shown in Fig. 1. For symmetric nuclear matter, the selected models provide similar results, which slightly deviate from each another at high density. Seemingly, DD-LZ1 presents slightly stiffer EoS compared to the others. However, for pure neutron matter, the softest EoS are obtained by both DD-LZ1 and DD-ME2, whereas PK1 containing non-linear self-coupling of$ \sigma $ - and$ \omega $ -mesons exhibits the hardest EoS. The results obtained by RHF models PKA1 and PKO1 are quite similar, lying between the softest and hardest. -
In this section, we first performed systematical calculations for a wide range of finite nuclei to appraise the quantitative accuracy of the new RMF Lagrangian DD-LZ1, as compared to the popular ones, including the RHF PKA1 [42] and PKO1 [30], the RMF DD-ME2 [55] and PK1 [51], and the relativistic point-coupling model PC-PK1 [52]. The selected nuclei range from light 16O to heavy 218U include the isotopes of oxygen (O), calcium (Ca), tin (Sn), and lead (Pb), as well as isotones of
$ N = 82 $ and 126. Most are spherical or near spherical, covering all the observable nuclei used in the parametrizations of the selected models. For the open shell nuclei, the pairing correlations are treated by the Bogoliubov method with the finite-range Gogny interaction D1S [14, 57], if not specified in the following.We first focus on the quantitative description of nuclear mass and charge radii. Afterwards, we appraise the reliability of DD-LZ1 in describing the nuclear structure properties, and particular effort is devoted on the elimination of the spurious shell closures
$ N/Z = 58 $ and 92, which commonly exist in past RMF calculations. Meanwhile, the restoration of the pseudo-spin symmetry is analyzed as combined with the modeling of the nuclear in-medium effects by DD-LZ1. -
Tables 3 and 4 show the binding energies
$ E_B $ (MeV) calculated by the new RMF Lagrangian DD-LZ1 for the selected nuclei with mass numbers of$ A<100 $ and$ A\geqslant 100 $ , respectively, in comparison with the results of PC-PK1, DD-ME2, PK1, PKA1, and PKO1, and the experimental data [65]. The last rows in these two tables show the root mean square deviations$ \Delta $ (MeV) from the data. The bold numbers in Tables 3 and 4 denote the calculations that deviate from the data by more than 2 and$ 2.5 $ MeV, respectively, and the bold nuclear symbols represent the observable nuclei used in the parametrization of DD-LZ1.nuclei Exp. DD-LZ1 PC-PK1 DD-ME2 PK1 PKA1 PKO1 16O −127.62 −128.21 −127.29 −127.75 −127.89 −126.84 −128.14 18O −139.81 −140.29 −141.63 −139.54 −139.95 −139.77 −140.98 20O −151.37 −151.00 −153.16 −150.42 −151.46 −151.76 −152.82 22O −162.03 −160.51 −162.91 −160.23 −161.82 −162.54 −163.17 24O −168.96 −168.80 −170.90 −167.88 −169.30 −171.67 −170.83 26O −168.92 −169.66 −175.10 −169.76 −172.66 −173.89 −173.72 36Ca −281.37 −282.37 −281.63 −278.96 −277.92 −283.76 −281.15 38Ca −313.12 −314.10 −313.46 −311.60 −311.62 −313.59 −313.58 40Ca −342.05 −344.01 −343.07 −342.61 −342.40 −341.37 −342.92 42Ca −361.90 −363.19 −364.06 −361.81 −362.05 −361.34 −363.13 44Ca −380.96 −381.28 −382.77 −380.11 −380.82 −380.33 −382.16 46Ca −398.77 −398.52 −399.86 −397.63 −398.70 −398.49 −400.10 48Ca −416.00 −415.14 −415.39 −414.46 −415.66 −415.93 −416.96 50Ca −427.51 −426.38 −427.34 −424.70 −425.29 −427.78 −427.34 52Ca −438.33 −436.87 −437.73 −434.10 −433.79 −439.25 −436.59 54Ca −445.37 −445.35 −446.65 −441.89 −442.43 −447.65 −445.08 18Ne −132.14 −132.39 −133.74 −131.61 −131.97 −132.49 −133.44 20Mg −134.56 −133.91 −136.23 −133.19 −134.12 −135.99 −136.61 34Si −283.43 −285.59 −284.63 −283.64 −284.10 −283.38 −284.32 36S −308.71 −309.92 −308.55 −306.10 −305.29 −308.74 −306.72 38Ar −327.34 −328.54 −327.54 −326.09 −325.91 −326.47 −326.73 42Ti −346.89 −348.19 −349.24 −346.85 −347.15 −347.13 −348.66 50Ti −437.79 −436.30 −437.27 −434.73 −436.26 −436.34 −436.94 56Ni −484.00 −484.42 −483.68 −480.68 −483.49 −485.68 −482.60 58Ni −506.46 −504.81 −504.08 −500.57 −503.11 −505.42 −502.63 72Ni −613.46 −612.80 −615.29 −611.56 −612.97 −612.02 −613.48 84Se −727.34 −724.23 −726.28 −725.06 −728.91 −723.37 −728.06 86Kr −749.23 −746.81 −748.46 −747.16 −750.13 −746.41 −749.96 88Sr −768.47 −766.67 −767.64 −766.33 −768.52 −766.58 −768.83 90Zr −783.90 −783.33 −783.72 −782.05 −783.96 −783.80 −784.33 92Mo −796.51 −796.26 −796.92 −794.70 −797.05 −796.58 −796.96 94Ru −806.86 −806.93 −807.67 −805.20 −808.14 −807.47 −807.46 98Cd −821.07 −822.62 −823.02 −820.65 −824.70 −824.28 −822.82 $ \Delta $ 

1.258 1.660 2.130 1.824 1.701 1.535 Table 3. Binding energies
$ E_B $ (MeV) of selected nuclei with mass number$ A < 100 $ calculated by DD-LZ1, PC-PK1, DD-ME2, PK1, PKA1, and PKO1, compared to the experimental data (Exp.) [65]. The last row shows the root-mean-square deviations$ \Delta $ (MeV) from the data. Details are given in the text.nuclei Exp. DD-LZ1 PC-PK1 DD-ME2 PK1 PKA1 PKO1 100Sn −825.30 −827.89 −827.99 −825.78 −830.23 −830.36 −827.78 106Sn −893.80 −891.21 −891.94 −889.84 −895.36 −891.52 −892.59 112Sn −953.53 −950.40 −950.80 −949.94 −953.67 −948.91 −951.56 116Sn −988.68 −986.98 −986.84 −985.92 −987.94 −984.05 −986.81 120Sn −1020.54 −1020.15 −1019.73 −1018.00 −1019.32 −1016.78 −1018.91 122Sn −1035.52 −1034.82 −1035.18 −1033.01 −1034.29 −1032.20 −1034.12 124Sn −1049.96 −1048.81 −1050.02 −1047.53 −1048.83 −1047.08 −1048.84 126Sn −1063.88 −1062.43 −1064.31 −1061.66 −1062.96 −1061.51 −1063.08 128Sn −1077.37 −1075.76 −1078.11 −1075.47 −1076.70 −1075.56 −1076.87 130Sn −1090.29 −1088.88 −1091.48 −1089.01 −1090.03 −1089.25 −1090.18 132Sn −1102.84 −1101.84 −1104.48 −1102.30 −1102.95 −1102.61 −1103.01 134Sn −1108.87 −1106.56 −1109.62 −1106.39 −1106.83 −1107.88 −1107.71 194Pb −1525.89 −1519.59 −1521.05 −1521.02 −1525.82 −1518.82 −1523.24 202Pb −1592.19 −1587.91 −1589.49 −1589.58 −1592.14 −1587.80 −1590.38 204Pb −1607.51 −1604.40 −1606.05 −1606.04 −1607.72 −1604.36 −1606.27 206Pb −1622.32 −1620.61 −1622.32 −1622.07 −1622.72 −1620.57 −1621.66 208Pb −1636.43 −1636.42 −1637.92 −1637.39 −1636.84 −1636.28 −1636.29 210Pb −1645.55 −1643.51 −1645.59 −1644.38 −1644.42 −1643.87 −1644.43 212Pb −1654.52 −1650.44 −1653.19 −1651.35 −1651.90 −1651.33 −1652.43 214Pb −1663.29 −1657.21 −1660.73 −1658.30 −1659.27 −1658.63 −1660.29 134Te −1123.41 −1121.86 −1124.96 −1122.98 −1124.83 −1121.95 −1124.42 136Xe −1141.88 −1140.19 −1143.43 −1141.95 −1144.93 −1139.64 −1143.89 138Ba −1158.29 −1156.79 −1159.99 −1159.22 −1163.26 −1155.65 −1161.45 140Ce −1172.68 −1171.47 −1174.51 −1174.70 −1179.73 −1169.46 −1177.01 142Nd −1185.14 −1183.70 −1186.60 −1186.06 −1190.72 −1182.25 −1188.37 144Sm −1195.73 −1193.95 −1196.50 −1195.59 −1200.07 −1192.91 −1197.91 146Gd −1204.43 −1202.33 −1204.50 −1203.33 −1207.85 −1201.78 −1205.68 148Dy −1210.78 −1208.85 −1210.73 −1209.34 −1214.12 −1208.67 −1211.77 150Er −1215.33 −1213.61 −1215.29 −1213.75 −1218.92 −1213.83 −1216.28 206Hg −1621.05 −1618.96 −1621.79 −1620.73 −1620.77 −1618.60 −1620.40 210Po −1645.21 −1645.02 −1647.25 −1646.98 −1647.98 −1644.40 −1646.76 212Rn −1652.50 −1652.30 −1655.11 −1655.22 −1657.66 −1651.26 −1655.69 214Ra −1658.32 −1658.26 −1661.55 −1662.13 −1665.93 −1656.83 −1663.13 216Th −1662.69 −1662.87 −1666.59 −1667.71 −1672.77 −1661.07 −1669.09 218U −1665.68 −1665.86 −1670.05 −1671.87 −1678.12 −1663.49 −1673.46 $ \Delta $ 

2.386 2.008 2.630 4.078 2.964 2.619 Table 4. Same as Table 3, for nuclei with
$ A\geqslant 100. $ For the nuclei with
$ A < 100 $ , all the selected models present a similar accuracy, given the$ \Delta $ values in the last row of Table 3 that$ \Delta\in (1.2,2.2) $ MeV. Nevertheless, the newly obtained DD-LZ1 still exhibits distinctive improvement on nuclear mass compared to others. Referring to the bold numbers in each column, there are only three cases whose deviations are beyond 2 MeV in both DD-LZ1 and PKO1 results. In particular, for the isotopes of oxygen and calcium only DD-LZ1 can reproduce all the available data with the deviations being less than 2 MeV, which may imply certain improvement on the isovector nature for the nuclei with$ A<100 $ . Furthermore, DD-LZ1 cannot precisely reproduce the drip line of oxygen isotopes, as seen in Table 3. Nevertheless, compared to the others, the accuracy is already significantly improved by DD-LZ1.For the heavier nuclei with
$ A \geqslant 100 $ , the last row of Table 3 shows that the discrepancies between models become notable, namely$ \Delta \in (2.0, 4.1) $ MeV. DD-LZ1 exhibits good agreement with the data, and the accuracy is only lower than PC-PK1. DD-LZ1 provides better agreement with the data than PC-PK1 for the nuclei with$ A<100 $ (Table 4). If focusing on the isotopic chains of tin and lead, PK1 reproduces the experimental data fairly well, as referred to the bold numbers that indicate the deviations larger than$ 2.5 $ MeV. In contrast, the deviations from the data given by PK1 become notable for the isotones of$ N = 82 $ and 126, which accounts for its fairly large$ \Delta $ value.As shown in Table 4, DD-LZ1 presents an appropriate description of the masses of the Sn and Pb isotopes, with the accuracy similar as PC-PK1 and DD-ME2, while less accurate than PKO1 and PK1, and slightly better than PKA1. It is worthwhile to emphasize that for the
$ N = 82 $ and 126 isotones, DD-LZ1 shows the best agreement with the data among the selected Lagrangians. Specifically, the selected Lagrangians, except DD-LZ1 and PKA1, present notable overestimation on the binding energies of both$ N = 82 $ and 126 isotones, particularly for the ones with$ Z = 58 $ and 92. As mentioned previously, this overestimation is tightly related to the emergence of the spurious shell closures of$ N/Z = 58 $ and 92 [62].For the charge radii, the novel RMF Lagrangian DD-LZ1 can also provide a similarly accurate description as the other popular Lagrangians. Table 5 shows the charge radii of 41 nuclei from the light 16O to heavy 214Ra, which are calculated by DD-LZ1, PC-PK1, DD-ME2, PK1, PKA1, and PKO1. As a quantitative qualification, the available experimental data from Ref. [75] are shown as a reference. The last row shows the root mean square deviations from the data, and the selected Lagrangians present a reasonable quantitative description on charge radius. Specifically, the new RMF Lagrangian DD-LZ1 provides similar accuracy as the RHF one PKO1, lower than PC-PK1 and DD-ME2, while better than PK1 and PKA1.
nuclei Exp. DD-LZ1 PC-PK1 DD-ME2 PK1 PKA1 PKO1 16O 2.699 2.752 2.768 2.727 2.697 2.859 2.731 18O 2.773 2.750 2.763 2.724 2.685 2.838 2.720 18Ne 2.971 2.997 2.960 2.960 2.919 3.057 2.931 36S 3.299 3.290 3.289 3.293 3.255 3.316 3.273 38Ar 3.403 3.397 3.391 3.385 3.355 3.445 3.376 40Ca 3.478 3.482 3.481 3.464 3.444 3.548 3.464 42Ca 3.508 3.479 3.482 3.465 3.441 3.538 3.462 46Ca 3.495 3.473 3.490 3.471 3.444 3.521 3.465 48Ca 3.477 3.466 3.494 3.474 3.447 3.509 3.467 50Ca 3.517 3.498 3.515 3.499 3.468 3.539 3.492 86Kr 4.184 4.155 4.180 4.171 4.148 4.189 4.163 88Sr 4.224 4.206 4.223 4.218 4.197 4.237 4.209 90Zr 4.269 4.257 4.267 4.267 4.246 4.289 4.258 92Mo 4.315 4.298 4.310 4.312 4.293 4.324 4.302 116Sn 4.625 4.601 4.614 4.614 4.590 4.618 4.600 120Sn 4.652 4.635 4.643 4.643 4.616 4.650 4.628 122Sn 4.663 4.644 4.657 4.655 4.629 4.662 4.641 124Sn 4.674 4.652 4.670 4.667 4.641 4.672 4.654 126Sn 4.683 4.660 4.683 4.678 4.654 4.681 4.666 128Sn 4.692 4.668 4.696 4.689 4.666 4.689 4.679 130Sn 4.702 4.675 4.709 4.700 4.678 4.697 4.691 132Sn 4.709 4.681 4.722 4.711 4.691 4.705 4.702 134Te 4.757 4.729 4.767 4.756 4.736 4.756 4.750 136Xe 4.796 4.774 4.809 4.798 4.779 4.803 4.793 138Ba 4.838 4.816 4.848 4.838 4.819 4.847 4.834 140Ce 4.877 4.853 4.885 4.875 4.857 4.890 4.873 142Nd 4.912 4.895 4.919 4.912 4.894 4.925 4.907 144Sm 4.952 4.934 4.951 4.948 4.930 4.960 4.941 146Gd 4.980 4.971 4.983 4.983 4.965 4.995 4.975 150Er 5.055 5.042 5.047 5.053 5.034 5.063 5.043 206Hg 5.484 5.472 5.503 5.494 5.478 5.499 5.491 200Pb 5.461 5.462 5.480 5.476 5.458 5.478 5.469 202Pb 5.471 5.469 5.490 5.486 5.468 5.487 5.480 204Pb 5.480 5.476 5.500 5.495 5.478 5.496 5.490 206Pb 5.490 5.484 5.509 5.504 5.487 5.505 5.499 208Pb 5.501 5.492 5.518 5.513 5.495 5.515 5.509 210Pb 5.521 5.507 5.538 5.531 5.516 5.529 5.530 212Pb 5.540 5.522 5.558 5.549 5.535 5.544 5.549 214Pb 5.558 5.537 5.578 5.566 5.555 5.558 5.568 212Rn 5.592 5.562 5.585 5.579 5.561 5.588 5.577 214Ra 5.608 5.595 5.617 5.610 5.592 5.623 5.609 $ \Delta $ 

0.019 0.015 0.014 0.029 0.033 0.018 Table 5. Charge radii
$ R_{\rm ch} $ (fm) of selected nuclei, calculated by DD-LZ1, PC-PK1, DD-ME2, PK1, PKA1, and PKO1, compared to experimental data (Exp.) [75]. The last row shows the root-mean-square deviations$ \Delta $ (fm) from the data. Details are given in the text. -
Because the new RMF Lagrangian DD-LZ1 brings significant improvement in describing the masses of both
$ N = 82 $ and 126 isotones, it is worthwhile to verify the systematics along the isotonic chains, and further the elimination of the so-called spurious shell closures$ Z = 58 $ and 92. As a quantitative qualification, here we introduce the two-proton shell gap$ \delta_{2p} $ as the observable [76],$ \begin{array}{l} \delta_{2p}(Z,N) = S_{2p}(Z,N)-S_{2p}(Z+2,N), \end{array} $

(19) where
$ S_{2p} = E_B(Z, N) - E_B(Z+2, N) $ is the two-proton separation energy, where$ E_B $ denotes the binding energies as shown in Tables 3 and 4.Figure 2 shows the two-proton shell gaps
$ \delta_{2p} $ (MeV) extracted from Table 4 for the selected$ N = 82 $ (upper panel) and$ N = 126 $ (lower panel) isotones. The results given by PC-PK1 and PK1 are not shown for simplicity, as they have similar systematics as DD-ME2. Both DD-ME2 and PKO1 present suddenly large$ \delta_{2p} $ values at$ Z = 58 $ for the$ N = 82 $ isotones, corresponding to the onset of the so-called spurious shell$ Z = 58 $ . In contrast to that, the$ \delta_{2p} $ value at$ Z = 58 $ is notably reduced by DD-LZ1, as well as by PKA1, showing appropriate agreement with the data [65], according to the upper panel of Fig. 2.
Figure 2. (color online) Two-proton shell gap
$\delta_{2p}$ for N = 82 (up panel) and 126 (down panel) isotonic chains obtained from RH(F)B calculations with the new effective interaction DD-LZ1. For comparison, the experimental data [65] and calculated results of PKA1, PKO1, and DD-ME2 are also given.Similar situation is also found in the results of the
$ N = 126 $ isotones. As seen from the lower panel of Fig. 2, the suddenly large$ \delta_{2p} $ values at$ Z = 92 $ given by both DD-ME2 and PKO1 are also remarkably reduced by DD-LZ1 and PKA1. Tthe occurrence of the$ Z = 92 $ subshell in this region has been ruled out by the recent experiment [77]. Thus, similarly to PKA1 [42], the new RMF Lagrangian DD-LZ1 also cures the common artifacts of the spurious shell closures$ N/Z = 58 $ and 92 which appear in previous RMF calculations. In the following context, we focus on the spurious shell closure$ Z = 92 $ , considering similar mechanism of the emergence of spurious shell closures$ Z = 58 $ and 92, namely the distinctive violation of the PSS.Consistently with the elimination of the spurious shell closures, the novel RMF Lagrangian DD-LZ1 also shows systematical improvements in describing the single-particle (s.p.) structure properties. Taking the doubly magic 208Pb as an example, Fig. 3 shows the neutron (
$ \nu $ , left panel) and proton ($ \pi $ , right panel) s.p. spectra given by DD-LZ1, as compared to PKA1, DD-ME2, and PKO1. As the reference, the experimental data taken from Ref. [78] are also shown, and we use the same colors to denote the pseudo-spin (PS) doublets. Restricted on the level of the mean field approach, all the selected Lagrangians show reasonable agreement with the reference data.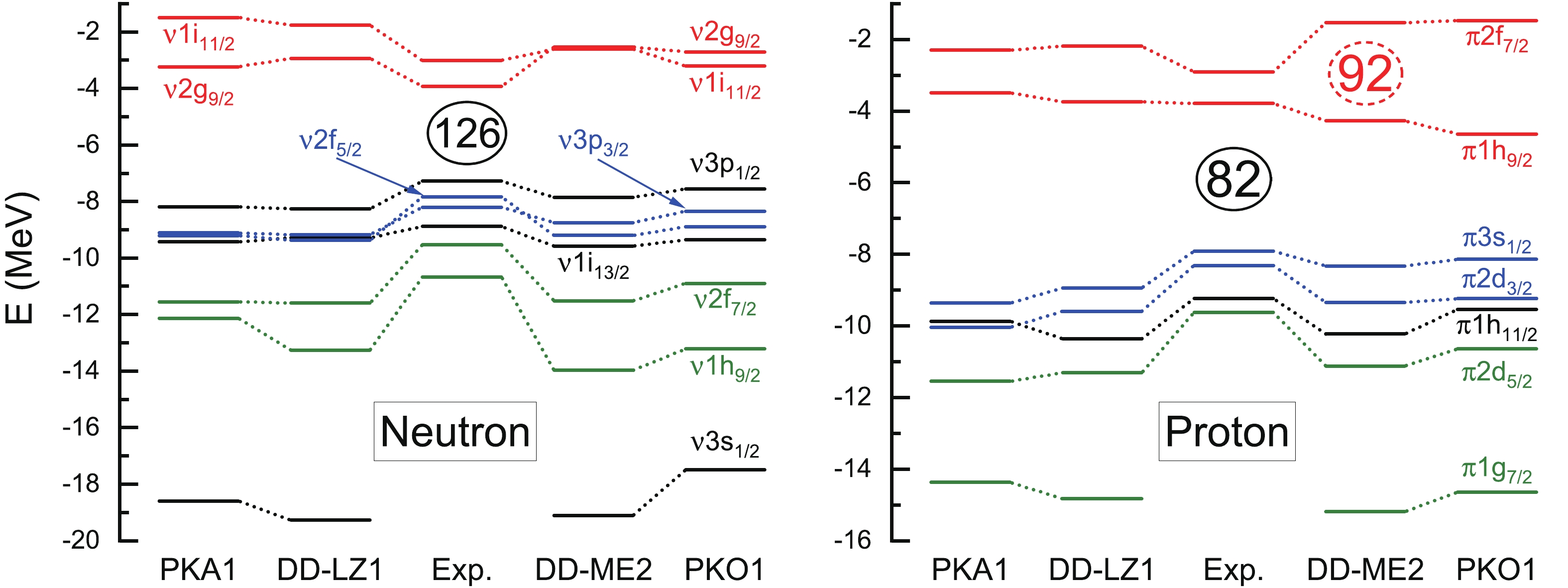
Figure 3. (color online) Neutron (left panel) and proton (right panel) single-particle spectra of 208Pb calculated by PKA1, DD-LZ1, DD-ME2, and PKO1, as referred to experimental data from Ref. [78]. The pseudo-spin doublets are denoted in the same colors.
As seen from the right panel of Fig. 3 shows the new RMF Lagrangian DD-LZ1, similar to PKA1, properly restoring the pseudo-spin symmetry (PSS) for the proton PS doublet
$ (\pi2f_{7/2}, \pi1h_{9/2}) $ , which eliminates the spurious shell$ Z = 92 $ existing in the DD-ME2 and PKO1 calculations. Consistently, both PKA1 and DD-LZ1 yield the notable proton magic shell$ Z = 82 $ , while the ones less pronounced than the reference data are obtained by DD-ME2 and PKO1. Considering the beyond mean field effects, such as particle vibration couplings, the relevant orbits may shift towards the Fermi levels to further squeeze the underestimated shell gaps by DD-ME2 and PKO1. In fact, not only on the shell structures, DD-LZ1 also shows distinct improvement on the ordering of the orbits, such as the neutron ones$ \nu1i_{11/2} $ and$ \nu2g_{9/2} $ , from the left panel of Fig. 3.The results of DD-LZ1 and PKA1 in Fig. 3 indicate that the PSS is properly restored around the Fermi surfaces not only for the low-l PS partners (
$ \nu3p_{3/2},\nu2f_{5/2} $ ) and$ (\pi3s_{1/2},\pi2d_{3/2}) $ , but also for the high-l ones$ (\nu2g_{9/2}, \nu1i_{11/2}) $ and$ (\pi2f_{7/2}, \pi1h_{9/2}) $ . As indicated in Ref. [61], the restoration of the PSS for the high-l PS partners is essentially related to the in-medium balance between the nuclear attraction and repulsion, mainly carried by the$ \sigma $ -S and$ \omega $ -V couplings, respectively. As an implementation of the discussion, Fig. 4 shows the evolution of the proton pseudo-spin orbital (PSO) splittings$ \Delta E_{\rm{PSO}}^\pi $ (MeV) in 208Pb with respect to the pseudo orbit$ l' $ (left panel: Total), as well as the sum contributions of the kinetic energy terms, and the Hartree terms of the$ \sigma $ -S and$ \omega $ -V potential energies (right panel:$ E_{\rm{kin.}}+E_{\sigma{\rm{-S}}}^D + E_{\omega{\rm{-V}}}^D $ ). The results are extracted from the calculations of DD-LZ1, DD-ME2, and PKA1.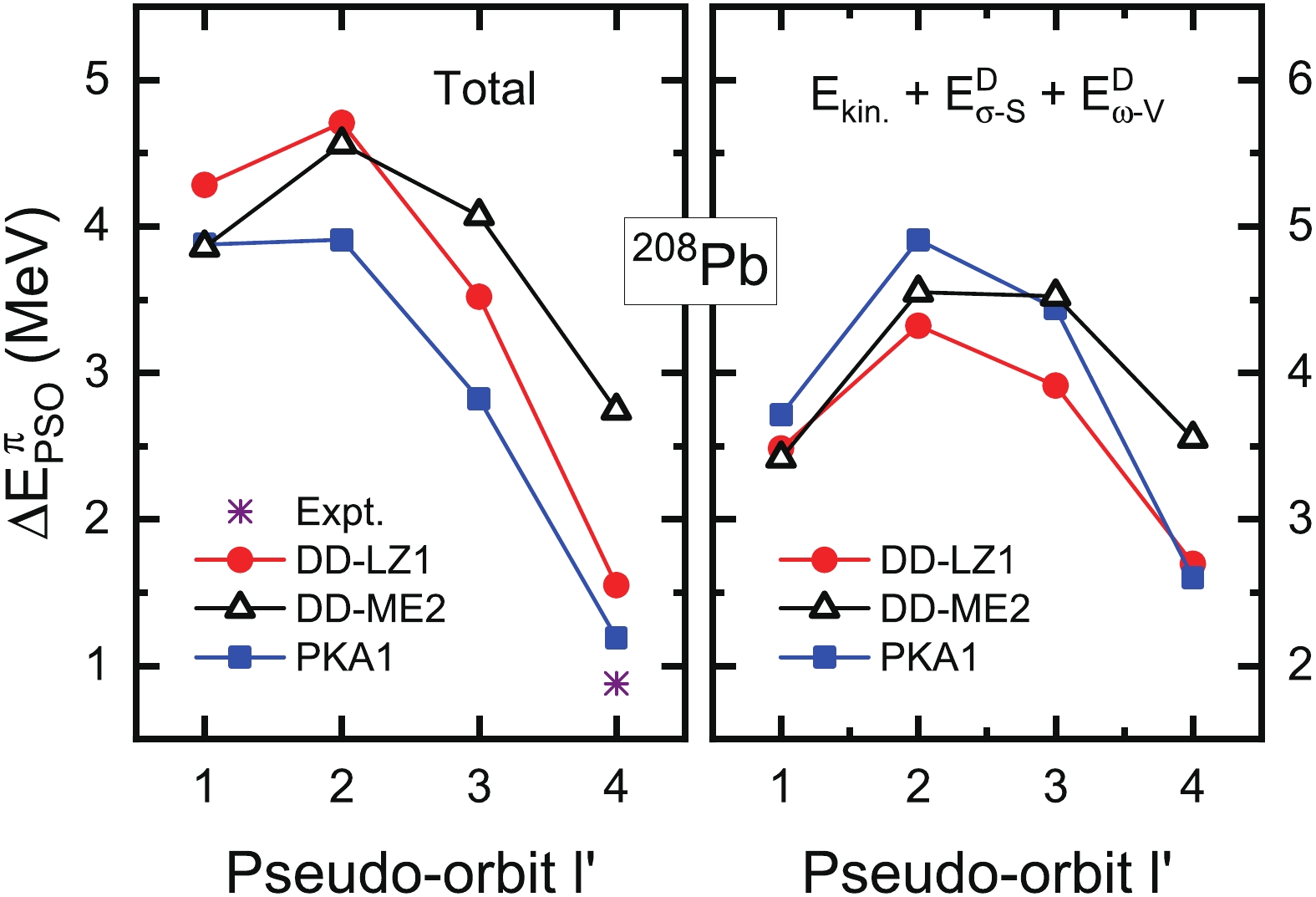
Figure 4. (color online) Proton (π) pseudo-spin orbital (PSO) splittings
$\Delta E_{\rm{PSO}}^{\pi}$ (MeV) (left panel), and sum contributions of kinetic energy terms, and Hartree terms of$\sigma$ -S and$\omega$ -V potential energies, namely$E_{\rm{kin.}}+ E_{\sigma{\rm{-S}}}^{D}+E_{\omega{\rm{-V}}}^{D}$ (right panel), in 208Pb with respect to pseudo-orbit$l^{\prime}$ . The results are obtained from the calculations with DD-LZ1, DD-ME2, and PKA1.Coincident with the systematics revealed in Ref. [61], DD-LZ1 shows a similar strong
$ l' $ -dependence as PKA1 for the$ \Delta E_{\rm{PSO}}^\pi $ values from the deeply bound PS doublet$ (\pi2s_{1/2}, \pi1d_{3/2}) $ ($ l' = 1 $ ) to the one$ (\pi2f_{7/2}, \pi1h_{9/2}) $ ($ l' = 4 $ ) around the Fermi surface, from the left panel of Fig. 4. Referring to the experimental data (in star symbol) [79], both DD-LZ1 and PKA1 properly restore the PSS for high-l PS doublet$ (\pi2f_{7/2}, \pi1h_{9/2}) $ . The right panel of Fig. 4 shows that the sum terms$ E_{\rm{kin.}}+E_{\sigma{\rm{-S}}}^D + E_{\omega{\rm{-V}}}^D $ play a dominant role in determining the strong$ l' $ -dependence of the$ \Delta E_{\rm{PSO}}^\pi $ values. On the contrary, DD-ME2 presents rather weakly$ l' $ -dependent$ \Delta E_{\rm{PSO}}^\pi $ values, as well as the sum contributions$ E_{\rm{kin.}}+E_{\sigma{\rm{-S}}}^D + E_{\omega{\rm{-V}}}^D $ . In fact, this distinct discrepancy between the RMF Lagrangians DD-LZ1 and DD-ME2 in restoring the PSS can be qualitatively interpreted by the density dependencies of the coupling strengths, from which one can deduce qualitatively the difference in the in-medium balance between nuclear attraction and repulsion.To provide a complete understanding on the in-medium balance, we also show the density dependence of the coupling strengths for the selected Lagrangians in Figs. 5 (a) and (b-c), corresponding to the isoscalar and isovector channels, respectively. As shown in Fig. 5 (a), the density-dependent behaviors of
$ g_\sigma $ and$ g_\omega $ given by DD-ME2 are in parallel with each another, which can be commonly found in other density-dependent RMF Lagrangians. In contrast, the coupling strengths$ g_\sigma $ and$ g_\omega $ of DD-LZ1 decrease with respect to the density$ \rho_b $ , albeit not simultaneously. Consequently, the in-medium balance between the isoscalar$ \sigma $ -S and$ \omega $ -V channels described by DD-LZ1, which dominates the PSO splittings$ \Delta E_{\rm{PSO}}^\pi $ , is essentially changed as compared to DD-ME2. As pointed out in Ref. [61], this effect benchmarks the strong$ l' $ -dependence of the PSO splittings shown in Fig. 4. In realistic nuclei, the enhanced centrifugal repulsion with respect to the orbit angular momentum drives nucleons from the center to the surface, and meanwhile nucleon density changes from nearly saturated to zero values. Thus, a consistent relation is revealed between the PSS restoration and in-medium balance of nuclear attraction and repulsion, which are carried mainly in the$ \sigma $ -S and$ \omega $ -V couplings [61].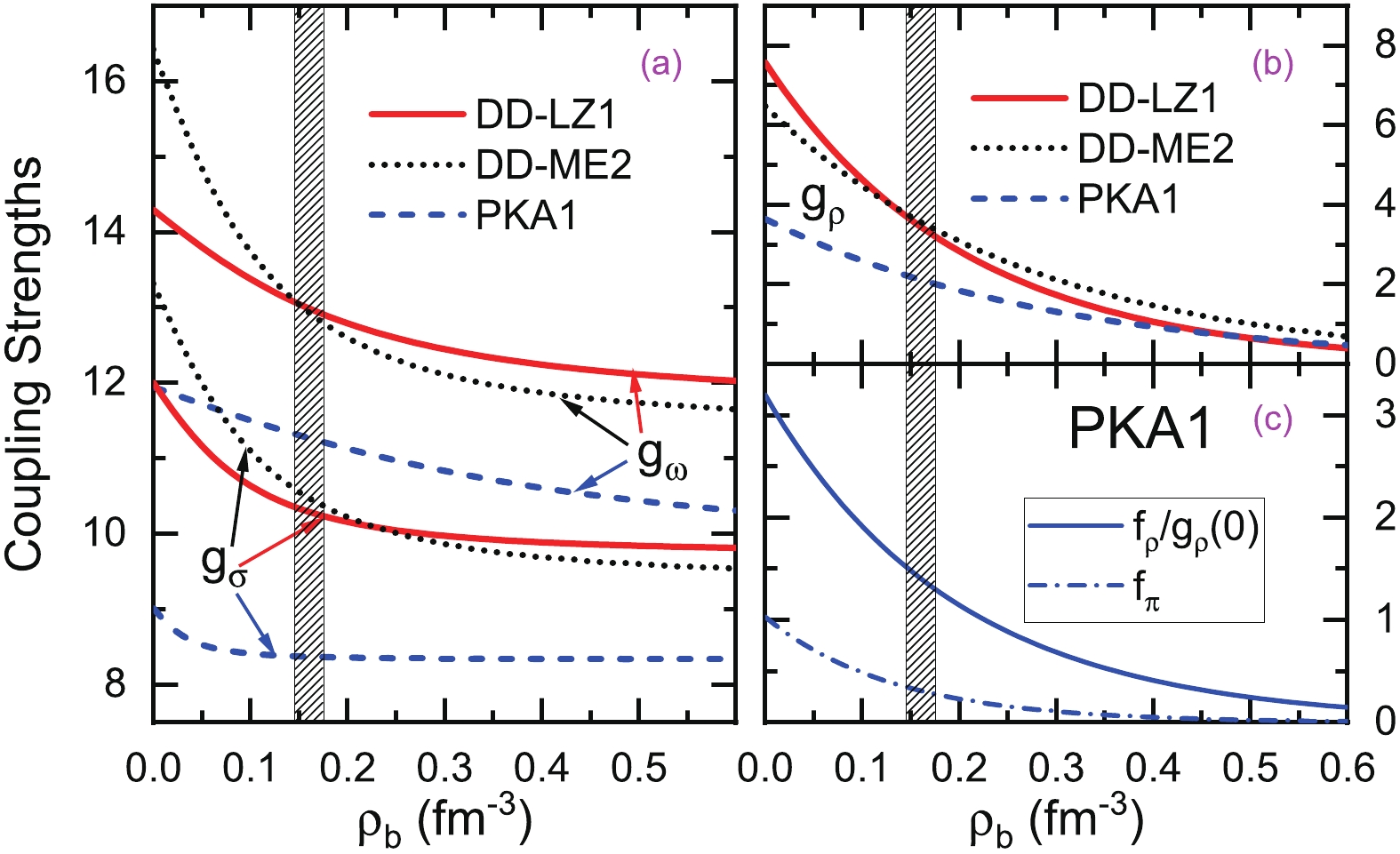
Figure 5. (color online) Density-dependent meson-nucleon couplings in isoscalar (plot (a):
$g_{\sigma}$ and$g_{\omega}$ ) and isovector (plot (b):$g_{\rho}$ ) channels as functions of baryonic density for the new DDRMF effective interaction DD-LZ1, compared with PKA1 in DDRHF and DD-ME2 in DDRMF. The density-dependent behaviors of$\rho$ -tensor ($f_{\rho}/ g_{\rho}$ ) and$\pi$ ($f_{\pi}$ ) are also shown (plot (c)). The shaded area indicates the empirical saturation density region of nuclear matter.Compared to DD-ME2, Fig. 5 (a) shows that the density dependence of
$ g_\sigma $ and$ g_\omega $ is notably reduced in DD-LZ1. Nevertheless, the$ g_\sigma $ and$ g_\omega $ in DD-LZ1 still show relatively stronger density dependencies than those in PKA1, which is necessary to provide an appropriate modeling of the nuclear in-medium effects. In PKA1, the$ \rho $ -T coupling presents strong attractive potential [61], and thus the strong density dependence of the coupling strength$ f_\rho $ carries a fairly large amount of the nuclear in-medium effects, according to$ f_\rho/g_\rho(0) $ in Fig. 5(c). In contrast, DD-LZ1 presents only slightly stronger density dependence on the coupling strength$ g_\rho $ than DD-ME2, as seen in Fig. 5(b). Therefore, the residual nuclear in-medium effects in the isoscalar channels, in fact enhanced by the unparallel density-dependent$ g_\sigma $ and$ g_\omega $ in DD-LZ1, are also meaningful in promising appropriate simulation of the nuclear in-medium effects.In a final remark, Ref. [61] demonstrated that the residual nuclear in-medium effects, manifested as the unparallel density-dependent behaviors of
$ g_\sigma $ and$ g_\omega $ , play an important role in restoring the PSS of the high-l PS partners and eliminating the spurious shells as well. It further indicates that the new in-medium balance between the nuclear attraction and repulsion can be optimized with respect to the PSS restoration on the mean field level, for instance given by the RHF Lagrangian PKA1. Therefore, within the RMF framework, the newly developed DD-LZ1 provides another example in optimizing the in-medium balance between the nuclear attraction and repulsion from the viewpoint of the PSS restoration. -
Aiming at the elimination of the spurious shell closures, which commonly appear in previous relativistic mean field (RMF) calculations, a new effective Lagrangian DD-LZ1 is proposed in this work for the RMF model with the density-dependent meson-nucleon couplings. DD-LZ1 presents a different in-medium balance between the dominant
$ \sigma $ -S and$ \omega $ -V coupling channels from the existing RMF Lagrangians, which is essential to eliminate the so-called spurious shell closures and properly retore the pseudo-spin symmetry (PSS) for the high-l pseudo-spin doublets around the Fermi levels. Because of these systematical improvements on the nuclear structure, DD-LZ1 also improves the accuracy in describing the bulk properties of the widely selected nuclei, particularly for the nuclear mass in the light region, and the evolution along the isotonic and isotopic chains.In contrast, as indicated by Ref. [61], the PSS restoration of the high-l pseudo-spin doublet is essentially related to the in-medium balance of nuclear attraction and repulsion, which is represented as the unparallel density dependence of the
$ \sigma $ -S and$ \omega $ -V coupling strengths. In this study, the successes achieved by the parametrization of DD-LZ1 demonstrate that it is an efficient way to qualitatively constrain the in-medium nuclear interactions via the PSS restoration. The better accuracy obtained by DD-LZ1 in describing nuclear mass is also quite desirable in further applications.
Novel relativistic mean field Lagrangian guided by pseudo-spin symmetry restoration
- Received Date: 2020-02-20
- Available Online: 2020-07-01
Abstract: The relativistic mean field (RMF) model has achieved great success in describing various nuclear phenomena. However, several serious defects are common. For instance, the pseudo-spin symmetry of high-l orbits is distinctly violated in general, leading to spurious shell closures





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: