-
Despite enormously successful descriptions of numerous experimental observations, the standard model (SM) carries certain lacunae. Apart from this, with little experimental validation, a significant possibility of physics beyond the SM remains. In the past few years, some discrepancies have been observed in various meson decays, most notably in the angular observable
${P}'_{5}$ [1] of$B\to {K}^{*}{\mu }^{+}{\mu }^{-}$ , branching ratio of$B\to \phi {\mu }^{+}{\mu }^{-}$ [2], lepton flavor non-universality parameter${R}_{{K}^{\left(*\right)}}$ [3-7], and${R}_{{D}^{\left(*\right)}}$ [8]. Because of the deficit in the SM theory, these anomalies motivate us to search for new physics (NP). High energy experiments at the LHC for the indirect search of rare decays of beauty and charm hadrons are dedicated to make precision measurements within and beyond the SM.After the CLEO observation of the b→sγ transition [9], rare decays of
$ {B}_{u,d,s}$ mesons become the main topic of interest. These studies become more reliable by including the results of the Bc meson discovered by the CDF collaboration [10-11]. Experimentally, the CDF collaboration discovered the Bc meson in 1998 via the semileptonic channel${B}_{c}^{+}\to J/\psi {l}^{+}\nu$ . The study of the Bc meson is itself quite exotic due to some outstanding features [12-14]. The Bc meson [15] is composed of two heavy quarks b and c, which are of different charge and flavor. Those heavy quarks are bound to the lowest state to form the Bc meson, and thus several properties of its decay modes are different from other flavor neutral processes. The main difference between the weak decays of Bc and${B_{u,d,s}}$ is that the latter can be described in the background of a heavy quark limit, which yields some relations between the form factors of the physical process. However, in the case of the Bc meson, heavy flavor and spin symmetries must be reconsidered, as both constituent quarks are heavy. Another important distinction between the weak decays of the Bc meson associated with b and c quark decays includes a significant difference in allowed kinematical region. The accessible kinematic range is broader in the decays of the Bc meson to charmonium and D mesons than for the decays o thef Bs and Bd meson. Consequently, numerous weak decays are kinematically allowed in the former case, whereas they are restricted in the latter. Because other excited states of${\bar{b}}c$ lie below the threshold of decay into the pair of B and D mesons, the strong and electromagnetic decay channels for these states are forbidden, while the weak decays are allowed. The Bc meson persists in more decay channels with a larger final phase space as the heavy quarks b and c can decay independently, or both take part in a single process. The phase space for the c→s transition is found to be smaller than that for the b→c transition; however, the CKM matrix element |Vcs|~1 is considerably larger than |Vcb|~0.04. Thus, decay modes of the c quark yield a dominant contribution (~70%) to the decay width of the Bc meson [16].This meson offers a rich laboratory for the study of various decay channels, which are essential in both theoretical and experimental aspects. With the possibility of an upcoming production of a large number of Bc mesons (about 108~1010) per year [17-21] at the future LHC run (with the luminosity values of
${\cal{L}}={10}^{34}$ cm−2s−1 and$\sqrt{s}=$ 14 TeV), one might explore the rare semileptonic Bc decays to$({D}_{s}^{\left(*\right)},{D}_{d}^{\left(*\right)}){l}^{+}{l}^{-}$ induced by the single-quark flavor-changing neutral current (FCNC)$b\to s,d$ transitions. According to the GIM mechanism [22], these transitions are forbidden at the tree level, but allowed through electroweak loop diagrams. This indicates a highly suppressed SM contribution. Due to this large suppression, it is important to study these channels beyond the SM with new physics (NP) effects. This might provide useful probes to test the SM and indirectly detect the NP.The processes induced by the
$b\to sl{\bar{l}}$ transition have been widely discussed in$B\to {K}^{\left(*\right)}l{\bar{l}}$ decays, where$b\to sl{\bar{l}}$ has a dominant contribution. The annihilation diagrams are CKM suppressed$\left|{V}_{ub}^{*}{V}_{us}\right|/\left|{V}_{ts}^{*}{V}_{tb}\right| \sim {\lambda }^{2}$ , and the spectator scattering is at the next order of${\alpha }_{s}$ . The CP violation in these channels is strongly suppressed in the SM due to the presence of only one independent CKM factor${V}_{ts}^{*}{V}_{tb}$ . In contrast, for$ b\to d$ modes, all three CKM factors$ {V}_{td}^{*}{V}_{tb}, {V}_{cd}^{*}{V}_{cb}, {V}_{ud}^{*}{V}_{ub}$ are of same order and hence can induce a notable CP-violating difference between the decay rates of$b\to d{l}^{+}{l}^{-}$ and$ {\bar{b}}\to {\bar{d}}{l}^{+}{l}^{-}$ . The theoretical investigation of these rare exclusive transitions is performed through two steps. First, the effective Hamiltonian of these processes is calculated from leading and next-to-leading loop diagrams in the SM using operator product expansion and renormalization group techniques. The reviews on this part are described in Refs. [23, 24]. Second, the matrix elements of the effective Hamiltonian between hadronic states are required. This part is model-dependent, as it requires nonperturbative QCD.There are several approaches in the literature where semileptonic Bc decays have been extensively investigated. In Ref. [25], authors described a detailed study of the exclusive semileptonic Bc decays in the framework of Bauer-Stech-Wirbel. In Refs. [26-28], the studies were performed in the relativistic and/or constituent quark model, whereas in Refs. [29, 30],
${{B}_{c}\to D}_{s}^{*}{l}^{+}{l}^{-}$ channels have been investigated in the SM with the fourth generation and supersymmetric models. In Refs. [31, 32], the authors have presented the three-point QCD approach for their analysis. The light-front quark model was adopted by the authors in Refs. [27, 33] for their needful probes. In Ref. [34], authors have explored the perturbative QCD approach to study semileptonic Bc decay channels. New physics contributions to${{B}_{c}\to D}_{s}^{*}{l}^{+}{l}^{-}$ decay have been studied extensively in the single universal extra dimension model [35] and also analyzed in a model-independent manner using an effective Hamiltonian approach [36, 37].In this study, we assume the QCD-motivated relativistic quark background and supplement the previous analysis of different decay observables of
${B}_{c}\to ({D}_{s}^{\left(*\right)}, {D}_{d}^{\left(*\right)}){l}^{+}{l}^{-}$ by considering the effect of the non-universal${Z'}$ boson. In the relativistic quark model, the quasipotential approach has been considered, where a meson is described as a bound state with a wave function consisting of the solution of the Schrodinger-type quasipotential equation. This model provides particular attention to the inclusion of negative-energy contributions and the relativistic transformation of the wave function from the resting to the moving reference frame. The numerical calculations are based on these relativistic wave functions, which were obtained previously from the meson mass spectra. Another advantage of this approach is that the electroweak matrix elements between meson states with a consistent relativistic effect allow to determine the form factor dependence on the momentum transfer. This dependence is reliable in the whole accessible kinematic range without using any ad hoc assumption and extrapolation. The form factors have been expressed as overlap integrals of the meson wave function. Here, one has to verify the fulfillment of model-independent symmetry relations among the form factors arising in heavy quark and large energy limits. We follow the calculation in Ref. [38] for the values of${B}_{c}\to {D}_{s}^{\left(*\right)},{D}_{d}^{\left(*\right)}$ form factors. This paper is organized as follows. In Section 2, the formalism of the effective Hamiltonian for${B}_{c}\to ({D}_{s}^{\left(*\right)},{D}_{d}^{\left(*\right)}){l}^{+}{l}^{-}$ decay modes has been presented. In Section 3, different decay observables for the above processes are given in terms of helicity amplitudes. In Section 4, the outline of the non-universal${Z'}$ model is provided. In Section 5, we analyze our predicted results. Section 6 comprises a summary and concluding remarks. -
Typically rare B decays are described by low energy effective Hamiltonian obtained by integrating out the heavy degrees of freedom of the top quark and W boson. Short-distance contributions contained in Wilson coefficients are separated by the operator product expansion and calculated perturbatively. Long-distance contributions are contained in matrix elements of local operators, which are calculated in a non-perturbative approach.
The effective Hamiltonian for the
$b\to q{l}^{+}{l}^{-}$ (where$q=s,d$ ) transition renormalized at a scale μ ≈ mb is given by [39]$ {\cal{H}}_{\rm eff}=-\frac{4{G}_{F}}{\sqrt{2}}{V}_{tq}^{*}{V}_{tb}\sum \limits_{i=1}^{10}{C}_{i}{\cal{O}}_{i}, $

(1) where GF is the Fermi constant, Vtj are CKM matrix elements, Ci denote the Wilson coefficients, and
${\cal{O}}_{i}$ denote the standard model operator basis, which is found in Ref. [23].${O}_{i}\left(\mu \right) \left(i=1,\cdots 6\right)$ represent the four-quark operators,$ i=7, 8$ are dipole operators, and$i=9, 10$ represent semileptonic electroweak operators. Here, the operators$ {\cal{O}}_{7}, {\cal{O}}_{9}$ , and${\cal{O}}_{10}$ are mainly responsible for these decay modes. From the reduced effective Hamiltonian, we can obtain the free quark decay amplitude, which is written as$\begin{split} {\cal{M}}\left( {b \to q{l^ + }{l^ - }} \right) =& \frac{{{G_F}{\alpha _{em}}}}{{2\sqrt 2 \pi }}{V_{tb}}V_{ts}^{\rm{*}}\{ C_9^{\rm eff}\left( \mu \right)\bar q{\gamma _\mu }\left( {1 - {\gamma _5}} \right)b\left( {\bar l{\gamma ^\mu }l} \right) \\&+ {C_{10}}\left( \mu \right)\bar q{\gamma _\mu }\left( {1 - {\gamma _5}} \right)b\left( {\bar l{\gamma ^\mu }{\gamma _5}l} \right)\\ &- \frac{{2{m_b}}}{{{q^2}}}C_7^{\rm eff}\left( \mu \right)\bar qi{\sigma _{\mu \nu }}{q^\nu }\left( {1 + {\gamma _5}} \right)b\left( {\bar l{\gamma ^\mu }l} \right)\} , \end{split} $

(2) where αem is the fine structure constant. Within the SM,
${C}_{7}^{\rm eff}$ in the leading logarithm approximation is written as [40]$\begin{split} {C}_{7}^{\rm eff}\left(\mu \right)=&{\eta }^{\frac{16}{23}}{C}_{7}\left({m}_{W}\right)+\frac{8}{3}\left({\eta }^{\frac{14}{23}}-{\eta }^{\frac{16}{23}}\right){C}_{8}\left({m}_{W}\right)\\&+{C}_{2}\left({m}_{W}\right)\sum\limits_{i=1}^{8}{h}_{i}{\eta }^{{a}_{i}}, \end{split}$

(3) where
$ {C}_{2}\left({m}_{W}\right)=1$ and$ {C}_{7}\left({m}_{W}\right), {C}_{8}\left({m}_{W}\right)$ are given in Ref. [41]. The coefficients ai and hi are given as [24, 42],$ \begin{split} {{a_i} = }&{(14/23,}\quad{16/23,}\quad{6/23,}\quad{-12/23,}\\&{0.4086,}\quad{-0.4230,}\quad{-0.8994,}\quad{0.1456),}\\ {{h_i} = }&{(2.2996,}\quad{-1.0880,}\quad{-3/7,}\quad{-1/14,}\\&{-0.6494,}\quad{-0.0380,}\quad{-0.0186,}\quad{-0.0057).} \end{split} $

The parameter η in Eq. (7) is defined as
$\eta =\frac{{{\alpha }_{s}(\mu }_{W})}{{\alpha }_{s}\left({\mu }_{b}\right)}$ .${C}_{9}^{\rm eff}$ contains short-distance perturbative contribution and long-distance contribution terms. Within the SM,${C}_{9}^{\rm eff}$ is written as$ {C}_{9}^{\rm eff}={C}_{9}+{y}_{\rm pert}\left({q}^{2}\right)+{y}_{\rm BW}\left({q}^{2}\right), $

(4) where q2 is the four-momentum squared of the lepton pair. The short-distance contribution (perturbative part) denoted by
${y}_{\rm pert}\left({q}^{2}\right)$ [38] involves the indirect contributions coming from the matrix element of four quark operators. The long-distance part denoted by${y}_{\rm BW}\left({q}^{2}\right)$ has$c{\bar{c}}$ intermediate states, i.e., the$ J/\psi $ family [43]. By introducing the Breit-Wigner formula, the explicit expression of${y}_{\rm BW}\left({q}^{2}\right)$ is parameterized [37], and it is provided in Appendix A.$c{\bar{c}}$ resonances cause a large peak in the decay distribution, due to which hadronic uncertainties are coming to the semileptonic decay modes. To apply these relations in Bc decay modes, we must find the matrix elements of the operators${\bar{q}}{\gamma }_{\mu }\left(1-{\gamma }_{5}\right)b$ and${\bar{q}}{\sigma }_{\mu \nu }{q}^{\nu }\left(1+{\gamma }_{5}\right)b$ between the initial and final hadronic states, which is based on a non-perturbative approach.The long-distance processes considered here are induced by resonance cascade modes, such as
${B}_{c}\to {D}_{s\left(d\right)}^{\left(*\right)}V\to {D}_{s\left(d\right)}^{\left(*\right)}l{\bar{l}}$ . The contributions of these transitions could be termed after the relationship$Br({B}_{c}\to { {D}_{s\left(d\right)}^{\left(*\right)}l{\bar{l}})}_{\rm cascade} \sim Br({B}_{c}\to {D}_{s\left(d\right)}^{\left(*\right)}V)\times Br(V\to l{\bar{l}})$ . The resonances V denote${J}^{PC}={1}^{--}$ mesons, which could be$ {\bar{u}}u, {\bar{d}}d, {\bar{s}}s$ , and${\bar{c}}c$ bound states. In our analysis, we neglect the effects of the${B}_{c}\to {D}_{s\left(d\right)}^{\left(*\right)}\rho (\omega ,\phi )$ cascade decays. Because Okubo-Zweig-Iizuka (OZI) rules allow the strong decays of$ \rho , \omega $ , and$\phi$ mesons, while the decay modes of$ J/\psi \left(\psi \right(2S\left)\right)$ are suppressed by OZI rules. Thus, the transitions$ \rho \left(\omega ,\phi \right)\to l{\bar{l}}$ induced by electromagnetic interaction are of a smaller branching fraction than the processes$ J/\psi \left(\psi \right(2S\left)\right)\to l{\bar{l}}$ . In contrast,$ {B}_{c}\to {D}_{s}^{\left(*\right)}\rho (\omega ,\phi )$ modes are suppressed because of small CKM matrix elements$ {V}_{ub}$ and$ {V}_{us}$ . Consequently, Wilson coefficients${C}_{3-6}$ are also small, yielding a lower branching fraction of$ {B}_{c}\to {D}_{s,d}^{\left(*\right)}\rho (\omega ,\phi )$ . Hence, here we have considered only${B_c} \to D_{s\left( d \right)}^{\left( * \right)}J/\psi \left( {\psi \left( {2S} \right)} \right) \to D_{s\left( d \right)}^{\left( * \right)}l{\bar{l}}$ processes [44, 45]. -
In this section, we present the explicit expressions of different decay observables of the semileptonic decay channels
$ {B}_{c}\to \left({D}_{s,d}^{\left(*\right)}\right){l}^{+}{l}^{-}$ . The matrix elements can be parameterized in terms of different hadronic form factors and are given in Appendix A. The obtained form factors are consistent with all model independent symmetry relations [46, 47] within the limit of infinitely heavy quark mass and large energy of the final meson. For the helicity amplitudes, we recall that the techniques of Refs. [48-50] followed Ref. [37]. These amplitudes are likewise given in Appendix A. The subscripts$ \pm , 0, t$ denote transverse, longitudinal, and time helicity components. As the final mesons$ {D}_{s,d}$ are pseudo-scalar mesons and do not have any polarization direction, the transverse helicity amplitudes for${B}_{c}\to {D}_{s,d}{l}^{+}{l}^{-}$ channels are zero.Based on the calculation in Refs. [37, 44], the three-body
${B}_{c}\to {D}_{s\left(d\right)}{l}^{+}{l}^{-}$ and${B}_{c}\to {D}_{s\left(d\right)}^{*}{l}^{+}{l}^{-}$ differential decay rates are given by,$\begin{split} \frac{{{\rm d}{\Gamma _{s\left( d \right)}}}}{{{\rm d}{q^2}}} =& \frac{{G_F^2}}{{{{\left( {2\pi } \right)}^3}}}{\left( {\frac{{{\alpha _e}\left| {{V_{tb}}V_{ts\left( {td} \right)}^*} \right|}}{{2\pi }}} \right)^2}\frac{{{\lambda ^{1/2}}{q^2}}}{{48M_{{B_c}}^3}}\sqrt {1 - \frac{{4m_l^2}}{{{q^2}}}}\\&\times \left[ {{H^{\left( 1 \right)}}{H^{\dagger \left( 1 \right)}}\left( {1 + \frac{{4m_l^2}}{{{q^2}}}} \right)} \right.\\ &\left. { + {H^{\left( 2 \right)}}{H^{\dagger \left( 2 \right)}}\left( {1 - \frac{{4m_l^2}}{{{q^2}}}} \right) + \frac{{2m_l^2}}{{{q^2}}}3H_t^{\left( 2 \right)}H_t^{\dagger \left( 2 \right)}} \right], \end{split} $

(5) where ml is the lepton mass and
$ {H}^{\left(i\right)}{H}^{\dagger\left(i\right)}={H}_{+}^{\left(i\right)}{H}_{+}^{\dagger\left(i\right)}+{H}_{-}^{\left(i\right)}{H}_{-}^{\dagger\left(i\right)}+{H}_{0}^{\left(i\right)}{H}_{0}^{\dagger\left(i\right)}. $

(6) Further, we also study some other observables like the forward-backward asymmetry (AFB) and the longitudinal polarization fraction (PL) of the final vector meson in the decay
${B}_{c}\to {D}_{s,d}^{*}{l}^{+}{l}^{-}$ . While analyzing the channel$B\to {K}^{*}{l}^{+}{l}^{-}$ , AFB and PL have received significant attention both theoretically and experimentally. It is expected to collect further information on the Wilson coefficient by investigating these observables. The forward-backward asymmetry (AFB) is given by [37]$\begin{split} {A}_{FB}\left({q}^{2}\right)={\frac{3}{4}\sqrt{1-\frac{4{m}_{l}^{2}}{{q}^{2}}}} \times{\left\{\frac{{\rm Re}\left({H}_{+}^{\left(1\right)}{H}_{+}^{\dagger\left(2\right)}\right)-{\rm Re}\left({H}_{-}^{\left(1\right)}{H}_{-}^{\dagger\left(2\right)}\right)}{{H}^{\left(1\right)}{H}^{\dagger\left(1\right)}\left(1+\dfrac{4{m}_{l}^{2}}{{q}^{2}}\right)+{H}^{\left(2\right)}{H}^{\dagger\left(2\right)}\left(1-\dfrac{4{m}_{l}^{2}}{{q}^{2}}\right)+\dfrac{2{m}_{l}^{2}}{{q}^{2}}3{H}_{t}^{\left(2\right)}{H}_{t}^{\dagger\left(2\right)}}\right\}.} \end{split} $

(7) Notably, the forward-backward asymmetry observable for the
${B}_{c}\to {D}_{s,d}{l}^{+}{l}^{-}$ channel is zero in the SM, which consequently states parity-even nature. The non-zero value of AFB indicates parity-odd effects arising due to the parity-conserving contribution coming from scalar-vector interference. AFB ≠ 0 might be possible, if it receives contribution from scalar, pseudoscalar, or tensor new physics operators. However, in our model no new operator has been introduced, and instead only the Wilson coefficients have been modified. Thus, we maintain the zero forward backward asymmetry and do not discuss this observable for${B}_{c}\to {D}_{s,d}{l}^{+}{l}^{-}$ .Similarly, the longitudinal polarization fraction (PL) of the
${D}_{s\left(d\right)}^{*}$ meson is written as [37]$ \begin{split} {{P}_{L}\left({q}^{2}\right)} {=\frac{{H}_{0}^{\left(1\right)}{H}_{0}^{\dagger\left(1\right)}\left(1+\dfrac{4{m}_{l}^{2}}{{q}^{2}}\right)+{H}_{0}^{\left(2\right)}{H}_{0}^{\dagger\left(2\right)}\left(1-\dfrac{4{m}_{l}^{2}}{{q}^{2}}\right)+\dfrac{2{m}_{l}^{2}}{{q}^{2}}3{H}_{t}^{\left(2\right)}{H}_{t}^{\dagger\left(2\right)}}{{H}^{\left(1\right)}{H}^{\dagger\left(1\right)}\left(1+\dfrac{4{m}_{l}^{2}}{{q}^{2}}\right)+{H}^{\left(2\right)}{H}^{\dagger\left(2\right)}\left(1-\dfrac{4{m}_{l}^{2}}{{q}^{2}}\right)+\dfrac{2{m}_{l}^{2}}{{q}^{2}}3{H}_{t}^{\left(2\right)}{H}_{t}^{\dagger\left(2\right)}}. } \end{split} $

(8) Here, we only investigate the longitudinal polarization of the final vector meson. The transverse polarizations PT could be obtained from the relation
${P}_{T}=1-{P}_{L}$ . Furthermore, the leptonic polarization asymmetry$\left({A}_{{P}_{L}}\right)$ is defined as [44],$ \begin{split} {A}_{{P}_{L}}={\frac{\dfrac{{{\rm d}Br}_{h=-1}}{{\rm d}{q}^{2}}-\dfrac{{{\rm d}Br}_{h=1}}{{\rm d}{q}^{2}}}{\dfrac{{{\rm d}Br}_{h=-1}}{{\rm d}{q}^{2}}+\dfrac{{{\rm d}Br}_{h=1}}{{\rm d}{q}^{2}}}} ={\sqrt{1-\frac{4{m}_{l}^{2}}{{q}^{2}}}\frac{2\left[{\rm Re}\left({H}_{+}^{\left(1\right)}{H}_{+}^{\dagger\left(2\right)}\right)+{\rm Re}\left({H}_{-}^{\left(1\right)}{H}_{-}^{\dagger\left(2\right)}\right)+{\rm Re}\left({H}_{0}^{\left(1\right)}{H}_{0}^{\dagger\left(2\right)}\right)\right]}{{H}^{\left(1\right)}{H}^{\dagger\left(1\right)}\left(1+\dfrac{4{m}_{l}^{2}}{{q}^{2}}\right)+{H}^{\left(2\right)}{H}^{\dagger\left(2\right)}\left(1-\dfrac{4{m}_{l}^{2}}{{q}^{2}}\right)+\dfrac{2{m}_{l}^{2}}{{q}^{2}}3{H}_{t}^{\left(2\right)}{H}_{t}^{\dagger\left(2\right)}}}. \end{split} $

(9) -
There are several models beyond the SM that predict the existence of exotic fermions. If the new exotic fermions have different
$U(1)'$ charges as in E6 models [49-53], mixing between ordinary (doublet) and exotic singlet left-handed fermions induces undesirable FCNC mediated by the SM Z boson. In contrast, the mixing between right handed ordinary and exotic fermions induces FCNC mediated by the${Z'}$ boson.Here, the choice of the non-universal
${Z'}$ model [54-57] is considered to be the most economical, as it requires one extra$U(1)'$ gauge symmetry associated with a neutral gauge boson called${Z'}$ boson. Basic formalism of the family non-universal${Z'}$ model with FCNCs can be found in [55, 58, 59]. The main attraction of this model is that the FCNC transitions could occur at tree level due to the off-diagonal (flavor changing) couplings of non-universal${Z'}$ with fermions, which is not allowed under SM consideration. Various studies of the non-universal${Z'}$ model have been conducted assuming diagonal as well as vanishing right-handed quark couplings with the${Z'}$ boson. It is observed that this can help resolve the puzzles of rare B meson decays, such as the$B-{\bar{B}}$ mixing phase [60],$ \pi -K$ puzzle [59, 61],$\pi -\pi $ puzzle [62, 63], etc.In this model, the
${Z'}$ part of the neutral-current Lagrangian within the basis of gauge eigenstates of all fields is written as$ {\cal{L}}^{Z'}={-g'}{{J'}_{\mu }}{Z'}^{\mu }, $

(10) where
$g'$ is the new gauge coupling of the$U(1)'$ group at the MW scale.The
$U(1)'$ current for${Z'}$ boson in the appropriate gauge basis is$ {J'}_{\mu }=\mathop\sum\nolimits _{i,j}{\bar{\psi}}_{i}{\gamma }_{\mu }\left[{{\epsilon}_{{\psi }_{{L}_{ij}}}P}_{L}+{\epsilon}_{{\psi }_{{R}_{ij}}}{P}_{R}\right]{\psi }_{j}, $

(11) where i is the family index, and ψ denotes the fermions (up- or down-type quarks, or charged or neutral leptons).
${P}_{L,R}= (1\mp {\gamma }_{5})/2$ and${\epsilon}_{{\psi }_{{R,L}_{ij}}}$ represent the chiral couplings of the${Z'}$ boson. The chiral${Z'}$ coupling matrices in the fermion mass eigenstate basis are given as$ {B}_{ij}^{{\psi }_{L}}\equiv {\left({V}_{L}^{\psi }{\epsilon}_{{\psi }_{L}}{V}_{L}^{{\psi }^{\dagger}}\right)}_{ij}, {B}_{ij}^{{\psi }_{R}}\equiv {\left({V}_{R}^{\psi }{\epsilon}_{{\psi }_{R}}{V}_{R}^{{\psi }^{\dagger}}\right)}_{ij}. $

(12) These couplings may contain CP-violating phases beyond the SM. As long as the ϵ matrices are not proportional to the identity, the B matrices will have non-zero off-diagonal elements that induce the FCNC interaction at the tree level. We chose the basis such that
$ {\epsilon}_{{\psi }_{R}}\propto I$ ; hence the right-handed couplings vanish within this framework. If${B}_{ij}^{{\psi }_{R}}$ is non-diagonal, different chirality structures will be induced in B decays, which generate new operators to the effective Hamiltonian. The presence of new chirally flipped operators might treat these transitions differently and may cause deviations from the SM. However, those discussions are beyond the scope of this study, as we only modify the Wilson coefficients in our analysis and do not create any new operators apart from the SM semileptonic operators.For the
$b\to q(q=s,d )$ transition, the${Z'}bq$ couplings are generated as [64],${{\cal{L}}}_{\rm FCNC}^{Z'}={-{\rm{g}}'}\left({B}_{sb}^{L}{{\bar{s}}}_{L}{\gamma }_{\mu }{b}_{L}+{B}_{sb}^{R}{{\bar{s}}}_{R}{\gamma }_{\mu }{b}_{R}\right){Z'}^{\mu }+h.c. $

(13) The effective Hamiltonian for the above transition mediated by the
${Z'}$ boson can be written as$ { H}_{\rm eff}^{{{\rm{Z}}'}}=\frac{8{G}_{F}}{\sqrt{2}}\left({\rho }_{sb}^{L}{{\bar{s}}}_{L}{\gamma }_{\mu }{b}_{L}+{\rho }_{sb}^{R}{{\bar{s}}}_{R}{\gamma }_{\mu }{b}_{R}\right)\left({\rho }_{ll}^{L}{{\bar{l}}}_{L}{\gamma }_{\mu }{l}_{L}+{\rho }_{ll}^{R}{{\bar{l}}}_{R}{\gamma }_{\mu }{l}_{R}\right), $

(14) where
$ {\rho}_{f{f'}}^{L,R}\equiv \frac{{{\rm{g}}'}{M}_{Z}}{{\rm{g}}{M}_{Z'}}{B}_{f{f'}}^{L,R}. $

(15) The value of
$ \left|\frac{{\rm{g}}'}{{\rm{g}}}\right|$ is not determined yet. However, it is expected that$\left|\frac{{\rm{g}}'}{{\rm{g}}}\right|\sim 1$ , as both$U(1)$ groups arise from the same GUT. Throughout the entire analysis, we ignore the renormalization group running effects due to these new contributions. To avoid too many free parameters, we assume that the FCNC couplings of the${Z'}$ and quarks only occur in the left-handed sector. Therefore,${\rho }_{sb}^{R}=0$ and the effects of the${Z'}$ FCNC currents simply modify the Wilson coefficients C9 and C10. Because the${Z'}$ boson has not yet been discovered, its mass is unknown. However, there are stringent limits on the mass of an extra${Z'}$ boson obtained by CDF, DØ, and LEP 2, and on the Z-Z' mixing angle${\theta }_{Z{Z'}}$ [65-66]. The precision electroweak (EW) data strongly constrain${\theta }_{Z{Z'}}$ to be very small, i.e.,$\left|{\theta }_{Z{Z'}} \right|\le 8.1\times {10}^{-3}$ . Using the current LHC Drell-Yan data, the authors of Refs. [67-69] obtained the lower limit of mass of${Z'}$ as$M_{Z'}> 4.4 \;{\rm{TeV}}$ . Recently, in Ref. [70] the constraints on the mixing angle${\theta }_{Z{Z'}}$ have been derived from resonant diboson searches at the LHC at$\sqrt{s}=13\;{\rm{TeV}}$ , which is on the order of a few ×10-4. Because of the small${\theta }_{Z{Z'}}$ , we can neglect the$Z-{Z'}$ mixing and consider that the couplings of only the right-handed quarks with${Z'}$ are diagonal. Hence, we can write the effective Hamiltonian for the transition$b\to q{l}^{+}{l}^{-}$ mediated by${Z'}$ FCNC as$\begin{split} H_{\rm eff}^{{\rm{Z'}}} =& \frac{{2{G_F}}}{{\sqrt 2 \pi }}{V_{tb}}V_{tq}^*\left[ {\frac{{B_{qb}^LS_{ll}^L}}{{{V_{tb}}V_{tq}^*}}\bar q{\gamma _\mu }\left( {1 - {\gamma _5}} \right)b\bar l{\gamma ^\mu }\left( {1 - {\gamma _5}} \right)l} \right.\\ &\left. { + \frac{{B_{qb}^LS_{ll}^R}}{{{V_{tb}}V_{tq}^*}}\bar q{\gamma _\mu }\left( {1 - {\gamma _5}} \right)b\bar l{\gamma ^\mu }\left( {1 + {\gamma _5}} \right)l} \right], \end{split} $

(16) where
${B}_{qb}^{L}=\left|{B}_{qb}^{L}\right|{\rm e}^{-{\rm i}{\varphi }_{qb}}$ represents the off-diagonal left-handed couplings of${Z'}$ boson with the quark sector, and φqb is the new weak phase angle. The concise effective Hamiltonian is thus given by [71]$ {H}_{\rm eff}^{Z'}=-\frac{4{G}_{F}}{\sqrt{2}}{V}_{tb}{V}_{ts}^{*}\left[{\wedge }_{sb}{C}_{9}^{Z'}{O}_{9}+{\wedge }_{sb}{C}_{10}^{Z'}{O}_{10}\right], $

(17) where
$ {\wedge }_{sb}=\frac{4\pi {\rm e}^{-{\rm i}{\varphi }_{sb}}}{\alpha {V}_{tb}{V}_{td}^{*}}, $

$ {C}_{9}^{Z'}=\left|{B}_{sb}\right|{S}_{LL}, $

and
$ {C}_{10}^{Z'}=\left|{B}_{sb}\right|{D}_{LL}. $

(18) Here,
$ {S}_{LL}={S}_{ll}^{L}+{S}_{ll}^{R}$ and$ {D}_{LL}={S}_{ll}^{L}-{S}_{ll}^{R}$ .The terms
${S}_{ll}^{L}$ and${S}_{ll}^{R}$ denote the couplings of the${Z'}$ boson with left- and right-handed leptons respectively. The numerical values of the${Z'}$ couplings suffer from several constraints that arise due to different exclusive and inclusive B decays [60, 72, 73]. We consider two scenarios, as described in Table 1 in our calculation, corresponding to different fitting values of${B}_{s}-{{\bar{B}}}_{s}$ and$ {B}_{d}-{{\bar{B}}}_{d}$ mixing data that present the couplings as well as the weak phase angle. The values of input parameters of |Bsb| and ϕsb are set by UTfit collaborations [74], whereas |Bdb| and ϕdb are recollected from Ref. [75].|Bsb|×10−3 ϕsb(Degree) |Bdb|×10−3 ϕdb(Degree) SLL×10−2 DLL×10−2 ${\cal{S}}_{1}$ 

1.09 ± 0.22 −72 ± 7 0.16±0.08 −33±45 −2.8 ± 3.9 −6.7 ± 2.6 ${\cal{S}}_{2}$ 

2.20 ± 0.15 −82 ± 4 0.19±0.05 −50±20 −1.2 ± 1.4 −2.5 ± 0.9 The contributions of the non-universal
${Z'}$ boson to the branching ratio, FB asymmetry, and lepton polarization asymmetry described in the following section are considered only for muonic channels i.e.,${B}_{c}\to {D}_{s,d}^{\left(*\right)}{\mu }^{+}{\mu }^{-}$ decay modes. -
In this study, we analyzed different decay observables like the branching ratio, forward-backward asymmetry, polarization fraction, and lepton polarization asymmetry in the non-universal
${Z'}$ model. The pictorial descriptions provide a good representation of the deviations of these observables in the NP model from their SM predictions. We plotted all these parameters with the variation of the total momentum transfer squared, i.e., q2, and their graphical representations are shown below. We also plotted the dependence of the branching ratio on the NP model parameters DLL and SLL with different ϕsb. Our whole study could lead us to the following conclusions.(i) Figs. 1–8 depict the dependence of the branching fraction on the model parameters. Here, we assumed the central values of |Bsb| and |Bdb| for both scenarios
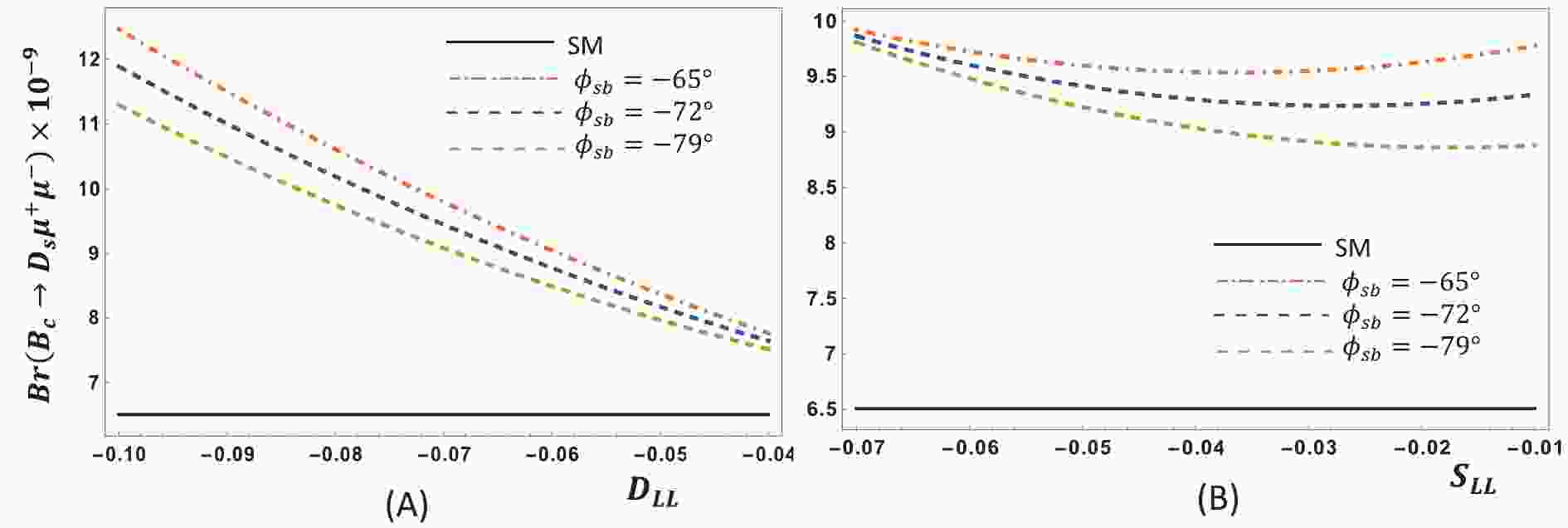
$ {\cal{S}}_{1}$ and$ {\cal{S}}_{2}$ , and the values of new weak phase angles ϕsb and ϕdb are changed accordingly. For${B}_{c}\to ({D}_{s},{D}_{s}^{*}){\mu }^{+}{\mu }^{-}$ (Figs. 1 and 3), we found that ϕsb = –65° maximally increases the value of the branching fraction in the first scenario$ {\cal{S}}_{1}$ . Fig. 1(A) and Fig. 3(A) show that for smaller DLL, the branching fraction is increased, whereas a saturated dependency on SLL is observable in Fig. 1(B) and Fig. 3(B). In scenario$ {\cal{S}}_{2}$ , the branching fraction depends on DLL, SLL, and ϕsb in an almost similar fashion (Fig. 2 and Fig. 4). Figs. 5 (A), 6 (A), 7 (A), and 8 (A) clearly indicate that the branching ratio of${B}_{c}\to ({D}_{d},{D}_{d}^{*}){\mu }^{+}{\mu }^{-}$ directly depends on ϕdb but inversely depends on DLL. In contrast, Fig. 5(B) and 7 (B) also show direct dependence of branching ratio on SLL, and Figs. 6 (B) and 7 (B) show the same trend, but below the cuts:${S}_{LL}=0.03$ for$ {B}_{c}\to {D}_{d}{\mu }^{+}{\mu }^{-}$ and$ {S}_{LL}=0.04$ for${B}_{c}\to {D}_{d}^{*}{\mu }^{+}{\mu }^{-}$ . The branching fraction variations (Figs. 9–12) of all decays above some noticeable deviation from their SM values are found in low recoil, i.e., in the high q2 region.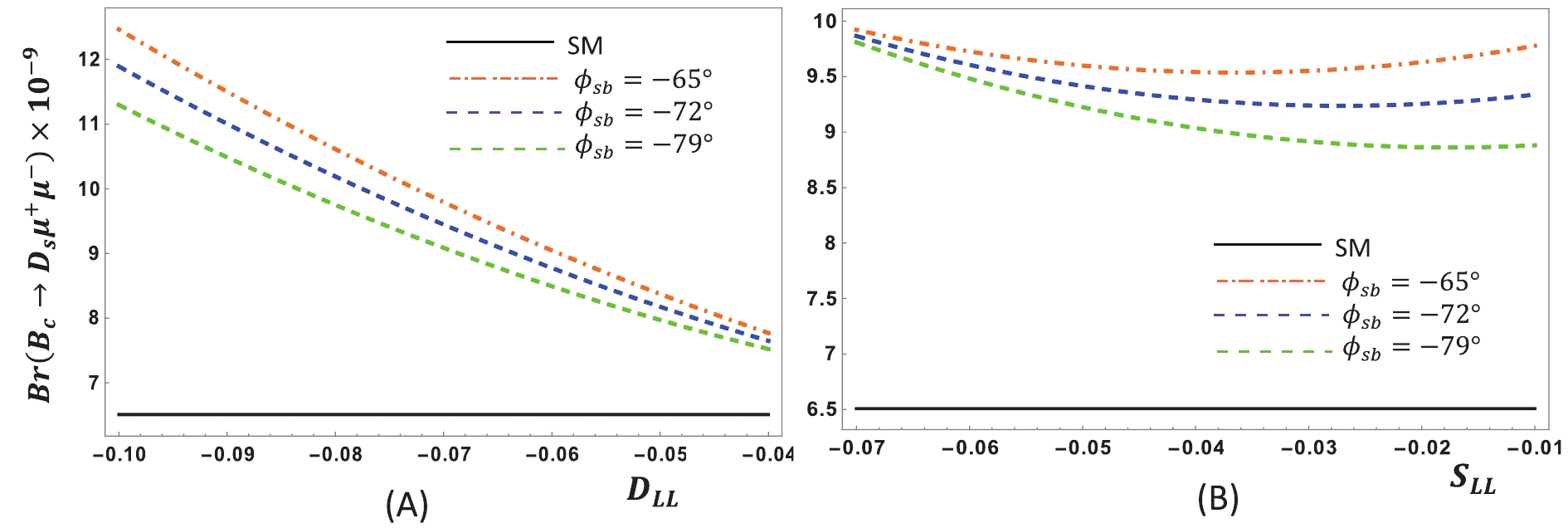
Figure 1. (color online) Dependence of
$Br\left({B}_{c}\to {D}_{s}{\mu }^{+}{\mu }^{-}\right)$ with respect to${D}_{LL}$ (A) and${S}_{LL} $ (B) for various$ {\phi }_{sb}$ in$ {\cal{S}}_{1}$ .
Figure 2. (color online)
$ Br\left({B}_{c}\to {D}_{s}{\mu }^{+}{\mu }^{-}\right)$ with respect to$ {D}_{LL}$ (A) and$ {S}_{LL}$ (B) for various${\phi }_{sb}$ in${\cal{S}}_{2}$ .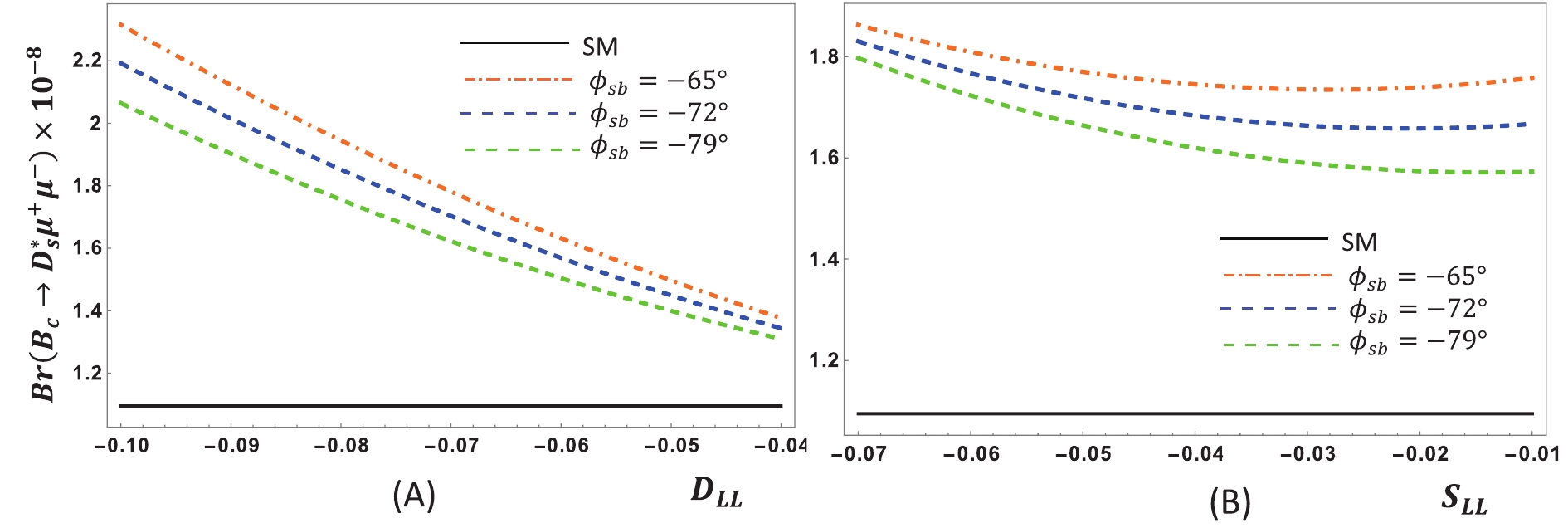
Figure 3. (color online)
$Br\left( {{B_c} \to D_s^*{\mu ^ + }{\mu ^ - }} \right)$ with respect to$ {D}_{LL}$ (A) and${S}_{LL} $ (B) for various$ {\phi }_{sb}$ in$ {\cal{S}}_{1}$ .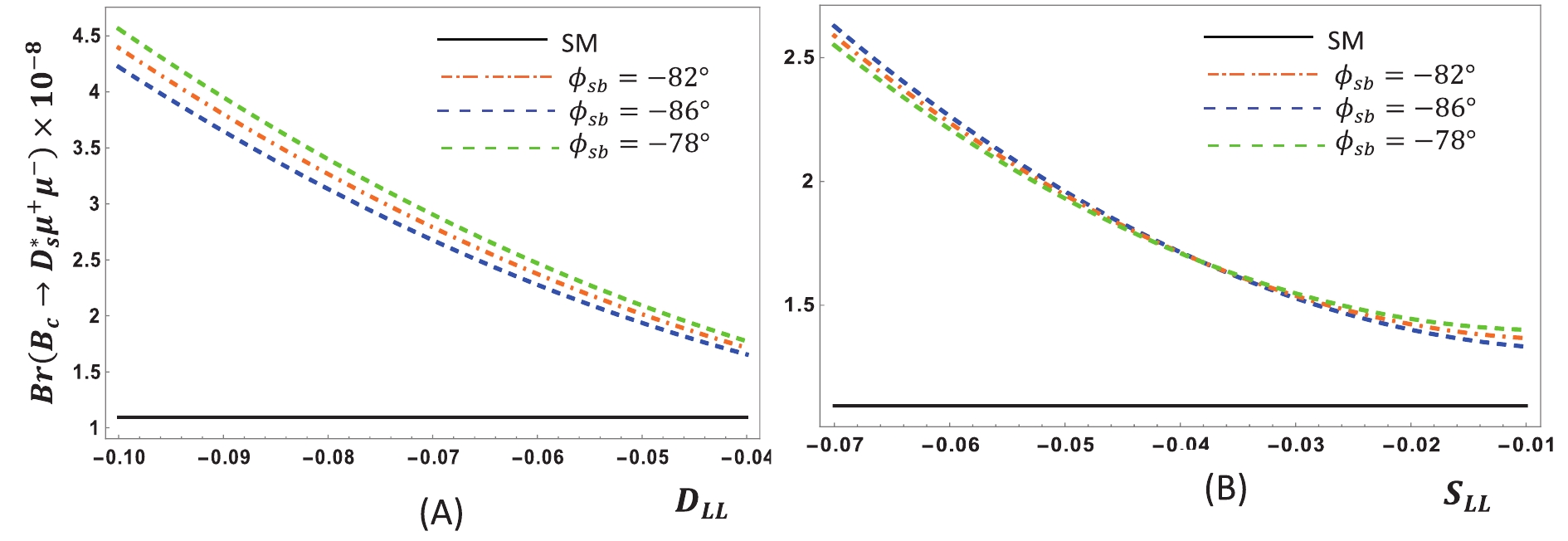
Figure 4. (color online)
$Br\left( {{B_c} \to D_s^*{\mu ^ + }{\mu ^ - }} \right)$ with respect to${D}_{LL}$ (A) and$ {S}_{LL}$ (B) for various$ {\phi }_{sb}$ in$ {\cal{S}}_{2}$ .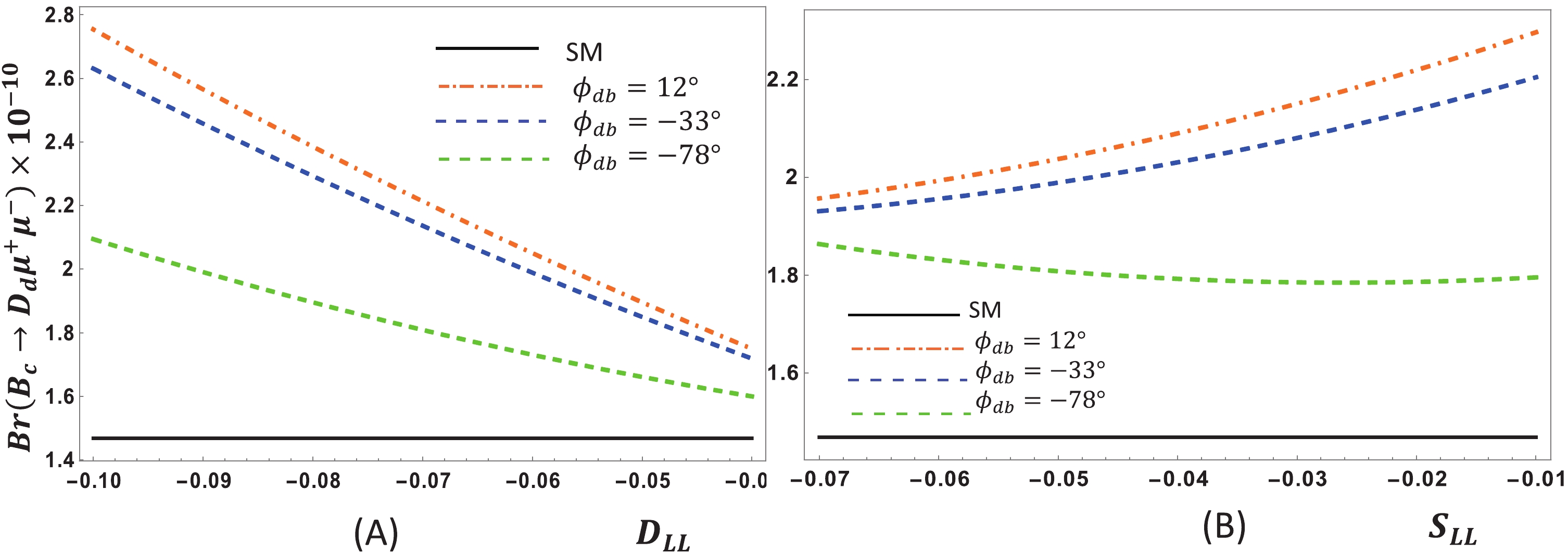
Figure 5. (color online)
$Br\left({B}_{c}\to {D}_{d}{\mu }^{+}{\mu }^{-}\right)$ with respect to${D}_{LL}$ (A) and$ {S}_{LL}$ (B) for various$ {\phi }_{db}$ in$ {\cal{S}}_{1}$ .
Figure 6. (color online)
$Br\left({B}_{c}\to {D}_{d}{\mu }^{+}{\mu }^{-}\right)$ with respect to$ {D}_{LL}$ (A) and${S}_{LL} $ (B) for various${\phi }_{db}$ in${\cal{S}}_{2}$ .
Figure 7. (color online)
$Br\left({B}_{c}\to {D}_{d}^{*}{\mu }^{+}{\mu }^{-}\right)$ with respect to$ {D}_{LL}$ (A) and$ {S}_{LL}$ (B) for various${\phi }_{db}$ in${\cal{S}}_{1}$ .
Figure 8. (color online) The dependence of
$Br\left({B}_{c}\to {D}_{d}^{*}{\mu }^{+}{\mu }^{-}\right)$ with respect to$ {D}_{LL}$ (A) and$ {S}_{LL}$ (B) for various${\phi }_{db}$ in$ {\cal{S}}_{2}$ .
Figure 9. (color online) Variation of branching fraction of
${B}_{c}\to {D}_{s}{\mu }^{+}{\mu }^{-}$ with respect to${q}^{2}$ .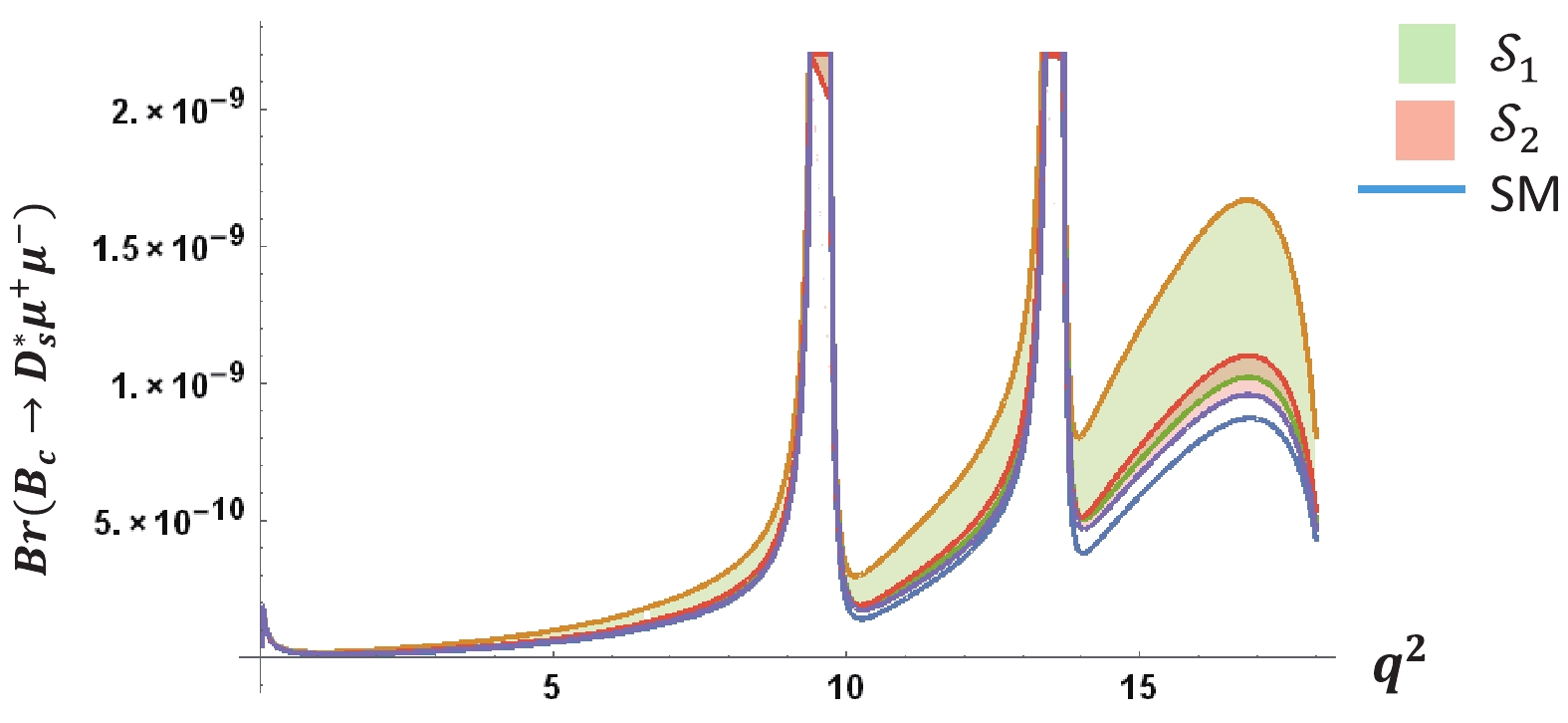
Figure 10. (color online) Variation of branching fraction of
${B_c} \to D_s^*{\mu ^ + }{\mu ^ - }$ with respect to$ {q}^{2}$ .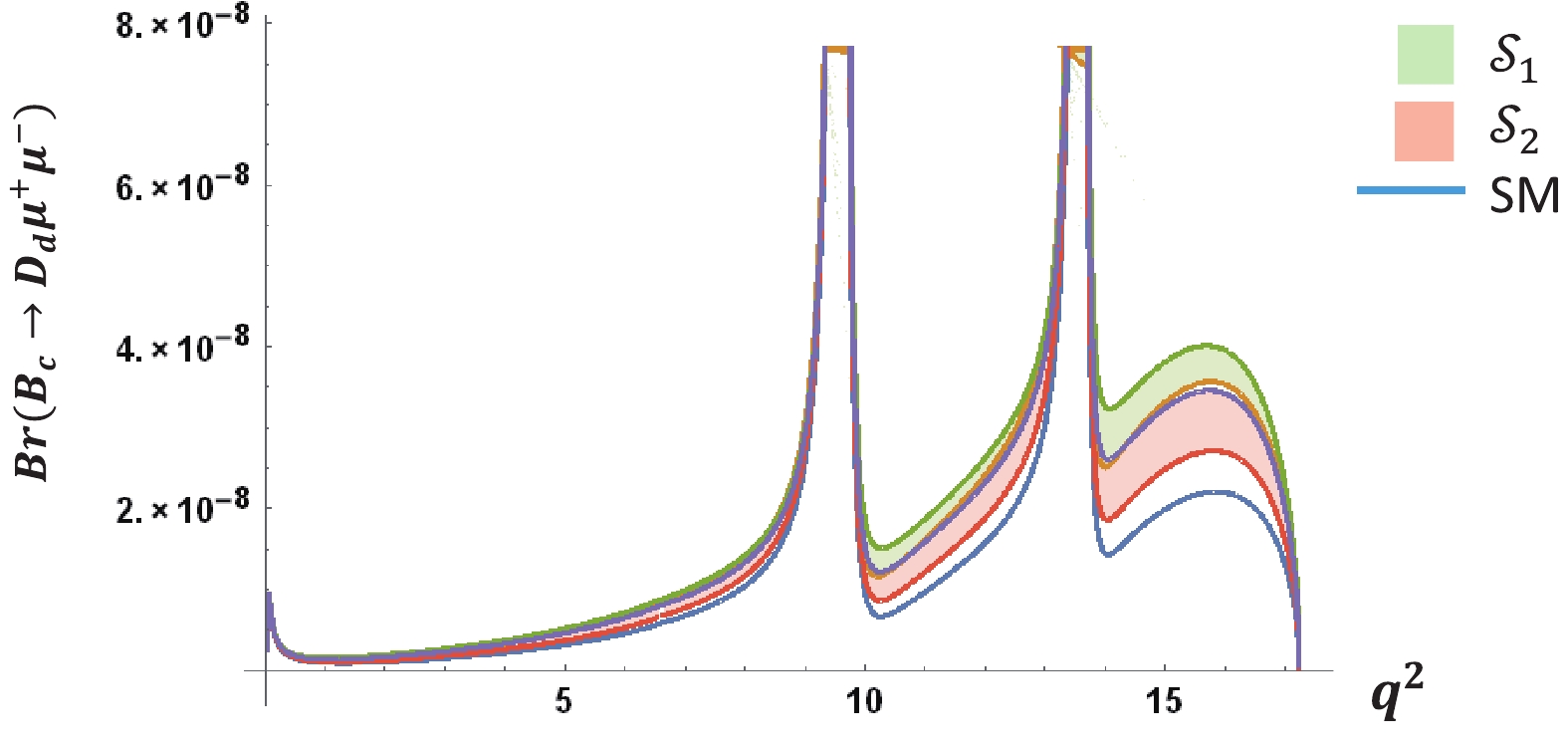
Figure 11. (color online) Variation of branching fraction of
${B_c} \to {D_d}{\mu ^ + }{\mu ^ - }$ with respect to$ {q}^{2}$ .
Figure 12. (color online) Variation of branching fraction of
${B_c} \to D_d^*{\mu ^ + }{\mu ^ - }$ with respect to$ {q}^{2}$ .(ii) Figs. 13 and 14 show the variation in the forward-backward asymmetry with respect to q2. This observable is a considerably interesting property for the decay channel, as it is sensitive to the parity status of any interaction. In the low q2 region, the parity conserving photonic interaction is relatively dominant, leading to a small FB asymmetry. However, in the higher momentum region (i.e., large q2), the parity-violating Z- and W-boson contributions become more significant. As a consequence, the FB asymmetry becomes larger. For
${B}_{c}\to {D}_{s}^{*}{\mu }^{+}{\mu }^{-}$ the zero crossing is shifted to 3.2 GeV2 from 2.1 GeV2 in the NP model, and both scenarios overlap with each other and lie below the SM. However, there is no such shift of zero-crossing found for the$ {B}_{c}\to {D}_{d}^{*}{\mu }^{+}{\mu }^{-}$ channel, and$ {\cal{S}}_{2}$ reaches slightly above the SM, whereas$ {\cal{S}}_{1}$ remains below it.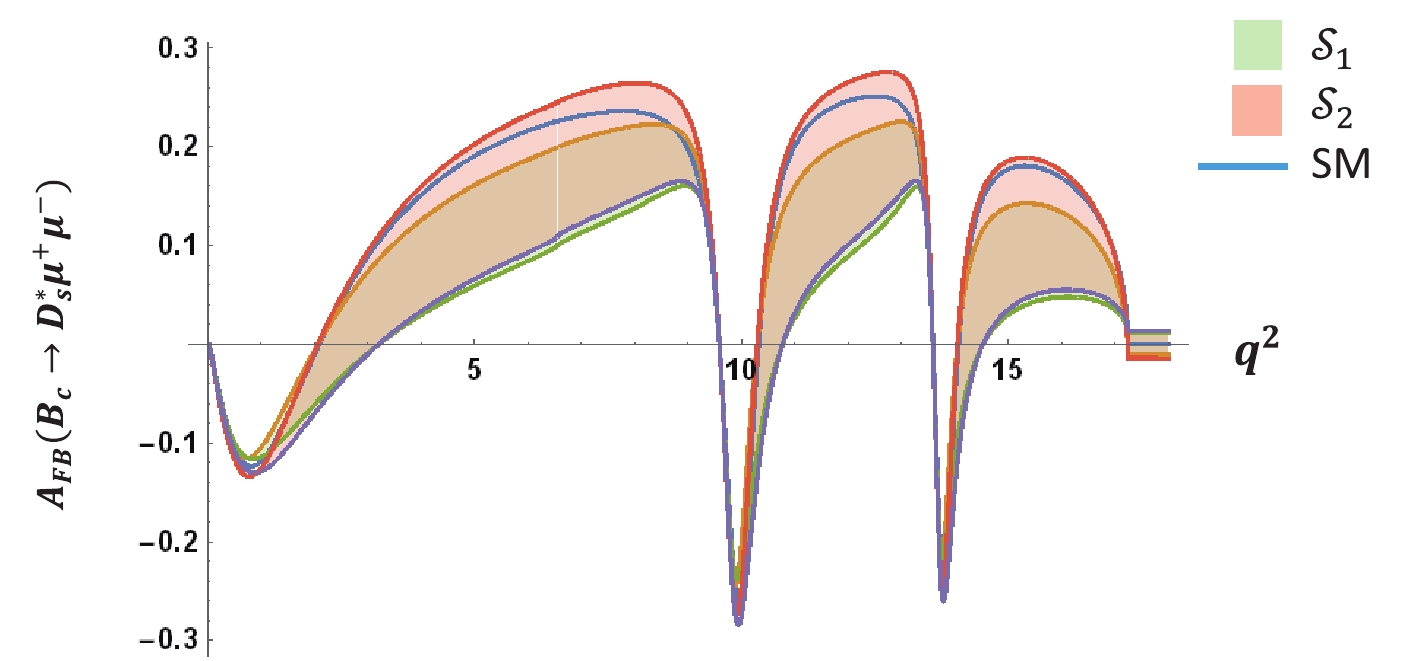
Figure 13. (color online) Variation of forward-backward asymmetry of
${B}_{c}\to {D}_{s}^{*}{\mu }^{+}{\mu }^{-}$ with respect to$ {q}^{2}$ .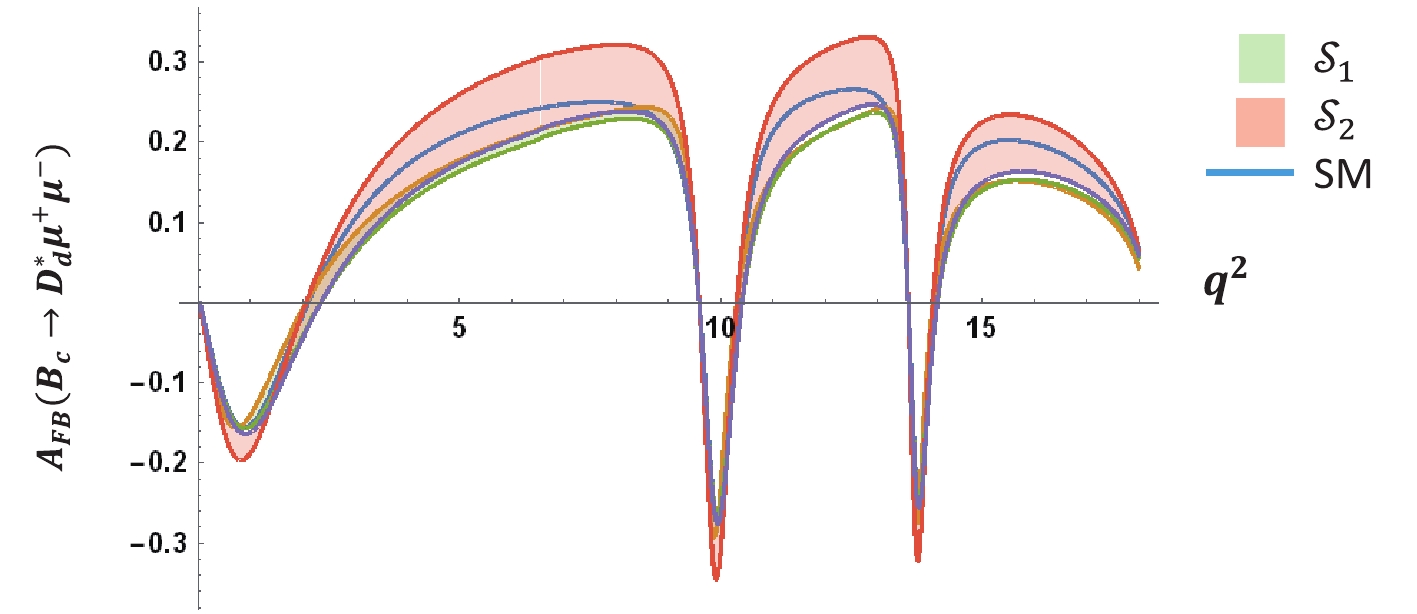
Figure 14. (color online) Variation of forward-backward asymmetry of
${B}_{c}\to {D}_{d}^{*}{\mu }^{+}{\mu }^{-}$ with respect to${q}^{2}$ .(iii) Fig. 15 and Fig. 16 depict the polarization fraction of
${B}_{c}\to ({D}_{s}^{*},{D}_{d}^{*}){\mu }^{+}{\mu }^{-}$ decay channels, and no NP contribution is noticeable for this observable.
Figure 15. (color online) Variation of polarization fraction of
${B}_{c}\to {D}_{s}^{*}{\mu }^{+}{\mu }^{-}$ with respect to$ {q}^{2}$ .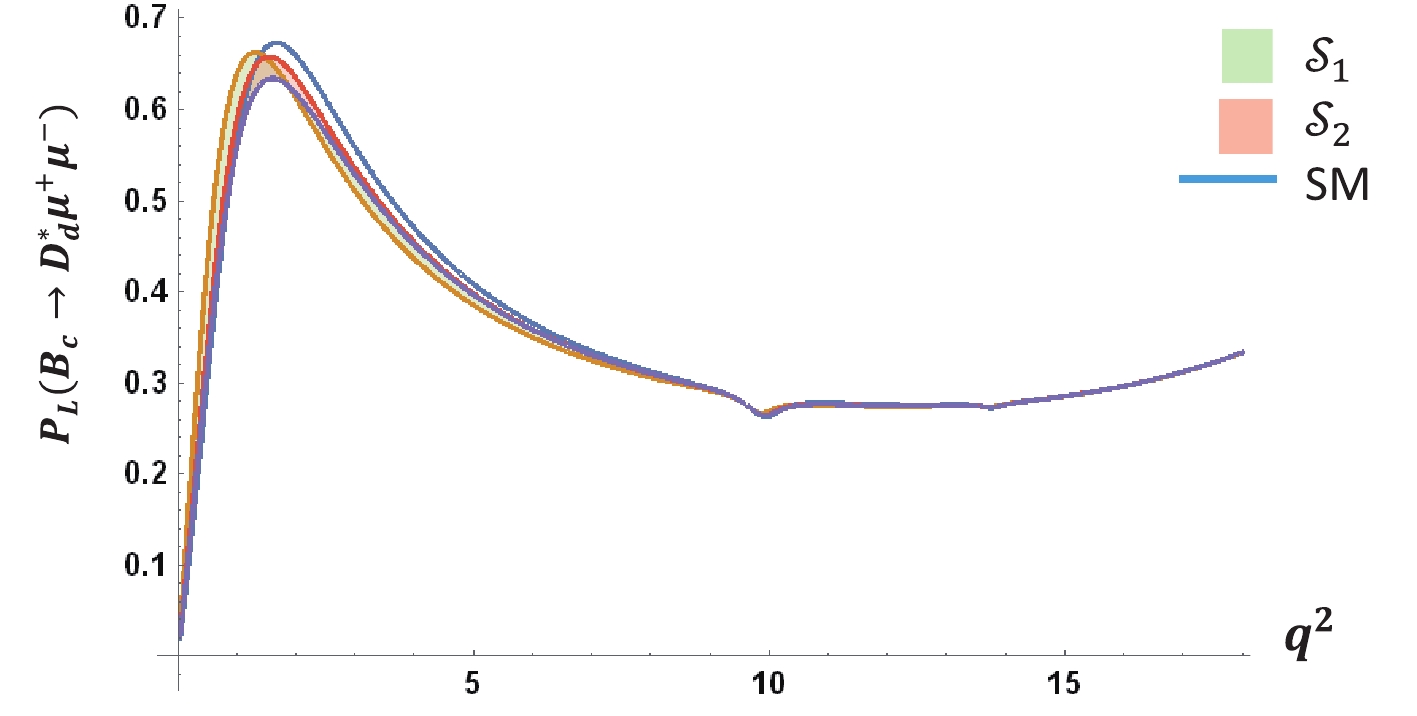
Figure 16. (color online) Variation of polarization fraction of
${B}_{c}\to {D}_{d}^{*}{\mu }^{+}{\mu }^{-}$ with respect to$ {q}^{2}$ .(iv) In Figs. 17–20, the lepton polarization asymmetry for all four decay modes is presented. In the SM,
$ {A}_{{P}_{L}} $ is approximately −0.1. In the non-universal${Z'}$ model, the lepton polarization asymmetry of${B}_{c}\to ({D}_{s},{D}_{s}^{*}){\mu }^{+}{\mu }^{-}$ received a noticeable increment from –0.1 for both scenarios$ {\cal{S}}_{1}$ and$ {\cal{S}}_{2}$ . For${B}_{c}\to ({D}_{d},{D}_{d}^{*}){\mu }^{+}{\mu }^{-}$ decay channels, we found a significant increment for$ {\cal{S}}_{1}$ and a comparably lower increase in$ {\cal{S}}_{2}$ . An interesting finding of this study is that the lepton longitudinal polarization asymmetry for${B}_{c}\to {D}_{s,d}^{*}{\mu }^{+}{\mu }^{-}$ yielded a positive value in the very low q2 region. This phenomenon could be an ideal probe to investigate the spin direction of final state leptons in vector meson decay.
Figure 17. (color online) Variation of lepton polarization asymmetry of
${B}_{c}\to {D}_{s}{\mu }^{+}{\mu }^{-}$ with respect to${q}^{2}$ .
Figure 18. (color online) Variation of lepton polarization asymmetry of
${B}_{c}\to {D}_{s}^{*}{\mu }^{+}{\mu }^{-}$ with respect to${q}^{2}$ .
Figure 19. (color online) Variation of lepton polarization asymmetry of
${B}_{c}\to {D}_{d}{\mu }^{+}{\mu }^{-}$ with respect to${q}^{2}$ .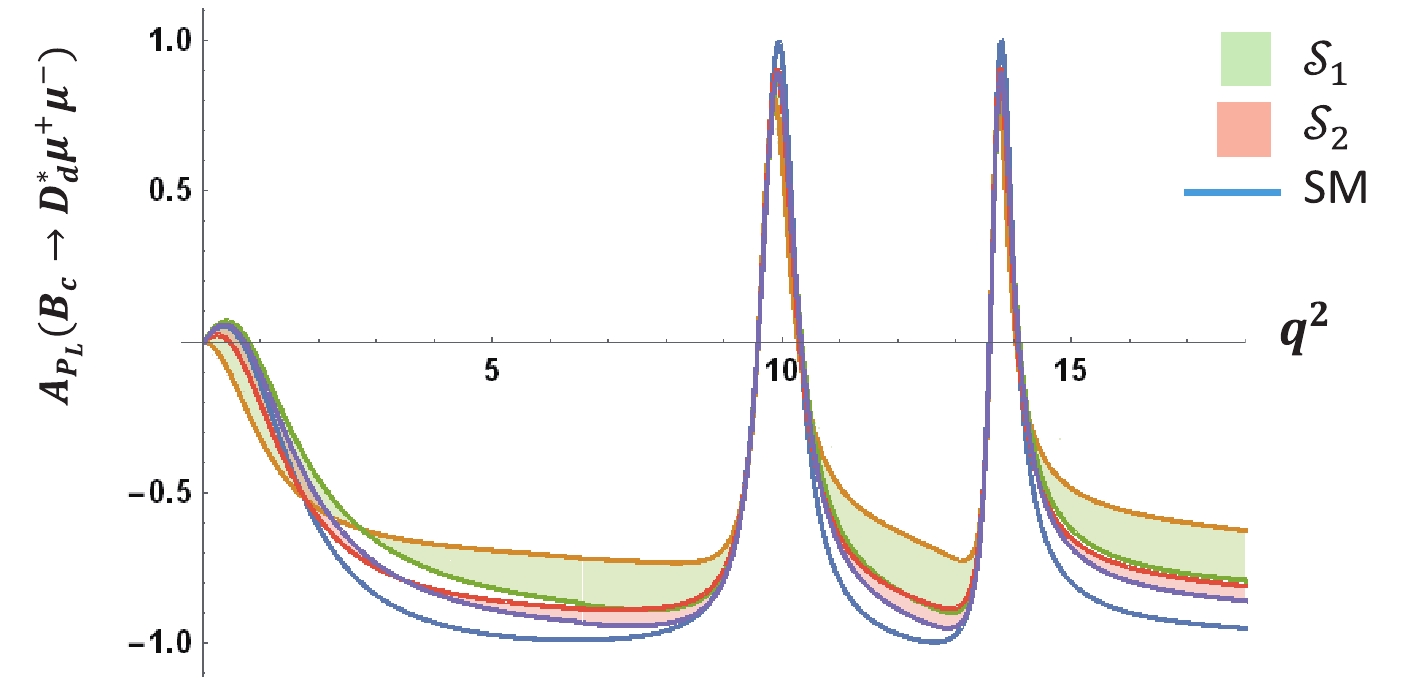
Figure 20. (color online) Variation of lepton polarization asymmetry of
${B}_{c}\to {D}_{d}^{*}{\mu }^{+}{\mu }^{-}$ with respect to${q}^{2}$ .Further, we plotted some correlation graphs between different decay observables and shown them below. We evaluate these graphs in the low
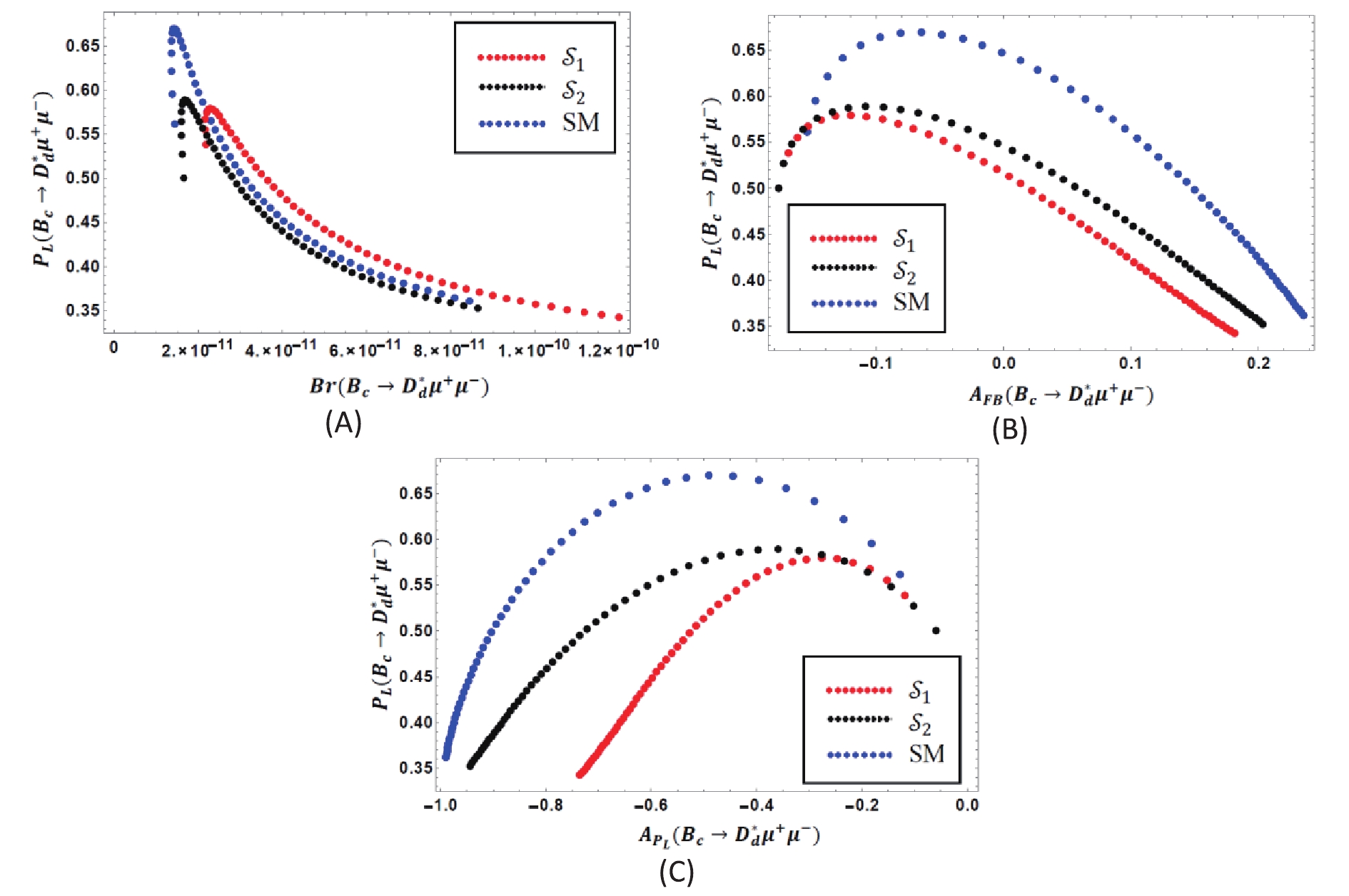
${q}^{2}$ region i.e.,$1<{q}^{2}<6$ GeV2.From the figures above, we can gather some information about the interdependence of different observables. Fig. 21 (A, B, C, D) show that for both the scenarios of
${Z'}$ model, the branching ratio and lepton polarization asymmetry enhance their SM predictions. In the${Z'}$ model, we found that the NP contribution to${B}_{c}\to {D}_{s}^{*}{\mu }^{+}{\mu }^{-}$ channel drives the polarization asymmetry,$ {A}_{{P}_{L}} $ , maximally up to approximately −0.4, which is significantly larger than the SM. Whereas the increment of$ {A}_{{P}_{L}} $ is not ast high, while still above the SM values of other channels. These large deviations could hold remarkable NP signatures. Fig. 22(A, B) is important, as it illustrates the dependence of the forward-backward asymmetry on the branching ratio of${B}_{c}\to {D}_{s}^{*}{\mu }^{+}{\mu }^{-}$ and$ {B}_{c}\to {D}_{d}^{*}{\mu }^{+}{\mu }^{-}$ channels. A higher branching ratio indicates higher FB asymmetry, and the correlation curves of both scenarios of the NP model lie below the SM prediction in the low momentum transfer region. While plotting the correlation between FB asymmetry and lepton polarization asymmetry of${B}_{c}\to {D}_{s}^{*}{\mu }^{+}{\mu }^{-}$ and$ {B}_{c}\to {D}_{d}^{*}{\mu }^{+}{\mu }^{-}$ channels in Figs. 23, we observed that the graphs for NP reach above the SM and for higher FB asymmetry, the lepton polarization asymmetry decreases. The correlation graphs for the longitudinal polarization fraction with other observables are shown in Figs. 24 (for${B}_{c}\to {D}_{s}^{*}{\mu }^{+}{\mu }^{-}$ ) and 25 (for${B}_{c}\to {D}_{s}^{*}{\mu }^{+}{\mu }^{-}$ ).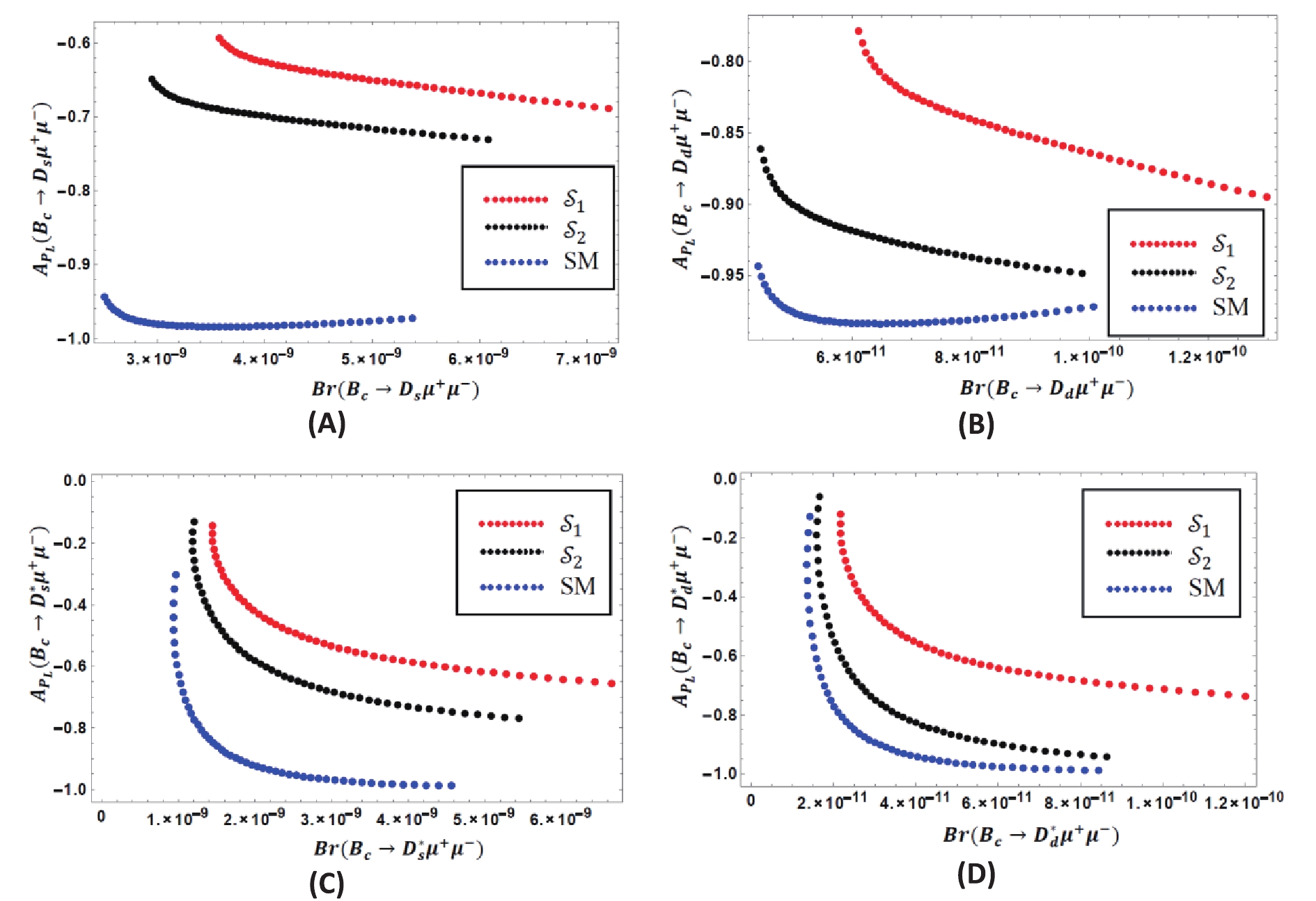
Figure 21. (color online) Correlation between branching ratio (
$Br$ ) and lepton polarization asymmetry ($ {A}_{{P}_{L}}$ ) for : (A)${B}_{c}\to {D}_{s}{\mu }^{+}{\mu }^{-}$ , (B)$ {B}_{c}\to {D}_{d}{\mu }^{+}{\mu }^{-}$ , (C)${B}_{c}\to {D}_{s}^{*}{\mu }^{+}{\mu }^{-}$ , (D)${B}_{c}\to {D}_{d}^{*}{\mu }^{+}{\mu }^{-}$ channels.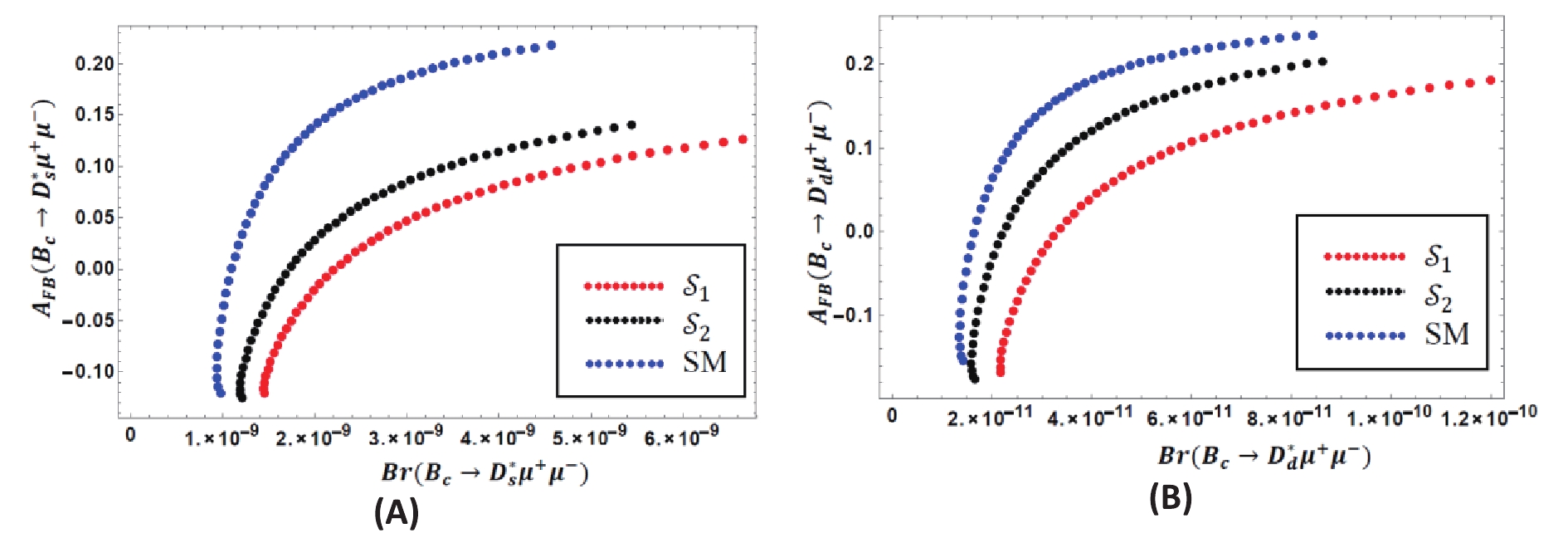
Figure 22. (color online) Correlation between branching ratio (
$Br$ ) and forward-backward asymmetry ($A_{FB}$ ) for: (A)${B_c} \to D_s^*{\mu ^ + }{\mu ^ - }$ , (B)${B_c} \to D_d^*{\mu ^ + }{\mu ^ - }$ channels.
Figure 23. (color online) Correlation between forward-backward asymmetry (
$A_{FB}$ ) and lepton polarization asymmetry (${A_{{P_L}}}$ ) for: (A)${B_c} \to D_s^*{\mu ^ + }{\mu ^ - }$ , (B)${B_c} \to D_d^*{\mu ^ + }{\mu ^ - }$ channels. -
The decay modes
${B_c} \to D_{s,d}^{\left( * \right)}{\mu ^ + }{\mu ^ - }$ are still in the process of experimental verification. In our analysis, we adopted the QCD motivated relativistic quark approach for the form factors. These form factors satisfy all the heavy quark and large energy symmetry relations that explicitly allow such transitions in the whole accessible kinematical range. Our study shows a noticeable effect of the non-universal${Z'}$ boson to these rare decay modes of the Bc meson, which can be investigated in the LHCb experiment as Bc mesons are expected to be produced copiously in the near future.The contribution of the cascade decays of J/ψ(ψ) meson lying in the long-distance terms of matrix elements could be cut down in any experimental as well as theoretical approach, as they produce significant uncertainties in decay distributions. From our study, we obtained the cuts around
$9\;{\rm{Ge}}{{\rm{V}}^2} < {q^2} < 15\;{\rm{Ge}}{{\rm{V}}^2}$ . The dependence of branching fraction to the${Z'}$ model parameters shown here is basically for negative DLL and SLL as their large positive values are forbidden by the constraints from${A_{FB}}{\left( {{{\bar{B}}_d} = {K^*}{\mu ^ + }{\mu ^ - }} \right)_{0 < {q^2} < 2\;{\rm{Ge}}{{\rm{V}}^2}}}$ . All branching fractions are increased in the high q2 region, and the best increment appears for scenario$ {\cal{S}}_{1}$ . Other parameters, such as FB asymmetry and lepton polarization asymmetry, also increased in the NP model. The longitudinal polarization fraction of the vector mesons$D_{s,d}^*$ does not show a significant deviation from its SM value, which indicates that the${Z'}$ boson would not change the polarization direction of those mesons. Furthermore, we provided several illustrative descriptions of correlations between different decay observables, which might be worthy of further investigation of these decay channels. As a concluding remark, we state that the presence of a non-universal${Z'}$ boson provides a considerable rise in the decay rate as well as other decay observables of${B_c} \to D_{s,d}^{\left( * \right)}{\mu ^ + }{\mu ^ - }$ decay channels. This might be helpful for the search of these decay modes with a highly sensitive experimental setup in future.We thank the reviewer for useful comments and suggestions that improved the quality of this paper. Maji is thankful to DST, Govt. of India for the INSPIRE Fellowship (IF160115). Nayek and Sahoo are grateful to SERB, DST, Govt. of India for financial support through project (EMR/2015/000817). Mahata and Biswas thank NIT Durgapur for the fellowship.
-
$\tag{A1}\begin{split} {y}_{\rm pert}\left({q}^{2}\right)=& {h\left(\frac{{m}_{c}}{{m}_{b}},\frac{{q}^{2}}{{m}_{b}^{2}}\right)\left(3{C}_{1}+{C}_{2}+3{C}_{3}+{C}_{4}+3{C}_{5}+{C}_{6}\right)}\\&-\frac{1}{2}h\left(1,\frac{{q}^{2}}{{m}_{b}^{2}}\right)(4{C}_{3}+4{C}_{4}+3{C}_{5}+ {C}_{6})\\&{-\frac{1}{2}h\left(0,\frac{{q}^{2}}{{m}_{b}^{2}}\right)\left({C}_{3}+3{C}_{4}\right)+\frac{2}{9}\left(3{C}_{3}+{C}_{4}+3{C}_{5}+{C}_{6}\right)}, \end{split} $

(A1) where
$\tag{A2} \begin{split} h\left(z,s\right)=&-\frac{8}{9}{\rm ln}\left(z\right)+\frac{8}{27}+\frac{4}{9}x-\frac{2}{9}\left(2+x\right)\sqrt{\left|1-x\right|}\\&\left\{\begin{array}{c}{\rm ln}\left|\frac{\sqrt{1-x}+1}{\sqrt{1-x}-1}\right|-{\rm i}\pi , x\equiv \frac{4{z}^{2}}{s'} < 1\\ 2{\rm arctan}\frac{1}{\sqrt{x-1}}, x\equiv \frac{4{z}^{2}}{s'}> 1\end{array}\right.\\ h\left(0,{s'}\right)=&{\frac{8}{27}-\frac{8}{9}{\rm ln}\frac{{m}_{b}}{\mu }-\frac{4}{9}{\rm ln}\left({s'}\right)+\frac{4}{9}{\rm i}\pi .} \end{split} $

(A2) Here,
$z=\frac{{m}_{c}}{{m}_{b}}, s=\frac{{q}^{2}}{{m}_{b}^{2}}$ .$\tag{A3} {y}_{\rm BW}\left({q}^{2}\right)=\frac{3\pi }{{\alpha }^{2}}\sum\limits_{{V}_{i}=J/\psi ,\psi }\frac{\varGamma \left({V}_{i}\to {l}^{+}{l}^{-}\right){m}_{{V}_{i}}}{{m}_{{V}_{i}}^{2}-{q}^{2}-{\rm i}{m}_{{V}_{i}}{\varGamma }_{{V}_{i}}}. $

(A3) The hadronic matrix elements for
${B}_{c}\to {D}_{s\left(d\right)}{\mu }^{+}{\mu }^{-}$ decays are written in terms of three invariant meson to meson transition form factors. These are$\tag{A4}\begin{split} \left\langle {{D_{s\left( d \right)}}{\rm{|}}{\bar{s}}{\gamma ^\mu }b{\rm{|}}{B_c}} \right\rangle =& {f_ + }\left( {{q^2}} \right)\left[ {p_{{B_c}}^\mu + p_{{D_{s\left( d \right)}}}^\mu - \frac{{M_{{B_c}}^2 - M_{{D_{s\left( d \right)}}}^2}}{{{q^2}}}{q^\mu }} \right] \\&+ {f_0}\left( {{q^2}} \right)\frac{{M_{{B_c}}^2 - M_{{D_{s\left( d \right)}}}^2}}{{{q^2}}}{q^\mu },\\ \left\langle {{D_{s\left( d \right)}}{\rm{|}}{\bar{s}}{\sigma ^{\mu \nu }}{q_\nu }b{\rm{|}}{B_c}} \right\rangle =& \frac{{{\rm i}{f_T}\left( {{q^2}} \right)}}{{{M_{{B_c}}} + {M_{{D_{s\left( d \right)}}}}}}\left[ {{q^2}\left( {p_{{B_c}}^\mu + p_{{D_{s\left( d \right)}}}^\mu } \right) }\right.\\&\left.- \left( {M_{{B_c}}^2 - M_{{D_{s\left( d \right)}}}^2} \right){q^\mu } \right]. \end{split} $

(A4) Similarly, for
$ {B}_{c}\to {D}_{s\left(d\right)}^{*}{\mu }^{+}{\mu }^{-}$ channels, the hadronic matrix elements can be parameterized in terms of seven invariant form factors. These are$\tag{A5} \begin{split} \left\langle {{D}_{s\left(d\right)}^*|{\bar{s}}{\gamma }^{\mu }b|{B}_{c}} \right\rangle=&\frac{2{\rm i}V\left({q}^{2}\right)}{{M}_{{B}_{c}}+{M}_{{\rm{D}}_{s\left(d\right)}^*}}{\epsilon}^{\mu \nu \rho \sigma }{\epsilon}_{\nu }^*{p}_{{B}_{{c}_{\rho }}}{p}_{{D}_{{s\left(d\right)}_{\sigma }}^*},\\ \left\langle {{D}_{s\left(d\right)}^*|{\bar{s}}{\gamma }^{\mu }{\gamma }_{5}b|{B}_{c}} \right\rangle=&2{M}_{{D}_{s\left(d\right)}^*}{A}_{0}\left({q}^{2}\right)\frac{{\epsilon}^*.q}{{q}^{2}}{q}^{\mu }+\left({M}_{{B}_{c}}+{M}_{{\rm{D}}_{s\left(d\right)}^*}\right){A}_{1}\left({q}^{2}\right)\left({\epsilon}^{*\mu }-\frac{{\epsilon}^*.q}{{q}^{2}}{q}^{\mu }\right)\\&{ -{A}_{2}\left({q}^{2}\right)\frac{{\epsilon}^*.q}{\left({M}_{{B}_{c}}+{M}_{{\rm{D}}_{s\left(d\right)}^*}\right)}\left[{p}_{{B}_{c}}^{\mu }+{p}_{{D}_{s}^*}^{\mu }-\frac{{M}_{{B}_{c}}^{2}-{M}_{{D}_{s\left(d\right)}^*}^{2}}{{q}^{2}}{q}^{\mu }\right],}\\ \left\langle {{D}_{s\left(d\right)}^*|{\bar{s}}{\sigma }^{\mu \nu }{q}_{\nu }b|{B}_{c}} \right\rangle=&2{T}_{1}\left({q}^{2}\right){\epsilon}^{\mu \nu \rho \sigma }{\epsilon}_{\nu }^*{p}_{{B}_{{c}_{\rho }}}{p}_{{D}_{{s\left(d\right)}_{\sigma }}^*},\\ \left\langle {{D}_{s\left(d\right)}^*|{\bar{s}}{\sigma }^{\mu \nu }{\gamma }_{5}{q}_{\nu }b|{B}_{c}} \right\rangle=&{T}_{2}\left({q}^{2}\right)\left[\left({M}_{{B}_{c}}^{2}-{M}_{{D}_{s\left(d\right)}^*}^{2}\right){\epsilon}^{*\mu }-{(\epsilon}^*.q)\left({p}_{{B}_{c}}^{\mu }+{p}_{{D}_{s\left(d\right)}^*}^{\mu }\right)\right]\\&{ +{T}_{3}\left({q}^{2}\right){(\epsilon}^*.q)\left[{q}^{\mu }-\frac{{q}^{2}}{{M}_{{B}_{c}}^{2}-{M}_{{D}_{s\left(d\right)}^*}^{2}}\left({p}_{{B}_{c}}^{\mu }+{p}_{{D}_{s\left(d\right)}^*}^{\mu }\right)\right],} \end{split} $

(A5) where
$ {q}^{\mu }={({p}_{B}-{p}_{{D}_{s\left(d\right)}},{p}_{{D}_{s\left(d\right)}^{*}})}^{\mu }$ is the four momentum transfer, and$ {\epsilon}_{\mu }$ is the polarization vector of the$ {D}_{s\left(d\right)}^{*}$ meson.The helicity amplitudes for the
$ {B}_{c}\to {D}_{s\left(d\right)}{l}^{+}{l}^{-}$ decay mode are written as$\tag{A6} \begin{split} { {H}_{\pm }^{\left(i\right)}}=&0,\\ {H}_{0}^{\left(1\right)}=&{\sqrt{\frac{\lambda }{{q}^{2}}}\left[{C}_{9}^{\rm eff}{f}_{+}\left({q}^{2}\right)+{C}_{7}^{\rm eff}\frac{2{m}_{b}}{{M}_{{B}_{c}}+{M}_{{D}_{s\left(d\right)}}}{f}_{T}\left({q}^{2}\right)\right], }\\ {H}_{0}^{\left(2\right)}=&{\sqrt{\frac{\lambda }{{q}^{2}}}{\rm{C}}_{10}{f}_{+}\left({q}^{2}\right),}\\ {H}_{\rm{t}}^{\left(1\right)}=&{\frac{{M}_{{B}_{c}}^{2}-{M}_{{D}_{s\left(d\right)}}^{2}}{{q}^{2}}{C}_{9}^{\rm eff}{f}_{0}\left({q}^{2}\right),}\\ {H}_{\rm{t}}^{\left(2\right)}=&{\frac{{M}_{{B}_{c}}^{2}-{M}_{{D}_{s\left(d\right)}}^{2}}{{q}^{2}}{\rm{C}}_{10}{f}_{0}\left({q}^{2}\right).} \end{split} $

(A6) Similarly, for
$ {B}_{c}\to {D}_{s\left(d\right)}^{*}{l}^{+}{l}^{-}$ modes, the hadronic helicity amplitudes are$\tag{A7} \begin{split} {H}_{\pm }^{\left(1\right)}=&{-\left({M}_{{B}_{c}}^{2}-{M}_{{D}_{s\left(d\right)}^*}^{2}\right)\left[{C}_{9}^{\rm eff}\frac{{A}_{1}\left({q}^{2}\right)}{\left({M}_{{B}_{c}}-{M}_{{\rm{D}}_{s\left(d\right)}^*}\right)}+\frac{2{m}_{b}}{{q}^{2}}{C}_{7}^{\rm eff}{T}_{2}\left({q}^{2}\right)\right]} {\pm \sqrt{\lambda }\left[{C}_{9}^{\rm eff}\frac{V\left({q}^{2}\right)}{\left({M}_{{B}_{c}}+{M}_{{\rm{D}}_{s\left(d\right)}^*}\right)}+\frac{2{m}_{b}}{{q}^{2}}{C}_{7}^{\rm eff}{T}_{1}\left({q}^{2}\right)\right],}\\ {H}_{\pm }^{\left(2\right)}=&{{\rm{C}}_{10}\left[-\left({M}_{{B}_{c}}+{M}_{{\rm{D}}_{s\left(d\right)}^*}\right){A}_{1}\left({q}^{2}\right)\right]\pm \frac{\sqrt{\lambda }}{\left({M}_{{B}_{c}}+{M}_{{\rm{D}}_{s\left(d\right)}^*}\right)}{\rm{C}}_{10}V\left({q}^{2}\right),}\\ {H}_{0}^{\left(1\right)}=& {-\frac{1}{2{M}_{{D}_{s\left(d\right)}^*}\sqrt{{q}^{2}}}\left\{{{C}_{9}^{\rm eff}\left[\left({M}_{{B}_{c}}^{2}-{M}_{{D}_{s\left(d\right)}^*}^{2}-{q}^{2}\right)\left({M}_{{B}_{c}}+{M}_{{\rm{D}}_{s\left(d\right)}^*}\right){A}_{1}\left({q}^{2}\right)-\frac{\lambda }{{M}_{{B}_{c}}+{M}_{{\rm{D}}_{s\left(d\right)}^*}}{A}_{2}\left({q}^{2}\right)\right]} \right.}\\ &+{\left. { 2{m}_{b}{C}_{7}^{\rm eff}\left[\left({M}_{{B}_{c}}^{2}+3{M}_{{D}_{s\left(d\right)}^*}^{2}-{q}^{2}\right){T}_{2}\left({q}^{2}\right)-\frac{\lambda }{{M}_{{B}_{c}}^{2}-{M}_{{D}_{s\left(d\right)}^*}^{2}}{T}_{3}\left({q}^{2}\right)\right]}\right\},}\\ {H}_{0}^{\left(2\right)}=&-\frac{1}{2{M}_{{D}_{s\left(d\right)}^*}\sqrt{{q}^{2}}}{\rm{C}}_{10} \left[\left({M}_{{B}_{c}}^{2}-{M}_{{D}_{s\left(d\right)}^*}^{2}-{q}^{2}\right)\left({M}_{{B}_{c}}+{M}_{{\rm{D}}_{s\left(d\right)}^*}\right){A}_{1}\left({q}^{2}\right){} {-\frac{\lambda }{{M}_{{B}_{c}}+{M}_{{\rm{D}}_{s\left(d\right)}^*}}{A}_{2}\left({q}^{2}\right)}\right],\\ {H}_{\rm{t}}^{\left(1\right)}=&{\sqrt{\frac{\lambda }{{q}^{2}}}{C}_{9}^{\rm eff}{A}_{0}\left({q}^{2}\right),}\\ {H}_{\rm{t}}^{\left(2\right)}=&{\sqrt{\frac{\lambda }{{q}^{2}}}{\rm{C}}_{10}{A}_{0}\left({q}^{2}\right), } \end{split} $

(A7) where
$\lambda ={M}_{{B}_{c}}^{4}+{M}_{{D}_{s\left(d\right)}^{\left(*\right)}}^{4}+{q}^{4}-2\left({M}_{{B}_{c}}^{2}{M}_{{D}_{s\left(d\right)}^{\left(*\right)}}^{2}+{M}_{{D}_{s\left(d\right)}^{\left(*\right)}}^{2}{q}^{2}+{M}_{{B}_{c}}^{2}{q}^{2}\right). $

Investigation of rare semileptonic ${{B}_{c}\to \left({D}_{s,d}^{\left(*\right)}\right){\mu }^{+}{\mu }^{-}} $ decays with non-universal Z′ effect
- Received Date: 2020-02-09
- Available Online: 2020-07-01
Abstract: We analyze different decay observables of semileptonic decays







 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: