-
The two-Higgs-doublet model (2HDM) [1] is a popular extension of the SM that introduces another
$ SU(2)_L $ Higgs doublet, which contains neutral CP-even Higgs bosons h and H, a neutral pseudoscalar A, and charged Higgs$ H^{\pm} $ . Four typical 2HDMs have absent flavor changing neutral currents at the tree level, namely type-I [2, 3], type II [2, 4], lepton-specific models, and flipped models [5–8]. In the type II model, the Yukawa couplings of leptons and down-type quarks can be enhanced by a factor$ \tan\beta $ . Therefore, the flavor observables and the LHC search for Higgs places stricter restrictions to the type II model than to the other three models. In the type II 2HDM, the 125 GeV Higgs can have a wrong sign Yukawa coupling besides an SM-like coupling. In comparison with the SM, at least one of the Yukawa couplings of the 125 GeV Higgs has an opposite sign in the couplings of gauge bosons, which was extensively studied in Refs. [9–24].In beginning of 2017, we used the LHC Higgs data available at that time to explore the parameter space of type II 2HDM, and found that the
$ H/A\to \tau^+\tau^- $ and$ A\to hZ $ modes can place strong restrictions on the parameter space of the wrong sign Yukawa coupling [22]. Recently, Refs. [23, 24] examined the parameter space with degenerate heavy Higgs masses in the framework of this model. In this study, we re-examine the wrong sign Yukawa coupling in the type II 2HDM and extensively scan over the parameter space by considering recent ATLAS and CMS Higgs data.Our paper is organized as follows. In Sec. 2, we briefly introduce the type II 2HDM. Detailed numerical calculations are implemented in Sec. 3. We display the allowed parameter space by considering relevant theoretical and experimental restrictions in Sec. 4. In Sec. 5, we provide our conclusions.
-
The scalar potential with a softly broken discrete
$ Z_2 $ symmetry is given by [25]$ \begin{split} {\rm{V}} =& m_{11}^2(\Phi _1^\dagger {\Phi _1}) + m_{22}^2(\Phi _2^\dagger {\Phi _2}) - \left[ {m_{12}^2(\Phi _1^\dagger {\Phi _2} + {\rm{h}}.{\rm{c}}.)} \right]\\ & + \frac{{{\lambda _1}}}{2}{(\Phi _1^\dagger {\Phi _1})^2} + \frac{{{\lambda _2}}}{2}{(\Phi _2^\dagger {\Phi _2})^2} + {\lambda _3}(\Phi _1^\dagger {\Phi _1})(\Phi _2^\dagger {\Phi _2}) \\&+ {\lambda _4}(\Phi _1^\dagger {\Phi _2})(\Phi _2^\dagger {\Phi _1}) + \left[ {\frac{{{\lambda _5}}}{2}{{(\Phi _1^\dagger {\Phi _2})}^2} + {\rm{h}}.{\rm{c}}.} \right]. \end{split}$

(1) We focus on the CP-conserving case, where all
$ \lambda_i $ and$ m_{12}^2 $ are real. The two complex Higgs doublets have the hypercharge$ Y = 1 $ :$\begin{split} \Phi_1 =& \left(\begin{array}{c} \phi_1^+ \\ \dfrac{1}{\sqrt{2}}\,(v_1+\phi_1^0+ia_1) \end{array}\right)\,,\\ \Phi_2 =& \left(\begin{array}{c} \phi_2^+ \\ \dfrac{1}{\sqrt{2}}\,(v_2+\phi_2^0+ia_2) \end{array}\right). \end{split}$

(2) In the above formula,
$ v_1 $ and$ v_2 $ are the electroweak vacuum expectation values (VEVs) with$v^2 = v^2_1 + v^2_2 = $ $ (246\; \rm GeV)^2 $ and$ \tan\beta = v_2 /v_1 $ . After breaking of the spontaneous electroweak symmetry, we obtain five physical Higgs particles, two neutral CP-even h and H, one neutral pseudoscalar A, and a pair of charged scalars$ H^{\pm} $ .The Yukawa interactions are given as
$ - {\cal L} = Y_{u2}\,\overline{Q}_L \, \tilde{{ \Phi}}_2 \,u_R +\,Y_{d1}\, \overline{Q}_L\,{\Phi}_1 \, d_R\, + \, Y_{\ell 1}\,\overline{L}_L \, {\Phi}_1\,e_R+\, {\rm{{h.c.}}}\,, $

(3) where
$ Q_L^T = (u_L\,,d_L) $ ,$ L_L^T = (\nu_L\,,l_L) $ , and$ \widetilde\Phi_{1,2} = i\tau_2 \Phi_{1,2}^* $ .$ Y_{u2} $ ,$ Y_{d1} $ and$ Y_{\ell 1} $ are$ 3 \times 3 $ matrices.The neutral Higgs Yukawa couplings normalized to the SM are as follows.
$ \begin{split} & y_{h}^{f_i} = \left[\sin(\beta-\alpha)+\cos(\beta-\alpha)\kappa_f\right], \\ &y_{H}^{f_i} = \left[\cos(\beta-\alpha)-\sin(\beta-\alpha)\kappa_f\right], \\ &y_{A}^{f_i} = -i\kappa_f\; {({\rm{for}}\; {\rm{u}})},\; \; \; \; y_{A}^{f_i} = i \kappa_f\; {({\rm{for}}\; {\rm{d}},\; \ell)},\\ &{\rm{with}}\; \kappa_d = \kappa_\ell\equiv-\tan\beta,\; \; \; \kappa_u\equiv 1/\tan\beta. \end{split} $

(4) The Yukawa interactions of the charged Higgs are given as,
$\begin{split} {\cal{L}}_Y =& - \frac{\sqrt{2}}{v}\, H^+\, \Big\{\bar{u}_i \left[\kappa_d\,(V_{\rm CKM})_{ij}\; m_{dj} P_R - \kappa_u\,m_{ui}\; (V_{\rm CKM})_{ij} \; P_L\right]d_j\\& + \kappa_\ell\,\bar{\nu} m_\ell P_R \ell \Big\}+ {\rm h.c.}, \end{split}$

(5) where
$ i,j = 1,2,3 $ .The neutral Higgs couplings with gauge bosons normalized to the SM are
$ y^{V}_h = \sin(\beta-\alpha),\; \; \; y^{V}_H = \cos(\beta-\alpha), $

(6) with V denoting W or Z.
In type II 2HDM, the SM-like Higgs has not only the SM-like coupling, but also the wrong sign Yukawa coupling,
$ \begin{array}{l} y_h^{{f_i}}\; \times \;y_h^V > 0\;{\rm{for}}\;{\rm{SM - like}}\;{\rm{coupling}},\;\;\;\\ y_h^{{f_i}}\; \times \;y_h^V < 0\;{\rm{for}}\;{\rm{wrong}}\;{\rm{sign}}\;{\rm{Yukawa}}\;{\rm{coupling}}. \end{array} $

(7) In case of the SM-like coupling, the 125 GeV Higgs couplings are very close to those in the SM, which has an alignment limit. Here, we introduce the wrong sign Yukawa coupling. The absolute values of
$ y_h^{f_i} $ and$ y^{V}_h $ should be close to 1.0 because of the restrictions in 125 GeV Higgs signal data. Hence, we obtain$\begin{split} & y_h^{{f_i}} = - 1 + \epsilon,\;\;y_h^V \simeq 1 - 0.5{\cos ^2}(\beta - \alpha )\;\;{\rm{for}}\;\\&\sin (\beta - \alpha ) > 0\;{\rm{and}}\;\cos (\beta - \alpha ) > 0\;,\\ &y_h^{{f_i}} = 1 - \epsilon,\;\;y_h^V \simeq - 1 + 0.5{\cos ^2}(\beta - \alpha )\;\;{\rm{for}}\;\\&\sin (\beta - \alpha ) < 0\;{\rm{and}}\;\cos (\beta - \alpha ) > 0. \end{split} $

(8) Here,
$ \mid\epsilon\mid $ and$ \mid\cos(\beta-\alpha)\mid $ are significantly less than 1. From Eq. (4), we can obtain$\begin{split} &{\kappa _f} = \frac{{ - 2 + \varepsilon + 0.5\cos {{(\beta - \alpha )}^2}}}{{\cos (\beta - \alpha )}} < < - 1\;{\rm{for}}\;\\&\sin (\beta - \alpha ) > 0\;{\rm{and}}\;\cos (\beta - \alpha ) > 0\;,\\ &{\kappa _f} = \frac{{2 - \varepsilon - 0.5\cos {{(\beta - \alpha )}^2}}}{{\cos (\beta - \alpha )}} > > 1\;{\rm{for}}\\&\sin (\beta - \alpha ) < 0\;{\rm{and}}\;\cos (\beta - \alpha ) > 0\;. \end{split} $

(9) In type II 2HDM, the constraints of the B-meson and
$ R_b $ require$ \tan\beta $ to be greater than 1, which leads to$ \kappa_d < -1 $ ,$ \kappa_\ell < -1 $ , and$ 0 < \kappa_u < 1 $ . Therefore, there is no wrong sign Yukawa coupling for the up-type quark. The wrong sign Yukawa couplings of the down-type quark and lepton for$ \sin(\beta-\alpha) > 0 $ and$ \cos(\beta-\alpha) >0 $ may exist. Because of the factor "–2" in the numerator in Eq. (9),$ \cos(\beta-\alpha) $ and$ \tan\beta $ in the wrong sign Yukawa coupling region are greater than those in the SM-like coupling region. -
We choose the light CP-even Higgs boson h as the SM-like Higgs with the mass of
$ 125 $ GeV. The branching ratio of$ b \to s\gamma $ places stringent restrictions on the charged Higgs mass of the type II 2HDM, which requires$ m_{H^{\pm}} > 570 $ GeV [26].In the calculation, we take account the following constraints and observables:
$ (1) $ The electroweak precision data and theoretical constraints: We use the$ \textsf{2HDMC} $ [27] to consider the theoretical constraints from the vacuum stability, unitarity and perturbativity, and calculate the oblique parameters (S, T, U). We take the recent fit results for S, T, U in Ref. [28],$ S = 0.02\pm 0.10, \; \; T = 0.07\pm 0.12,\; \; U = 0.00 \pm 0.09, $

(10) with correlation coefficients,
$ \rho_{ST} = 0.89, \; \; \rho_{SU} = −0.54, \; \; \rho_{TU} = −0.83. $

(11) $ (2) $ The heavy-flavor observables and$ R_b $ constraints: We use$ \textsf{SuperIso-3.4} $ [29] to calculate the branching ratio of$ B\to X_s\gamma $ .$ \Delta m_{B_s} $ is calculated following the formulas of Ref. [30]. Furthermore, we consider the$ R_b $ constraints of bottom quarks in Z decays, which are calculated following the formulas of Refs. [31, 32]. Recently, the$ R_b $ observable was also considered in some studies on the 2HDM [33, 34]$ (3) $ The 125 GeV Higgs signal data: We use the version 2.0 of$ \textsf{Lilith} $ [35] to perform the calculation of$ \chi^2 $ for the 125 GeV Higgs signal data combining the LHC run-I and run-II data (up to datasets of$ 36 {\rm fb}^{-1} $ ). We are particularly concerned with the surviving samples for$ \chi^2-\chi^2_{\rm min} \leqslant 6.18 $ , where$ \chi^2_{\rm min} $ is the minimum of$ \chi^2 $ . These samples are within the$ 2\sigma $ range in the two-dimensional plane of model parameters.$ (4) $ The LHC search for additional Higgs bosons: We use the$ \textsf{HiggsBounds-4.3.1} $ [36, 37] to perform the exclusion limits from the Higgs search at LEP at 95% confidence level.At the LHC run-I and run-II, the ATLAS and CMS searched the additional Higgs via its decay into various SM modes and some exotic channels. Because of the destructive interference contributions to
$ gg\to A $ production, which arise from the top-quark loop and the bottom-quark loop in the type II 2HDM, the cross-section decreases with the increasing$ \tan\beta $ , and reaches a minimum value for a moderate$ \tan\beta $ , which is dominated by the bottom-quark loop for a large enough value of$ \tan\beta $ . The cross-section of$ gg\to H $ production not only depends on$ \tan\beta $ and$ m_H $ , but also$ \sin(\beta-\alpha) $ . We calculate the cross-sections for A and H in the gluon fusion and$ b\bar{b} $ -associated production at NNLO in QCD via$ \textsf{SusHi} $ [38]. The cross-sections of H via the vector boson fusion process are derived from the data of the LHC Higgs Cross Section Working Group [39]. We use the$ \textsf{2HDMC} $ to calculate the branching ratios of various decay channels of A and H. In Table 1 and Table 2, we show a complete list of the additional Higgs searches considered in this study. When 1$ \leqslant \tan\beta \leqslant 30 $ , the heavy charged scalar searches at LHC cannot impose restrictions on the model for$ m_{H^{\pm}}>500 $ GeV [40]. Thus, we do not include the heavy charged Higgs search.Channel Experiment/TeV Mass range/GeV Luminosity/fb−1 $ gg/b\bar{b}\to H/A \to \tau^{+}\tau^{-} $ 

ATLAS 8 [41] 90-1000 19.5-20.3 $ gg/b\bar{b}\to H/A \to \tau^{+}\tau^{-} $ 

CMS 8 [42] 90-1000 19.7 $ gg/b\bar{b}\to H/A \to \tau^{+}\tau^{-} $ 

ATLAS 13 [43] 200-1200 13.3 $ gg/b\bar{b}\to H/A \to \tau^{+}\tau^{-} $ 

CMS 13 [44] 90-3200 12.9 $ gg\to H/A \to \tau^{+}\tau^{-} $ 

CMS 13 [45] 200-2250 36.1 $ b\bar{b}\to H/A \to \tau^{+}\tau^{-} $ 

CMS 13 [45] 200-2250 36.1 $ b\bar{b}\to H/A \to \tau^{+}\tau^{-} $ 

CMS 8 [46] 25-80 19.7 $ b\bar{b}\to H/A \to \mu^{+}\mu^{-} $ 

CMS 8 [47] 25-60 19.7 $ pp\to H/A \to \gamma\gamma $ 

ATLAS 13 [48] 200-2400 15.4 $ gg\to H/A \to \gamma\gamma $ 

CMS 8+13 [49] 500-4000 12.9 $ gg\to H/A \to \gamma\gamma $ +

$ t\bar{t}H/A\; (H/A\to \gamma\gamma) $ 

CMS 8 [50] 80-110 19.7 $ gg\to H/A \to \gamma\gamma $ +

$ t\bar{t}H/A\; (H/A\to \gamma\gamma) $ 

CMS 13 [50] 70-110 35.9 $ VV\to H \to \gamma\gamma $ +

$ VH\; (H\to \gamma\gamma) $ 

CMS 8 [50] 80-110 19.7 $ VV\to H \to \gamma\gamma $ +

$ VH\; (H\to \gamma\gamma) $ 

CMS 13 [50] 70-110 35.9 $ gg/VV\to H\to W^{+}W^{-} $ 

ATLAS 8 [51] 300-1500 20.3 $ gg/VV\to H\to W^{+}W^{-}\; (\ell\nu\ell\nu) $ 

ATLAS 13 [52] 300-3000 13.2 $ gg\to H\to W^{+}W^{-}\; (\ell\nu qq) $ 

ATLAS 13 [53] 500-3000 13.2 $ gg/VV\to H\to W^{+}W^{-}\; (\ell\nu qq) $ 

ATLAS 13 [54] 200-3000 36.1 $ gg/VV\to H\to W^{+}W^{-}\; (e\nu \mu\nu) $ 

ATLAS 13 [55] 200-3000 36.1 $ gg/VV\to H\to ZZ $ 

ATLAS 8 [56] 160-1000 20.3 $ gg\to H \to ZZ(\ell \ell \nu \nu) $ 

ATLAS 13 [57] 300-1000 13.3 $ gg\to H\to ZZ(\nu \nu qq) $ 

ATLAS 13 [58] 300-3000 13.2 $ gg/VV\to H\to ZZ(\ell \ell qq) $ 

ATLAS 13 [58] 300-3000 13.2 $ gg/VV\to H\to ZZ(\ell\ell\ell\ell) $ 

ATLAS 13 [59] 200-3000 14.8 $ gg/VV\to H\to ZZ(\ell\ell\ell\ell+\ell\ell\nu\nu) $ 

ATLAS 13 [60] 200-2000 36.1 $ gg/VV\to H\to ZZ(\nu\nu qq+\ell\ell qq) $ 

ATLAS 13 [61] 300-5000 36.1 Table 1. Upper bounds on production cross-section times branching ratio of
$ \tau^+\tau^- $ ,$ \mu^+\mu^- $ ,$ \gamma\gamma $ ,$ WW $ , and$ ZZ $ for H and$ A $ searches at 95% C.L..Channel Experiment/TeV Mass range/GeV Luminosity /fb−1 $ gg\to H\to hh \to (\gamma \gamma) (b \bar{b}) $ 

CMS 8 [62] 250-1100 19.7 $ gg\to H\to hh \to (b\bar{b}) (b\bar{b}) $ 

CMS 8 [63] 270-1100 17.9 $ gg\to H\to hh \to (b\bar{b}) (\tau^{+}\tau^{-}) $ 

CMS 8 [64] 260-350 19.7 $ gg \to H\to hh \to b\bar{b}b\bar{b} $ 

ATLAS 13 [65] 300-3000 13.3 $ gg \to H\to hh \to b\bar{b}b\bar{b} $ 

CMS 13 [66] 750-3000 35.9 $ gg \to H\to hh \to (b\bar{b}) (\tau^{+}\tau^{-}) $ 

CMS 13 [67] 250-900 35.9 $ pp \to H\to hh $ 

CMS 13 [68] 250-3000 35.9 $ gg\to A\to hZ \to (\tau^{+}\tau^{-}) (\ell \ell) $ 

CMS 8 [64] 220-350 19.7 $ gg\to A\to hZ \to (b\bar{b}) (\ell \ell) $ 

CMS 8 [69] 225-600 19.7 $ gg\to A\to hZ\to (\tau^{+}\tau^{-}) Z $ 

ATLAS 8 [70] 220-1000 20.3 $ gg\to A\to hZ\to (b\bar{b})Z $ 

ATLAS 8 [70] 220-1000 20.3 $ gg/b\bar{b}\to A\to hZ\to (b\bar{b})Z $ 

ATLAS 13 [71] 200-2000 36.1 $ gg/b\bar{b}\to A\to hZ\to (b\bar{b})Z $ 

CMS 13 [72] 225-1000 35.9 $ gg\to h \to AA \to \tau^{+}\tau^{-}\tau^{+}\tau^{-} $ 

ATLAS 8 [73] 4-50 20.3 $ pp\to h \to AA \to \tau^{+}\tau^{-}\tau^{+}\tau^{-} $ 

CMS 8 [74] 5-15 19.7 $ pp\to h \to AA \to (\mu^{+}\mu^{-})(b\bar{b}) $ 

CMS 8 [74] 25-62.5 19.7 $ pp\to h \to AA \to (\mu^{+}\mu^{-})(\tau^{+}\tau^{-}) $ 

CMS 8 [74] 15-62.5 19.7 $ pp\to h \to AA \to (b\bar{b})(\tau^{+}\tau^{-}) $ 

CMS 13 [75] 15-60 35.9 $ pp\to h \to AA \to \tau^{+}\tau^{-}\tau^{+}\tau^{-} $ 

CMS 13 [76] 4-15 35.9 $ gg\to A(H)\to H(A)Z\to (b\bar{b}) (\ell \ell) $ 

CMS 8 [77] 40-1000 19.8 $ gg\to A(H)\to H(A)Z\to (\tau^{+}\tau^{-}) (\ell \ell) $ 

CMS 8 [77] 20-1000 19.8 Table 2. Upper bounds on production cross-section times branching ratio for channels of Higgs-pair and a Higgs production in association with Z at 95% C.L..
For the
$ A\to hZ $ channel, the CMS collaboration presented the result of$ h \to \tau^+\tau^- $ at the 13 TeV LHC with an integrated luminosity of 35.9 fb-1 in Ref. [78]. However, compared to the results of Refs. [71, 72], the decay width$ \Gamma_A/m_A $ corresponding to the bound of Ref. [78] is not clearly given. Therefore, we do not include the experimental bound of$ A\to hZ\to (\tau^+\tau^-)Z $ channel from Ref. [78]. -
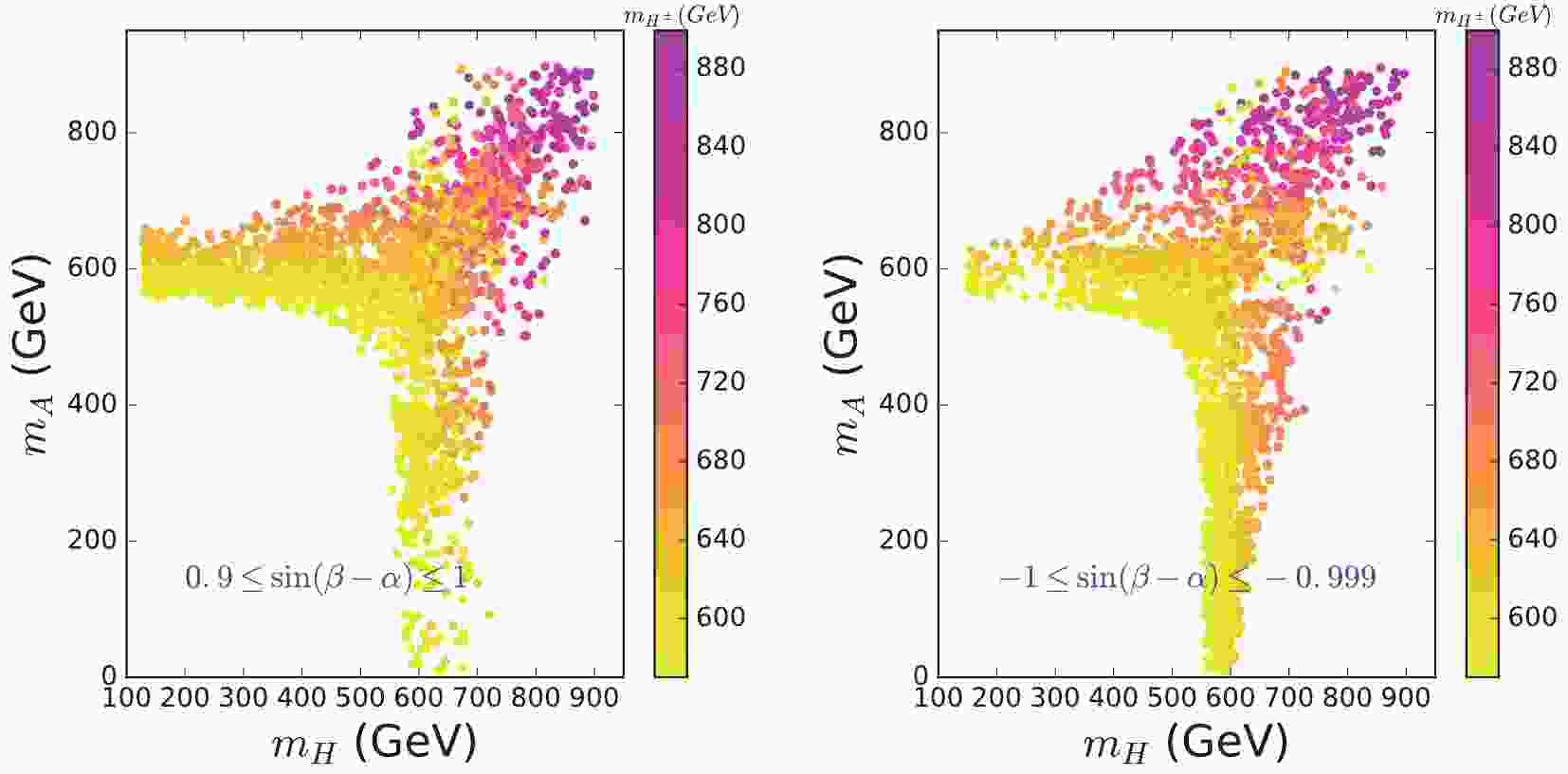
In Fig. 1, we display the permitted
$ m_A $ and$ m_H $ under the constraints of theory and oblique parameters. Since the branching fraction of$ b \to s\gamma $ imposes a lower bound on the mass of$ H^\pm $ ,$ m_{H^{\pm}} > 570 $ GeV [26], we take 570 GeV$ \leqslant m_{H^{\pm}}\leqslant $ 900 GeV. When either$ m_A $ or$ m_H $ are very close to$ m_{H^{\pm}} $ , the contributions of 2HDM to oblique parameters are considerably suppressed, and the other mass is permitted to have a large mass splitting with$ m_{H^{\pm}} $ . Therefore, as shown in Fig. 1, it is not feasible that both$ m_A $ and$ m_H $ are less than 480 GeV, and at least one of the A or H is required to have a greater mass. When either$ m_A $ or$ m_H $ is approximately 600 GeV, the other mass may have a large mass range, particularly for a low mass. However, when$ m_H $ is significantly larger than 600 GeV and even$ m_H = m_{H^{\pm}} $ ,$ m_A $ cannot be very small. The main reason is due to the requirements of vacuum stability,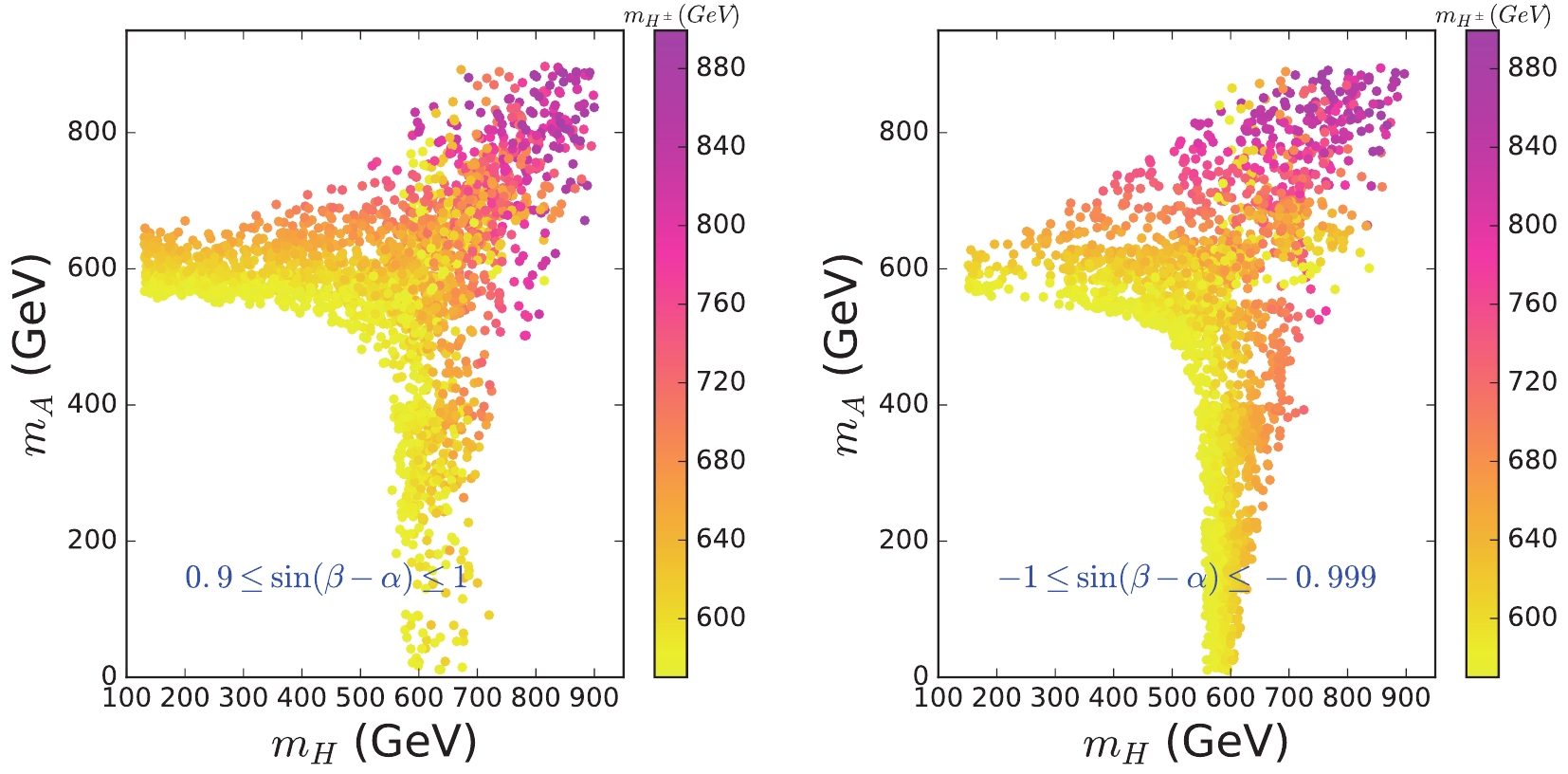
Figure 1. (color online) Scatter plots of
$ m_A $ and$ m_H $ satisfying constraints of vacuum stability, unitarity, perturbativity, and oblique parameters for 570$ \leqslant m_{H^{\pm}}\leqslant $ 900 GeV.$ \lambda_1>0,\; \; \lambda_2>0,\; \; \lambda_3>-\sqrt{\lambda_1\lambda_2}\,,\; \; \lambda_3+\lambda_4-\mid\lambda_5\mid>-\sqrt{\lambda_1\lambda_2}\,. $

(12) To better understand this point, we assume a very small
$ \cos(\beta-\alpha) $ and obtain the following relations [18],$ \begin{split} v^2 \lambda_1 & = m_h^2 - \frac{t_\beta\,(m_{12}^2 -m_H^2 s_\beta c_\beta ) }{ c_\beta^2}\,, \\ v^2 \lambda_2 & = m_h^2 - \frac{ (m_{12}^2 -m_H^2 s_\beta c_\beta) }{ t_\beta s_\beta^2 }\,,\\ v^2 \lambda_3 & = m_h^2 + 2 m_{H^{\pm}}^2 - 2m_H^2 - \frac{(m_{12}^2 -m_H^2 s_\beta c_\beta)}{ s_\beta c_\beta }\,,\\ v^2 \lambda_4 & = m_A^2- 2 m_{H^{\pm}}^2 + m_H^2+ \frac{ (m_{12}^2 -m_H^2 s_\beta c_\beta)}{ s_\beta c_\beta }\,,\\ v^2 \lambda_5 & = m_H^2 - m_A^2+ \frac{ (m_{12}^2 -m_H^2 s_\beta c_\beta)}{ s_\beta c_\beta } \,, \end{split} $

(13) with
$ t_\beta\equiv\tan\beta $ ,$ s_\beta\equiv\sin\beta $ , and$ c_\beta\equiv\cos\beta $ . The first two requirements in Eq. (12) are simultaneously satisfied for$ m^2_{12}- m^2_H s_\beta c_\beta $ $ \to $ 0, and the last two are respectively satisfied for$ m_h^2 + m_{H^{\pm}}^2 - m_H^2 > 0\,, \quad \quad m_h^2 + m_{A}^2 - m_H^2 > 0\,. $

(14) The right relation of Eq. (14) implies that
$ m_A $ cannot be very small for a very large$ m_H $ . Eq. (14) is obtained in the two limits,$ \cos(\beta-\alpha)\to 0 $ and$ m^2_{12}- m^2_H s_\beta c_\beta\to 0 $ . In this study, we perform an exact numerical calculation on the requirements of vacuum stability. The bounds of Eq. (14) can be appropriately loosened by tunning$ \cos(\beta-\alpha) $ ,$ t_\beta $ , and$ m_{12}^2 $ .Using the survival samples in Fig. 1 and imposing the restrictions of the 125 GeV Higgs signal data, we obtain the scatter plots of
$ \tan\beta $ and$ \sin(\beta-\alpha) $ in Fig. 2. Fig. 2 shows that the 125 GeV Higgs data can provide very stringent constraints on$ \tan\beta $ and$ \sin(\beta-\alpha) $ . As discussed above, the Yukawa coupling with the wrong sign can be achieved only for$ \sin(\beta-\alpha) > 0 $ . In the left panel of Fig. 2,$ \tan\beta $ and$ \sin(\beta-\alpha) $ are respectively required to be larger than 5.0 and as low as 0.94 in case of wrong sign coupling. When the SM-like coupling is applied,$ \sin(\beta-\alpha) $ is restricted to exist in two very narrow bands of$ 0.994\sim1.0 $ and$ -1.0\sim-0.99993 $ , which can be seen in the left and right panels of Fig. 2. For a given$ \sin(\beta-\alpha) $ ,$ \tan\beta $ is imposed a lower limit in case of the Yukawa coupling with wrong sign, and it is required to be as low as 1.0 in case of the SM-like Higgs coupling.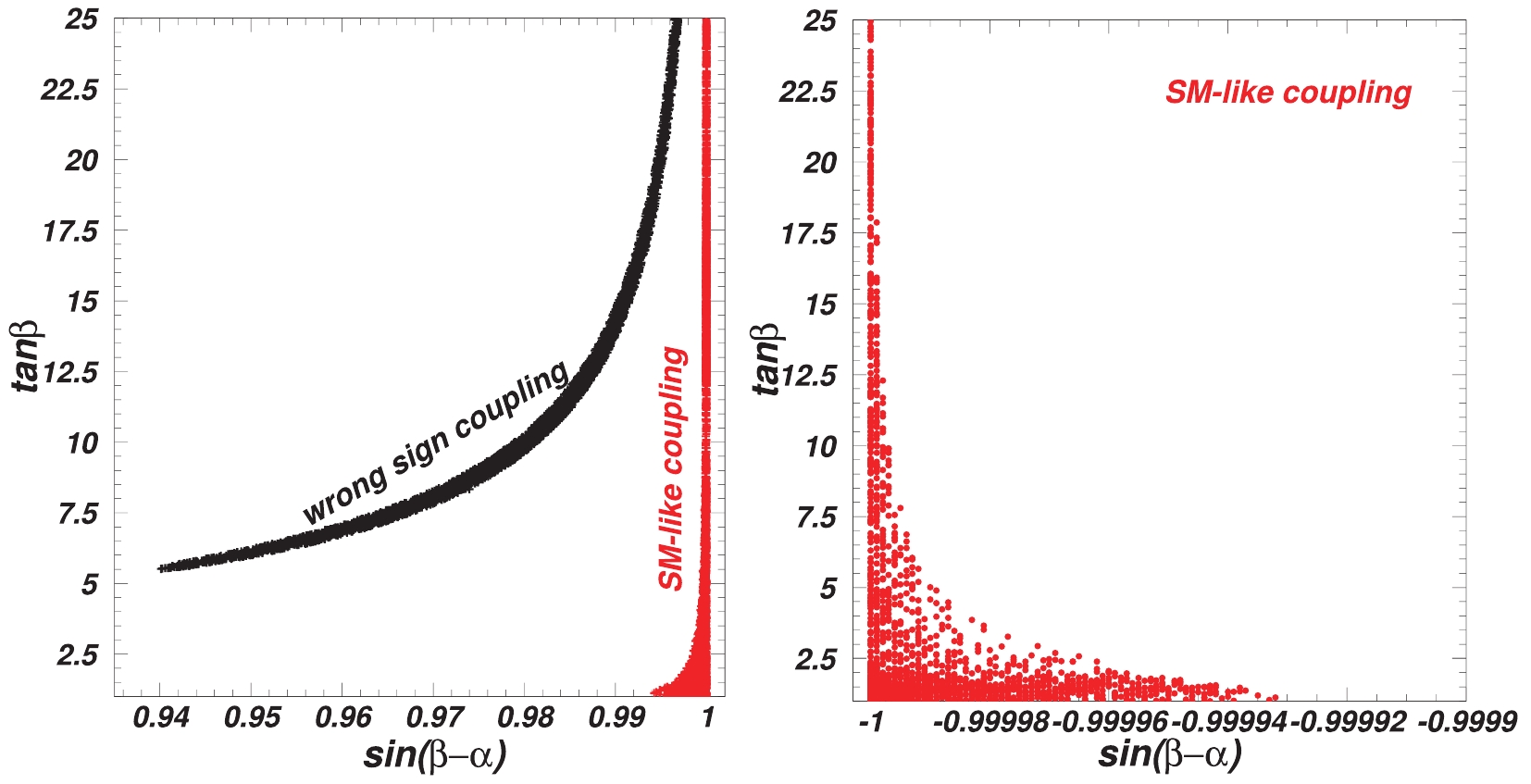
Figure 2. (color online) Scatter plots of
$ \sin(\beta-\alpha) $ and$ \tan\beta $ satisfying constraints of theory, oblique parameters, and 125 GeV Higgs signal data.To explicitly show the dependence of
$ m_A $ ($ m_H $ ) on the other parameters and the specific excluded parameter space from each channel, we do not simultaneously scan over$ m_A $ and$ m_H $ . In the following discussions, considering the allowed Higgs mass spectrum shown in Fig. 1, we will respectively set$ m_A $ or$ m_H $ as 600 GeV, and the other can have a wide mass range, especially for the low mass. Because heavy Higgs can easily avoid the restrictions of the LHC direct search easily, the Higgs with a moderate and low mass is more interesting. We scan the parameters for wrong sign Yukawa coupling in the following two scenarios:$\begin{split} &0.93 \leqslant \sin (\beta - \alpha ) \leqslant 1.0,\;\;1 \leqslant \tan \beta \leqslant 25,\;\\&570\;{\rm{GeV}} \leqslant \;{m_{{H^ \pm }}} \leqslant 900\;{\rm{GeV}},\\ &{\rm{scenario}}\;{\rm{A}}:\;\;{m_H} = 600\;{\rm{GeV}},\;\;10\;{\rm{GeV}} \leqslant {m_A} \leqslant \;900\;{\rm{GeV}},\\ &{\rm{scenario}}\;{\rm{B}}:\;\;{m_A} = 600\;{\rm{GeV}},\;\;150\;{\rm{GeV}} \leqslant {m_H} \leqslant \;900\;{\rm{GeV}}. \end{split}$

(15) The free parameter
$ m_{12}^2 $ is adjusted to satisfy the theoretical constraint. Here, we employ the conventional method [27], 0$ \leqslant\beta\leqslant \dfrac{\pi}{2} $ and$ -\dfrac{\pi}{2}\leqslant\beta-\alpha\leqslant \dfrac{\pi}{2} $ . Namely,$0 \leqslant $ $ \cos(\beta-\alpha) \leqslant 1 $ and$ -1 \leqslant \sin(\beta-\alpha) \leqslant 1 $ . -
We extract the permitted parameter space of scenario A after considering the joint constraints from pre-LHC (i.e., theoretical constraints, electroweak precision data, flavor observables,
$ R_b $ , and exclusions from the search for Higgs at LEP), 125 GeV Higgs signal data, and the search for additional Higgs particles at the LHC. The surviving samples are projected on the planes of$ m_A $ versus$ \tan\beta $ and$ m_A $ versus$ \sin(\beta-\alpha) $ in Fig. 3. In case of the wrong sign Yukawa coupling, the restrictions mentioned above require$ \tan\beta > 5 $ . For this range of$ \tan\beta $ , the cross-section of scalar A in the gluon fusion production is considerably suppressed, and all samples are favored by the$ A\to \gamma\gamma $ and$ A\to HZ $ modes. Because the 125 GeV Higgs signal data place large restrictions on the branching ratio of$ h\to AA $ , the LHC search for$ h\to AA $ cannot impose constraints on the parameter space.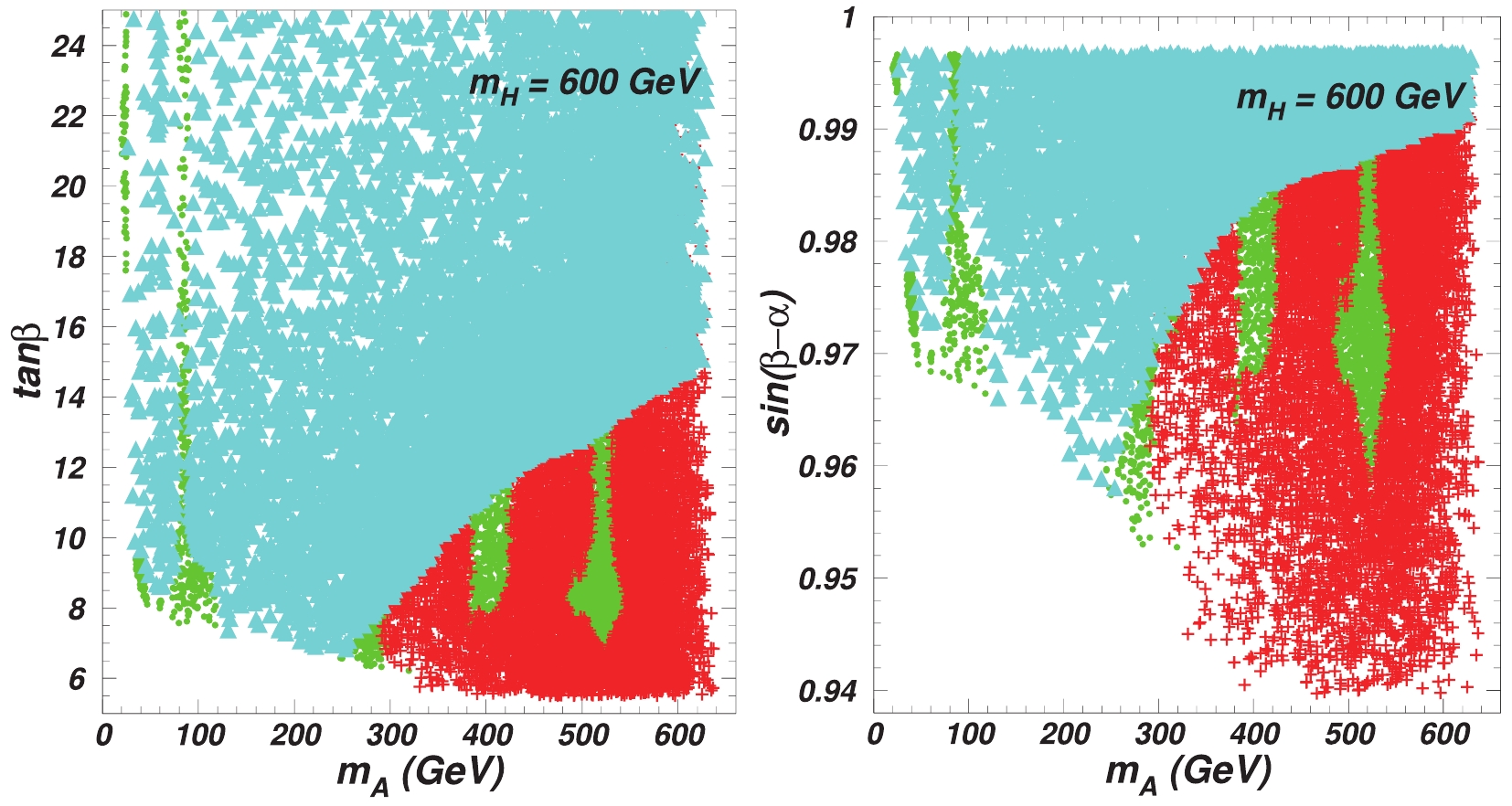
Figure 3. (color online) Scatter plots of
$ m_A $ with respect to$ \tan\beta $ and$ m_A $ with respect to$ \sin(\beta-\alpha) $ satifying constraints of pre-LHC and 125 GeV Higgs signal data. Triangles (sky blue) and pluses (red) are excluded by$ A/H\to \tau^+ \tau^- $ and$ A\to hZ $ channels at the LHC, respectively. Bullets (green) are permitted by various LHC direct searches.The
$ b\bar{b}\to A \to \tau^+ \tau^- $ channel excludes most of the parameter space for large$ \tan\beta $ and$ gg/b\bar{b}\to A\to hZ $ for small$ \tan\beta $ . Because the coupling of$ AhZ $ is proportional to$ \cos(\beta-\alpha) $ , the$ A\to hZ $ channel tends to exclude samples with small$ \mid\sin(\beta-\alpha)\mid $ . The permitted samples are mainly distributed across several corners and narrow bands. As shown in Table 1, the experimental bound of$ A \to \tau^+ \tau^- $ channel is absent for$ m_A<20 $ GeV and 80$ <m_A<90 $ GeV. Therefore,$ m_A $ in these mass ranges are permitted. Furthermore, most samples with$ m_A $ in the ranges of$ 30\sim 120 $ GeV,$ 240\sim 300 $ GeV,$ 380\sim 430 $ GeV, and$ 480\sim 550 $ GeV are allowed for appropriate$ \tan\beta $ and$ \sin(\beta-\alpha) $ . For the last two bands, the experimental bounds of$ A\to hZ $ [72] are larger than those of the neighbouring mass ranges. Therefore, in the regions of 380$ \leqslant m_A\leqslant $ 430 GeV and 480 GeV$ \leqslant m_A\leqslant $ 550 GeV, numerous samples with large$ \sin(\beta-\alpha) $ can accommodate the bound of the$ A\to hZ $ channel. -
We study the permitted parameter space in scenario B when imposing the joint restrictions (1)–(4) in Section 3. The surviving samples are shown in the scatter plots of
$ m_H $ with respect to$ \tan\beta $ and$ \sin\,(\beta-\alpha) $ in Fig. 4. Similar to the discussion in scenario A, the pre-LHC and 125 GeV Higgs signal data require$ \tan\beta > 5 $ , and all samples are favored by the$ H\to VV,\; \gamma\gamma,\; hh $ , and$ A\to HZ $ channels.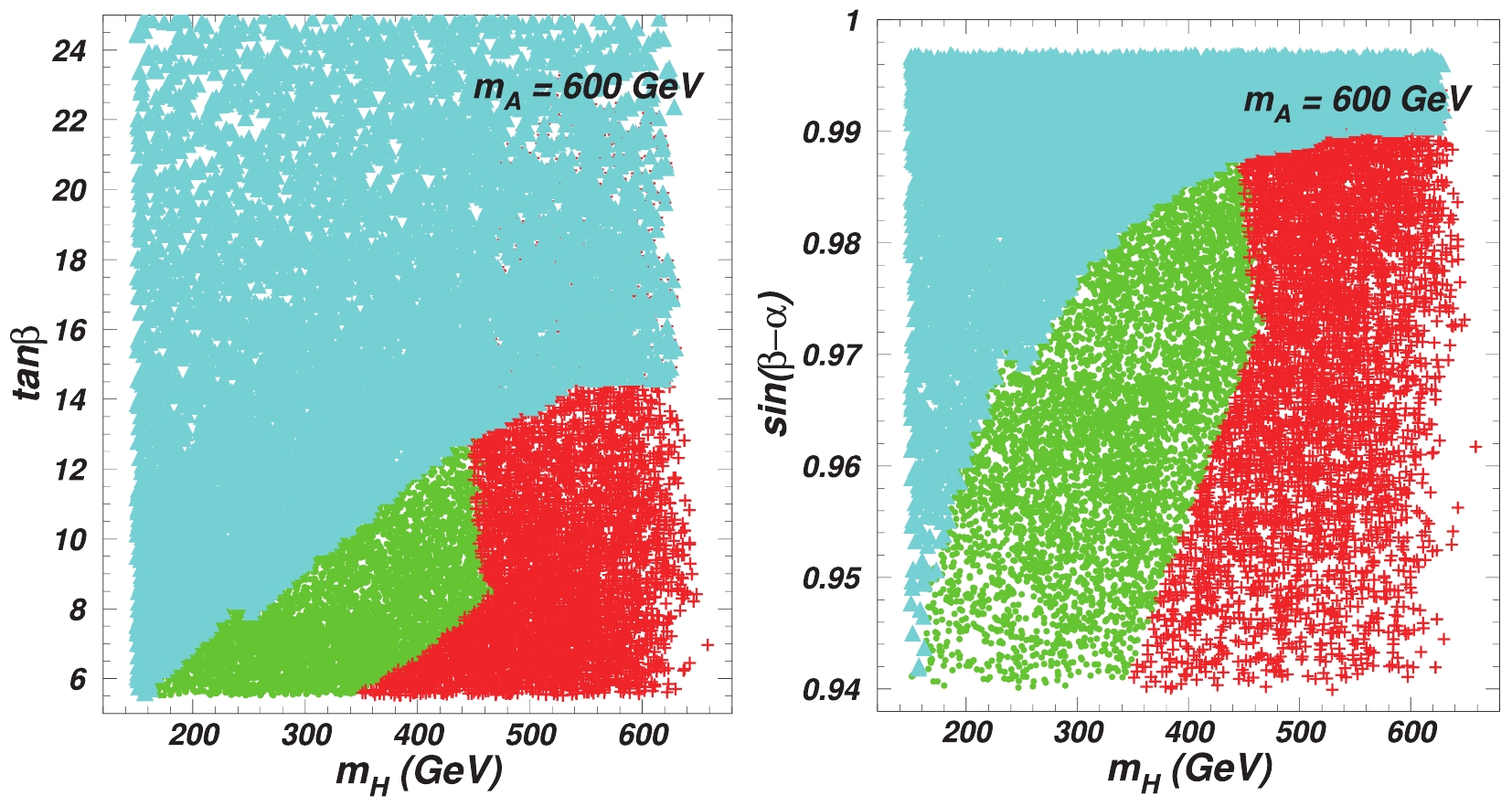
Figure 4. (color online) Scatter plots of
$ m_H $ with respect to$ \tan\beta $ and$ m_H $ versus$ \sin(\beta-\alpha) $ satisfying constraints of pre-LHC and 125 GeV Higgs signal data. Triangles (sky blue) and pluses (red) are excluded by$ H/A\to \tau^+ \tau^- $ and$ A\to hZ $ channels at LHC, respectively. Bullets (green) are permitted by various LHC direct searches.Fixing
$ m_A = $ 600 GeV, the channel$ b\bar{b}\to H \to \tau^+ \tau^- $ provides upper bounds on$ \tan\beta $ and$ \sin(\beta-\alpha) $ . For instance,$ \tan\beta< $ 7.0 (9.2, 14,4) and$ \sin(\beta-\alpha)< $ 0.96 (0.98, 0.99) for$ m_H = $ 200 GeV (300 GeV, 600 GeV). All samples with$ m_H< $ 350 GeV can accommodate the constraints from the channel$ A\to hZ $ . For such$ m_H $ values, the mode$ A\to HZ $ can increase the total width of A and considerably suppress the branching ratio of$ A\to hZ $ . The channels$ A\to\tau^+ \tau^- $ and$ A\to hZ $ exclude all samples with$ m_H> $ 470 GeV, and some samples with 150$ <m_H< $ 470 GeV survive for appropriate$ \tan\beta $ and$ \sin(\beta-\alpha) $ .In comparison with the results of Ref. [22], recent LHC Higgs data considerably reduce the parameter space. For
$ m_H = 600 $ GeV, the whole range of$ m_A< $ 700 GeV is permitted in Ref. [22], while$ m_A $ is only allowed to vary within several ranges in this study, namely$ m_A<20 $ GeV, 30$ <m_A<120 $ GeV, 240 GeV$ <m_A<300 $ GeV, 380 GeV$ <m_A< 430 $ GeV, and 480 GeV$ <m_A< 550 $ GeV. For$ m_A = 600 $ GeV, the entire range of$ m_H< $ 700 GeV is permitted in Ref. [22], while$ m_H< $ 470 GeV is required in this study. Such differences are mainly due to the experimental data of$ gg/b\bar{b}\to A\to hZ $ from Refs. [71, 72], which are not included in Ref. [22]. -
We studied the status of wrong sign Yukawa coupling of type II 2HDM in light of recent LHC Higgs data, obtaining some interesting conclusions. The channels
$ b\bar{b}\to A/H \to \tau^+ \tau^- $ and$ gg/b\bar{b}\to A\to hZ $ exclude most of the parameter space for large$ \tan\beta $ and small$ \tan\beta $ , respectively. For$ m_H = $ 600 GeV, the allowed samples are mainly distributed in several corners and narrow bands of$ m_A<20 $ GeV, 30$ <m_A<120 $ GeV, 240 GeV$ <m_A<300 $ GeV, 380$ <m_A< 430 $ GeV, and 480 GeV$ <m_A< 550 $ GeV. For$ m_A = $ 600 GeV,$ m_H $ is required to be lower than 470 GeV.
Revisiting wrong sign Yukawa coupling of type II two-Higgs-doublet model in light of recent LHC data
- Received Date: 2020-01-17
- Available Online: 2020-07-01
Abstract: In light of the recently obtained LHC Higgs data, we examine the parameter space of the type II two-Higgs-doublet model, in which the 125 GeV Higgs bosons exhibit wrong sign Yukawa couplings. Combining the relevant theoretical and experimental limits, we find that the LHC Higgs data exclude most of the parameter space of the wrong sign Yukawa coupling. For






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: