-
In the past forty years, the chiral effective field theory (ChEFT) and lattice quantum chromodynamics (LQCD) have been powerful tools to solve the problems of strong interactions at the low energy scale due to non-perturbative behaviors. The realization of LQCD simulation is strongly dependent on the computing resource. It is very difficult to describe the properties of hadrons at physical pion mass,
$ m_\pi\approx 140 $ MeV. However, these properties can be generated as functions of pion masses in ChEFT. Therefore, there have been numerous attempts to extrapolate the LQCD results of hadrons to the physical pion mass with the help of ChEFT, including the baryon masses, axial coupling constants, magnetic moments [1–4], etc. These studies largely improved our understanding of the QCD theory for single hadrons in the low energy region.For the nucleon-nucleon (NN) system, the potentials from ChEFT at different expansion orders were constructed, whose lower-energy constants (LECs) were determined by fitting the NN scattering data [5-13]. To date, the next-to-next-to-next-to-next-to-leading order (N4LO, fifth order) has been completely included in the chiral NN potentials [14–19], which were adopted to calculate the properties of light nuclei and infinite nuclear matter [17, 20, 21]. As for the LQCD, the information of the nucleon-nucleon interaction was extracted from the Wilson quark action in several studies [22–25]. The pion-mass-dependent NN forces were obtained from the HALQCD collaboration in the LQCD [26–29]. Although the pion masses (quark masses) in these calculations were far from the physical mass point (
$ m_\pi = 468.6, ..., 1170.9 $ MeV), they were readily applied to investigate the properties of nuclear many-body problems [30-33].The case of ChEFT for single nucleon at various pion masses provided important information on chiral dynamics. Hence, the ChEFT for the two-nucleon system should provide valuable information on the role of the pion in a complex nuclear system. However, the investigations on the connection of the ChEFT and LQCD for the nuclear force are few to date. Recently, Song et al. adopted the available hyperon-hyperon scattering data from LQCD simulations to discuss the relativistic baryon-baryon interaction [34]. Barnea et al. predicted the binding energies of light nuclei with the NN interaction generated by the pionless EFT using the hyperspherical harmonics and auxiliary-field diffusion Monte Carlo methods at
$ m_\pi = 805 $ MeV, where the leading-order (LO) LECs were fitted to the deuteron, dineutron, and triton energies obtained by the NPLQCD group [35, 36].In this study, we construct a bridge between ChEFT and LQCD in terms of the NN force and extract the LECs from LQCD simulations for the first time. Although not possible for the ChEFT at larger pion mass, it remains important to extract the pion-mass dependence of LECs to elucidate the role of the pion in a complex system from LQCD, which can freely change the pion mass. The chiral NN potentials are generated from the available HALQCD lattice simulations, which have strong pion-mass dependence. Because the statistical errors of lattice simulations are still considerably large, the chiral expansion order is restricted to the lowest order, i.e., leading order, where only two LECs,
$ C_S $ , and$ C_T $ can be extracted. We discuss the pion-mass dependence of LECs and the pion form factors in the following section. Furthermore, we apply these chiral potentials to study the properties of nuclear matter and obtain their equations of state with different pion masses. -
Because the chiral effective Lagrangian at leading order originates from two-nucleon tree diagrams, the NN potential is written as a one-pion-exchange component and contact terms. In the center-of-mass system, its explicit expression is as follows [37, 38],
$V_{NN}^{(0)}({\vec p_1},{\vec p_2}) = - \frac{{g_A^2}}{{4f_\pi ^2}}\frac{{{{\vec \sigma }_1} \cdot \vec q{{\vec \sigma }_2} \cdot \vec q}}{{{{\vec q}^2} + m_\pi ^2}}{\vec \tau _1} \cdot {\vec \tau _2} + {C_S} + {C_T}{\vec \sigma _1} \cdot {\vec \sigma _2},$

(1) where
$ g_A,\; f_\pi $ , and$ m_\pi $ denote the nucleon axial coupling constant, pion decay constant, and pion mass, respectively.$ \vec q = \vec p_1-\vec p_2 $ is the momentum transfer between two nucleons, where$ \vec p_1 $ and$ \vec p_2 $ denote the initial and final nucleon momenta in the center-of-mass system, respectively. The superscript (0) denotes the chiral expansion order. The LECs in the LO contact terms can be expressed in terms of the partial wave components in the$ ^1S_0 $ and$ ^3S_1 $ channels [18],$\begin{split} V_{{\rm{ct}}}^{(0)}{(^1}{S_0}) =& {\widetilde C_{^1{S_0}}} = 4\pi ({C_S} - 3{C_T}),\\ V_{{\rm{ct}}}^{(0)}{(^3}{S_1}) =& {\widetilde C_{^3{S_1}}} = 4\pi ({C_S} + {C_T}). \end{split}$

(2) To determine the LECs,
$ \widetilde C_{^1S_0} $ , and$ \widetilde C_{^3S_1} $ , the LO chiral potential,$ V^{(0)}_{NN}(\vec p_1,\vec p_2) $ , is inserted to a scattering equation to generate the phase shifts of NN collisions. We follow the choice of Entem et al. with a relativistic version, the Blankenbeclar-Sugar equation, which is shown explicitly in Refs. [18, 39]. Furthermore, a regular function should be multiplied with the chiral potential,$ \widehat V $ , to avoid divergence at high momenta in the scattering equation, with an exponential function in momentum space [18, 19],$f({p_1},{p_2}) = \exp \left[ { - {{({p_1}/\Lambda )}^{(2n)}} - {{({p_2}/\Lambda )}^{(2n)}}} \right].$

(3) The cut-off momentum,
$ \Lambda $ , and the power, n, will be fixed by fitting the phase shifts from the lattice forces in this study [40]. Once these chiral NN potentials are obtained, the properties of symmetric nuclear matter and pure neutron matter are calculated by the Brueckner-Hartree-Fock (BHF) method [41-43]. -
In the lattice NN forces obtained from the HALQCD collaboration, the pion masses range from 468.6 to 1170.9 MeV with different
$ u,\; d $ quark masses. The corresponding nucleon masses change from 1161 to 2274 MeV [28, 30]. Furthermore, the axial-vector coupling constant$ g_A $ and pion-decay constant$ f_\pi $ can be evaluated by the LQCD method as a function of the pion mass. The available studies indicate that the axial-vector coupling constant is not particularly sensitive to the pion mass [1]. Therefore, it is fixed to$ g_A = 1.20 $ in the present study for all potentials, as shown in Ref. [1]. In contrast, the pion-decay constant is strongly dependent on the pion mass from the present LQCD simulations. Its value can be compared with the predictions of SU(2) chiral perturbation theory at next-to-next-to-leading order, which can be expressed by the chiral logarithms in terms of pion masses [2]. Therefore, we can use these achievements to fix the pion-decay constants at the corresponding pion masses from 468.6 to 1170.9 MeV.Once these physical constants are determined, there are four free parameters in the LO chiral NN potentials, two LECs in contact terms,
$ \widetilde C_{^1S_0}, \; \widetilde C_{^3S_1} $ , the power of cut-off, n, and cut-off momenta$ \Lambda $ at each pion mass.$ \Lambda $ in this study is only a cut-off momenta in the form factor, rather than the breaking scale in the conventional ChEFT. These parameters are fitted with the least square method to the phase shifts in the$ ^1S_0 $ and$ ^3S_1 $ channels for the neutron-proton system from the HALQCD lattice NN potentials, below the laboratory energy$ E_\text{lab} = 150.0 $ MeV. The best fitting results are obtained for the exponential cutoff function at$ n = 1 $ , and we first fix n at this value and simulate the phase shifts of HALQCD NN potentials at long distance. All physical constants and free parameters, which are pion-mass dependent, are listed in Table 1. All pion-decay constants$ f_\pi $ , LECs of contact terms (in unit of$ 10^4 $ GeV-2), and cut-off momenta increase with the pion masses. These LO chiral potentials are named LO469, LO672, LO837, LO1015, and LO1171, corresponding to different pion masses,$ m_\pi = 468.6,\; 672.3,\; 836.5,\; 1015.2 $ , and 1170.9 MeV, respectively, for convenience.LO469 LO672 LO837 LO1015 LO1171 $ m_\pi $ /MeV

468.6 672.3 836.5 1015.2 1170.9 $ M_N $ /MeV

1161.0 1484.0 1749.0 2031.0 2274.0 $ f_\pi $ /MeV

118.0 133.0 145.0 159.0 172.0 $ \widetilde C_{^1S_0} $ 

−0.077 −0.027 −0.024 −0.021 −0.016 $ \widetilde C_{^3S_1} $ 

−0.091 −0.029 −0.028 −0.025 −0.022 $ \Lambda $ /MeV

334.37 550.00 569.81 622.93 664.91 $ \chi^2/{\rm d.o.f} $ 

9.385 8.805 0.389 2.665 0.928 Table 1. Pion mass, nucleon mass, pion-decay constant, LECs of contact terms and cut-off momenta at LO chiral potential from LQCD data with different pion masses from 468.6 to 1170.9 MeV. The LO LECs are in units of
$ 10^4 $ GeV-2.In Fig. 1, the NN scattering phase shifts in the
$ ^{1}S_0 $ and$ ^{3}S_1 $ channels from the HALQCD calculations and the LO chiral NN potentials are compared at different pion masses. The solid and dashed curves are generated by the LO chiral NN potentials. The square and diamond symbols represent the HALQCD data. The LO chiral potentials efficiently describe the results from lattice simulations at larger pion masses from LO837 to LO1171 potentials. This situation exacerbates for lower pion masses, i.e., LO469 and LO672 potentials, at higher laboratory energy$ E_\text{lab} $ , which is related to the strong repulsions of NN potential in the short range region. This demonstrates that the contact terms of LO chiral potentials cannot completely display the complexities of lattice data in the short range region and the next-to-leading order in the chiral expansion must be included at lower pion masses.
Figure 1. (color online) Phase shifts in
$ ^{1}S_0 $ and$ ^{3}S_1 $ channels from lattice NN potentials (discretized symbols) and chiral NN potentials (solid and dashed lines) with different pion masses from 468.6 to 1170.9 MeV.The phase shifts from the HALQCD collaboration involved stochastic and systematic errors due to complicated Monte Carlo simulations, which have been shown in Fig. 4 of Ref. [29] and Fig. 2 of Ref. [30]. Therefore, it is necessary to discuss the influences of such uncertainties on the chiral potential, especially for the LECs,
$ \widetilde C_{^1S_0} $ and$ \widetilde C_{^3S_1} $ . Therefore, these LECs are refitted by considering the error bars appearing in HALQCD phase shifts at$ ^1S_0 $ and$ ^{3}S_1 $ channels with$ m_\pi = 468.6 $ MeV at a fixed cut-off momentum$ \Lambda = 334.37 $ MeV. Here, the corresponding LECs assume the values of$ \widetilde C_{^1S_0} = -0.077\pm0.012 $ and$ \widetilde C_{^3S_1} = -0.091\pm0.010 $ . The phase shifts from LO chiral potentials with such LECs are shown as shaded regions in Fig. 2 for$ ^1S_0 $ and$ ^{3}S_1 $ channels in panels (a) and (b), respectively. The phase shifts from HALQCD with uncertainties are presented with square symbols and error bars for comparison. The lattice data are within the LO chiral potentials' uncertainty regions for phase shifts in the low energy region. The differences between chiral potentials and HALQCD data become larger with increasing energy, because the cut-off momentum is relatively small in LO469 potentials. Here, the uncertainties of LECs in present chiral potentials are approximately ~10%–15% in the LQCD data, whereas they are only about 1% for the chiral potential generated by the NN scattering data [19]. Due to the lack of the uncertainties of HALQCD data at larger pion masses, a more systematical analysis cannot be performed in present framework, such as the Bayesian method in Ref. [44]. Furthermore, the calculations in HALQCD were performed in the discretized space. However, the present phase shifts are derived from the continuum momentum space. Therefore, the present uncertainties in LECs also include some finite-size effects.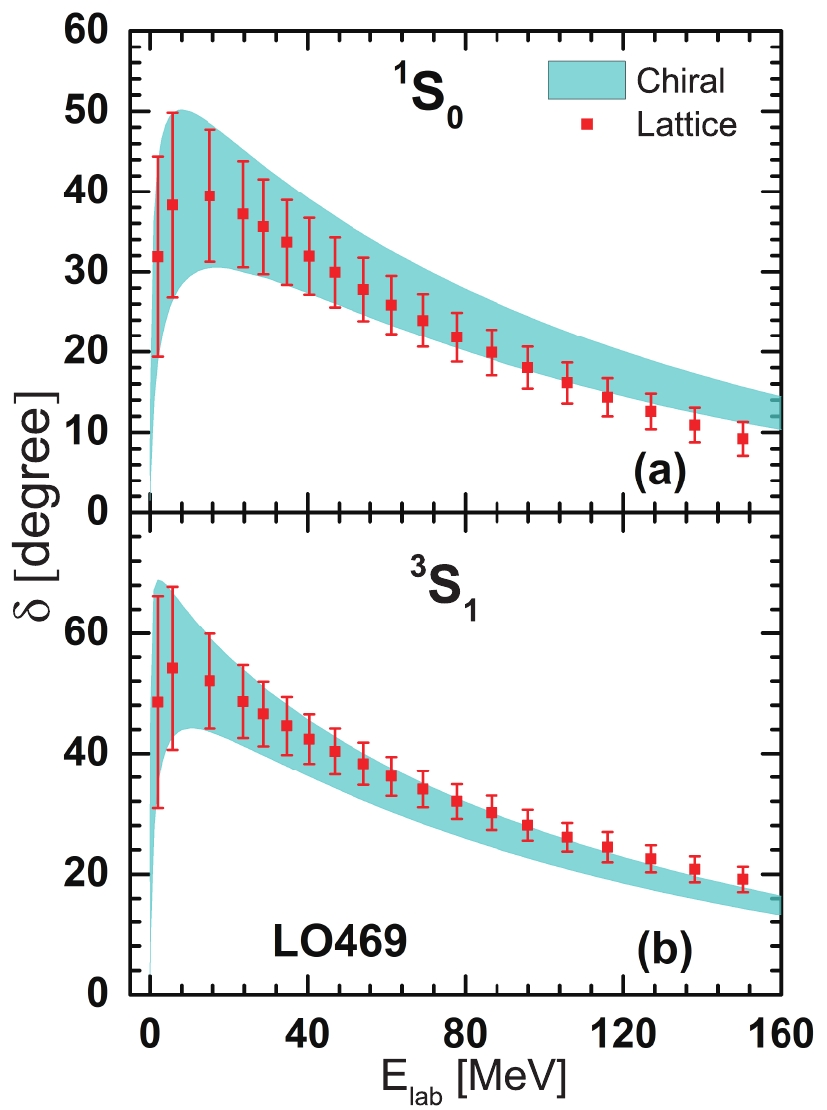
Figure 2. (color online) Uncertainties of phase shifts in
$^{1}S_0$ and$^{3}S_1$ channels from lattice NN potential (square symbols with error bars) and chiral NN potential (shadow regions) with$m_\pi = 468.6$ MeV.It is interesting to compare these chiral NN potentials from the LQCD data with the ones at the physical mass point. Therefore, a LO chiral potential is obtained by fitting the phase shifts at
$ ^{1}S_0 $ and$ ^{3}S_1 $ channels extracted from the experimental data of NN scattering at$ m_\pi = 140 $ MeV, where$ M_N = 939 $ MeV and$ f_\pi = 92.4 $ MeV, referred to as the LO140 potential. The phase shifts are better reproduced than the ones of the conventional LO chiral NN potentials in the lower energy region$ E_{\rm lab}<150 $ MeV [16]. We use the order of the cutoff function$ n = 1 $ instead of 2 in the other studies. This indicates that the exponential regulator in this study is weaker than in the others, such as the LO chiral potential provided by Entem et al. [18]. Its cutoff momentum is$ \Lambda = 500 $ MeV. Therefore, we can obtain more repulsive contributions in phase shifts.At the physical point, the strengths of contact terms and cut-off momenta are given as
$ \widetilde C_{^1S_0} = -0.152, \; \widetilde C_{^3S_1} =$ −0.214, and$ \Lambda = 322.49 $ MeV. With these parameters, the LO140 potentials at the physical pion-mass point efficiently describe the phase shifts from experimental data, as shown in Fig. 3, whereas the LO chiral potential with larger cutoff momentum depicted by the dashed line cannot reproduce the phase shifts at larger incident energies. In comparison to the present lattice simulations at heavier pion masses, it is obvious that the phase shifts at$ m_\pi = 140 $ MeV are larger in the$ ^{1}S_0 $ and$ ^{3}S_1 $ channels, which indicates that there are more attractive contributions in realistic NN potentials. In the study of Inoue et al. of the HALQCD group [30], the potentials of$ ^{1}S_0 $ and$ ^{3}S_1 $ channels only provide the maximum attractions around –40 MeV in the intermediate range, whereas these values are closer to –100 MeV for realistic potentials, such as AV18 and CD Bonn potentials.
Figure 3. (color online) Phase shifts of
$^{1}S_0$ and$^{3}S_1$ channels from Nijmegen PWA (discretized symbols), chiral NN potentials (solid lines) with physical pion mass$m_\pi = 140.0$ MeV and small cut-off momentum in present study, and chiral LO potential with$\Lambda = 500$ MeV (dashed lines), provided by Entem et al. [18].In Fig. 4, the LECs at leading order,
$ \widetilde{C}_{^1S_0} $ and$ \widetilde{C}_{^3S_1} $ , are given as a function of pion mass from$ m_\pi = 140.0 $ MeV to$ m_\pi = 1170.9 $ MeV. At larger pion masses, these LECs in the$ ^{1}S_0 $ and$ ^{3}S_1 $ channels are almost identical. With the pion mass approaching the physical value, their differences suddenly become larger. With the presently available HALQCD data, it is difficult to extrapolate the LECs of chiral potential at a physical pion mass from the lattice data. In comparison to the LQCD simulations on meson and one-baryon sectors, the uncertainties of two-nucleon system from HALQCD are relatively larger. Furthermore, the mechanism behind the NN interaction is more complicated. In this study, we only attempt to build the connections between the ChEFT and LQCD in NN potentials. With more comprehensive LQCD calculations on few-body systems in future, we expect that the NN interaction at the physical pion mass can be extracted using the lattice results at larger pion masses in the chiral expansion technique, as previously performed for the single nucleon.
Figure 4. (color online) LECs at leading order,
$\widetilde{C}_{^1S_0}$ and$\widetilde{C}_{^3S_1}$ with different pion masses from 140.0 to 1170.9 MeV.Recently, an interesting study on the two-nucleon system for axion production and gamma absorption was reported, assuming
$ \widetilde{C}_{^1S_0} = \widetilde{C}_{^3S_1} $ , which corresponds the Wigner symmetry [45]. The Wigner symmetry is obtained in the large number of colors limit of QCD. The present study indicates that the Wigner symmetry is realized even when the color number is three for the case of a large pion mass, which corresponds to a large quark mass.However, in nature, the scattering lengths are
$ a_{^1S_0} = -23.740\pm 0.020 $ fm and$ a_{^3S_1} = 5.419\pm 0.007 $ fm for a proton-neutron system [46, 47]. Therefore,$ \widetilde{C}_{^1S_0} $ and$ \widetilde{C}_{^3S_1} $ are expected to exhibit distinct differences when the pion mass is close to the physical pion mass.The LO chiral NN potentials from HALQCD data are adopted to investigate the properties of nuclear matter in the framework of the BHF method. In these calculations, only four channels,
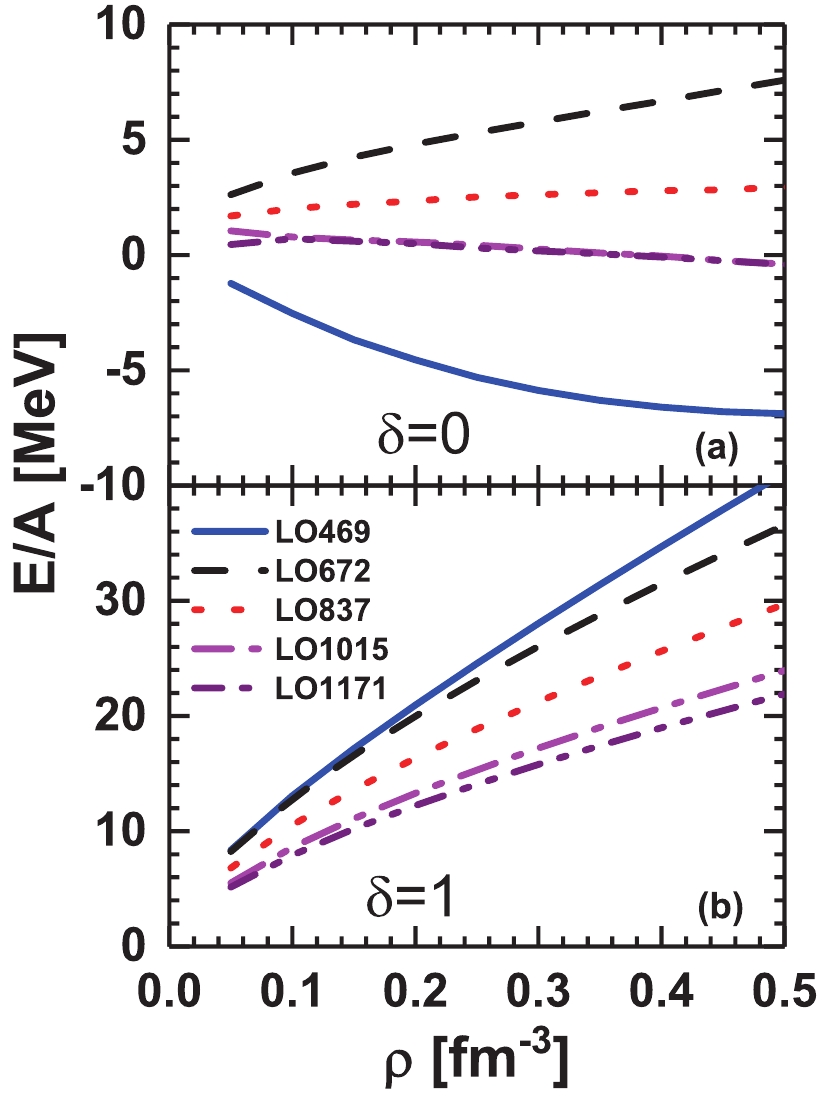
$ ^1S_0,\; ^3S_1,\; ^3D_1 $ , and$ ^3S_1 $ -$ ^3D_1 $ are included for the available LQCD simulations. In Fig. 5, the equations of state of symmetric nuclear matter (panel (a),$ \delta = (N-Z)/A = 0 $ ) and pure neutron matter (panel (b),$ \delta = (N-Z)/A = 1 $ ) are shown with different pion masses. There is a saturation binding energy,$ E/A = -6.80 $ MeV at$ \rho_B = 0.45 $ fm−3 for the LO469 potential in symmetric nuclear matter, while the bound system is not found in LO672 and LO837 potentials. With the pion mass, the systems have very weak bound states with LO1015 and LO1171 potentials at high density. Actually, the behaviors can be explained by the phase shifts of chiral potentials given in Fig. 1. The LO469 potential provides the largest phase shifts in the$ ^1S_0 $ and$ ^3S_1 $ channels, which generates the strongest attractive contributions. In the LO672 potential, the phase shifts in the$ ^1S_0 $ and$ ^3S_1 $ channels suddenly decrease and amount to only one half of the LO469 potential. The magnitudes of phase shifts become larger with increasing pion mass. Therefore, the energy per nucleon in the corresponding equations of state is changed from positive values to negative ones. Furthermore, the saturation binding energy of the LO469 potential in present study is larger than in the similar HALQCD simulation potential calculated directly by Inoue et al., where the saturation point is$ E/A = -5.4 $ MeV at$ \rho_B = 0.414 $ fm−3 [30]. This is because the phase shifts of$ ^1S_0 $ channel obtained by the LO469 potential are more attractive than the lattice data at larger$ E_\text{lab} $ . In the pure neutron matter, only the$ ^1S_0 $ channel provides a contribution due to the Pauli principle. The LO469 potential yields the most repulsive equation of state, while the LO1171 potential generates the most attractive one. In general, the behaviors of equations of state of nuclear matter in the LO chiral potentials are similar to those in HALQCD potentials obtained by Inoue et al. -
Nature behaves as it does because the pion mass is the one in the free space. The pion-mass dependence of NN potentials is highly important to understand the QCD theory in the low energy scale. The NN potentials with pion-mass dependence were constructed in terms of the one-pion exchange and contact terms, for the first time, based on the chiral effective field theory with leading-order expansion and recent lattice QCD achievements obtained by the HALQCD group. In these potentials, the attractions progressively weakened, and the LECs,
$ \widetilde C_{^1S_0} $ and$ \widetilde C_{^3S_1} $ increased with the pion mass. Furthermore, the magnitudes of$ \widetilde C_{^1S_0} $ and$ \widetilde C_{^3S_1} $ at larger pion masses were very close to each other, while their differences became obvious when the pion mass approached the physical point.We constructed the equations of state of symmetric nuclear matter and pure neutron matter with these LO chiral potentials in the framework of the BHF method. The LO469 potential generated the bound states in symmetric nuclear matter. As for pure neutron matter, there was only the contribution from the
$ ^1S_0 $ channel due to the Pauli principle, and the potentials with larger pion masses provided more repulsive contributions. These results showed that the properties of nuclear many-body system were strongly dependent on the pion mass, which is a contradiction of the conclusions from the pionless ChEFT. To interpret the relations between the lattice simulation and ChEFT in the two-nucleon system, more partial waves need to be calculated in the lattice QCD, as the next-to-leading order NN interaction is combined by the LECs in terms of$ ^1S_0, ^3P_0, ^1P_1, ^3P_1, ^3S_1, ^3S_1 $ -$ ^3D_1 $ , and$ ^3P_2 $ channels.
One-pion-exchange potential with contact terms from lattice QCD simulations
- Received Date: 2019-12-18
- Accepted Date: 2020-03-02
- Available Online: 2020-07-01
Abstract: Pion-mass-dependent nucleon-nucleon (NN) potentials are obtained in terms of the one-pion exchange and contact terms from the latest lattice QCD simulations of the two-nucleon system. They assume the forms of the leading order (LO) NN potential from the chiral effective field theory and thus are referred to as the LO chiral potential in this study. We extract the coefficients of contact terms and cut-off momenta in these potentials, for the first time, by fitting the phase shifts of





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: