-
In recent years, many decay and in-beam spectroscopic studies have been performed on the light superheavy nuclei around the mass region
$ Z = 100,\; A = 250 $ . Valuable experimental data are available concerning the detailed structure and can be used to constrain various nuclear theories (see Refs. [1–3] and references therein).$ ^{254} {\rm{No}}$ is the pioneer nucleus for an experimental spectroscopy study in this mass region due to its relatively high production rate. Pioneering research included both the extension of the ground state bands (GSB) to the high angular momentum [4–6], and the observation of the high-K multi-particle states [7–12].In 1973, a
$ (0.28\pm0.04) $ s isomer of$ ^{254} {\rm{No}}$ was reported, which was suspected to be the$ K^{\pi} = 8^- $ state arising from either a two-proton$ \pi\frac{7}{2}^{-}[514]\otimes\pi\frac{9}{2}^+[624] $ or two-neutron$\nu\frac{9}{2}^â[734]\otimes $ $ \nu\frac{7}{2}^+[613] $ configuration [7]. More than thirty years later, the$ 8^- $ isomer was identified with the excitation energy of$ 1.293-1.297 $ MeV in several experiments [9–12]. The configuration of this state is still an open issue. A two-neutron state is favored in Ref. [12], while a two-proton state with a configuration$ \pi\frac{7}{2}^{-}[514]\otimes$ $ \pi\frac{9}{2}^+[624] $ is favored in the other works [9–11]. Rotational structure on top of the$ 8^- $ isomer was reported independently by two contemporary studies, where different detailed level schemes were proposed [11, 12]. Heßberger et al. suggested that all seven observed transitions constitute a single$ \Delta I = 1 $ rotational sequence based on the$ K^{\pi} = 8^- $ state [11], while Clark et al. placed only the first two members in the$ K^{\pi} = 8^- $ band and the rest of the transitions in a new band which was assigned as the$ K^{\pi} = 10^+ $ band.The second isomer discovered in
$ ^{254} {\rm{No}}$ is a four-particle state with the energy$ E>2.5 $ MeV and half-life of 171-198 µs [9–12]. Its configuration is not yet determined.$ K^{\pi} = 16^+ $ was assumed in Refs. [10–12], while$ K^{\pi} = 14^+ $ was tentatively suggested by Tandel et al. [9]. Note that this is one of only two four-particle isomers reported experimentally in this region. The other one is the recently observed 247(73) µs$ K^{\pi} = 16^+ $ isomer in 254Rf [13].The two-particle
$ K^{\pi} = 3^+ $ state is assigned unambiguously as the two-proton state with the configuration$ \pi\frac{7}{2}^-[514]\otimes\pi\frac{1}{2}^-[521] $ [9–12]. The$ 3^{+} $ state is of particular interest since the proton orbital$ \pi\frac{1}{2}^-[521] $ stems from the spherical$ 2f_{5/2} $ orbital. The spin-orbit interaction strength of the$ 2f_{5/2}-2f_{7/2} $ partners governs the size of the$ Z = 114 $ spherical shell gap, which is predicted as the possible next magic proton number beyond lead. The properties of single-particle orbitals$ \pi\frac{7}{2}^-[514] $ and$ \pi\frac{1}{2}^-[521] $ affect strongly the properties of the neighboring odd-Z nuclei [14–17].These observed high-K multi-particle states in
$ ^{254} {\rm{No}}$ can provide valuable information about the single-particle structure, deformation, pairing correlations, K conservation, etc. [18]. The rotational bands built upon these multi-particle states provide insight into the angular momentum alignment, high-j intruder orbital, pairing reduction, etc. In addition, the knowledge of the transfermium nuclei provides indirect information about the single-particle structure of the superheavy nuclei, which is crucial for the synthesis of the superheavy elements.A comparison of the experimental kinematic moment of inertia (MoI)
$ J^{(1)} $ of the two-particle high-K bands with GSB of$ ^{254} {\rm{No}}$ is displayed in Fig. 1. Compared to GSB, a 20%~25% increase of$ J^{(1)} $ is seen for the high-K bands in the low frequency region. As the rotational frequency increases, GSB increases smoothly, while the high-K bands are almost constant ($ 8^{-} $ and$ 10^{+} $ bands) or decrease ($ 3^{+} $ band). This behavior can be explained by the pairing correlations, angular momentum alignment and Pauli blocking effect.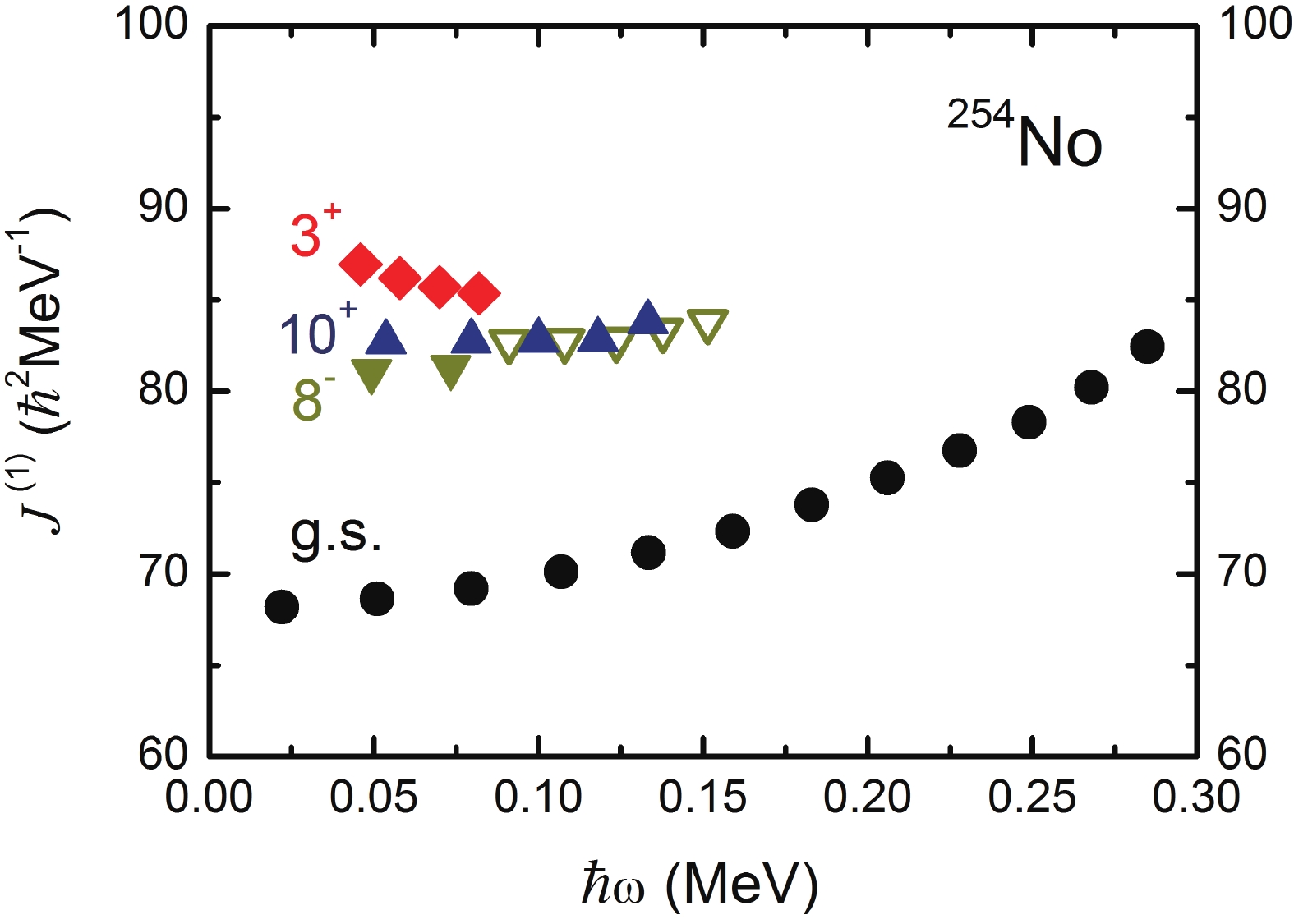
Figure 1. (color online) Experimental kinematic moment of inertia
$ J^{(1)}$ for the ground state and two-particle state bands$ K^{\pi} = 3^+,\;8^-,\;10^+$ in$ ^{254}{\rm{No}}$ . The experimental data are from Refs. [8, 10–12, 19]. The last five transitions in the$ K^{\pi} = 8^-$ band in Ref. [11], which are placed in the$ K^{\pi} = 10^+$ band in Ref. [12], are denoted by open down-triangles.In terms of theoretical investigations, most spectroscopic studies of
$ ^{254} {\rm{No}}$ focused on the properties of the yrast band [16, 20–36]. The strength of the pairing correlations in the$ A = 250 $ region and its influence on MoI of GSB were compared with the lighter nuclear system in Refs. [32, 35]. As for the observed high-K multi-particle states, few theoretical studies have been carried out. Liu et al. calculated the observed high-K isomers in$ ^{254} {\rm{No}}$ with special attention on the influence of the high-order deformation$ \varepsilon_{6} $ on the excitation energies and the nuclear potential energy [37]. Jolos et al. studied the low-lying and collective states in$ Z\sim100 $ nuclei with particular discussion of the effects of octupole and hexadecupole residual forces [38]. To our best knowledge, there is still no detailed theoretical investigation of the two-particle$ K^{\pi} = 3^+, \;8^- $ and$ 10^+ $ bands in$ ^{254} {\rm{No}}$ .In the present work, the multi-particle states in
$ ^{254} {\rm{No}}$ and the rotational bands on top of them are investigated by the cranked shell model (CSM) with the pairing correlations treated by the particle-number conserving (PNC) method. To our knowledge, this is the first time that detailed theoretical calculations are performed of the observed rotational bands beyond the yrast band in$ ^{254} {\rm{No}}$ . The pairing correlations and blocking effect are very important for describing multi-particle states. In the PNC-CSM method, the cranked shell model Hamiltonian with monopole and quadrupole pairing correlations is solved directly in the truncated Fock space. Hence, the particle number is conserved and the Pauli blocking effect is taken into account exactly. -
The CSM Hamiltonian in the rotating frame is
$ H_{\rm CSM} = H_{\rm SP}-\omega J_x + H_{\rm P}(0)+H_{\rm P}(2). $

(1) $ H_{\rm SP} = \sum_{\xi}(h_{\rm Nil})_{\xi} $ is the single-particle part, where$ h_{{\rm Nil}} $ is the Nilsson Hamiltonian,$ \xi $ ($ \eta $ ) is the eigenstate of the Hamiltonian$ h_{\xi(\eta)} $ , and$ \bar{\xi} $ ($ \bar{\eta} $ ) is the time-reversed state.$ -\omega J_x $ is the Coriolis interaction with the rotational frequency ω about the x axis (perpendicular to the nuclear symmetry z axis). The cranked Nilsson levels$ \epsilon_{\mu} $ and cranked state$ |\mu\rangle $ are obtained by diagonalizing the cranked single-particle Hamiltonian$ h_{0}(\omega) = h_{\xi}-\omega j_{x} $ .The pairing includes monopole and quadrupole pairing correlations
$ \ H_{\rm{P}}(0) = -G_{0}\sum\limits_{\xi \eta } a_{\xi }^{\dagger}a_{\overline{\xi }}^{\dagger }a_{\overline{\eta }}a_{\eta }\ , $

(2) $ H_{\rm{P}}(2) = -G_{2}\sum\limits_{\xi \eta } q_{2}(\xi) q_{2}(\eta) a_{\xi}^{\dagger } a_{\overline{\xi}}^{\dagger} a_{\overline{\eta}}a_{\eta}\ , $

(3) where
$ a_{\xi }^{\dagger}a_{\overline{\xi }}^{\dagger } $ $ (a_{\bar{\eta}} a_\eta) $ is the pair creation (annihilation) operator.$ q_{2}(\xi) = \sqrt{{16\pi}/{5}}\langle \xi |r^{2}Y_{20} | \xi \rangle $ is the diagonal element of the stretched quadrupole operator.In the rotating frame, the time reversal symmetry is broken, while the symmetry with respect to the rotation by π around the x axis,
$ R_{x}(\pi) = {\rm e}^{-{\rm i}\pi\alpha} $ , is retained. The signature$ \alpha = \pm1/2 $ , eigenvalues of$ R_{x}(\pi) $ , remains a good quantum number. By transforming the Hamiltonian into the cranked basis, we have$ \begin{split} H_{\rm CSM} =& \displaystyle\sum\limits_{\mu}\epsilon_{\mu}b_{\mu}^{\dagger}b_{\mu} -G_0\sum\limits_{\mu\mu{\prime}\nu\nu{\prime}}f^{\ast}_{\mu\mu{\prime}}f_{\nu{\prime}\nu}b_{\mu+}^{\dagger}b_{\mu{\prime}-}^{\dagger}b_{\nu-}b_{\nu{\prime}-}\\ & -G_2\sum\limits_{\mu\mu{\prime}\nu\nu{\prime}}g^{\ast}_{\mu\mu{\prime}}g_{\nu{\prime}\nu} b_{\mu+}^{\dagger}b_{\mu{\prime}-}^{\dagger}b_{\nu-}b_{\nu{\prime}+}, \end{split} $

(4) where
$ b_{\mu}^{\dagger} $ is the real particle creation operator in the cranked state$ |\mu\rangle $ . To investigate the pairing reduction due to rotation and blocking, the PNC method (see Refs. [39–43] for details) is employed to deal with the pairing correlations. The CSM Hamiltonian Eq. (4) is diagonalized in the truncated Cranked Many-Particle Configuration (CMPC) space [40]. The effective pairing strengths$ G_0 $ and$ G_2 $ are connected with the dimension of the truncated CMPC space. In the following calculations, the CMPC space for$ ^{254} {\rm{No}}$ is constructed in the proton$ N = 4,\; 5,\; 6 $ and neutron$ N = 6, \;7 $ shells. The dimension of the CMPC space is about 1000, and the corresponding effective monopole and quadrupole pairing strengths are$ G_{0} = 0.25 $ MeV and$ G_{2} = 0.02 $ MeV for both protons and neutrons. The effective pairing strength is usually determined by the odd-even differences in binding energies. However, in the transfermium mass region, due to the lack of experimental data, the effective pairing strength is determined by the odd-even differences in MoI. Since the total Hamiltonian is diagonalized directly in the truncated Fock space, a sufficiently accurate solution can be obtained in a comparatively small diagonalization space for the yrast and low-lying excited states. In this way, like in the standard shell model approach, the particle number is conserved and the Pauli blocking effect is taken into account exactly.The eigenstate of
$ H_{ \rm{CSM}} $ is$ | \psi \rangle = \sum_{i} C_i | i \rangle $ with CMPC$ | i \rangle $ defined by the occupation of real particles on the cranked single-particle orbitals. A converged solution$ | \psi \rangle $ can always be obtained even for a pair-broken state, while the conventional cranked Hartree-Fock-Bogoliubov model does not converge in many cases [44, 45]. This makes it very convenient to treat the multi-particle states in a nucleus. The PNC-CSM method provides a reliable way to assign the configuration for a multi-particle state. Once the wave function$ | \psi \rangle $ is obtained, the configurations of all low-lying excited multi-particle states can be obtained using the occupation probability of a specific$ | i \rangle $ , with the unpaired particle blocked in the single-particle orbitals near the Fermi surface [43]. -
The Nilsson parameters
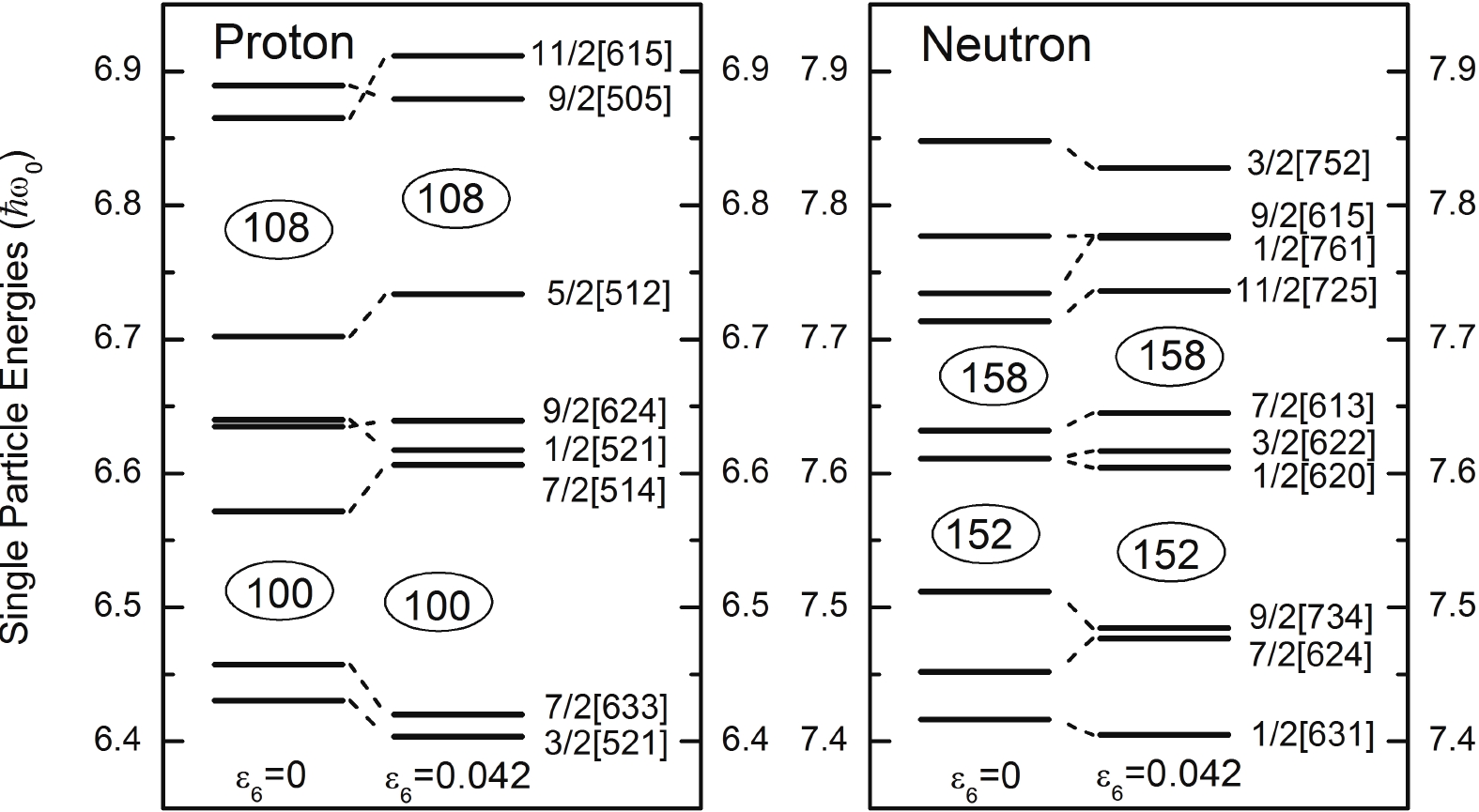
$ (\kappa,\mu) $ , which were optimized to reproduce the experimental level schemes for light superheavy nuclei in the$ A = 250 $ mass region in Refs. [26, 46], are used in this work. The values of proton$ \kappa_{5},\;\mu_{5} $ and neutron$ \kappa_{6},\;\mu_{6} $ are modified slightly to reproduce the correct single-particle level sequence when$ \varepsilon_{6} $ is included. The deformation parameters$ \varepsilon_{2} = 0.26,\ \varepsilon_{4} = 0.02 $ are taken from Ref. [26], and$ \varepsilon_{6} = 0.042 $ is taken from Ref. [47].The Nilsson single-particle levels with and without high-order deformation
$ \varepsilon_{6} $ are compared at the rotational frequency$ \hbar\omega = 0 $ in Fig. 2. It can be seen that the calculations including the$ \varepsilon_{6} $ deformation lead to enlarged proton$ Z = 100 $ and neutron$ N = 152 $ deformed shell gaps, which is consistent with the predictions using the Woods-Saxon potential by Liu et al. [37] and Patyk et al. [48]. Note that the existence of these two deformed shell gaps has been confirmed in the experiment [49]. In addition, compared with the results without the$ \varepsilon_{6} $ deformation, the proton deformed shell gap for$ Z = 106 $ is larger and the one for$ Z = 108 $ smaller, while the neutron shell gaps for$ N = 148,160 $ appear and the one for$ N = 150 $ disappears. The changes of the deformed single-particle level structure further influence the excitation energy and MoI of the multi-particle states. We note that the influence of the high-order deformation is still intricate, especially in the region of heavy and superheavy nuclei where the single-particle level density is high and the knowledge of the single-particle level structure is limited. Moreover, the value of$ \varepsilon_{6} $ is strongly model dependent. Therefore, a more comprehensive investigation of the effect of$ \varepsilon_{6} $ deformation on the single-particle levels is needed for heavy and superheavy nuclei. -
The multi-particle states predicted by various models are compared with the experimental data in Fig. 3. The predictions of PNC-CSM are listed in Table 1. Our model in its present version does not include the residual spin-spin interaction. In Table 1, both values of
$ K^{\pi} = |\Omega_1\pm\Omega_2|^\pi $ are shown for the two-particle states, with the value favored by the Gallagher-Moszkowski (GM) rules [53] underlined. According to the GM rules, the spin-singlet coupling is energetically favored for the pair-broken states in an even-even nucleus.$ K^\pi $ 

configuration $ E_{\rm x} $ /MeV(

$ \varepsilon_{6}\neq0 $ )

$ E_{\rm x} $ /MeV(

$ \varepsilon_{6} = 0 $ )

$ E_{\rm x}^{\rm exp} $ /MeV

$ \underline{3}^+,4^+ $ 

$ \pi\frac{7}{2}^{-}[514]\otimes\pi\frac{1}{2}^{-}[521] $ 

1.154 1.508 0.988 $ \underline{8}^-,1^- $ 

$ \pi\frac{7}{2}^{-}[514]\otimes\pi\frac{9}{2}^{+}[624] $ 

1.272 1.431 1.297 $ \underline{5}^-,4^- $ 

$ \pi\frac{9}{2}^{+}[624]\otimes\pi\frac{1}{2}^{-}[521] $ 

1.324 1.749 $ \underline{6}^+,1^+ $ 

$ \pi\frac{7}{2}^{-}[514]\otimes\pi\frac{5}{2}^{-}[512] $ 

1.794 1.807 $ \underline{3}^+,2^+ $ 

$ \pi\frac{5}{2}^{-}[512]\otimes\pi\frac{1}{2}^{-}[521] $ 

1.902 2.235 $ 7^-,\underline{2}^- $ 

$ \pi\frac{9}{2}^{+}[624]\otimes\pi\frac{5}{2}^{-}[512] $ 

2.007 2.142 $ \underline{4}^-,3^- $ 

$ \pi\frac{7}{2}^{+}[633]\otimes\pi\frac{1}{2}^{-}[521] $ 

2.200 2.145 $ \underline{7}^-,0^- $ 

$ \pi\frac{7}{2}^{+}[633]\otimes\pi\frac{7}{2}^{-}[514] $ 

2.229 $ \underline{2}^+,1^+ $ 

$ \pi\frac{1}{2}^{-}[521]\otimes\pi\frac{3}{2}^{-}[521] $ 

2.279 $ \underline{4}^-,5^- $ 

$ \nu\frac{9}{2}^{-}[734]\otimes\nu\frac{1}{2}^{+}[620] $ 

1.686 1.678 $ \underline{6}^-,3^- $ 

$ \nu\frac{9}{2}^{-}[734]\otimes\nu\frac{3}{2}^{+}[622] $ 

1.718 1.675 $ \underline{4}^+,3^+ $ 

$ \nu\frac{7}{2}^{+}[624]\otimes\nu\frac{1}{2}^{+}[620] $ 

1.757 2.142 $ 5^+,\underline{2}^+ $ 

$ \nu\frac{7}{2}^{+}[624]\otimes\nu\frac{3}{2}^{+}[622] $ 

1.793 2.145 $ 8^-,\underline{1}^- $ 

$ \nu\frac{9}{2}^{-}[734]\otimes\nu\frac{7}{2}^{+}[613] $ 

1.944 1.848 $ \underline{7}^+,0^+ $ 

$ \nu\frac{7}{2}^{+}[624]\otimes\nu\frac{7}{2}^{+}[613] $ 

2.025 2.303 $ \underline{2}^+,1^+ $ 

$ \nu\frac{1}{2}^{+}[620]\otimes\nu\frac{3}{2}^{+}[622] $ 

2.277 $ \underline{8}^-,1^- $ 

$ \nu\frac{9}{2}^{-}[734]\otimes\nu\frac{7}{2}^{+}[624] $ 

2.301 2.286 $ \underline{2}^+,3^+ $ 

$ \nu\frac{1}{2}^{+}[620]\otimes\nu\frac{5}{2}^{+}[622] $ 

2.421 2.517 $ \underline{1}^+,0^+ $ 

$ \nu\frac{1}{2}^{+}[620]\otimes\nu\frac{1}{2}^{+}[631] $ 

2.448 $ \underline{3}^+,4^+ $ 

$ \nu\frac{1}{2}^{+}[620]\otimes\nu\frac{7}{2}^{+}[613] $ 

2.470 $ \underline{4}^+,1^+ $ 

$ \nu\frac{5}{2}^{+}[622]\otimes\nu\frac{3}{2}^{+}[622] $ 

2.499 $ 10^+,\underline{1}^+ $ 

$ \nu\frac{9}{2}^{-}[734]\otimes\nu\frac{11}{2}^{-}[725] $ 

2.526 2.454 2.013 $ 14^+ $ 

$ \nu\frac{9}{2}^{-}[734]\otimes\nu\frac{3}{2}^{+}[622]\otimes\pi\frac{7}{2}^{-}[514]\otimes\pi\frac{9}{2}^{+}[624] $ 

2.991 2.928 $ 16^+ $ 

$ \nu\frac{5}{2}^{-}[523]\otimes\nu\frac{7}{2}^{+}[613]\otimes\pi\frac{7}{2}^{-}[514]\otimes\pi\frac{9}{2}^{+}[624] $ 

3.215 2.928 $ 16^+ $ 

$ \nu\frac{9}{2}^{-}[734]\otimes\nu\frac{7}{2}^{+}[624]\otimes\pi\frac{7}{2}^{-}[514]\otimes\pi\frac{9}{2}^{+}[624] $ 

3.572 1 The $ K^{\pi} $ values favored by the GM rules [53] are underlined for two-particle states.

Table 1. Low-lying multi-particle states in 254No predicted by the PNC-CSM method.

Figure 3. Comparison between the excitation energies of the experimentally deduced and calculated multi-particle states in
$^{254}{\rm{No}}$ . The experimental data are taken from Refs. [10, 12]. The calculations are from a) PNC-CSM method in this work; b) configuration constrained potential energy surfaces method [37]; c) projected shell model [10]; d) configuration constrained potential energy surfaces method [50]; e) quasiparticle phonon nuclear model [51]; f) the Woods-Saxon potential plus the Lipkin-Nogami formalism for pairing [9]; g) semi-microscopic approach [52]; h) the Skyrme Hartree-Fock Bogolyubov model with the SLy4 force [9]. This plot extends a similar figure shown in Refs. [10, 12]. The$8^-$ state with the two-proton configuration$\pi\frac{7}{2}^{-}[514]\otimes\pi\frac{9}{2}^{+}[624]$ is indicated by dotted lines. The$8^-_1$ stands for the two-neutron state with the configuration$\nu\frac{9}{2}^{-}[734]\otimes\nu\frac{7}{2}^{+}[613]$ , and$8^-_2$ for$\nu\frac{9}{2}^{-}[734]\otimes\nu\frac{7}{2}^{+}[624]$ . The$16^+_1$ stands for the four-particle state with the configuration$\nu\frac{9}{2}^{-}[734]\otimes \nu\frac{7}{2}^{+}[613]\otimes \pi\frac{7}{2}^{-}[514]\otimes\pi\frac{9}{2}^{+}[624]$ , and$16^+_2$ for$\nu\frac{9}{2}^{-}[734]\otimes \nu\frac{7}{2}^{+}[624]\otimes\pi\frac{7}{2}^{-}[514]\otimes\pi\frac{9}{2}^{+}[624]$ .The two-particle state at 0.988 MeV is firmly assigned as the two-proton
$ 3^+ $ state with the configuration$ \pi\frac{1}{2}^{-}[521]\otimes\pi\frac{7}{2}^{-}[514] $ [9–12]. Thus, this assignment can be used to constrain the parametrizations of theoretical models. As shown in Fig. 3, the$ 3^+ $ state is predicted as the lowest two-particle state in the present PNC-CSM calculations, the configuration constrained calculations of potential-energy surfaces (PES) [37], the Woods-Saxon potential plus the Lipkin-Nogami formalism for pairing [9] and the Skyrme Hartree-Fock Bogolyubov (SHFB) model with the SLy4 force [9].In Table 1, the effect of high-order deformation
$ \varepsilon_{6} $ on the excitation energies of multi-particle states is demonstrated. The calculations without$ \varepsilon_{6} $ lead to the result that the$ 8^{-} $ ($ \pi\frac{9}{2}^+[624]\otimes\pi\frac{7}{2}^-[514] $ ) instead of the$ 3^+ $ ($ \pi\frac{1}{2}^{-}[521]\otimes\pi\frac{7}{2}^{-}[514] $ ) state, is the lowest two-particle state, which disagrees with the experimental data. When$ \varepsilon_{6} = 0.042 $ is considered, the$ 3^{+} $ state becomes the lowest lying two-particle state, and the calculated energy reproduces the experimental data very well. This is because once$ \varepsilon_{6} $ is included, the proton orbitals$ \pi\frac{7}{2}^{-}[514] $ and$ \pi\frac{1}{2}^{-}[521] $ get closer, and the positions of$ \pi\frac{1}{2}^{-}[521] $ and$ \pi\frac{9}{2}^{+}[624] $ orbitals are reversed (see Fig. 2). Apart from the$ 3^+ $ state, the theoretical results with$ \varepsilon_{6} $ in general reproduce the experimental data better also for the other multi-particle states. Thus, the inclusion of$ \varepsilon_{6} $ leads to a more reasonable single-particle level structure in this mass region.The
$ K^{\pi} = 8^{-} $ isomer is observed systematically in this mass region. Unlike the$ 8^{-} $ isomer in$ N = 150 $ isotones, its configuration is accepted to be a two-neutron state with the configuration$ \nu\frac{9}{2}^{-}[734]\otimes\nu\frac{7}{2}^{+}[624] $ in$ ^{252} {\rm{No}}$ [54], 250Fm [49] and$ ^{244} {\rm{Pu}}$ [55]. However, the configuration of the$ 8^{-} $ isomer at 1.297 MeV in$ ^{254} {\rm{No}}$ is still being discussed. A two-neutron configuration is favored by the recent experiment study [12], whereas a two-proton configuration$ \pi\frac{7}{2}^{-}[514]\otimes\pi\frac{9}{2}^{+}[624] $ is suggested in the earlier experimental works [9–11].Theoretically, the Skyrme Hartree-Fock Bogoliubov model with the SLy4 force gives only one low-lying
$ 8^- $ state with the two-proton configuration, and it is too high in energy. All calculations using the macroscopic-microscopic (MM) method predict at least two low-lying$ 8^- $ states with similar excitation energies, one is a two-proton state and the other a two-neutron state. The projected shell model [10, 56] and the quasiparticle phonon nuclear model [51] favor the two-neutron configuration of the lowest-lying$ 8^- $ state. In contrast, the other MM methods, including the present PNC-CSM, the Woods-Saxon plus the Lipkin-Nogami treatment for pairing [9], the configuration constrained PES [37] and the semi-microscopic approach [52], favor the two-proton configuration. The configuration constrained PES leads to the lowest two-neutron$ 8^- $ state in the earlier work [50]. However, when the high-order$ \varepsilon_{6} $ deformation is included, the proton configuration instead of the neutron configuration is assigned as the lowest lying$ 8^- $ state [37]. In the present PNC-CSM calculations, three low-lying$ 8^- $ states are predicted. The lowest$ 8^{-} $ state is the two-proton state with the configuration$ \pi\frac{9}{2}^{+}[624]\otimes\pi\frac{7}{2}^{-}[514] $ at the energy$ 1.272 $ MeV ($ \varepsilon_{6} = 0.042 $ ), which reproduces the experimental result of 1.297 MeV very well. The predicted low-lying two-neutron$ 8^{-} $ states are$ \nu\frac{9}{2}^{-}[734]\otimes\nu\frac{7}{2}^{+}[613] $ (denoted as$ 8^{-}_{1} $ ), and$ \nu\frac{9}{2}^{-}[734]\otimes\nu\frac{7}{2}^{+}[624] $ (denoted as$ 8^{-}_{2} $ ). The latter is too high in energy to be the observed isomer. Since$ 8^{-}_{1} $ is not the energetically favored state of the GM doublet, the excitation energy would be even higher when the residual spin-spin interaction is taken into account. However, the$ 8^{-}_{1} $ state can not be completely excluded from a study of the rotational behavior, which will be discussed in the next section.A four-particle isomer formed by the coupling of two-proton and two-neutron states was observed in
$ ^{254} {\rm{No}}$ . Two possible spin-parity assignments, i.e.$ K^{\pi} = 16^{+} $ and$ K^{\pi} = 14^{+} $ , were suggested in Refs. [10–12] and Ref. [9], respectively. The present PNC-CSM calculations predict one$ 14^+ $ state and two$ 16^+ $ states. As shown in Fig 3,$ K^{\pi} = 14^{+} $ state with the configuration$\nu\frac{9}{2}^{-}[734]\otimes \nu\frac{3}{2}^{+}[622]\otimes $ $ \pi\frac{7}{2}^{-}[514]\otimes\pi\frac{9}{2}^{+}[624] $ reproduces the experimental data very well. The lower$ K^{\pi} = 16^+_{1} $ state with the configuration$ \nu\frac{9}{2}^{-}[734]\otimes \nu\frac{7}{2}^{+}[613]\otimes \pi\frac{7}{2}^{-}[514]\otimes\pi\frac{9}{2}^{+}[624] $ is higher than the experimental data by about 0.287 MeV. The deviation is acceptable, and this configuration is favored by the recent experimental work [12] and the Wood-Saxon potential calculations [37]. Therefore, neither the$ K^{\pi} = 16^+_1 $ state nor the$ K^{\pi} = 14^{+} $ state can be ruled out by the present calculations. The excitation energy of the second$ K^{\pi} = 16^+_2 $ state with the configuration$ \nu\frac{9}{2}^{-}[734]\otimes $ $ \nu\frac{7}{2}^{+}[624]\otimes\pi\frac{7}{2}^{-}[514]\otimes\pi\frac{9}{2}^{+}[624] $ is much higher than the experimental data, and is too high to be the observed as a four-particle isomer.It can be seen in Table 1 that all four-particle states are built by coupling different two-neutron states with the same two-proton state
$ \pi\frac{7}{2}^{-}[514]\otimes\pi\frac{9}{2}^{+}[624] $ . Therefore, the main uncertainty is brought by the two-neutron states. The neutron single-particle level density is very high and its structure is complicated in the heavy and superheavy mass region. Different potentials result in quite different single-particle level structure, which is very sensitive to the adopted parameters. Therefore, a further investigation of the single-particle level structure, especially for neutrons, is needed for this mass region.A
$ K^{\pi} = 10^+ $ state was reported in the recent experiment [12]. As shown in Fig. 3, the$ 10^+ $ state is predicted by the PNC-CSM method, the configuration constrained PES [37] and the semi-microscopic approach [52]. The two latter calculations are based on the Woods-Saxon single-particle levels and show a deformed shell gap at$ N = 162 $ and the neutron orbital$ \nu\frac{11}{2}^{-}[725] $ located below this gap [52, 57]. In contrast, PNC-CSM is based on the Nilsson single-particle levels. It differs from the Woods-Saxon potential, and as shown in Fig. 2, a deformed shell gap appears at$ N = 158 $ , and the$ \nu\frac{11}{2}^{-}[725] $ level is located just above this gap. Moreover, including$ \varepsilon_{6} $ makes the$ N = 158 $ deformed shell gaps even larger, which results in the increase of the excitation energies of the$ K^{\pi} = 8^{-} $ and$ K^{\pi} = 10^{+} $ states. Based on such a single-particle level structure, the excitation energy of the$ K^{\pi} = 10^{+} $ state given by the Nilsson potential in the present calculations is 0.513 MeV higher than the experimental data, whereas the results with the Woods-Saxon potential are 0.534 and 0.413 MeV lower than the experimental data in Ref. [37] and Ref. [52], respectively. It should be noted that the$ K^{\pi} = 10^+ $ coupling is not the energetically favored state of the GM doublet. When the residual spin-spin interaction is taken into account, the excitation energy would be even higher. -
The kinematic MoI of the state
$ \left\vert \psi \right\rangle $ is given by$ J^{(1)} = \left\langle \psi \right\vert J_{x}\left\vert\psi \right\rangle/\omega $ , where the angular momentum alignment is$ \left\langle \psi \right| J_{x} \left| \psi \right\rangle = \sum_{i}\left|C_{i}\right| ^{2} \left\langle i\right| J_{x}\left| i\right\rangle + 2\sum_{i<j}C_{i}^{\ast }C_{j} \left\langle i\right| J_{x}\left| j\right\rangle $ . The calculated$ J^{(1)} $ versus the rotational frequency, based on the ground state and two-particle$ K^{\pi} = 3^+,\;8^- $ and$ 10^+ $ states in$ ^{254} {\rm{No}}$ , are compared with the experimental data in Fig. 4. In general, the experimental data are reproduced quite well.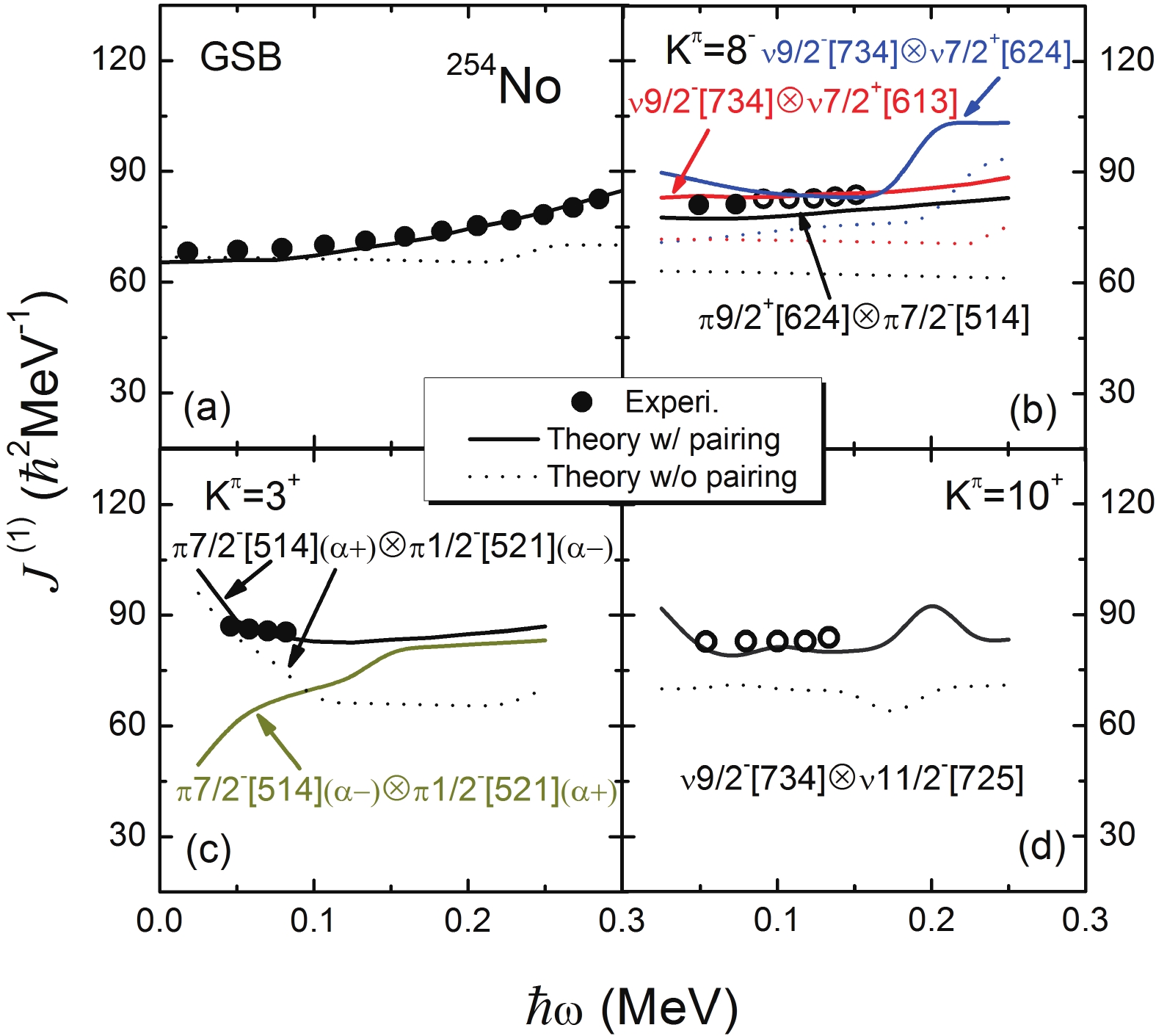
Figure 4. (color online) Kinematic moment of inertia
$J^{(1)}$ versus the rotational frequency for the ground state and two-particle ($K^{\pi} = 3^+,\;8^-$ and$10^+$ ) bands in$^{254}$ No. The experimental data [8, 10–12, 19] are denoted by symbols, and the theoretical results with/without pairing by solid/dotted lines. The last five transitions in the$K^{\pi} = 8^-$ band [11], which are placed in the$K^{\pi} = 10^+$ band [12], are denoted by open circles. The theoretical results without pairing, shown by dotted lines, are shifted down by 40$\hbar^{2}$ ${\rm MeV}^{-1}$ in order to make a comparison with the results with pairing.The
$ 3^{+} $ state is of particular interest since the$ \pi\frac{1}{2}^{-}[521] $ orbital originates from the spherical$ 2f_{5/2} $ orbital. The spin-orbit interaction strength of the$ 2f_{5/2}-2f_{7/2} $ partners determines whether$ Z = 114 $ is a magic number in the "island of stability" for shell stabilized superheavy nuclei. Rotational bands based on the$ \pi\frac{1}{2}^{-}[521] $ orbital were observed in odd-proton nuclei$ ^{251} {\rm{Md}}$ [14] and$ ^{255} {\rm{Lr}}$ [15]. Studies of these rotational bands found a signature of splitting [16, 17]. The result for the$ 3^{+} $ band in$ ^{254} {\rm{No}}$ is similar. While the bandhead energy of the$ \pi\frac{7}{2}^{-}[514] $ $(\alpha = +1/2)\otimes\pi\frac{1}{2}^{-}[521](\alpha = -1/2) $ band is lower only by about 0.6 keV than the$ \pi\frac{7}{2}^{-}[514](\alpha = -1/2)\otimes\pi\frac{1}{2}^{-}[521]$ $(\alpha = +1/2) $ band, the rotational behavior is quite different. As shown in Fig. 4(c), only the former can reproduce the experimental data well.For the
$ 8^{-} $ band, as shown in Fig. 4(b), the calculated$ J^{(1)} $ of the$ \nu\frac{9}{2}^{-}[734]\otimes\nu\frac{7}{2}^{+}[624] $ band can not reproduce the trend of the experimental data. In Ref. [12], there are only two excited members in the$ K^{\pi} = 8^- $ band, denoted by solid circles in Fig. 4(b). In this case, the experimentally deduced$ J^{(1)} $ is located in between the theoretical two-neutron$ \nu\frac{9}{2}^{-}[734]\otimes\nu\frac{7}{2}^{+}[613] $ and two-proton$ \pi\frac{7}{2}^{-}[514]\otimes$ $ \pi\frac{9}{2}^{+}[624] $ bands. In Ref. [11], the$ K^\pi = 8^- $ band is extended to spin$ I = 15\hbar $ . The data corresponding to the possible$ K^\pi = 8^- $ band extension [open circles in Fig. 4(b)] are placed in the$ K^\pi = 10^+ $ band in Ref. [12] [open circles in Fig. 4(d)]. If the possible$ K^{\pi} = 8^- $ band extension is considered, the calculated two-neutron$ \nu\frac{9}{2}^{-}[734]\otimes$ $\nu\frac{7}{2}^{+}[613] $ band agrees better with the experimental data. Nevertheless, although the calculated$ J^{(1)} $ of the$ \pi\frac{7}{2}^{-}[514]\otimes\pi\frac{9}{2}^{+}[624] $ band is a bit lower than the experimental data, it is still good enough. The lower values may come from the influence of the effective pairing strengths. When considered together with the result for the excitation energies, neither the proton configuration$ \pi\frac{7}{2}^{-}[514]\otimes\pi\frac{9}{2}^{+}[624] $ nor the neutron configuration$ \nu\frac{9}{2}^{-}[734]\otimes\nu\frac{7}{2}^{+}[613] $ can be ruled out. Further investigations are needed on both the experimental and theoretical sides.The excitation energy of the
$ K^\pi = 10^+ $ band is comparatively high, and the configuration mixing is significant. The occupation of the$ \nu\frac{9}{2}^{-}[734]\otimes\nu\frac{11}{2}^{-}[725] $ configuration is less pure. A comparatively large probability amplitude of other components in the wave function influences strongly the behavior of the$ K^\pi = 10^+ $ band. The hump in$ J^{(1)} $ at$ \hbar\omega\approx0.2 $ MeV is attributed to the contribution of the$ \nu\frac{9}{2}^{-}[734]\otimes\nu\frac{1}{2}^{-}[761] $ configuration.As shown in Fig. 1, compared with GSB,
$ J^{(1)} $ of the rotational bands based on the three two-particle states$ (K^{\pi} = 3^+,\; 8^-,\;10^+) $ are larger by about 25% in the low frequency region. A similar increase is seen in two-particle bands in the$ A = 180 $ region and has been attributed to the pairing reduction [58]. To determine if the$ J^{(1)} $ increase comes from the pairing reduction in the high-K bands in$ ^{254} {\rm{No}}$ ,$ J^{(1)} $ was calculated without pairing. We note that to make a suitable comparison with the results including pairing, the results without pairing shown in Fig. 4 (dotted lines) are shifted down by 40$ \hbar^{2} $ ${\rm MeV}^{-1} $ . The results without pairing show that the three two-particle bands have similar$ J^{(1)} $ values as GSB, and are almost constant versus the frequency$ \hbar\omega $ . Thus, we conclude that the increase of$ J^{(1)} $ in the high-K bands compared with GSB at low frequency, and the gradual increase of$ J^{(1)} $ versus frequency, can be mainly attributed to the pairing reduction. -
The nuclear pairing gap [59, 60] in the PNC-CSM formalism is defined as
$ \tilde{\Delta} = G_{0}\left[ -\frac{1}{G_{0}}\left\langle\psi\right| H_{{\rm P}}\left|\psi\right\rangle\right]^{1/2}. $

(5) For the quasi-particle vacuum band,
$ \tilde{\Delta} $ is reduced to the usual definition of the nuclear pairing gap$ \Delta $ when the Hamiltonian includes only the monopole pairing correlation [60]. Figure 5 shows the calculated neutron and proton pairing gaps$ \tilde{\Delta} $ versus the rotational frequency for GSB and the two-particle$ K^{\pi} = 3^+,8^- $ and$ 10^+ $ bands in$ ^{254} {\rm{No}}$ . The effective pairing strengths in the calculations are the same for neutrons and protons, and the difference in the pairing gaps is purely from the wave functions. In general, as shown in Fig. 5, the pairing gaps of neutrons are larger than of protons. The pairing gaps decrease with increasing frequency. The reduction in pairing with frequency is due to the rotation and the gradual alignment of the paired nucleons. The pairing gaps of GSB are larger than of the two-particle bands. The reduction in pairing for the high-K bands is due to the Pauli blocking of the orbitals near the Fermi surface.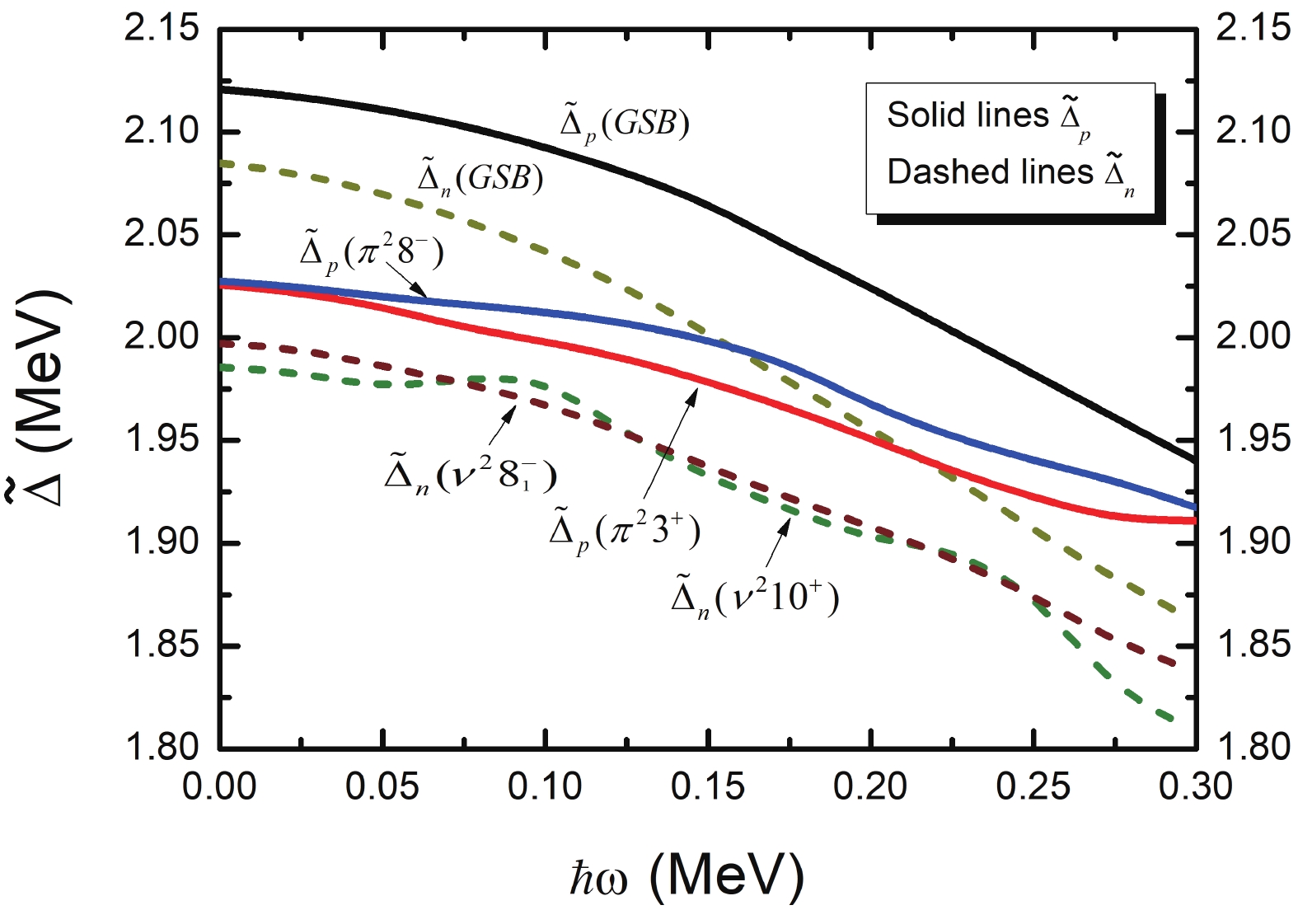
Figure 5. (color online) Calculated pairing gap
$ \tilde{\Delta} $ for the ground state and two-particle bands in$ ^{254} {\rm{No}}$ . The configurations of two-particle bands are$ \pi^2 8^- \{\frac{9}{2}^+[624]\otimes\frac{7}{2}^-[514]\} $ ,$\pi^2 3^+ \{\frac{1}{2}^-[521]\otimes $ $ \frac{7}{2}^-[514]\} $ ,$ \nu^2 8^-_1 \{\frac{9}{2}^-[734]\otimes\frac{7}{2}^+[613]\} $ and$ \nu^2 10^+ \{\frac{9}{2}^-[734]\otimes $ $\frac{11}{2}^-[725]\} $ .To examine quantitatively the dependence of the pairing gap on the rotational frequency ω and seniority ν (number of the unpaired particles), the relative pairing gap reduction factors are defined as
$ \begin{split} R_{\tau}(\omega) = & \frac{\tilde{\Delta}_{\tau}(\omega)-\tilde{\Delta}_{\tau}(\omega = {0})}{\tilde{\Delta}_{\tau}(\omega = {0})}, \\ R_{\tau}(\nu) = & \frac{\tilde{\Delta}_{\tau}(\nu)-\tilde{\Delta}_{\tau}(\nu = {0})}{\tilde{\Delta}_{\tau}(\nu = {0})}, \ \ \ \ \ \ \ \ \ \tau = p\ {\rm or}\ n. \end{split} $

(6) In the following, the seniority dependence of the pairing gap
$ R_{\tau}(\nu) $ is calculated at the bandhead$ \hbar\omega = 0 $ , and$ \tilde{\Delta}_\tau (\nu = 0) $ is adopted as$ \tilde{\Delta} $ of GSB:$ \begin{split} & {\rm GSB}:\ R_{p}(\hbar\omega = 0.3 \;{\rm MeV})\approx18.1{\text{%}},\ \ \\ &\pi^{2}3^{+}:\ R_{p}(\hbar\omega = 0.3 \;{\rm MeV})\approx5.7{\text{%}},\ \ R_{p}(\nu = 2)\approx4.5{\text{%}},\\ &\pi^{2}8^{-}:\ R_{p}(\hbar\omega = 0.3 \;{\rm MeV})\approx5.4{\text{%}},\ \ R_{p}(\nu = 2)\approx4.4{\text{%}},\\ \\ &{\rm GSB}:\ R_{n}(\hbar\omega = 0.3 \;{\rm MeV})\approx22.3{\text{%}},\ \ \\ &\nu^{2}8^{-}_{1}:\ R_{n}(\hbar\omega = 0.3 \;{\rm MeV})\approx8.0{\text{%}},\ \ R_{n}(\nu = 2)\approx4.2{\text{%}},\\ &\nu^{2}10^{+}:\ R_{n}(\hbar\omega = 0.3 \;{\rm MeV})\approx8.0{\text{%}},\ \ R_{n}(\nu = 2)\approx4.8{\text{%}}. \end{split} $

The different behavior of the observed GSB and high-K bands in
$ ^{254} {\rm{No}}$ can be explained in the following way. At the bandhead$ \hbar\omega = 0 $ , the seniority dependence of the relative pairing gap is reduced by about ~4.5%, which is due to the Pauli blocking of the unpaired nucleons occupying single-particle orbitals near the Fermi surface. This contributes to the ~25% increase of$ J^{(1)} $ for the high-K (seniority$ \nu = 2 $ ) bands compared with the ground state band (seniority$ \nu = 0 $ ). The frequency dependences of the relative pairing gap reduction at$ \hbar\omega = 0.3 $ MeV is about 20% for GSB, and about 5% (8%) for the two-proton (two-neutron) high-K bands. Therefore,$ J^{(1)} $ of the two-particle$ K^{\pi} = 3^+,\;8^- $ and$ 10^+ $ bands displays a flat behavior, while that of GSB shows a smooth increase with frequency. -
The multi-particle states and rotational properties of the two-particle
$ K^{\pi} = 3^+, \;8^- $ and$ 10^+ $ bands in$ ^{254} {\rm{No}}$ were investigated by the cranked shell model with pairing correlations treated by the particle number conserving method. The experimental excitation energies and moments of inertia of the multi-particle states are reproduced well by the calculations. The calculated Nilsson levels with the high-order deformation$ \varepsilon_{6} $ show enlarged proton$ Z = 100 $ and neutron$ N = 152 $ deformed shell gaps. Better agreement with the experimental data is achieved with such single-particle levels structures. There is a signature of splitting of the Nilsson proton orbital$ \pi\frac{1}{2}^-[521] $ . Only the state with the configuration$ \pi\frac{7}{2}^{-}[514](\alpha = +1/2)\otimes$ $\pi\frac{1}{2}^{-}[521](\alpha = -1/2) $ reproduces the experimental rotational behavior of the$ 3^+ $ state.$ J^{(1)} $ in the two-particle bands is larger than the ground state band by about 25%. A detailed investigation of the pairing shows that the increase of$ J^{(1)} $ in the two-particle bands can be attributed to the pairing reduction due to the Pauli blocking effect.One of the authors, X.-T. He, is grateful to Prof. P. Walker for his very useful comments and for carefully reading the manuscript.
High-K multi-particle bands and pairing reduction in 254No
- Received Date: 2019-10-21
- Available Online: 2020-03-01
Abstract: The multi-particle states and rotational properties of the two-particle bands in





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




















 DownLoad:
DownLoad: