The Buchdahl stability bound in Eddington-inspired Born-Infeld gravity

Despite general relativity (GR) being the most successful theory to describe gravity, there have been a number of modified theories of GR to resolve various problems, such as singularities, local energy problems and incompatibilities with our quantum world. To regularize the singularities Deser and Gibbons (1998) [1], motivated by Born-Infeld electrodynamics [2], discussed the possible forms of the gravitational analogue of Born-Infeld theory in the metric formalism, and the necessary conditions without running into the ghost problem. On the other hand, the ghost problem can also be avoided in the Palatini formalism. In particular, Vollick (2004) [3] first considered a Born-Infeld-like action for gravity in the Palatini formalism. Later on, Bañados and Ferreira (2010) [4] showed that this action can be regarded as the Eddington action if the matter action is absent [5]. Furthermore, when matter solely couples to the metric, the highly nonlinear coupling between matter and gravity could avoid the cosmological singularity in the radiation dominated era, resulting in significant deviations from GR in the extremely high density environment. Since then, this model has aroused much interest, dubbed Eddington-inspired Born-Infeld (EiBI) gravity [6].

It is known that when we apply a modified theory of gravity to a stellar sphere, the junction conditions must be dealt with carefully. For example, in $ f(R) $ gravity the matching of the first and second fundamental forms [7] is not sufficient to merge the two spacetime regions since the derivative terms of curvatures in the field equations play important roles [8,9]. In contrast to the higher derivative theory, EiBI is equivalent to GR in vacuum, so that the junction conditions are the same as those in GR. This advantage makes EiBI an interesting modification of GR. Nevertheless, when applying EiBI to compact stars, it has been found that there are some pathologies, such as the surface singularities [10] , and anomalies associated with phase transitions [11]. However, the surface singularities can be prevented if the equations of state (EoS) is modified by the geodesic deviation (Jacobi) equation near the surface of a star [12]. This aspect is quite similar to EoS in $ f(R) $ theories, in which more stringent junction conditions are needed [13,14].

In GR, the Buchdahl stability bound implies that the radius of a stable stellar sphere cannot be smaller than $ 9/8 $ of its gravitational radius [15]. This inequality is independent of EoS contained in the sphere, which is a generic feature of GR. For EiBI gravity, it is not clear if there is a similar Buchdahl bound. However, it is expected that the bound in GR should be different from that in EiBI gravity.

To address this issue, we start from the EiBI action [3,4] with the geometric units $ G = c = 1 $, given by

where $ {{g}} $ and $ {{\cal{R}}} $ correspond to the metric tensor and Ricci curvature based on the connection $ \Gamma $ with the matrix elements $ g_{\mu\nu} $ and $ \cal{R}_{\mu\nu} $, respectively, and $ S_{M}[g,\Psi] $ is the matter action, in which the generic matter field $ \Psi $ couples only to the metric tensor $ g $. Note that the cosmological constant is defined as $ \Lambda = (\lambda-1)/\kappa $ in this model. However, when it comes to compact stars, it is reasonable to set $ \lambda = 1 $ such that $ \Lambda = 0 $. In the Palatini formalism, varying the action with respect to $ g $ and $ \Gamma $ independently gives the equations of motion of EiBI gravity as follows:

where $ \tau = \sqrt{{\left| {{{g}}} \right|}/{\left| {{{q}}} \right|}} $ with $ {\left| {\bullet} \right|} $ denoting the absolute value of the determinant of the matrix, $ T^{\mu\nu} $ is the physical energy momentum tensor, and $ q^{\mu\nu}\equiv q_{\mu\nu}^{-1} $. Here, the auxiliary metric is used for raising/lowering the index in the geometric sector, while the metric tensor is for the matter sector. As a result, it follows that

By defining $ {\cal{R}}\equiv {\cal{R}}^{\mu}_{\mu} $ and $ T\equiv T^{\mu}_{\mu} $, the field equations can be recast into the GR-like ones with the Einstein tensor built with the auxiliary metric [16], given by

where $ {\cal{P}} = (\tau-1)/(8\pi\kappa)-\tau T/2 $ is the isotropic pressure and $ {\cal{T}}^{\mu}_{\nu} $ is defined as the "auxiliary" energy momentum tensor. Furthermore, by taking the determinant of Eq. (4), we can express $ \tau $ solely in terms of $ T^{\mu}_{\nu} $ as

If we model the self-gravitating sphere by a perfect fluid with $ T^{\mu}_{\nu} = (\rho+p)u^{\mu}u_{\nu}+p\delta^{\mu}_{\nu} $, where $ \rho $, $ p $ and $ u^{\mu} $ denote the energy density, pressure and four-velocity of the fluid with $ u^{\mu}u_{\mu} = -1 $, respectively, we can further write $ \tau $ in terms of $ \rho $ and $ p $ as

where $ a\equiv\sqrt{1+8\pi\kappa\rho} $ and $ b\equiv\sqrt{1-8\pi\kappa p} $ are required to be positive real number. In addition, we can define the "auxiliary" density $ \tilde{\rho} $ and pressure $ \tilde{p} $ in terms of $ a $ and $ b $ by:

In a spherically symmetric and static spacetime, the physical and auxiliary metrics are given by

respectively, where $ {\rm d}\Omega^2 = {\rm d}\theta^2+\sin^2\theta\; {\rm d}\phi^2 $. For a perfect fluid, $ T^{\mu\nu} = (\rho+p)u^{\mu}u^{\nu}+pg^{\mu\nu} $, the relations between the two sets of metrics $ g_{\mu\nu} $ and $ q_{\mu\nu} $ via Eq. (3) are given by

Once the auxiliary metric is solved, the physical one can be obtained immediately, and vice versa. We note that these two metrics are identical to those in the absence of matter, i.e. vacuum, in which $ a = b = 1 $.

With the auxiliary metric at hand, we can also solve the auxiliary Einstein equations in Eq. (5) as in GR. First, we give an ansatz $ B^2\equiv\big[1-2m(r)/r\big]^{-1} $, where $ m(r) $ represents the auxiliary mass within the radial distance $ r $. The $ tt $ and $ rr$-components lead to

and

respectively, where the “ ' ” denotes the derivative with respect to the coordinate $ r $. Together with $ \tilde{\nabla}_{\alpha}{\cal{T}}^{\alpha}_{\beta} = 0 $ ($ \tilde{\nabla} $ denotes the covariant derivative associated with $ q_{\alpha\beta} $), we find

which is the Tolman-Oppenheimer-Volkoff (TOV) equation [17] for auxiliary quantities, as expected. With the help of Eq. (9), the derivative of $ \tilde{p}(\rho,p) $ with respect to $ r $ can be written in terms of $ {\rm d}p/{\rm d}r $, resulting in the modified TOV equation in EiBI gravity, given by

where $ c_{s}^2\equiv {\rm d}p/{\rm d}\rho $ with $ c_{s} $ the speed of sound. From this equation, both $ \kappa>0 $ and $ \kappa<0 $ are allowed to support an equilibrium stellar structure [18-20]. However, for $ \kappa<0 $, when some generic first-order phase transitions are present inside a star [11], the energy density $ \rho $ can not be monotonically non-increasing throughout the star interior. As a result, we will only focus on the case of $ \kappa>0 $ in this study.

By taking the derivative of $ \tilde{p} $ in Eq. (12) and substituting the expression into Eq. (13), we find

which characterizes how the average auxiliary density changes in accordance with the auxiliary potentials, and plays the key role in proving the Buchdahl stability bound. Naively, we would expect the same Buchdahl stability bound as in GR due to the GR-like field equations of the auxiliary quantities. However, in order to examine the bound, we need to express these auxiliary quantities in terms of the physical ones. Due to the highly nonlinear coupling of matter to gravity in EiBI, EoS clearly affects the determination of the bound.

For a star submerged in the Schwarzshild vacuum, we use the Darmois-Israel matching conditions [7] since EiBI is equivalent to GR in vacuum due to $ B^{-2}(r) = A^{2}(r) = G^{-2}(r) = F^{2}(r) = 1-2{\cal{M}}/r $, where $ \cal{M} $ is the Schwarzschild mass in the spherically static spacetime. As the auxiliary mass $ m(r) $ is quite different from the physical one, with the mass function appearing in the physical metric inside the interior of a star, it should match $ m(r_{s}) = \cal{M} $ at radius $ r_{s} $ with the condition $ p(r_{s}) = 0 $. This suggests that we should take another ansatz $ G^2\equiv\big[1-2M(r)/r\big]^{-1} $ together with $ G^2 = B^2/ab $, where $ M(r) $ stands for the physical mass, to obtain

or equivalently

The "effective" density associated with $ M(r) $ can be defined by $ \rho_{\rm{eff}}\equiv M'(r)/4\pi r^2 $ in analogy to Eq. (11). Subsequently, we derive

Instead of the auxiliary density $ \tilde{\rho} $, $ \rho_{\rm{eff}} $ is the one in EiBI, corresponding to the physical density $ \rho $ in GR. Therefore, the non-increasing monotonicity of $ \rho_{\rm{eff}} $ must be assumed to show the Buchdahl stability bound. On the other hand, it is worth noting that the second term of $ (1-ab)/8\pi r^2 $ in Eq. (17) is potentially divergent as $ r\rightarrow 0 $ unless $ ab = 1 $. To avoid the singularity of $ \rho_{\rm{eff}} $ in this model, we must have $ ab = 1 $ at the center of a star as $ r\rightarrow 0 $. This situation is analogous to the surface singularities of the Ricci curvature associated with the metric tensor $ g_{\mu\nu} $ [10,12].

A crucial assumption in proving the Buchdahl stability bound in GR is the monotonically non-increasing property of the physical density $ \rho $. However, is the monotonically non-increasing $ \rho $ sufficient to have the same monotonic behavior of $ \tilde{\rho}(\rho,p) $ and $ \rho_{\rm{eff}}(\rho,p) $? To answer this question, let us examine the differential relation between $ \tilde{\rho} $ and $ \rho $:

The term in the numerator with $24\pi\kappa(\rho+p)a^2c_{s}^2+ (3b^2+$$ a^2)b^2>0 $ is required to guarantee the non-increasing monotonicity of $ \tilde{\rho} $ once $ \rho $ is such. For a positive $ \kappa $, the positivity is true if the null energy condition holds, i.e. $ \rho+p\geqslant 0 $.

For the effective density, taking the derivative of Eq. (17) with respect to $ r $ gives

Since the derivative terms associated with $ a $ and $ b $ will pick out one order higher of $ \kappa $, we collect them as $ \cal{O}(\kappa) $ terms. Clearly, the first term in Eq. (19) is negative if $ \rho $ is monotonically non-increasing according to Eq. (18). However, the assumption of the monotonically non-increasing $ \rho $ cannot lead to the same monotonicity of $ \rho_{\rm{eff}} $ due to the potentially positive terms in Eq. (19). To elaborate, we define the $ \kappa $ energy condition $ ab\geqslant 1 ( \rho-p\geqslant$ $ 8\pi\kappa\rho p $) and consider if this condition is violated or not. For $ ab\geqslant 1 $ ($ \rho-p\geqslant 8\pi\kappa\rho p $), $ a^2c_{s}^2\leqslant b^2 $, while in the GR case with $ \kappa\rightarrow 0 $, $ \rho-p\geqslant 0 $ ($ c_{s}^2\leqslant 1 $), which is just the requirement for the causal energy condition with positive density and pressure. On the other hand, $ ab<1 $ ($ \rho-p< 8\pi\kappa\rho p $) gives $ a^2c_{s}^2>b^2 $, which violates the causality condition if $ \kappa\rightarrow 0 $, but is allowed for any finite value of $ \kappa $. In these two cases, the net effect can be offset only if the terms in the square bracket of Eq. (19) are positive, i.e.

For $ \cal{O}(\kappa) $, we are obliged to impose this condition as an additional assumption, if we want to interpret this effective density as the physical one corresponding to GR, i.e. the density contributing to the physical mass $ M(r) $. Since the profile of $ \rho $ depends on EoS contained inside the star as well as the modified TOV equation in Eq. (14), the assumption of the monotonically non-increasing $ \rho_{\rm{eff}} $ limits the possible classes of EoS in the EiBI theory. Note that the three densities tend to be the same in the GR limit of $ \kappa\rightarrow 0 $.

We now show the corresponding Buchdahl stability bound in the EiBI theory based on the assumptions made above. To begin with, we can prove that if $ \rho_{\rm{eff}} $ is a monotonically non-increasing function, then

where $ r_{s} $ is the radius of the star at which $ p(r_{s}) = 0 $ and $ {\cal{M}}\equiv M(r_{s}) $.

Proof. By definition, $ M(r) = \int^{r}_{0}4\pi\xi^2\rho_{\rm{eff}}(\xi){\rm d}\xi $. Using the mean-value theorem, there exists $ \bar{r}\in(0,r) $, such that

resulting in

where $ \bar{\rho}_{\rm{eff}}(r)\geqslant\bar{\rho}_{\rm{eff}}(r_{s}) $ due to the non-increasing monotonicity, and $ M(r_{s}) = \cal{M} $.

Together with Eq. (16), we readily obtain

On the other hand, if $ \tilde{\rho} $ is a monotonically non-increasing function, then

where we have used the fact that $ m(r_{s}) = M(r_{s})\equiv\cal{M} $ at the surface ($ a = b = 1 $) of the star.

From the inequalities in Eqs. (22) and (23), we get the dual relations between the two mass functions. In order not to form a black hole, we must have $ r-2m>0 $ as well as $ r-2M>0 $ throughout the interior of the star. The signs of the extra terms in the inequalities, which are absent in GR due to $ a = b = 1 $, depend on the sign of $ (ab-1) $. If the $ \kappa $ energy condition holds ($ ab\geqslant 1 $), the inequality in Eq. (22) is stronger than (or equal to) that in Eq. (23), and the other way around if it is violated ($ ab<1 $). When proving the Buchdahl stability bound, we will use the stricter assumption depending on the $ \kappa $ energy condition.

Furthermore, if $ \tilde{\rho} $ is a monotonically non-increasing function, then

Proof.

where $ \bar{r}\in(0,r) $. Here, we have used the mean-value theorem and non-increasing monotonicity of $ \tilde{\rho} $ to obtain the inequality.

Theorem. If (i) both $ \tilde{\rho} $ and $ \rho_{\rm{eff}} $ are finite and monotonically non-increasing functions, (ii) $ A^2 $ and $ B^2 $ are positive definite, and (iii) the $ \kappa $ energy condition ($ ab\geqslant 1 $) holds, the Buchdahl stability bound in EiBI gravity is given by

where

Proof. With Eq. (24) and $ A(B)>0 $, integrating Eq. (15) from $ r $ to $ r_{s} $, one gets

To match the second fundamental form to the Schwarzchild vacuum, it is required that

leading to

and

If the $ \kappa $ energy condition ($ ab\geqslant 1 $) holds, by writing $ m(r) $ in terms of $ M(r) $ we have $ r-2m = (r-2M)/ab $, which yields $ M(r)\geqslant\displaystyle\frac{r^3}{r_{s}^3}\cal{M} $ from Eq. (22). As a result, we obtain

All of the above imply

solving the inequality with the desired result.

If the $ \kappa $ energy condition ($ ab\geqslant 1 $) holds throughout the interior of the sphere, $ g $ is positive definite. This means that the lower bound of the stable radius in EiBI gravity is larger than $ (9/4)\cal{M} $. On the other hand, if the $ \kappa $ energy condition ($ ab<1 $) is violated, we replace Eq. (23) with $ m(r)\geqslant\displaystyle\frac{r^3}{r_{s}^3}\cal{M} $ in the proof to get the same bound as in GR.

The intuitive explanation is the EoS switch-on of the "repulsive effect" in EiBI gravity. It becomes clear by expanding the auxiliary quantities in Eqs. (8) and (9) to the leading order of $ \cal{O}(\kappa) $, given by

We observe that the repulsive effect with $ \tilde{\rho}<\rho $ and $ \tilde{p}>p $ in EiBI is significant only when $ \rho>[(3+2\sqrt{3})/5]p\simeq $$ 1.29p $. Note that we do not consider the case with $ \rho<[(3-2\sqrt{3})/5]p\simeq -0.09p $ if the physical density and pressure are both positive inside the star. For $ \tilde{\rho}>\rho $ and $ \tilde{p}>p $, the effect is reduced due to the increased density in $ \tilde{\rho} $ compared to $ \rho $. When including all orders of $ \kappa $, the two cases correspond to $ ab>1 $ and $ ab<1 $, respectively. Note that the criteria for the repulsive effect to become significant depend on the $ \kappa $ energy condition and the specific value of $ \kappa $, but the mechanism is the same as from the contributions of $ \cal{O}(\kappa) $. In Fig. 1, we plot the difference between the auxiliary and physical densities $ 8\pi \kappa (\tilde\rho-\rho) $ v.s. the corresponding pressures $ 8\pi \kappa (\tilde{p}-p) $ , for $ ab $ ranging from $ 0.85 $ to $ 1.2 $ , to show the regions where the repulsive effect is significant or not. The borderline near $ ab\simeq 1 $ corresponds to $ \tilde{\rho}\simeq\rho $, where the repulsive effect switches on/off. Moreover, as we shall see, the critical value of $ ab = 1 $ corresponds to an exotic EoS.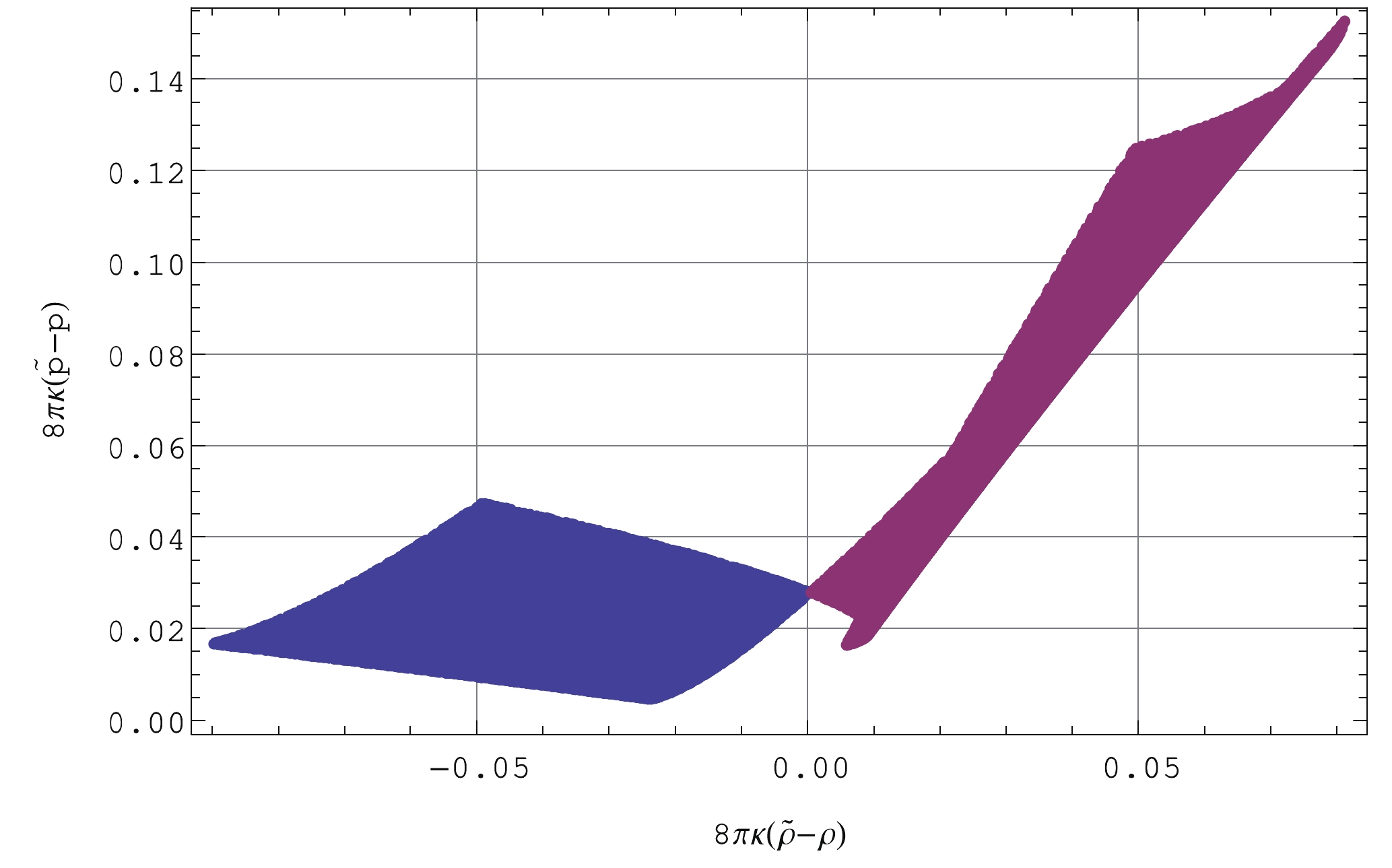

Figure 1.  (color online) Difference between the auxiliary and physical densities $ 8\pi \kappa (\tilde\rho-\rho) $ v.s. the corresponding pressures $ 8\pi \kappa (\tilde{p}-p) $ in terms of $ ab $, where the blue (left) and purple (right) regions represent $ ab\gtrsim1 $ with $ 1.1<a<1.2 $ and $ 0.942<b<1.0 $ , and $ ab\lesssim1 $ with $ 1.0<a<1.1 $ and $ 0.85<b<0.942 $, respectively. The borderline near $ ab\simeq 1 $ corresponds to $ \tilde{\rho}\simeq\rho $. Here, $ a\equiv\sqrt{1+8\pi\kappa\rho} $ and $ b\equiv\sqrt{1-8\pi\kappa p} $, while $ \tilde{\rho} $ and $ \tilde{p} $ are given in terms of $ a $ and $ b $ from Eqs. (8) and (9), respectively.

The "singularity avoidance" feature of this model [16] relies on the fact that as $ b\rightarrow 0 $, i.e. $ 8\pi\kappa p\rightarrow 1 $, the auxiliary energy density (pressure) diverges but with a finite physical energy density (pressure). In this regard, $ \kappa $ can be taken as a cutoff near the Planck scale. However, as noted previously, if we assume $ b\neq 0 $ inside the star, $ \rho_{\rm{eff}} $ is still potentially divergent due to $ (1-ab)/8\pi r^2 $ as $ r\rightarrow 0 $. The remedy to cure the pathology is to set $ ab = 1 $, or equivalently

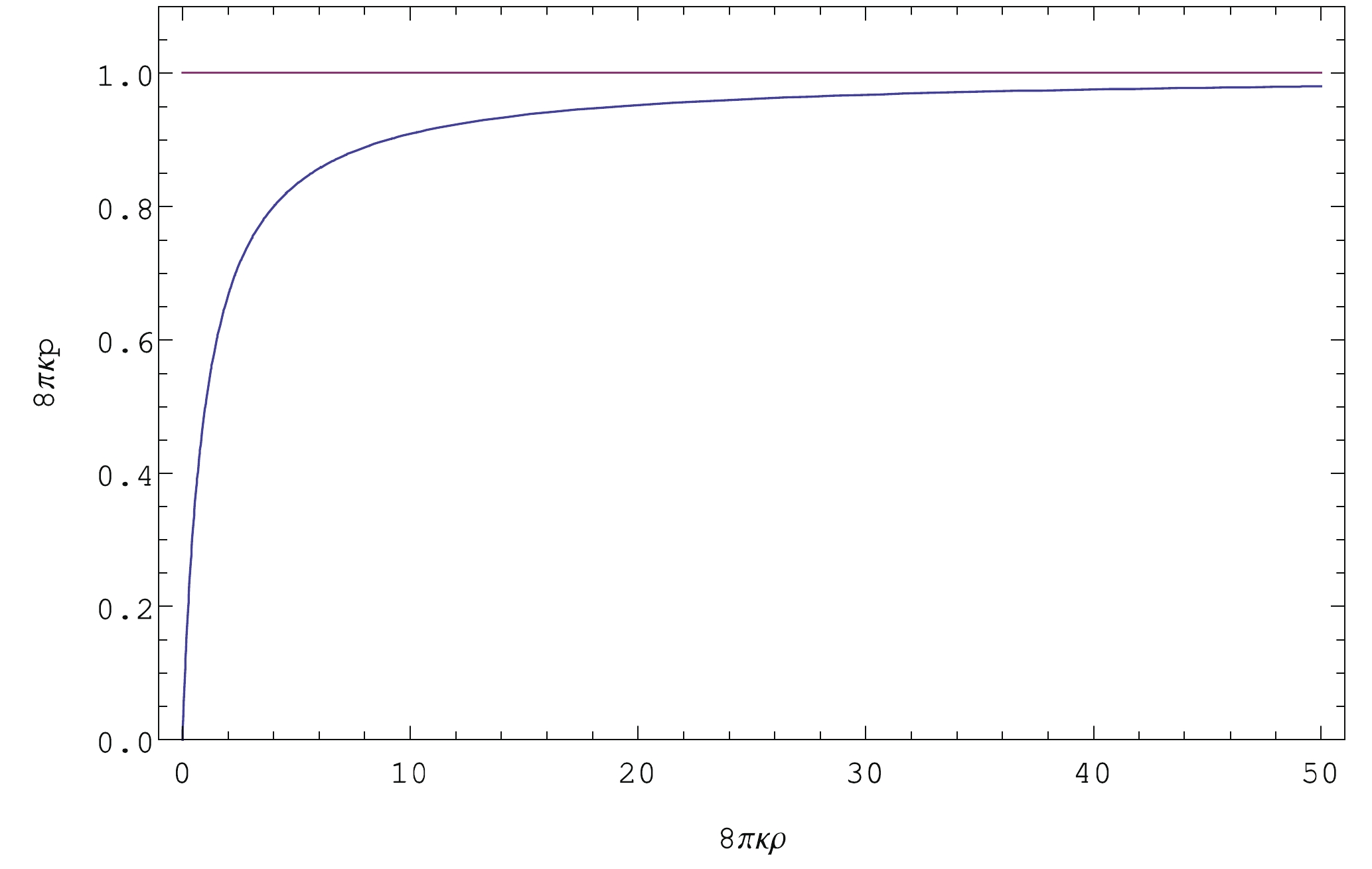
around $ r = 0 $. Physically, this leads to an exotic EoS controlled by $ \kappa $ near the center ($ r\lesssim\sqrt{\kappa} $) of a star regardless of the real matter content. For this exotic EoS, the physical pressure $ p $ is bounded by $ 1/8\pi\kappa $. On the other hand, there is no bound on the physical density $ \rho $ , as $ \rho\rightarrow\infty $ if $ p\rightarrow 1/8\pi\kappa $. In other words, the cutoff of the physical pressure does not prevent the divergence of the physical density, as shown in Fig. 2. Remarkably, this situation is in close analogy to the Hagedorn temperature [21], in which the energy and entropy diverge but with a fixed and finite (Hagedorn) temperature. This Hagedorn-like EoS [22,23] manifests somewhat a deep connection of EiBI with the string theory [23-25], which deserves further investigation. However, the discussions above are only at the classical level. The pressure near the cutoff scale may signal a breakdown of EiBI or Hagedorn-like phase transition. Whether the divergence of $ \rho $ really occurs during the gravitational collapse [26-28] requires a real understanding of EiBI as well as its quantized version.

Figure 2.  (color online) Exotic EoS behavior (blue curve) at the center of a star in the $\rho - p$ plane, which is analogous to the effect of the Hagedorn temperature, where the straight line (purple) represents the pressure bound $1/8\pi \kappa $

The Buchdahl stability bound in EiBI is larger than (or equal to) $ (9/4){\cal{M}} $ in GR due to the repulsive effect if the $ \kappa $ energy condition ($ ab\geqslant 1 $) holds throughout a star. To elaborate this statement, we see that $ g $ in Eq. (26) can be calculated using the mean-value theorem such that

where $ \bar{a} = \bar{a}(r_{s})\equiv a(\bar{r}) $ and $ \bar{b} = \bar{b}(r_{s})\equiv b(\bar{r}) $, respectively, for $ \bar{r}\in(0,r_{s}) $. Expanding in terms of $ \kappa $, we have $ r_{s}/2{\cal{M}}\geqslant 9/8+(3\pi/8)\kappa(\bar{\rho}-\bar{p})+{\cal{O}}(\kappa^2) $. This inequality provides a direct way to constrain $ \kappa $ just by examining the radii and masses of the most compact spherical objects in the sky. For instance, the typical density $ \bar{\rho}\sim 10^{18}\; {\rm{kg}}/{\rm{m}}^3 $, radius $ r_{s}\sim 12\; {\rm{km}} $ and gravitational radius $ 2{\cal{M}}\sim 6\; {\rm{km}} $ with $ {\cal{M}}\sim 2M_{\odot}\sim 3\; {\rm{km}} $ of a neutron star (NS) [29,30] yield the bound $ \kappa\lesssim 10^{9}\;{\rm{m}}^2 $. Even though this gives a constraint on $ \kappa $ of similar order of magnitude as those in Refs. [18,31], the bound on $ \kappa $ can be further improved by one order if a NS with the same radius but a mass around $ 3M_{\odot} $ is observed in the future.

On the other hand, if we believe that EiBI gravity is a viable theory down to the cutoff scale $ \kappa $ , with the observed minimally stable radius of a spherical compact object of $ (9/4)\cal{M} $, this would indicate that an unusual EoS, violating the $ \kappa $ energy condition ($ ab<1 $), is contained inside the compact object. This sheds a new light on how we can probe EoS contained inside a compact star just by examining its smallest stable radius. However, the Buchdahl stability bound is modified, as that in GR, if an anisotropic fluid is considered [32-34]. Such a situation merits further studies in the future.

We thank Professor W.-T. Ni for useful suggestions during a visit of W.-X. Feng at National Center for Theoretical Sciences (NCTS), Taiwan. W.-X. Feng was grateful to J. C. Baez and M. Mulligan for helpful discussions as well as V. Hubeny and C.-S. Chu on the relevant issues during the Formosa Summer School on High Energy Physics 2018.

In Table 1, we show the nomenclature and notation used in EiBI gravity.

symbol	description
$\kappa $	EiBI model parameter (of length-squared dimension)
${g_{\mu \nu }}$	physical metric tensor
${q_{\mu \nu }}$	auxiliary metric tensor
${{\cal{R}}_{\mu \nu }}$	Ricci tensor associated with ${q_{\mu \nu }}$
${{\cal{G}}_{\mu \nu }}$	Einstein tensor associated with ${q_{\mu \nu }}$
${T_{\mu \nu }}$	physical energy momentum tensor
${{\cal{T}}_{\mu \nu }}$	auxiliary energy momentum tensor
$\rho $	physical energy density
p	physical pressure
$a = \sqrt {1 + 8\pi \kappa \rho } $	transformation factor between the two metrics depending on ρ
$b = \sqrt {1 - 8\pi \kappa p} $	transformation factor between the two metrics depending on p
m	auxiliary mass function associated with qµν
$\tilde \rho $	auxiliary energy density associated with m
$\tilde p$	auxiliary pressure
M	physical mass function associated with gµν
ρeff	effective energy density associated with M
rs	radius of the self-gravitating sphere (star)
${\cal{M}} = m\left( {{r_s}} \right) = M\left( {{r_s}} \right)$	total mass of the self-gravitating sphere (star)

Table 1.  Nomenclature and notation of EiBI gravity