-
An unsolved problem in cosmic ray physics is the "knee" structure in the energy spectrum, namely a significant bending of the spectrum from the power-law index of approximately –2.7 to –3.1 around a few PeV. The reasons for the knee structure are closely related to the origin, acceleration and propagation mechanisms of cosmic rays, but there is no consistent measurement so far. Several experiments have measured all-particle spectra around the knee region, such as KASCADE-Grand [1], Tibet-AS
$ \gamma $ [2], EAS-TOP [3]. These experiments exhibited a similar knee-like structure at energies of about 4 PeV, within a factor of two in flux values [4].In addition, the energy spectra of individual components are very different. For example, the unfolded proton spectrum measured by the KASCADE experiment shows a steepening at 2 PeV or 3PeV, based on QGSJET01 and SIBYLL2.1 models, respectively [5]. However, the hybrid experiment ARGO-YBJ and two prototypes of WFCTA show that the energy spectrum for H&He has a knee-like structure at 700 TeV [6]. The main reasons for this situation are the lack of absolute energy scale and of the way to identify the type of primary particles in cosmic rays. LHAASO [7, 8], located in Daocheng Haizishan, 4410 m a.s.l., Sichuan Province, China, will throw new light on this long-standing issue.
The LHAASO site is at an ideal altitude for knee physics research because the atmospheric depth is close to the maximum of development of the cosmic ray extensive air shower (EAS) [9], so that the fluctuation of EAS and the dependence on the interaction model will be minimum. Similar to the ARGO-YBJ experiment, WCDA can obtain the absolute energy scale using measurement of the Moon shadow [10]. Because the detection threshold of WCDA can be as low as several hundred GeV, it can be directly compared with the measurement results of space experiments to study the error of the energy scale.
Furthermore, LHAASO contains four types of detectors, which can detect electromagnetic particles, muons, Cherenkov and fluorescent photons in EAS. Multi-variable measurements of EAS can effectively distinguish the components of cosmic rays. Thus, the energy spectra of the individual components can be precisely measured by LHAASO using multi-variable analysis (MVA).
LHAASO plans to obtain consecutive measurement of energy spectra in four stages. In the first stage, WCDA delivers the absolute energy scale to WFCTA by hybrid observation of cosmic rays from 10 TeV to 100 TeV. In this energy range, the energy spectra measured by LHAASO overlap with the spectra from space experiments. The second stage is mainly for knee observation of the light nuclei components of cosmic rays with energies from 100 TeV to 10 PeV by hybrid detection with WFCTA, WCDA, and KM2A. In the third stage, the layout of WFCTA will be changed to measure the knee of the heavy nuclei from 10 PeV to 100 PeV [11]. WCDA will not be included in the hybrid detection due to saturation. The last stage is for the second knee study from 100 PeV to 1 EeV, in which WFCTA will be operated in the fluorescence observation mode [12].
In the first three observation stages, the elevation angles of WFCTA are
$ 90^{\circ} $ ,$ 60^{\circ} $ ,$ 45^{\circ} $ , respectively. Their corresponding atmospheric depths are around the shower maximum positions of cosmic rays in their respective observation stages. This paper is devoted to the prospect of energy spectra measurement of pure proton and H&He in the second stage using simulations. -
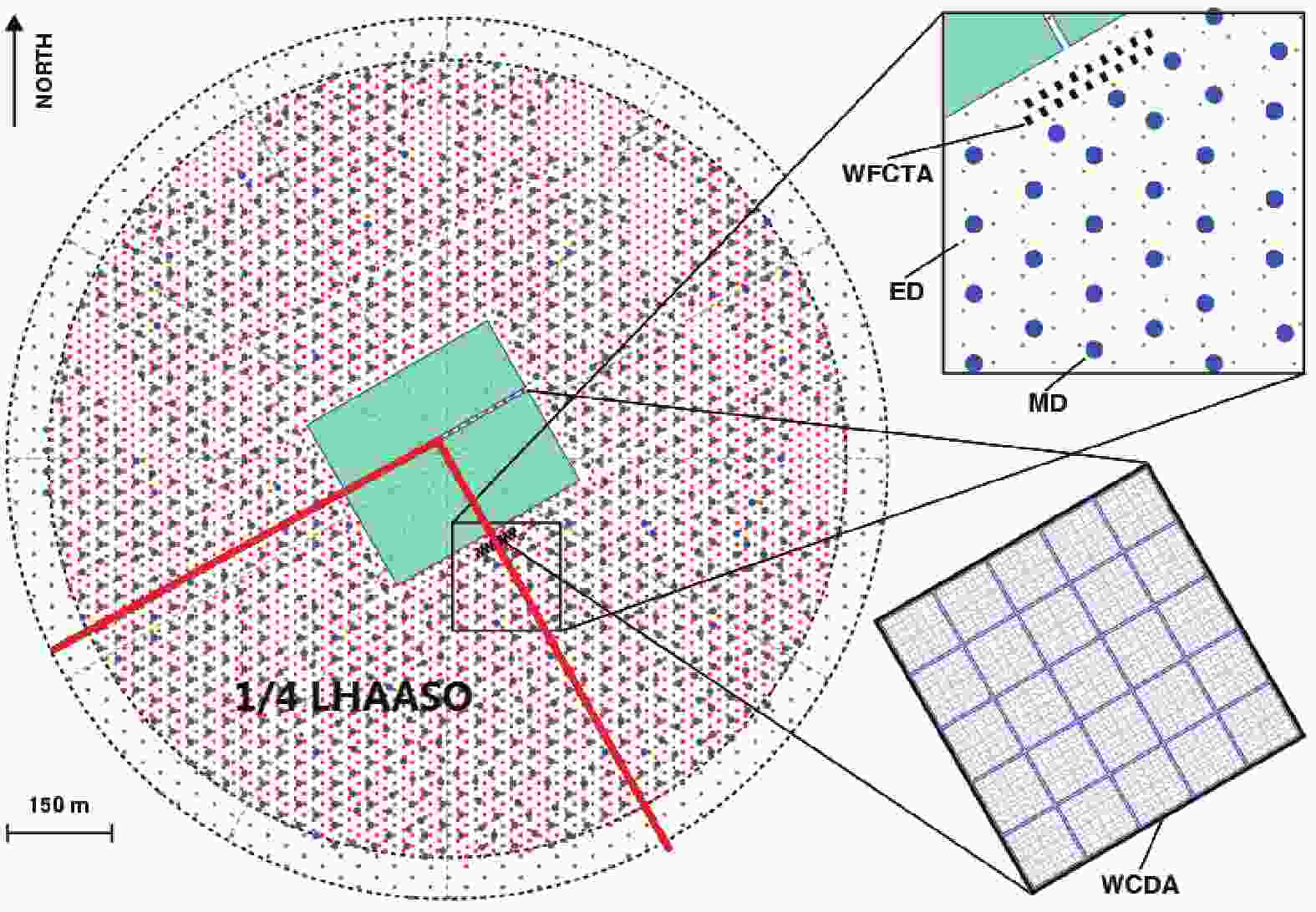
LHAASO was formally approved on December 31, 2015 and is now in construction. The detector layout of the LHAASO experiment is shown in Fig. 1. LHAASO consists of four types of detectors: electromagnetic detectors (red dots), muon detectors (blue dots), water Cherenkov detector (blue squares) and wide field-of-view (FOV) Cherenkov telescopes (black rectangles). There are many vacant slots in the distribution of muon detectors (blue dots), because the terrain makes it impossible to install them.
WCDA [13], located at the center of LHAASO, is a water Cherenkov detector array with a total area of 78000
$\rm m^2 $ . It detects Cherenkov light produced in water by the cascade of secondary particles in EAS. WCDA consists of three water ponds: two have an area of$\rm 150~ m\times 150~ m $ , and one has an area of$\rm 300~ m\times110~ m $ . All ponds have a water depth of 4.5 m. Each pond is divided into small cells with an area of$\rm 5~ m\times 5~ m $ , with two photomultiplier tubes (PMT) anchored to the bottom at the center of the cell. In one of the$\rm 150~ m\times 150~ m $ ponds, in the lower left quarter in Fig. 1, a 1-inch PMT is placed right next to a 8-inch PMT to enlarge the dynamic range to 200000 photoelectrons. It allows measurement of cosmic rays with energy up to 10 PeV [14]. This pond is called WCDA++ , and is used to achieve hybrid detection with WFCTA.WFCTA is located 85 meters away from the center of WCDA++. It detects Cherenkov and fluorescence photons in the air shower. The angle of elevation of the telescope's main axis is set to
$ 60^{\circ} $ . Each telescope includes a spherical mirror to collect Cherenkov and fluorescence photons and to reflect them onto the camera [15] with the effective area of$\rm 5~m^2 $ . The camera is located at the focal point of the spherical mirror and its function is to convert Cherenkov/fluorescence photons into electrical signals. The optical sensor of the camera is SiPM [16], with 1024 pixels in total. The pixel of each SiPM is$ 0.5^{\circ}\times0.5^{\circ} $ and the camera sees a FOV of$ 16^{\circ}\times16^{\circ} $ . All parts of the telescope are placed in a container for convenience of movement and arrangement. Two telescope prototypes have been operated successfully at Yangbajing cosmic ray observatory in Tibet [17].KM2A contains two sub-arrays: electromagnetic detector array (ED) and muon detector array (MD). ED array [18] covers an area of 1.3 km2 consisting of 5195 plastic scintillator detectors with a spacing of 15 meters. One ED detector has an effective area of 1 m2. As its name says, ED detects the electromagnetic particles in EAS. The MD array is an underground water Cherenkov detector array [19]. There are 1171 muon detectors, covering an area of 1 km2 , with a spacing of 30 meters. The area of one muon detector is 36 m2, and it detects muons in EAS.
The 1/4 LHAASO array includes WCDA++, six Cherenkov telescopes, 1272 EDs and 300 MDs. The layout of the 1/4 array is shown in Fig. 1. It will run for a few years to achieve the goal of measuring energy spectra of the light nuclei components.
Since full-coverage array can provide more accurate geometric information of air showers, the secondary particles are mainly measured by WCDA++ in the second hybrid detection stage. This means that the shower core position at this stage is outside of the ED array. Therefore, ED is not included in our simulations.
-
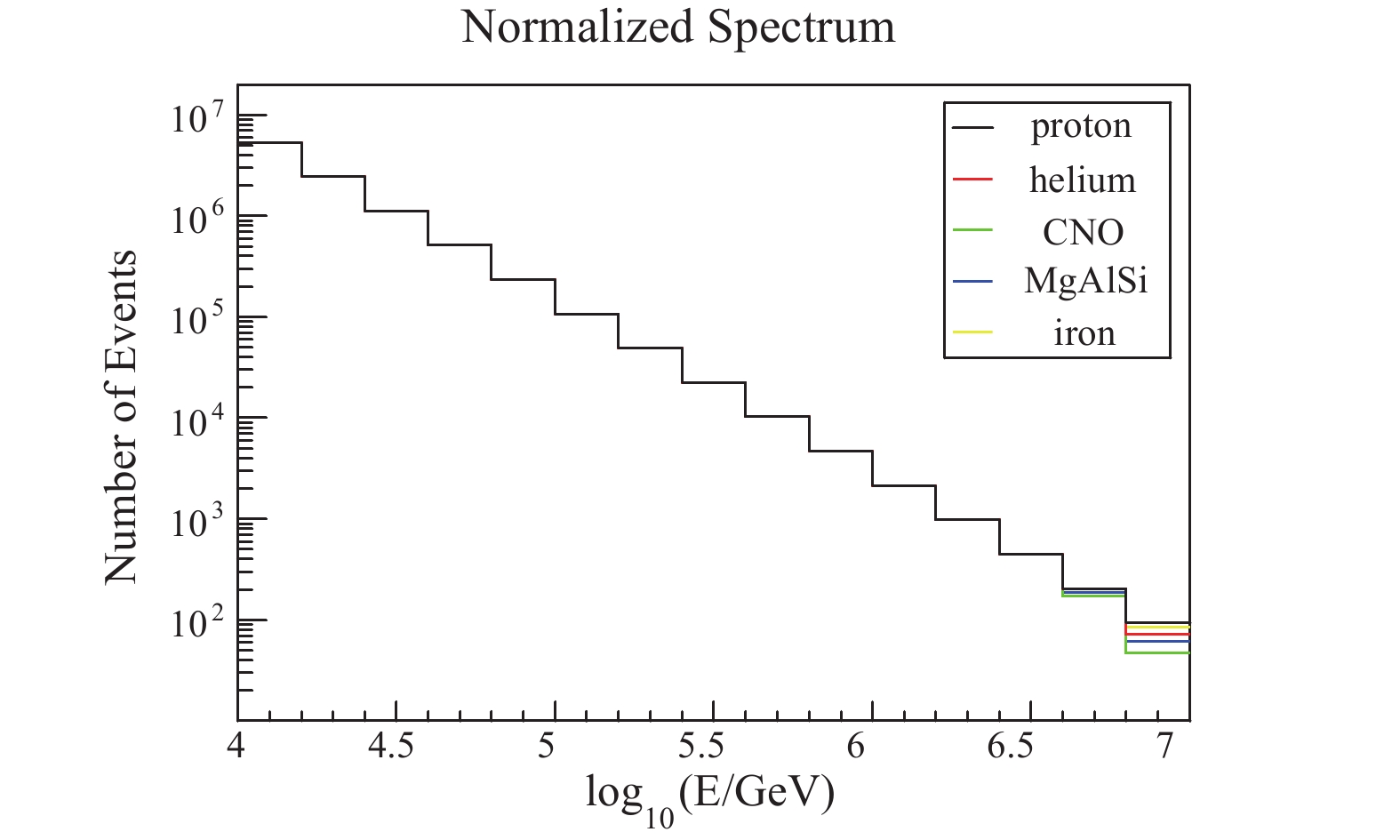
The cascade processes of primary cosmic rays in the atmosphere are simulated with the CORSIKA [20] program, version 6990. The EGS4 model is chosen for electromagnetic interactions. The QGSJET02 and GHEISHA models are chosen for the high and low energy hadronic processes, respectively. The information about Cherenkov photons and secondary particles at the level of the observatory are recorded to simulate hybrid observation. Five components, protons, helium, CNO, MgAlSi, and iron are generated with energies from 10 TeV to 10 PeV according to a power law spectrum with an index of −2.7. The directions of the showers are from
$ 24^{\circ} $ to$ 38^{\circ} $ in zenith, and from$ 77^{\circ} $ to$ 103^{\circ} $ in azimuth. The shower core position is evenly distributed in an area of 260 m$ \times $ 260 m. The primary energy spectrum is normalized to the exponent of −2.7 from 10 TeV to 10 PeV, as shown in Fig. 2. Different components are normalized to that of protons.In addition, the five components are also normalized according to the Hörandel model. The relationship between the original proton spectrum and the two normalized proton spectra is that the number of original proton events, the number of proton events with the exponent −2.7 and the number of proton events with the exponent from the Hörandel model are the same at 100 TeV. The event number in the other energy bins and other components are normalized in proportion. The normalized statistics of each component are equivalent to the observation data for one year with 10% duty cycle according to the Hörandel model [21].
The simulation of the response of three LHAASO detector arrays to EAS is performed separately. In the simulation, the actual coordinates of the detector arrays are transferred to the CORSIKA coordinate system. The program of photon ray-tracing is used for WFCTA simulation. The trigger pattern of the telescope is set to 7, namely seven neighboring pixels should be triggered. The fast simulation program [22] is used for the simulation of WCDA++ and MD. Only photoelectrons are sampled according to the energy, direction and particle id of the secondary particles in EAS. The time response is not included. The simulated results of different detectors are then merged before reconstruction.
-
According to the actual data acquisition, as long as the Cherenkov telescope is triggered, the events measured by three detector arrays are reconstructed.
First, the shower core position is given by WCDA++ using NKG fitting [23]. Due to the lack of time response information in the WCDA++ fast simulation program, there is no information about the shower fronts. Therefore, the arrival direction of the shower is obtained by Gauss sampling with an angular resolution of
$0.3 ^{\circ} $ .Secondly, the perpendicular distance between the telescope and the shower axis (
$ R_p $ ) is calculated. The Cherenkov image cleaning is then performed. The first step is to remove the fired pixels which contain less than 30 photoelectrons in the image. The second step is to find a fired pixel with the largest number of photoelectrons, and use it as the center for projecting the whole image outward. Then, all isolated fired pixels are removed.After the image cleaning, the Hillas parameters [24], are obtained, as well as the total number of photoelectrons (
$ N^{pe} $ ) in the image.$ N^{pe} $ is a good energy estimator. Before energy reconstruction,$ N^{pe} $ should be normalized to$ R_p = 0 $ and$ \alpha = 0 $ , namely$ N_{0}^{pe} = \lg(N^{pe})+a{\times}(R_p/1m)+b{\times}\tan(\alpha) ,$

(1) where
$ \alpha $ is the space angle between the shower direction and the optical axis of the telescope, and the parameters$ a $ and$ b $ depend on the primary component of cosmic rays.Finally, the lateral distribution of muons is fitted by an empirical formula Eq. (2) using maximum likelihood fitting [9]. The normalized muon size is given by
$ {\rho}(r, N_{\mu}) = k_G N_{\mu} \left(\frac{r}{r_G}\right)^{-k_1} \left(1+\frac{r}{r_G}\right)^{-k_2} [m^{-2}], $

(2) where
$ k_1\cong1.4 $ ,$ k_2\cong1.0 $ ,$ r_G\cong220\;{\rm m} $ . These three parameters are reconfirmed according to the layout of the MD array. -
There are three basic principles for event selection: first, the shower core position must fall in WCDA++; second, the Cherenkov image is complete; and third, the muon lateral distribution is well fitted.
Specifically, the reconstructed shower core located within
$ 130\;{\rm m}\times 130\;{\rm m} $ around WCDA++ is selected. For the Cherenkov image, the number of fired pixels must be more than 10, and the angular distance between the weighted center of the image and the center of the camera plane less than$ 6^{\circ} $ . For muon lateral distribution fitting, the fitted normalized muon size ($ k_G N_{\mu} $ ) should be more than$ 10^{-7} $ .The number of events in each energy bin after selection is shown in Fig. 3 (left). The dotted line represents the number of proton events in the simulation, which is consistent with the black line in Fig. 2. The solid lines represent the number of events after selection, and different colors represent different components. Fig. 3 (left) shows that the hybrid observation becomes nearly fully efficient above 100 TeV for all components.
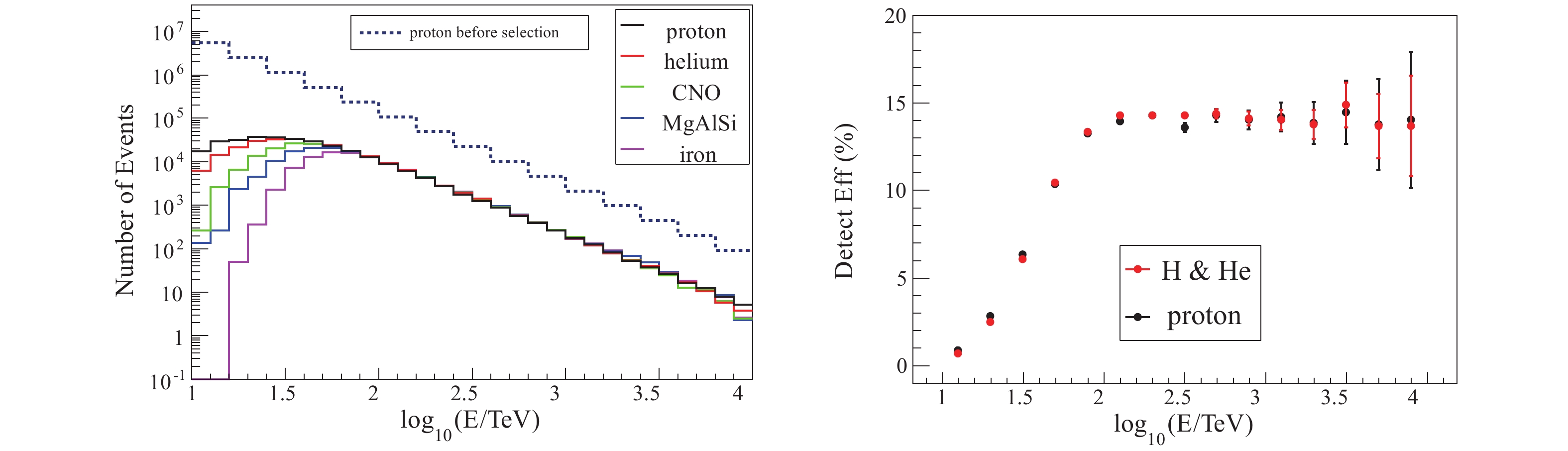
Figure 3. (color online) Left: energy distribution after event selection. Right: detection efficiency for protons and H&He.
The detection efficiency is defined as the ratio of the number of selected events to the number of simulation events in each energy bin, i.e. the black solid line divided by the blue dotted line in Fig. 3 (left). In our simulations, the detection efficiency is about 15% above 100 TeV for all components, as shown in Fig. 3 (right). The red dots show the detection efficiency of H&He and the black dots show the the detection efficiency for protons. It is obvious that the error bars of the last two points in Fig. 3 (right) are large due to small statistics. Therefore the results for
$ \lg(E/{\rm TeV}) > 3.6 $ are masked in the subsequent analysis. -
In this section, the parameters of the three types of detector arrays are analyzed according to the development characteristics of EAS. The component sensitive parameters of LHAASO hybrid observation are introduced. The toolkit for multivariate analysis (TMVA) [25, 26] is used and selected results are presented.
-
It is known that the iron induced air showers are larger, develop faster and have a smaller interaction mean free path than the primary particles, which travel in the atmosphere [9]. Thus, the proton induced shower develops its maximum later than the iron shower. The atmospheric depth of the shower maximum,
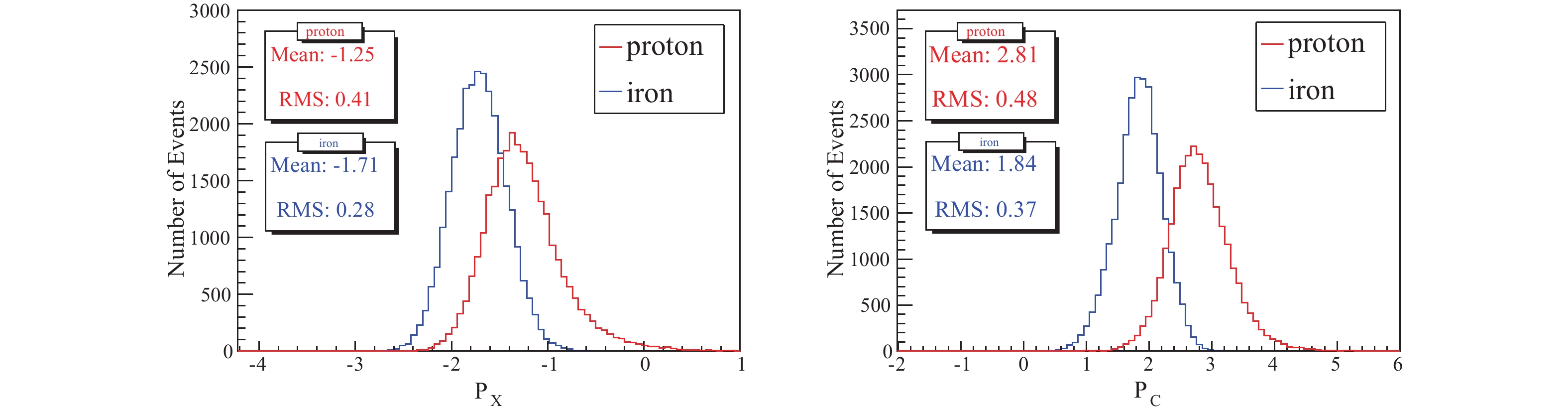
$ X_{\max} $ , is a traditional mass sensitive parameter. We use$ {\Delta}{\theta} $ , the parameter used to reconstruct$ X_{\max} $ , instead of the reconstructed$ X_{\max} $ .$ {\Delta}{\theta} $ is the angular distance between the direction of the arriving shower and the gravity center of the Cherenkov image. It can not be used directly to classify the primary particles because of the$ R_{p} $ and shower energy ($ N_{0}^{pe} $ ) dependence. After normalization, the structure of the mass sensitive parameter$ P_{X} $ is as follows:$ P_{X} = {\Delta}{\theta}-0.0103\times R_p - 0.404\times N_{0}^{pe}. $

(3) Moreover, the proton induced showers exhibit an elongated elliptic shape [24]. The ratio of the length and width of the Cherenkov image is also a traditional effective parameter:
$ P_{C} = L/W-0.0137\times R_p+0.239\times N_{0}^{pe}. $

(4) The distributions of
$ P_{X} $ and$ P_{C} $ for proton and iron showers are shown in Fig. 4. -
The muon size
$ N_{\mu} $ of a shower heavily depends on the atomic number ($ A $ ) of the primary particle:$ N_{\mu}^{A}/N_{\mu}^{p} \approx A^{(1-\eta )} $ , where$ \eta $ is approximately 0.9 [9] , and$ p $ indicates the proton shower.Therefore, the fitted muon size (
$ N_{\mu}^{F} $ ), the total number of detected muons ($ N_{\mu}^{M} $ ) and the number of fired MDs (NMD) are significant variables for identification of the primary particles:$ P_{\mu1} = \lg(N_{\mu}^{F})-0.9823 \times N_{0}^{pe}, $

(5) $ P_{\mu2} = \lg(N_{\mu}^{M})+0.00226 \times Rlp-0.873 \times N_{0}^{pe}, $

(6) $ P_{\mu3} = \lg(NMD+0.098\times Rlp)-0.552\times N_{0}^{pe}, $

(7) $ Rlp $ is the perpendicular distance between the center of the MD array and the shower axis. The distributions of the three parameters$ P_{\mu1} $ ,$ P_{\mu2} $ and$ P_{\mu3} $ for proton and iron showers are shown in Fig. 5. -
It is also known that the iron induced shower is more extensive at the same observation level. This means that the lateral extension of secondary particles in iron induced air shower is larger. WCDA++, the fully covered detector array, can detect the lateral distribution of secondary particles well. The formulas for the average lateral distribution
$ <ER> $ and its$ {\rm RMS} $ are given using Eq. (2) to Eq. (5) as$ <ER> = \dfrac{\sum R_{i} \times Pe_{i}}{\sum Pe_{i}}, $

(8) where
$ R_{i} $ is the distance between the shower core position and the$ ith $ fired cell in WCDA++ and$ Pe_{i} $ are the photoelectrons measured by the$ ith $ fired cell, and$ \begin{align} {\rm RMS}_{x} = \sqrt{ \dfrac{\sum x_{i}^{2}\times Pe_{i}}{\sum Pe_{i}} - x_{\rm weight}^{2} } \end{align}, $

(9) $ \begin{align} {\rm RMS}_{y} = \sqrt{ \dfrac{\sum y_{i}^{2}\times Pe_{i}}{\sum Pe_{i}} - y_{\rm weight}^{2} } \end{align}, $

(10) $ \begin{align} {\rm RMS} = \sqrt{ \dfrac{\sum R_{i}^{2}\times Pe_{i}}{\sum Pe_{i}} - <ER>^{2} } \end{align}, $

(11) where
$ x_{\rm weight} $ and$ y_{\rm weight} $ are the centroids of the distribution of secondary particles in WCDA++:$ \begin{align} x_{\rm weight} = \dfrac{\sum x_{i}\times Pe_{i}}{\sum Pe_{i}} \end{align}, $

(12) $ \begin{align} y_{\rm weight} = \dfrac{\sum y_{i}\times Pe_{i}}{\sum Pe_{i}} \end{align}. $

(13) These parameters are not only related to the primary component but also to the shower direction and energy, hence they should be corrected before MVA:
$ P_{F2} = \lg<ER>-0.343\times \theta_{\rm rec}+0.1159\times N_{0}^{pe}, $

(14) $ P_{F3} = {\rm RMS}_{x}-6.921\times \theta_{\rm rec}+2.82\times N_{0}^{pe}, $

(15) $ P_{F4} = {\rm RMS}-6.084\times \theta_{\rm rec}+1.917\times N_{0}^{pe}. $

(16) The distributions of the three parameters
$ P_{F2} $ ,$ P_{F3} $ and$ P_{F4} $ for proton and iron showers are shown in Fig. 5.In addition, near the shower core axis, the particle density of the iron-shower is lower than that of the proton shower [6]. Hence, the number of photoelectrons in the brightest cell (
$ N_{\max} $ ) measured by WCDA++ is sensitive to components:$ P_{F} = \lg(N_{\max}) -1.391\times N_{0}^{pe}. $

(17) The total number of photoelectrons (
$ N_{w}^{pe} $ ) measured by WCDA++ is also a mass sensitive variable, even if it is weaker than$ N_{\max} $ :$ P_{E} = \lg(N_{w}^{pe}) -1.163\times N_{0}^{pe}. $

(18) The distributions of the two parameters
$ P_{F} $ and$ P_{E} $ for proton and iron showers are shown in Fig. 6.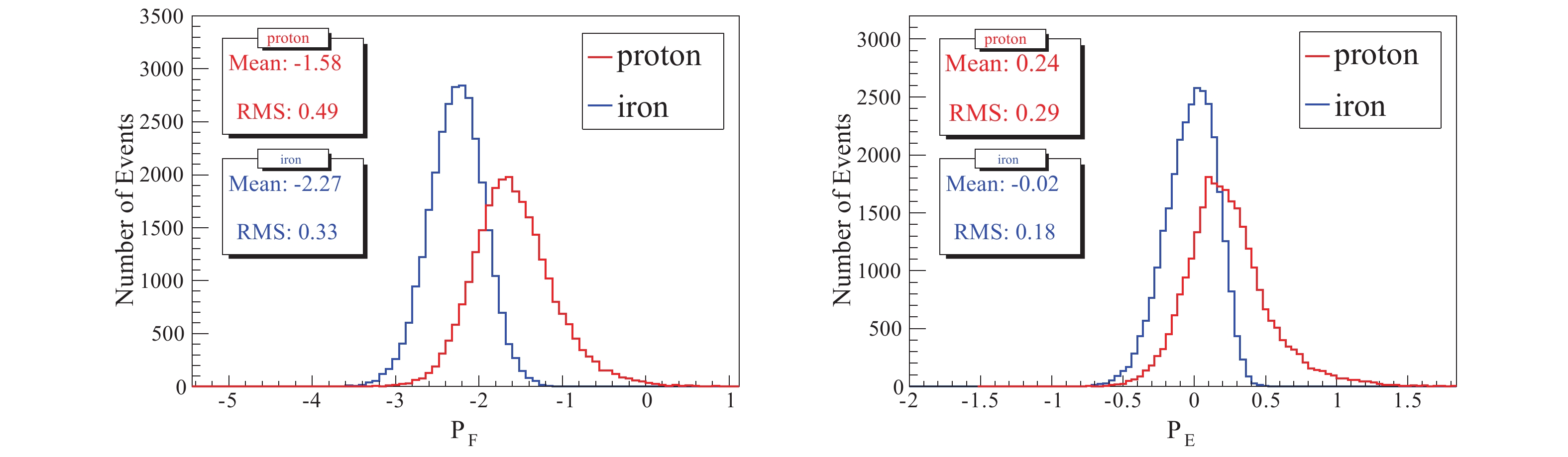
Figure 6. (color online) Distributions of mass sensitive parameters
$P_{F}$ (left) and$P_{E}$ (right) for the proton (red line) and iron (blue) induced showers.Other parameters have also been studied, such as the photoelectrons measured by the brightest pixel in air Cherenkov image (
$ P_{C1} $ ), the total photoelectrons located 45 meters away from the shower core in WCDA++ ($ P_{F1} $ ), the muon density detected at 80 m to 100 m away from the shower core position ($ P_{\mu4} $ ), etc. Nevertheless, the particle classification of these variables is weak. After tuning of the parameters, the above ten parameters are used as input for the BDTG classifiers. -
The parameters described above are not independent. There is a correlation between some of them. Parameters provided by the same detector array are highly correlated, such as
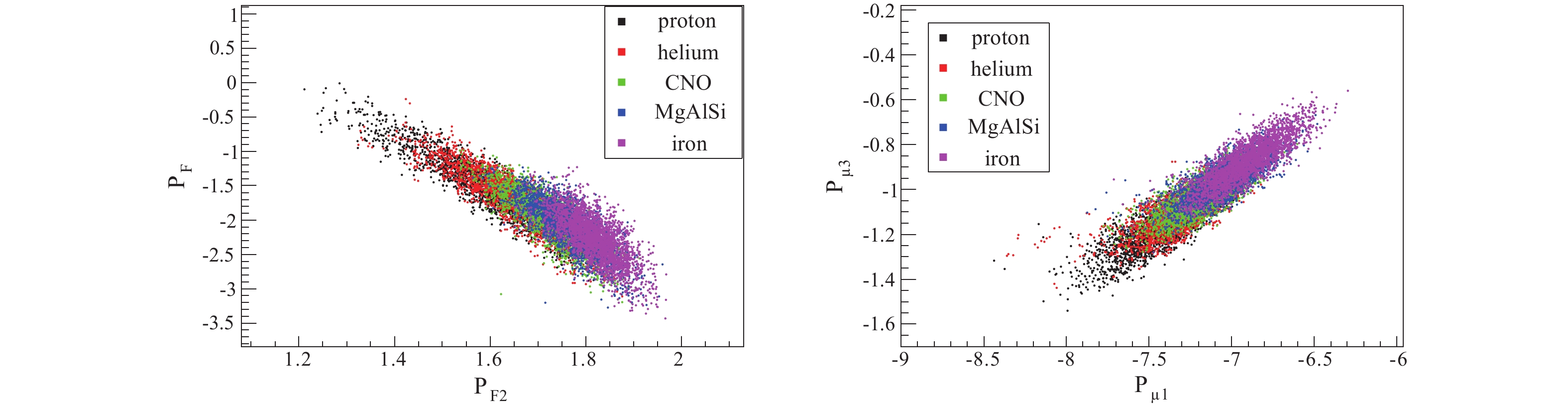
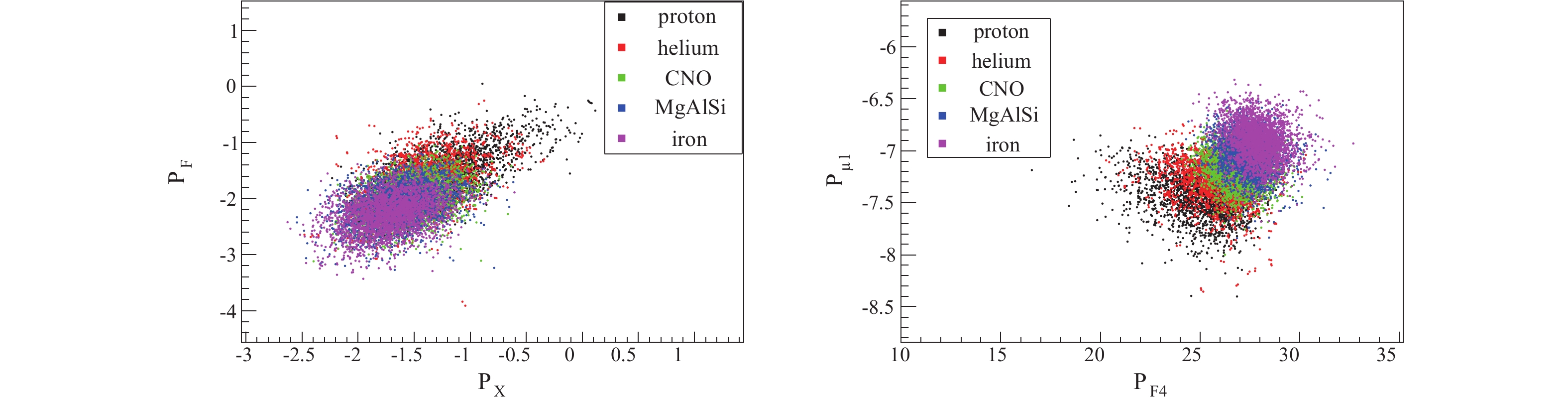
$ P_{F} $ and$ P_{F2} $ ,$ P_{\mu1} $ and$ P_{\mu3} $ . The correlations of parameters from WCDA and MD for five components of cosmic rays are shown in Fig. 7. The parameters$ P_{F} $ and$ P_{F2} $ have negative correlation (left plot), while$ P_{\mu1} $ and$ P_{\mu3} $ are position correlated (right plot). According to the development characteristics of EAS, it is easy to understand that as the lateral distribution of the secondary particles becomes more extensive there are less particles near the shower core. Also, as more muon detectors are fired there is a larger muon content in the shower.The correlation of parameters provided by the different detector arrays is weak, such as
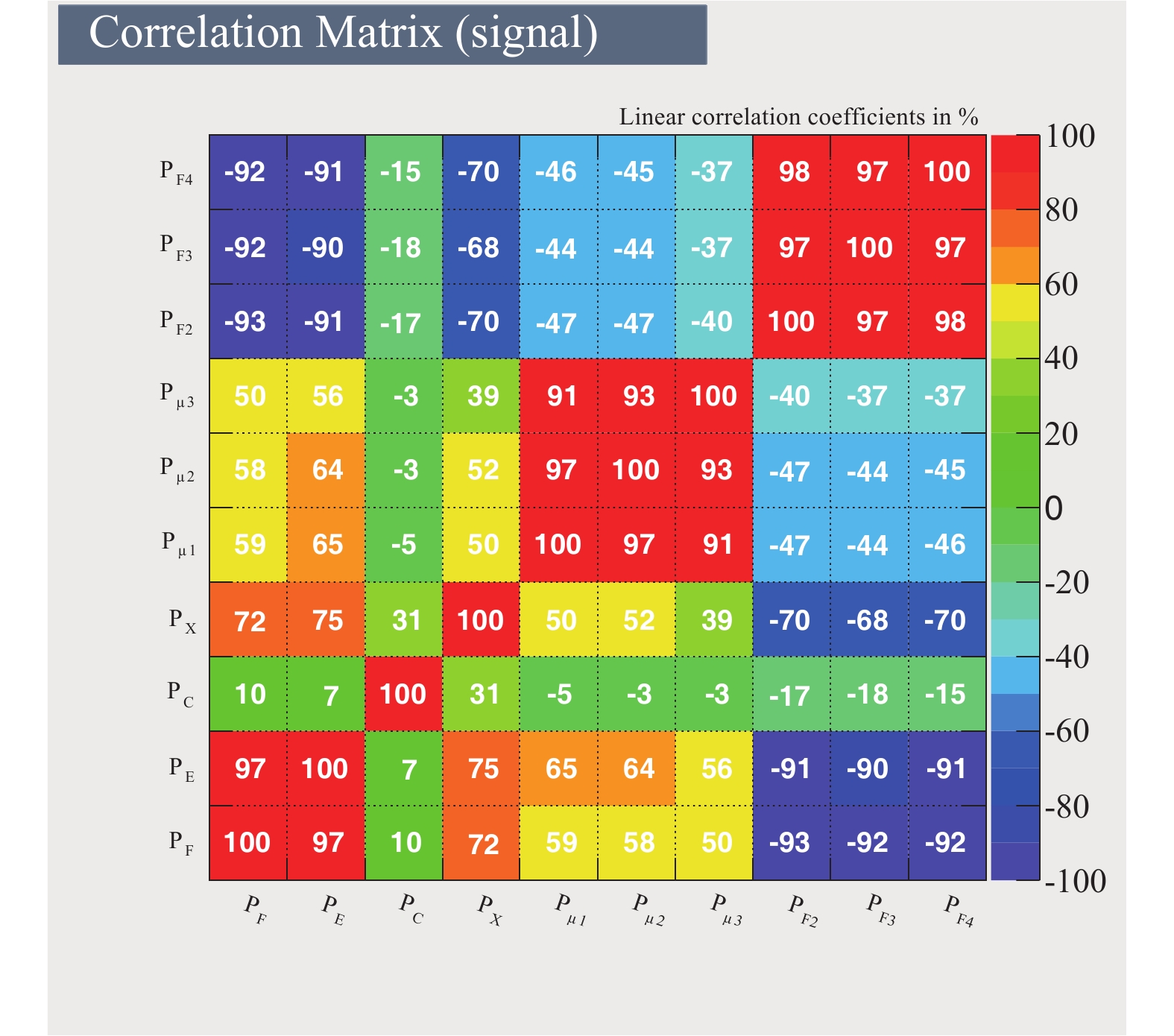
$ P_{F} $ and$ P_{X} $ , and$ P_{\mu1} $ and$ P_{F4} $ . The correlation of parameters from different detector arrays for five components are shown in Fig. 8. The distributions are approximately circular. However, the correlation between parameters of different components is slightly different. The parameters for protons tend to be more correlated, as shown by black dots in Fig. 8.The correlation matrix of the ten variables for proton induced showers is shown in Fig. 9. The correlation coefficient of 100% means a linear positive correlation, and −100% means linear negative correlation. A zero correlation coefficient means no correlation among parameters. It should be noted that the parameter
$ P_{C} $ is basically independent of other parameters, as shown in the third column or in the eighth row in Fig. 9. This is because$ P_{C} $ reflects the overall development characteristic, not just the lateral or longitude distribution of the air shower.After removing the highly correlated parameters (97% or 98% correlation coefficient), six parameters,
$ P_{C} $ ,$ P_{X} $ ,$ P_{F} $ ,$ P_{F4} $ ,$ P_{\mu2} $ and$ P_{\mu3} $ , are used for TMVA training and analysis. -
Drawing on the experience of ARGO-YBJ/WFCT hybrid detection, two parameters are used for particle identification [27] in the event-by-event cut. However, having too many variables is not suitable for particle identification when using event-by-event cuts because it is complicated to get an optimal cut for each parameter. Therefore, MVA is used.
As an important branch of statistics, multivariate analysis has been applied in most disciplines. TMVA is specially developed for high energy physics based on the ROOT integrated environment. It is powerful for signal and background classification. In accelerator physics, it can effectively screen out the b-tagging signals from a large number of background particles in a jet [28]. Likewise, it enables to identify the components of cosmic rays [29].
TMVA is based on machine learning. It integrates multiple advanced algorithms, such as Boosted Decision Trees (BDT), Artificial Neural Networks (ANN), Support Vector Machine (SVM), etc. Users need to input variable samples and select the algorithm, and the machine training and testing are then carried out. The result is one variable which is used by the user to select signals.
Here, Boosted Decision Trees with Gradient (BDTG) is chosen, which is the most widely used algorithm. The classification of protons and H&He from other mass components is carried out independently.
The selected hybrid events are divided into two equal parts. One is used for TMVA training and testing and the other is used as data. The statistics of the signal (proton or H&He) and background (others) are shown in Table 1.
NO. of events proton H&He signal 40215 61098 background 91330 70447 Table 1. The number of events for BDTG classifier training and testing.
To avoid overtraining, several parameters are adjusted to achieve best performance of the classifier. Parameters of BDTG classifiers for the separation of protons from the other nuclei are as follows:
-Number of trees in the forest is 380;
-Minimum training events required in the leaf node are 30;
-Maximum depth of the decision tree is 2.
Parameters of BDTG classifiers for the separation of H&He from the other nuclei are as follow:
-Number of trees in the forest is 300;
-Minimum training events required in the leaf node are 50;
-Maximum depth of the decision tree is 2.
The other parameters are set at their default values.
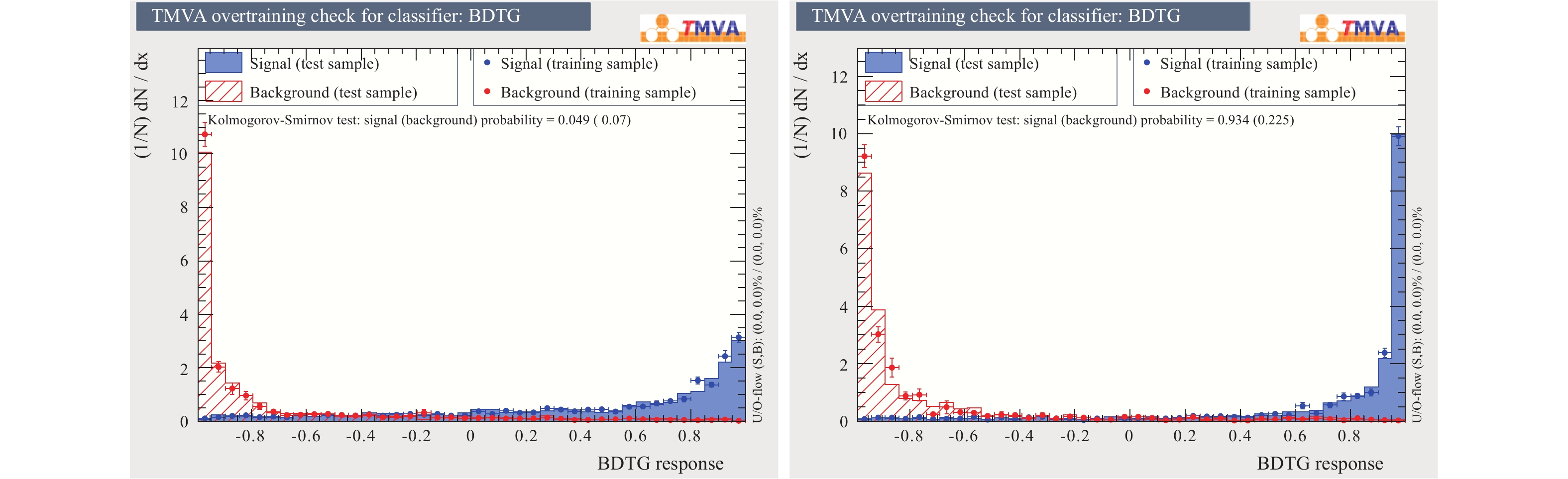
The training results are shown in Fig. 10.
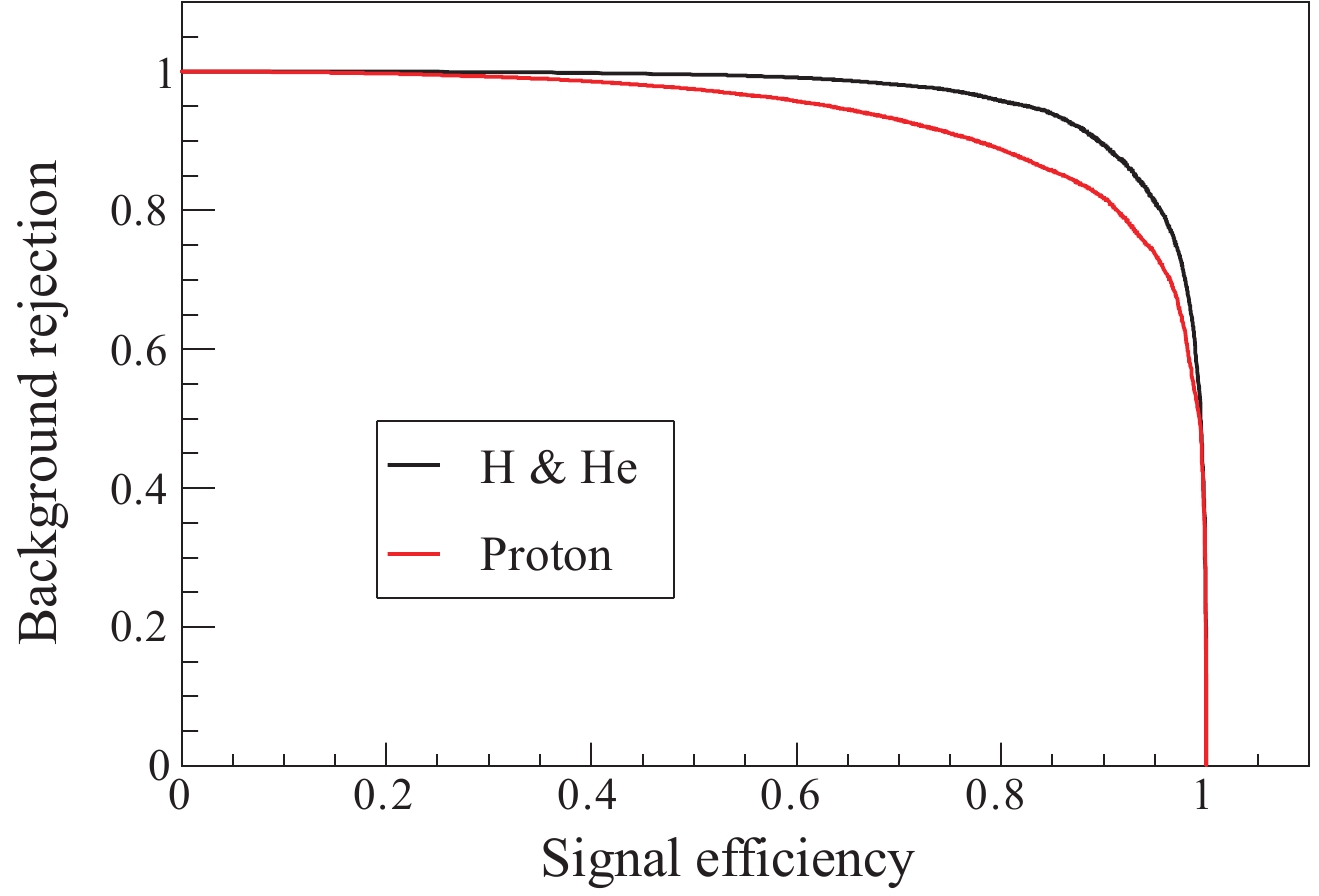
$ {\rm H\&He} $ can be well separated from the other components. However, separation of protons from the other nuclei is barely satisfactory. The background rejection versus signal efficiency ("ROC curve") is obtained by cuts in the BDTG classifier outputs for proton and H&He samples, as shown in Fig. 11. It is obvious that for the same signal efficiency, the background rejection of the other heavy nuclei (H&He vs. other nuclei) is higher. -
The training results are applied to the other half of the data sample. Generally, signal events can be selected according to the best cut points provided by TMVA. However, because our final goal is to obtain selection efficiency with different energy bins, the distribution of the output BDTG classifier versus reconstructed energy is studied first. As shown in Fig. 12, the separation of the output BDTG classifiers between H&He and heavy nuclei becomes larger as the primary energy increases. The mean value of the signal (red dots) in each energy bin is slightly higher than the background (black dots), and the RMS of the signal gradually decreases. The reason for larger separation is that the performance of the input parameters gets better at higher energies.

Figure 12. (color online) Distribution of the BDTG output parameter as a function of reconstructed energy. The error bars show the RMS in each bin.
To get a coincident selection efficiency, the cut values are scaled following Eq. (19) and Eq. (20):
$\rm Cut~ Value (H) = 0.09\times lg(Energy/TeV)+0.55, $

(19) $\rm Cut~ Value (H\&He) = 0.33\times lg(Energy/TeV)-0.26. $

(20) After the cut described above, the aperture and contamination of hybrid observation are calculated. The aperture for a pure proton is about
$ 900\;{\rm m}^{2}\rm Sr $ , and the aperture for H&He is about$ 1800\;{\rm m}^{2}\rm Sr $ , as shown in Fig. 13 (left). The contamination of the proton sample is about 10% , and the contamination of H&He sample is less than 3% according to the Hörandel model, as shown in Fig. 13 (right).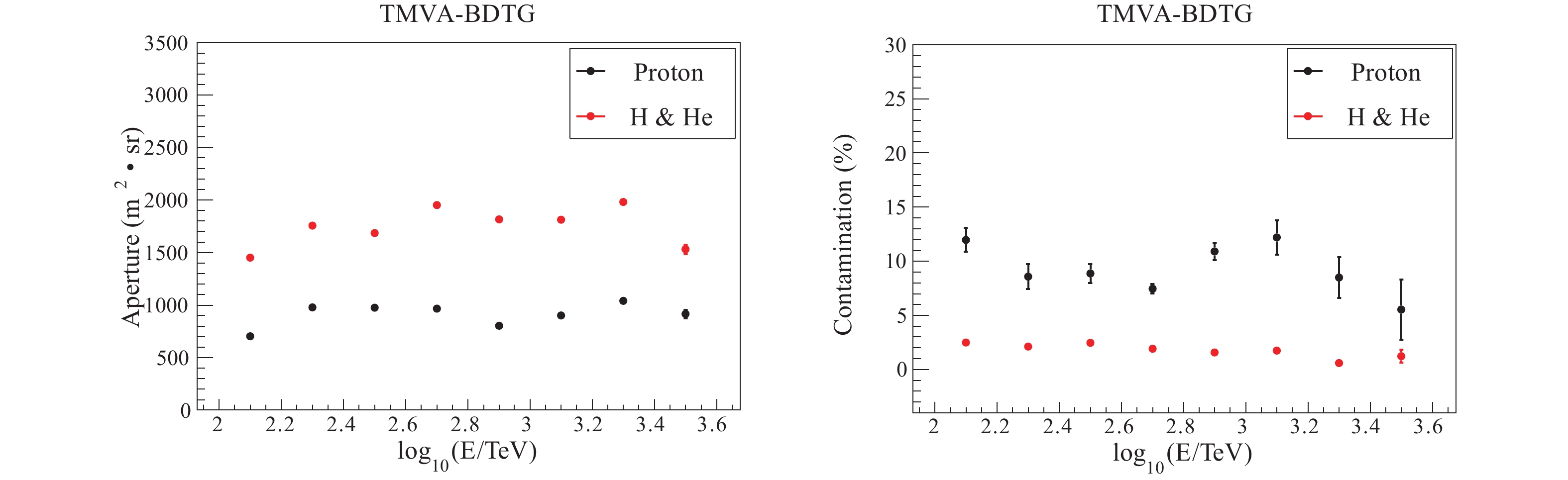
Figure 13. (color online) The final selected aperture (left) and contamination (right) for protons and H&He.
Considering the uncertainty due to the hadronic interaction models, two batches of data, QGSJET-FLUKA and EPOS-FLUKA, were used for error analysis. It is found that the aperture for H&He is consistent within
$ \pm 5 $ %. -
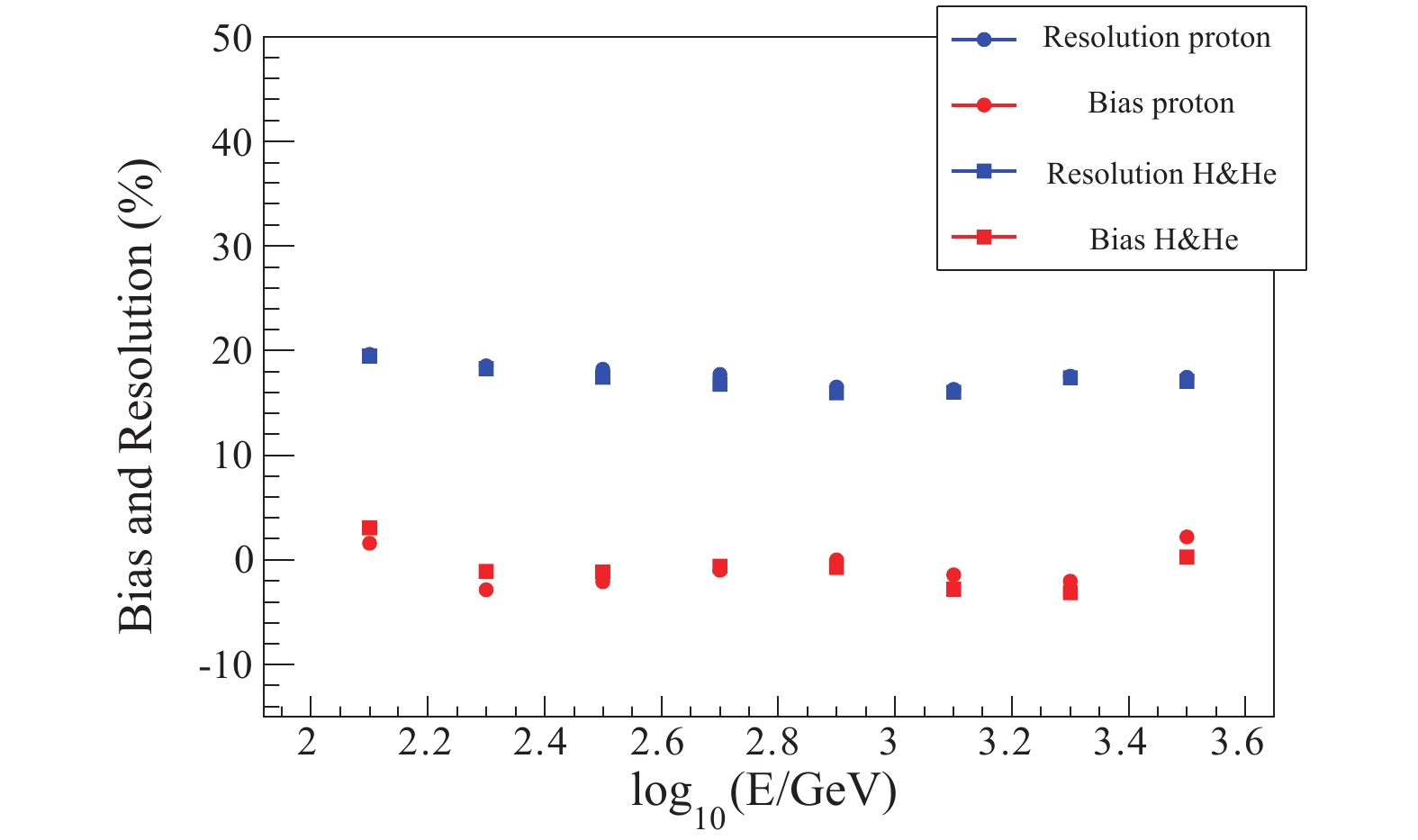
After the primary particle identification, the accuracy of event reconstruction for light components is obtained. For protons and H&He, the shower core resolution is less than 3 m. The energy reconstruction is obtained by WFCTA, as described in Section 3. There is a linear correlation between the shower energy E and the corrected number of Cherenkov photoelectrons,
$ N_{0}^{pe} $ . For protons,$ a = 0.00916 $ and$ b = 0.0182 $ ; the reconstructed energy is$ E_{\rm rec} = 10^{0.9558{\times}N_{0}^{pe}-2.31} $ . The variables$ a $ and$ b $ for H&He energy reconstruction are approximately equal to that for protons. The reconstructed bias and resolution for protons and H&He are shown in Fig. 14. The bias is about 4% and the resolution is less than 20%.Based on the aperture described above, the cosmic ray spectra of protons and H&He are predicted according to the Hörandel model [21], and the ARGO-YBJ/WFCT model [6], which is an experimental model. The exposure time is set to one year with a 10% duty cycle. Since the experimental model ARGO-YBJ/WFCT only gives the energy spectrum of H&He, the spectrum of pure protons is obtained by dividing by 2, that is, the ratio of protons to helium is 1:1. The bending of the knee is unchanged.
In Fig. 15, the left panel shows the spectrum with the Hörandel model, and the right panel with the ARGO-YBJ/WFCT model. The black dots are for protons and the red dots for
${\rm H\&He} $ . The statistical errors are very small with the aperture and effective time given above. The corresponding event rate for one year is shown in Fig. 16.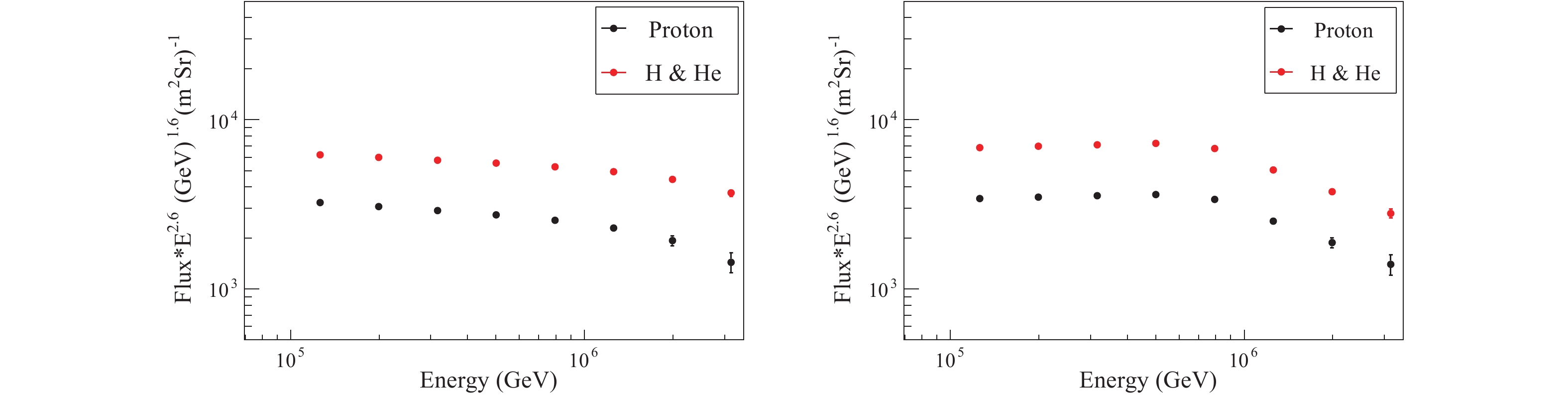
Figure 15. (color online) Expected spectra with the Hörandel model (left) and the ARGO-YBJ/WFCT model (right).

Figure 16. (color online) The statistics for one year with a 10% duty cycle for the Hörandel model (left) and the ARGO-YBJ/WFCT model (right).
At 800 TeV, 5121/6461 H&He events and 1130/1476 proton events can be selected in one year according to the Hörandel model and the ARGO-YBJ/WFCT model, respectively. At 2 PeV, 1023/849 H&He events and 222/210 proton events can be selected in one year according to the Hörandel model and the ARGO-YBJ/WFCT model, respectively.
Therefore, if the knee of the cosmic ray light component is below 1 PeV, the 1/4 LHAASO array can give good measurements within one year. If the knee of the light component is higher than 3 PeV, more observation time, or a more effective method, is needed to get sufficient statistics. The use of SiPM allows observations during a Moon night with WFCTA, and the duty cycle of the hybrid observation can be extended. Moreover, additional Cherenkov telescopes installed during the construction of LHAASO can also increase the statistics effectively.
-
The simulation of the second stage of 1/4 LHAASO hybrid detection was performed. Three types of detectors, WFCTA, WCDA and MD, are included in this study. Parameters for each detector array were studied in detail and tuned. After removing the highly correlated parameters, six parameters were used as input for the BDTG classifier for TMVA machine training and testing. The results show that the classification of pure protons is weaker than of H&He.
After the cuts, high purity light component samples were selected. The aperture for pure protons is 900 m2 Sr, and the contamination is around 10% according to the Hörandel model. The aperture for H&He is 1800 m2 Sr, and the contamination is less than 3%. For the H&He aperture, the uncertainty from the different strong interaction models is about ±5%. Moreover, the bias of energy reconstruction is about ±4% and the resolution is less than 20% for both pure proton and H&He samples.
According to the energy spectrum expected from the ARGO-YBJ/WFCT model, the spectrum of the light component of cosmic rays could be measured accurately in a short time with the 1/4 LHAASO array.
Expected energy spectrum of cosmic ray protons and helium below 4 PeV measured by LHAASO
- Received Date: 2019-03-18
- Available Online: 2019-07-01
Abstract: The Large High Altitude Air Shower Observatory (LHAASO) is a composite cosmic ray observatory consisting of three detector arrays: kilometer square array (KM2A), which includes the electromagnetic detector array and muon detector array, water Cherenkov detector array (WCDA) and wide field-of-view Cherenkov telescope array (WFCTA). One of the main scientific objectives of LHAASO is to precisely measure the cosmic rays energy spectrum of individual components from





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: