-
The evaluation of the static and dynamic properties of the hadrons has always been a major concern for nuclear and particle physicists. The new experimental observations in the field of light baryons, heavy baryons, and exotic states have been determined very recently. Different research groups have provided light baryon resonances with increasing confidence levels [1-4]. These experimental observations have generated interest in the theoretical study of light baryon spectra (radial and orbital excited states). A description of all the baryon systems can be found in review articles [5-10].
The combination of three confined light quarks with the flavors up, down, and strange provides a basis for the study of light baryons; it belongs to the
$SU(3)_f$ symmetry multiplet. It also provides a basis to understand the non-abelian character of quantum chromodynamics (QCD). The light baryons can be in the following multiplets:$10_S \oplus 8_M \oplus 8_M \oplus 1_A$

We study the
$N^*$ baryon system, which is a combination of two$d$ quarks and one$u$ quark. The nature and interactions of the compound system can be evaluated by hadron spectroscopy.$N^*$ can provide us with critical insights into the nature of QCD in the confinement domain and its relevance to nuclear and low energy hadron physics [11]. Particle Data Group(PDG) has provided many excited states resonances of N baryons [4]. The search for these resonances is the main focus of the baryon programs at JLab [12], Mainzer Mikrotron (MAMI) [13], the Beijing Spectrometer (BES), the Electron Stretcher and Accelerator (ELSA) facility (the Crystal Barrel collaboration) [14], GRAAL [15, 16] and the Two Arms Photon Spectrometer (TAPS) [17 ], SAPHIR [18, 19], and CLAS [20]. In addition, we can expect new results from analysis projects such as EBAC, Julich, SAID, and MAID. Many theoretical studies have investigated the excited resonances of nucleons using various quark models [21-28], basis light-front quantization approach [29], BnGa partial wave analysis [30], chiral Lagrangian theory [31], Fadeev approach [32, 33] Lattice QCD [34-36], etc.We determined the spectra of
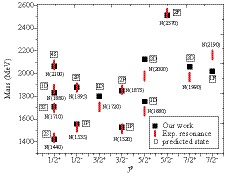
$N^*$ resonances in the framework of hypercentral constituent quark model (hCQM). The model has already been extended to obtain the excited state baryon resonances for heavy baryons. The excited states masses of singly, doubly, and triply heavy baryons in both the charm and bottom sectors are in good agreement with other theoretical predictions, as well as with the recent experimental outcomes [37-43]. Further, the magnetic moments of heavy baryons are also determined at L= 0, and radiative and strong decays are calculated [44]. Moreover, using the Regge trajectories the unknown quantum states and$J^P$ values are also identified. In this study, we use the hCQM and identify several hadronic properties of$N^*$ baryons. Giannini et al. used this model to study light flavored baryons for low-lying radial, as well as orbital and excited states below 2 GeV. Here, we calculated the spectra for 1S-5S, 1P-5P, 1D-4D, and 1F-2F states and constructed Regge trajectories upto 3.3 GeV. From Fig. 1, it is clear that the new experimental resonances agree well with our predicted states. A brief description of the model is given in Section 2. Further, we determined several hadronic properties, such as Regge trajectories, magnetic moments, and decay widths of excited states, using the obtained masses. The hadronic propeties are discussed in Section 3, which is followed by the conclusion in Section 4. -
Spectroscopy is a powerful tool to observe the constituents of a compound system in order to study their nature and interactions. Hadron spectroscopy has provided many unexpected results. In our previous work, we studied heavy baryon spectra for singly, doubly, and triply heavy baryons excited states, starting from S state to F states, using hCQM with all isospin splittings [37-43].
In the present study, we predict the radial and orbital excited states of
$N$ baryon in the hypercentral approach [9, 45]. The two relative coordinates are rewritten as a single six-dimensional vector, and the non-relativistic Schr$\ddot o$ dinger equation. We numerically solve six-dimensional space equation in the Mathematica notebook [46]. The potential, expressed in terms of the hypercentral radial coordinate, effectively considers the three-body interactions. We employ the Coulomb plus linear confinement potential with the first-order correction for the quarks. The relative Jacobi coordinates can be expressed as [47]$ \vec{\rho} = \dfrac{1}{\sqrt{2}}(\vec{r_{1}} - \vec{r_{2}}), \tag{1a} $

$ \vec{\lambda} =\dfrac{m_1\vec{r_1}+m_2\vec{r_2}-(m_1+m_2)\vec{r_3}}{\sqrt{m_1^2+m_2^2+(m_1+m_2)^2}}. \tag{1b} $

The Hamiltonian of the baryonic system in the hCQM is then expressed as
$ H=\dfrac{P_{x}^{2}}{2m} +V(x). $

(2) where
$m=\displaystyle\frac{2 m_{\rho} m_{\lambda}}{m_{\rho} + m_{\lambda}}$ is the reduced mass, and$x$ is the six-dimensional radial hyper central coordinate of the three-body system. The quark masses are$m_u$ =$m_d$ = 0.290 GeV. We add the first-order correction to the energy term of the potential to observe the effect. For heavy baryons, we demonstrate results without adding correction as well as with first-order correction. Here, however, we only considered the excited state masses adding the first-order correction. The model is formed by a linear confining interaction with a spin, flavor, and orbital angular momentum dependent hyperfine interaction. The potential is of the form$ V(x) = V^{0}(x) + \left(\dfrac{1}{m_{\rho}}+ \dfrac{1}{m_{\lambda}}\right) V^{(1)}(x)+V_{SD}(x). $

(3) where
$V^{0}(x)$ and the first-order correction$V^{1}(x)$ is given by$ V^{(0)}(x)= \dfrac{\tau}{x}+ \beta x, \quad V^{(1)}(x)= - C_{F}C_{A} \dfrac{\alpha_{s}^{2}}{4 x^{2}}. $

(4) $V^{(0)}(x)$ is the sum of hyper Coulomb (hC) (vector) interaction and a confinement (scalar) term. Here, the hC strength$\tau = -\displaystyle\frac{2}{3} \alpha_{s}$ , where$\alpha_{s}$ corresponds to the strong running coupling constant;$\beta$ corresponds to the string tension of the confinement.$C_{F}$ and$C_{A}$ are the Casimir charges of the fundamental and adjoint representation, respectively.For computing the mass difference between different degenerate baryonic states, we consider the spin-dependent part of the usual one gluon exchange potential. The spin-dependent part,
$V_{SD}(x)$ , contains three types of the interaction terms: the spin-spin term$V_{SS} (x)$ , spin-orbit term$V_{\gamma S}(x)$ , and tensor term$V_{T}(x)$ . It is given by$ \begin{split} V_{SD}(x)=& V_{SS}(x)(\vec{S_{\rho}}.\vec{S_\lambda}) + V_{\gamma S}(x) (\vec{\gamma} \cdot \vec{S}) + V_{T} (x)\\ & {\times}\left[S^2-\dfrac{3(\vec{S }\cdot \vec{x})(\vec{S} \cdot \vec{x})}{x^{2}}\right]. \end{split} $

(5) The coefficient of the spin-dependent terms can be written as
$ V_{\gamma S} (x) = \dfrac{1}{2 m_{\rho} m_{\lambda}x} \left(3\dfrac{{\rm d}V_{V}}{{\rm d}x} -\dfrac{{\rm d}V_{S}}{{\rm d}x} \right), \tag{6a} $

$ V_{T}(x)=\dfrac{1}{6 m_{\rho} m_{\lambda}} \left(3\dfrac{{\rm d}^{2}V_{V}}{{\rm d}x^{2}} -\dfrac{1}{x}\dfrac{{\rm d}V_{V}}{{\rm d}x} \right), \tag{6b} $

$ V_{SS}(x)= \dfrac{1}{3 m_{\rho} m_{\lambda}} \bigtriangledown^{2} V_{V}. \tag{6c} $

The spin-orbit and tensor terms describe the fine structure of the states, while the spin-spin term gives the spin singlet triplet splittings.
-
N baryon has isospin I=
$\frac{1}{2}$ and strangeness$S$ = 0. We constructed a complete classification of$N^{*}$ baryons spectrum in this study. Indeed, many experimentally known excited state resonances agree well with our predicted states. Theses resonances are listed in Table 1 along with their mass, experimental status, and respective$J^{P}$ values. The status (*) indicates the likelihood of the existence: four stars indicates that it the existence is certain; three star indicates that the existence is likely to certain, and more information is desirable; two stars indicate that the probability of existence is fair; and one star indicates that the existence is poor. Further, few additional three and four star baryons are mentioned in PDG(2018) [4], such as, N(1650), N(1675), N(1700), N(1900) with$J^{P}$ values$\displaystyle\frac{1}{2}^{-}$ ,$\displaystyle\frac{5}{2}^{-}$ ,$\displaystyle\frac{3}{2}^{-}$ ,$\displaystyle\frac{3}{2}^{+}$ and the two star baryons N(1860), N(2120), N(2300); these values do not fit our obtained resonances.state J P M(exp.) status N(939) 1/2+ 939 **** N(1440) 1/2+ 1420-1470 **** N(1710) 1/2+ 1680-1740 *** N(2100) 1/2+ 2100 * N(1535) 1/2− 1525-1545 **** N(1520) 3/2− 1515-1525 **** N(1895) 1/2− 1880-1910 ** N(1680) 5/2+ 1680-1690 **** N(1875) 3/2− 1820-1920 *** N(2000) 5/2+ 1950-2150 ** N(1720) 3/2+ 1700-1750 **** N(1880) 1/2+ − ** N(1990) 7/2+ 1950-2100 ** N(2190) 7/2− 2100-2200 **** N(2250) 9/2− 2250-2320 **** N(2570) 5/2− − ** Table 1. List of the N resonances from baryon summary Table of PDG (2018).
Table 2 lists the light baryon masses from 1S-5S, 1P-5P, 1D-4D, and 1F-2F states. The obtained
$N$ baryon masses are tabulated with the experimental resonances and other theoretical approaches. The radial excited states are calculated for$J^{P}= \displaystyle\frac{1}{2}^{+}$ , and the orbital excited P, D, and F states are calculated for$J^{P}$ values,$\left(\displaystyle\frac{1}{2}^{-}\right.$ ,$\displaystyle\frac{3}{2}^{-}$ ,$\left.\displaystyle\frac{5}{2}^{-}\right)$ ,$\left(\displaystyle\frac{1}{2}^{+}\right.$ ,$\displaystyle\frac{3}{2}^{+}$ ,$\displaystyle\frac{5}{2}^{+}$ ,$\left.\displaystyle\frac{7}{2}^{+}\right)$ , and$\left(\displaystyle\frac{3}{2}^{-}\right.$ ,$\displaystyle\frac{5}{2}^{-}$ ,$\displaystyle\frac{7}{2}^{-}$ ,$\left.\displaystyle\frac{9}{2}^{-}\right)$ , respectively.state J P mass exp. [4] [48] [24] [49] [24] [50] [51] [52] [30] [26] [27] 1S 1/2+ 939 938 938 938 939 938 938 939 938 960 2S 1/2+ 1425 1420-1470 1444 1448 1511 1463 1467 1440 1492 1430 3S 1/2+ 1721 1680-1740 1832 1795 1776 1752 1710 1710 1763 1710 4S 1/2+ 2089 2100 2100 5S 1/2+ 2515 1P 1/2− 1565 1525-1545 1567 1543 1537 1524 1535 1511 1501 1490 1460 1P 3/2− 1535 1515-1525 1567 1543 1537 1524 1536 1520 1511 1517 1535 1495 1P 5/2− 1495 1630 2P 1/2− 1898 1880-1910 1888 1650 1895 2P 3/2− 1865 1820-1920 1700 1880 2P 5/2− 1820 1675 3P 1/2− 2288 2090 3P 3/2− 2251 2150 2080 2150 3P 5/2− 2202 4P 1/2− 2741 4P 3/2− 2697 4P 5/2− 2628 5P 1/2− 3242 5P 3/2− 3192 5P 5/2− 3126 1D 1/2+ 1849 1835-1910 1890 1870 1D 3/2+ 1815 1700-1750 1648 1735 1690 Table 2. Predicted excited state masses of N baryon (in MeV).
The states,
$N(1440)$ ,$N(1710)$ ,$N(1535)$ , and$N(1520)$ are listed as a four-star states. They are determined as 2S, 3S, 1P$\left(\displaystyle\frac{1}{2}^{-}\right)$ , and 1P$\left(\displaystyle\frac{3}{2}^{-}\right)$ states by many other theoretical approaches. All the masses are close to the experimental values. We suggest baryons resonances$N(1895)$ and$N(1875)$ should be the 2P states with$J^{P}$ vales$\displaystyle\frac{1}{2}^{-}$ and$\displaystyle\frac{3}{2}^{-}$ . The mass obtained by Ref. [49] shows a difference of only 10 MeV difference with our mass of 2P. Further, the calculated masses of the 3P state have a difference of$\approx$ 200 MeV with Ref. [51].The assigned
$J^{P}$ value of$N(1720)$ is$\displaystyle\frac{3}{2}^{+}$ . Our 1D$\left(\displaystyle\frac{3}{2}^{+}\right)$ state mass is 65 MeV greater than the upper bound of the experimental mass, and 80 MeV greater than Ref. [52], so that we predict as 1D state. Our predicted 1D$\left(\displaystyle\frac{5}{2}^{+}\right)$ state mass is$\approx$ 80 MeV greater than the baryon$N(1680)$ mass, and it also shows a difference of 30, 65, and 34 MeV with Refs. [49, 50, 52]The other two baryon resonances,
$N(1990)$ and$N(2000)$ , have$J^{P}$ values$\displaystyle\frac{5}{2}^{+}$ and$\displaystyle\frac{7}{2}^{+}$ , respectively, and our 2D state masses with same$J^{P}$ values agrees well with them.For the greater excited negative parity resonances,
$N(2190)$ ,$N(2250)$ , and$N(2570)$ baryons, our 1F state mass is 55 MeV less than experimental mass, while the 2F$\left(\displaystyle\frac{9}{2}^{-}\right)$ state is 59 MeV greater than the experimental mass. The mass of baryon$N(2570)$ is experimentally unknown; if we consider it to be equal to 2570 MeV, then it has a difference of 20 MeV with our 2F state with$J^{P}=\displaystyle\frac{5}{2}^{-}$ .We do not find any results which gives the masses for higher negative and positive parity excited states (which can be determined as 4P, 5P, 2D, 3D, 4D, and 2F states). The
$N$ resonances are compared with the experimental masses and possible$J^P$ values in Fig. 1. -
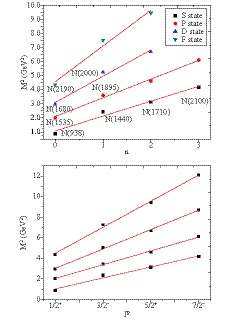
Another important property of hadronic spectroscopy is the Regge trajectory. The Regge trajectories are useful for spectral as well as nonspectral purposes. The spin and mass of the hadrons are related in these plots. Using the obtained results of Table 2, we plot the graphs in (n,
$M^{2}$ ) and (J,$M^{2}$ ) planes [See Fig. 2]. The relation is,$ n= \beta M^2+ \beta_0~~~~\&~~~~~~ J= \alpha M^2+ \alpha_0, $

(7) where n is a principal quantum number;
$\beta$ ,$\alpha$ are slopes; and$\beta_0$ ,$\alpha_0$ are intercepts. The ground and radial excited states S$\left( {\rm{with}} \;J^{P}={\displaystyle\frac{1}{2}}^{+}\right)$ and the orbital excited state P$\left({\rm{with}} \;J^{P}= {\displaystyle\frac{1}{2}}^{-}\right)$ , D$\left({\rm{with}} \;J^{P}= {\displaystyle\frac{5}{2}}^{+}\right)$ , and F$\left({\rm{with}} \;J^{P}= {\displaystyle\frac{7}{2}}^{-}\right)$ are plotted from bottom to top in ($M^2\rightarrow$ n) plot. In ($M^2\rightarrow$ J) plot, we use$\left(J^{P}=\displaystyle\frac{1}{2}^{+}\right.$ ,$J^{P}=\displaystyle\frac{3}{2}^{-}$ ,$J^{P}=\displaystyle\frac{5}{2}^{+}$ ,$\left. J^{P}=\displaystyle\frac{7}{2}^{-}\right)$ for n= 1 to 4. We have already introduced these plots and determined the experimentally unknown heavy baryons in our previous work [37-43]. Here, we aim to study the nature of the graphs for light baryons. -
The magnetic moment of the nucleon is also an important hadronic property because it is an important input for electromagnetic transitions, form factor, and radiative decays of baryons. Here, we determined the magnetic moment of
$N(939)$ state with$J^{P}=\displaystyle\frac{1}{2}^{+}$ and$N(1535)$ states with$J^{P}=\displaystyle\frac{1}{2}^{-}$ . The magnetic moments of the baryons are obtained in terms of the spin, charge, and effective mass of the bound quarks as in Ref. [37]$ \begin{align} \mu_{B}=\sum_{i}\langle \phi_{sf}\vert \mu_{iz}\vert\phi_{sf}\rangle);~~~ \mu_{i}=\frac{e_i \sigma_i}{2m_{i}^{{\rm eff}}}, \end{align} $

(8) where
$e_i$ is a charge and$\sigma_i$ is the spin of the respective constituent quark. The effective mass for each constituting quark$m_{i}^{{\rm eff}}$ can be defined as$ m_{i}^{{\rm eff}}= m_i\left( 1+ \frac{\langle H \rangle}{\displaystyle\sum_{i} m_i} \right), $

(9) where
$\langle H \rangle$ = E +$\langle V_{{\rm spin}} \rangle$ . The wave-function and obtained magnetic moment are provided in Table 3.Table 3. Magnetic moment (in nuclear magneton) for
${N(939)}$ baryon.The magnetic moment is also carried out by orbital excitation. The final spin flavor wave function from the quark model for the nucleons with
$J^{P}= \displaystyle\frac{1}{2}^{-}$ are given by [56] as:$ \begin{split} &\mu(1535)=\left( \frac{1}{9} \mu_{u}+ \frac{2}{9} \mu_{d} \right)\cos^{2} \theta +\left( \frac{1}{3} \mu_{u}+ \mu_{d}\right) \sin^{2} \theta -\\&\quad\left(-\frac{8}{9} \mu_{u}+\frac{8}{9} \mu_{d} \right)\cos \theta \sin \theta, \end{split} $

$ \begin{align} &\mu(1535)=\left( \frac{2}{9} \mu_{u}+ \frac{1}{9} \mu_{d} \right)\cos^{2} \theta +\left( \frac{8}{9} \mu_{u}+ \frac{1}{3} \mu_{d}\right) \sin^{2} \theta \\ &\quad -\left(\frac{8}{9} \mu_{u}-\frac{8}{9} \mu_{d} \right)\cos \theta \sin \theta. \end{align} $

The value of the mixing angle
$\theta$ = −31.7. The obtained magnetic moment value for N(1535) is −0.7695 and 1.8299 (in nuclear magneton), and the values in Ref. [56] were are −1.284 and 1.894. Other Refs. [57, 58, 59, 60] obtained the values for$J^P= \displaystyle\frac{1}{2}^{-}$ as −0.9, −0.56, −0.54 and −0.84. -
The wave functions of nucleons will be bilinear combinations of spin, flavor, and orbital wave functions and then the product of two Jacobi coordinates of the three-quark system. S. Capstick et al. had already determined the decay widths of light baryons in their work [61]. The decay width relations will depend on the orbital wave functions of the baryons. The decay widths are expressed as in Ref. [62]. We used the pion-nucleon coupling constants (
$f$ ) from [62] and determined the widths using our masses as the input. The energy ($E$ ) and the momentum of pion$\kappa$ are,$ E=\frac{m^{* 2}- m_\pi^2+ m_N^2}{2m^*}, \tag{10a} $

(10a) $ \kappa=\frac{\sqrt{[m^{* 2}-(m_N+ m_\pi)^{2}][m^{* 2}-(m_N-m_\pi)^{2}]}}{2m^*}, \tag{10b} $

(10b) where,
$m_N$ = 939 MeV and$m_\pi$ = 139 MeV are the mass of the nucleon and pion, respectively.$m^*$ is the resonance mass, from Table 2, for each case. We calculate some of the decay widths of the excited nucleons:1.
$N(1440) \rightarrow N\pi$ $ \Gamma = \frac{3f^2}{4\pi} \frac{E-m_N}{m^*} \frac{\kappa}{m_\pi^{2}}(m^*+m_N)^{2} $

(11) is 62%, which is in the range of PDG 55%−75% with
$f$ = 0.39 and$m^*$ =1425.2.
$N(1535) \rightarrow N\pi$ $ \Gamma = \frac{f^2}{4\pi} \frac{E+m_N}{m^*} \frac{\kappa}{m_\pi^{2}}(m^*-m_N)^{2} $

(12) is 86%, which is higher than the range of PDG 55%−65% and 25%−65% of Ref. [63], with
$f$ =0.36 and$m^*$ = 1565.3.
$N(1520) \rightarrow N\pi$ $ \Gamma =\frac{1}{3} \frac{f^2}{4\pi} \frac{E-m_N}{m^*} \frac{\kappa^3}{m_\pi^{2}} $

(13) is 16%, which is lower than the range of PDG 32%−52%, with
$f$ = 1.56 and$m^*$ = 1535.4.
$N(1720) \rightarrow N\pi$ $ \Gamma = \frac{1}{3}\frac{f^2}{4\pi} \frac{E+m_N}{m^*} \frac{\kappa^{3}}{m_\pi^{2}} $

(14) is 11%, which is in the range of PDG 8%−14% with
$f$ = 0.25 and$m^*$ = 1815.5.
$N(1680) \rightarrow N\pi$ $ \Gamma = \frac{2}{5}\frac{f^2}{4\pi} \frac{E-m_N}{m^*} \frac{\kappa^{5}}{m_\pi^{4}} $

(15) is 118%, which is higher than the range of PDG 60%−70% with
$f$ =0.42 and$m^*$ =1769. -
$N^{*}$ resonances are determined using the hCQM model by adding the first-order correction to the potential. The complete mass spectra with individual states and predicted$J^{P}$ values are presented in Table 2 and graphically compared with the experimental states in Fig. 1. We can observe that the resonances are predicted from the first radial excited state (2S) to the orbital excited state (2F). The major results are summarized below:● We compared 14 experimentally known states with our prediction. We also plotted their masses against their
$J^{P}$ values. The conclusion of the plot suggests that the states$N(1440)$ ,$N(1710)$ ,$N(1880)$ ,$N(2100)$ ,$N(1535)$ ,$N(1895)$ ,$N(1520)$ ,$N(1875)$ , and$N(2570)$ are close to our determined resonances. While the states,$N(1720)$ ,$N(1680)$ ,$N(2000)$ ,$N(1990)$ , and$N(2190)$ did not agree with our predicted values. All the determined states are presented according to our predictions of the isospin splitting states.● The radial excited states (2S-4S) masses are agree with our predicted values within the range of an experimental error.
● It can be concluded that the mass spectra of hadrons can be conveniently described through Regge trajectories. These trajectories will aid in identifying the quantum number of particular resonance states. From Fig. 1, we can see that the trajectories are linear but not parallel, similar to Ref. [64].
● The magnetic moment was calculated for
$J^{P}=\displaystyle\frac{1}{2}^{+}$ and$J^{P}=\displaystyle\frac{1}{2}^{-}$ . We will attempt to reproduce the nucleon magnetic moments of other excited states after this preliminary calculation.● Nucleons
$N(1440)$ ,$N(1535)$ ,$N(1520)$ ,$N(1720)$ , and$N(1680)$ for$N\pi$ decay widths were calculated. In case of$N(1680)$ , the ratio of$\displaystyle\frac{\Gamma_{N\pi}}{\Gamma_{{\rm tot}}} $ was very high. For other cases, it was near/in range.● We successfully studied the mass spectra of
$N^*$ baryons using the hCQM. We would like to extend the model for other light baryons as well.
Spectroscopy of light
${{N^*}}$
baryons
- Received Date: 2018-10-01
Abstract: We present the masses of N baryons up to 3300 MeV. The radial and orbital excited states are determined using hypercentral constituent quark model with the first-order correction. The obtained masses are compared with the experimental results and other theoretical predictions. The Regge trajectories are also determined in (n,







 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: