-
The
$ \alpha $ -decay process is essentially a quantum tunneling effect, which was first described by Gamow and by Condon and Gurney [1, 2]. Several theoretical calculations have been performed to understand the microscopic nature of this phenomenon, obtain the$ \alpha $ -decay width and gain information about the structure of the nuclei. These studies are based on various theoretical models such as the shell model, fission-like model, and cluster model [3–10]. In general, the$ \alpha $ -decay constant$ \lambda $ is the product of the preformation factor$ P_{\alpha} $ , alpha particle penetration through the potential barrier$ P_{0} $ , and the assault frequency$ \nu_{0} $ . The nuclear values of these parameters are generally dependent on nuclear structure and internuclear potential.Because the formation of the alpha particle, including valence nucleons, is closely related to the nuclear structure and alpha preformation factor containing most of the nuclear structure information, the preformation factor is an important component of the
$ \alpha $ -decay study. Consequently, the parent nucleus can be approximated as a simple two-particle system before emission, such that the alpha emitter is assumed as a system consisting of a core nucleus and a single alpha cluster [11, 12]. The surface nucleons and isospin asymmetry of these is expected to play a more important role in the preformation of the alpha nucleus [11–16].The neutron skin thickness is defined as the difference between neutron and proton root-mean-squares;
$ \Delta{r_{np}}\equiv R_{n}-R_{p} $ , which can be related to the difference in nuclear asymmetric equation states inside and on the surface of the nucleus. Various studies have been conducted on the determination of proton and neutron density distributions, the experimental root-mean-square (rms) measurements of nuclei and the effect of neutron skin thickness on$ \alpha $ -decay [17-19]. In some studies, to determine the$ \Delta{r_{np}} $ , it is assumed that the proton diffuseness$ a_{p} $ and neutron diffuseness$ a_{n} $ are the same, while in fact, at the nucleus surface this is not exactly the case. Although this assumption is true for light nuclei with$ N = Z $ , it is not validated for the nuclei with$ N>Z $ , as the proton and neutron density distributions of heavy nuclei are not exactly the same on the nuclear surface. Moreover, the shape of the neutron density distribution is more diffuse than the charge density distribution [18, 20, 21].The HF formalism and Skyrme forces parameterized to describe various ground state properties of nuclei are successful theories for the determination of more realistic nuclei densities [16, 17, 22–24]. The effects of the isospin asymmetry are embedded so well in this formalism that it can be applied to surface studies of the nuclei. The specifics of the effects of these different isospin asymmetries on the half-lives of the
$ \alpha $ -decay can be expected within the different$ \Delta{r_{np}} $ originated by HF formalism and the NST case.For this purpose, using isospin asymmetry data obtained from the HF formalism and the NST case, we aim to determine their effects on the
$ \alpha $ -decay width, half-life, and on the preformation factor of$ \alpha $ -decay for even-even isotope groups with$ 82\leqslant Z\leqslant92 $ .This paper is organized as follows: In Sec. 2, the theoretical framework of the double folding (DF) model is presented in the calculation of nuclear potential, half-life, and the preformation factor. Sec. 3 presents the results and discussion. A summary is provided in Sec. 4.
-
The total alpha core potential is constructed by nuclear and Coulomb terms, and it is given by
$ V_{\rm T}(r) = V_{\rm C}(r)+ V_{\rm N}(r). $

(1) Nuclear and Coulomb potentials are obtained from the DF model by folding the densities of the alpha particle and the daughter nuclei with effective M3Y interactions [25–29],
$\begin{split} V_{\rm N}({{r}}) =& \lambda V_{\rm F}({{r}}) = \lambda \iint{\rho_{1}({{r}}_{1})\, \nu(s = |{{r}}+{{r}}_{2}-{{r}}_{1}|)}\,\\ &{\times\rho_{2}({{r}}_{2})\, {\rm d}^{3}{{r}}_{1}\,{\rm d}^{3}{{r}}_{2}}, \end{split}$

(2) where
$ {{s}} $ is the distance between the two interacting nucleons, and$ \rho_{1}({{r}}_{1}) $ and$ \rho_{2}({{r}}_{2}) $ are the density distributions of the alpha particle and daughter nuclei, respectively. The$ \nu(s = |{{r}}+{{r}}_{2}-{{r}}_{1}|) $ is the effective nucleon-nucleon interaction, where we employ M3Y Paris-NN forces with zero range approximation for the nucleon-nucleon interaction [28].The parameter
$ \lambda $ in Eq. (2) is a re-normalization factor. To reproduce the experimental$ \alpha $ -decay energies, the$ \lambda $ -value is determined under the Bohr-Sommerfeld quantization condition [30],$ \int_{r_{1}}^{r_{2}}\sqrt{\frac{2\mu}{\hbar^{2}}|V(r)-Q|}\, {\rm d}r = (2n + 1)\frac{\pi}{2} = (G-L+1)\frac{\pi}{2}, $

(3) where
$ r_{1} $ and$ r_{2} $ (and later$ r_{3} $ ) are the classical return points, determined from the relation$ V(R) = Q $ (decay energy of alpha). The global quantum number G is estimated by the Wildermuth rule [31],$ G = 2N + L = \sum\limits_{i = 1}^{4}(2n_{i}+l_{i}) = \sum\limits_{i = 1}^{4}g_{i}, $

(4) where N is the number of nodes in the alpha core wave function, L is the angular momentum of the cluster motion, and
$ g_{i} $ is the oscillation quantum number of the cluster nucleon. For N and Z, the parent nucleus is for$ (Z, N) \leqslant 82 $ ,$ g_{i} = 4 $ , for$ 82 <(Z, N) \leqslant126 $ ,$ g_{i} = 5 $ , and for$ (Z, N)> 126 $ ,$ g_{i} = 6 $ , corresponding to the order on the oscillator layers of$ 4\hbar\omega $ ,$ 5\hbar\omega $ , and$ 6\hbar\omega $ , respectively. In the quasiclassical approximation, the$ \alpha $ -decay width$ \Gamma_{\alpha} $ is obtained by [30, 32]$ \Gamma_{\alpha} = P_{\alpha} F \frac{\hbar^{2}}{4\mu}{\rm exp}\left( -2\int_{r_{2}}^{r_{3}} k(r)\,{\rm d}r \right), $

(5) where
$ P_{\alpha} $ is the alpha preformation factor, which can be extracted from the ratio of the experimental decay width to the calculated one [27].The normalization factor is,
$ F\int_{r_1}^{r_2}\frac{{\rm d}r}{2k(r)}\, = 1, $

(6) where
$ k(r) = \sqrt{\frac{2\mu}{\hbar^2}|V(r)-Q|} $ is the wave number. Then, the$ \alpha $ -decay half-life is related to the width by$ T_{1/2} = \hbar \ln2/\Gamma_{\alpha} $ .In Eq. (2), the mass density distribution of the spherical alpha particle
$ \rho_{1}(r_{1}) $ has a Gaussian form given by$ \rho_{1}(r_{1}) = 0.4229\,\exp(-0.7024\,r_{1}^{2}), $

(7) and the mass density distribution of the daughter nucleus is written as
$ \rho_{2}^{\tau}(r_{2}) = \frac{\rho_{0}^{\tau}}{1+\exp[(r_{2}-R_{1/2}^{\tau})/a_{\tau}]}, $

(8) where
$ \tau = {n} $ or p and the value of$ {\rho_{0}^{\tau}} $ is fixed by integrating the density distribution equivalent to the mass number of the daughter nucleus. The half-density radius$ R_{1/2}^{\tau} $ is related to the mass number of the nucleus. The neutron and proton rms radii of the daughter nuclei are$ R_{\tau}^{(S)}\equiv <r^{2}>^{1/2} = \left[ \frac{\int \rho_{2}^{\tau}(r)r^{4}{\rm d}r}{\int \rho_{2}^{\tau}(r)r^{2}{\rm d}r} \right]^{\frac{1}{2}}. $

(9) Considering the importance of deformation of the nuclei on the calculation of this parameter and
$ \alpha $ -decay study [6, 26, 33], we have employed the axially symmetric deformed distribution of the daughter nucleus in the DF model calculations using the following profile [33],$ \rho_{2}^{\tau}(r_{2},\theta) = \frac{\rho_{0}^{\tau}}{1+\exp\{[r_{2}-R_{1/2}^{\tau}(\theta)]/a_{\tau}\}}, $

(10) where the half-density radius
$ R_{1/2}^{\tau}(\theta) $ is parameterized as$ R_{1/2}^{\tau}(\theta) = r_{\tau}A^{1/3}[1+\beta_{2}Y_{20}(\theta) + \beta_{4}Y_{40}(\theta)], $

(11) where
$ \beta_{2} $ and$ \beta_{4} $ are the quadrupole and hexadecapole deformation parameters of daughter nuclei, respectively, with their values taken from Ref. [34]. The rms neutron and proton radii using the deformed nuclear distributions are calculated by$ R_{\tau}^{(D)}\equiv\left[ \frac{\int \rho_{2}^{\tau}(r,\theta)r^{4}{\rm d}r\,{\rm d}\Omega }{\int \rho_{2}^{\tau}(r,\theta)r^{2}{\rm d}r\,{\rm d}\Omega} \right]^{\frac{1}{2}}. $

(12) The multipole expansion of the deformed distribution
$ \rho_{2}^{\tau}(r_{2}) $ is used and then the orientation-dependent DF potential can be evaluated as the sum of different multipole components [18, 33]. The effect of nuclear deformations on the decay width could also be evaluated by integrating the partial width along the direction,$ \Gamma = \int_{0}^{\pi/2}\Gamma(\beta)\sin\beta\,{\rm d}\beta, $

(13) where
$ \beta $ is the angle between the symmetry axis of the daughter nucleus and the direction of the$ \alpha $ -particle emission.We studied two cases. In the first case, the radius and diffuseness parameters were obtained by HF calculations based on the Skyrme-SLy4 effective interaction that successfully explains the ground state properties of nuclei [35–37]. The other case is the NST with the assumption
$ r_{n} > r_{p} $ and$ a_{n} = a_{p} = 0.54 $ that the radius parameters$ r_{n} $ and$ r_{p} $ have determined in terms of the neutron and protons rms radii. The proton root-mean-square radius$ R_{p} $ is extracted by empirical data, and the neutron rms radius$ R_{n} $ is determined by the relation$ R_{n} = R_{p}+ \Delta r_{np} $ , in which the$ \Delta r_{np} $ is obtained by$ \Delta r_{np} = (-0.04 \pm 0.03)+(1.01 \pm 0.15)\delta, $

(14) which presents the linear relationship between the isospin asymmetry
$ \delta = (N-Z)/(N+Z) $ and$ \Delta r_{np} $ [38]. -
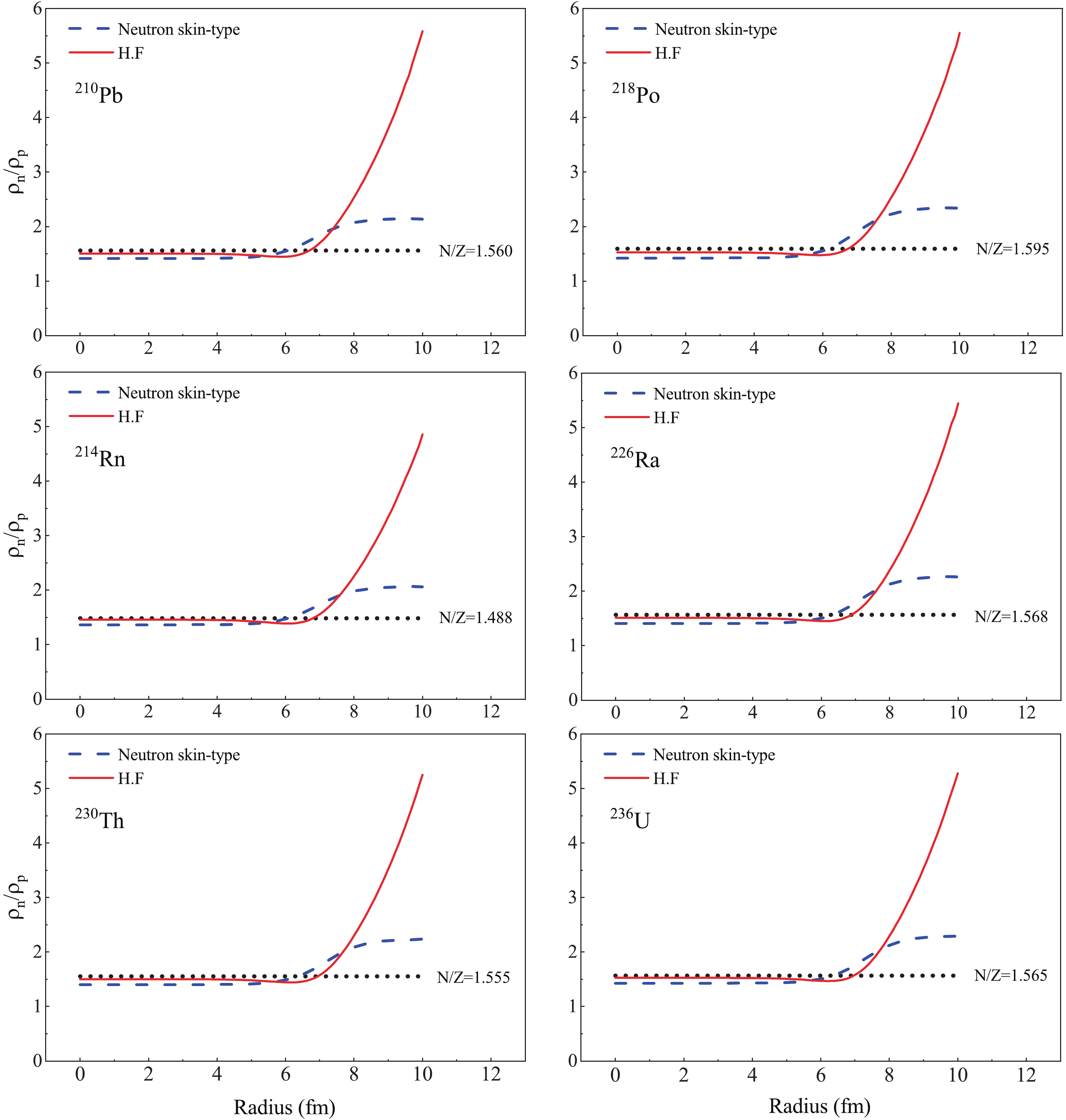
For the nuclei with
$ N>Z $ , the rms of the neutron density distribution is larger than the rms of the proton density distribution, hence the neutron density distribution can be different from the proton density distribution. Accordingly, to calculate the nucleus density distribution, it is not generally correct to assume that$ \rho_{n} = \frac{N}{Z}\rho_{p} $ when$ N>Z $ . Instead, it is better to separately employ the neutron-to-proton densities.The ratio of the neutron-to-proton density versus distance from the nucleus center was plotted for some neutron-rich nuclei
$ ^{210}{\rm Pb} $ ,$ ^{218}{\rm Po} $ ,$ ^{214}{\rm Rn} $ ,$ ^{226}{\rm Ra} $ ,$ ^{230}{\rm Th} $ , and$ ^{236}{\rm U} $ in Fig. 1. The ratio of densities is equal to$ N/Z $ in the range$ R = 0-4 $ fm, followed by a sharp rise. This rising trend is more dramatic in HF compared to NST. To determine the effect of the neutron skin thickness on the$ \alpha $ -decay, the neutron skin thickness was calculated by the NST and HF formalism versus the isospin asymmetry parameter$ \delta $ compared in Fig. 2. This figure illustrates the variation between the calculated values of$ \Delta r_{np} $ within these two different approaches.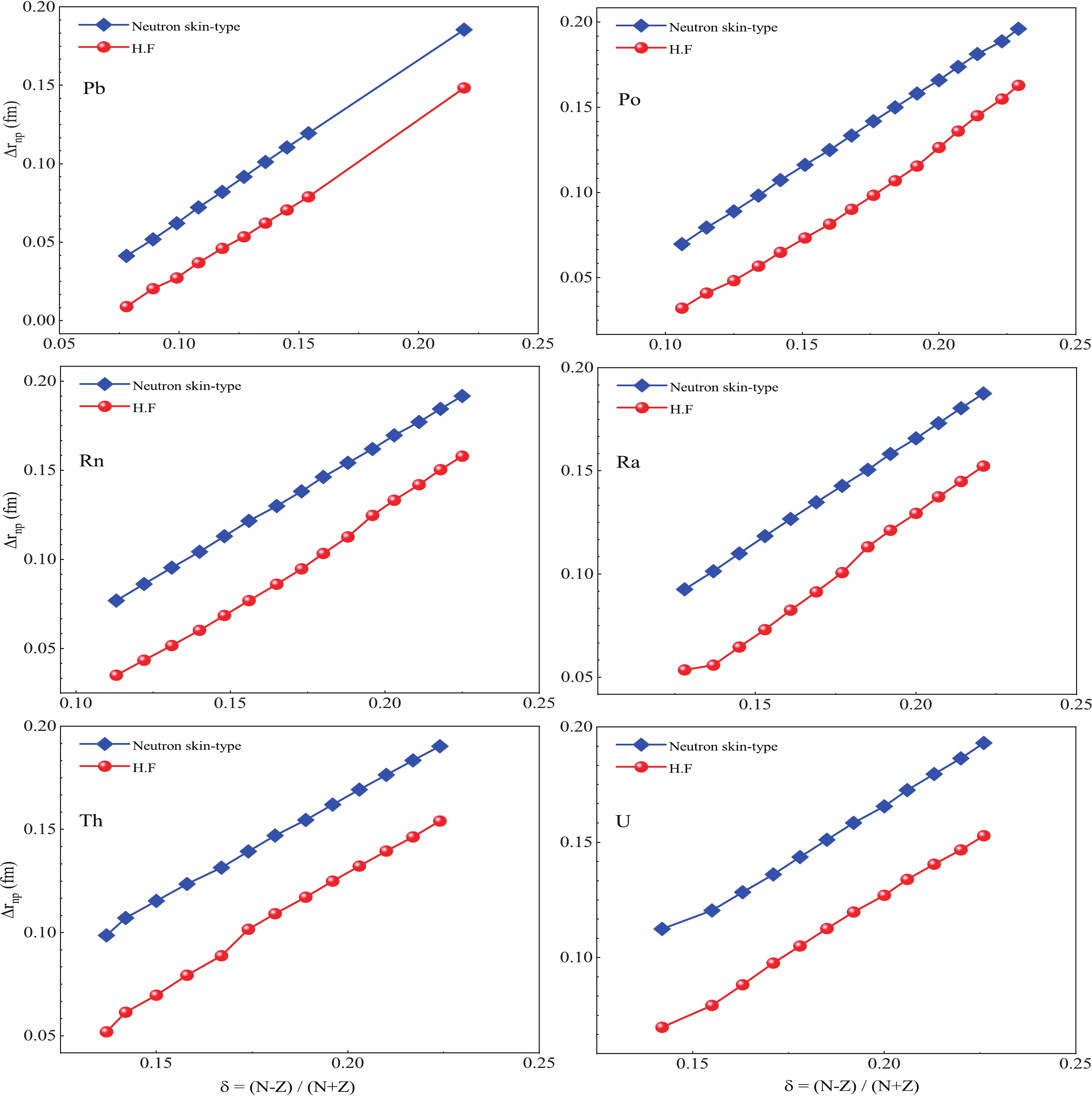
Figure 2. (color online) Neutron skin thickness
$ \Delta r_{np} $ versus asymmetry parameter$ \delta $ for isotope groups of elements$ {\rm Pb, Po, Rn, Ra, Th} $ and U for two cases NST and HF.Because of the important role of the neutron and proton density distributions in calculating the nuclear potential, typically, the total potential for the
$ ^{216}{\rm Po} $ , whose deformation parameters are zero, in the NST and HF cases were plotted in Fig. 3(a). In the range of$ R = 9.9-12.5 $ (fm), the potential value in the HF case is greater by 0.15% to 2.5% in comparison with the NST case. Because of the effect of the neutron skin thickness in NST and HF cases on the total potential, it is expected that the potential variations will affect the penetration probabilities and consequently affect the$ \alpha $ -decay width. Therefore, the$ \alpha $ -decay width was investigated in NST and HF cases for isotope groups of elements${\rm Pb, Po, Rn, Ra, Th} $ , and U. Typically, the treatment of the calculated$ \alpha $ -decay width for the Po isotope group in terms of the neutron number was presented in Fig. 3(b). In this figure, the$ \alpha $ -decay widths of the NST case are greater by about 30% than their equivalent values of HF case. Therefore, this can affect the$ \alpha $ -decay half-life and the extracted preformation factor. Within the calculated potentials,$ \alpha $ -decay half-lives were calculated for the even-even isotope groups of elements$ {\rm Pb, Po, Rn, Ra, Th} $ , and U by employing relations 6 to 8. In the NST case, the diffuseness parameters were fixed, and the radius parameters$ r_{n} $ and$ r_{p} $ were determined in terms of the neutron and proton rms radii. The rms proton radius$ R_{p} $ was taken from the experimental rms charge radii, and the rms neutron radius$ R_{n} $ was obtained from the relationship$ R_{n} = R_{p}+ \Delta r_{np} $ . Since the experimental rms charge radii for some isotopes was not available, we have assumed the values of rms charge radii for these isotopes from a simple relationship, given by$ R_{p} = (r_0 + r_{1}A^{-2/3}+r_{2}A^{-4/3})A^{1/3} $ with$ r_{0} = 0.891(2) $ fm,$ r_{1} = 1.52(3) $ fm, and$ r_{2} = -2.8(1) $ fm. This relationship was adapted from a systematic study on available data of the experimental rms charge radii [39].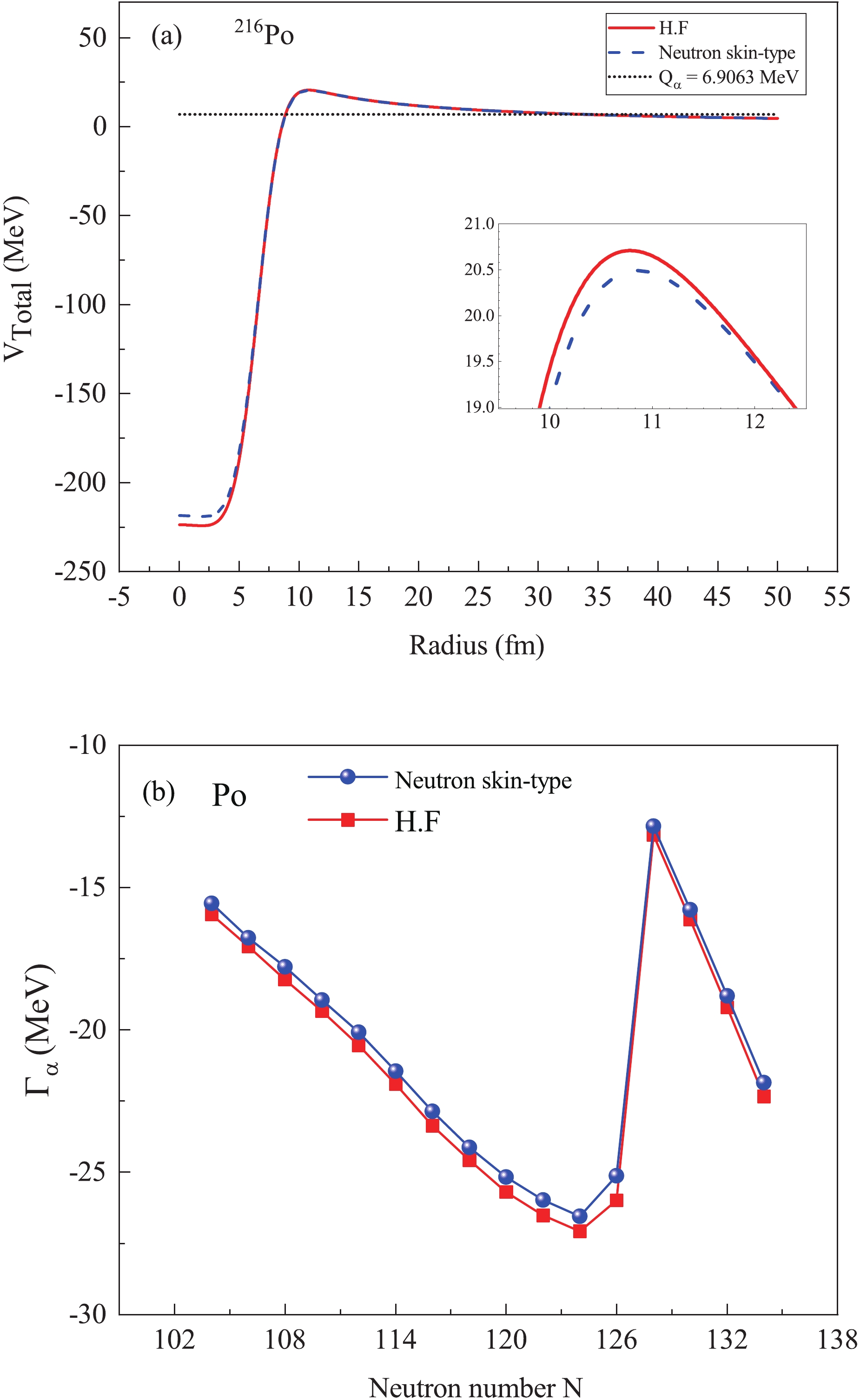
Figure 3. (color online) (a) Total potential in terms of distance from center of nucleus for
$ ^{216}{\rm Po} $ , assuming that HF and NST and (b) is the$ \alpha $ -decay width versus neutron number for even-even Po isotopes.In Fig. 4, the logarithm of the preformation factor, calculated from the relation
$ P_{\alpha} = \Gamma_{\alpha}^{\rm exp}/\Gamma_{\alpha}^{\rm cal} $ [27], is plotted according to the parent neutron number for even-even isotopes with the atomic number in the range$ 82\leqslant Z\leqslant92 $ . In general, the variation treatments in NST and HF cases are the same. Results indicate that the curve of HF has a value closer to the experimental data. The standard deviation from the experimental data obtained by$ \sigma = \{ \sum^{N}_{i = 1}[{\rm log}_{10}(T^{i}_{\rm cal}/T^{i}_{\rm exp})]^{2}/{N}\}^{1/2} $ is equal to$ 0.438 $ and$ 0.391 $ for NST and HF cases, respectively. This confirms that the calculated half-lives in the HF case are closer to experimental data. -
In this study, we investigated the effects of isospin asymmetries resulting from different proton and neutron density distributions on the total potentials,
$ \alpha $ -decay widths, and half-lives of even-even alpha emission nuclei with the atomic number in the range$ 82\leqslant Z\leqslant92 $ . The neutron and proton density distributions of the daughter nuclei were calculated in the two-parameter Fermi form of nucleon density distributions. The radius and diffuseness parameter values of the nuclei were obtained from the NST and HF formalism, leading to different isospin asymmetries. The results indicated that the values of$ \Delta r_{np} $ for the two NST and HF cases affect the$ \alpha $ -decay half-life and the preformation factor.The standard deviation of the calculated half-lives from experimental data reached about 0.438 for the NST case. However, the results illustrated that the isospin asymmetry within HF formalism lowered the standard deviation in comparison with its equivalent value obtained from NST. The standard deviation for the HF case is about 0.391, which indicates that the calculated half-life, in this case, is closer to the value obtained by experimental data.
Determination of isospin asymmetry effects on α-decay
- Received Date: 2019-05-06
- Accepted Date: 2019-09-16
- Available Online: 2019-12-01
Abstract: In this study, we compared the effect of the isospin asymmetry of proton and neutron density distributions in the neutron skin-type (NST) case and in the Hartree-Fock formalism (HF) on the half-life of alpha emitters with the atomic number in the range of





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: