-
Hadrons, subatomic particles that are composed of quarks and gluons, cover a large spectrum of masses: the lightest hadron, the pion, has a mass
$ M_\pi \approx 0.14 \;{\rm GeV} $ , while the heavy hadrons are heavier than$ 10 \;{\rm GeV} $ [1]. It is expected that the underling theory, quantum chromodynamics (QCD) [2], can explain the hadron spectrum and unify the description of light and heavy hadrons. QCD is a non-Abelian local gauge field theory of strong interaction and is consistent with experimental observations. Due to the phenomena that emerge at the hadronic scale, i.e. confinement and dynamical chiral symmetry breaking (DCSB), non-perturbative QCD is an important part of the Standard Model.Confinement provides an intrinsic wavelength,
$ \lambda_c\approx 0.5 \;{\rm fm} $ , for the propagation of quarks and gluons. They behave like partons for$ r<\lambda_c $ , and show different propagation mode for$ r>\lambda_c $ .The propagation of quarks and gluons is certainly affected by the finite size of hadrons. Studying hadron physics with QCD needs non-perturbative methods. As a well-established non-perturbative approach, the lattice QCD (lQCD) [3–5], a lattice gauge theory formulated on a grid, has achieved many successes in hadron physics. While lQCD resorts to brute force calculation, functional methods like the Dyson-Schwinger and Bethe-Salpeter equations (DSBSE) [6–8] are complementary to lQCD.
In this work, we aim at unifying the description of light, heavy and heavy-light mesons via the DSBSE approach. In the Poincaré covariant framework, the quark propagator is presented by the Gap equation [6–8]①,
$ \begin{split} S_f^{-1}(k) = & Z_2 (i\gamma\cdot k + Z_m m_f) \\ & + \frac{4}{3}\bar{g}^2 Z_1 \int^\Lambda_{d q} D_{\mu\nu}(l)\gamma_\mu S_{f}(q)\Gamma^f_\nu(k,q), \end{split} $

(1) where
$ f = \{u,d,s,c,b,t\} $ represents the quark flavor,$ l = k-q $ ,$ S_{f} $ is the quark propagator,$ m_f $ the current quark mass,$ \Gamma^f_\nu $ the quark-gluon vertex,$ D_{\mu\nu} $ the gluon propagator,$ \bar{g} $ the coupling constant.$ Z_1 $ ,$ Z_2 $ ,$ Z_m $ are the renormalization constants of the quark-gluon vertex, the quark field and the quark mass, respectively.$ \int^\Lambda_{d q} = \int ^{\Lambda} {\rm d}^{4} q/(2\pi)^{4} $ stands for the Poincaré invariant regularized integration, with$ \Lambda $ the regularization scale. A meson corresponds to a pole in the quark-antiquark scattering kernel [9]. The Bethe-Salpeter amplitude (BSA),$ \Gamma^{fg}(k;P) $ , where$ k $ and$ P $ are the relative and total momentum of the meson,$ P^2 = -M^2 $ , and$ M $ the meson mass, is solved by the Bethe-Salpeter equation (BSE) [8–10],$ \big{[} \Gamma^{fg}(k;P) \big{]}^{\alpha}_{\beta} = \int^\Lambda_{d q} \big{[} K^{fg}(k,q;P) \big{]}^{\alpha\delta}_{\sigma\beta} \big{[} \chi^{fg}(q;P) \big{]}^{\sigma}_{\delta} , $

(2) where
$ K^{fg}(k,q;P) $ is the quark-antiquark scattering kernel, and$ \alpha $ ,$ \beta $ ,$ \sigma $ and$ \delta $ are the Dirac indexes.$ \chi^{fg}(q;P) = S_{f}(q_{+}) \Gamma^{fg}(q;P) S_{g}(q_{-}) $ is the wave function,$ q_{+} = q + \iota P/2 $ ,$ q_{-} = q - (1-\iota) P/2 $ .$ \iota $ is the partitioning parameter describing the momentum partition between the quark and antiquark, and does not affect the physical observables.A promising and consistent way to solve the problem of meson spectrum is to build a quark-gluon vertex and construct a scattering kernel. The form of the quark-gluon vertex and of the scattering kernel have been investigated in [11], and the most widely used and technically simplest is the rainbow-ladder (RL) approximation,
$ \bar{g}^2 Z_1 D_{\mu\nu}(l) \Gamma^f_\nu(k,q) \to [Z_{2}]^{2} \tilde{D}^{f}_{\mu\nu}(l) \gamma_\nu, $

(3) $ \big{[} K^{fg}(k,q;P) \big{]}^{\alpha\delta}_{\sigma\beta} \to -\frac{4}{3}[Z_{2}]^{2} \tilde{D}^{fg}_{\mu\nu}(l) [\gamma_{\mu}]^{\alpha}_\sigma [\gamma_{\nu}]^\delta_\beta, $

(4) where
$ \tilde{D}^{fg}_{\mu\nu}(l) \!=\! \left(\delta_{\mu\nu}\!-\!\frac{l_{\mu}l_{\nu}}{l^{2}}\right){\cal G}^{fg}(l^2) $ and$ \tilde{D}^{f}_{\mu\nu}(l)\! =\! \left(\delta_{\mu\nu}\!-\!\frac{l_{\mu}l_{\nu}}{l^{2}}\right){\cal G}^f(l^2) $ are the effective quark-antiquark interactions. In the original RL approximation,$ {\cal G}^{fg} = {\cal G}^{f} $ is flavor symmetrical and modeled by [12]$ {\cal G}^f(s) = {\cal G}^f_{\rm IR}(s) + {\cal G}_{\rm UV}(s), $

(5) $ {\cal G}^f_{\rm IR}(s) = 8\pi^2\frac{D_f^2}{\omega_f^4} {\rm e}^{-s/\omega_f^2}, $

(6) $ {{\cal G}_{\rm UV}}(s){\rm{ }} = \frac{{8{\pi ^2}\gamma _m{\cal F}(s)}}{{{\rm{ln}}[\tau + {{(1 + s/\Lambda _{\rm QCD}^2)}^2}]}}, $

(7) where
$ s = l^2 $ .$ {\cal G}^f_{\rm IR}(s) $ is the infrared interaction responsible for DCSB, with$ D_f^2\omega_f $ expressing the interaction strength and$ \omega_f $ the interaction width in momentum space. The form in Eq. (6) is used as it enables a natural extraction of a monotonic running-coupling and gluon mass [12], whose relation to QCD can be traced [13].$ {\cal G}_{\rm UV}(s) $ keeps the one-loop perturbative QCD limit in the ultraviolet.$ {\cal F}(s) = [1 - \exp(-s^2/[4m_{t}^{4}])]/s $ ,$ \gamma_{m} = 12/(33-2N_{f}) $ , with$ m_{t} = 1.0 \;{\rm GeV}\, $ ,$ \tau = {\rm e}^{10} - 1 $ ,$ N_f = 5 $ , and$ \Lambda_{{\rm {QCD}}} = 0.21 $ GeV. The values of$ m_{t} $ and$ \tau $ are chosen different from Ref. [12] so that$ {\cal G}_{\rm UV}(s) $ is well suppressed in the infrared, and the dressed function$ {\cal G}_{\rm IR}^{fg}(s) $ is qualitatively correct in the limit$ m_f \to \infty $ or$ m_g \to \infty $ .A nontrivial property of
$ \Gamma^f_\nu $ is its dependence on the quark flavor due to the dressing effect. By the same token,$ K^{fg} $ depends on the flavors of scattered quark and antiquark. For a unified description of the system with different quarks, the flavor dependence of$ \Gamma^f_\nu $ and$ K^{fg} $ should be taken into account properly, whatever model is used. The RL approximation is phenomenologically successful for pseudoscalar and vector mesons [12, 14–16]. The best parameters are$ (D_f^2\omega_f)^{1/3} = $ $ 0.8\;{\rm GeV} $ and$ \omega_f = 0.5\;{\rm GeV} $ for light mesons [12], and$ (D_f^2\omega_f)^{1/3} \approx [0.6,0.7] \;{\rm GeV} $ and$ \omega_f = 0.8\;{\rm GeV} $ for heavy mesons [17, 18]. The strength decreases and$ \omega_f $ increases for an increasing quark mass, indicating that heavy-flavor quarks probe shorter distances than light-flavor quarks at the corresponding quark-gluon vertexes [19]. The RL approximation fails to describe heavy-light mesons due to the lack of flavor asymmetry in Eq. (5)-Eq. (7). The spectrum has a larger error than for quarkonia and the decay constants are incorrect [20, 21]. The heavy-light meson problem has been studied for 20 years in this approach [22–27], but no satisfactory solution has been found yet. -
To introduce flavor asymmetry, one should consider the axial-vector Ward-Takahashi identity (av-WTI), which guarantees that the ground state pseudoscalar mesons are Goldstone bosons of DCSB [14, 15],
$ \begin{split} P_\mu \Gamma^{fg}_{5\mu}(k;P) = & S^{-1}_f(k_+)i\gamma_5 + i\gamma_5 S^{-1}_g(k_-)\\ & - i[m_f + m_g]\Gamma^{fg}_5(k;P), \end{split} $

(8) where
$ \Gamma^{fg}_{5\mu} $ and$ \Gamma^{fg}_5 $ are the axial-vector and pseudoscalar vertexes, respectively. Considering the equations for$ S^{f,g} $ ,$ \Gamma^{fg}_{5\mu} $ and$ \Gamma^{fg}_5 $ in the RL approximation, Eq. (8) leads to$ \begin{array}{l} \displaystyle\int^\Lambda_{d q} {\cal G}^{fg}(s)\gamma_\alpha [S_{f}(q_+)i\gamma_5 + i\gamma_5 S_{g}(q_-)]\gamma_\beta = \displaystyle\int^\Lambda_{d q} \gamma_\alpha [{\cal G}^{f}(s) S_{f}(q_+)i\gamma_5 + {\cal G}^{g}(s) i\gamma_5S_{g}(q_-)]\gamma_\beta. \end{array} $

(9) Eq. (9) says that
$ {\cal G}^{fg}(s) $ is a median value of$ {\cal G}^{f}(s) $ and$ {\cal G}^{g}(s) $ . Considering the scalar part of the propagator,$ S^f(q) = -i{\not\!{q}}\sigma^f_v(q^2) + \sigma^f_s(q^2) $ , we get$ {\cal G}^{fg}(s) = (\sigma^f_s(q^2_+){\cal G}^{f}(s) + $ $(\sigma^f_s(q^2_+){\cal G}^{f}(s) + \sigma^g_s(q^2_-){\cal G}^{g}(s))/(\sigma^f_s(q^2_+) + \sigma^g_s(q^2_-)) $ . It is well known that the infrared value of$ \sigma^f_s(q^2) $ is proportional to the inverse of the interaction strength, and the width of$ \sigma^f_s(q^2) $ is proportional to$ \omega_f $ . Thus, we assume$ {\cal G}^{fg}(s) $ to be$ {\cal G}^{fg}(s) = {\cal G}^{fg}_{\rm IR}(s) + {\cal G}_{\rm UV}(s), $

(10) $ {\cal G}^{fg}_{\rm IR}(s) =8\pi^2\frac{D_f}{\omega_f^2}\frac{D_g}{\omega_g^2} {\rm e}^{-s/(\omega_f\omega_g)}. $

(11) $ {\cal G}_{\rm UV}(s) $ is unchanged from Eq. (7), and as we are dealing with 5 active quarks,$ {\cal G}_{\rm UV}(s) $ is independent of the quark flavor. The effective interaction$ \tilde{D}^{fg}_{\mu\nu} $ represents the total dressing effect of the gluon propagator and of the two quark-gluon vertexes. Eq. (11) means that quarks and antiquarks contribute equally to the interaction strength and width.The preservation of av-WTI can be checked numerically by the Gell-Mann-Oakes-Renner (GMOR) relation, which is equivalent to av-WTI [14, 15],
$ \tilde{f}_{0^-} : = (m_f + m_g)\rho_{0^-}/M^2_{0^-} = f_{0^-}, $

(12) where
$ M_{0^-} $ is the mass of the pseudoscalar meson, and$ f_{0^-} $ the leptonic decay constant.$ f_{0^-} $ and$ \rho_{0^-} $ are defined by$ {f_{{0^ - }}}{P_\mu }\;: = {Z_2}{N_c}\;{\rm{tr}}\int_{dk}^\Lambda \gamma _5^{}\gamma _\mu ^{}{S_f}({k_ + })\Gamma _{{0^ - }}^{fg}(k;P){S_g}({k_ - }),$

(13) ${\rho _{{0^ - }}}{\rm{ }}: = {Z_4}{N_c}\;{\rm{tr}}\int_{dk}^\Lambda \gamma _5^{}{S_f}({k_ + })\Gamma _{{0^ - }}^{fg}(k;P){S_g}({k_ - }), $

(14) where
$ Z_4 = Z_2 Z_m $ ,$ N_c $ is the color number, tr the trace of the Dirac index, and$ \Gamma^{fg}_{0^{-}} $ is BSA of pseudoscalar mesons. BSA is normalized by [28]$ \begin{split} 2P_\mu = & N_c \frac{\partial}{\partial P_\mu}\int^{\Lambda}_{d q} \;{\rm tr} [ \Gamma(q;-K) \\ & \times S(q_+)\Gamma(q;K)S(q_-) ]|_{P^2 = K^2 = -M^2}, \end{split} $

(15) where
$ N_c = 3 $ is the color number. Before discussing the details and results, we first demonstrate the preservation of av-WTI by comparing$ f_{0^-} $ and$ \tilde{f}_{0^-} $ in Fig. 1. The two deviate by not more than 3% for all pseudoscalar mesons considered. We conclude that av-WTI is perfectly preserved in our approach.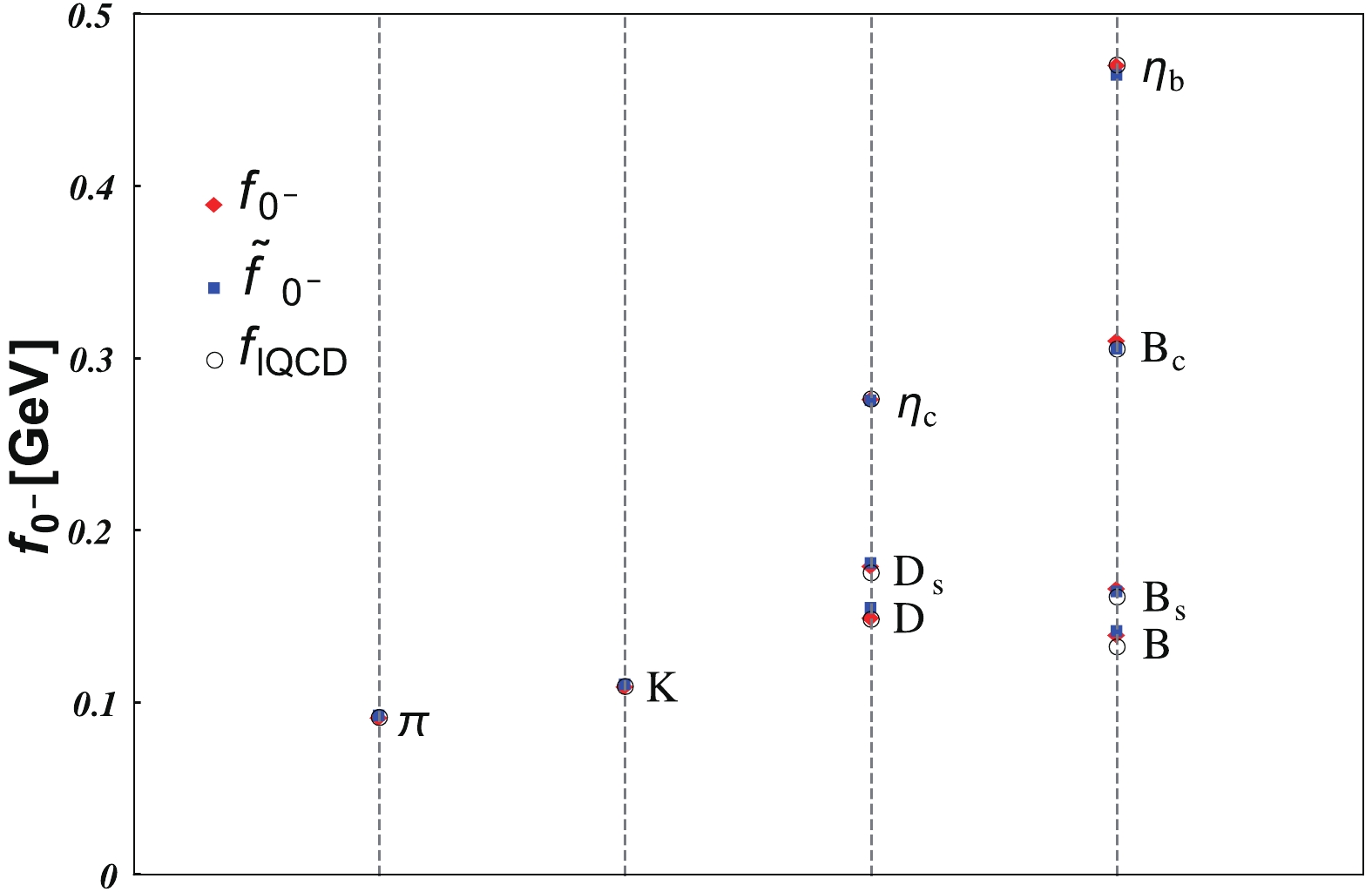
Figure 1. (color online) Decay constants of the ground state pseudoscalar mesons:
$f_{0^-}$ is given by Eq. (13), and$\tilde{f}_{0^-}$ by Eq. (12) and Eq. (14).$f_{\;{\rm lQCD}}$ are the lattice QCD data given in Table 1. -
In Eq. (11),
$ D_{f,g} $ and$ \omega_{f,g} $ express the flavor dependent quark-antiquark interaction. However, the flavor dependence of these parameters is a priori unknown. Here, we treat$ D_{f} $ and$ \omega_{f} $ for each flavor as free parameters. Working in the isospin symmetry limit, we have 4 independent quarks up to the$ b $ quark mass:$ u $ (or$ d $ ),$ s $ ,$ c $ and$ b $ . There are 3 parameters for each flavor:$ D_f $ ,$ \omega_f $ and$ m_f $ . In total there are 12 parameters.$ \omega_u $ is treated as an independent variable, the other 11 parameters are dependent variables, which are fitted by 11 observables: the masses and decay constants of$ \pi $ ,$ K $ ,$ \eta_c $ and$ \eta_b $ , and the masses of D,$ D_s $ and$ B $ . All masses and decay constants of the ground state pseudoscalar mesons (except$ \eta $ and$ \eta^\prime $ ), and all the ground state vector mesons are predicted.The masses and decay constants of the ground state pseudoscalar mesons are listed in Table 1. Our results are quite stable when
$ \omega_u $ varies by 10% around$ 0.5 \;{\rm GeV} $ . With$ \omega_u \in [0.45,0.55] \;{\rm GeV} $ , the masses are almost unchanged and the decay constants vary within 1.2%. Our result for$ M_{B^{\pm}_s} $ deviates from the experimental value by only$ 0.01 \;{\rm GeV} $ , which is impossible to get in the original RL truncated DSBSE. The flavor dependence of the quark gluon interaction has even a significant effect on$ B_c $ meson.$ M_{B_c} $ given by the original RL truncated DSBSE is$ 0.11\;{\rm GeV} $ larger than the experimental value [18]. Here, the error is reduced to less than$ 0.02 \;{\rm GeV} $ . Our results for$ f_D $ ,$ f_{D^{\pm}_s} $ ,$ f_{B} $ ,$ f_{B^{\pm}_s} $ and$ f_{B_c} $ are all consistent with the lattice QCD, with deviations of less than 6%. Note that our$ f_{D^{\pm}_s} $ is also in good agreement with the recent experimental measurement [29]. The only mesons absent in Table 1 are$ \eta $ and$ \eta^\prime $ , which are affected by the axial anomaly [30, 31] and beyond our present study.herein lQCD expt. herein lQCD $M_{\pi}$ 

$\underline{0.138}$ 

$\ast$ 

$\underline{0.138(1)}$ 

$f_{\pi}$ 

$\underline{0.0093}$ 

$\underline{0.0093(1)}$ 

$M_K$ 

$\underline{0.496}$ 

$\ast$ 

$\underline{0.496(1)}$ 

$f_K$ 

$\underline{0.111}$ 

$\underline{0.111(1)}$ 

$M_D$ 

$\underline{1.867}$ 

1.865(3) $\underline{1.867(1)}$ 

$f_D$ 

0.151(1) 0.150(1) $M_{D^{\pm}_s}$ 

$\underline{1.968}$ 

1.968(3) $\underline{1.968(1)}$ 

$f_{D^{\pm}_s}$ 

0.181(1) 0.177(1) $M_{\eta_c}$ 

$\underline{2.984}$ 

$\ast$ 

$\underline{2.984(1)}$ 

$f_{\eta_c}$ 

$\underline{0.278}$ 

$\underline{0.278(2)}$ 

$M_{B}$ 

$\underline{5.279}$ 

5.283(8) $\underline{5.279(1)}$ 

$f_{B}$ 

0.141(2) 0.134(1) $M_{B^{\pm}_s}$ 

5.377(1) 5.366(8) 5.367(1) $f_{B^{\pm}_s}$ 

0.168(2) 0.163(1) $M_{B_c}$ 

6.290(3) 6.276(7) 6.275(1) $f_{B_c}$ 

0.312(1) 0.307(10) $M_{\eta_b}$ 

$\underline{9.399}$ 

$\ast$ 

$\underline{9.399(2)}$ 

$f_{\eta_b}$ 

$\underline{0.472}$ 

$\underline{0.472(5)}$ 

Table 1. Masses and decay constants of the ground state pseudoscalar mesons (in GeV). We use the convention
$f_\pi = 0.093\;{\rm GeV}$ . The lQCD data are taken from:$M_D$ and$M_{D_s}$ - Ref. [32];$M_B$ and$M_{B_s}$ - Ref. [33];$M_{B_c}$ - Ref. [34];$f_\pi$ and$f_K$ - Ref. [35];$f_D$ ,$f_{D_s}$ ,$f_B$ and$f_{B_s}$ - Ref. [36];$f_{\eta_c}$ and$f_{\eta_b}$ - Ref. [37];$f_{B_c}$ - Ref. [38].$M_{\pi}$ ,$M_K$ ,$M_{\eta_c}$ ,$M_{\eta_b}$ in this table and$M_\Upsilon$ in Table 2 are usually used to fit the quark masses in lQCD calculations [39], so there are no lQCD predictions for these quantities. The experimental data are taken from Ref. [1]. Note that we work in the isospin symmetry limit, so that the average value among or between the isospin multiplets is cited for$\pi$ , K, D and B mesons. All data are cited with an accuracy of$0.001 \;{\rm GeV}$ . In our calculations, the underlined values are used to fit the 11 dependent variables, and the others are our results with the uncertainty corresponding to$\omega_u \in [0.45,0.55] \;{\rm GeV}$ . The decay constants are fitted to the lQCD data because an accurate and complete experimental estimate is still lacking.A further confirmation of our model is given by vector mesons. Our predictions of the static vector meson masses and decay constants are listed in Table 2. The decay constants are defined in analogy to Eq. (13)
herein lQCD expt. herein lQCD $M_{\rho}$ 

0.724(2) 0.780(16) 0.775(1) $f_{\rho}$ 

0.149(1) – $M_{K^*}$ 

0.924(2) 0.933(1) 0.896(1) $f_{K^*}$ 

0.160(2) – $M_\phi$ 

1.070(1) 1.032(16) 1.019(1) $f_\phi$ 

0.191(1) 0.170(13) $M_{D^*}$ 

2.108(4) 2.013(14) 2.009(1) $f_{D^*}$ 

0.174(4) 0.158(6) $M_{D^{*\pm}_s}$ 

2.166(7) 2.116(11) 2.112(1) $f_{D^{*\pm}_s}$ 

0.206(2) 0.190(5) $M_{J/\psi}$ 

3.132(2) 3.098(3) 3.097(1) $f_{J/\psi}$ 

0.304(1) 0.286(4) $M_{B^*}$ 

5.369(5) 5.321(8) 5.325(1) $f_{B^*}$ 

0.132(3) 0.131(5) $M_{B^{*\pm}_s}$ 

5.440(1) 5.411(5) 5.415(2) $f_{B^{*\pm}_s}$ 

0.152(2) 0.158(4) $M_{B^*_c}$ 

6.357(3) 6.331(7) – $f_{B^*_c}$ 

0.305(5) 0.298(9) $M_\Upsilon$ 

9.454(1) $\ast$ 

9.460(1) $f_\Upsilon$ 

0.442(3) 0.459(22) Table 2. Masses and decay constants of the ground state vector mesons (in GeV). The lQCD data are taken from:
$M_{\rho}$ - Ref. [40];$M_{K^*}$ - Ref. [41];$M_\phi$ and$f_\phi$ - Ref. [42];$M_{D^*}$ ,$f_{D^*}$ ,$M_{D^{*\pm}_s}$ ,$f_{D^{*\pm}_s}$ ,$M_{B^*}$ ,$f_{B^*}$ ,$M_{B^{*\pm}_s}$ and$f_{B^{*\pm}_s}$ - Ref. [43];$M_{J/\psi}$ and$f_{J/\psi}$ - Ref. [44];$M_{B^*_c}$ - Ref. [34];$f_{B^*_c}$ - Ref. [38];$f_\Upsilon$ - Ref. [45]. The experimental data are taken from Ref. [1], the average value for the isospin multiplet is cited for$M_{D^*}$ .$B^*_c$ meson has not been discovered experimentally. All data are cited with an accuracy of$0.001 \;{\rm GeV}$ . The uncertainties of our results correspond to$\omega_u \in [0.45,0.55] \;{\rm GeV}$ .$ f_{1^{-}}M_{1^-} = Z_{2} N_{c} \;{\rm {tr}} \! \int^{\Lambda}_{d k} \! \gamma_{\mu} S_f(k_+)\Gamma^{\mu,fg}_{1^{-}}(k;P)S_g(k_-), $

(16) where
$ M_{1^-} $ is the vector meson, and$ \Gamma^{\mu,fg}_{1^{-}} $ the vector meson BSA. Vector mesons also show a weak dependence on$ \omega_u \in [0.45,0.55] \;{\rm GeV} $ . The deviation from experimental or lQCD values decreases as the mass increases. The mass deviation is about 6% for$ \rho $ meson, decreasing to about 1% for heavy mesons. The deviation of the decay constant is about 12% for$ \phi $ meson, decreasing to less than 7% for heavy mesons. This deviation is attributed to the systematic error of RL truncation [16]. The success of the pattern of flavor dependent interaction, Eq. (10,11,7), is demonstrated by the fact that the deviation is of the same order for open-flavor mesons and quarkonia. We can see again that the flavor dependence has a significant effect on$ B_c $ mesons. While$ M_{B^*_c}\approx 6.54 \;{\rm GeV} $ and$ f_{B^*_c} \approx 0.43 \;{\rm GeV} $ in the original RL truncated DSBSE [18], our result$ M_{B^*_c} \approx 6.357 \;{\rm GeV} $ and$ f_{B^*_c} \approx 0.305 \;{\rm GeV} $ is more consistent with the lQCD predictions.$ B^*_c $ has not been discovered experimentally, and both our and lQCD predictions wait for experimental verification.Finally, we investigate the flavor dependence of the quark-antiquark interaction. In the heavy quark limit, the dressing of the quark-gluon vertex may be ignored and the interaction we have adopted is in agreement with QCD [13], and should saturate
$ {\cal G}^{ff}(l^2) \xrightarrow{m_f\to\infty} $ $ 4\pi\alpha_s \dfrac{Z(l^2)}{l^2} $ , where$ \alpha_s $ is the strong-interaction constant, and$ Z(l^2) $ the dressing function of the gluon propagator defined by$ \Delta_{\mu\nu}(l) = \left(\delta_{\mu\nu}-\dfrac{l_\mu l_\nu}{l^2}\right)\dfrac{Z(l^2)}{l^2} $ , with$ \Delta_{\mu\nu}(l) $ the dressed gluon propagator. As we fix$ N_f = 5 $ , both$ \alpha_s $ and$ Z(l^2) $ are independent of the interacting quarks. Phenomenologically, the parameters$ D_f $ and$ \omega_f $ should become constant as the quark mass increases. In the chiral limit, the interaction is enhanced because of the dressing of the quark-gluon vertex [46–50], which is necessary to trigger chiral symmetry breaking. The potential is properly defined by the Fourier transform of the interaction. For the interesting infrared part of our model we have$ {\cal V}_{\;{\rm IR}}^{ff}(\vec{r}) =\int \;{\rm d}^3\vec{l}\, {\cal G}_{\;{\rm IR}}^{ff}(l^2)\;{\rm e}^{-\vec{l}\cdot\vec{r}/\omega^2_f} \propto {\rm {e}}^{-\vec{r}^2/R_{f}^2} $

(17) where
$ \vec{r} $ is the space coordinate, and$ R_{f} = 2/\omega_f $ expresses the radius of the quark-gluon interaction. Additionally, we adopt the following quantity to describe the interaction strength [51]:$ \sigma_f = \frac{1}{4\pi}\int_{\Lambda_{\;{\rm QCD}}^2}^{(10\Lambda_{\;{\rm QCD}})^2}\;{{\rm d}s}\,{\cal G}^{ff}(s)*s. $

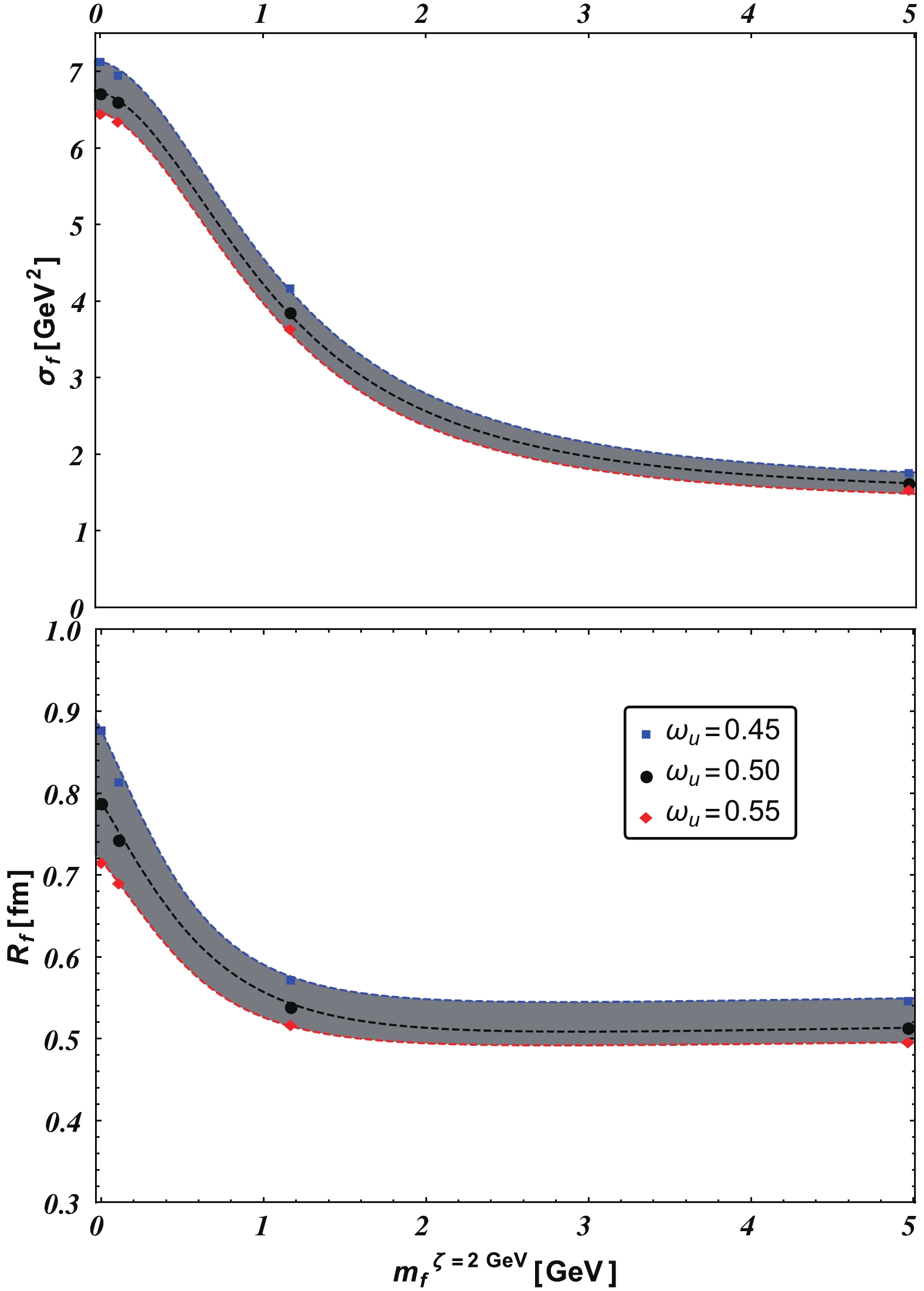
(18) The dependence of
$ \sigma_f $ and$ R_{f} $ on the quark mass is depicted in Fig. 2. The interaction strength and radius reduce as the quark mass increases, which is expected since the effect of quark-gluon vertex dressing decreases as the quark mass increases [47]. The interaction radius,$ 2/\sqrt{\omega_{f}\omega_{g}} $ , also expresses the fact that quarks and gluons have a maximum wavelength of the size of a hadron [52]. -
The flavor dependence of the full quark-antiquark interaction is an intrinsic property of QCD and crucial for a unified description of light and heavy hadrons. While a perfect quark-gluon vertex that has the proper flavor dependence of QCD has not been found, we constructed a flavor dependent kernel based on the RL truncation of DSBSE. The quark-antiquark interaction is composed of a flavor dependent infrared part and a flavor independent ultraviolet part. With the parameters fixed by physical observables, our model takes into account not only the flavor dependence, but also the hadron size. Our model, with perfectly preserved av-WTI, provides a successful unified description of light, heavy and heavy-light ground state pseudoscalar and vector mesons. Our model shows, for the first time, that the infrared enhanced quark-antiquark interaction is stronger and wider for lighter quarks. This flavor dependence pattern is universal, and is supposed to be applicable to baryons, for example, the double charm baryons in the Faddeev approach. Our approach also provides a proper description of the inner structure of heavy-light mesons, which can be used to calculate scattering processes, such as the
$ B $ to$ \pi $ transition form factor.Work supported by: the Chinese Government’s Thousand Talents Plan for Young Professionals.
-
The fit parameters corresponding to
$ \omega_u = 0.45, 0.50, 0.55 \;{\rm GeV} $ are listed in Table A1. The quark mass$ \bar{m}_f^{\zeta} $ is defined by$\tag{A1} \begin{array}{l} \bar{m}_f^{\zeta} = \hat{m}_f/\left[\dfrac{1}{2}\;{\rm Ln}\frac{\zeta^2}{\Lambda^2_{\;{\rm QCD}}}\right]^{\gamma_m}, \end{array} $

$\tag{A2} \begin{array}{l} \hat{m}_f = \lim_{p^2 \to \infty}\left[\dfrac{1}{2}\;{\rm Ln}\frac{p^2}{\Lambda^2_{\;{\rm QCD}}}\right]^{\gamma_m} M_f(p^2), \end{array} $

where
$ \zeta $ is the renormalization scale,$ \hat{m}_f $ the renormalization group invariant current quark mass, and$ M_f(p^2) $ the quark mass function,$ S_f(p) = \frac{Z_f(p^2,\zeta^2)}{i\gamma\cdot p + M_f(p^2)} $ .flavor $\bar{m}_f^{\zeta=2\;{\rm GeV}}$ 

$w_f $ 

$D_f^2$ 

$w_f $ 

$D_f^2$ 

$w_f $ 

$D_f^2$ 

u 0.0049 0.450 1.133 0.500 1.060 0.550 1.014 s 0.112 0.490 1.090 0.530 1.040 0.570 0.998 c 1.17 0.690 0.645 0.730 0.599 0.760 0.570 b 4.97 0.722 0.258 0.766 0.241 0.792 0.231 Table A1. Fitted parameters correspond to
$\omega_u = 0.45, 0.50, 0.55 \;{\rm GeV}$ .$\bar{m}_f^{\zeta = 2\;{\rm GeV}}$ ,$\omega_f$ and$D_f$ are all measured in GeV.
A pattern for the flavor dependent quark-antiquark interaction
- Received Date: 2019-07-19
- Available Online: 2019-11-01
Abstract: A flavor dependent kernel is constructed based on the rainbow-ladder truncation of the Dyson-Schwinger and Bethe-Salpeter equations in quantum chromodynamics. The quark-antiquark interaction is composed of a flavor dependent infrared part and a flavor independent ultraviolet part. Our model gives a successful and unified description of the light, heavy and heavy-light ground state pseudoscalar and vector mesons. Our model shows, for the first time, that the infrared enhanced quark-antiquark interaction is stronger and wider for lighter quarks.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: