-
Photonuclear cross-sections are necessary for energy, safety, and medical applications, as well as for nuclear physics and astrophysics [1, 2]. The total photoabsorption is the fundamental parameter that determines various competitive photonuclear reactions, which can be described using photon strength functions (PSF) [3]. In recent years, to systematically improve the quality of current photonuclear cross-sections and remove unreliable and discrepant data, a new international coordinated research project (CRP) is held by International Atomic Energy Agency (IAEA) to update the IAEA photonuclear data and generate a reference database for PSF in 2016–2020 [4–7]. Meanwhile, an international measurement collaboration under this CRP, photoexcitation, and neutron emission cross-sections (Phoenix), is also carried out to measure photonuclear data, and a series of new measurements for the
$ \gamma $ -ray data have been obtained in NewSUBARU, Oslo et al. to support the improvement.Among all electric and magnetic transitions with different multipolarities, dipole electric
$ \gamma $ -transitions (E1) are usually dominant. The total photoabsorption cross-sections above the neutron separation energy are usually described by E1 strength functions [8, 9]. Both microscopic and phenomenological approaches were investigated with generated E1 strength functions in the past.In microscopic approaches, the E1 strength function can be derived from many models, such as the finite Fermi systems [10], semi-classical thermodynamic pole approach [11], and random phase approximation (RPA) based the ground description with Hartree-Fock calculations [12] or relativistic mean field calculations [13–16]. Recently, the E1 strength function based on the Hartree-Fock-Bogoliubov (HFB) and Quasi-particle RPA (QRPA) model with a realistic Skyrme interaction [8, 17] and Gogny interaction [18] by Goriely et al., is constructed for the entire nuclear chart. Ring et al. used time-dependent relativistic mean field theory to derive the fully self-consistent relativistic quasiparticle random phase approximation (RQRPA) [14, 15].
In the phenomenological approaches, the photoabsorption cross-section is normally estimated within the Lorentzian representation of the giant dipole resonance (GDR). In spherical nuclei, this depends on the GDR parameters: the peak energy
$ E_r $ , the width$ \Gamma_r $ and the value$ \sigma_r $ of the photoabsorption cross-section around the GDR energy. In the axially deformed nuclei, it is taken as a sum of two components with two sets of GDR parameters. There are several most frequently used phenomenological models of the photoabsorption cross-sections description: the standard Lorentzian (SLO) model [19, 20], the enhanced generalized Lorentzian (EGLO) model [21, 22], the generalized Fermi-liquid (GFL) model [23], the Hybrid model (GH) [24], the modified Lorentzian (MLO) approach [11], and its simplified version SMLO [3]. The main difference in various phenomenological models is the width$ \Gamma(\epsilon_\gamma) $ . The width$ \Gamma(\epsilon_\gamma) $ reflects the description of the collective state damping, and also depends on the temperature.In this work, we wish to determine the systematic GDR parameters for nuclei with medium to heavy-mass. In Section 2, details of the theoretical models are described, which are used to calculate the GDR component of the photoabsorption cross-section. Section 3 presents our calculation and the obtained results of the systematic GDR parameters for the entire nuclear chart. Related discussions are also contained in the section. Finally, the work is summarized in Section 4.
-
The theoretical photoabsorption cross-section
$ \sigma_{\rm abs}(\epsilon_\gamma) $ as a function of$ \gamma $ -ray energy$ \epsilon_\gamma $ is taken as a sum of the terms$ \sigma_{\rm abs}(\epsilon_\gamma) = \sigma_{\rm GDR}(\epsilon_\gamma)+\sigma_{\rm QD}(\epsilon_\gamma), $

(1) where the component
$ \sigma_{\rm GDR}(\epsilon_\gamma) $ corresponds to GDR excitation, and$ \sigma_{\rm QD}(\epsilon_\gamma) $ is a quasideuteron contribution (a photoabsorption by a neutron–proton pair), which is taken in accordance with the model proposed by Chadwick et al. [25].The GDR component
$ \sigma_{\rm GDR}(\epsilon_\gamma) $ of the total photoabsorption cross-section is equal to the photoabsorption cross-section of electric dipole$ \gamma $ rays$ \sigma_{\rm E1}(\epsilon_\gamma) $ , which is proportional to the strength function$ S_{\rm E1}(\epsilon_\gamma) $ $ \sigma_{\rm E1}(\epsilon_\gamma) = \frac{16\pi^3}{9}\frac{e^2}{\hbar c}\epsilon_\gamma S_{\rm E1}(\epsilon_\gamma), $

(2) where the isovector dipole strength function
$ S_{\rm E1}(E_\gamma) $ can be calculated by a microscopic model, such as: RQRPA equations [13–15, 26]. In standard notation, these equations can be written in matrix form as$ \left(\begin{array}{cc} A^J&B^J\\-B^{*J}&-A^{*J} \end{array}\right)\left(\begin{array}{c} X^{\nu J}\\Y^{\nu J} \end{array}\right) = \omega^\nu\left( \begin{array}{c} X^{\nu J}\\Y^{\nu J} \end{array}\right). $

(3) Then, the reduced electric transition probability from the ground to an excited state with angular momentum J and excitation energy
$ \omega_\nu $ for a multipole operator$ \hat{Q}^J $ is given by$ \begin{split} B(J,\omega_\nu) =& \bigg|\sum\limits_{kk'}(\langle k||\hat{Q}^J||k'\rangle X_{kk'}^{\nu J}+(-1)^{j_k-j_{k'}+J}\langle k'||\hat{Q}^J||k\rangle Y_{kk'}^{\nu J})\\&\times(u_kv_{k'}+(-1)^Jv_ku_{k'})\bigg|^2 . \end{split} $

(4) The isovector dipole strength function
$ S_{\rm E1}(E_\gamma) $ can be calculated by$ S_{\rm E1}(\epsilon_\gamma) = \sum\limits_\nu\frac{B(1,\omega_\nu)}{\pi}\frac{\Gamma(\epsilon_\gamma)/2}{(\epsilon_\gamma-\omega_\nu)^2+(\Gamma(\epsilon_\gamma)/2)^2}, $

(5) where
$ \Gamma(\epsilon_\gamma) $ is the width of the Lorentzian distribution.Phenomenological models assume that the total photoabsorption cross-section has a Lorentzian shape with various expressions for the "width"
$ \Gamma_r(\epsilon_\gamma) $ . The standard Lorentzian (SLO) model [19, 20] is based on the Brink hypothesis. In the SLO model, the width$ \Gamma_r(\epsilon_\gamma) $ is taken as the constant$ \Gamma_r $ :$ \sigma_{\rm{{GDR,SLO}}}(\epsilon_\gamma) = \sigma_r\Gamma_r \frac{\epsilon_\gamma^2\Gamma_r}{(\epsilon_\gamma^2-E_r^2)^2+[\Gamma_r\cdot \epsilon_\gamma]^2}, $

(6) where
$ E_r $ and$ \sigma_r $ are the GDR energy (in$ {\rm MeV} $ ) and the peak cross-section (in$ {\rm mb} $ ), respectively. The SLO approach can be used to describe the photon absorption data for medium and heavy-mass nuclei [27, 28]. However, for$ \gamma $ -emission, the SLO model underestimates the$ \gamma $ -decay spectra at low energies [29].In the low energy range, the generalized Fermi liquid (GFL) [23] and the enhanced generalized Lorentzian (EGLO) [21, 22] models are based on Kadmenskij-Markushev-Furman (KMF) model [10, 30] and give a better description of the
$ {\rm E1} $ strengths at the energies$ \epsilon_\gamma $ close to zero. The photoaborption cross-section of the EGLO is given by the following expression:$ \begin{split} \sigma_{\rm{{GDR,EGLO}}}(\epsilon_\gamma)=& \sigma_r\Gamma_r\epsilon_\gamma\\&\times\left[\frac{\epsilon_\gamma\Gamma_K(\epsilon_\gamma)}{(\epsilon_\gamma^2-E_r^2)^2+\epsilon_\gamma^2\Gamma_K^2(\epsilon_\gamma)}\right.+\left.\frac{0.7\Gamma_K(\epsilon_\gamma = 0)}{E_r^3}\right]\end{split}$

(7) with a width equal to
$ \begin{split} \;\;\Gamma_K(\epsilon_\gamma)=& C_{\rm coll}(\epsilon_\gamma)(\epsilon_\gamma^2+4\pi T_f^2),\\ C_{\rm coll}(\epsilon_\gamma) =& \frac{\Gamma_\gamma}{\epsilon_\gamma^2}\chi(\epsilon_\gamma) = C_{\rm KMF}\chi(\epsilon_\gamma)\equiv C_k(\epsilon_\gamma) \end{split}, $

(8) where the empirical factor
$ \chi(\epsilon_\gamma) $ is obtained from fitting to experimental data,$ \chi(\epsilon_\gamma) = k+(1-k)(\epsilon_\gamma-\epsilon_0)/(E_r-\epsilon_0), $

(9) and the parameter k reproduces the experimental
$ {\rm E1} $ strength around a reference energy$ \epsilon_0 $ ;$ \chi(E-\gamma = E_r) = 1 $ and$ C_K(E_r) = C_{\rm KMF} $ . The value of the factor k depends on the model adopted to describe the nuclear state density, and was obtained from the average resonance capture data, where$ \epsilon_0 = 4.5 $ MeV. If the Fermi gas model is used, k is given by$ k = \left\{ {\begin{array}{*{20}{l}} {1,}&{A<148}\\ {1+0.09(A-148)^2{\rm exp}{-0.18(A-148)}}&{A\geqslant 148}. \end{array}} \right. $

The expression for the GFL model photoabsorption cross-section has the following form
$ \begin{aligned} \sigma_{\rm{{GDR,GFL}}}(\epsilon_\gamma) = \sigma_r\Gamma_r\epsilon_\gamma \times \frac{K\cdot E_r\cdot\Gamma_m(\epsilon_\gamma)}{(\epsilon_\gamma^2-E_r^2)^2+K[\Gamma_m(\epsilon_\gamma)\epsilon_\gamma]^2}, \end{aligned} $

(10) where the quantity K depicts the Landau parameters of the quasi-particle interaction in the isovector channel of Fermi system, and the energy-dependent width
$ \Gamma_m(\epsilon_\gamma) $ is written as:$ \Gamma_m(\epsilon_\gamma) = \Gamma_{\rm coll}(\epsilon_\gamma)+\Gamma_{dq}(\epsilon_\gamma), $

(11) the collisional component is taken as
$ \Gamma_{\rm coll}(\epsilon_\gamma)\equiv C_{\rm coll}(\epsilon_\gamma^2+4\pi^2T_f^2), $

(12) with
$ C_{\rm coll} $ determined by normalizing the total width$ \Gamma_m(\epsilon_\gamma) $ at$ \epsilon_\gamma = E_r $ and$ T_f = 0 $ to the GDR width of a cold nucleus, i.e.$ \Gamma_m(\epsilon_\gamma = E_r) = \Gamma_r $ . The component$ \Gamma_{dq} $ is assumed in the following form:$ \Gamma_{dq}(\epsilon_\gamma) = C_{dq}\sqrt{\epsilon_\gamma^2\bar{\beta}_2^2+\epsilon_\gamma s_2}, $

(13) where
$ C_{dq} = \sqrt{5\ln2/\pi} = 1.05 $ ;$ s_2 = E_2+\bar{\beta}_2^2\approx217.16/A^2 $ with$ E_{2+} $ as the energy of the first vibrational quadrupole state, and$ \bar{\beta}_2 $ being the effective deformation parameter.It can be noted that the SLO, EGLO, and GFL expressions are not consistent with the general relations between the imaginary part of the response function and photoabsorption cross-section. To avoid this shortcoming, the Modified Lorentzian approach (MLO) was proposed [11]. The photoabsorption cross-section within the MLO model has the following form:
$\begin{split} \sigma_{\rm{{GDR,MLO}}}(\epsilon_\gamma)=& \sigma_r\Gamma_r\epsilon_\gamma\frac{\epsilon_\gamma}{1-\exp(\epsilon_\gamma/T_f)}\\ & \times\frac{\Gamma_\gamma(\epsilon_\gamma)}{(\epsilon_\gamma^2-E_r^2)^2+[\Gamma_\gamma(\epsilon_\gamma)\cdot \epsilon_\gamma]^2}, \end{split} $

(14) where at zero excitation energy
$ \Gamma_r = \Gamma_\gamma(\epsilon_\gamma = E_r) $ .In the case where the excitation energy is not too high and
$ \epsilon_\gamma $ ranges from zero up to the GDR energy, the MLO1 width$ \Gamma(\epsilon_\gamma) $ can be expressed as$ \Gamma(\epsilon_\gamma) = \left\{ {\begin{array}{*{20}{l}} {a(\epsilon_\gamma+U_f) = aU,}&{\rm{for}} \ \gamma-{\rm{decay}}\\ {a\epsilon_\gamma,}&{\rm{for\ photoabsorption}} \end{array}} \right. $

(15) where
$ a = \Gamma_r/E_r = C_{\rm KMF}\cdot \epsilon_\gamma $ if the normalization condition$ \Gamma_r = \Gamma_\gamma(\epsilon_\gamma = E_r) $ is adopted for cold nuclei. This model is denoted as the simplified modified Lorentzian (SMLO) model [3]. The values of the parameter a are obtained by fitting the SMLO shape to the experimental photoabsorption cross-sections in spherical nuclei. -
In this section, we construct two kinds of systematic GDR parameters for medium to heavy nuclei. One is based on the microscopic RQRPA calculation. The other is achieved by phenomenological models. The shape of parameters is obtained by fitting the theoretical calculation to the experiment photoabsorption cross-sections from the EXFOR library [31]. In Table 1 and 2 we have listed 47 nuclei, which we use to fit the systematic GDR parameters. Therein are 25 spherical nuclei and 22 axially deformed nuclei.
nucleus points energy range /MeV Ref. def. $ \beta_2 $ 

34S 29 12.0 - 26.0 [32] 0.00 40Ar 61 10.0 - 40.0 [33] 0.00 40Ca 70 11.25 - 28.1 [34] 0.00 42Ca 151 10.0 - 40.0 [35] 0.00 44Ca 58 11.5 - 40.0 [35] 0.00 48Ca 60 10.5 - 40.0 [35] 0.00 48Ti 58 11.5 - 40.0 [35] 0.00 51V 41 10.47 - 32.69 [36] 0.00 52Cr 115 11.5 - 40.0 [33] 0.00 90Zr 46 12.2 - 25.7 [37] 0.035 91Zr 101 10.8 - 30.0 [38] 0.053 92Zr 105 15.8 - 27.8 [39] 0.053 94Zr 92 7.85 - 31.0 [38] 0.063 112Sn 167 10.9 - 27.5 [40] 0.018 114Sn 168 10.4 - 27.1 [40] 0.00 116Sn 200 9.70 - 29.6 [40] 0.00 117Sn 232 7.40 - 30.9 [40] −0.044 118Sn 211 9.40 - 30.7 [40] 0.00 119Sn 233 7.40 - 31.1 [40] 0.00 120Sn 207 9.20 - 29.8 [40] 0.00 122Sn 184 8.90 - 27.2 [40] 0.00 124Sn 220 8.60 - 30.9 [40] 0.00 138Ba 61 8.48 - 27.1 [41] 0.00 208Pb 101 7.50 - 37.5 [42] 0.00 209Bi 109 8.01 - 26.4 [41] −0.008 Table 1. Experimental values of spherical nuclei used to fit systematic GDR parameters.
nucleus points energy range /MeV Ref. def. $ \beta_2 $ 

23Na 110 12.8 - 40.0 [43] 0.390 24Mg 82 11.0 - 29.75 [34] 0.356 25Mg 154 9.4 - 40.0 [33] 0.323 27Al 150 10.2 - 40.0 [33] −0.541 28Si 151 10.0 - 40.0 [33] −0.583 29Si 158 8.6 - 40.0 [33] −0.334 63Cu 60 10.5 - 40.0 [33] 0.161 65Cu 60 10.5 - 40.0 [33] −0.155 80Se 68 9.92 - 28.1 [44] 0.150 127I 86 8.78 - 29.5 [45] −0.128 133Cs 66 9.05 - 29.5 [41] −0.103 159Tb 198 7.70 - 27.4 [46] 0.288 181Ta 59 7.50 - 36.5 [47] 0.248 182W 65 8.02 - 20.8 [48] 0.240 184W 65 8.02 - 20.8 [48] 0.221 186W 65 8.02 - 20.8 [48] 0.210 186Os 45 1.11 - 19.7 [49] 0.205 188Os 84 7.44 - 30.4 [49] 0.179 189Os 77 7.44 - 29.9 [49] 0.170 190Os 84 7.44 - 30.4 [49] 0.153 192Os 82 7.44 - 29.9 [49] 0.145 235U 38 5.22 - 18.3 [50] 0.241 Table 2. Experimental values of axially deformed nuclei used to fit systematic GDR parameters.
-
In this section, we construct the microscopic GDR parameters within the relativistic quasiparticle random phase approximation (RQRPA) calculation, which is obtained with the NL3 interaction [26]. RQRPA has been proved to be able to provide a reliable description of the GDR centroid and fraction of the energy-weighted sum rule exhausted by the E1 mode. However, this can only be used to solve the spherical nuclei, and if we want to reproduce the photoabsorption cross-section of the experimental data, it is necessary to find a good width of the Lorentzian distribution. In previous RQRPA calculations, the width of the Lorentzian distribution is usually treated as a constant [15, 16]. Here, we follow the method in Ref. [51] and define an energy-dependent width parameter as
$ \Gamma(\epsilon_\gamma) = \Gamma\sqrt{\epsilon_\gamma/E_{\rm E1}} $ in Eq.(5), where$ E_{\rm E1} $ is the peak energy of the giant dipole resonance, and$ \Gamma $ is one of the parameters we use to fit the experimental data. To reproduce the photoabsorption cross-section of the experimental data, we add another parameter G in Eq.(2) to adjust the height of the curve of the photoaborption cross-section$ \sigma_{\rm E1}(\epsilon_\gamma) = \frac{16\pi^3}{9}\frac{e^2}{\hbar c}G\epsilon_\gamma S_{\rm E1}(\epsilon_\gamma). $

(16) With the help of the MINUIT package, we adjust G and
$ \Gamma $ to improve the RQRPA calculation of the photoabsorption cross-section in Table 1. As shown in Table 3, the total$ \chi^2_{\rm tot} $ of the RQRPA with experimental photoabsorption cross-section has been improved more than 10 times.$\Gamma$ 

G $\chi_{\rm tot}^2$ 

RQRPA 2.0 (C) 1.0 270.0 RQRPA(fitted) 1.59 (ED) 0.65 21.0 Table 3. Parameters and
$\chi_{\rm tot}^2$ of microscopic GDR parameters within RQRPA. C depicts constant width of Lorentzian distribution.,$ED$ denotes energy-dependent width.In Fig. 1, we present the comparison of our microscopic GDR parameters (RQRPA) calculations with the experimental photoabsorption cross-sections and other GDR calculations such as: QRPA, MLO1, and SMLO for 52Cr, 90Zr, 120Sn, and 208Pb. The QRPA calculations are based on the Sly4 Skyrme force [8], and the results of MLO1* are based on the parameters from RIPL-3 [2]. The curves of the SMLO are calculated by phenomenological GDR parameters, which we discuss in the next section. Fig. 1shows that the centroid energy of RQRPA is closer to the experimental GDR energy. By adjusting G and
$ \Gamma $ parameters, we can reproduce the experimental photoabsorption cross-section as well as the MLO1*. Our microscopic GDR parameter calculations can be used to estimate the spherical nuclei, and the cross-section for heavy-mass nuclei are lower than the ones obtained by experimental data.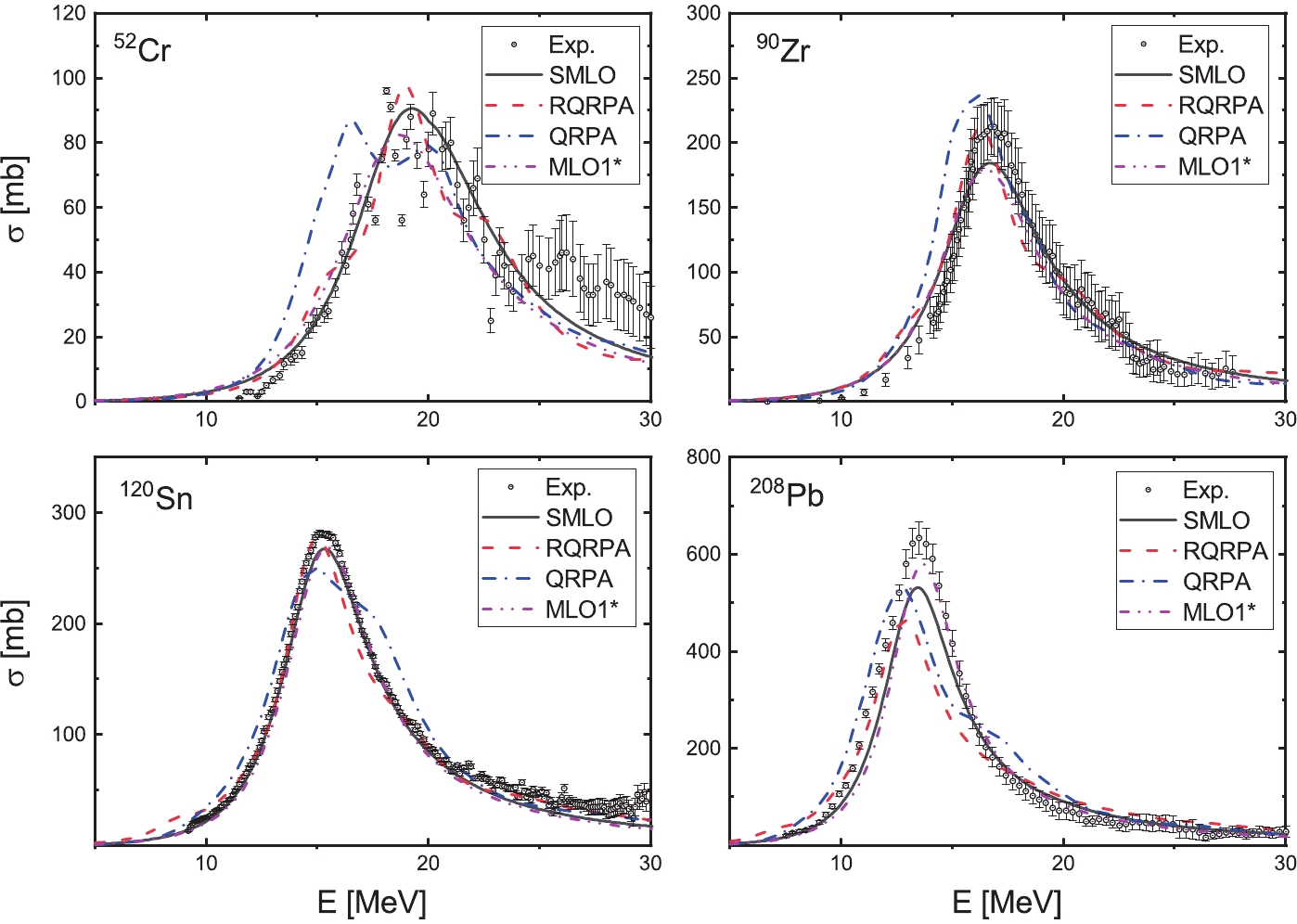
Figure 1. (color online) Comparison of SMLO (black solid line) and RQRPA (red dashed line) calculations with experimental photoabsorption cross-sections and other systematic GDR parameters calculations QRPA [8] (blue dash-dot line) and MLO1* from RIPL-3 [2] (magenta dash-dot-dot line) for 52Cr, 90Zr, 120Sn and 208Pb.
-
In this section, systematic GDR parameters, based on phenomenological models, are systematically constructed. As introduced in Section 2, the phenomenological models assume that the total photoabsorption cross-section has a Lorentzian shape. In spherical nuclei, this depends on GDR parameters: the energy
$ E_r $ , the value$ \sigma_r $ of the photoabsorption cross-section, and width$ \Gamma_r $ at GDR energy. In axially deformed nuclei, this is taken as a sum of two components with two sets of the GDR parameters.There are several different models of the photoabsorption cross-section description. The major difference of various models is the expressions for the width of the curve. In the standard Lorentzian model (SLO) [19, 20], the width is adopted as a constant that is equal to the GDR width
$ \Gamma_r $ . In other models, such as the enhanced generalized Lorentzian model (EGLO) [21, 22], generalized Fermi liquid model (GFL) [23], hybrid model (GH) [24], and modified Lorentzian model (MLO) [11], the width is taken as dependent on the$ \gamma $ -ray energy$ \Gamma(\epsilon_\gamma) $ . Although in the different models,$ \Gamma(\epsilon_\gamma) $ has various formulas,$ \Gamma_r $ is the only parameter of the$ \gamma $ -ray energy dependent width.Hence, in our phenomenological GDR parameters, first we have to define three basic values for the photoabsorption cross-section. They are assumed in the form of the mass number A and deformation
$ \beta_2 $ :$ \begin{split}E_r =& a_1(1+a_6I^2)/A^{1/3}+a_2(1+a_7I^2)/A^{1/6},\\ \Gamma_r =& a_3E_r^{a_4}-a_8E_r\beta_2,\\ \sigma_r =& \frac{2}{\pi}a_5\cdot\sigma_{TRK}/\Gamma_r.\end{split}$

(17) where
$ a_i(i = 1,\cdots,8) $ are adjustable parameters,$ I = (N-Z)/A $ , and$ \sigma_{\rm{{TRK}}} = 60NZ/A $ is the classical dipole Thomas-Reiche-Kuhn sum rule [52]. Comparing with the Eq.(137) in RIPL-3 Ref. [2], we added three extra parts with three more parameters, which correspond to the neutron-proton asymmetry I and deformation$ \beta_2 $ of the nuclei. Our phenomenological GDR parameters are not only for the spherical nuclei, but also can be used to calculate axially deformed nuclei. We adopt the following formula:$\begin{split} E_{r,2} =& E_r\frac{1}{b_0}[1-1.51\cdot10^{-2}(a_0^2-b_0^2)],\\ E_{r,1} =& E_{r,2}/\left[0.911\frac{a_0}{b_0}+0.089\right],\\ \Gamma_{r,2} =& b_2E_{r,2}^{b_3}-E_{r,2}b_6\beta_2,\; \; \; \; \Gamma_{r,1} = b_4E_{r,1}^{b_5}-E_{r,1}b_7\beta_2,\\ \sigma_{r,2} =& \sigma_r|1-b_8+b_1\beta_2|,\; \; \; \; \sigma_{r,1} = \sigma_r|b_8-b_1\beta_2|.\end{split}$

(18) where indexes
$ 1 $ and$ 2 $ correspond to the collective motion along and perpendicular to the axis of symmetry, respectively, with the relative semi-axes of a spheroid. We added eight parameters$ b_i (i = 1,\cdots,8) $ to change the value of width$ \Gamma_{r} $ and photoabsorption cross-section$ \sigma_r $ with deformation$ \beta_2 $ .$\begin{split} a_0 =& (1+\alpha_2)/\lambda,\\ b_0 =& (1-0.5\alpha_2)/\lambda,\\ \lambda^3 =& 1+\frac{3}{5}\alpha_2^2+\frac{2}{35}\alpha_2^3. \end{split} $

(19) Effective quadrupole deformation parameters
$ \alpha_2 $ or$ \beta_2 $ were determined from ground state deformation parameters$ \beta_n\equiv\alpha_n/\sqrt{(2n+1)/4\pi} $ , with the nuclear radius expansion expressed in spherical harmonics.$ \beta_n $ parameters were provided by Ref. [53].In Table 4, we display all the phenomenological GDR parameters and total
$ \chi^2 $ -values of MLO1, MLO2, MLO3, EGLO, GFL, SLO, GH, and SMLO models. Symbols SLO* and MLO1* denote the parameters in RIPL-3 [2]. In Fig. 2, we display the$ \chi^2 $ of each nucleus with different models. The red and blue points are$ \chi^2 $ values for the spherical and deformed nuclei, respectively. Comparing with the global GDR parameters of RIPL-3, our systematic approach, Eq. (17) and (18), represents a significantly better fit of the experimental photoabsorption cross-section, especially for the deformed nuclei, since the total$ \chi^2 $ value of the SMLO model is the smallest, and the formula of the SMLO is very simple. Therefore, the SMLO model performs better than others.MLO1 MLO2 MLO3 EGLO GFL SLO GH SMLO SLO* MLO1* $ a_1 $ 

42.722 41.504 42.563 43.1769 39.2025 39.7783 38.4423 42.0152 27.47 28.69 $ a_2 $ 

16.0865 16.7204 16.1593 16.0834 18.8849 17.6336 18.6947 16.4032 22.063 21.731 $ a_3 $ 

0.0111 0.0124 0.0122 0.0048 0.0104 0.012 0.01 0.0062 0.0277 0.0285 $ a_4 $ 

1.0375 1.0157 1.0071 1.1963 1.0186 1.0095 1.0114 1.1682 1.9 1.9 $ a_5 $ 

0.0452 0.0477 0.0457 0.0309 0.0395 0.0459 0.0384 0.0364 1.222 1.267 $ a_6 $ 

-9.0294 -10.4079 -10.3748 -5.00 -6.6123 -11.7035 -10.4802 -10.5713 0 0 $ a_7 $ 

8.8811 9.6039 10.3457 4.1809 4.4196 9.7693 7.6594 10.3444 0 0 $ a_8 $ 

0.0039 0.0049 0.0043 0.0017 0.0023 0.0051 0.0039 0.0014 0 0 $ b_1 $ 

−0.8837 −0.903 −0.8877 −0.7608 −0.8142 −0.8966 −0.8669 −0.7962 0 0 $ b_2 $ 

0.2753 0.5083 0.395 0.0086 0.2809 0.5838 0.5052 0.0629 0.026 0.026 $ b_3 $ 

1.0789 0.8666 0.9495 2.2425 1.1868 0.7884 0.9247 1.5836 1.91 1.91 $ b_4 $ 

0.0855 0.0503 0.0758 0.1945 0.4745 0.0757 0.1551 0.1821 0.026 0.026 $ b_5 $ 

1.4629 1.5903 1.4809 1.4222 0.9907 1.4819 1.3278 1.2703 1.91 1.91 $ b_6 $ 

−0.184 −0.1789 −0.1604 −0.1539 −0.3373 −0.1666 −0.2366 −0.1882 0 0 $ b_7 $ 

0.0815 −0.0221 0.036 1.0276 0.3179 0.1194 0.2426 0.2623 0 0 $ b_8 $ 

0.2448 0.2307 0.2474 0.2914 0.2475 0.229 0.2303 0.304 0.333 0.333 $ \chi^2 $ 

9.8769 12.8526 10.7246 9.742 10.1275 15.9214 15.6991 9.5161 25.8048 19.0095 Table 4. Parameters and
$ \chi^2 $ -values of systematics within MLO1, MLO2, MLO3, EGLO, GFL, SLO, GH, and SMLO models.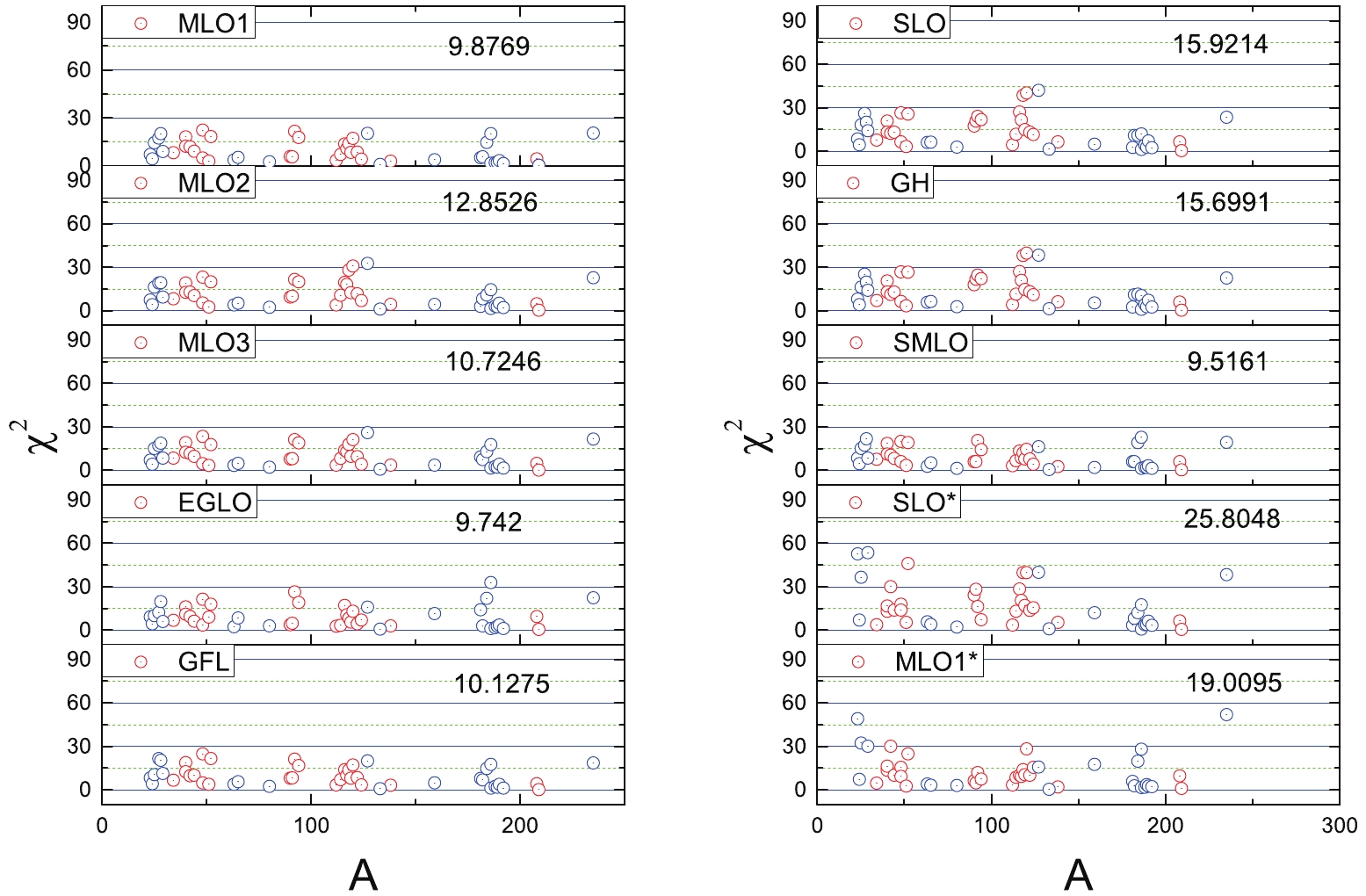
Figure 2. (color online) The
$\chi^2$ of each nuclei with different models, red and blue points depict$\chi^2$ values for spherical and deformed nuclei, respectively.In Figs. 1 and 3, we displayed the comparison of the results of SMLO with the experimental photoabsorption cross-sections and other systematic calculations such as: QRPA and MLO1*. In Fig. 1, we compare cross-sections of the spherical nuclei, and in Fig. 3 the deformed nuclei including: 28Si, 80Se, 127I and 186W are taken into account. The QRPA calculations are based on the Sly4 Skyrme force [8] and MLO1* is the result of the GDR parameters in RIPL-3 [2]. As observed in Figs. 1 and 3, the SMLO model can provide a good description of the GDR peak energy for both spherical and deformed nuclei. Around the GDR region, the agreement of the phtotoabsorption cross-sections between SMLO and experimental data are rather satisfactory.
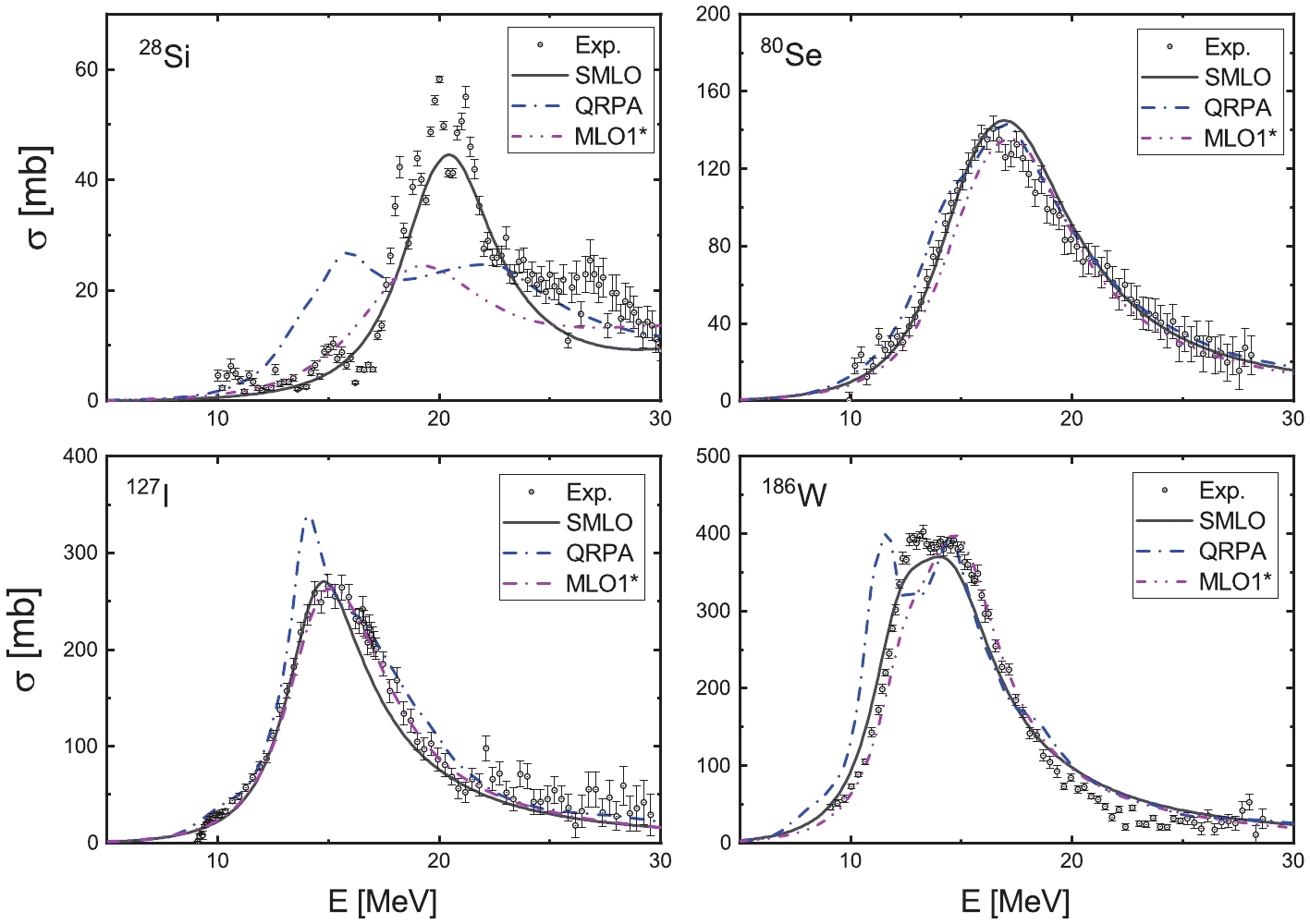
Figure 3. (color online) Comparison of SMLO (solid line) calculations with experimental photoabsorption cross-sections for 28Si, 80Se, 127I, and 186W. The QRPA (dash dot line) calculations are based on the Sly4 Skyrme force [8], and MLO1* (dash dot dot line) are the results of GDR parameters recommended by RIPL-3 [2].
-
In this work, we constructed two kinds of systematic GDR parameters to describe the photoabsorption cross-section of medium to heavy-mass nuclei. The microscopic GDR parameters are based on RQRPA calculations, which can be used to describe the photoabsorption cross-section of the spherical nuclei with only two parameters. At the same time, we systematically explore phenomenological GDR parameters in various Lorentzian models with 16 parameters, and the SMLO model is recommended at last, considering its brief formula expression and the smallest
$ \chi^2 $ .To further test the predictive ability of the two methods, we produce the GDR peak energies in the broad mass range 20
$ \leqslant $ A$ \leqslant$ 209, and compare them with the measurements in Fig. 4, where the black squares represent the experimental data [3], the blue triangles are the calculations of RQRPA with NL3 interaction for 58 even-even spherical nuclei from 30Si to 208Pb, and the red circles are the results of 266 nuclei from 20Ne to 209Bi using the systematic SMLO parameters in Table 4. Both methods yield reliable productions of the measured points. The GDR peak energies in the RQRPA scheme keep good consistency with the experimental data for A$ \geqslant $ 40 spherical nuclei. The GDR parameters from SMLO cover not only the spherical nuclei, but also the deformed medium to heavy-mass nuclei, and better performance is demonstrated around the mass A$ \geqslant $ 120.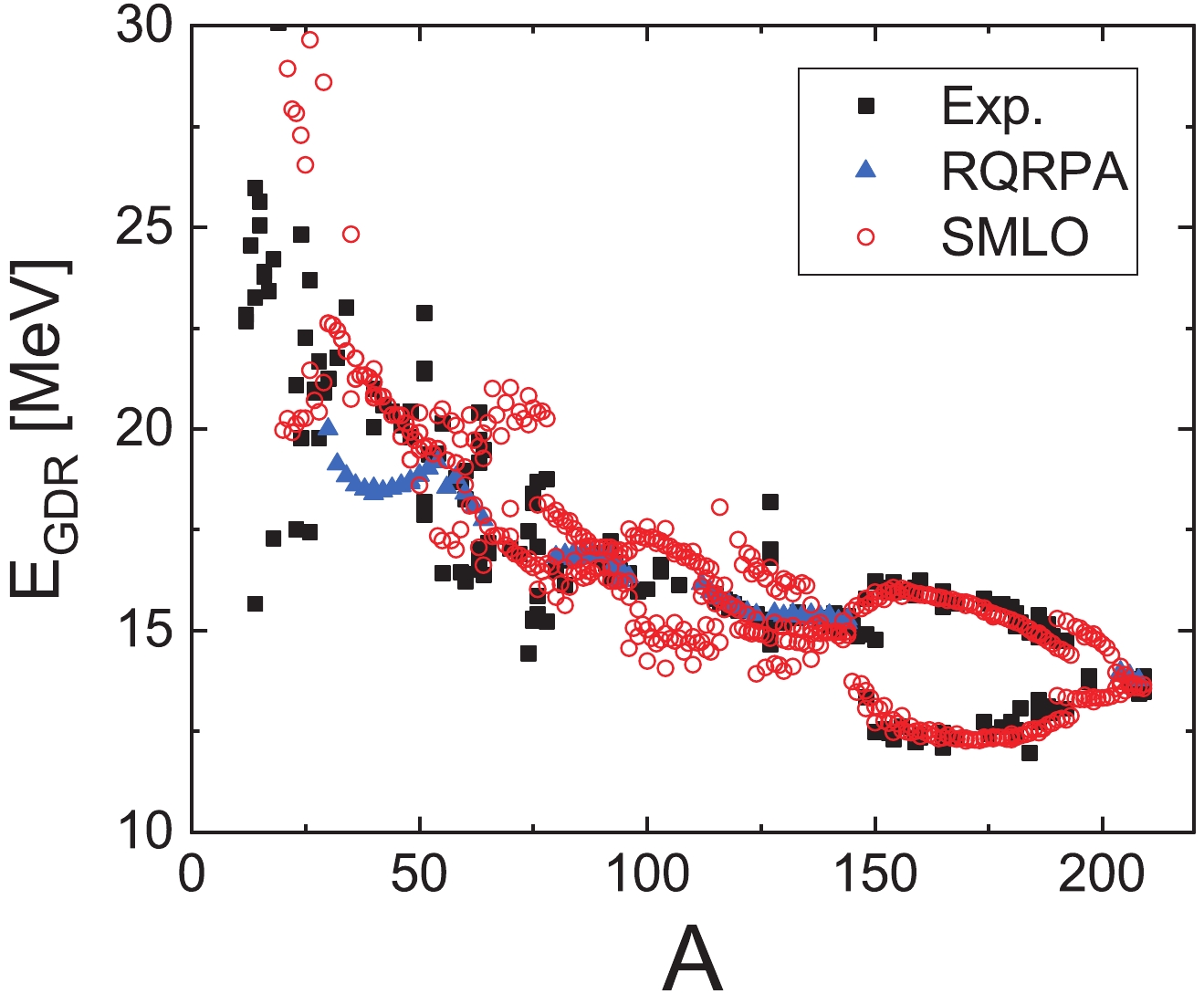
Figure 4. (color online) Comparison of experimental GDR energy [3] with RQRPA calculation obtained with NL3 interaction and SMLO calculations. RQRPA energies are displayed for 58 spherical nuclei only.
We would like to thank C.H. Cai (Nankai University), J.S. Zhang, Q.B.Shen, Y.L. Han (CNDC), and T. Kawano (LANL) for their kind discussions on the photon-nuclear reaction calculation; B.S. Yu (CNDC), H.W. Wang(SINAP), W. Luo (Nanhua University) and V.Varlamov (MSU) for their help on the experimental data evaluation of W isotopes; P. Dimitriou (IAEA) and A. Koning (IAEA) for their help on the evaluation.
Giant dipole resonance parameters from photoabsorption cross-sections
- Received Date: 2019-07-02
- Available Online: 2019-11-01
Abstract: The structural effect is believed to have no influence on the decay properties of medium and heavy-mass nuclei at excitation energies above the pairing gap. These properties can be described by statistical properties using so-called photon strength functions for different multipolarities, and directly related to the photoabsorption cross-section (





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: