-
Study of the exotic nuclear structure has been a hot subject in modern nuclear physics [1–3]. Exotic nuclei refer to nuclei that are far away from the
$ \beta $ -stability line. The nuclear structure properties of Ca isotopes have been one of the most attractive topics in the research of exotic nuclear structures [4–30]. Many properties of Ca isotopes with neutron number$N \leqslant 28 $ , such as the binding energies, charge radii, nucleon density distributions, single-particle energies, and low-lying excitation energies have been measured [24–33]. In recent years, experimental measurements of the properties of neutron-rich Ca isotopes have made a great progress [34–40]. Steppenbeck et al. reported a direct experimental evidence of a new magic number N = 34 by measuring the 2+ excitation energies of 54Ca [34]. Precise mass measurements of 49-57Ca established prominent shell closures at neutron numbers N = 32 and 34 [35–38]. Garcia Ruiz et al. measured the charge radii of 49,51,52Ca in the laser spectroscopy experiments, which suggested a large and unexpected increase of charge radii beyond N = 28 [39]. Very recently, the discovery of 59,60Ca was reported in the fragmentation of the 345 MeV/u primary 70Zn beam on a Be target at the radioactive ion-beam factory of the RIKEN Nishina Center [40].The Skyrme energy density functional theory is one of the most important approaches in microscopic studies of the nuclear structure [41–44]. It has been used to investigate the bulk properties and microscopic structure of stable and exotic nuclei [45–48]. In recent years, many studies have shown that the Skyrme tensor force plays a crucial role in describing the exotic nuclear structure [49–63]. The details of the Skyrme energy density functional with the tensor force can be found in a recent review [64]. In fact, the tensor force was included in the Skyrme interaction when it was proposed [65]. However, the tensor component was usually neglected in nuclear structure studies because of its complexity, instability, and small influence on the nuclear structure. Thus, in most Skyrme parametrizations, the tensor force has not yet been included. In order to study its effect on exotic nuclear structures, the tensor force was usually added as a perturbation to the Skyrme parametrization, for example the SLy5+T parametrization [51, 64]. Lesinski et al. proposed 36 sets of TIJ parametrizations which include the tensor force using the SLy interaction fit protocol [54], in which the spin-orbit strength
$ W_{0} $ varies from 103.7 MeV fm5 for T11 to 195.3 MeV fm5 for T66. This variation is correlated to the tensor force strength, which has the tendency to reduce the spin-orbit splitting in spin-unsaturated nuclei. Since the calculated nuclear properties are dependent on the accuracy of the nucleon-nucleon interaction, it is important to find reliable interactions among these parametrizations. The above mentioned experimental data for neutron-rich Ca isotopes provide a solid ground for testing these Skyrme interactions.The properties of the extreme neutron-rich Ca isotopes have been investigated using various models [6, 13, 14, 16, 17, 66–74]. For example, a neutron giant halo in some nuclei near the neutron drip-line was predicted by the relativistic continuum Hartree-Bogoliubov (RCHB) method [66–68], which is one of the most interesting studies of the extreme neutron-rich Ca isotopes. The giant halo in the very neutron-rich Ca isotopes has also been studied in the SHFB theory. It was found that the existence of the giant halo is strongly dependent on the Skyrme parametrization [69–71]. However, the tensor force has not been considered in these studies. The tensor force effect on the exotic nuclear structure has been discussed in the relativistic Hartree-Fock theory, such as the giant halo structure of Ce isotopes [75], and the evolution of single-particle energies of Ca isotopes [76, 77]. Therefore, it is of current interest to study the giant halo and other exotic structures of Ca isotopes in the Skyrme mean-field theory with the tensor force.
In this work, we first test the Skyrme interactions including the tensor force in the framework of the SHFB approach by comparing our systematic calculations with the experimental data for Ca isotopes, and determine the Skyrme interactions that lead to reliable predictions of exotic nuclear structures of Ca isotopes. We then search for the giant halo and other exotic structures in nuclei near the neutron drip-line with the selected interactions.
The paper is organized in the following way. In Sec. 2, the SHFB theoretical framework is introduced. The numerical results and corresponding discussions are given in Sec. 3. In the last section, conclusions are drawn.
-
In this work, the tensor force is taken into account using the spherical SHFB code (HRBRAD) [44]. In the framework of the spherical SHFB approach, the Skyrme interaction includes two parts,
$ V_{\rm Skyrme} = V_{12}+V_{12}^{T}, $

(1) where
$ V_{12} $ and$ V_{12}^{T} $ denote the usual part and the tensor part, respectively.$ V_{12} $ is written as [44]$ \begin{split} V_{12} =& t_{0}\left( 1+x_{0}P_{\sigma }\right) \delta ({{r}}_{1}- {{r}}_{2}) \\ &+\frac{1}{2}t_{1}\left( 1+x_{1}P_{\sigma }\right) \left[ \delta ({{r}} _{1}-{{r}}_{2}){{k}}^{^{\prime }2}+\delta ({{r}}_{1}-{{r}}_{2}){{k}}^{2}\right] \\ &+t_{2}\left( 1+x_{2}P_{\sigma }\right) \delta ({{r}}_{1}-{{r}} _{2}){{k}}^{\prime }\cdot {{k}} \\ & +\frac{1}{6}t_{3}\left( 1+x_{3}P_{\sigma }\right) \delta ({{r}}_{1}- {{r}}_{2})\rho ^{\gamma }\left( \frac{1}{2}({{r}}_{1}-{{r}} _{2})\right) \\ & +iW_{0}\delta ({{r}}_{1}-{{r}}_{2})\left( \sigma _{1}+\sigma _{2}\right) \cdot {{k}}^{\prime }\times {{k}}, \end{split} $

(2) where
$t _{i} $ ,$ x_{i} $ , and$ W_{0} $ are the parameters of the interaction,$ P_{\sigma} $ is the spin-exchange operator, and$ \sigma_{i} $ is the Pauli spin operator. The operator k = ($ \nabla _{1}-\nabla_{2} $ )/2i acts on the right and k' = –($ \nabla _{1}-\nabla _{2} $ )/2i acts on the left.$V _{12}^{T} $ is expressed as [49–65]$\begin{split} V_{12}^{T} =& \frac{T}{2} \left[ \left( \sigma _{1}\cdot {{k}} ^{\prime }\right) \left( \sigma _{2}\cdot {{k}}^{\prime }\right) -\frac{1}{3}\left( \sigma _{1}\cdot \sigma _{2}\right) {{k}}^{\prime 2}\right] \delta \left( {{r}}_{1}-{{r}}_{2}\right) \\ & +\frac{T}{2}\delta \left( {{r}}_{1}- {{r}}_{2}\right) \left[ \left( \sigma _{1}\cdot {{k}}\right) \left( \sigma _{2}\cdot {{k}}\right) -\frac{1}{3}\left( \sigma _{1}\cdot \sigma _{2}\right) {{k}}^{2}\right] \\ & +\frac{U}{2}\left[ \left( \sigma _{1}\cdot {{k}}^{\prime }\right) \delta \left( {{r}}_{1}- {{r}}_{2}\right) \left( \sigma _{2}\cdot {{k}}\right) \right.\\&\left.+\left( \sigma _{2}\cdot {{k}}^{\prime }\right) \delta \left( {{r}}_{1}- {{r}} _{2}\right) \left( \sigma _{1}\cdot {{k}}\right) \right] \\ & -\frac{1}{3}U\left( \sigma _{1}\cdot \sigma _{2}\right) {{k}}^{\prime }\cdot \delta \left( {{r}}_{1}- {{r}}_{2}\right) {{k}}, \end{split} $

(3) where T and U are the strengths of the triplet-even and triple-odd tensor interactions, respectively.
In the pairing channel, a zero range density dependent pairing interaction is used [44]
$ V_{\rm pair} = \left( t_{0}^{\prime }+\frac{t_{3}^{\prime }}{6}\rho ^{\gamma ^{\prime }}\right) \delta, $

(4) where
$ \gamma ^{\prime } = 1 $ , and$ t_{3}^{\prime } = -18.5t_{0}^{\prime} $ corresponds to the mixed pairing force.$t _{0}^{\prime } $ is the pairing strength parameter and determined by the pairing energy gap extracted from the following empirical formula [78–80]$ \begin{split}\Delta _{p} =& \frac{1}{8}[B(Z+2,N)-4B(Z+1,N)+6B(Z,N) \\ & -4B(Z-1,N)+B(Z-2,N)],\end{split} $

(5) where B is the experimental binding energy taken from the nuclear mass table of 2016 [31].
The total energy E is the sum of the kinetic, usual Skyrme, pairing, Coulomb, and tensor terms
$ \begin{split}E =& K+E_{\rm Skyrme}+E_{\rm Pair}+E_{\rm Coul}+E_{\rm Tensor} \\ =& \int {\rm d}^{3}{{r}}\left[ k({{r}})+\varepsilon _{\rm Skyrme}({{r}} )+\varepsilon _{\rm Pair}({{r}})+\varepsilon _{\rm Coul}({{r}})+\varepsilon _{\rm Tensor}({{r}})\right] . \end{split} $

(6) The kinetic, Skyrme, pairing and Coulomb energy densities in Eq. (6) can be found in Ref. [44]. The expression for the tensor energy density is written as [49–64]
$ \varepsilon _{\rm Tensor}(r) = \frac{5}{24}(T+U)J_{n}J_{p}+\frac{5}{24} U(J_{n}^{2}+J_{p}^{2}). $

(7) Here,
$ J_{q} $ (r) is the abnormal spin current density, and can be expressed as$ \begin{split} J_{q}(r) =& \frac{1}{4\pi r^{3}}\sum\limits_{i}\left( 2j_{i}+1\right) \\ & \times \left[ j_{i}\left( j_{i}+1\right) -l_{i}\left( l_{i}+1\right) - \frac{3}{4}\right] R_{qi}^{2}(r). \end{split} $

(8) Since the particle number can not be preserved by the Bogolyubov transformation, two Lagrange multipliers
$ \lambda _{N} $ and$ \lambda _{Z} $ are introduced to conserve the average neutron and proton numbers. The SHFB equations are then obtained from the stationary condition$ \delta \left[ E -\langle \lambda _{N}N+\lambda _{Z}Z\rangle \right] = 0 $ .The spin-orbit field with the tensor contribution has the following form [49–64]
$ \begin{split} B_{q} =& \frac{W_{0}}{2r}\left( 2\frac{{\rm d}\rho _{q}}{{\rm d}r}+\frac{{\rm d}\rho _{q^{\prime }}}{{\rm d}r}\right) \\ & +\left[ \frac{1}{8}\left( t_{1}-t_{2}\right) -\frac{1}{8}\left( t_{1}x_{1}+t_{2}x_{2}\right) +\frac{5}{12}U\right] \frac{J_{q}}{r} \\ & +\left[ \frac{5}{24}(T+U)-\frac{1}{8}\left( t_{1}x_{1}+t_{2}x_{2}\right) \right] \frac{J_{q^{\prime }}}{r}. \end{split}$

(9) In Eqs. (8) and (9), q stands for neutrons (protons) and
$ q^{\prime } $ for protons (neutrons), where i = n, l, j runs over all states having the given q ($ q^{\prime } $ ), and$ R_{qi} $ (r) is the radial part of the wave function.The expressions for the normal effective mass
$ M_{q} $ , abnormal effective mass$ \widetilde{M}_{q} $ and other potential fields (the particle-hole field$ U_{q} $ , particle-particle field$ \widetilde U_{q} $ , Coulomb field$ V_{C}({{r}}) $ and abnormal spin-orbit field$ \widetilde B_{q} $ ) can be found in Ref. [44].The above mentioned fields can be written in a matrix form
$ \mathcal{M} = \left( \begin{array}{cc} M & \widetilde{M} \\ \widetilde{M} & -M \end{array} \right) ,\mathcal{U} = \left( \begin{array}{cc} U-\lambda & \widetilde{U} \\ \widetilde{U} & -U+\lambda \end{array} \right), $

(10) $ \mathcal{U}_{so} = \left( \begin{array}{cc} B & \widetilde{B} \\ \widetilde{B} & -B \end{array} \right) \frac{j(j+1)-l(l+1)-\frac{3}{4}}{2r}. $

(11) Finally, the bulk and microscopic properties can be obtained by solving the following SHFB equation
$ \left[ -\frac{{\rm d}}{{\rm d}r}\mathcal{M}\frac{{\rm d}}{{\rm d}r}+\mathcal{U}+\mathcal{M}\frac{l(l+1) }{r^{2}}+\frac{\mathcal{M}^{\prime }}{r}+\mathcal{U}_{so}\right] \left( \begin{array}{c} u_{1} \\ u_{2} \end{array} \right) = E\left( \begin{array}{c} u_{1} \\ u_{2} \end{array} \right), $

(12) where
$ \mathcal{M}^{\prime } $ is the first order derivative with respect to radial coordinate r , and$u_{1} $ and$u _{2} $ are the components of the quasi-particle wave function. -
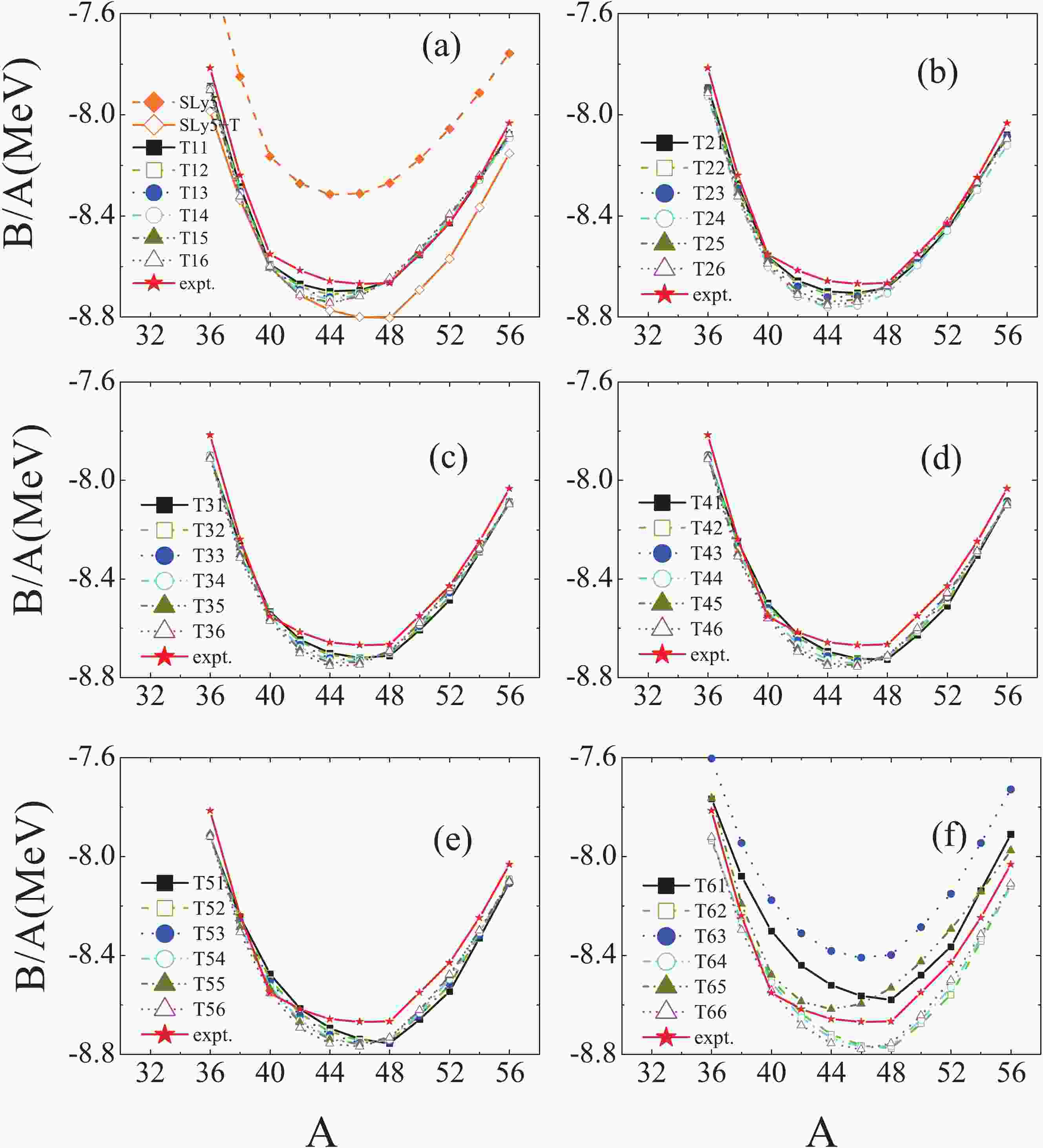
We have performed calculations of the average binding energies B/A of Ca isotopes in the spherical SHFB approach using SLy5, SLy5+T and 36 sets of TIJ parametrizations, whose values as function of mass number A are shown in Fig. 1. Note that in our calculations the spherical box and mesh sizes are 30 fm and 0.1 fm, respectively. The quasi-particle energies are cut off at 60 MeV. The maximum angular momentum of the quasi-particles
$ j_{\max } $ is set to$ \frac{25}{2}\hbar $ . All calculations converged with these conditions.From Fig. 1, it is seen that the experimental data for B/A can be reproduced accurately by the Skyrme interactions, except for the SLy5, T61, T63 and T65 parametrizations. In the case of T61, T63 and T65 parametrizations, the deviation between the experimental and calculated values is small. The deviation in the case of SLy5 interaction can be as large as 0.5 MeV. Comparing the results of SLy5 parametrization with SLy5+T, it is found that the experimental data are reproduced significantly better with the SLy5+T interaction, which indicates that the isospin dependence of B/A can be improved by adding the tensor force to the Skyrme parametrizations.
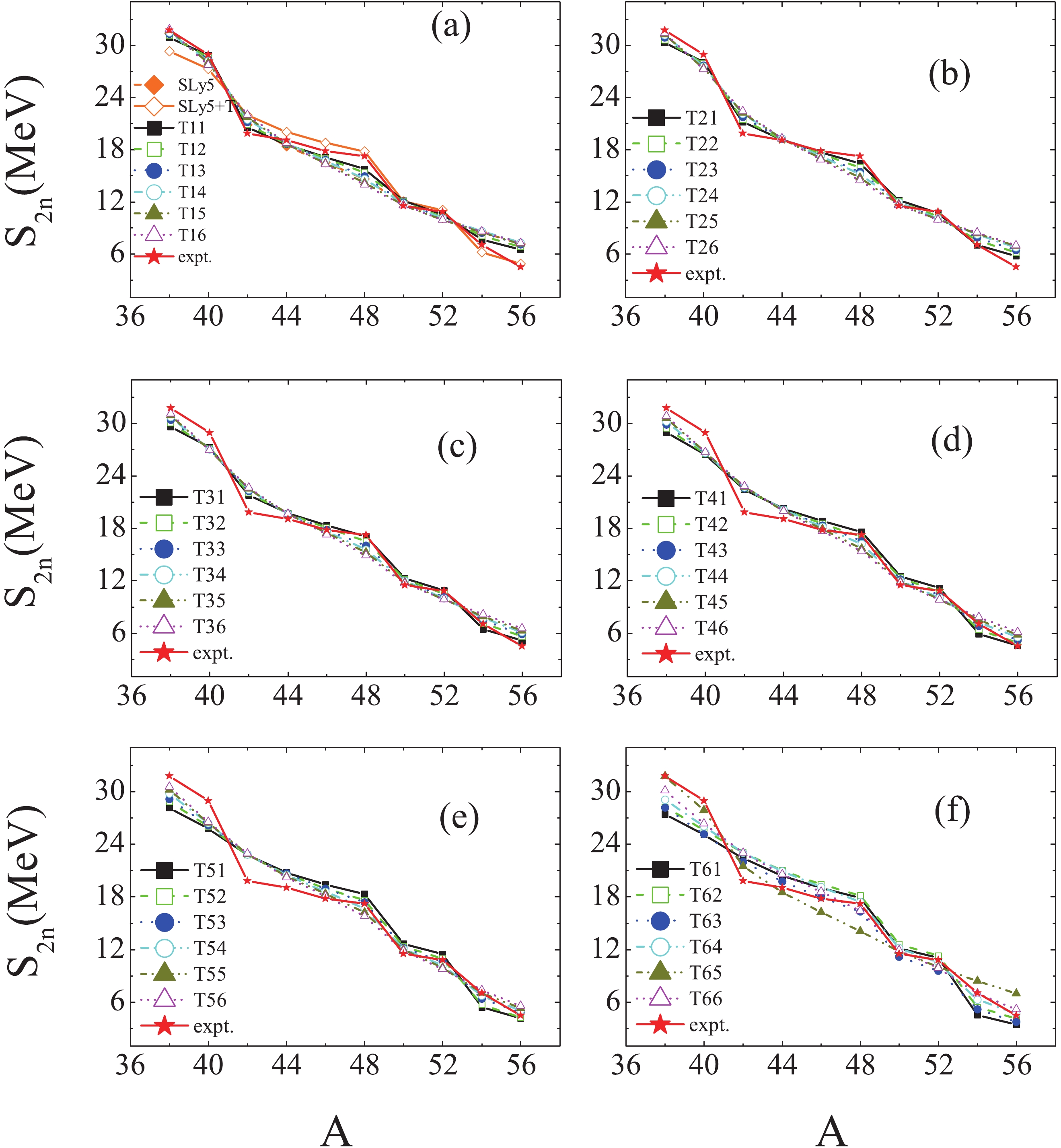
We extract the two-neutron separation energies
$ S_{2n} $ using the calculated B values for each interaction, which are plotted in Fig. 2. From the experimental data for$ S_{2n} $ versus A, we can see the shell effects at 40Ca (N = 20), 48Ca (N = 28), and 52Ca (N = 32). From Fig. 2, it can be seen that only the SLy5+T, T31, and T32 parametrizations reproduce the shell effects at N= 20, 28, and 32, and the experimental value of$S_{2n} $ for 56Ca. Recently, Michimasa et al. provided experimental evidence for the magic nature of N = 34 in the neutron-rich Ca nuclei [38] by measuring the masses of 55-57Ca. However, it is not so easy to see the shell effect for 54Ca in the experimental data for$ S_{2n} $ as shown in Fig. 2, which indicates that the shell effect becomes weaker with increasing A. To show the shell effect at N = 34 clearly, the experimental data for$ S_{2n} $ of 50-56Ca as function of A are displayed in Fig. 3. The calculated$ S_{2n} $ using the SLy5+T, T31 and T32 interactions are also plotted in Fig. 3. A weak kink can be seen at 54Ca in the experimental$ S_{2n} $ , and the kink is reproduced by the SLy5+T, T31 and T32 interactions, as shown in Fig. 3. The shell effect at N = 34 given by the three interactions is more evident than in the experimental data.
Figure 3. (color online) Comparison between the experimental data and calculated
$S _{2n} $ for 50-56Ca with the SLy5+T, T31 and T32 interactions.The experimental data for the charge radii
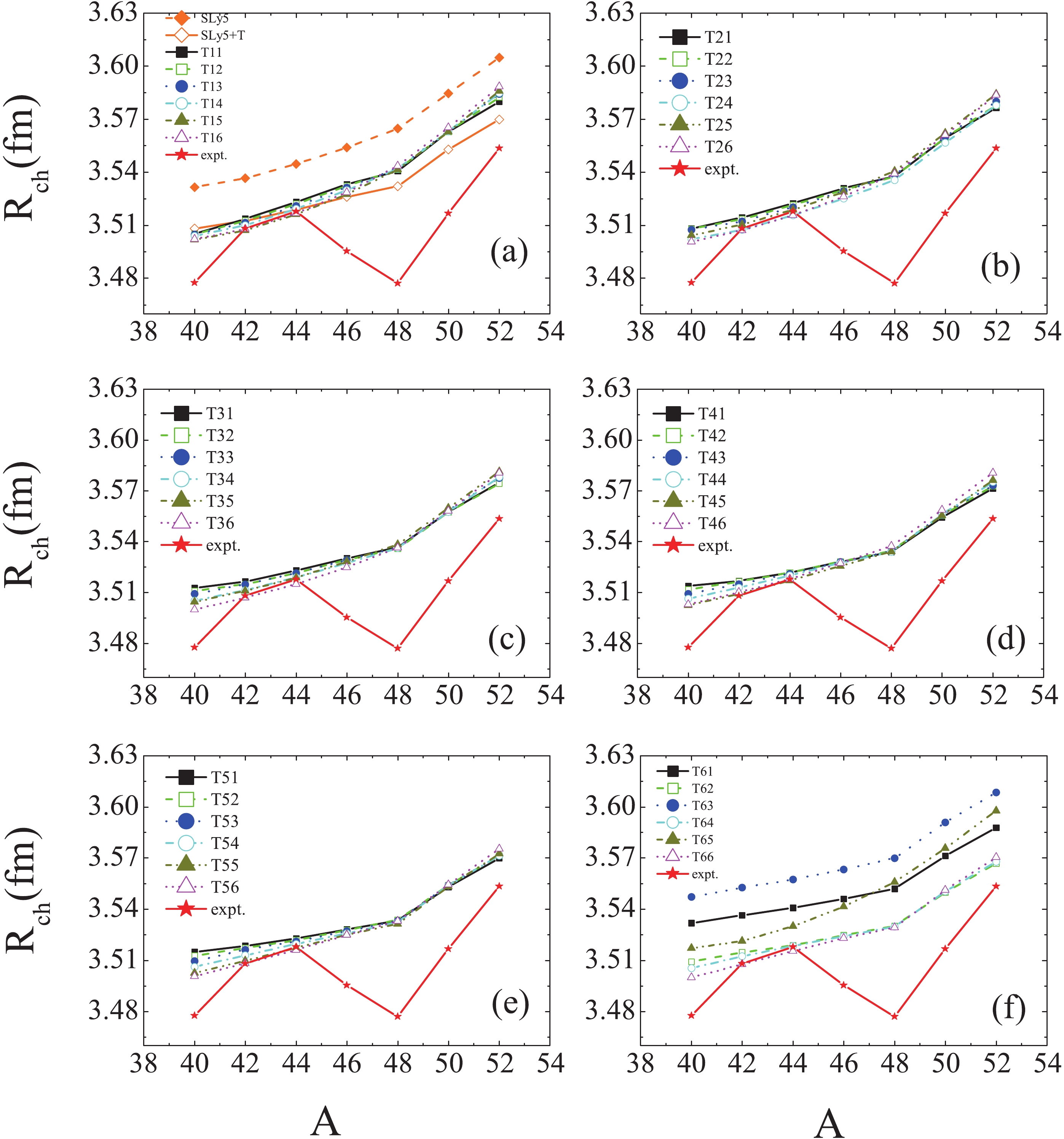
$ R_{ch} $ and the calculated values using SLy5, SLy5+T and 36 sets of the TIJ parametrizations are displayed in Fig. 4. Observing the experimental data for$ R_{ch} $ , a minimum at 48Ca can be clearly seen. However, the minimum does not appear in all interactions, as displayed in Fig. 4, which implies that the minimum at 48Ca might have some unknown origin beyond the mean field. In addition, it is seen in Fig. 4 that the agreement between the experimental data and$ R_{ch} $ calculated using the SLy5, T61, T63, and T65 parametrizations is worse. For the other 34 sets, the experimental data for$ R_{ch} $ are not reproduced well, although the differences between the calculated and experimental values are small. For example, the largest deviation is 0.07 fm for 48Ca. In addition, the kink at 48Ca is obtained with most interactions, but it is very small. For the SLy5+T interaction, the resulting accuracy is improved considerably by taking into account the tensor force, similarly to the situation in Fig. 1.According to the above discussion, the SLy5+T, T31 and T32 interactions may be seen to describe best the experimental data for Ca isotopes. In the following, we predict the properties of the very neutron-rich Ca isotopes using the SLy5+T and T31 parametrizations and compare them with the results obtained with the SLy5 parametrization.
The
$S _{2n} $ values for nuclei with$ A\geqslant 56 $ obtained with the SLy5, SLy5+T and T31 interactions are plotted in Fig. 5 as function of A. The figure shows that the two-neutron drip line is located at 70Ca for the SLy5+T and T31 interactions. However, for the SLy5 interaction, it is at 68Ca. Note that a kink was predicted at 60Ca (N = 40) by the RCHB approach [66–68]. However, the shell gap at 60Ca is not seen in Fig. 5. In the$ S_{2n} $ plot for the SLy5+T interaction, a weak shell effect at 70Ca (N = 50) can be seen. The recent discovery of 60Ca does not support predictions of ab initio models. Furthermore, it was found that the Skyrme energy density functionals (HFB-22 and UNEDF0) can describe the experimentally established limits, and predict that the even-mass Ca isotopes are bound up to at least 70Ca [40]. Our predictions with the SLy5+T and T31 interactions are consistent with the HFB-22 and UNEDF0 models.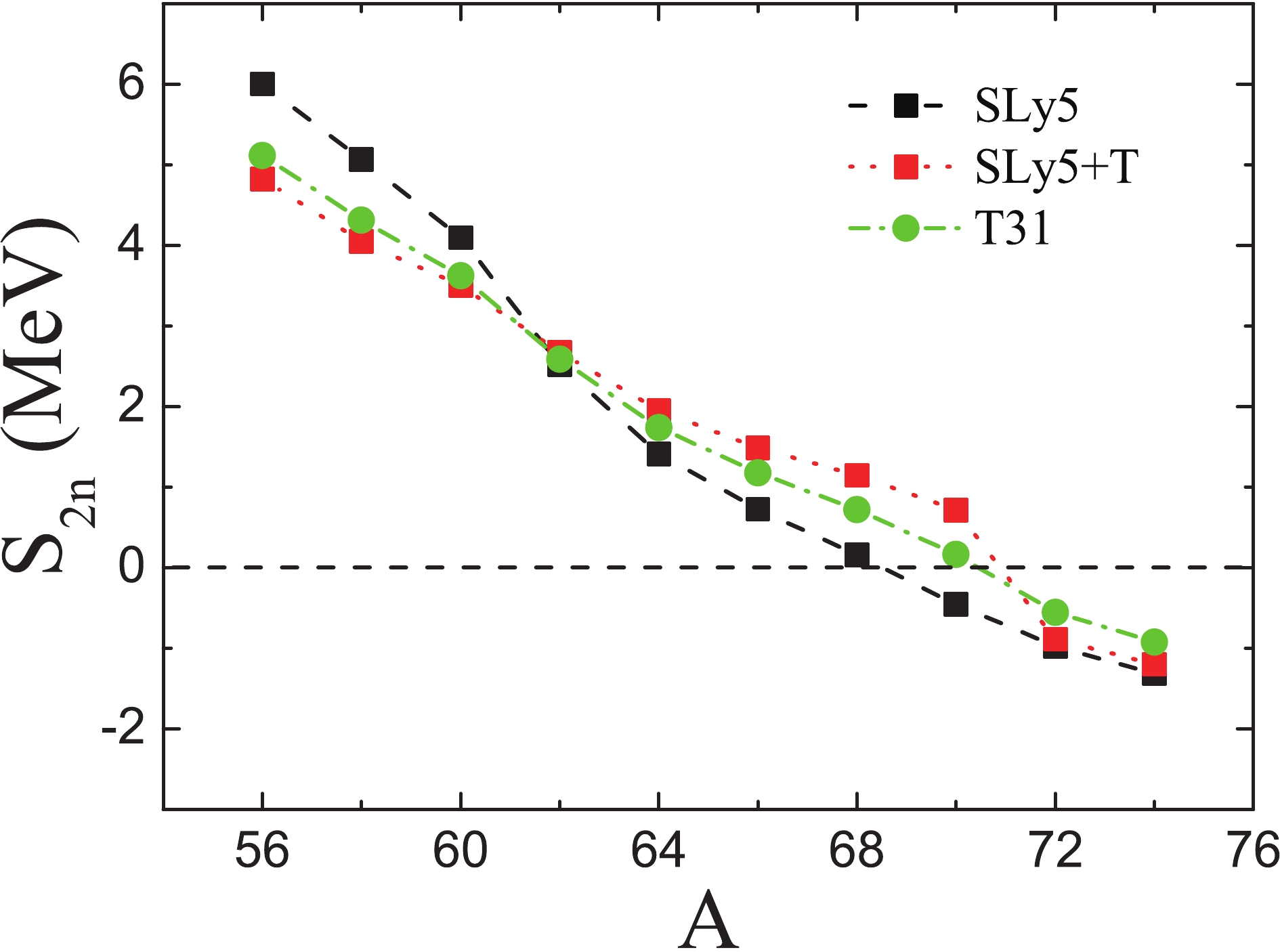
Figure 5. (color online)
$ S_{2n} $ for nuclei with$ A\geqslant 56 $ as function of A obtained with the SLy5, SLy5+T and T31 interactions.In Fig. 6 , we show the neutron radii
$ R_{n} $ of Ca isotopes predicted by the SLy5, SLy5+T and T31 interactions, and the$ r_{0} $ $ N^{1/3} $ curve. From Fig. 6 , we see that the$ R_{n} $ dependence on the neutron number N obtained with the SLy5 interaction is close to the SLy5+T and T31 interactions. A strong kink is observed in Fig. 6 at 70Ca for each interaction. The slope of$ R_{n} $ with the SLy5 interaction is much more pronounced than with the SLy5+T and T31 interactions. This suggests that a neutron giant halo exists for isotopes with N > 50, which is suppressed by the tensor force. To see the reason why the giant halo is suppressed by the tensor force, the properties of the single-neutron states near the Fermi energy for 72Ca as an example are listed in Table 1. As can be seen from Table 1, the rms radius of the 3$ s_{1/2} $ state ($r _{3s_{1/2}} $ ) is the largest for each interaction. Because the centrifugal potential of the s orbital is 0, its wave function can extend up to a very large r . As a result, the$ 3s_{1/2} $ state contributes most to$ R_{n} $ . From Table 1, it is also seen that the$ 3s_{1/2} $ state is below the Fermi energy for the SLy5 interaction, but it is above the Fermi energy for the SLy5+T and T31 interactions. As a result, the occupation probability of the$ 3s_{1/2} $ state and$r _{3s_{1/2}} $ become smaller with the tensor force in the SLy5+T and T31 interactions, and$ R_{n} $ is accordingly suppressed. However, as N increases, the neutron drip line is reached before the halo structure starts to form for the three Skyrme interactions. As a result, the neutron giant halo is unlikely to appear for the extreme neutron-rich Ca isotopes. In addition, it is seen in Fig. 6 that the$ R_{n} $ values for the neutron-rich Ca isotopes are in agreement with the$r _{0} $ $N ^{1/3} $ law. However, in the neutron-deficient region, the$ R_{n} $ values deviate from the curve considerably.
Figure 6. (color online)
$ R_{n} $ for Ca isotopes obtained with the SLy5, SLy5+T and T31 interactions.$ R_{n} $ calculated by the law$ r_{0} $ $ N^{1/3} $ ($ r_{0} $ = 1.190 fm) is shown by the solid line.$ nl_{j} $ 

SLy5 SLy5+T T31 E /MeV $v ^{2} $ 

$r _{nlj} $ /fm

E /MeV $ v^{2} $ 

$ r_{nlj} $ /fm

E /MeV $ v^{2} $ 

$r _{nlj} $ /fm

$1f _{5/2} $ 

−6.27 0.977 4.46 −4.81 0.982 4.52 −4.83 0.968 4.56 $1 g_{9/2} $ 

−0.71 0.784 5.03 −2.45 0.967 4.91 −2.00 0.921 4.97 $3s _{1/2} $ 

0.37 0.747 13.19 0.29 0.432 11.93 0.21 0.331 10.43 $2d _{5/2} $ 

0.90 0.095 7.79 0.67 0.138 6.91 0.57 0.186 6.66 Fermi energy 0.49 – – 0.25 – – 0.13 – – Table 1. The properties of the single-neutron states near the Fermi energy of 72Ca obtained with the SLy5, SLy5+T and T31 interactions. E,
$ v^{2} $ and$r _{nlj} $ represent the single-neutron energy, occupation probability and rms radius of each orbital, respectively.In order to further study the giant halo structure, the neutron density distribution in Ca isotopes obtained with the SLy5+T and T31 interactions are plotted in Fig. 7. Since the density distribution in the exterior region is related to the skin and halo structures, the logarithmic neutron density is shown in the insets of this figure to indicate more clearly the density distribution in the exterior region. From the two insets in Fig. 7, it is seen clearly that the neutron density tail becomes longer as N increases. Nevertheless, the tails for nuclei near the neutron drip-line are shorter and thinner than those obtained with the RCHB approach [67]. This suggests that the existence of a neutron giant halo in the extreme neutron-rich Ca isotopes is not supported by the spherical SHFB calculations. It is also seen from the insets in Fig. 7 that the tail of 70Ca obtained with the T31 interaction is wider than with the SLy5+T interaction, which is caused by the difference of the squared radial wave functions of the
$3 s_{1/2} $ state ($ R_{3s_{1/2}}^{2}(r) $ ) in the two interactions. In Fig. 8, we show the$ R_{3s_{1/2}}^{2}(r) $ distribution in 70Ca with the SLy5+T and T31 interactions. As can be seen in Fig. 8, the tail obtained with the T31 interaction extends to larger r than with the SLy5+T interaction.
Figure 7. (color online) Neutron density distribution in Ca isotopes obtained with the SLy5+T and T31 interactions. The insets are the same plots in logarithmic scale.
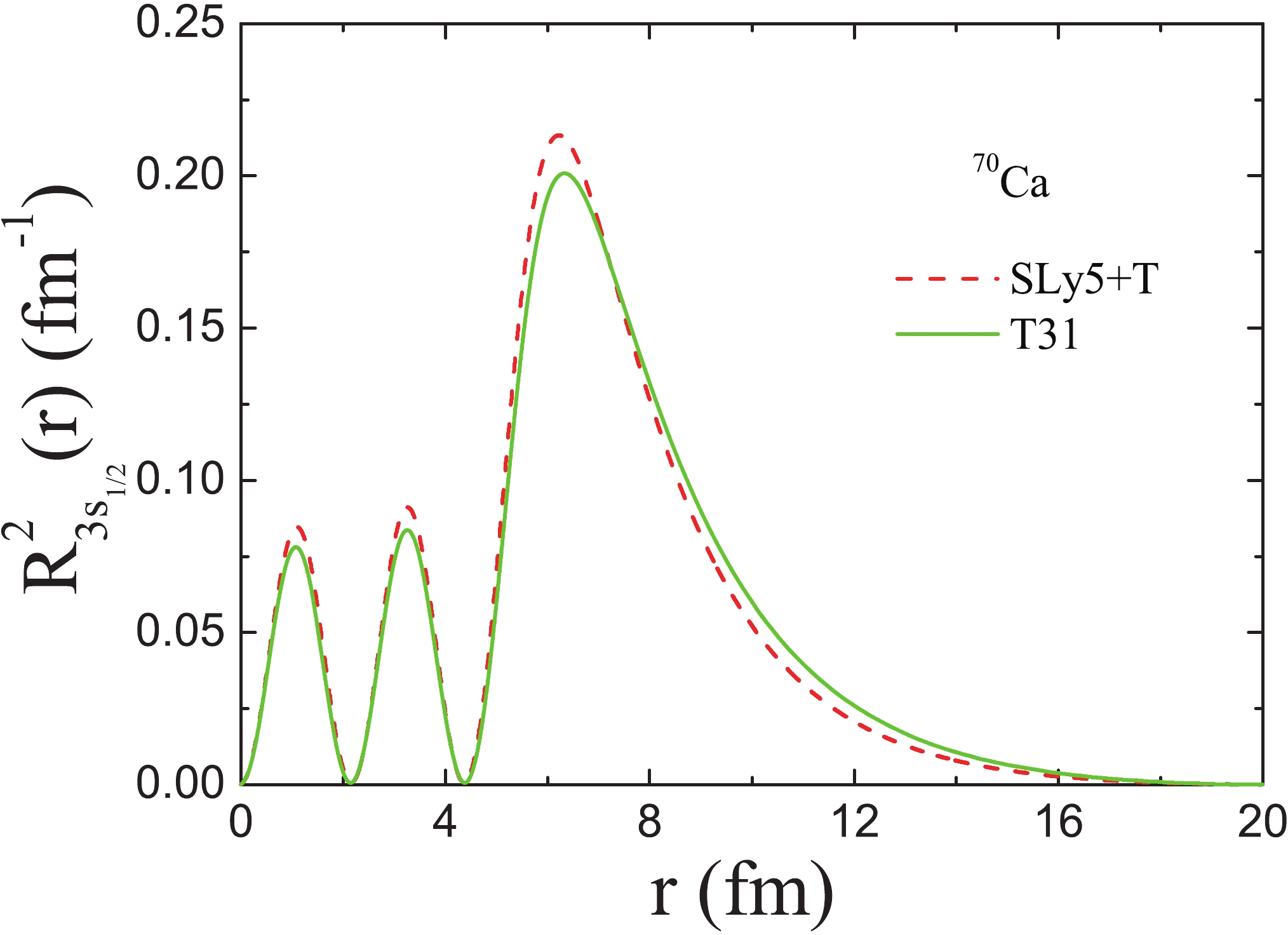
Figure 8. (color online) Radial wave function squared of the neutron
$ 3s_{1/2} $ state in 70Ca obtained with the SLy5+T and T31 interactions.From Figs. 5-8, one can see that the details of the nuclear structure of the extreme neutron-rich Ca isotopes are different for the SLy5+T and T31 interactions, although both were selected as best. In Ref. [54], 36 sets of the TIJ parametrizations were analyzed in order to determine the impact of the tensor force on a large variety of observables in calculations with a pure mean-field. Combining the work of Lesinski et al. [54] and our calculations, it seems that it is even more important to analyze the effects of the tensor force by comparing the details of different tensor forces, although it is essential to find best parametrizations of the tensor force based on experimental data. Moreover, in addition to the TIJ interactions, other Skyrme parametrizations with the tensor force, such as SLy5+T
$ _{\rm new} $ [62], SIII+T$ _{\rm new} $ [62], T41$ _{\rm new} $ [62], Skxta [50], Skxtb [50], SIII+T [52], and SLy5+T$ _{w} $ [49, 58], are also used to study nuclear structure. Using 35 sets of TIJ interactions (T31 is not included) and the above mentioned Skyrme interactions, we further investigate the properties of Ca isotopes near the neutron drip line. The predicted locations of the two-neutron drip line are listed in Table 2. From Table 2, it is seen that the location of the two-neutron drip line is strongly dependent on the type of parametrization. Furthermore, an increase of the slope of$ R_{n} $ is not seen in the two-neutron drip line for every interaction, suggesting that the non-existence of a neutron giant halo in Ca isotopes is not dependent on the type of Skyrme energy density functional with tensor force. To analyze this independence, the single-neutron spectra for 68Ca obtained with the T22, T32, T43, T56, T63, T66, SIII+T$ _{\rm new} $ and Skxta interactions are shown in Fig. 9. From Fig. 9, it is seen that the details of energy spectra are different for different Skyrme parametrizations. However, the ordering of the energy levels around the N = 50 gap ($ 3s_{1/2} $ and$ 1g_{9/2} $ orbitals) is the same for each interaction. For nuclei with 40 < N < 50, many more neutrons occupy the$ 1g_{9/2} $ state compared with the number of neutrons scattered to the$ 3s_{1/2} $ orbital for each interaction. This neutron filling pattern is the same for the eight sets of interactions. Thus, the dependence of the giant halo on the type of Skyrme interaction with tensor force can not be seen. However, it is necessary to point out that there are considerably less Skyrme parametrizations with tensor force than without it. It is believed that additional Skyrme parametrizations with a tensor component will be proposed in the near future, and it may still be possible to see the dependence of the giant halo on parametrizations with tensor force.Two-neutron drip line Skyrme parametrization sets 70Ca T41, T42, T51, T52, T53, T61, T62, T64, SIII+T 68Ca T21, T22, T32, T33, T34, T43, T44, T45, T46, T54, T55, T56, T63, T66, SIII+Tnew, Skxta 66Ca T11, T12, T13, T14, T23, T24, T25, T26, T35, T36, SLy5+Tnew, T41new 64Ca T15, T16, T65, SLy5+Tw, Skxtb Table 2. Predicted location of the two-neutron drip line in Ca isotopes obtained with different Skyrme parametrizations containing the tensor force.
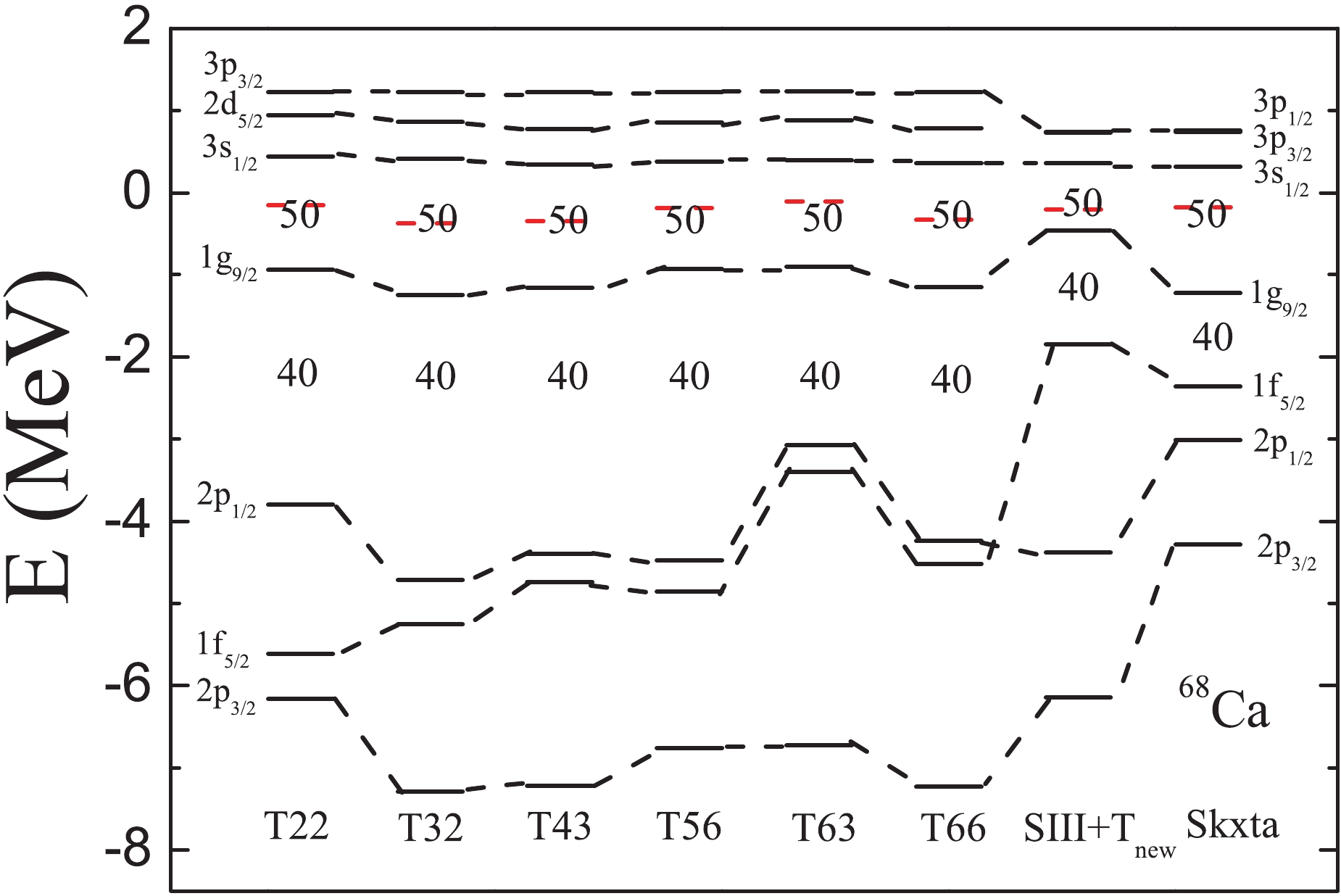
Figure 9. (color online) Single-neutron energy levels in 68Ca obtained with the T22, T32, T43, T56, T63, T66, SIII+T
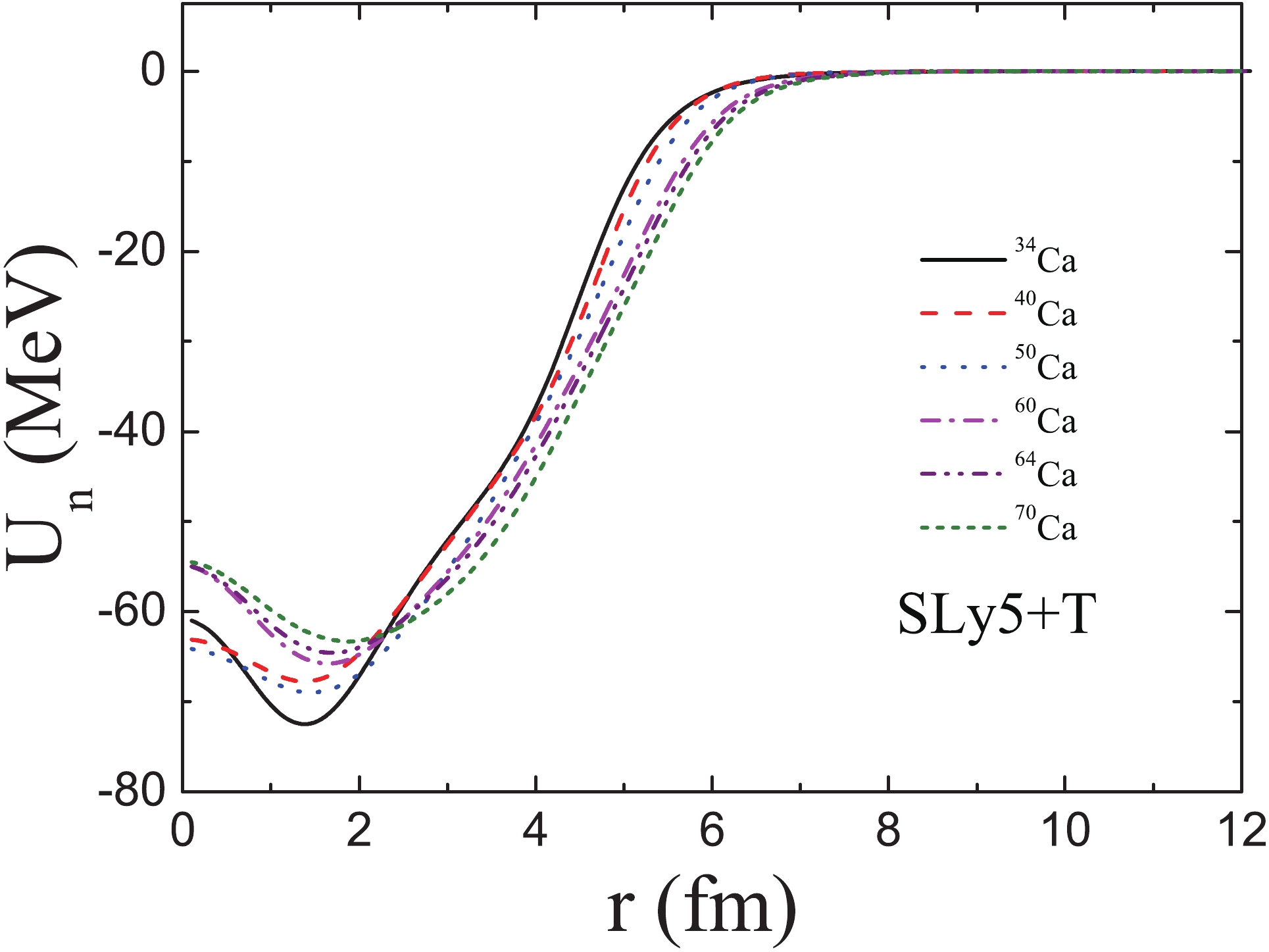
$ _{\rm new} $ and Skxta interactions. The red dash line represents the Fermi energy.In addition to the properties of the exterior region, the neutron density distribution in the interior region can be clearly seen in Fig. 7 in the normal scale. For 34Ca, the central density is depleted significantly. The nucleus with a depleted central density is called a “bubble” nucleus, and the depletion is caused by the lower occupation probability of the s state. The discussion of its formation mechanism can be found in the relevant studies [53, 81–92]. To our surprise, bubble-like structures can also be found in 52-70Ca, which is different from the predictions of RCHB. To explain this phenomenon, we plot in Fig. 10 the neutron mean-potential in 34,40,50,60,64,70Ca obtained with the SLy5+T interaction. For the mean-potential in 34,60,64,70Ca, there is a maximum at r = 0 and a minimum at some distance. The mean-potential looks like a “wine-bottle” in the region of small r . Due to the “wine-bottle” shaped mean-potential, the single-neutron energy level with a low orbital angular momentum l is pushed up, while the one with a large l is pulled down. As a result, the ordering of the energy levels can be changed, and the central density lowered. However, the bottom of the mean-potential in 40,50Ca is flat, so that a bubble-like structure can not be found. Therefore, we may conclude that the density distribution in the nuclear interior is strongly dependent on the shape of the bottom of the mean-potential.
-
In this work, the binding energies, two-neutron separation energies, and charge radii of the Ca isotopes were calculated with SLy5, SLy5+T, and 36 sets of TIJ parametrizations in the framework of the spherical SHFB approach. Comparing the calculated results with the experimental data, it was shown that the SLy5+T, T31, and T32 parametrizations reproduce best the experimental properties, especially the neutron shell effects at N = 20, 28, and 32, and the recent experimental
$ S_{2n} $ value for 56Ca. Using the SLy5+T and T31 interactions, structural properties of nuclei near the neutron drip-line were predicted. It was found that the neutron giant halo for isotopes with N > 50 is suppressed by the tensor force. However, the neutron drip-line is reached before the halo structure starts to develop. Thus, the neutron giant halo structure does not exist in the very neutron-rich Ca isotopes. However, depleted central densities in these nuclei were found, which are determined by the shape of the bottom of the mean-potential. Finally, it is necessary to point out that only mixed pairing was used in this work. Relevant studies suggest that the properties of neutron-rich nuclei are strongly dependent on the pairing form [93, 94]. It would be interesting to predict the structure of neutron-rich Ca isotopes with surface and volume pairings in the framework of the SHFB approach with tensor force, which is a work in progress.We thank professors Shangui Zhou, Ramon Wyss, Roberto Liotta, and Fengshou Zhang for helpful discussions.
Tensor force effect on the exotic structure of neutron-rich Ca isotopes
- Received Date: 2019-02-28
- Accepted Date: 2019-08-10
- Available Online: 2019-11-01
Abstract: The structure of neutron-rich Ca isotopes is studied in the spherical Skyrme-Hartree-Fock-Bogoliubov (SHFB) approach with SLy5, SLy5+T, and 36 sets of TIJ parametrizations. The calculated results are compared with the available experimental data for the average binding energies, two-neutron separation energies and charge radii. It is found that the SLy5+T, T31, and T32 parametrizations reproduce best the experimental properties, especially the neutron shell effects at N = 20, 28 and 32, and the recently measured two-neutron separation energy of 56Ca. The calculations with the SLy5+T and T31 parametrizations are extended to isotopes near the neutron drip line. The neutron giant halo structure in the very neutron-rich Ca isotopes is not seen with these two interactions. However, depleted neutron central densities are found in these nuclei. By analyzing the neutron mean-potential, the reason for the bubble-like structure formation is given.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: