-
As it does not release greenhouse gases and chemical pollutants, nuclear energy is one of the low-carbon power sources that can overcome the shortage of energy and solve the environmental problems in the world [1, 2]. However, nuclear energy still faces some challenges. One of them is the highly radioactive long-lived nuclear waste generated during power production [3]. At present, most of the nuclear waste is first kept under surveillance in storage facilities, and subsequently stored permanently in deep underground storage. Due to the risk of leaks and proliferation in biosphere of nuclear waste [4], a new concept of transmutation based on the accelerator driven systems (ADS) has been introduced for disposal of the long-lived nuclear waste. The idea of ADS was first mentioned in the early 1950s [5]. Since 1980s, several countries have started research projects in ADS, including France, Japan, USA, and some other European countries [6], but there has been no successfully constructed ADS in any country yet [7]. In China, the research in ADS began in 1990s [8, 9]. In 2010, the ADS research project was started by the Chinese Academy of Sciences, and the project China initiative Accelerator Driven System (CiADS) was approved in 2015. Its goal is to build a megawatt grade ADS demonstration facility in Huizhou, Guangdong [10–18].
ADS consists of three sub-systems: proton accelerator, spallation target and sub-critical reactor [19–22]. As the accelerator and the reactor are coupled by the spallation target, the spallation reaction plays an important role in ADS [23–25]. The cross-section data for different target nuclei in a spallation reaction are required for the construction of ADS. However, each set of experimental data is limited and can only be used to verify part of the spallation reaction mechanism owing to the large projectile energy range, the broad target nucleus spectrum and the quantity of output results. It is impossible to cover every type of spallation reaction using only one code. Furthermore, proton and deuteron-induced spallation reactions are considered as promising mechanisms for transmutation of the long-lived fission products (LLFPs) [26]. However, the experimental cross-section data for deuteron-induced spallation of LLFPs are quite rare. The cross-sections of the spallation reactions of
$ ^{90} {\rm Sr}$ and$ ^{137} {\rm Cs}$ induced by deuterons at 185 MeV/nucleon were measured in Japan [27]. For projectile energies greater than 200 MeV/nucleon, there are no experimental data. Hence, the development of spallation models is necessary [28].Several dynamical models based on a microscopic approach have been developed to simulate the out-of-equilibrium process of spallation. Two examples are the Boltzmann-Uehling-Uhlenbeck models [29, 30], and the quantum molecular dynamics models [31–33]. To describe the decay process of spallation, principally evaporation or fission, several statistical models have been developed based on the Weisskopf [34] or Hauser-Feshbach [35] formalisms, such as ABLA [36], GEM [37], GEMINI [38], and SMM [39]. A decade ago, the International Atomic Energy Agency (IAEA) has organized an international benchmark of different spallation models in the world [40]. An effort was made to collect the data and estimate the prediction capacities of these models [28]. The codes in the IAEA benchmark are based on a two-step process, where the excitation stage of the spallation reaction uses dynamical models, and the de-excitation stage is based on the statistical models [40]. The two-step process has been successful in modeling nuclear spallation. However, there are still some observables, such as the production of the intermediate mass fragments (IMFs), where the discrepancy between the results of the models and the experimental data highlight the necessity for further improvement of the existing models. In our previous work, by increasing the dynamics evolution time, a two-step model was developed [41, 42]. In order to improve the description of IMFs, the phase space density constraint was considered, and the dynamical simulation is performed until the excitation energy of hot fragments is below the threshold energy for multi-fragmentation.
In this paper, we predict the cross-sections of isotopes produced in deuteron-induced spallation of LLFPs in the GeV/nucleon energy region in the framework of isospin dependent quantum molecular dynamics (IQMD) model [43, 44] followed by the GEMINI code [45]. The version of the IQMD model is IQMD-BNU, which was introduced and compared with the other versions in the transport code comparison project [46]. The paper is organized as follows. In Sec. 2, the method is introduced. In Sec. 3, the results are presented. In Sec. 4, a summary is given.
-
In the IQMD model, each nucleon is described by the wave function in the form of a Gaussian wave packet. To describe the N-body system, the total wave function is the direct product of these Gaussian wave packets. Applying the Wigner transformation of the quantum wave function, the N-body phase-space density is given by the Hamiltonian, which consists of three terms,
$ H = T + U_{\rm Coul} + \int V [\rho ({ r})] {\rm d}{{r}}, $

(1) where T is the kinetic energy and
$ {U}_{\rm Coul} $ is the Coulomb potential energy. The third term is the nuclear potential energy density of the asymmetric nuclear matter with density ρ and asymmetry δ$ V(\rho, \delta) = \frac{\alpha}{2} \frac{\rho^2}{\rho_0} + \frac{\beta}{\gamma+1} \frac{\rho^{\gamma+1}}{\rho_0^{\gamma}} + \frac{C_{sp}}{2}(\frac{\rho}{\rho_{0}})^{\gamma_{i}} \rho \delta ^{2} +\frac{g_{s}}{2\rho_0}[\nabla \rho({ r})]^{2}, $

(2) where
$ \rho_0 $ is the normal density. The parameters used in this paper are$ \alpha = -356.00 \;{\rm MeV} $ ,$ \beta = 303.00 \;{\rm MeV}$ ,$ \gamma = 7/6$ ,$ C_{sp} $ = 38.06 MeV, and$ \gamma_{i} $ = 0.75,$ g_{s} $ = 120.00 MeV/fm2.The time evolution of nucleons in the generated mean-field is governed by Hamilton's equations of motion,
$ \begin{array}{l} \dot{{{r}}}_{i} = \nabla_{{{p}}_{i}} H , \\ \dot{{{p}}}_{i} = -\nabla_{{{r}}_{i}} H . \end{array} $

(3) In addition, the nucleon-nucleon (NN) collisions are included in the IQMD code to simulate the short-range residual interaction. The differential cross-section of the NN collision is the product of three parameters,
$ \left( \frac{{\rm d} \sigma}{{\rm d} \Omega} \right)_{i} = \sigma _{i}^{\rm free} f_{i}^{\rm angl} f _{i}^{ \rm med}, $

(4) where
$ \sigma^{\rm free} $ is the cross-section of the NN collision in free space,$ f^{\rm angl} $ refers to the angular distribution, and$ f^{\rm med} $ is the in-medium factor. The parametrization used above of the cross-section$ \sigma^{\rm free} $ and the angular distribution$ f^{\rm angl} $ are taken from Ref. [47]. The in-medium factor$ f^{\rm med} $ is from Ref. [48]. The subscript i represents different channels of the NN collision: i = pp represents elastic proton-proton scattering, i = nn elastic neutron-neutron scattering, i = np elastic neutron-proton scattering, and i = in inelastic NN collision.In order to include the fermionic nature of the N-body system, the method of phase space density constraint and the Pauli blocking, which were introduced in the constrained molecular dynamics (CoMD) model proposed by M. Papa et al. [49], are applied in the IQMD model. According to the phase space density constraint, the integration is performed on a hypercube of volume
$ h^{3} $ in the phase space, centered around the i-th nucleon, and the phase space occupancy probability is calculated as,$ \overline{f}_{i} = \sum\limits_{n} \delta _{\tau_{n},\tau_{i}} \delta _{s_{n},s_{i}} \int _{h^{3}} \frac{1}{\pi ^{3} \hbar ^{3}} {\rm e}^{ -\frac{({ r}-{ r}_{n})^{2}}{2L} -\frac{({ p}-{ p}_{n})^{2}L}{\hbar ^{2}} } {\rm d}^{3}r{\rm d}^{3}p. $

(5) At each time step, the phase space occupancy probability of each nucleon is calculated. The parameter
$ k_{\rm fcon} $ in the IQMD model is used to estimate the phase space occupancy probability. If$ f_{i} > k_{\rm fcon} $ , the many-body elastic scattering is carried out for the i-th nucleon. Moreover,$ f_{i} $ is calculated for each NN collision. By taking into account the Pauli blocking, only those NN collisions with$ f_{i} $ < 1.0 in the final state are accepted. We choose$ k_{\rm fcon} $ = 1.15. -
The two-step process in the IAEA benchmark includes the dynamical code, and the statistical code. The dynamical code is used to model the excitation stage of the target nucleus impacted by the incident particle. The emission of heavy fragments and light particles is then simulated by the statistical code. In this work, the model used is different: the decay process of the excited nucleus is included in the IQMD code, so that the dynamical evolution calculated by the IQMD code is longer than in the IAEA benchmark. A parameter
$ { E}_{\rm stop} $ is used in the IQMD code to extend the dynamical description of a spallation reaction. After the excitation stage, the simulation in the IQMD code continues until the excitation energy of the heaviest hot fragments of the target nucleus is below the model parameter$ {E}_{\rm stop} $ , when the statistical code GEMINI is turned on. The smaller the value of${ E} _{\rm stop} $ , the longer is the simulation by the IQMD code. In this work,$ { E}_{\rm stop} $ = 2 MeV/nucleon. The output of the IQMD code, which is the charge, mass number and the excitation energy of each hot fragment, is the input for GEMINI. By using the Monte Carlo method [42], the GEMINI code simulates the sequential decay of hot fragments, including the light-particle evaporation and symmetric fission. The simulation continues until the excitation energy of the hot fragments reaches zero. The partial decay width from the Hauser-Feshbach formalism, is given by,$\begin{split} \Gamma_{J_{2}}(Z_{1}, A_{1}, Z_{2}, A_{2}) =& \frac{2J_{1}+1}{2\pi \rho_{0}} \sum\limits_{l = |J_{0}-J_{2}|}^{J_{0}+J_{2}} \int_{0}^{E^{*}-B-E_{\rm rot}} T_{l}(\varepsilon) \rho_{2}\\&\times(E^{*}-B-E_{\rm rot}-\varepsilon, J_{2}) {\rm d}\varepsilon, \end{split}$

(6) where
${ Z} _{i} $ ,$ { A}_{i} $ ,$ { J}_{i} $ and$ \rho{_i} $ are the charge, mass number, spin and level density. The subscript i takes the value of 0 for the initial fragment, 1 for the emitted light particle, and 2 for the residual fragments. E*,$ { E}_{\rm rot} $ , B and ε refer to the excitation energy, rotational energy of the ground-state configuration, separation energy and kinetic energy. The separation energy B is calculated from the nuclear masses, where the tabulated masses are employed [50, 51]. -
Transmutation of LLFPs in nuclear waste by spallation has attracted attention for minimizing radioactive hazard of nuclear waste. However, there is a lack of experimental cross-section data for LLFPs, especially for reactions induced by deuterons at energies greater than 200 MeV/nucleon. Therefore, the above model is applied to predict the cross-sections of LLFPs produced in deuteron-induced spallation reactions.
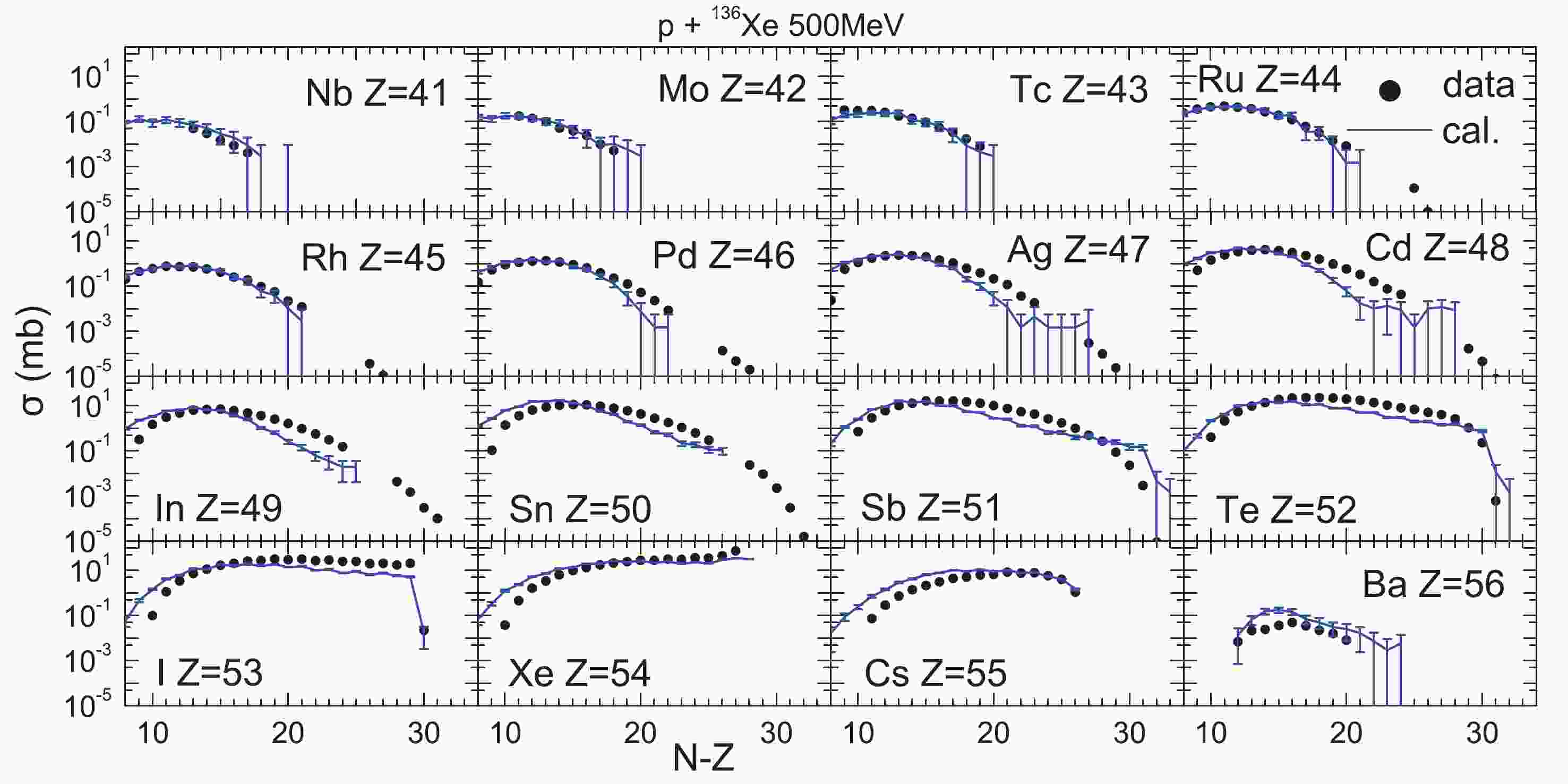
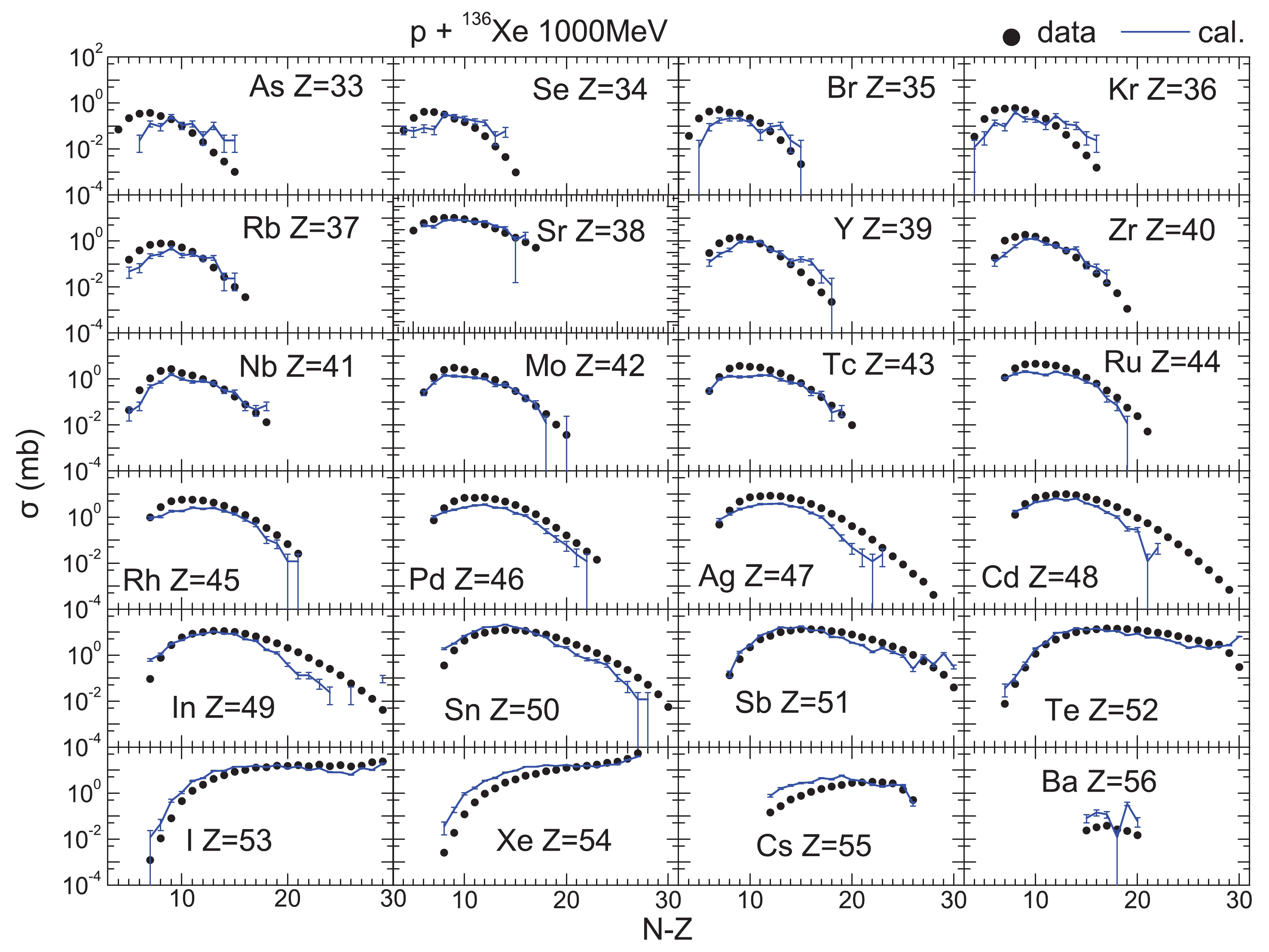
Before simulating deuteron-induced spallation reactions, the reliability of the simulations needs to be verified. Figs. 1 and 2 show the cross-sections of isotopes produced in the spallation reactions
$ ^{136} {\rm Xe}$ + p at 500 and 1000 MeV/nucleon. The elements are from Nb to Ba for 500 MeV/nucleon, and from As to Ba for 1000 MeV/nucleon. The solid circles in the figures refer to the experimental data and the blue curves to the simulations. The figures show that the simulations agree with the experimental data. The discrepancies mainly appear on both sides of the peaks, where the cross-sections are small. In the zone around the peaks, the cross-sections are more significant, and the simulations agree quite well with the data. Hence, in the case of calculations of transmutation, the discrepancies have only a small influence on the results, and the calculations by the model can be considered as reliable.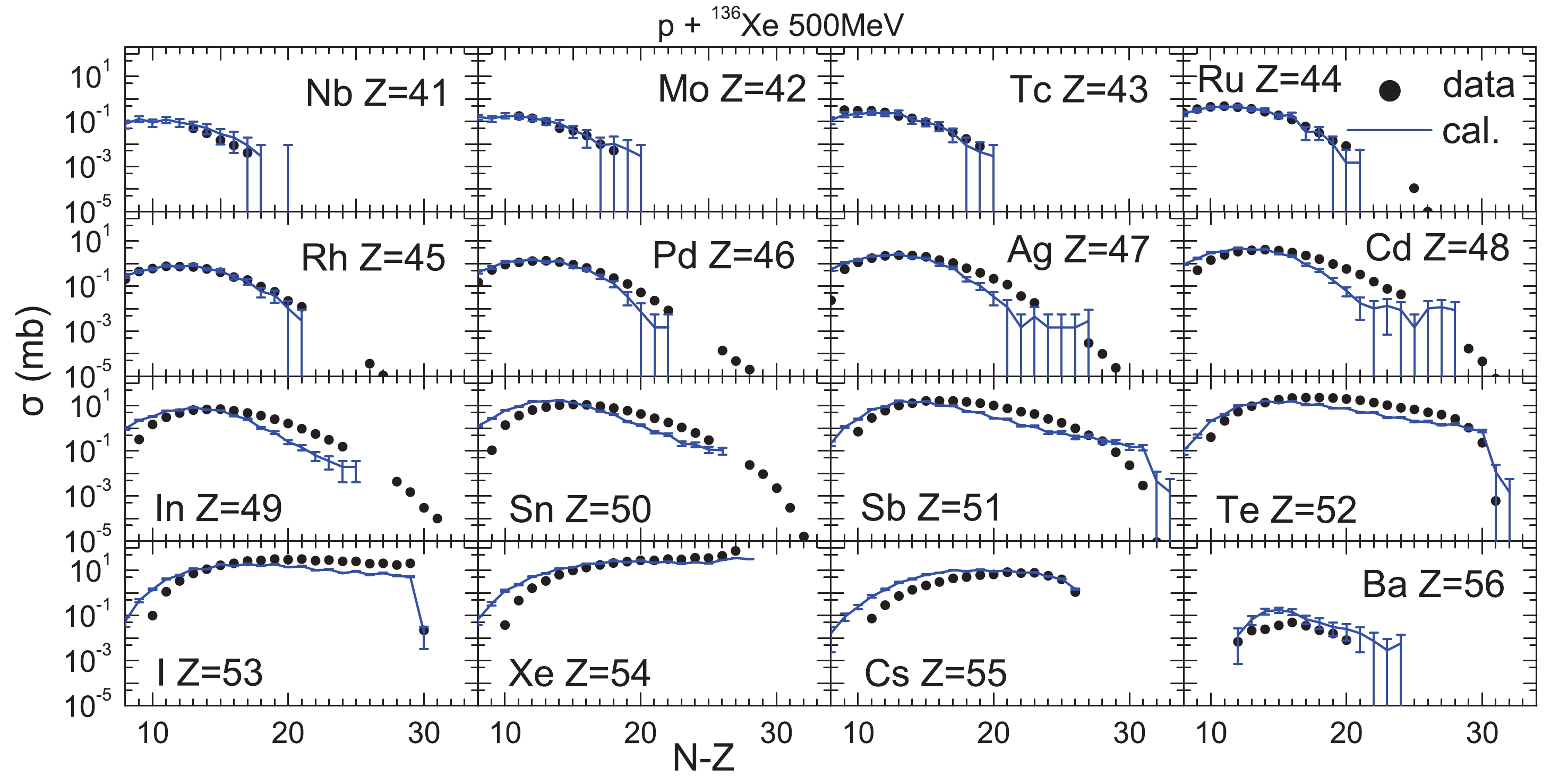
Figure 1. (color online) Isotope distribution of cross-sections for the residual nuclei (Z from 33 to 56) produced in 136Xe + p at 500 MeV/nucleon. The experimental data, shown as solid circles, are taken from Ref. [52].
After verifying the performance of the model, the deuteron-induced spallation reactions of four LLFPs,
$ ^{90} {\rm Sr}$ ,$ ^{93} {\rm Zr}$ ,$ ^{107} {\rm Pd}$ and$ ^{137} {\rm Cs}$ , at 200, 500 and 1000 MeV/nucleon were simulated. As an example, the predictions of the cross-sections of isotopes produced in$ ^{2} {\rm H}$ +$ ^{137} {\rm Cs}$ are shown in Fig. 3. The black circles in the figure correspond to the spallation reaction at 200 MeV/nucleon, the blue squares at 500 MeV/nucleon, and the red triangles at 1000 MeV/nucleon. The cross-sections display a peak near the stable isotope, except for Z > 53. For the elements near the target nucleus, there is another peak near A = 137. For the elements from Se to In, the cross-sections increase with increasing projectile energy. However, the energy dependence becomes weak as the atomic number of the element increases. The calculations overlap for elements from Sn to Ba. During transmutation of LLFPs, large production of noble gases may be harmful for ADS. When noble gases contain long-lived nuclei, there is a risk of radioactive leaks. The cross-sections predicted for the noble gas Kr have a maximum around 10 mb. The predictions suggest that the minima of the cross-sections for spallation of$ ^{90} {\rm Sr}$ ,$ ^{93} {\rm Zr}$ is at 1000 MeV/nucleon, and of$ ^{107} {\rm Pd}$ ,$ ^{137} {\rm Cs}$ at 200 MeV/nucleon. Hence, in order to reduce the production of long-lived nuclei$ ^{81} {\rm Kr}$ and$ ^{85} {\rm Kr}$ , the projectile energy should be as high as possible for$ ^{90} {\rm Sr}$ +$ ^{2} {\rm H}$ and$ ^{93} {\rm Zr}$ +$ ^{2} {\rm H}$ , and as low as possible for$ ^{107} {\rm Pd}$ +$ ^{2} {\rm H}$ and$ ^{137} {\rm Cs}$ +$ ^{2} {\rm H}$ .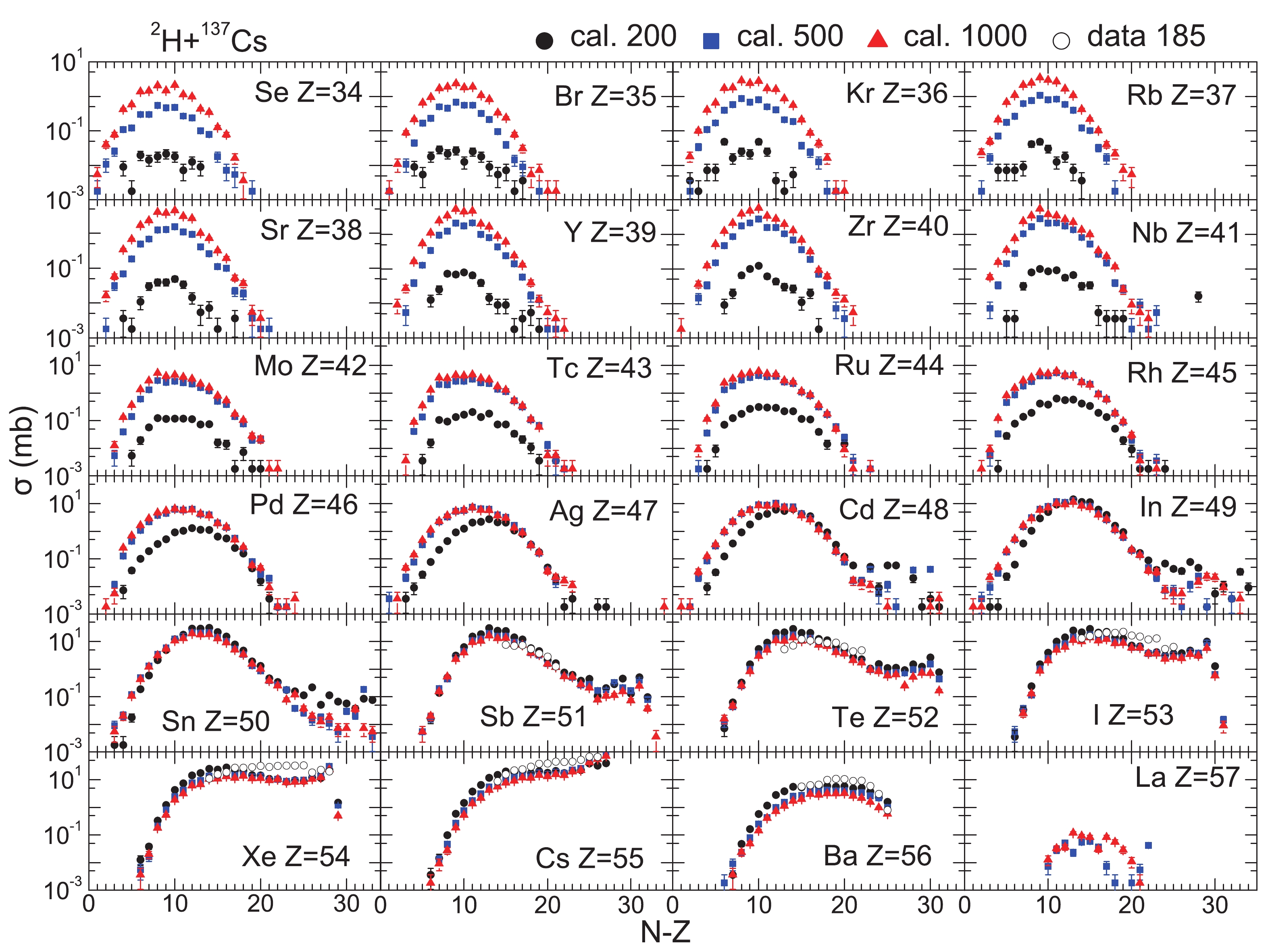
Figure 3. (color online) Isotope distribution of cross-sections for the residual nuclei (Z from 34 to 57) produced in 137Cs + 2H spallation at 200, 500 and 1000 MeV/nucleon. The data for 185 MeV/nucleon are also shown.
The transmutation of LLFPs with ADS aims at burning the long-lived radioactive nuclei by producing short-lived nuclei using the spallation reaction. However, the spallation reaction can also produce long-lived nuclei, reducing the efficiency of transmutation. Hence, production of long-lived nuclei in a spallation reaction should also be considered. The cross-sections of the long-lived nuclei in deuteron-induced spallation are presented in Table 1. For the long-lived nuclei
$ ^{41} {\rm Ca}$ to$ ^{63} {\rm Ni}$ , produced in$ ^{90} {\rm Sr}$ +$ ^{2} {\rm H}$ and$ ^{93} {\rm Zr}$ +$ ^{2} {\rm H}$ at 200 Mev/nucleon, the cross-sections increase as the projectile energy increases. The production of long-lived nuclei from$ ^{79} {\rm Se}$ to$ ^{93} {\rm Mo}$ is inversely proportional to the projectile energy in these two spallation reactions. As the projectile energy in the spallation$ ^{107} {\rm Pd}$ +$ ^{2} {\rm H}$ increases, the production of long-lived nuclei from$ ^{53} {\rm Mn}$ to$ ^{81} {\rm Kr}$ increases, and from$ ^{85} {\rm Kr}$ to$ ^{101} {\rm Rh}$ decreases. For$ ^{137} {\rm Cs}$ +$ ^{2} {\rm H}$ , the cross-sections of long-lived nuclei from$ ^{60} {\rm Co}$ to$ ^{107} {\rm Pd}$ and from$ ^{126} {\rm Sn}$ to$ ^{133} {\rm Ba}$ are respectively directly and inversely proportional to the projectile energy. Globally, when the projectile energy increases, the cross-sections of long-lived nuclei in the above spallation reactions first increase until a certain nucleus, and then decrease.137Cs 107Pd 93Zr 90Sr 200 500 1000 200 500 1000 200 500 1000 200 500 1000 53Mn 0.09 0.56 2.06 0.32 1.86 4.26 0.40 2.09 4.80 55Fe 0.11 0.66 2.17 0.38 2.08 4.58 0.55 2.61 5.18 60Fe 0.02 0.19 0.61 0.10 0.58 1.02 0.24 1.01 1.51 60Co 0.01 0.15 0.61 0.10 0.61 1.80 0.46 2.18 3.70 0.93 3.30 4.62 59Ni 0.01 0.12 0.48 0.12 1.04 3.17 0.83 3.69 6.52 1.29 4.53 6.73 63 Ni 0.02 0.21 0.77 0.10 0.80 2.08 0.81 2.72 4.13 2.06 4.32 5.52 79Se 0.00 0.29 1.10 0.34 0.84 0.99 1.18 0.80 0.81 2.72 2.08 1.98 81Kr 0.01 0.68 2.30 3.62 5.40 5.47 12.66 8.70 7.65 17.08 13.24 11.73 85Kr 0.01 0.24 0.76 0.14 0.09 0.11 0.58 0.48 0.42 3.95 3.64 3.39 90Sr 0.00 0.30 0.66 0.03 0.02 0.02 2.47 2.37 2.17 93Zr 0.05 1.07 1.78 0.35 0.26 0.26 92Nb 0.09 1.91 3.66 6.26 4.13 3.94 1.50 1.19 0.63 94Nb 0.09 1.59 2.63 1.14 0.96 0.84 93Mo 0.14 2.37 4.10 14.86 9.80 8.35 97Tc 0.20 3.23 4.60 6.13 5.16 4.43 98Tc 0.16 2.43 3.40 3.12 2.76 2.41 99Tc 0.19 2.30 3.03 2.52 2.01 1.93 101Rh 0.58 5.35 6.19 13.55 13.22 11.65 107Pd 0.64 1.85 1.86 126Sn 0.12 0.06 0.03 125Sb 0.58 0.51 0.47 129I 4.19 4.07 3.89 134Cs 15.65 18.74 16.52 135Cs 22.37 32.44 28.98 133Ba 4.91 3.41 2.30 Table 1. Cross-sections (µb) of the long-lived nuclei in deuteron-induced spallation at 200, 500, and 1000 MeV/nucleon.
Figure 4 shows the cross-sections of the long-lived and short-lived nuclei produced in the transmutation of
$ ^{137} {\rm Cs}$ predicted by the model. The results are compared to the calculated cross-sections from TENDL-2015 [55] and the experimental data for$ ^{136} {\rm Xe}$ . The spallation reaction is induced by protons. The open circles refer to the data for$ ^{136} {\rm Xe}$ , the solid squares to the calculations of our model, and the lines to TENDL-2015. The red color corresponds to the long-lived and the black color to the short-lived nuclei. The cross-sections obtained by TENDL-2015 are only for projectile energies less than 200 MeV/nucleon. Our model gives cross-sections from 50 to 1000 MeV/nucleon. The results of our model agree much better with the experimental data than TENDL-2015. Thus, the model is suitable for predicting the cross-sections of LLFPs produced in transmutation due to the wider range of projectile energies and higher accuracy.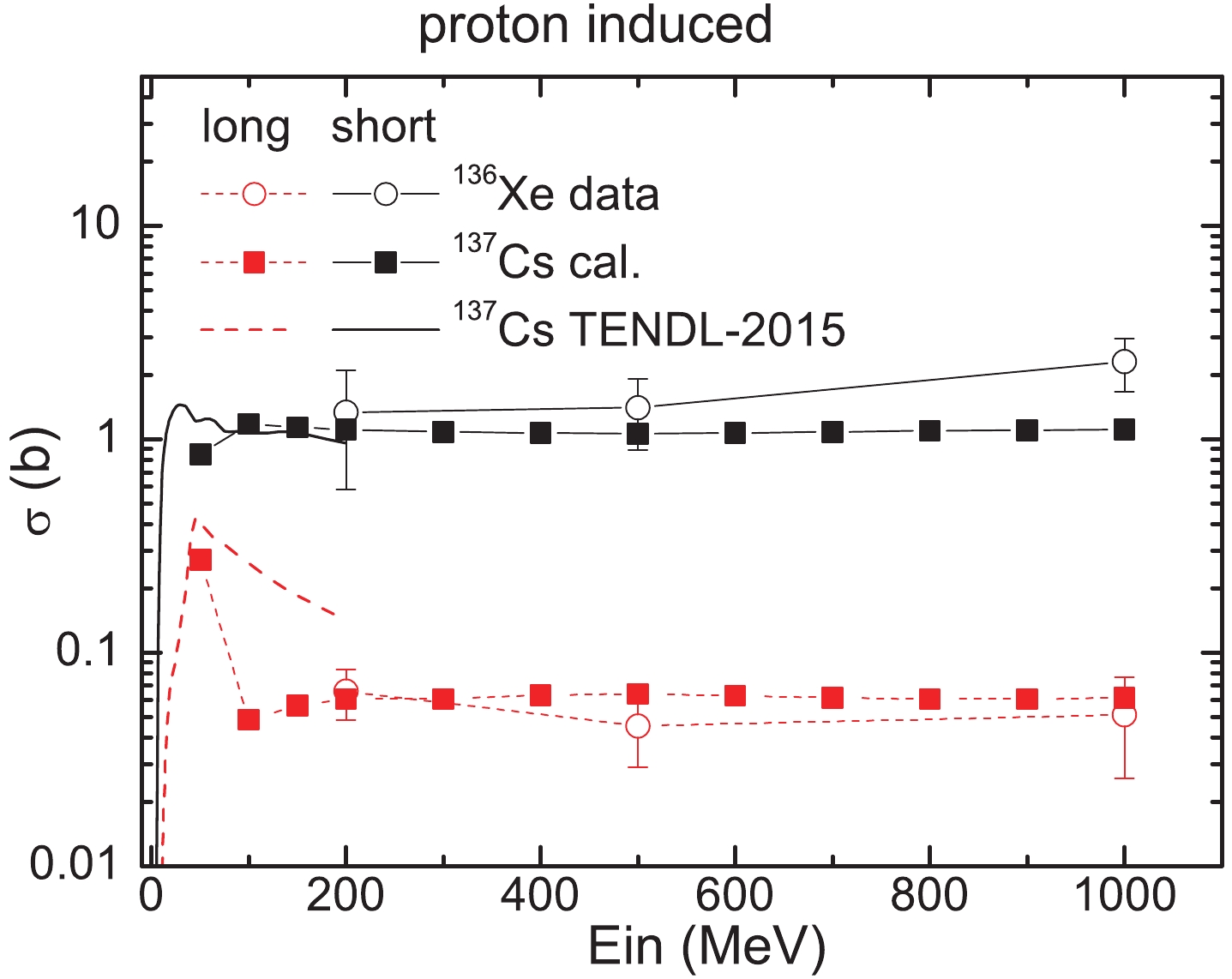
Figure 4. (color online) Cross-sections of the long-lived and short-lived nuclei produced in proton-induced spallation as a function of projectile energy. The experimental data for the target nucleus 136Xe are taken from Refs. [52-54]. The calculated cross-sections of the target nucleus 137Cs are from the IQMD+GEMINI model and TENDL-2015 [55].
The cross-sections of the long-lived and short-lived nuclei produced in deuteron-induced spallation reactions given by the model and TENDL-2015 are shown in Fig. 5. The total number of produced nuclei are shown as function of the projectile energy for the reactions
$ ^{90} {\rm Sr}$ +$ ^{2} {\rm H}$ ,$ ^{93} {\rm Zr}$ +$ ^{2} {\rm H}$ ,$ ^{107} {\rm Pd}$ +$ ^{2} {\rm H}$ and$ ^{137} {\rm Cs}$ +$ ^{2} {\rm H}$ . The results obtained by TENDL-2015 are for projectile energies less than 200 MeV/nucleon, while the results of our model are for the range 200 to 1000 MeV/nucleon. The cross-sections predicted by the model show that the production of long-lived nuclei is one to two orders of magnitude lower than of short-lived nuclei. These results indicate that the transmutation of LLFPs by deuterons has sufficient efficiency for applications. Moreover, the cross-sections of long-lived nuclei produced in these spallation reactions increase with projectile energy. Thus, a lower projectile energy is suggested for transmutation of LLFPs with the purpose of reducing the production of long-lived nuclei.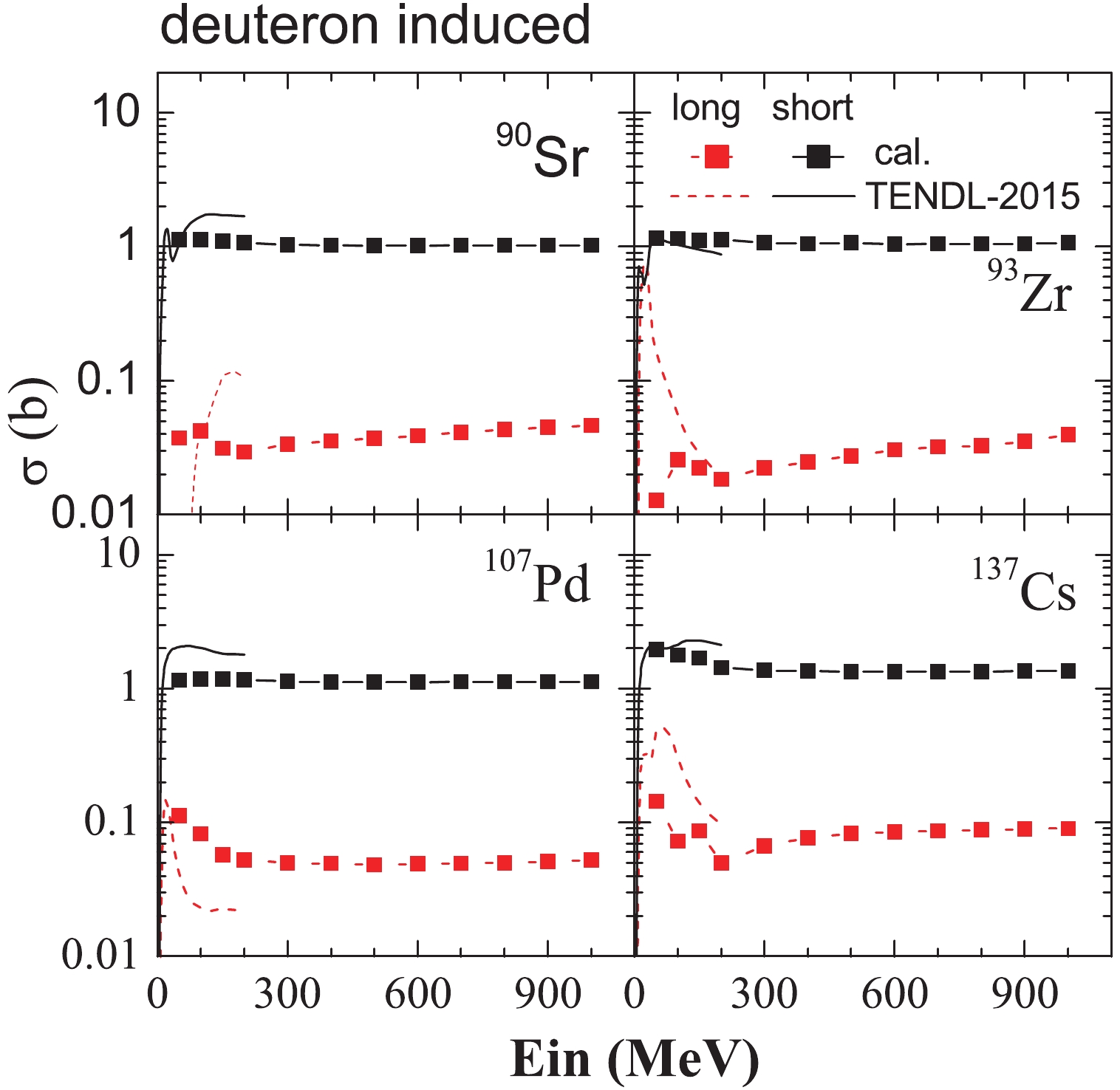
Figure 5. (color online) Cross-sections of long-lived and short-lived nuclei as a function of projectile energy. The spallation reactions are 90Sr + 2H, 93Zr + 2H, 107Pd + 2H, and 137Cs + 2H.
Figure 6 shows the probability distribution of the energy released in the spallation reactions of four LLFPs,
$ ^{90} {\rm Sr}$ ,$ ^{93} {\rm Zr}$ ,$ ^{107} {\rm Pd}$ , and$ ^{137} {\rm Cs}$ , for projectile energies of 200, 500 and 1000 MeV/nucleon. The black circles correspond to the projectile energy of 200 MeV/nucleon, the blue squares to 500 MeV/nucleon, and the red triangles to 1000 MeV/nucleon. The simulations are given by the IQMD+GEMINI model, and are important for determining the temperature field inside ADS. The energies released presented in the figure are all with a negative sign, which indicates that these spallation reactions are endothermic. The probability distribution curves of the four spallation reactions have the same bow shape for the three projectile energies. They all reach their peaks at the absorbed energy of around 100 MeV. Around the peak, the probability of spallation is inversely proportional to the projectile energy. However, when the absorbed energy is greater than 180 MeV, or less than 40 MeV, the probability increases with projectile energy. In general, the area under the probability curve increases with projectile energy, meaning that the energy absorbed in the spallation reaction is higher for a higher projectile energy. Considering the generating efficiency of ADS, a lower projectile energy is recommended. -
Transmutation of long-lived fission products in nuclear waste and the development of accelerator driven systems require a large amount of data for cross-sections of spallation reactions. The isospin dependent quantum molecular dynamics model was applied to study the cross-sections of spallation reactions. The predictions of the model were verified for the spallation reactions
$ ^{136} {\rm Xe}$ + p at 500 and 1000 MeV/nucleon, and$ ^{137} {\rm Cs}$ +$ ^{2} {\rm H}$ at 185 MeV/nucleon. The model was then applied to the transmutation of four LLFPs,$ ^{90} {\rm Sr}$ ,$ ^{93} {\rm Zr}$ ,$ ^{107} {\rm Pd}$ and$ ^{137} {\rm Cs}$ , induced by deuterons. The projectile energy was between 200 and 1000 MeV/nucleon. The predicted cross-sections of isotopes produced in spallation reactions were presented. The results allow to fill in the blank regions in the experimental data, and give some recommendations for the practical cases. For example, to reduce the production of radioactive noble gas Kr, higher projectile energy in$ ^{90} {\rm Sr}$ + d,$ ^{93} {\rm Zr}$ + d , and lower projectile energy in$ ^{107} {\rm Pd}$ +$ ^{2} {\rm H}$ ,$ ^{137} {\rm Cs}$ +$ ^{2} {\rm H}$ , are suggested. A comparison of the production of long-lived and short-lived nuclei and the energy released in spallation reactions were also discussed. The production of long-lived nuclei was related to the efficiency of transmutation of LLFPs. The cross-sections of the long-lived nuclei are predicted to be one to two orders of magnitude lower than of the short-lived nuclei. Thus, transmutation of LLFPs could be considerable. The obtained probability of energy released contributes to the calculation of the temperature field inside ADS. The predictions show that the most probable energy absorbed in the four spallation reactions is around 100 MeV, and that the energy absorbed in a spallation reaction is higher for a higher projectile energy. Hence, a lower projectile energy is recommended to increase the generating efficiency of ADS.
Prediction of the cross-sections of isotopes produced in deuteron-induced spallation of long-lived fission products
- Received Date: 2019-04-19
- Available Online: 2019-10-01
Abstract: The spallation cross-section data for the long-lived fission products (LLFPs) are scarce but required for the design of accelerator driven systems. In this paper, the isospin dependent quantum molecular dynamics model and the statistical code GEMINI are applied to simulate deuteron-induced spallation in the energy region of GeV/nucleon. By comparing the calculations with the experimental data, the applicability of the model is verified. The model is then applied to simulate the spallation of 90Sr, 93Zr, 107Pd, and 137Cs induced by deuterons at 200, 500 and 1000 MeV/nucleon. The cross-sections of isotopes, the cross-sections of long-lived nuclei, and the reaction energy are presented. Using the above observables, the feasibility of LLFP transmutation by spallation is discussed.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: