Role of magnetic fields on the outer crust in a magnetar

The origins of soft γ-ray repeaters and some anomalous x-ray pulsars are generally associated with a kind of special neutron stars, the so-called magnetars, which possess very strong magnetic fields (MF) of the order of 10$ ^{14} $$ - $10$ ^{15} $ G on the surface [1−6]. The accurate description of the crust of a magnetar is essential to understand some astrophysical phenomena involving magnetars, such as the oscillations [7−12] and cooling [13−15] in magnetars. In the present work, we will focus on the study on the outer crust in magnetars, where the fully ionized atoms are thought to be arranged in a Coulomb lattice embedded in a gas of degenerate electrons [16] and the high MF can have non-negligible influence on the composition and equation of state due to the Landau-Rabi quantization of electron motion [17−21]. Moreover, the MF with $ B\gtrsim10^{17} $ G may modify appreciably the nuclear structure due to the alteration of the size and even the ordering of energy levels [22−25]. The calculations about the outer crust in neutron stars are based on the method proposed by Baym, Pethick, and Sutherland [26], where the masses of nuclei act as input parameters. Until now, there are very few studies about the effects of the change of nuclear masses in the presence of MF on the outer crust [27]. It is mainly due to the fact that the surface fields of magnetars inferred from the current observations are up to a few times 10$ ^{15} $ G [3, 6] and $ 3.2 \times 10^{16} $ G from the latest work [28], and the fields with such order of magnitude play a small role in the nuclear masses. Nonetheless, considering the upper limit of the interior magnetic fields being the order of 10$ ^{18} $ G according to the virial theorem [17] and numerical simulations [29−34], it is still worth investigating the nuclear masses under the extreme high magnetic fields and the corresponding effects on the crustal properties in magnetars prior to possible astronomical observations.

For studying the properties of nuclei in the presence of magnetic fields, we use the publicly available Sky3D code based on the Skyrme density functional theory [35, 36] in the present work to solve the time-independent Hartree-Fock (HF) equations on a three-dimensional grid without further symmetry assumptions. This code has been used to study a wide range of problems, such as the nuclear structure, collective vibrational excitations and heavy-ion collisions.

This article is organized as follows. In Sec. 2, we describe the formulas for the present work. In Sec. 3, the calculated results and some discussions are given. Finally, the summary is present in Sec. 4.

The energy eigenvalue of an electron under MF presents the Landau-Rabi levels whose energies are given by

where c is the speed of light, $ m_e $ is the rest mass of the electron, $ p_z $ is the component of the momentum along the field, $ \nu=n+1/2+s/2=0,1,2,... $ with n being the principal quantum number and s the spin along the magnetic field axis with $ +1 $ for spin-up and $ -1 $ for spin-down cases. Note that $ \nu=0 $ corresponds to one single spin state while all $ \nu>0 $ states correspond to two spin states. Here $ B_{\star}=B/B_c $ is the magnetic field B measured in units of the critical field $ B_c $ defined as

at which the electronic cyclotron energy reaches the electron rest mass energy.

In the case of temperature $ T=0 $ K, the Fermi momenta of electrons $ k_{Fe} $ for different numbers of ν are related to the electronic chemical potential $ \mu_e $ in the magnetar's crust in equilibrium as $ \mu_e^2= c^2p_{Fe}(\nu)^2 + m_e^2c^4(1 + 2\nu B_{\star}) $. The requirement that $ p_{Fe}\geq 0 $ determines the maximum number of ν labeled as $ \nu_{max} $. Then the expression of the electron density under MF can be given by

where $ \lambda_e=\hbar/{m_e}c $ is the Compton wavelength, the degeneracy $ g_{\nu} $ is 1 for $ \nu=0 $ and 2 for $ \nu\geq 1 $ and the dimensionless Fermi momentum is defined by $ x_e(\nu)=p_{Fe}(\nu)/m_ec $. The electronic energy density and pressure are respectively given by

where $ {\psi _ \pm }(x) = x\sqrt {1 + {x^2}} \pm \ln (x + \sqrt {1 + {x^2}}) $. Also the results in the absence of the MF ($ B = 0 $ G) corresponding to Eqs. (4) and (5) are given in this work by

where $ x=\lambda_e(3\pi^2n_e)^{1/3} $.

For $ B=0 $ G case, the ions are believed to be arranged in a body-centered cubic lattice, the lattice energy per baryon is approximately given by [27]

where the baryonic Fermi momentum $ p_{F_b} $ is in MeV. The associated lattice pressure is $ P_l= \varepsilon_l/3 $. The total pressure is therefore $ P=P_e+P_l $. Following the arguments in Ref. [27], this work still use Eq. (8) to give the contribution of the lattice energy in the presence of magnetic fields.

The Gibbs free energy per nucleon can be written as [27]

where $ M(A,Z,B) $ is the mass of the nuclei with proton number Z and atomic number A, and is the function of B because we will consider the effects of the MF on nuclear masses in this work. Then the distribution of nuclei in the outer crust of neutron stars in equilibrium can be obtained by searching a series of nuclei for the minimum of these Gibbs free energies.

In this work, we follow the line of Ref. [25] where the Sky3D code is used to calculate the masses of nuclei under the MF. The effects of external MF are included by introducing the B-field-related hamilton operators $ \hat{H}_{p,n}^{(B)} $ into the original Hamiltonian in the Sky3D code, which are given by

where $ m_p $ and $ m_n $ are the proton and neutron masses, respectively, $ g_p=5.5856 $ and $ g_n=-3.8263 $ are the g-factors of a proton and neutron, and $ \vec L $ and $ \vec S $ are the orbital and spin angular momenta, respectively.

The following are some settings for the Sky3D code: we consider, in an isolated system, 24 grid points in each direction in three-dimensional Cartesian coordinates, with a distance of $ 1.0\ \text {fm} $ between each grid point. The force chosen in the type of Skyrme force is 'SLy6', which is mainly applied to neutron-rich nuclei and neutron matter in the field of astrophysics [37]. For the setting of the Newtonian gradient iteration method, the damping step is adjusted to $ x_0=0.4 $ and the damping adjustment parameter to $ E_0 = 100 $. The initial radii of the harmonic oscillator state are set to $ 3.1\ \text {fm} $. We begin the calculation in the absence of MF, which is used as the input values to obtain the results at $ B=10^{16} $ G. Then these results at $ B=10^{16} $ G are used for the higher MF and similar procedures are carried until $ B=10^{18} $ G. The maximum number of iterations are set to 1500 and the convergence criterion is that the energy fluctuation is less than $ 10^{-6}\ \text {MeV} $.

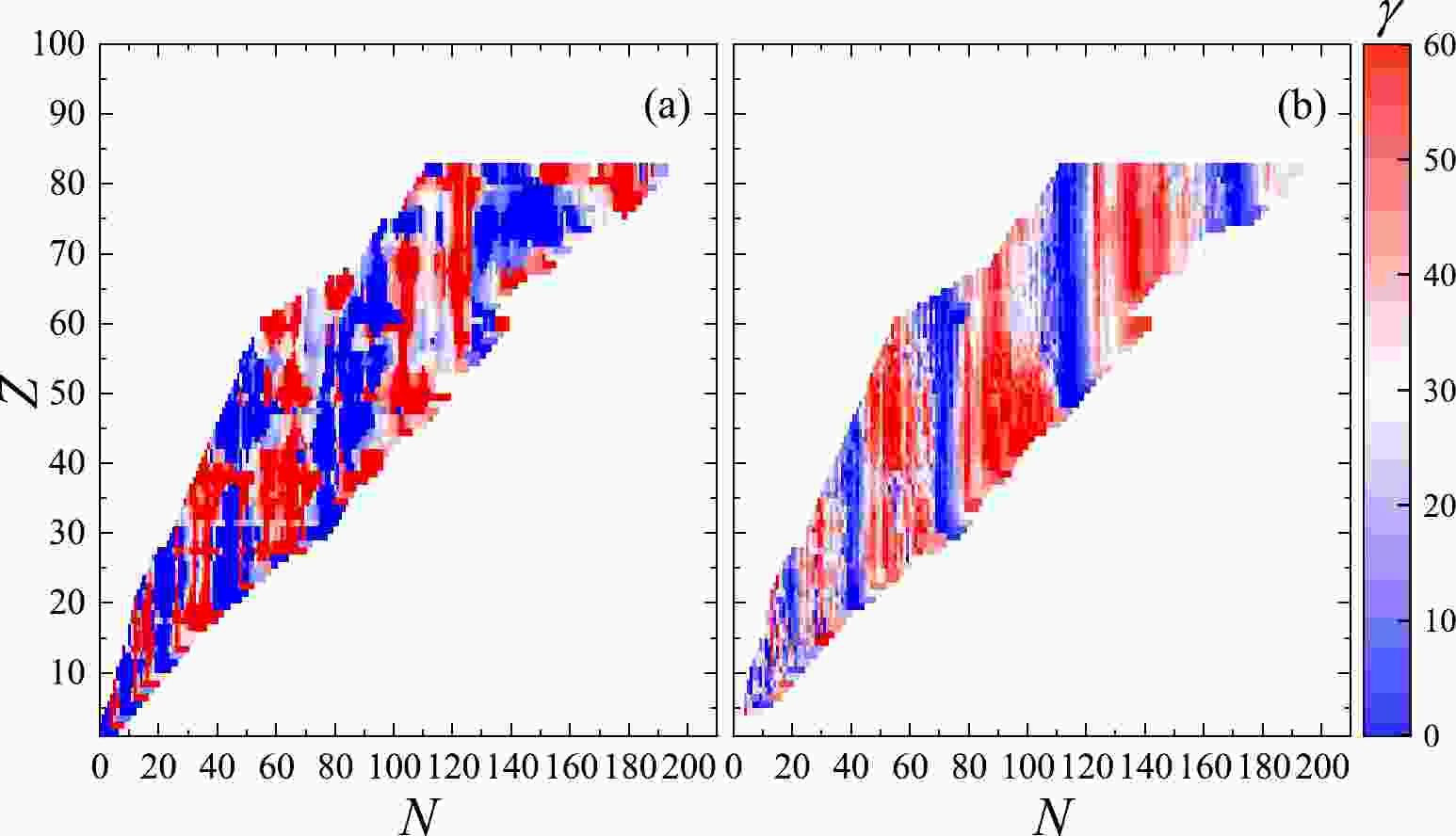
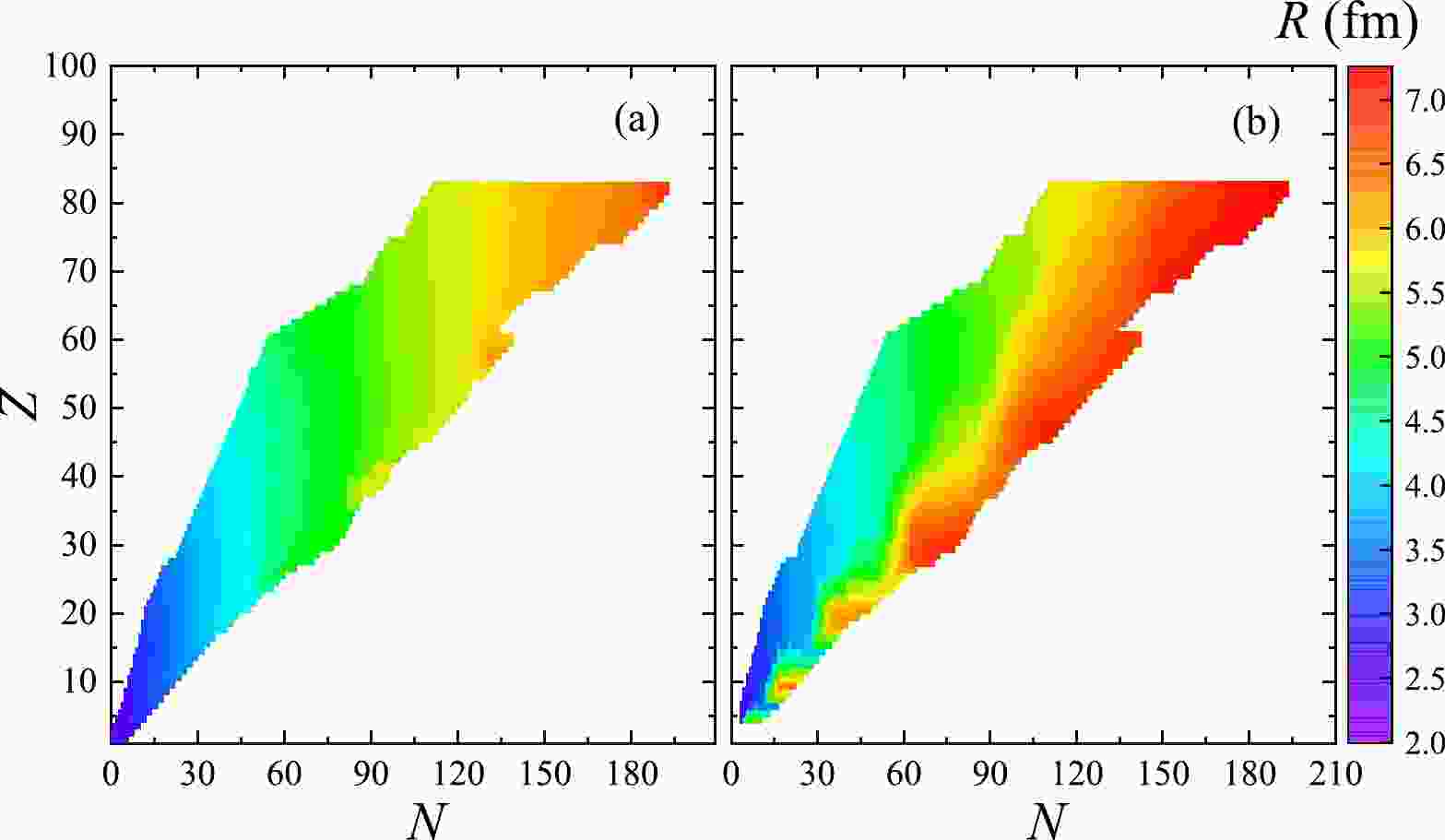
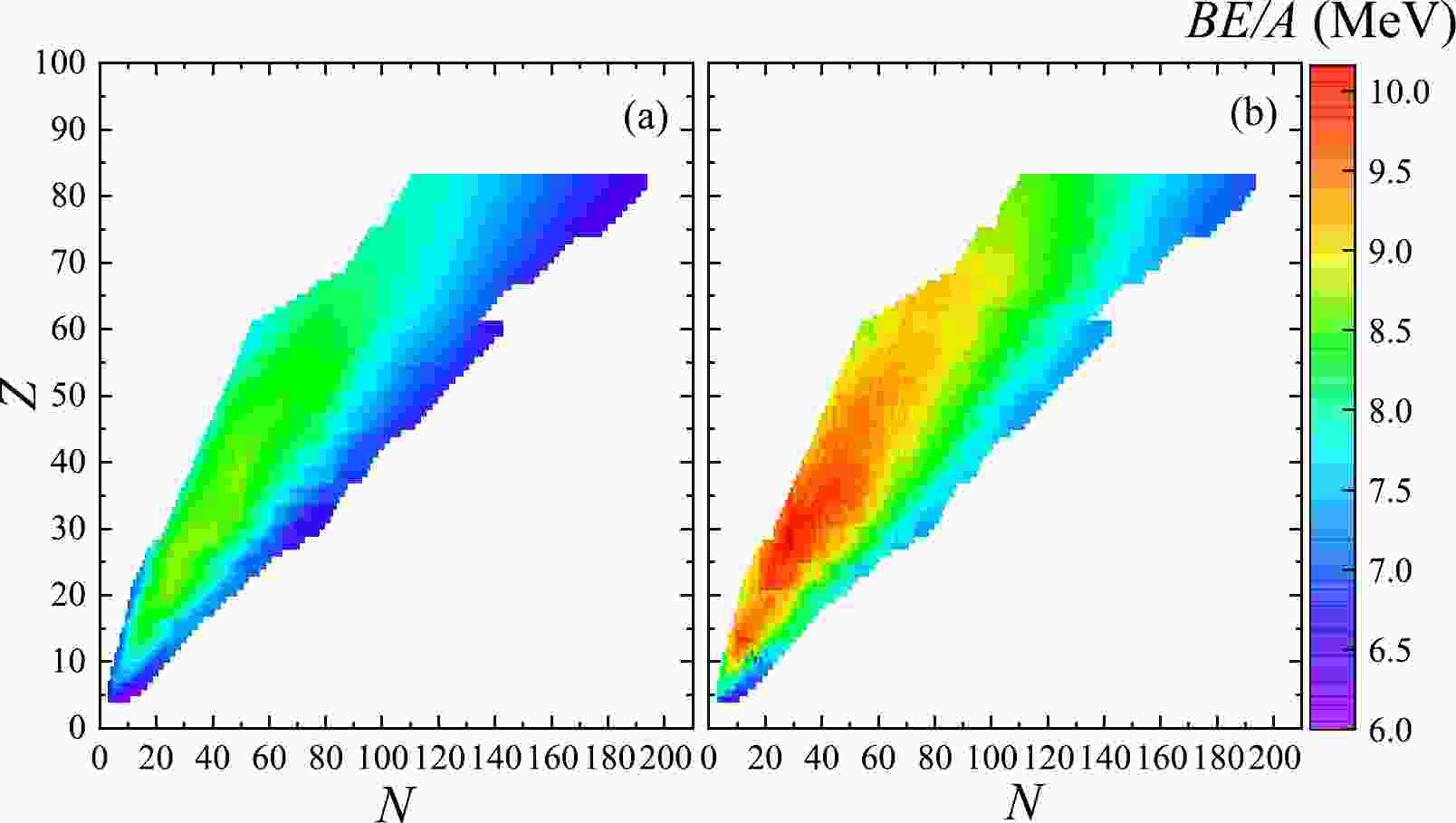
In Figs. 1-4, the calculations on 4110 nuclides from $ Z=5 $ to $ Z=82 $, ranging from neutron fraction 0.54 to 0.73, are made for the MF with $ B=0 $ G (left panels) and $ B=10^{18} $ G (right panels). Since the strong MF break the pairing in nuclei, these figures and the remainder of this work neglect the pairing energy in $ B\neq 0 $ G cases for simplicity. Comparing Fig. 1(a) and (b), we see that this super-strong MF increase the binding energies $BE$s of these nuclei by 8%$ \sim $15%. At $ B=10^{18} $ G, shown in Fig. 2, the root mean square radii R are seen to be larger than in the absence of MF.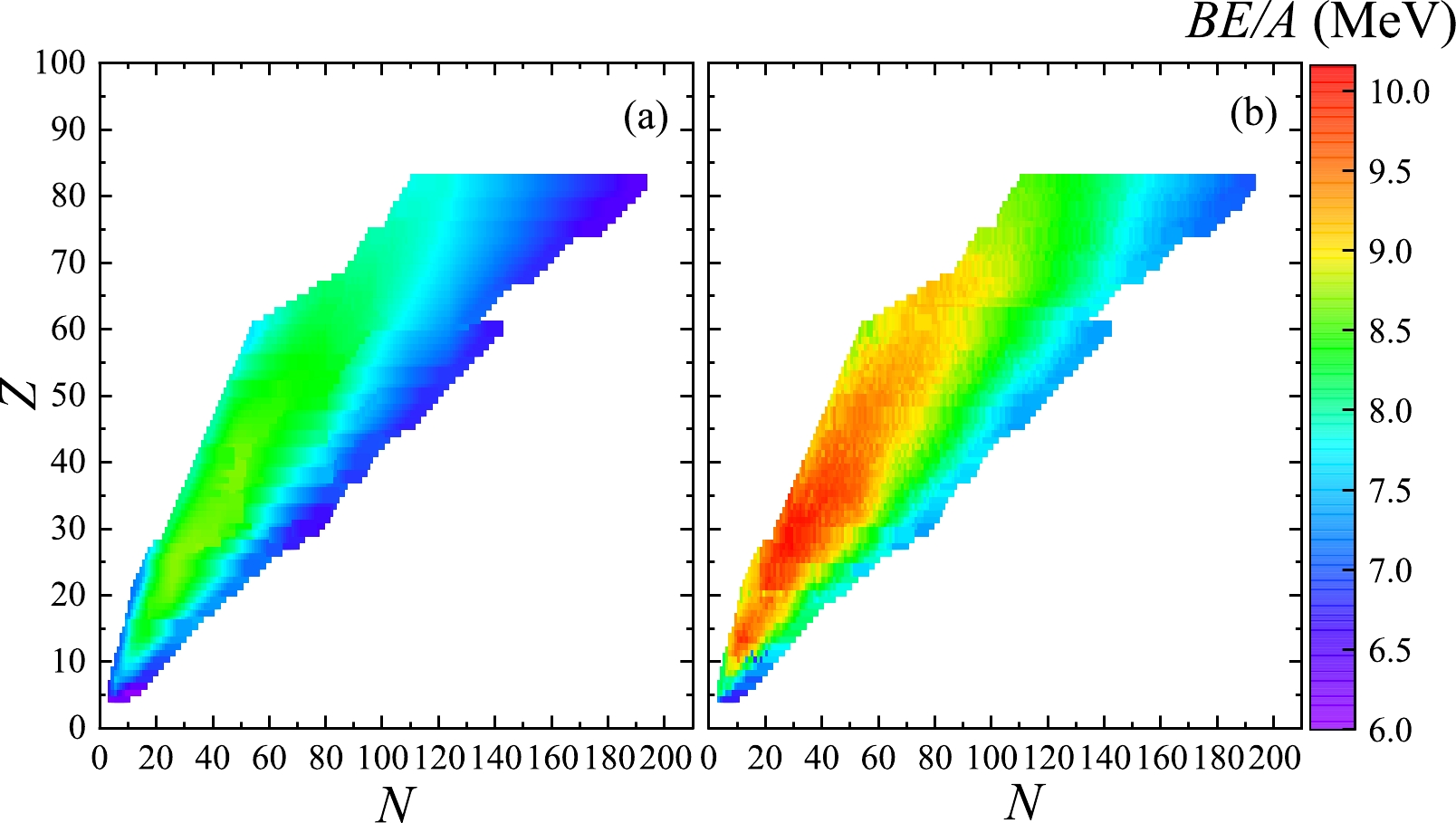

Figure 1.  (color online) Binding energy per nucleon $BE/A$ (in MeV) for the nuclides with the neutron (N) and proton (Z) numbers at (a) $B = 0$ G (left panel) and (b) $B= 10^{18}$ G (right panel).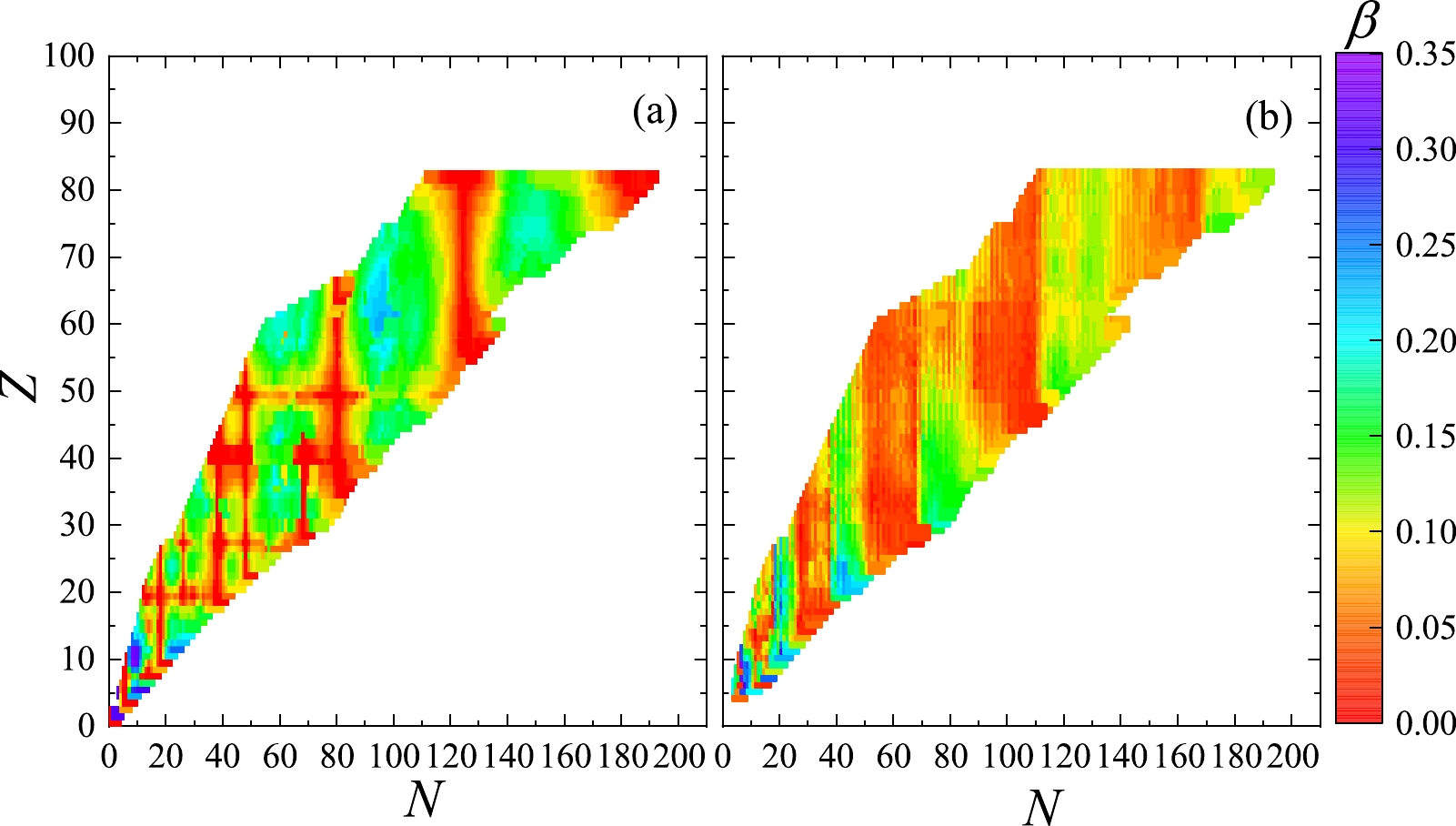

Figure 3.  (color online) Total deformation β for the nuclides with the neutron (N) and proton (Z) numbers at (a) $B = 0$ G (left panel) and (b) $B= 10^{18}$ G (right panel).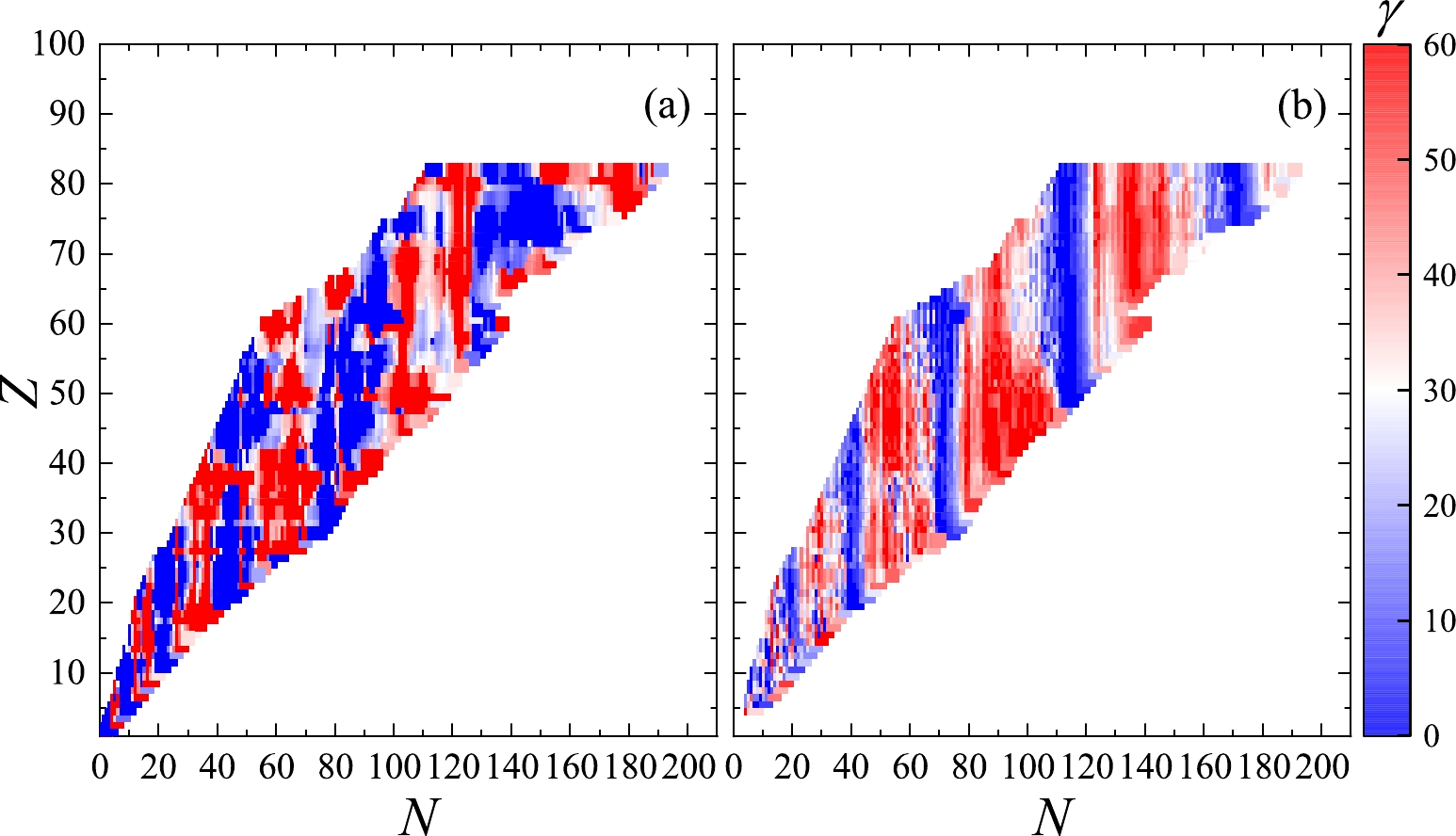

Figure 4.  (color online) Triaxiality γ for the nuclides with the neutron (N) and proton (Z) numbers at (a) $B = 0$ G (left panel) and (b) $B= 10^{18}$ G (right panel).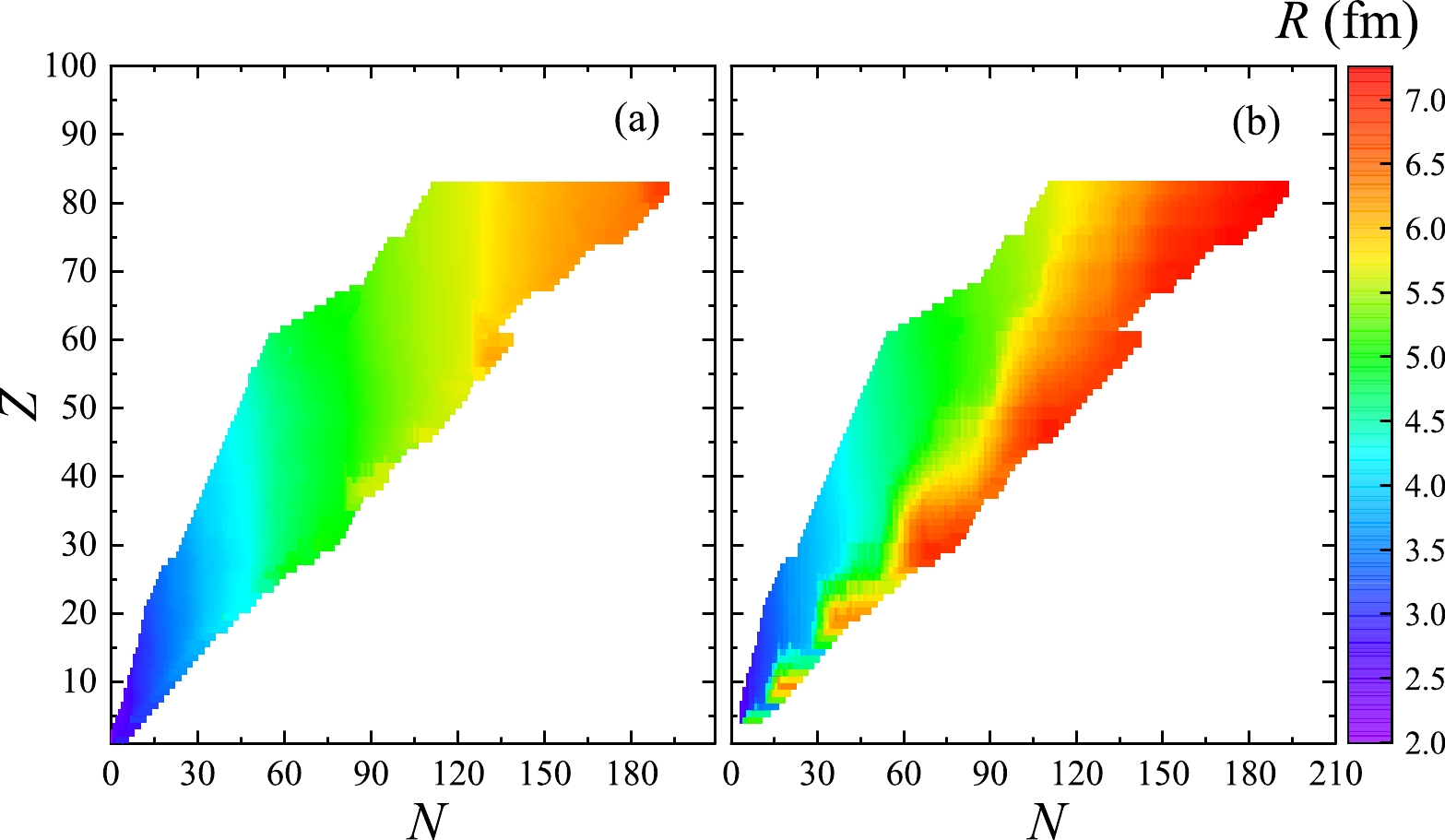

Figure 2.  (color online) Root mean square radii R (in fm) for the nuclides with the neutron (N) and proton (Z) numbers at (a) $B = 0$ G (left panel) and (b) $B= 10^{18}$ G (right panel).

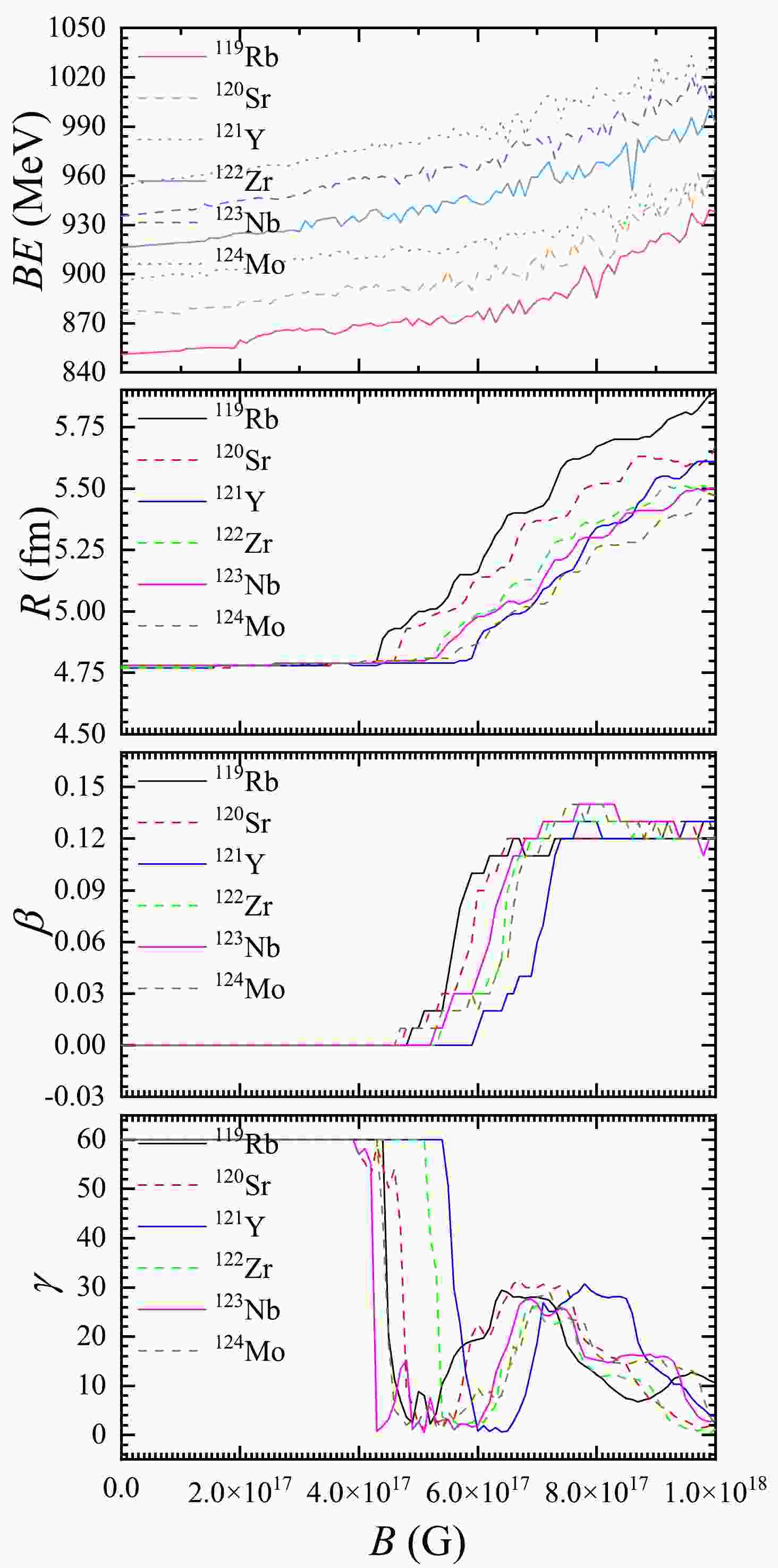
The MF also play an important role in the shape of the nucleus. In this work, we show the total deformation β and the triaxiality γ in Figs. 3-4, respectively. Here the parameters β and γ are known as Bohr-Mottelson parameters [38]. $ \beta = 0 $ refers to a spherical nucleus, which is non-deformed. When β is non-zero, the nucleus is deformed. The shape of a nucleus is prolate if $ \gamma=0 ^\circ $, oblate if $ \gamma=60 ^\circ $, and between the prolate and oblate deformations for $ 0 ^\circ<\gamma<60 ^\circ $. In Fig. 3(a), the nuclides in the region near the magic numbers have β = 0, which means they are non-deformed. But in Fig. 3(b), this phenomenon does not appear and almost all the nuclides are deformed. The low β regions ($ \beta <0.05 $) mainly focus on the areas with N=26$ \sim $36, 52$ \sim $68 and 96$ \sim $112. Note that some regions with large β in the absence of MF may become the small-β ones in the strong MF, e.g., the blue area around $ Z=58-68 $ and $ N=92-102 $ in Fig. 3(a), where β is greater than 0.2, can not be seen in Fig. 3(b). Thus, the strong MF may cause some nuclei with large deformation to become more 'spherical'. Compared with the results in Fig. 4(a), the triaxialities vary considerably in Fig. 4(b), and interestingly, we see $ \gamma=0^\circ $ around $ N=44, 74,114,172 $, between which $ \gamma=60^\circ $ shows up. This means that in the super-strong MF, in general, the prolate and oblate deformations of a nucleus emerge alternately with increasing neutron numbers.

In Fig. 5, we calculate the binding energy BE, radius R, and deformation parameters β and γ of six nuclides which may exist in the outer crust of a cold nonaccreting neutron star as a function of magnetic field strength. What is the most obvious in this figure is that $BE$s are not simply positively correlated with the strength of the magnetic field, but rise jaggedly. It is because the spin-up and spin-down states split under the MF, and the energy levels of a nucleus may undergo the rearrangement for B $ \gtrsim 10^{17} $ G [25]. The analogue in atomic physics is the transition from Zeeman to Paschen-Back effect when the MF become very strong. In this figure, we see that R, β and γ are nearly unchanged for $ B\lesssim 4.1\times 10^{17} $ G, but $BE$s still increase. At $ B\gtrsim 4.1\times 10^{17} $ G, Rs increase with increasing MF, while βs rise initially then have small changes above some certain values of magnetic field strength. In addition, at $ B\gtrsim 4.1\times 10^{17} $ G, the phenomenon that γs become $ \gamma=0^\circ $ rapidly when the MF increase, then increase to about $ \gamma=30^\circ $ and subsequently return to $ \gamma=0^\circ $ at higher MF implies that the nuclei may not become more prolate with higher MF and might relate to the alternate emergence of the prolate and oblate deformation of a nucleus with increasing neutron numbers, seen in Fig. 4(b).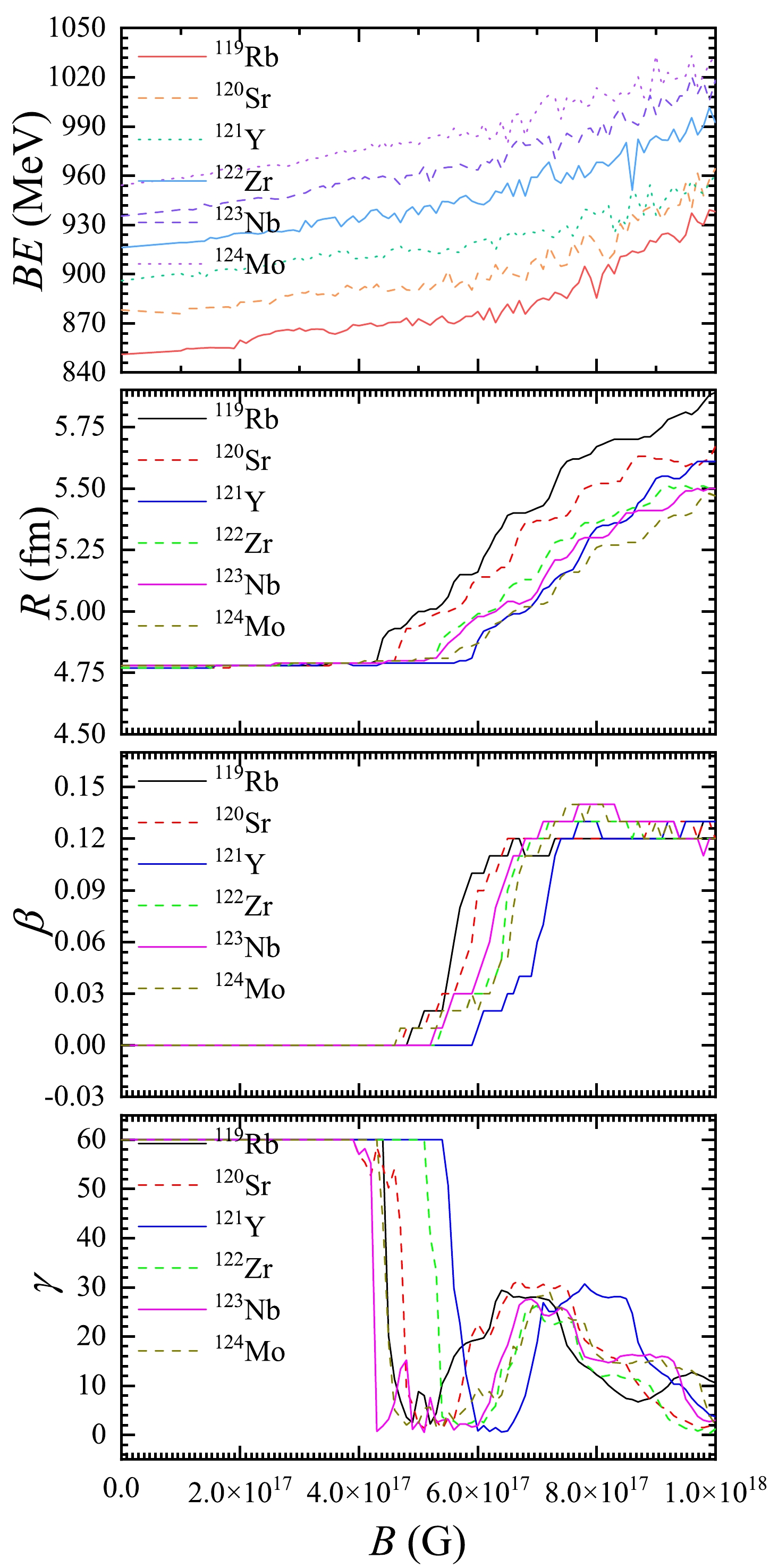

Figure 5.  (color online) Binding energy (BE), radius R, and deformation parameters β and γ of six nuclides which may exist in the outer crust of a cold nonaccreting neutron star as a function of magnetic field strength.

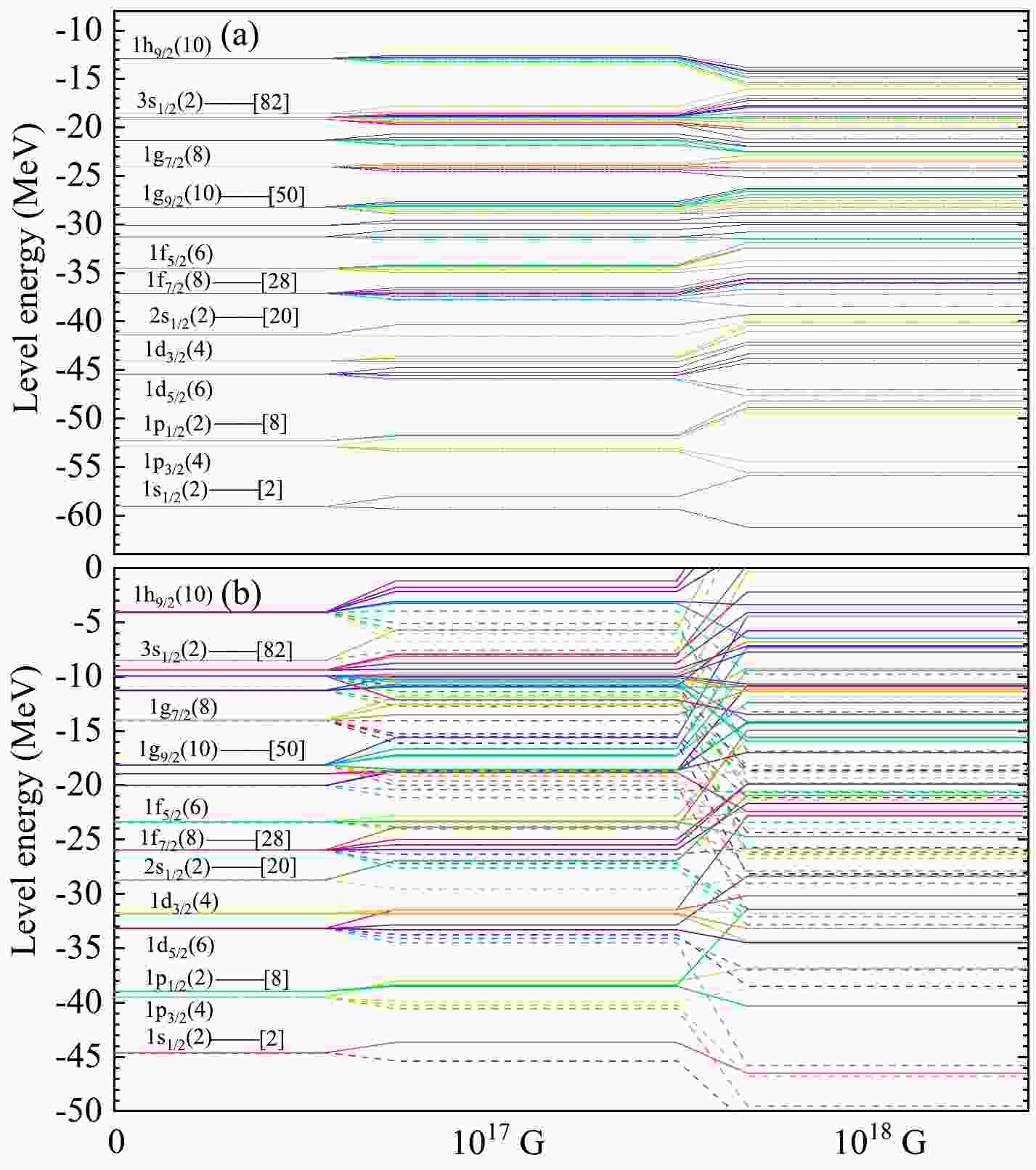
To understand the jaggedness of the $BE$ in Fig. 5 more thoroughly, we display in Fig. 6 the neutron and proton energy levels of $ {}^{208} $Pb, for $ B=0 $ G, $ B=10^{17} $ G and $ B=10^{18} $ G. The interaction between the MF and the magnetic moment for $ B\neq 0 $ splits the energy levels. The neutrons have no orbital magnetic moment, thus the gaps between the neutron magic numbers are still obvious at $ B=10^{17} $ G, and higher MF ($ B=10^{18} $ G here) are needed to modify or even eliminate the neutron shell structure. On the other hand, the effects of the MF on the protons are enough due to the orbital magnetic moment so that some outer and inner energy levels in the absence of MF cross over at $ B=10^{17} $ G and more energy levels cross over at $ B=10^{18} $ G. This rearrangement of energy levels leads to the appearance of the jaggedness for the $BE$.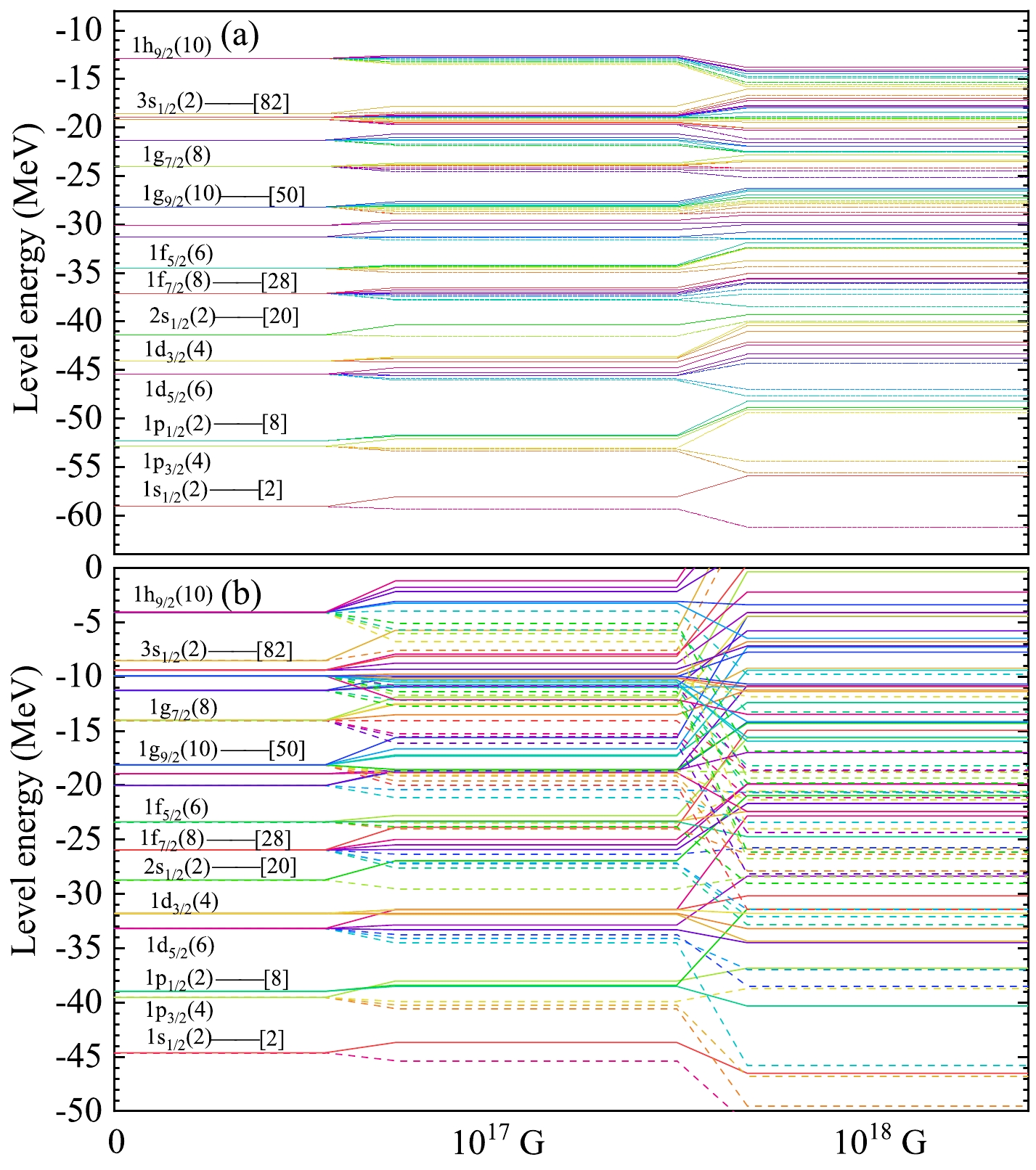

Figure 6.  (color online) Energy levels of (a) neutron (upper panel) and (b) proton (lower panel) (in MeV) of ${}^{208}$Pb at $B=0$ G, $B=10^{17}$ G and $B=10^{18}$ G.

In Fig. 7, we illustrate the equilibrium composition of the outer crust in the absence of MF by minimizing Eq. (9). The nuclear masses are calculated with the Skyrme force SLy6 [37] by Sky3D code. For comparison, the results based on the Hartree-Fock-Bogoliubov (HFB) method labeled by HFB-21 and the relativistic mean-field model labeled by DD-ME2 are also shown in this figure, respectively [18, 27]. We see some trends in common for these three models. The equilibrium element in the outermost part of crust is $ ^{56} $Fe. With the increasing pressure, two constant plateaus of neutron number appear, which correspond to two magic numbers, i.e., $ N=50 $ and $ 82 $, respectively. Accompanied by these two plateaus is the obvious lift of proton number with the subsequent decrease. All the maximum pressures for these models are similar $ \sim 4.7\times 10^{-4} $ MeV fm$ ^{-3} $, at which the neutrons begin to drip out of the nuclei, indicating the boundary between the outer and inner crusts of the neutron stars. Nonetheless, there are some model-dependent features for these models, e.g., DD-ME2 displays a dip for the neutron and proton numbers in the interval between $ P\sim 10^{-7}-10^{-6} $ MeV fm$ ^{-3} $ and the $ N=50 $ plateau begins to appear in HFB-21 at higher pressure.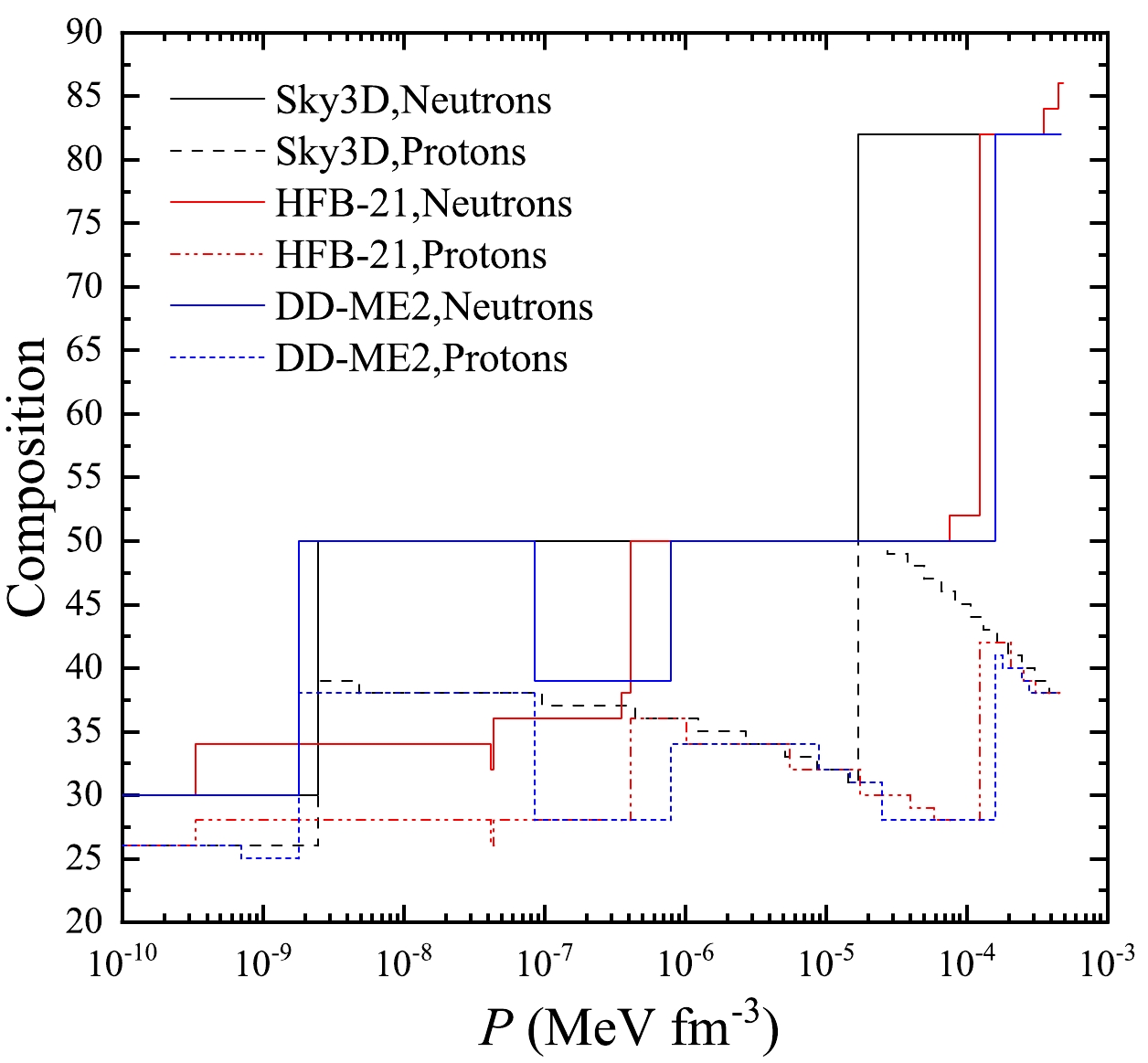

Figure 7.  (color online) Composition of the outer crust of a cold nonaccreting neutron star in the absence of a magnetic field $(B=0\ \text G)$ where the nuclear masses are obtained with the Skyrme force SLy6 [37] by Sky3D code, the Hartree-Fock-Bogoliubov method labeled by HFB-21 [18] and the relativistic mean-field model labeled by DD-ME2 [27].

Fig. 8 displays the neutron-drip transition pressure $ P_{\text{drip}} $ as a function of the magnetic field, where $ P_{\text{drip}} $ is obtained by requiring Gibbs energy in Eq. (9) equaling to the neutron mass. It is shown that the effects of MF on $ P_{\text{drip}} $ are almost nothing other than for $ B>10^{16} $ G. Furthermore, we see that when $ B\gtrsim10^{17} $ G, $ P_{\text{drip}} $ is nearly a linear function of magnetic field. These results are in agreement with that in Refs [18, 27]. In addition, the variation on the nuclear masses due to the MF ($ B_n=B $) plays a ignorable role for $ B\lesssim10^{17} $ G because the MF with such orders of magnitude can not affect the nuclei obviously. For the extreme high MF, $ B=10^{18} $ G, $ P_{\text{drip}} $ in the $ B_n=B $ case increases about 20% in comparison with that in the case without taking the change of the nuclear masses into account ($ B_n=0 $).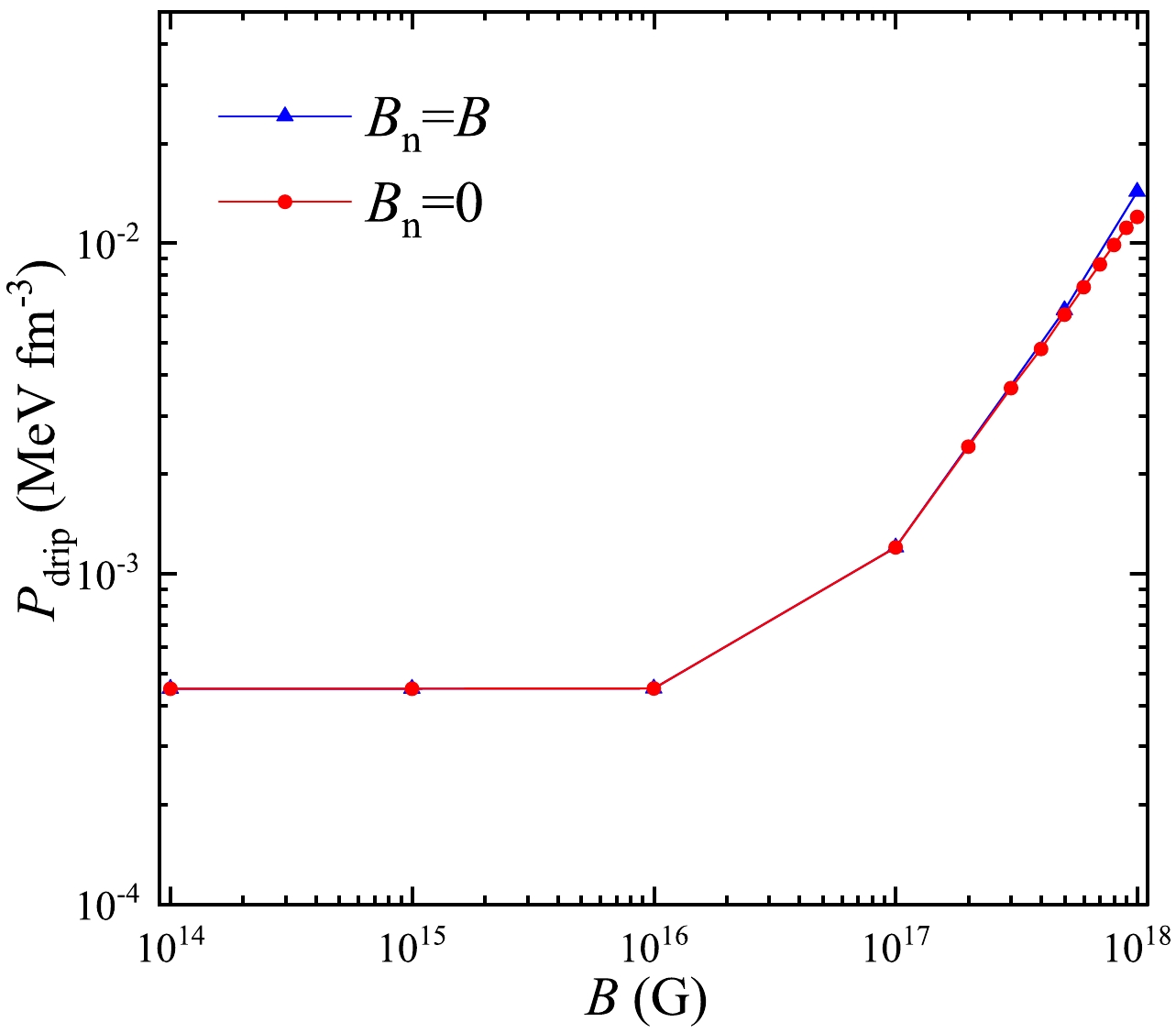

Figure 8.  (color online) Neutron-drip transition pressure $P_{\text{drip}}$ versus magnetic field strength B, where the effect of the magnetic fields on the nuclear masses is included ($B_{\text n}=B$) and not included $(B_{\text n}=0)$.

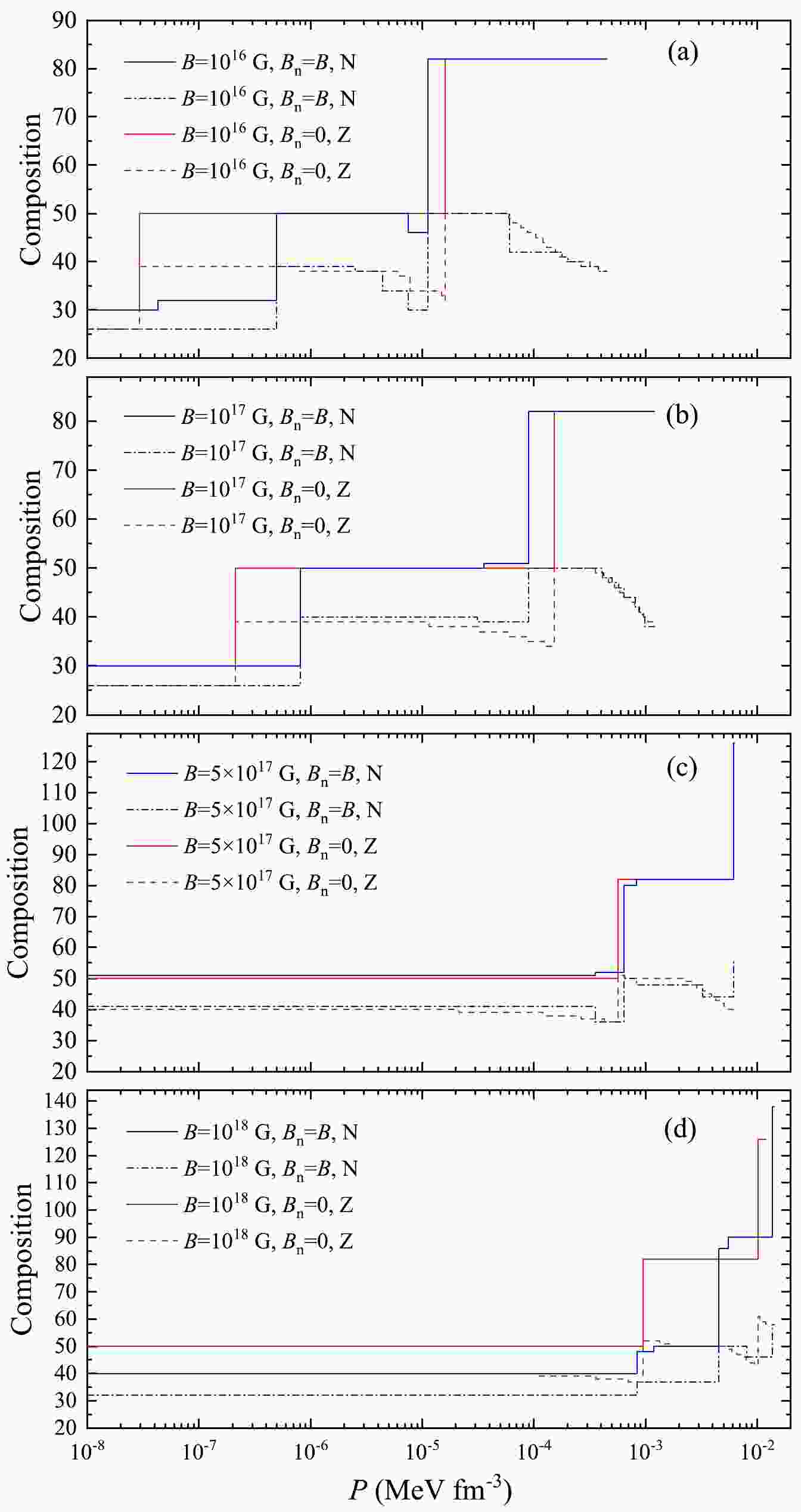
In Fig. 9, we illustrate the equilibrium composition of the outer crust for (a) $ B= 10^{16} $ G, (b) $ B= 10^{17} $ G, (c) $ B=5\times 10^{17} $ G, and (d) $ B= 10^{18} $ G. The variation on the nuclear masses due to the MF is considered ($ B_{\text n} = B $) and not considered ($ B_{\text n} = 0 $). The nuclear masses are affected slightly by the MF for $ B\leq 10^{17} $ G, but we can still find obvious discrepancy between the $ B_{\text n} = B $ and $ B_{\text n} = B $ cases in Fig. 9 (a) and Fig. 9 (b). However, this result may be model dependent [27]. It can be seen that the plateaus with $ N=50 $ and $ 82 $ are present in Fig. 9 (a) and (b). There is a clear shift for the $ N=50 $ plateau to higher pressures in comparison with that in the absence of MF seen in Fig. 1, but the pressure at which the $ N=82 $ plateau begins to emerge does not change very much for $ B=10^{16} $ G. This is in agreement with the results in Ref. [27]. We also show the composition in detail for $ B= 10^{16} $ G and $ B= 10^{17} $ G in Table. 1 and 2, where only the $ B_{\text n} = B $ case is listed. In both tables, from $ P_{\text{ion}} $ to the maximum pressure in the outer crust $ P_{\text{drip}} $, $ ^{56} $Fe occurs first, then $ ^{89} $Y on the $ N=50 $ plateau and $ ^{132} $Sn, $ ^{124} $Mo, $ ^{123} $Nb, $ ^{122} $Zr, $ ^{120} $Sr on the $ N=82 $ plateau are present. We notice that the same nuclides emerge at higher pressures in the stronger MF. It is mainly due to the reduced electronic Fermi energy under high MF. In addition, some nuclides may appear or disappear under the different magnetic field strength. $ ^{88} $Sr and $ ^{84} $Se existing in the $ B=10^{16} $ G case disappear on the $ N=50 $ plateau for $ B=10^{17} $ G, while $ ^{90} $Zr appear on this plateau. The nuclides not seen on the $ N=82 $ plateau for $ B=10^{16} $ G, i.e., $ ^{131} $In, $ ^{130} $Cd, $ ^{129} $Ag, $ ^{128} $Pd and $ ^{126} $Ru can exist in the $ B=10^{17} $ G case. Moreover, we find that the nuclide at the neutron-drip transition in Fig. 9 (a) and (b) is same, i.e., $ ^{120} $Sr, which is also one in the absence of MF (not shown in this paper). It is consistent with the observation in Ref. [18], but it is $ ^{124} $Sr there.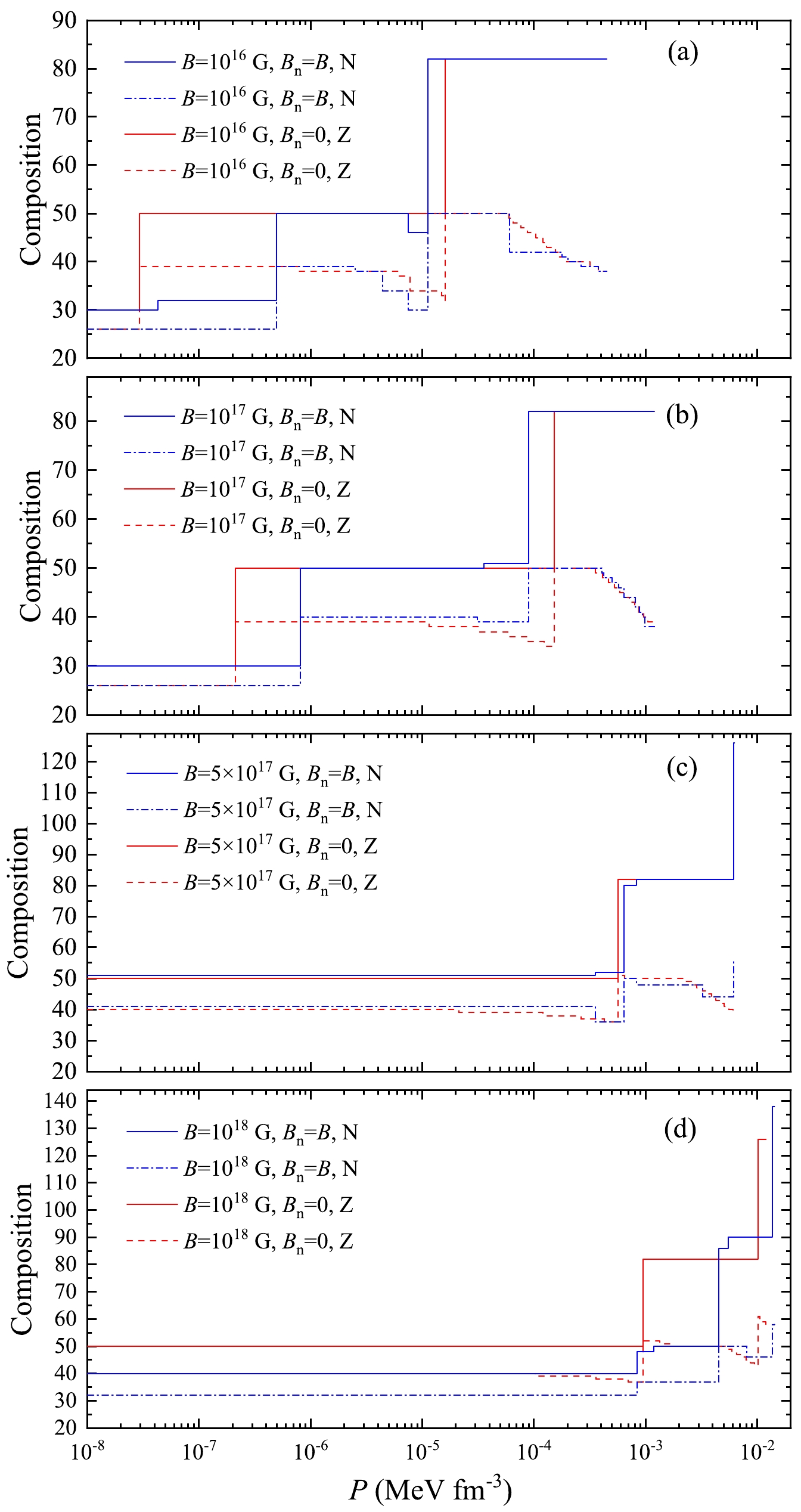

Figure 9.  (color online) Composition of the outer crust of a cold nonaccreting magnetar for the four cases, (a) $B = {10^{16}}$ G, (b) $B = {10^{17}}$ G, (c) $B=5\times 10^{17}$ G and (d) $B = {10^{18}}$ G, where the effect of the magnetic fields on the nuclear masses is included ($B_{\text n}=B$) and not included $(B_{\text n}=0)$.

Nucleus	$P_{\text {min}}$	$P_{\text {max}}$	$n_{\text {min}}$	$n_{\text {max}}$
${}_{26}^{56}$Fe	$P_{\text{ion}}$	$4.27\cdot 10^{-8}$	$n_{\text{ion}}$	$5.54\cdot 10^{-7}$
${}_{26}^{58}$Fe	$4.28\cdot 10^{-8}$	$4.98\cdot 10^{-7}$	$5.74\cdot 10^{-7}$	$1.53\cdot 10^{-6}$
${}_{39}^{89}$Y	$4.99\cdot 10^{-7}$	$2.50\cdot 10^{-6}$	$1.59\cdot 10^{-6}$	$3.34\cdot 10^{-6}$
${}_{38}^{88}$Sr	$2.51\cdot 10^{-6}$	$4.40\cdot 10^{-6}$	$3.39\cdot 10^{-6}$	$4.44\cdot 10^{-6}$
${}_{34}^{84}$Se	$4.41\cdot 10^{-6}$	$7.51\cdot 10^{-6}$	$4.62\cdot 10^{-6}$	$5.99\cdot 10^{-6}$
${}_{30}^{76}$Zn	$7.52\cdot 10^{-6}$	$1.13\cdot 10^{-5}$	$6.28\cdot 10^{-6}$	$7.63\cdot 10^{-6}$
${}_{50}^{132}$Sn	$1.14\cdot 10^{-5}$	$6.07\cdot 10^{-5}$	$8.03\cdot 10^{-6}$	$3.64\cdot 10^{-5}$
${}_{42}^{124}$Mo	$6.08\cdot 10^{-5}$	$1.79\cdot 10^{-4}$	$3.80\cdot 10^{-5}$	$1.07\cdot 10^{-4}$
${}_{41}^{123}$Nb	$1.80\cdot 10^{-4}$	$2.02\cdot 10^{-4}$	$1.09\cdot 10^{-4}$	$1.18\cdot 10^{-4}$
${}_{40}^{122}$Zr	$2.03\cdot 10^{-4}$	$2.64\cdot 10^{-4}$	$1.20\cdot 10^{-4}$	$1.49\cdot 10^{-4}$
${}_{39}^{121}$Y	$2.65\cdot 10^{-4}$	$3.77\cdot 10^{-4}$	$1.51\cdot 10^{-4}$	$1.91\cdot 10^{-4}$
${}_{38}^{120}$Sr	$3.79\cdot 10^{-4}$	$4.49\cdot 10^{-4}$	$1.95\cdot 10^{-4}$	$2.31\cdot 10^{-4}$

Table 1.  Composition of the outer crust of a magnetar at $B=10^{16}$ G. $P_{\text {min}}$ ($P_{\text{max}}$) is the minimum (maximum) pressure of the appearing nuclide, in units of $ \text{MeV fm}^{-3}$, at which $n_{\text {min}}$ ($n_{\text {max}}$), in units of $ \text{fm}^{-3}$, is the corresponding average minimum (maximum) baryon number density. $P_{\text {ion}}$ and $n_{\text {ion}}$ are the complete ionization pressure and density. Here only the $B_{\text n}=B$ case which includes the effect of the magnetic fields on the nuclear masses is shown.

Nucleus	$P_{\text {min}}$	$P_{\text {max}}$	$n_{\text {min}}$	$n_{\text {max}}$
${}_{26}^{56}$Fe	$P_{\text{ion}}$	$8.07\cdot 10^{-7}$	$n_{\text{ion}}$	$7.54\cdot 10^{-6}$
${}_{40}^{90}$Zr	$8.08\cdot 10^{-7}$	$3.10\cdot 10^{-5}$	$8.26\cdot 10^{-6}$	$3.75\cdot 10^{-5}$
${}_{39}^{89}$Y	$3.11\cdot 10^{-5}$	$3.58\cdot 10^{-5}$	$3.81\cdot 10^{-5}$	$4.06\cdot 10^{-5}$
${}_{39}^{90}$Y	$3.59\cdot 10^{-5}$	$8.99\cdot 10^{-5}$	$4.12\cdot 10^{-5}$	$6.38\cdot 10^{-5}$
${}_{50}^{132}$Sn	$9.00\cdot 10^{-5}$	$4.05\cdot 10^{-4}$	$7.35\cdot 10^{-5}$	$1.52\cdot 10^{-4}$
${}_{49}^{131}$In	$4.06\cdot 10^{-4}$	$4.24\cdot 10^{-4}$	$1.54\cdot 10^{-4}$	$1.58\cdot 10^{-4}$
${}_{48}^{130}$Cd	$4.25\cdot 10^{-4}$	$5.01\cdot 10^{-4}$	$1.60\cdot 10^{-4}$	$1.74\cdot 10^{-4}$
${}_{47}^{129}$Ag	$5.02\cdot 10^{-4}$	$5.71\cdot 10^{-4}$	$1.76\cdot 10^{-4}$	$1.87\cdot 10^{-4}$
${}_{46}^{128}$Pd	$5.72\cdot 10^{-4}$	$6.38\cdot 10^{-4}$	$1.90\cdot 10^{-4}$	$2.00\cdot 10^{-4}$
${}_{44}^{126}$Ru	$6.39\cdot 10^{-4}$	$8.13\cdot 10^{-4}$	$2.06\cdot 10^{-4}$	$2.33\cdot 10^{-4}$
${}_{42}^{124}$Mo	$8.14\cdot 10^{-4}$	$8.86\cdot 10^{-4}$	$2.40\cdot 10^{-4}$	$2.50\cdot 10^{-4}$
${}_{41}^{123}$Nb	$8.87\cdot 10^{-4}$	$9.41\cdot 10^{-4}$	$2.54\cdot 10^{-4}$	$2.62\cdot 10^{-4}$
${}_{40}^{122}$Zr	$9.42\cdot 10^{-4}$	$9.79\cdot 10^{-4}$	$2.66\cdot 10^{-4}$	$2.71\cdot 10^{-4}$
${}_{38}^{120}$Sr	$9.80\cdot 10^{-4}$	$1.20\cdot 10^{-3}$	$2.81\cdot 10^{-4}$	$3.10\cdot 10^{-4}$

Table 2.  Same as Table 1, but at $B=10^{17}$ G.

For $ B= 5\times10^{17} $ G and $ B= 10^{18} $ G, the composition in the neutron star outer crust is significantly changed. Firstly we focus on the $ B_{\text n} = 0 $ case. Fig. 9 (c) and (d) show that the outermost nuclide in the outer crust is not $ ^{56} $Fe, but $ ^{90} $Zr, which is just on the $ N=50 $ platform, and spans in the broad range of pressures. The plateau with $ N=82 $ is still present and delays to higher pressures compared with that in the weak MF. It is surprising that the neutron plateau with new magic number $ N=126 $ can be seen for $ B= 10^{18} $ G. This is in disagreement with the conclusion in Ref. [27], where the authors preset a medium-heavy nuclide as the upper limit of the composition in the outer crust. It is also pointed out by Ref. [39] where the HFB method is used and the effect of the MF on the nuclear masses is not included. Therefore, for the super-strong MF, such neutron-rich nuclide might be present in the outer crust. In the $ B_{\text n} = B $ case, we see from Fig. 9 (c) and Table 3 that for $ B=5\times10^{17} $ G the outermost nuclide is not on the $ N=50 $ platform, i.e., $ ^{92} $Nb, and the nuclide at $ P_{\text{drip}} $ is $ ^{182} $Ba, which is just on the $ N=126 $ plateau. For stronger MF, i.e., $ B=10^{18} $ G ($ B_{\text n} = B $), Fig. 4 (d) and Table 4 show that the platforms with $ N=82 $ and $ N=126 $ disappear. The outermost nuclide is $ ^{72} $Ge, and the nuclide at $ P_{\text{drip}} $ is $ ^{196} $Ce which differs evidently from $ N=126 $ plateau. It results from the fact that the binding energies rise jaggedly with increasing MF due to the rearrangement of the energy levels for $ B> 10^{17} $ G, as shown in Fig. 5. Thus, some concepts, e.g., magic numbers, should be reexamined when the effects of MF on nuclear masses are taken into account.

Nucleus	$P_{\text {min}}$	$P_{\text {max}}$	$n_{\text {min}}$	$n_{\text {max}}$
${}_{41}^{92}$Nb	$P_{\text{ion}}$	$3.53\cdot 10^{-4}$	$n_{\text{ion}}$	$2.85\cdot 10^{-4}$
${}_{36}^{88}$Kr	$3.54\cdot 10^{-4}$	$6.44\cdot 10^{-4}$	$3.09\cdot 10^{-4}$	$4.10\cdot 10^{-4}$
${}_{50}^{130}$Sn	$6.45\cdot 10^{-4}$	$8.27\cdot 10^{-4}$	$4.42\cdot 10^{-4}$	$4.97\cdot 10^{-4}$
${}_{48}^{130}$Cd	$8.28\cdot 10^{-4}$	$3.25\cdot 10^{-3}$	$5.17\cdot 10^{-4}$	$1.00\cdot 10^{-3}$
${}_{44}^{126}$Ru	$3.26\cdot 10^{-3}$	$6.16\cdot 10^{-3}$	$1.05\cdot 10^{-3}$	$1.44\cdot 10^{-3}$
${}_{56}^{182}$Ba	$6.17\cdot 10^{-3}$	$6.27\cdot 10^{-3}$	$1.65\cdot 10^{-3}$	$1.66\cdot 10^{-3}$

Table 3.  Same as Table 1, but at $B=5\times 10^{17}$ G.

Nucleus	$P_{\text {min}}$	$P_{\text {max}}$	$n_{\text {min}}$	$n_{\text {max}}$
${}_{32}^{72}$Ge	$P_{\text{ion}}$	$8.41\cdot 10^{-4}$	$n_{\text{ion}}$	$6.23\cdot 10^{-4}$
${}_{37}^{85}$Rb	$8.42\cdot 10^{-4}$	$1.18\cdot 10^{-3}$	$6.41\cdot 10^{-4}$	$7.48\cdot 10^{-4}$
${}_{37}^{87}$Rb	$1.19\cdot 10^{-3}$	$4.54\cdot 10^{-3}$	$7.69\cdot 10^{-4}$	$1.46\cdot 10^{-3}$
${}_{50}^{136}$Sn	$4.55\cdot 10^{-3}$	$5.49\cdot 10^{-3}$	$1.71\cdot 10^{-3}$	$1.87\cdot 10^{-3}$
${}_{50}^{140}$Sn	$5.50\cdot 10^{-3}$	$8.09\cdot 10^{-3}$	$1.93\cdot 10^{-3}$	$2.33\cdot 10^{-3}$
${}_{46}^{136}$Pd	$8.10\cdot 10^{-3}$	$1.36\cdot 10^{-2}$	$2.45\cdot 10^{-3}$	$3.14\cdot 10^{-3}$
${}_{58}^{196}$Ce	$1.37\cdot 10^{-2}$	$1.43\cdot 10^{-2}$	$3.63\cdot 10^{-3}$	$3.71\cdot 10^{-3}$

Table 4.  Same as Table 1, but at $B=10^{18}$ G.

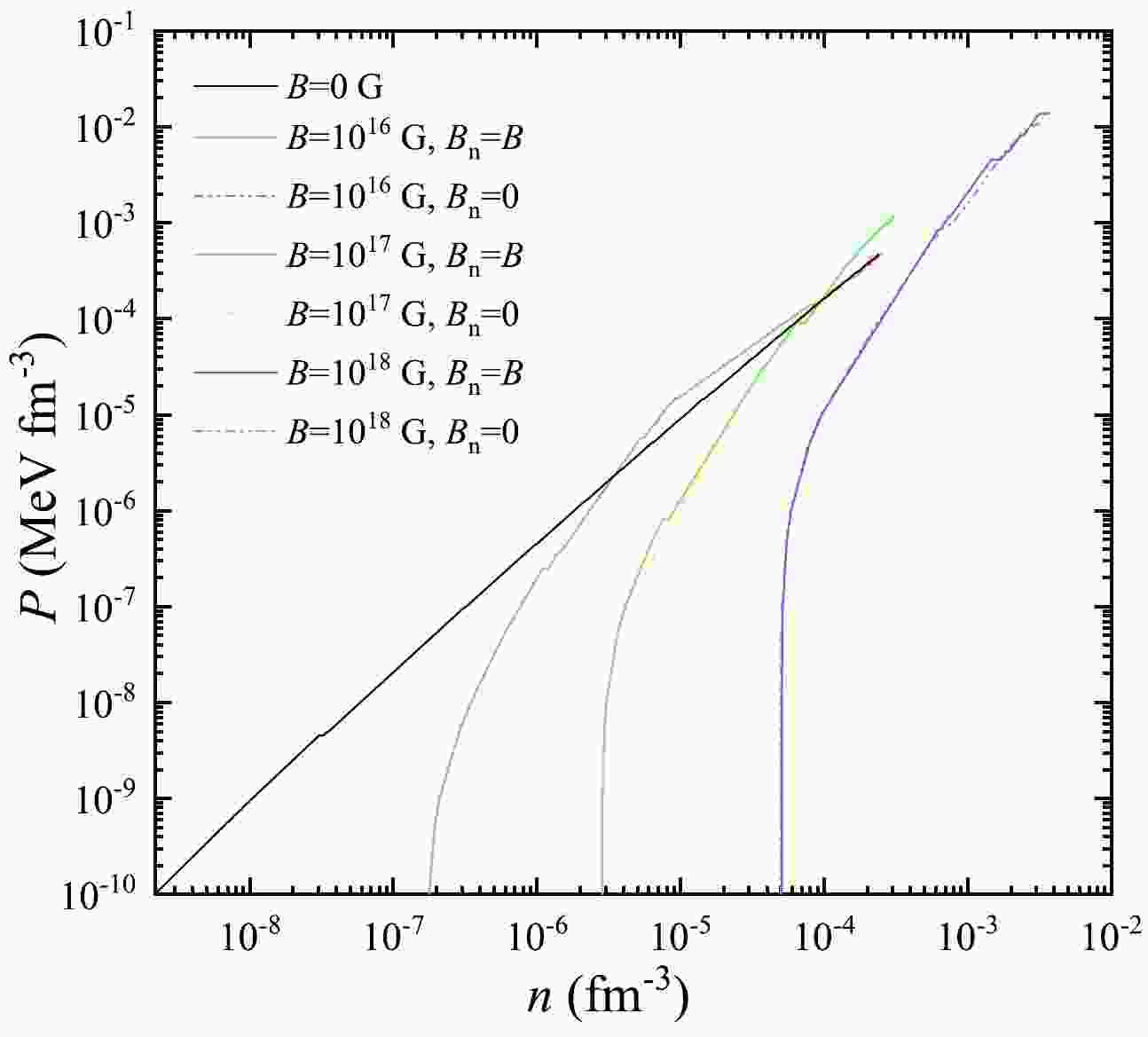
In Fig. 10, we compare the behavior of the pressure P as a function of the baryonic density n for the three magnetic field cases. The result for $ B=0 $ G is also shown for comparison. It can be seen that the effects of the variation on the nuclear masses due to the MF are negligible. In the low density region, the phenomenon that the density is almost unchanged over a wide range of pressures is more obvious under higher MF. It indicates that the outermost material of the magnetar is almost incompressible. This is because the electrons occupy only the lowest Landau level at low densities. On the other hand, the electrons may occupy a growing number of levels rapidly with increasing densities, and the effects of MF will become unimportant. It may result in the similar slope of these lines at higher densities to that for $ B=0 $ G which is approximately linear, as can be seen in this figure.

Figure 10.  (color online) Pressure P versus average nucleon number density n (equation of state) in the outer crust of a cold nonaccreting neutron star at four magnetic fields $B = 0\ \text G$, $B = {10^{16}}\ \text G$, $B = {10^{17}}\ \text G$, and $B = {10^{18}}\ \text G$, where the effect of the magnetic fields on the nuclear masses is included ($B_{\text n}=B$) and not included $(B_{\text n}=0)$.

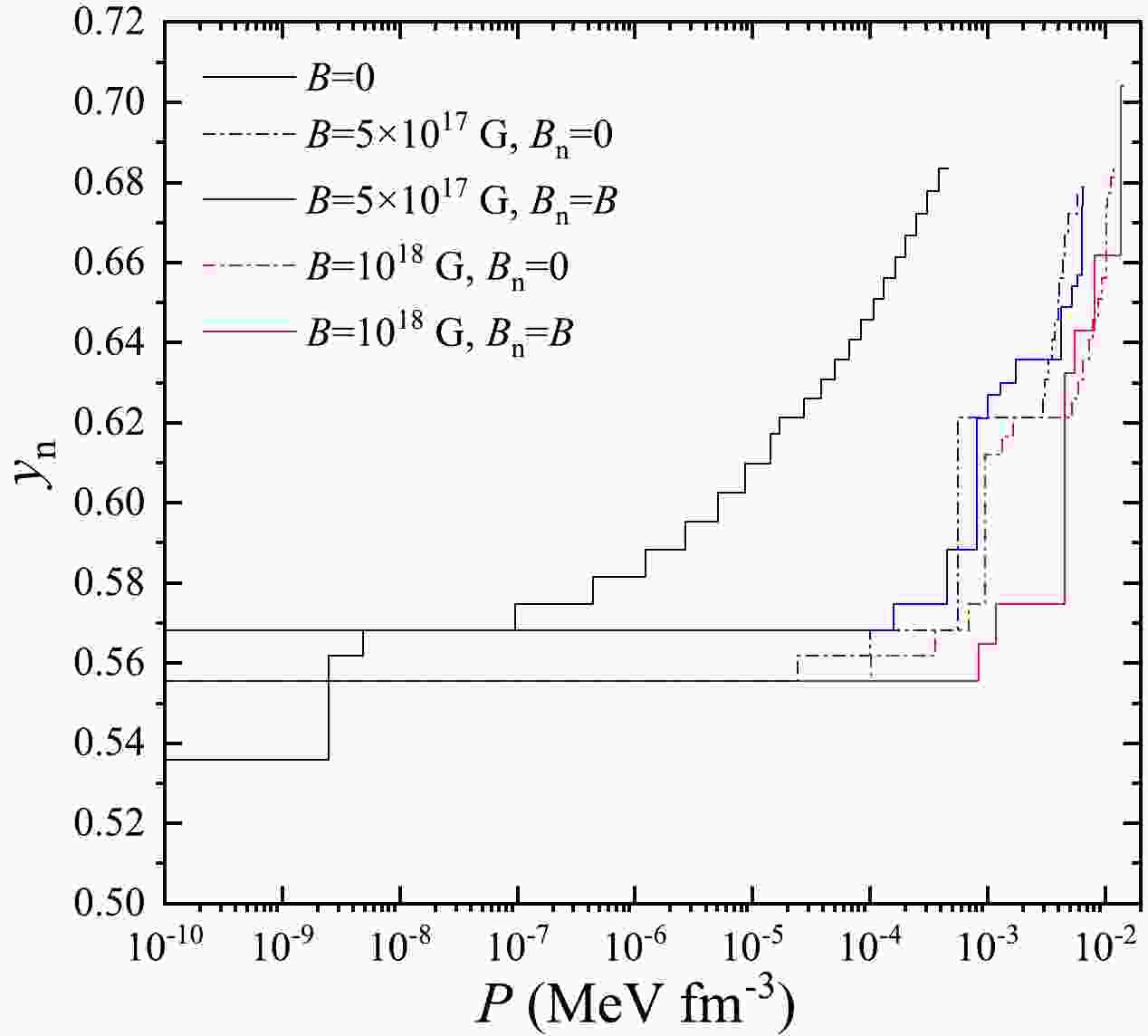
In Fig. 11, we compare the neutron fraction $ y_{\text n} $ in the outer crust for the cases $ B=0 $ G, $ 5\times10^{17} $ G, and $ 10^{18} $ G. It is shown that $ y_{\text n} $ is positively correlated with the pressure P in all cases. This is consistent with the physical intuition as the inverse $ \beta\text{-} $decay reaction becomes more intense with increasing depth of the magnetar, and the nuclei will become more and more neutron-rich. For $ B \neq 0 $ G, it is shown that no essential difference can be seen between $ B_{\text n}= 0 $ and $ B_{\text n}= B $ cases, and $ y_{\text n} $ is smaller than that in the $ B=0 $ G case at the same pressure (these ultra-strong MF, i.e., $ B>10^{17} $ G, can make the outermost nuclide become richer in neutron than $ ^{56} $Fe, and thus may lead to a neutron-richer region in the outer crust). It indicates that except in the outermost region for the ultra-strong MF case, the nuclei in the outer crust of a magnetar are more symmetric than those in an ordinary neutron star with weak MF at the same pressure.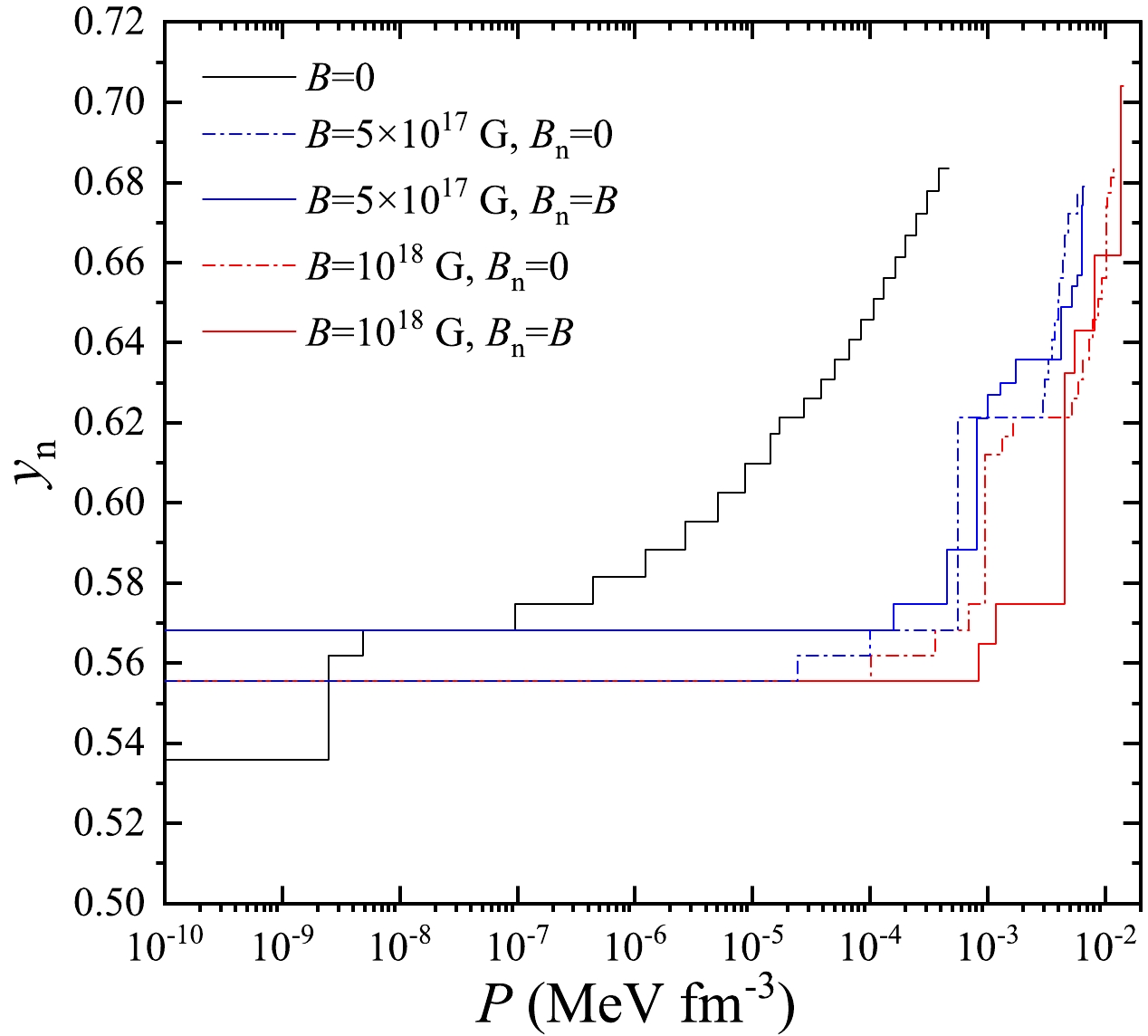

Figure 11.  (color online) Neutron fraction $y_{\text n}$ ($y_{\text n}$=$N/A$) versus pressure P in the outer crust of a neutron star for the magnetic field strength of $B=0\ \text G$, $B = {5\times 10^{17}}\ \text G$ and $B = {10^{18}}\ \text G$, where the effect of the magnetic fields on the nuclear masses is included ($B_{\text n}=B$) and not included $(B_{\text n}=0)$.

In summary, we explore the properties of 4110 nuclides from $ Z=5 $ to $ Z=82 $ with the Sky3D code and the composition of the outer crust of a cold non-accreting magnetar. The effects of the variation on the nuclear masses due to the MF have been investigated. The MF play an important role in the binding energies, size and shape of the nucleus. The strong MF increase the binding energies and nuclear radii. For the MF $ B \lesssim 10^{17} $ G, the nuclear shapes are nearly unchanged. At higher MF ($ B=10^{18} $ G in this work), almost all the nuclides are deformed while some nuclei with large deformation can become more 'spherical', moreover, the prolate and oblate deformations of a nucleus emerge alternately with increasing neutron numbers in general. For the MF $ B \lesssim 10^{17} $ G, there are some trends in common with the case in the absence of MF, i.e., $ ^{56} $Fe occurs first, the plateaus with $ N=50 $ and $ 82 $ are present, and the nuclide at the neutron-drip transition might not change, while these trends may be altered for $ B> 10^{17} $ G. If the effects of the MF on the nuclear masses are not taken into account ($ B_{\text n} = 0 $), the MF only influence the electrons but the outermost nuclide in the outer crust is $ ^{90} $Zr, not $ ^{56} $Fe. The $ N=50 $ and $ N=82 $ platforms are still present. Even the neutron plateau with new magic number $ N=126 $ can be seen for $ B= 10^{18} $ G. When the variation on the nuclear masses due to the MF is considered, the spin-up and spin-down states split. Thus the energy levels of a nucleus may undergo the rearrangement, and the situation may become more complex. In the case of $ B_n=B $, the outermost nuclide is $ ^{92} $Nb for $ B= 5\times10^{17} $ G and $ ^{72} $Ge for $ B= 10^{18} $ G. Moreover, the $ N=82 $ and $ N=126 $ plateaus disappear for $ B= 10^{18} $ G. Thus, some concepts, e.g., magic numbers, should be reexamined in the $ B_n=B $ case. In addition, we also study the neutron-drip transition pressure, the equation of state and neutron fraction of the outer crust in the presence of the MF. The effects of MF on $ P_{\text{drip}} $ are almost nothing other than for $ B>10^{16} $ G. At the extreme high MF, $ B=10^{18} $ G, $ P_{\text{drip}} $ in the $ B_{\text n}=B $ case increases about 20% in comparison with that for the case of $ B_{\text n}=0 $. The equation of state is affected by the MF mainly in the low density region, where the density is almost unchanged over a wide range of pressures while the variation on the nuclear masses due to the MF plays a negligible role. The neutron fractions do not show the essential difference between the $ B_{\text n}=0 $ and $ B_{\text n}=B $ cases.

The present work shows that the nuclei with the neutron number $ N\geq126 $ emerge in both $ B_{\text n}=0 $ and $ B_{\text n}=B $ cases for $ B= 10^{18} $ G, while the $ N=126 $ nuclei emerge in $ B_{\text n}=B $ case and not in $ B_{\text n}=0 $ one for $ B= 5\times10^{17} $ G. Thus, considering the effects of the MF on the nuclear masses or not may modify the conclusion about the composition of the outer crust under strong MF. It needs to be studied in more detail later.