Nuclear stability and ratio of kinetic to potential energy

Ke-Hu Wang; Zhang-Ya Wang; Ning Wang; Min Liu

doi:10.1088/1674-1137/adc3ff

Chinese Physics C> 2025, Vol. 49> Issue(6) : 064108 DOI: 10.1088/1674-1137/adc3ff

Nuclear stability and ratio of kinetic to potential energy

Ke-Hu Wang ¹ ,
Zhang-Ya Wang ¹ ,
Ning Wang ^1,2, ,
Min Liu ^{1,2,
,}

1.
Department of physics, Guangxi Normal University, Guilin 541004, China
2.
Guangxi Key Laboratory of Nuclear Physics and Technology, Guilin 541004, China

Abstract
HTML
Reference
Related

PDF

Abstract：
The Skyrme energy density functional was used to systematically analyze the ratio of repulsive kinetic to attractive potential energy ( $T/U$ ) for even-even nuclei in their ground states. Notably, the nuclei with maximal value of $T/U$ are generally stable for a certain isobaric chain with $Z\le 82$ . However, the known magic numbers can be more clearly observed from the $T/U$ ratio than from nuclear binding energy, particularly for the isobaric chains with semi-magic nuclei. Combining the predicted binding energies and the $T/U$ ratios from the Skyrme Hartree-Fock-Bogoliubov (HFB) code transformed harmoic oscilattor (HFBTHO) with the parameter set based on the Universal Nuclear Energy Density Funcitonal (UNEDF0), the possible magic numbers in super-heavy mass region were simultaneously studied. The neutron magic number $N=184$ can be clearly observed from the calculated values of $T/U$ and the extracted microscopic energies of the nuclei.
- nuclear stability ,
- energy density functional ,
- ratio of kinetic to potential energy ,
- super-heavy nuclei

I. INTRODUCTION

I. INTRODUCTION
II. FRAMEWORK OF THE MODEL
III. RESULTS AND DISCUSSIONS
IV. SUMMARY

Nuclear stability is a cornerstone research theme in nuclear physics, governed by nucleon-nucleon interactions and manifested through critical observables including binding energy systematics, magic number configurations, decay modes, and half-life patterns. This fundamental property not only dictates the synthesis pathways of new isotopes and superheavy elements (SHEs) but also serves as a stringent testbed for nuclear models. The nuclear shell model initially proposed in the 1960s predicted post- $^{208}$ Pb magic numbers at $Z=114$ and $N=184$ [1−3], suggesting an "island of stability" centered at ( $Z=114$ , $N=184$ ) where superheavy nuclei might exhibit enhanced stability. However, modern self-consistent mean-field calculations reveal competing predictions, proton shell closures at $Z=120$ or 126 and neutron shell closures spanning $N=172-184$ [4, 5]. These theoretical divergences highlight the critical role of SHE stability studies in validating nuclear many-body approaches. Through fusion-evaporation reactions, superheavy nuclei with $104 \leq Z\leq 118$ have already been successfully synthesized in experiments [6−12]. The heaviest nucleus $^{294}$ Og that has been synthesized so far has a half-life on the order of milliseconds and is neutron-deficient due to the limitations in available projectile-target combinations and experimental facilities. The determination of nuclear stability exhibits mass-dependent characteristics. For light and medium nuclei ( $A<150$ ), β-decay predominance makes binding energy minimization along isobaric chains the key stability indicator. For heavy and super-heavy nuclei ( $A>200$ ), multi-mode decay competition disrupts simple energy-based predictions. For example, although the ground state energy of $^{214}$ Po is smaller than that of $^{214}$ Pb by 2.7 MeV, the half-life of $^{214}$ Pb is much larger than that of $^{214}$ Po, due to the different decay modes: $^{214}$ Pb via β-decay in contrast to $^{214}$ Po via α-decay. Therefore, new stability metrics beyond traditional binding energy considerations should be developed, particularly for SHEs. The enduring mystery surrounding the existence and location of the "island of stability" continues to drive interdisciplinary efforts combining nuclear experiments, astrophysical observations, and exascale computational modeling.

The binding energy of atomic nuclei predominantly arises from the dynamic equilibrium between the nuclear strong force and Coulomb repulsion [13], which governs their β-decay stability. Quantitatively, a net energy difference is manifested between the absolute values of the attractive nuclear potential energy U and the repulsive kinetic energy T. Notably, the $T/U$ ratio constitutes a fundamental parameter in nuclear astrophysics [14, 15], as it correlates with two critical phenomena: nuclear matter compressibility and stability mechanisms. The ratio $T/U$ provides insights into the stiffness of nuclear matter, a key determinant of neutron star interior structure and equation of state. In neutron stars, gravitational binding stability requires the dominance of gravitational potential energy $U_{\rm grav}$ over rotational kinetic energy $T_{\rm rot}$ . A significant imbalance ( $|U_{\rm grav}|\gg T_{\rm rot}$ ) may trigger catastrophic collapse into black holes. For atomic nuclei, the $T/U$ ratio reflects the interplay between nucleon-nucleon interaction strength (governed by nuclear force saturation) and nucleon motion intensity (driven by Fermi energy). Higher $T/U$ values typically indicate reduced binding coherence, thereby influencing fission barriers and decay modes. This intrinsic connection between the $T/U$ ratio and multi-scale stability (from femtometer-scale nuclei to kilometer-scale neutron stars) underscores its significance in unified nuclear many-body theories. Systematic investigations of this ratio across nuclear chart regions can unveil universal constraints on hadronic matter under extreme conditions.

The Skyrme Hartree-Fock-Bogoliubov (HFB) model is a versatile microscopic theoretical framework widely used in nuclear physics research, allowing the nuclear structure at ground state such as binding energies, charge radii, deformation and shape coexistence to be investigated self-consistently [16−20]. In this study, we performed systematic calculations for 2318 even-even nuclei using the Skyrme HFB model to analyze nuclear stability and the energy components of nuclei.

II. FRAMEWORK OF THE MODEL

I. INTRODUCTION
II. FRAMEWORK OF THE MODEL
III. RESULTS AND DISCUSSIONS
IV. SUMMARY

In HFB calculations, the Hamiltonian of a system with interacting fermions is written in terms of the annihilation and creation operators $(c,c^{\dagger})$ as [16, 17]:

$\begin{aligned} H=\sum_{\mu\mu'}T_{\mu\mu'}c_{\mu}^{\dagger}c_{\mu}'+\frac{1}{4}\sum_{\mu\nu\mu'\nu'}\tilde{V}_{\mu\nu\mu'\nu'}c_{\mu}^{\dagger}c_{\nu}^{ \dagger}c_{\nu'}c_{\mu'}, \end{aligned}$

(1)

in which $T_{\mu\mu'} = -\dfrac{\hbar^2}{2m} \langle \mu|\nabla^{2}|\mu' \rangle$ and $\tilde{V}_{\mu\nu\mu'\nu'} = \langle \mu\nu|V(r_{12})|\mu'\nu'- \nu'\mu'\rangle$ are the single-particle kinetic energy matrix elements and anti-symmetrized two-body interaction matrix elements, respectively. In the HFB model, the particle operators are transformed into quasiparticle operators through the Bogoliubov transformation to handle the pairing correlation

$\begin{aligned}[b]& \alpha_{\mu}=\sum_{\nu}(U^{\ast}_{\nu \mu}c_{\nu}+V^{\ast}_{\nu \mu}c_{\nu}^{\dagger}), \\&\alpha_{\mu}^{ \dagger}=\sum_{\nu}(V_{\nu\mu}c_{\nu}+U_{\nu \mu}c_{\nu}^{\dagger}), \end{aligned}$

(2)

where U and V are the transformation matrices. The quasiparticle vacuum state is defined as the HFB ground state $|\Phi \rangle$ , satisfying the condition $\alpha_{\mu} |\Phi \rangle = 0$ . By applying Wick's theorem, the expectation value of the Hamiltonian H can be expressed as a function of the Hermitian density matrix ρ and pairing tensor κ [16]

$\begin{aligned} E[\rho,\kappa] = \langle\Phi|H|\Phi\rangle, \end{aligned}$

(3)

where $\rho_{\mu\mu^{\prime}}=\langle\Phi|c^{\dagger}_{\mu^{\prime}}c_{\mu}|\Phi\rangle$ and $\kappa_{\mu\mu^{\prime}}=\langle\Phi|c_{\mu^{\prime }}c_{\mu}|\Phi\rangle$ .

In coordinate space, the operators $c_{{\boldsymbol{r}}\sigma q}$ and $c^{\dagger}_{{\boldsymbol{r}}\sigma q}$ refer to annihilation and creation of nucleons, respectively, at point ${\boldsymbol{r}}$ with spin $\sigma = \pm {1}/{2}$ and isospin $q = \pm {1}/{2}$ , which using the quasiparticle operators are expressed as

$\begin{aligned}[b] c_{{\boldsymbol{r}}\sigma q} = \sum_{\nu} \left[ U_{\nu}({\boldsymbol{r}}, \sigma, q) \alpha_{\nu} + V_{\nu}^*({\boldsymbol{r}}, \sigma, q) \alpha_{\nu}^\dagger \right],\\ c^{\dagger}_{{\boldsymbol{r}}\sigma q} = \sum_{\nu} \left[ V_{\nu}({\boldsymbol{r}}, \sigma, q) \alpha_{\nu} + U_{\nu}^*({\boldsymbol{r}}, \sigma, q) \alpha_{\nu}^\dagger \right]. \end{aligned}$

(4)

The density matrix and the pairing tensor are expressed as

$\begin{aligned}[b] \rho({\boldsymbol{r}} \sigma q,{\boldsymbol{r}}' \sigma' q') =\;& \langle \Phi | c^{\dagger}_{{\boldsymbol{r}}'\sigma' q'} c_{{\boldsymbol{r}}\sigma q} | \Phi \rangle \\=\;& \sum_{\nu} V_{\nu}^*({\boldsymbol{r}}, \sigma, q) V_{\nu}({\boldsymbol{r}}', \sigma', q'),\\ \kappa({\boldsymbol{r}} \sigma q,{\boldsymbol{r}}' \sigma' q') =\;& \langle \Phi | c_{{\boldsymbol{r}}'\sigma' q'} c_{{\boldsymbol{r}}\sigma q} | \Phi \rangle \\= \;&\sum_{\nu} V_{\nu}^*({\boldsymbol{r}}, \sigma, q) U_{\nu}({\boldsymbol{r}}', \sigma', q'). \end{aligned}$

(5)

where κ can be replaced by the pairing density matrix via $\tilde{\rho}({\boldsymbol{r}} \sigma q,{\boldsymbol{r}}' \sigma' q') = -2 \sigma '\kappa({\boldsymbol{r}} \sigma q,{\boldsymbol{r}}' -\sigma'q')$ for convenience to describe time-even quasiparticle states when both ρ and $\tilde{\rho}$ are Hermitian and time-even [16].

With the Skyrme force characterized by zero-range and non-local interaction, the HFB energy in Eq. (3) can be expressed as the volume integral of the energy density

$\begin{aligned} E[\rho,\tilde{\rho}]=\int\text{d}^{3}{ \boldsymbol{r}}\,{\cal{H}}({\boldsymbol{r}})\, , \end{aligned}$

(6)

${\cal{H}}({\boldsymbol{r}})={\cal{H}}_{\rm S}({\boldsymbol{r}})+{\cal{\tilde{H}}}_{\rm P}({\boldsymbol{r}}) + {\cal{H}}_{\rm C}({\boldsymbol{r}})$ includes the energy densities of Skyrme interaction ${\cal{H}}_{\rm S}({\boldsymbol{r}})$ , pairing ${\cal{\tilde{H}}}_{\rm P}({\boldsymbol{r}})$ , and Coulomb interaction ${\cal{H}}_{\rm C}({\boldsymbol{r}})$ for protons. The mean field with Skyrme force ${\cal{H}}_{\rm S}({\boldsymbol{r}})$ is a functional of the particle density $\rho = \sum_{q}\rho_{q}$ , kinetic-energy density $\tau = \sum_{q}\tau_{q}$ , and spin-current tensor ${\boldsymbol{J}}_{ij} = \sum_{q}{\boldsymbol{J}}_{q,ij}$ , with index $q=p,n$ corresponding to proton and neutron, respectively:

$\begin{aligned}[b] {\cal{H}}_{\rm S}({\boldsymbol{r}}) =\;& \frac{\hbar^{2}}{2m}\tau+\frac{1}{2}t_{0}\bigg{[}\bigg{(}1+\frac{1 }{2}x_{0}\bigg{)}\rho^{2}-\bigg{(}\frac{1}{2}+x_{0}\bigg{)}\sum_{q}\rho_{q}^{2} \bigg{]}+\frac{1}{2}t_{1}\bigg{[}\bigg{(}1+\frac{1}{2}x_{1}\bigg{)}\rho\bigg{(}\tau-\frac{3}{4}\Delta\rho\bigg{)} -\bigg{(}\frac{1}{2}+x_{1}\bigg{)}\sum_{q}\rho_{q}\bigg{(}\tau_{q}-\frac{3}{4}\Delta\rho_{q}\bigg{)}\bigg{]}\\ &+\frac{1}{2}t_{2}\bigg{[}\bigg{(}1+\frac{1}{2}x_{2}\bigg{)}\rho\bigg{(}\tau+\frac{1}{4}\Delta\rho\bigg{)} -\bigg{(}\frac{1}{2}+x_{2}\bigg{)}\sum_{q}\rho_{q}\bigg{(}\tau_{q}+\frac{1}{4}\Delta\rho_{q}\bigg{)}\bigg{]}+ \frac{1}{12}t_{3}\rho^{\alpha}\bigg{[}\bigg{(}1+\frac{1}{2}x_{3}\bigg{)}\rho^{2}-\bigg{(}x_{3}+\frac{1}{2}\bigg{)}\sum_{q}\rho_{q}^{2}\bigg{]}\\ & -\frac{1}{8}(t_{1}x_{1}+t_{2}x_{2})\sum_{ij}{\boldsymbol{J}}_{ij}^{2}+\frac{1}{8}(t_{1}-t_{2})\sum_{q,ij}{\boldsymbol{J}}_{q,ij}^{2} -\frac{1}{2}W_{0}\sum_{ijk}\varepsilon_{ijk}\bigg{[}\rho\nabla_{k}{\boldsymbol{J}}_{ij}+\sum_{q}\rho_{q}\nabla_{k}{\boldsymbol{J}}_{q,ij}\bigg{]}, \end{aligned}$

(7)

where $\varepsilon_{ijk}$ is the Levi-Civita symbol with $i,j,k=$ (1, 2, 3), and $(x_{0},x_{1},x_{2},x_{3},t_{0},t_{1},t_{2},t_{3},W_{0},\alpha)$ are the parameters of the Skyrme force. The pairing energy density is expressed as

$\begin{aligned} {\cal{\tilde{H}}}_{\rm P}({\boldsymbol{r}})=\frac{1}{2} V_{0}\bigg{[}1-\frac{1}{2}\frac{\rho}{\rho_{0}}\bigg{]}\sum_{q}\tilde{\rho}_{q}^{2} \end{aligned}$

(8)

with $V_{0}$ the pairing strength and $\rho_{0}$ the saturation density determined by the Skyrme parameters. The Coulomb interaction should be included into the energy densities for the case of proton

$\begin{aligned} {\cal{H}}_{\rm C}({\boldsymbol{r}})=\frac{e^2}{2}\rho_{p} \int \text{d}^{3}{\boldsymbol{r'}}\,\frac{\rho_{p}({\boldsymbol{r'}})}{|{\boldsymbol{r}}-{\boldsymbol{r'}}|} - \frac{3}{4}e^2\bigg{(}\frac{3}{\pi}\bigg{)}^{1/3}\rho_{p}^{4/3} . \end{aligned}$

(9)

The Skyrme HFB equations can be obtained by varying the HFB energy in Eq. (6) with respect to ρ and $\tilde{\rho}$ . Detailed expressions are available in the literature [16−18]. After obtaining self-consistent solutions to the ground-state density matrix ρ and pairing density matrix $\tilde{\rho}$ using the Skyme HFB equations, the kinetic energy can be expressed as:

$\begin{aligned} T= \frac{\hbar^{2}}{2m} \int \tau \,\text{d}^{3}{\boldsymbol{r}} \end{aligned}$

(10)

and total energy $E_{\rm tot}$ in the ground state can be obtained. The contribution of the non-local term of the Skyrme interaction to the kinetic energy is incorporated via solving the density matrix under single-particle potential. The potential energy U is calculated by subtracting the kinetic energy from the total energy

$\begin{aligned} U = E_{\rm tot} - T, \end{aligned}$

(11)

which includes contributions from the mean field, pairing energy, and Coulomb energy. Based on the predicted kinetic and potential energies for a nucleus, the ratio $T/U$ for the nucleus in its ground state can be obtained.

The axially deformed solution of the Skyrme HFB equations can be obtained by using the transformed harmonic oscillator basis [16−18, 21−23], and the corresponding code HFBTHO (v2.00d) was used in the calculations. A series of Universal Nuclear Energy Density Functionals (UNEDFs) [24] are proposed to provide a more accurate description of the properties of the ground state nuclei. The HFBTHO (v2.00d) also implements HFB calculations adopting the UNEDF functional. In this work, the UNEDF0 functional and standard Skyrme functionals SLy4 [25], SkM* [26] and SIII [27] were adopted. The number of oscillator shells was set as $N_{\text{max}}^{\text{shells}}=20$ and the total number of states in the basis was $N_{\text{states}}=1771$ . The default value $b_{0}=-1.0$ fm was used for the oscillator length, which means that the code automatically sets $b_{0}=\sqrt{\hbar /m\omega }$ with $\hbar \omega = 1.2\times 41/A^{1/3}$ [17]. The pairing force was assumed to be $V_{\text{pair}}^{{n,p}}=V_{0}^{{n,p}}\left ( 1-\dfrac{1}{2} \dfrac{\rho \left ( \vec r \right ) }{\rho _{0}} \right ) \delta ( \vec r-\vec{r'} )$ with $\rho _{0}=0.16\; \rm{fm}^{-3}$ , and a pre-defined pairing strength $V_{0}^{{n,p}}$ was used for each Skyrme force for simplicity. The default value adopted for the quasi-particle cutoff energy was $E_{\text{cut}}=60.0$ MeV.

III. RESULTS AND DISCUSSIONS

I. INTRODUCTION
II. FRAMEWORK OF THE MODEL
III. RESULTS AND DISCUSSIONS
IV. SUMMARY

Based on the Skyrme HFB code HFBTHO (v2.00d) [17], we systematically investigated the ground state properties of even-even nuclei with $8\leq Z \leq 130$ . First, we checked the calculated binding energies by adopting different Skyrme parameter sets. In Fig. 1, we show the calculated ground state energies $E_{\rm{tot}}$ for the isobaric chains with $A=40$ , 100, 150, 208, 228, and 256 using UNEDF0, SLy4, SkM* and SIII. The experimental data from AME2020 [28] are also presented for comparison. The data are reasonably well reproduced for medium mass nuclei with all four Skyrme forces. For heavy nuclei with $A > 200$ , the uncertainties of the predictions from these Skyrme forces significantly increase, especially for neutron rich nuclei. Note that the calculated results with UNEDF0 are the best for nuclei shown in Fig. 1. UNEDF0 demonstrates better predictive capabilities in the region of heavy nuclei, possibly due to its refined treatment of isospin dependence. We therefore adopted UNEDF0 for the following analysis of the total energies and kinetic to potential energy $T/U$ ratios.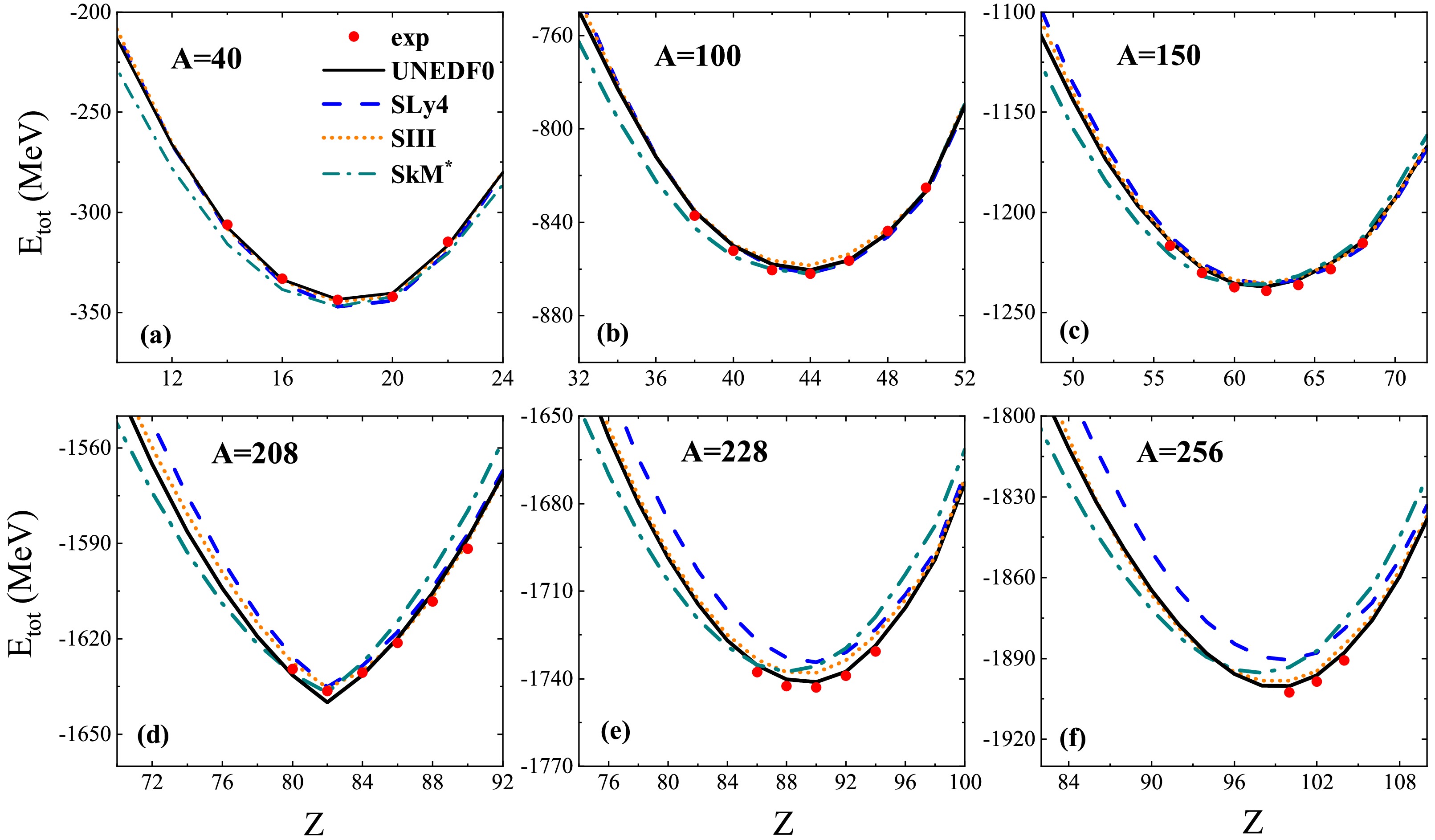

Figure 1

Figure 1. (color online) Nuclear ground state energies

$E_{\rm tot}$ for nuclei with

$A=40$ , 100, 150, 208, 228, 256. The curves denote the calculated results with UNEDF0, SLy4, SIII, and SkM*. The red circles denote the experimental data [28].

DownLoad: Full-Size Img PowerPoint

The nucleus with the minimal energy for certain light and medium isobars can be considered as the most stable nuclide on this isobaric chain as mentioned previously. According to the available data [28], in Fig. 1, the corresponding known stable nuclei (e.g. $^{40}$ Ar, $^{40}$ Ca, $^{100}$ Ru, $^{100}$ Mo, $^{150}$ Nd, $^{150}$ Sm and $^{208}$ Pb) are located around the valleys of the ground state energies for the isobaric chains with $Z\le 82$ . In addition to the nuclear ground state energy $E_{\rm tot}$ , we concurrently investigated the corresponding ratio $T/U$ . Fig. 2 shows the ground state energy $E_{\rm tot}$ and $T/U$ ratio for isobaric chains with $A=40$ , 48, 208, 298, 90, and 120. The nuclei with minimal energies are generally those with maximal values of $T/U$ , which indicates that the ratio $T/U$ also has a close relationship with nuclear stability in addition to nuclear binding energy. The values of $T/U$ essentially show the relationship between the average kinetic and potential energies per nucleon, reflecting the relevance of nuclear force strength to the intensity of nucleonic motion. A larger average kinetic energy per nucleon $T/A$ may indicate a more vigorous nucleon motion. Similarly, a larger absolute value of the average potential energy per nucleon $|U|/A$ indicates a stronger attractive potential acting on the nucleon. Nuclear stability is therefore significantly influenced by the balance of T and U.

Figure 2

Figure 2. (color online) Comparison of the ground state energy

$E_{\rm tot}$ and the ratio

$T/U$ for isobaric chains with

$A=40$ , 48, 208, 298, 90, and 120. The dashed lines serve as a guide.

DownLoad: Full-Size Img PowerPoint

In Fig. 2, notably the isobars with $A=40$ and 48 and maximal values of $T/U$ are located at the double magic nuclei $^{40}$ Ca and $^{48}$ Ca, respectively, whereas the corresponding values of minimal $E_{\rm tot}$ are found at nuclides $^{40}$ Ar and $^{48}$ Ti. To investigate the influence of shell closure on $E_{\rm tot}$ and $T/U$ , we further analyzed the $T/U$ and $E_{\rm tot}$ for nuclei around $^{208}$ Pb. The predicted ground state energy $E_{\rm tot}$ and corresponding $T/U$ ratio for isobaric chains with $A=202$ , 204, 206, and 210 are shown in Fig. 3. The peaks of $T/U$ for these isobars are all located at proton magic number $Z=82$ . For $^{210}$ Pb with proton shell closure and $^{210}$ Po with neutron shell closure, the predicted values of $T/U$ are very close to each other. Apparently, the known magic numbers can be more clearly observed from the ratio $T/U$ , which can be helpful for exploring the magic numbers in the super-heavy region.

Figure 3

Figure 3. (color online) The same as Fig. 2 but for isobaric chains with

$A=202$ , 204, 206, and 210.

DownLoad: Full-Size Img PowerPoint

To further analyze the difference between $E_{\rm tot}$ and $T/U$ , we systematically investigated the $T/U$ ratios for even-even nuclei with $8\leq Z \leq 130$ . Fig. 4 shows the nuclei with maximal $T/U$ on a given isobaric chain predicted by the HFBTHO calculations with UNEDF0. The solid curve denotes the predicted β-stability line according to Green's formula [29], $Z=A/2[1-0.4A/ (A+200)]$ . In the regions with known stable nuclei, the predicted nuclei with maximal $T/U$ are generally located around the β-stability line. In addition, the calculated nuclei with minimal total energy $E_{\rm tot}$ are also presented for comparison. In the super-heavy mass region, the number of nuclei obtained from $T/U$ is much more than that from $E_{\rm tot}$ at $N=184$ . Note that the nuclei with $Z=108$ and $Z=118$ obtained from $T/U$ are far more numerous than the neighboring nuclei.

Figure 4

Figure 4. (color online) Nuclear β-stability line. The gray squares denote the known even-even stable nuclei. The circles and red squares denote the calculated even-even nuclei with maximal

$T/U$ and those with minimal

$E_{\rm tot}$ , respectively. The solid curve denotes the results of Green's formula.

DownLoad: Full-Size Img PowerPoint

Notably, the central position of the "island of stability" is closely related to the microscopic shell correction energies of nuclei which are usually estimated by subtracting the smooth macroscopic part from $E_{\rm tot}$ . In this work, we studied the corresponding microscopic energies of nuclei by combining the modified Bethe-Weizsäcker mass formula [30, 31]

$\begin{aligned} E_{\rm LD}(A,Z)=a_{v} A + a_{s} A^{2/3}+ a_{c} \frac{Z(Z-1)}{A^{1/3}} \left ( 1- Z^{-2/3} \right) + a_{\rm sym} I^2 A. \end{aligned}$

(12)

Here, the parameters in Eq. (12) are determined by fitting the calculated ground-state energies of 2138 even-even nuclei with UNEDF0. In Fig. 5, we show the contour plots of the calculated microscopic energies $E_{\rm tot}-E_{\rm LD}$ for nuclei with $Z\ge 90$ . In the region $N>126$ , one can see two islands: one located around $N=152- 162$ , $Z=102-108$ and the other located around $N=184$ , which is consistent with the predicted $T/U$ ratios. The predicted microscopic energy for the super-heavy nucleus ( $Z=120,\; N=184$ ) is approximately 7 MeV, which is comparable with the results of macroscopic-microscopic mass models [32, 33].

Figure 5

Figure 5. (color online) Microscopic energy (in MeV)

$E_{\rm tot}-E_{\rm LD}$ based on the ground state energy from UNEDF0 and smoothed liquid-drop energy

$E_{\rm LD}$ from the modified Bethe-Weizsäcker mass formula. The dashed lines serve as a guide.

DownLoad: Full-Size Img PowerPoint

In Fig. 6(a), the peak values of $T/U$ are displayed for each isobaric chain as a function of mass number A. For heavy nuclei, the maximum of $T/U$ in general decreases linearly with A. The oscillations in the HFBTHO+UNEDF0 results are mainly due to the microscopic shell effects. For light stable nuclei with $A<50$ , the contribution of nuclear surface energy is evident from Eq. (12), and the average kinetic energy per nucleon is relatively low, which results in a larger $T/U$ ratio compared with those of the heavy nuclei. In Fig. 6 (b), the average kinetic energy per nucleon significantly increases with mass number A in the region $A<150$ . In the heavy and superheavy mass region ( $A>150$ ), the average kinetic energy per nucleon generally approaches a constant due to nuclear density saturation. Coulomb energy is known to significantly increase with charge number Z in the heavy mass region, which results in a reduction of the total potential energy in absolute value. For stable nuclei in the medium-heavy mass region, the nearly linear dependence of $T/U$ on mass number A is clearly observed in Fig. 6(a), which is mainly due to the competition between the significant increase in Coulomb energy and saturation behavior of the nuclear force.

Figure 6

Figure 6. (color online) (a) Maximum of the ratio

$T/U$ for each isobaric chain as a function of mass number A. (b) The corresponding average kinetic energy per nucleon

$T/A$ (dashed curve) and average potential energy per nucleon

$U/A$ (solid curve).

DownLoad: Full-Size Img PowerPoint

The virial theorem states that for an inverse square force field (such as Coulomb potential), the ratio of kinetic to potential energy is $T/|U| = 0.5$ . According to the HFBTHO calculations, the absolute values of $T/U$ for bound nuclei are approximately $0.65 \sim 0.75$ , which implies that the short-range characteristic and complexity of the nuclear force may lead to a different virial theorem. The linear dependence of $T/U$ on mass number A for heavy nuclei can be helpful in further exploring the virial theorem of nuclear forces and equation of state for neutron stars.

IV. SUMMARY

I. INTRODUCTION
II. FRAMEWORK OF THE MODEL
III. RESULTS AND DISCUSSIONS
IV. SUMMARY

In this study, we investigated the nuclear ground state energies and the ratios of kinetic energy T to potential energy U using HFBTHO. Based on the Skyrme energy density functional UNEDF0, the ratios $T/U$ for 2318 even-even nuclei were systematically calculated. We note that the nuclei with maximal value of $T/U$ for a certain isobaric chain are generally stable or long-lived. Also note that the known magic numbers can be more clearly observed from the ratio $T/U$ than from nuclear binding energy, particularly for isobaric chains with semi-magic nuclei (with magic numbers for either proton or neutron). Combining nuclear binding energies with the values of $T/U$ from the Skyrme HFB calculations, the magic numbers in super-heavy mass region were studied. In the super-heavy mass region, the neutron magic number $N=184$ was clearly observed from the obtained $T/U$ ratios and extracted microscopic energy of nuclei using UNEDF0. We also found that the nuclei with $Z=108$ and $Z=118$ obtained from $T/U$ are much more numerous than the neighboring nuclei, which is helpful for exploring the shell structure of superheavy nuclei. For super-heavy nuclei with $Z=118$ and $N=178-196$ , the calculated deformations of the nuclei were spherical or oblate in shape, whereas the predicted $^{292-300}$ Fl were all spherical in shape. Therefore, further investigations into the influence of nuclear oblate deformations on the stability of super-heavy nuclei are required in the future. The $T/U$ peak value can be used as a supplementary indicator in selecting potential long-lived superheavy nuclei. In addition, we note that the obtained $T/U$ ratios decreased almost linearly with mass number A for heavy nuclei around the β-stability line due to the competition between strong Coulomb repulsion and the saturation property of the nuclear force, which implies that the short-range characteristic and complexity of the nuclear force may lead to a different virial theorem.

References

[1]	W. D. Myers and W. J. Swiatecki, Nucl. Phys. A 81(1), 1 (1966) doi: 10.1016/0029-5582(66)90639-0
[2]	S. G. Nilsson, J. R. Nix, A. Sobiczewski, et al., Nucl. Phys. A 115(3), 545 (1968) doi: 10.1016/0375-9474(68)90748-3
[3]	S. G. Nilsson, C. F. Tsang, A. Sobiczewski, et al., Nucl. Phys. A 131(1), 1 (1969) doi: 10.1016/0375-9474(69)90809-4
[4]	M. Bender, W. Nazarewicz and P. G. Reinhard, Phys. Lett. B 515, 42 (2001) doi: 10.1016/S0370-2693(01)00863-2
[5]	A. T. Kruppa, M. Bender, W. Nazarewicz, et al., Phys. Rev. C 61, 034313 (2000) doi: 10.1103/PhysRevC.61.034313
[6]	K. Morita, K. Morimoto, D. Kaji, et al., J. Phys. Soc. Jpn. 73(10), 2593 (2004) doi: 10.1143/JPSJ.73.2593
[7]	K. Morita, K. Morimoto, D. Kaji, et al., J. Phys. Soc. Jpn. 76(4), 045001 (2007) doi: 10.1143/JPSJ.76.045001
[8]	Y. T. Oganessian, A. V. Yeremin, A. G. Popeko, et al., Nature 400, 242 (6741) doi: 10.1038/22281
[9]	Y. T. Oganessian, F. S. Abdullin, P. D. Bailey, et al., Phys. Rev. C 63, 011301 (2000) doi: 10.1103/PhysRevC.83.054315
[10]	Y. T. Oganessian, V. K. Utyonkov, Yu. V. Lobanov, et al., Phys. Rev. C 74, 044602 (2006) doi: 10.1103/PhysRevC.74.044602
[11]	Y. T. Oganessian, F. S. Abdullin, P. D. Bailey, et al., Phys. Rev. Lett. 104, 142502 (2010) doi: 10.1103/PhysRevLett.104.142502
[12]	Y. T. Oganessian, F. S. Abdullin, S. N. Dmitriev, et al., Phys. Rev. C 87, 014302 (2013) doi: 10.1103/PhysRevC.87.014302
[13]	S. Ćwiok, P. H. Heenen and W. Nazarewicz, Nature 433, 705 (7027) doi: 10.1038/nature03336
[14]	J. M. Lattimer and M. Prakash, Astrophys. J. 550, 426 (2001) doi: 10.1086/319702
[15]	F. Özel, D. Psaltis, T. Güver, et al., Astrophys. J. 820, 28 (2016) doi: 10.3847/0004-637X/820/1/28
[16]	J. Dobaczewski, H. Flocard and J. Treiner, Nucl. Phys. A 422, 103 (1984) doi: 10.1016/0375-9474(84)90433-0
[17]	M. V. Stoitsov, J. Dobaczewski, W. Nazarewicz, et al., Comput. Phys. Commun. 167, 43 (2005) doi: 10.1016/j.cpc.2005.01.001
[18]	M. V. Stoitsov, N. Schunck, M. Kortelainen, et al., Comput. Phys. Commun. 184, 1592 (2013) doi: 10.1016/j.cpc.2013.01.013
[19]	G. Scamps, S. Goriely, E. Olsen, et al., Eur. Phys. J. A 57, 333 (2021) doi: 10.1140/epja/s10050-021-00642-1
[20]	S. Goriely, N. Chamel, and J.M. Pearson, Phys. Rev. Lett. 102, 152503 (2009) doi: 10.1103/PhysRevLett.102.152503
[21]	M. Bender, P. H. Heenen and P. G. Reinhard, Rev. Mod. Phys. 75, 121 (2003) doi: 10.1103/RevModPhys.75.121
[22]	Y. El Bassem and M. Oulne, Nucl. Phys. A 957, 22 (2017) doi: 10.1016/j.nuclphysa.2016.07.005
[23]	Ali H. Taqi, Malik A. Hasan, Arab. J. Sci. Eng. 47, 761 (2022) doi: 10.1007/s13369-021-05345-9
[24]	M. Kortelainen, T. Lesinski, J. Moré, et al., Phys. Rev. C 82, 024313 (2010) doi: 10.1103/PhysRevC.82.024313
[25]	E. Chabanat, P. Bonche, P. Haensel, et al., Nucl. Phys. A 635, 231 (1998) doi: 10.1016/S0375-9474(98)00180-8
[26]	J. Bartel, P. Quentin, M. Brack, et al., Nucl. Phys. A 386, 79 (1982) doi: 10.1016/0375-9474(82)90403-1
[27]	M. Beiner, H. Flocard, N. Van Giai, et al., Nucl. Phys. A 238, 29 (1975) doi: 10.1016/0375-9474(75)90338-3
[28]	M. Wang, W. J. Huang, F. G. Kondev, et al., Chin. Phys. C 45, 030003 (2021) doi: 10.1088/1674-1137/abddaf
[29]	Alex E. S. Green, Phys. Rev. 99, 1410 (1955) doi: 10.1103/PhysRev.99.1410
[30]	H. A. Bethe and R. F. Bacher, Rev. Mod. Phys. 8, 82 (1936) doi: 10.1103/RevModPhys.8.82
[31]	N. Wang, M. Liu and X. Z. Wu, Phys. Rev. C 81, 044322 (2010) doi: 10.1103/PhysRevC.81.044322
[32]	N. Wang, M. Liu, X. Z. Wu, et al., Phys. Lett. B 734, 215 (2014) doi: 10.1016/j.physletb.2014.05.049
[33]	P. Möller, J. R. Nix, W. D. Myers, et al., At. Data Nucl. Data Tables 59(2), 185 (1995) doi: 10.1006/adnd.1995.1002

References

[1]	W. D. Myers and W. J. Swiatecki, Nucl. Phys. A 81(1), 1 (1966) doi: 10.1016/0029-5582(66)90639-0
[2]	S. G. Nilsson, J. R. Nix, A. Sobiczewski, et al., Nucl. Phys. A 115(3), 545 (1968) doi: 10.1016/0375-9474(68)90748-3
[3]	S. G. Nilsson, C. F. Tsang, A. Sobiczewski, et al., Nucl. Phys. A 131(1), 1 (1969) doi: 10.1016/0375-9474(69)90809-4
[4]	M. Bender, W. Nazarewicz and P. G. Reinhard, Phys. Lett. B 515, 42 (2001) doi: 10.1016/S0370-2693(01)00863-2
[5]	A. T. Kruppa, M. Bender, W. Nazarewicz, et al., Phys. Rev. C 61, 034313 (2000) doi: 10.1103/PhysRevC.61.034313
[6]	K. Morita, K. Morimoto, D. Kaji, et al., J. Phys. Soc. Jpn. 73(10), 2593 (2004) doi: 10.1143/JPSJ.73.2593
[7]	K. Morita, K. Morimoto, D. Kaji, et al., J. Phys. Soc. Jpn. 76(4), 045001 (2007) doi: 10.1143/JPSJ.76.045001
[8]	Y. T. Oganessian, A. V. Yeremin, A. G. Popeko, et al., Nature 400, 242 (6741) doi: 10.1038/22281
[9]	Y. T. Oganessian, F. S. Abdullin, P. D. Bailey, et al., Phys. Rev. C 63, 011301 (2000) doi: 10.1103/PhysRevC.83.054315
[10]	Y. T. Oganessian, V. K. Utyonkov, Yu. V. Lobanov, et al., Phys. Rev. C 74, 044602 (2006) doi: 10.1103/PhysRevC.74.044602
[11]	Y. T. Oganessian, F. S. Abdullin, P. D. Bailey, et al., Phys. Rev. Lett. 104, 142502 (2010) doi: 10.1103/PhysRevLett.104.142502
[12]	Y. T. Oganessian, F. S. Abdullin, S. N. Dmitriev, et al., Phys. Rev. C 87, 014302 (2013) doi: 10.1103/PhysRevC.87.014302
[13]	S. Ćwiok, P. H. Heenen and W. Nazarewicz, Nature 433, 705 (7027) doi: 10.1038/nature03336
[14]	J. M. Lattimer and M. Prakash, Astrophys. J. 550, 426 (2001) doi: 10.1086/319702
[15]	F. Özel, D. Psaltis, T. Güver, et al., Astrophys. J. 820, 28 (2016) doi: 10.3847/0004-637X/820/1/28
[16]	J. Dobaczewski, H. Flocard and J. Treiner, Nucl. Phys. A 422, 103 (1984) doi: 10.1016/0375-9474(84)90433-0
[17]	M. V. Stoitsov, J. Dobaczewski, W. Nazarewicz, et al., Comput. Phys. Commun. 167, 43 (2005) doi: 10.1016/j.cpc.2005.01.001
[18]	M. V. Stoitsov, N. Schunck, M. Kortelainen, et al., Comput. Phys. Commun. 184, 1592 (2013) doi: 10.1016/j.cpc.2013.01.013
[19]	G. Scamps, S. Goriely, E. Olsen, et al., Eur. Phys. J. A 57, 333 (2021) doi: 10.1140/epja/s10050-021-00642-1
[20]	S. Goriely, N. Chamel, and J.M. Pearson, Phys. Rev. Lett. 102, 152503 (2009) doi: 10.1103/PhysRevLett.102.152503
[21]	M. Bender, P. H. Heenen and P. G. Reinhard, Rev. Mod. Phys. 75, 121 (2003) doi: 10.1103/RevModPhys.75.121
[22]	Y. El Bassem and M. Oulne, Nucl. Phys. A 957, 22 (2017) doi: 10.1016/j.nuclphysa.2016.07.005
[23]	Ali H. Taqi, Malik A. Hasan, Arab. J. Sci. Eng. 47, 761 (2022) doi: 10.1007/s13369-021-05345-9
[24]	M. Kortelainen, T. Lesinski, J. Moré, et al., Phys. Rev. C 82, 024313 (2010) doi: 10.1103/PhysRevC.82.024313
[25]	E. Chabanat, P. Bonche, P. Haensel, et al., Nucl. Phys. A 635, 231 (1998) doi: 10.1016/S0375-9474(98)00180-8
[26]	J. Bartel, P. Quentin, M. Brack, et al., Nucl. Phys. A 386, 79 (1982) doi: 10.1016/0375-9474(82)90403-1
[27]	M. Beiner, H. Flocard, N. Van Giai, et al., Nucl. Phys. A 238, 29 (1975) doi: 10.1016/0375-9474(75)90338-3
[28]	M. Wang, W. J. Huang, F. G. Kondev, et al., Chin. Phys. C 45, 030003 (2021) doi: 10.1088/1674-1137/abddaf
[29]	Alex E. S. Green, Phys. Rev. 99, 1410 (1955) doi: 10.1103/PhysRev.99.1410
[30]	H. A. Bethe and R. F. Bacher, Rev. Mod. Phys. 8, 82 (1936) doi: 10.1103/RevModPhys.8.82
[31]	N. Wang, M. Liu and X. Z. Wu, Phys. Rev. C 81, 044322 (2010) doi: 10.1103/PhysRevC.81.044322
[32]	N. Wang, M. Liu, X. Z. Wu, et al., Phys. Lett. B 734, 215 (2014) doi: 10.1016/j.physletb.2014.05.049
[33]	P. Möller, J. R. Nix, W. D. Myers, et al., At. Data Nucl. Data Tables 59(2), 185 (1995) doi: 10.1006/adnd.1995.1002

[1]	K. S. Kim , Soonchul Choi , Hana Gil , Chang Ho Hyun . Inclusive quasielastic neutrino-nucleus scattering with energy density functional nuclear models. Chinese Physics C, 2024, 48(8): 084101. doi: 10.1088/1674-1137/ad4855
[2]	W. M. Seif , A. S. Hashem . Constraints on the nuclear symmetry energy and its density slope from the α decay process. Chinese Physics C, 2018, 42(6): 064104. doi: 10.1088/1674-1137/42/6/064104
[3]	S. S. Hosseini , H. Hassanabadi . Theoretical approaches to alpha decay half-lives of super-heavy nuclei. Chinese Physics C, 2017, 41(6): 064101. doi: 10.1088/1674-1137/41/6/064101
[4]	Zhong Xu , Zhi-Pan Li . Microscopic analysis of octupole shape transitions in neutron-rich actinides with relativistic energy density functional. Chinese Physics C, 2017, 41(12): 124107. doi: 10.1088/1674-1137/41/12/124107
[5]	Peng-Cheng Li , Hong-Fei Zhang , Yong-Jia Wang . Stability of super heavy nuclei associated with the updated nuclear data. Chinese Physics C, 2017, 41(11): 114103. doi: 10.1088/1674-1137/41/11/114103
[6]	M. Ismail , A. Y. Ellithi , A. Adel , Hisham Anwer . Islands of stability and quasi-magic numbers for super-and ultra-heavy nuclei. Chinese Physics C, 2016, 40(12): 124102. doi: 10.1088/1674-1137/40/12/124102
[7]	ZHANG Song , CHEN Jin-Hui , MA Yu-Gang , XU Zhang-Bu , CAI Xiang-Zhou , MA Guo-Liang , ZHONG Chen . Hypertriton and light nuclei production at Λ-production subthreshold energy in heavy-ion collisions. Chinese Physics C, 2011, 35(8): 741-746. doi: 10.1088/1674-1137/35/8/008
[8]	LIU Min , LI Zhu-Xia , WANG Ning , ZHANG Feng-Shou . Exploring nuclear symmetry energy with isospin dependence in neutron skin thickness of nuclei. Chinese Physics C, 2011, 35(7): 629-634. doi: 10.1088/1674-1137/35/7/006
[9]	WANG Nan , ZHOU Shan-Gui , ZHAO En-Guang . Influence of octupole deformation and orientation on the potential energy surface in the di-nuclear system model. Chinese Physics C, 2010, 34(10): 1615-1621. doi: 10.1088/1674-1137/34/10/012
[10]	YE Wei . Surveying the role of excitation energy in probing nuclear dissipation. Chinese Physics C, 2009, 33(7): 528-531. doi: 10.1088/1674-1137/33/7/005
[11]	CHEN Shuang , CHU Yan-Yun , REN Zhong-Zhou . Density-dependent potential for multi-neutron halo nuclei. Chinese Physics C, 2009, 33(8): 639-644. doi: 10.1088/1674-1137/33/8/008
[12]	CAO Xi-Guang , CHEN Jin-Gen , MA Yu-Gang , FANG De-Qing , TIAN Wen-Dong , YAN Ting-Zhi , CAI Xiang-Zhou . Density effect of the neutron halo nucleus induced reactions in intermediate energy heavy ion collisions. Chinese Physics C, 2009, 33(S1): 49-51. doi: 10.1088/1674-1137/33/S1/016
[13]	GUO Wen-Jun , LIU Jian-Ye . Isospin effects of the Skyrme potential and the momentum dependent interaction at intermediate energy heavy ion collisions. Chinese Physics C, 2008, 32(3): 172-176. doi: 10.1088/1674-1137/32/3/002
[14]	YE Yan-Lin , ZHOU Xiao-Hong , LIU Wei-Ping , MA Yu-Gang , ZHANG Yu-Hu , XU Fu-Rong . Outline of the progress in the study of radioactive nuclear physics and super-heavy nuclei. Chinese Physics C, 2008, 32(S2): 1-7.
[15]	Bai Ge , Li Jiarong . High Energy Unequal Nuclei Collision and Relaxation Time in a Relativistic Kinetic Equation. Chinese Physics C, 1994, 18(Z1): 55-60.
[16]	Liu Bo , Jiang Huanqing . The K⁺/π⁺ Ratio in High-Energy Nucleus Collisions and the Effect of Secondary Collisions. Chinese Physics C, 1993, 17(S4): 403-409.
[17]	Soren P. Sorensen , Zhao Weiqin . Influence of Finite Collision Time on Energy Density in Relativistic Heavy Ion Collisions. Chinese Physics C, 1993, 17(S1): 89-93.
[18]	Gao Yonghua , He Zhenmin , Huang Ruiwang , Peng Hong'an . The Influence of Nuclear Target on “Small” Mass Lepton Pair Production of High Energy Hadron-Nuclei Collision. Chinese Physics C, 1992, 16(S3): 281-289.
[19]	Zhuang Pengfei , Liu Lianshou . Estimation of the Maximum Energy Density in High Energy Heavy Ion Collisions and the Space-time Region for the Formation of Quark Matter. Chinese Physics C, 1991, 15(S3): 297-305.
[20]	Liu Yiming , Huo Lei , Jiang Yuzhen , Wang Shan , D. Keane , S. Y. Fung , S. Y. Chu . Source Density Distribution and Intensity Interferometry in High-energy Heavy-ion Collisions. Chinese Physics C, 1991, 15(S1): 33-41.

Access

Figures(6)

Get Citation

Ke-Hu Wang, Zhang-Ya Wang, Ning Wang and Min Liu. Nuclear stability and the ratio of kinetic to potential energy[J]. Chinese Physics C. doi: 10.1088/1674-1137/adc3ff

Ke-Hu Wang, Zhang-Ya Wang, Ning Wang and Min Liu. Nuclear stability and the ratio of kinetic to potential energy[J]. Chinese Physics C. doi: 10.1088/1674-1137/adc3ff shu

RIS(for EndNote,Reference Manager,ProCite)

BibTex

Txt

Milestone

Received: 2024-12-30

Article Metric

Article Views(588)
PDF Downloads(30)
Cited by(0)

Policy on re-use

To reuse of subscription content published by CPC, the users need to request permission from CPC, unless the content was published under an Open Access license which automatically permits that type of reuse.

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

HTML

I. INTRODUCTION

Nuclear stability is a cornerstone research theme in nuclear physics, governed by nucleon-nucleon interactions and manifested through critical observables including binding energy systematics, magic number configurations, decay modes, and half-life patterns. This fundamental property not only dictates the synthesis pathways of new isotopes and superheavy elements (SHEs) but also serves as a stringent testbed for nuclear models. The nuclear shell model initially proposed in the 1960s predicted post- $^{208}$ Pb magic numbers at $Z=114$ and $N=184$ [1−3], suggesting an "island of stability" centered at ( $Z=114$ , $N=184$ ) where superheavy nuclei might exhibit enhanced stability. However, modern self-consistent mean-field calculations reveal competing predictions, proton shell closures at $Z=120$ or 126 and neutron shell closures spanning $N=172-184$ [4, 5]. These theoretical divergences highlight the critical role of SHE stability studies in validating nuclear many-body approaches. Through fusion-evaporation reactions, superheavy nuclei with $104 \leq Z\leq 118$ have already been successfully synthesized in experiments [6−12]. The heaviest nucleus $^{294}$ Og that has been synthesized so far has a half-life on the order of milliseconds and is neutron-deficient due to the limitations in available projectile-target combinations and experimental facilities. The determination of nuclear stability exhibits mass-dependent characteristics. For light and medium nuclei ( $A<150$ ), β-decay predominance makes binding energy minimization along isobaric chains the key stability indicator. For heavy and super-heavy nuclei ( $A>200$ ), multi-mode decay competition disrupts simple energy-based predictions. For example, although the ground state energy of $^{214}$ Po is smaller than that of $^{214}$ Pb by 2.7 MeV, the half-life of $^{214}$ Pb is much larger than that of $^{214}$ Po, due to the different decay modes: $^{214}$ Pb via β-decay in contrast to $^{214}$ Po via α-decay. Therefore, new stability metrics beyond traditional binding energy considerations should be developed, particularly for SHEs. The enduring mystery surrounding the existence and location of the "island of stability" continues to drive interdisciplinary efforts combining nuclear experiments, astrophysical observations, and exascale computational modeling.

The binding energy of atomic nuclei predominantly arises from the dynamic equilibrium between the nuclear strong force and Coulomb repulsion [13], which governs their β-decay stability. Quantitatively, a net energy difference is manifested between the absolute values of the attractive nuclear potential energy U and the repulsive kinetic energy T. Notably, the $T/U$ ratio constitutes a fundamental parameter in nuclear astrophysics [14, 15], as it correlates with two critical phenomena: nuclear matter compressibility and stability mechanisms. The ratio $T/U$ provides insights into the stiffness of nuclear matter, a key determinant of neutron star interior structure and equation of state. In neutron stars, gravitational binding stability requires the dominance of gravitational potential energy $U_{\rm grav}$ over rotational kinetic energy $T_{\rm rot}$ . A significant imbalance ( $|U_{\rm grav}|\gg T_{\rm rot}$ ) may trigger catastrophic collapse into black holes. For atomic nuclei, the $T/U$ ratio reflects the interplay between nucleon-nucleon interaction strength (governed by nuclear force saturation) and nucleon motion intensity (driven by Fermi energy). Higher $T/U$ values typically indicate reduced binding coherence, thereby influencing fission barriers and decay modes. This intrinsic connection between the $T/U$ ratio and multi-scale stability (from femtometer-scale nuclei to kilometer-scale neutron stars) underscores its significance in unified nuclear many-body theories. Systematic investigations of this ratio across nuclear chart regions can unveil universal constraints on hadronic matter under extreme conditions.

The Skyrme Hartree-Fock-Bogoliubov (HFB) model is a versatile microscopic theoretical framework widely used in nuclear physics research, allowing the nuclear structure at ground state such as binding energies, charge radii, deformation and shape coexistence to be investigated self-consistently [16−20]. In this study, we performed systematic calculations for 2318 even-even nuclei using the Skyrme HFB model to analyze nuclear stability and the energy components of nuclei.

IV. SUMMARY

In this study, we investigated the nuclear ground state energies and the ratios of kinetic energy T to potential energy U using HFBTHO. Based on the Skyrme energy density functional UNEDF0, the ratios $T/U$ for 2318 even-even nuclei were systematically calculated. We note that the nuclei with maximal value of $T/U$ for a certain isobaric chain are generally stable or long-lived. Also note that the known magic numbers can be more clearly observed from the ratio $T/U$ than from nuclear binding energy, particularly for isobaric chains with semi-magic nuclei (with magic numbers for either proton or neutron). Combining nuclear binding energies with the values of $T/U$ from the Skyrme HFB calculations, the magic numbers in super-heavy mass region were studied. In the super-heavy mass region, the neutron magic number $N=184$ was clearly observed from the obtained $T/U$ ratios and extracted microscopic energy of nuclei using UNEDF0. We also found that the nuclei with $Z=108$ and $Z=118$ obtained from $T/U$ are much more numerous than the neighboring nuclei, which is helpful for exploring the shell structure of superheavy nuclei. For super-heavy nuclei with $Z=118$ and $N=178-196$ , the calculated deformations of the nuclei were spherical or oblate in shape, whereas the predicted $^{292-300}$ Fl were all spherical in shape. Therefore, further investigations into the influence of nuclear oblate deformations on the stability of super-heavy nuclei are required in the future. The $T/U$ peak value can be used as a supplementary indicator in selecting potential long-lived superheavy nuclei. In addition, we note that the obtained $T/U$ ratios decreased almost linearly with mass number A for heavy nuclei around the β-stability line due to the competition between strong Coulomb repulsion and the saturation property of the nuclear force, which implies that the short-range characteristic and complexity of the nuclear force may lead to a different virial theorem.

Reference (33)

Nuclear stability and ratio of kinetic to potential energy

Abstract：

I. INTRODUCTION

I. INTRODUCTION
II. FRAMEWORK OF THE MODEL
III. RESULTS AND DISCUSSIONS
IV. SUMMARY

II. FRAMEWORK OF THE MODEL

I. INTRODUCTION
II. FRAMEWORK OF THE MODEL
III. RESULTS AND DISCUSSIONS
IV. SUMMARY

III. RESULTS AND DISCUSSIONS

I. INTRODUCTION
II. FRAMEWORK OF THE MODEL
III. RESULTS AND DISCUSSIONS
IV. SUMMARY

Figure 1

Figure 2

Figure 3

Figure 4

Figure 5

Figure 6

IV. SUMMARY

I. INTRODUCTION
II. FRAMEWORK OF THE MODEL
III. RESULTS AND DISCUSSIONS
IV. SUMMARY

References

References

Access

Article Metrics

Metrics

通讯作者: 陈斌, bchen63@163.com

Email This Article