Plasma effects on weak gravitational lensing and shadows of Sen black holes

Gravitational lensing, a notable consequence of Einstein's general relativity, occurs when the curvature of spacetime around a massive object, such as a black hole, bends the path of light from a distant source [1]. This phenomenon was first confirmed by Eddington's observation of light deflected by the Sun, establishing the significance of gravitational lensing in astrophysical research [2].

In the context of black holes, gravitational lensing becomes particularly fascinating owing to the extreme gravitational fields involved [3]. The study of weak gravitational lensing by black holes – where the deflection of light is subtle and occurs at more considerable distances from the event horizon – offers valuable insights into the properties of these enigmatic objects and their surrounding spacetime. Additionally, gravitational lensing has been a crucial tool for testing theories of gravity with precision and detecting exotic objects in the universe [4−7]. Gravitational lensing is a crucial tool in astrophysics and cosmology for testing fundamental gravity theories [8] and detecting dark matter and dark energy [9−11]. The study of weak lensing by black holes aids in our understanding of their intrinsic properties, where the deflection angle is assumed to be small. Weak lensing has been extensively studied [12, 13] and has effectively accounted for experimental tests of general relativity. The subtle lensing effects observed at more considerable distances can reveal deviations from theoretical models and potentially indicate the presence of new physics.

Theoretical studies of weak gravitational lensing by black holes have explored how various black hole solutions deflect light [14−16]. For instance, Virbhadra and Ellis (2000) provided a detailed analysis of weak lensing in the context of Schwarzschild black holes [17]. These analyses underscore the potential of gravitational lensing as a tool for probing black hole properties and testing general relativity. In addition to classical black holes, research has been extended to more complex solutions, such as Kerr black holes, which include rotation effects. Sereno and de Luca (2006) investigated analytical lensing for Kerr black holes, highlighting how spin influences lensing signatures [18], and numerous aspects are investigated using various models in Refs. [19−26]. Furthermore, several studies have extensively analyzed the weak gravitational lensing effects of black holes [27−35], including those for rotating black holes [36−38].

The interplay between gravitational and plasma effects becomes particularly significant near black holes, where the intense gravitational field is coupled with the presence of an accretion disk or a surrounding plasma medium. The influence of plasma on gravitational lensing has been explored in various theoretical frameworks. Perlick made significant advancements in explaining plasma effects [39], and Bisnovatyi-Kogan and Tsupko [40] conducted subsequent studies on topics such as the scale of stellar-mass black holes in X-ray binaries [41]. The presence of plasma can change the observed lensing features [42−59] and influence the size and shape of the black hole's shadow [60−69].

Understanding these effects is crucial for interpreting observational data, particularly with recent advances in high-resolution imaging. Observations of black hole shadows by the Event Horizon Telescope (EHT) [70−73] have provided new insights into gravity in extreme conditions, highlighting the increasing relevance of studying plasma effects in gravitational lensing. Plasma effects can alter the effective refractive index around a black hole, impacting the size and shape of the observed shadow. The EHT and other observational efforts have begun to reveal the intricate details of black holes and their surroundings, making the study of plasma effects in gravitational lensing increasingly relevant.

An accurate understanding of these effects is essential for interpreting observational data and distinguishing between black hole models. The primary objective of this paper is to investigate the weak gravitational lensing and shadow properties of the Sen black hole. Considering plasma effects, we investigate weak gravitational lensing and the shadow of Sen black holes. We aim to analyze the influence of plasma on weak lensing observables for Sen black holes. We examine the effects of plasma on the size and shape of the black hole shadow.

The spherical Sen black hole under consideration is a solution to the low-energy effective field equations of heterotic string theory, and both electric and magnetic charges characterize it. These black holes have a richer structure than their classical counterparts, making studying their gravitational lensing effects particularly interesting. The unique properties of the Sen black hole, including its dilaton and axion fields, influence the spacetime curvature differently from Schwarzschild black holes [74]. Recently, different types of studies have investigated the Sen black hole and its rotating generalization (the Kerr Sen black hole); see, for example, Refs. [75−81].

The remainder of this paper is organized as follows: In Sec. II, we explore particle dynamics around the Sen black hole in the presence of plasma using the Hamilton-Jacobi equation. The plasma effect on weak gravitational lensing around Sen black hole is considered in Sec. III. In Sec. IV, using the lens equation, we study the magnification of images. Subsequently, the time delay of light around the Sen black hole is discussed in Sec. V. Finally, we discuss obtained results in Sec. VI. Throughout this paper, we use geometrical units ($ c=1 $ and $ G=1 $).

Here, we review and discuss Sen black hole spacetime. The Sen black hole is a solution in heterotic string theory that describes spacetime emerging in the low-energy limit [82]. It includes the electromagnetic field $ A^\mu $ with the field-strength tensor $ F^{\mu \nu} $, the second-rank antisymmetric tensor field $ B_{\mu\nu} $ (also known as the Kalb-Ramond field [83]), and the dilaton field Φ. These components significantly influence the spacetime geometry and key parameters of the black hole, including the effective charge $ q_m $, which combines electromagnetic and dilatonic contributions. With the combined effects of these fields, the Sen solution exhibits a complex structure and provides a more complete description of the black hole in the context of string theory.

The Less black hole, also associated with the Kalb-Ramond field, describes only the interaction between the gravitational and Kalb-Ramond fields, excluding the influence of additional fields such as the dilaton. This makes the Less solution less complex but more specialized as it does not involve all the elements of string theory [83−86].

Both models include the Kalb-Ramond field. However, the Sen black hole has a more intricate structure because of the inclusion of electromagnetic and dilatonic effects. This makes it a more detailed and extensive solution within the framework of string theory. The action describing the spacetime of the Sen black hole in the string frame is presented as follows [74] (see also [87−90] for other black hole and black p-brane solutions in the low-energy limit of string theory):

where the Lagrangian $ {\cal{L}} $ is given by

with $ H_{k\lambda\mu} $, the third-rank tensor field (Kalb-Ramond three-form), defined in terms of the tensor gauge field and field-strength tensor of the electromagnetic field as

The general spherical symmetric metric ansatz is

The metric function derived in this configuration was determined by Sen in Ref. [74] and is expressed as

where $ q_m $ is an effective charge (including both the electric charge and an effective charge associated with the dilation field) measured by a static observer at infinity, which characterizes specific hair. The horizon properties indicate that the following condition must be satisfied: $ q_m \leqslant \sqrt{2} $. We easily observe that, at $ q_m=0 $, the Sen metric of the black hole coincides with the Schwarzschild metric. Here, we have introduced a new variable $ q_m^2=q $ for convenience.

In this subsection, we investigate the behavior of photon motion in the vicinity of a black hole when it is surrounded by plasma. To analyze this scenario, we can conveniently utilize the Hamilton-Jacobi equation, which is given by [91]

Here, $ x^\alpha $ describes the spacetime coordinates. We can use definition of the effective metric tensor $ \tilde{g}^{\alpha \beta} $ as [91]

where $ u^{\beta} $is the four velocity of the photon, and n denotes the refractive index of the medium. Its formula is [41]

where e and $ m_e $ are the electron charge and mass, respectively, and N is the number density of the electrons. The photon frequency $ \omega(r) $ measured by a static observer is determined using the gravitational redshift formula [41]

Here, $ \omega_0=\text{const} $ is the frequency measured by the observer at infinity. Light can propagate in plasma only when its frequency is greater than that of the plasma; therefore, the $ n > 0 $ condition must be satisfied.

The radius of a circular orbit of light around a black hole, particularly the one that forms a photon sphere of radius $ r_{ph} $, is determined by solving the following equation [92]:

where

By substituting Eq. (9) into Eq. (10), we can determine an algebraic equation for the photon radius $ r_{ph} $ in the presence of a plasma medium, which can be expressed as

Here, the prime denotes the derivative concerning the radial coordinate r. For most variants of $ \omega_p(r) $, the roots of the equation cannot be obtained analytically; however, we consider a few simplified cases in the following subsections.

First, we consider a homogeneous (uniform) plasma case with $ \omega^2_p(r)=\text{const} $. Here, we can solve Eq. (11) analytically and express it as

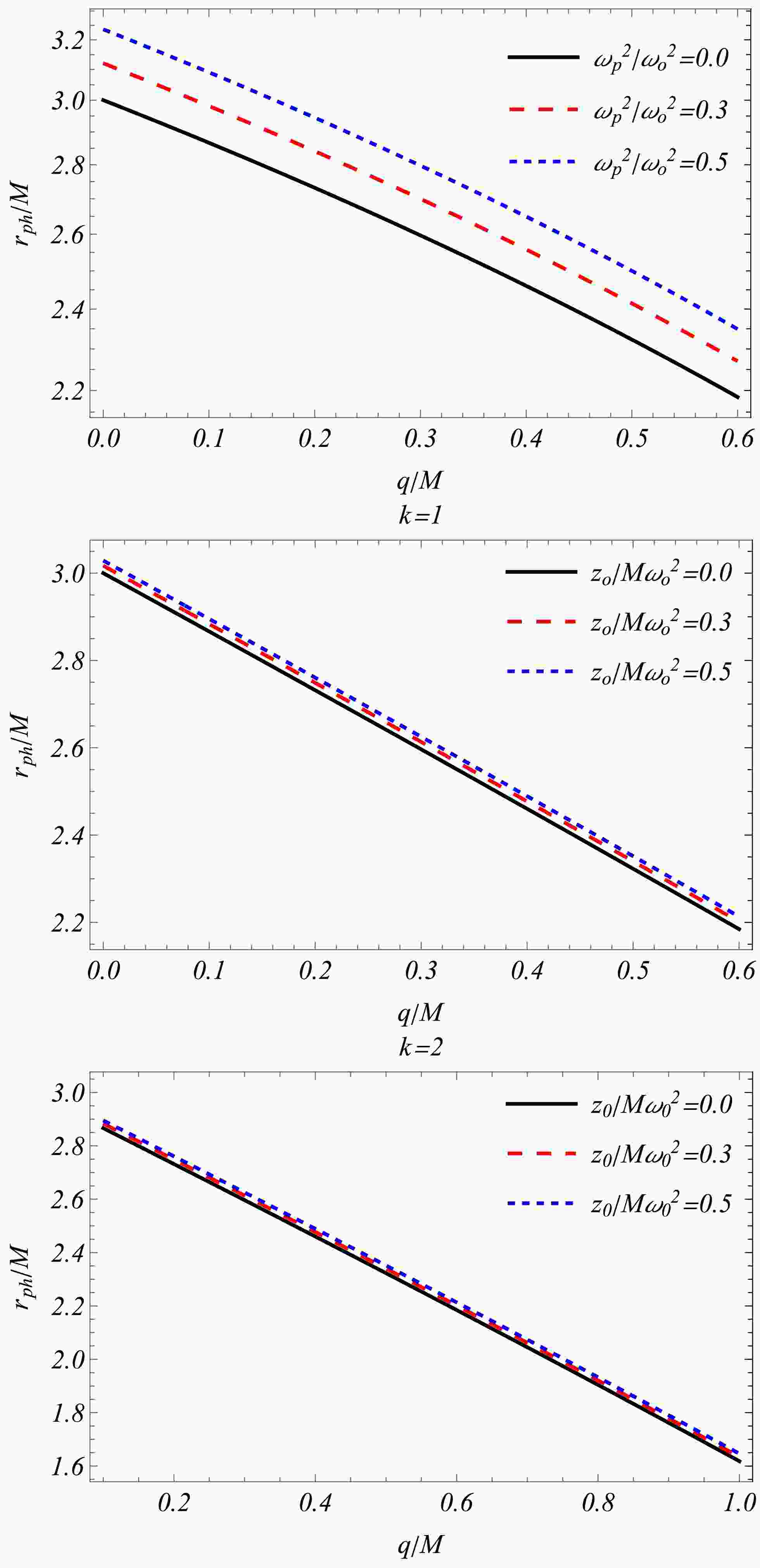
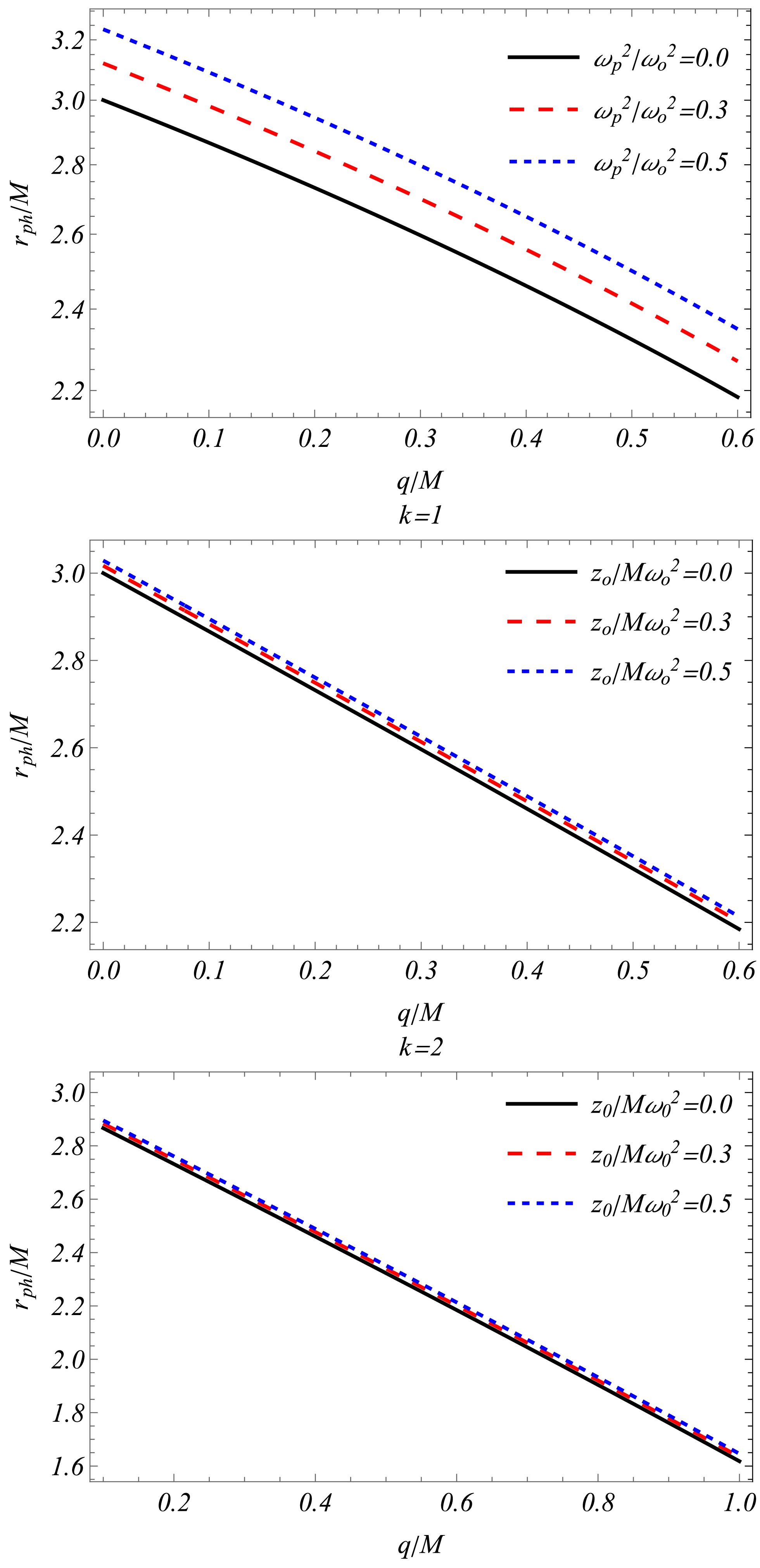
Fig. 1(upper panel) shows that, for homogeneous plasma, the radius of the photon sphere decreases with increasing parameter $ q/M $ and increases with increasing plasma frequency.

Figure 1.  (color online) Relationship between the photon radius of the black hole and the effective charge for various frequency values in homogeneous (upper panels) and inhomogeneous (middle and lower panels) plasma media.

In this subsection, we study photonic spheres in the presence of inhomogeneous plasma, where the plasma frequency must satisfy a simple power law of the form [42]

where $ z_0 $ and $ k > 0 $ are free parameters. To analyze the main features of the power-law model, we restrict ourselves to $ k=1 $ and $ z_0 $ as a constant, and using Eqs. (11) and (13), we can obtain the radius of the photon sphere in the analytical form for inhomogeneous plasma as follows:

where

Fig. 1(middle and lower panels) shows that, for inhomogeneous plasma, the photon sphere radius decreases with increasing $ q/M $and k and increases with increasing ratio $ z_0/M\omega^2_0 $.

Now, we consider the radius of the shadow of the Sen spacetime metric in the presence of a plasma medium. The angular radius of the black hole shadow $ \alpha_{sh} $ is determined using a geometric approach, which leads to the following expression [66, 85, 92, 93]:

where $ r_0 $ and $ r_p $ indicate the positions of the observer and radius of photon sphere, respectively. If the observer is at a sufficiently large distance from the black hole, then the radius of the shadow of the black hole can be approximated as [92, 94]

This is based on the fact that $ h(r) \rightarrow r $, which follows from Eq. (5) at spatial infinity for both plasma models. For a black hole surrounded by a uniform plasma medium, the shadow radius can be expressed analytically as

where

Based on Eqs. (14) and (17), we derive the expressions for the shadow radius in the scenario of inhomogeneous plasma where $ z_0= $ const and $ k=1 $.

where

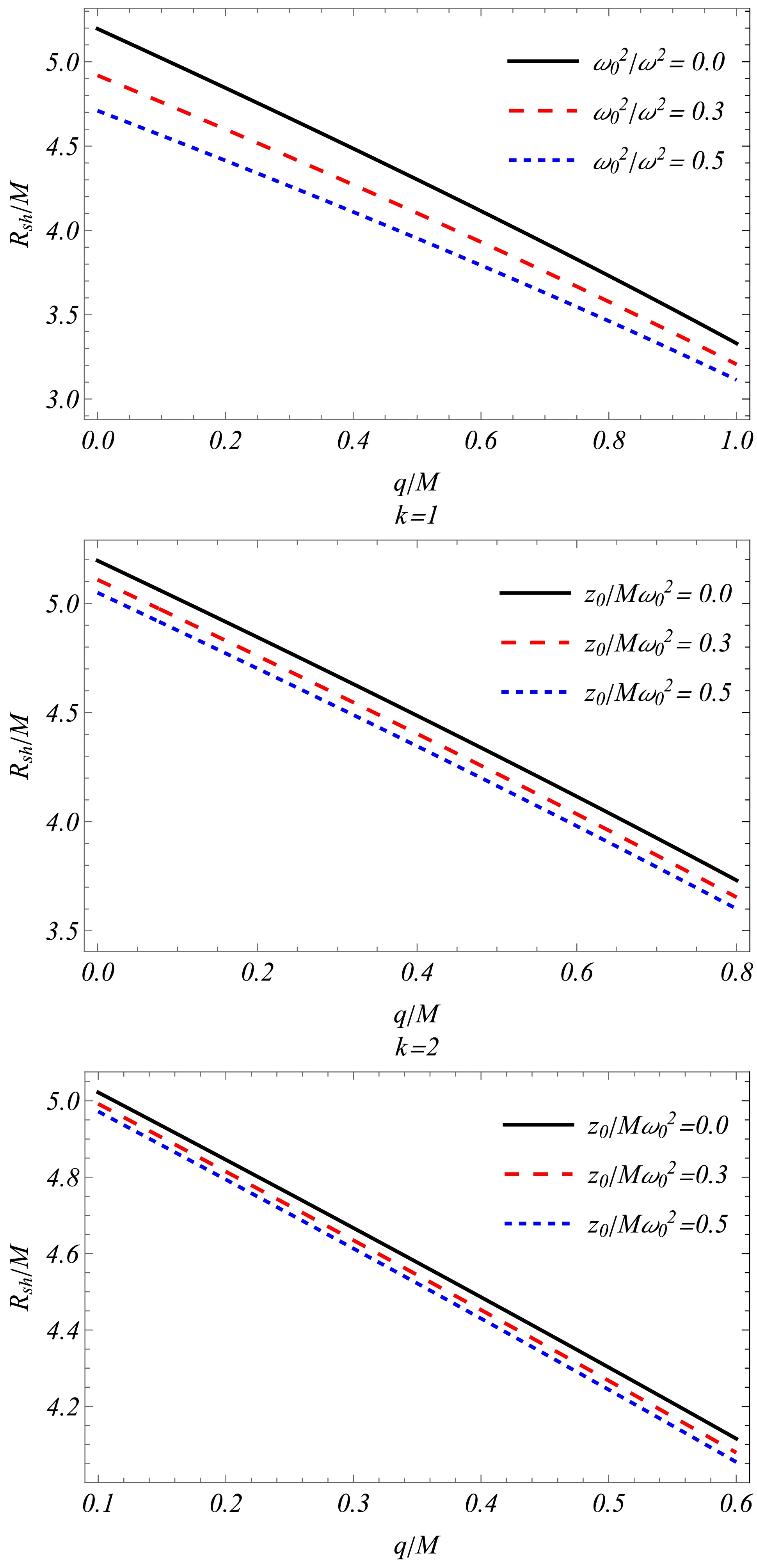
Eq. (20) shows that, in the absence of plasma ($ z_0=0 $) and charge $ q=0 $, the shadow radius is identical to that of the Schwarzschild black hole, $ R_{sh}=3\sqrt{3}M $. Fig. 2 shows that the shadow radius of the Sen black hole in the presence of both uniform and non-uniform plasma is smaller than that in vacuum and decreases with increasing effective charge q and k (middle and lower panels).

Figure 2.  (color online) Relationship between the shadow radius of the black hole and the effective charge for various frequency values in homogeneous (upper panel) and inhomogeneous (middle and lower panels) plasma media.

In this section, we assess the influence of plasma surrounding a black hole on light propagation, as outlined by Synge [91]. We can investigate the gravitational influences in the weak-field approximation by employing the subsequent breakdown of the spacetime surrounding a compact object [41]:

where $ \eta_{\alpha \beta} $ and $ h_{\alpha \beta} $ connote the Minkowski and perturbation metrics, respectively:

The phase speed of the electromagnetic wave in a plasma is given by $ v=c/n $. Eq. (7) shows that, when $ \omega_p > \omega $, the plasma medium plays the role of a refractive medium. In the other words, under this condition, electromagnetic waves cannot propagate in such dense plasma. Only when $ \omega_p < \omega $ can the plasma medium exhibit reflective medium effects, and in the limit $ \omega_p \ll \omega $ $ (n \rightarrow 1) $, Eq. (7) reduces to the vacuum case.

Now, we examine the plasma effects on the bending angle of the light rays. For a plasma medium, the deflection angle can be expressed as [41, 66]

where b is the impact parameter, which is characterized by the radius-vector $ r^2=b^2+z^2 $.

Note that negative values of $ \hat{\alpha}_b $ correspond to the bending of the light ray towards the central object and vice versa. At a large r, we have $\dfrac{R_s}{r}\gg (\dfrac{R_s}{r})^2$. Thus, the black hole metric is approximated to

where ${\rm d}s^2_0=-{\rm d}t^2+{\rm d}r^2+r^2({\rm d}\theta^2+\sin^2\theta {\rm d}^2\phi)$.

Now, we investigate the effects of plasma medium together with the gravitational field of the Sen black hole as an application of the above-described formalism. In Cartesian coordinates, the components $ h_{\alpha \beta} $ can be expressed as

where $ R_s=2M $, $ \cos{x}=z/\sqrt{b^2+z^2} $, and $ r=\sqrt{b^2+z^2} $; b is the impact parameter signifying the closest approach of the photons to the black hole. Using the above-mentioned expressions in Eq. (24), we can compute the light deflection angle with respect to b for a black hole surrounded by plasma as

Eq. (27) shows that the expression includes the effects of gravity and plasma. Here, we rewrite the integral form of deflection angle by separating the effects as [45]

Now, we calculate the integrals for the deflection angle for the different configurations of the plasma distribution.

First, we explore the effects of uniform plasma. We begin by calculating the terms related to only the effects of spacetime curvature:

Eq. (31) indicates that, when $ q=0 $, we obtain $ \hat{\alpha}_1=R_s/b $. The second one is a mixed term reflecting the spacetime and plasma effects, which has the following form:

where $ \omega^2_0=\omega^2_e=\text{const} $. Eq. (32) also becomes $ \hat{\alpha}_2=R_s/b $ at $ q=0 $. Thus, we may obtain the expression for the deflection angle for the Schwarschild case $ \hat{\alpha}_b=2Rs/b $ when $ q=0 $. Under a uniform plasma distribution, the third term of the deflection angle specified by Eq. (30) becomes zero. Finally, we can express the deflection angle of light for uniform plasma around the Sen black hole as

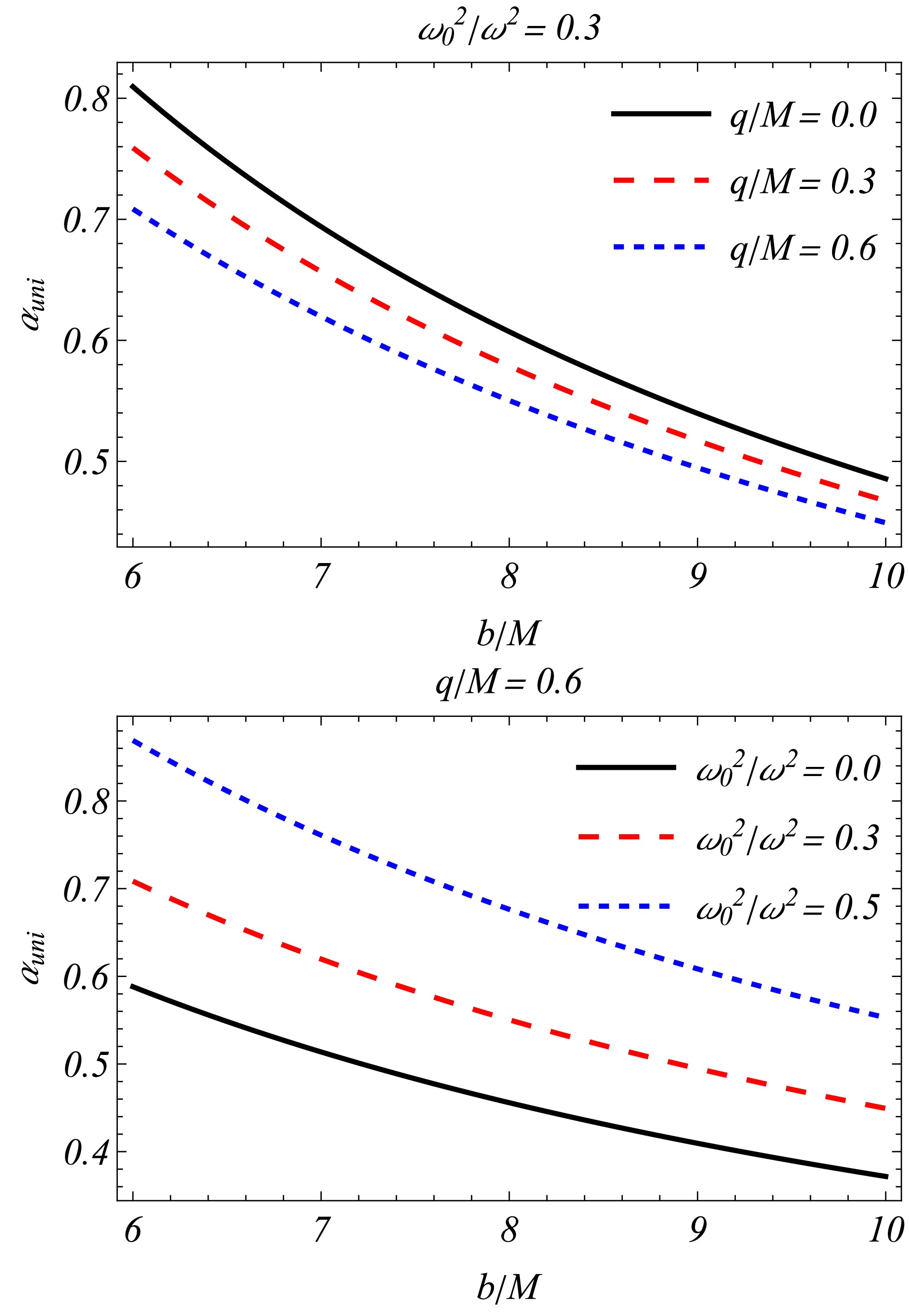
Figure 3 shows the photon deflection angle $ \hat{\alpha}_{\rm uni} $ as a function of the impact parameter b for different values of the coupling constant q (upper panel) and the plasma parameter ${\omega^2_0}/{\omega^2}$(lower panel). Increasing the impact parameter and effective charge decreases the deflection angle. Additionally, the deflection angle can be greater in the presence of uniform plasma than in vacuum.

Figure 3.  (color online) Dependence of the deflection angle of the light rays in the presence of uniform plasma on the impact parameter for different values of charge (upper panel) and plasma frequency (lower panel).

The Singular Isothermal Sphere (SIS) is the most suitable model for understanding the characteristics of a photon's gravitational lens. It was primarily introduced to explore the lens property and clusters. The SIS is a spherical cloud of gas with a single feature of density up to infinity at its center. The density distribution of a SIS is given by [41, 42]

where $ \sigma_\nu^2 $ refers to a one-dimensional velocity dispersion. The plasma concentration admits the following analytic expression [41, 42]:

where $ m_p $ is the proton mass, and k is a dimensionless constant coefficient generally associated with the dark matter universe. Utilizing the plasma frequency yields the following:

Now, we can calculate the deflection angle in the presence of the plasma with the SIS distribution around the Sen black hole using Eq. (28). Here, we have separated the deflection angle as Eqs. (28)–(30) and expressed it as [48]

Because the first term does not include the plasma effects, it takes the same form as Eq. (31):

where $ \omega^2_c=\dfrac{K_e\sigma^2}{2km_pR^2_s} $.

Obtaining all integrals, we have

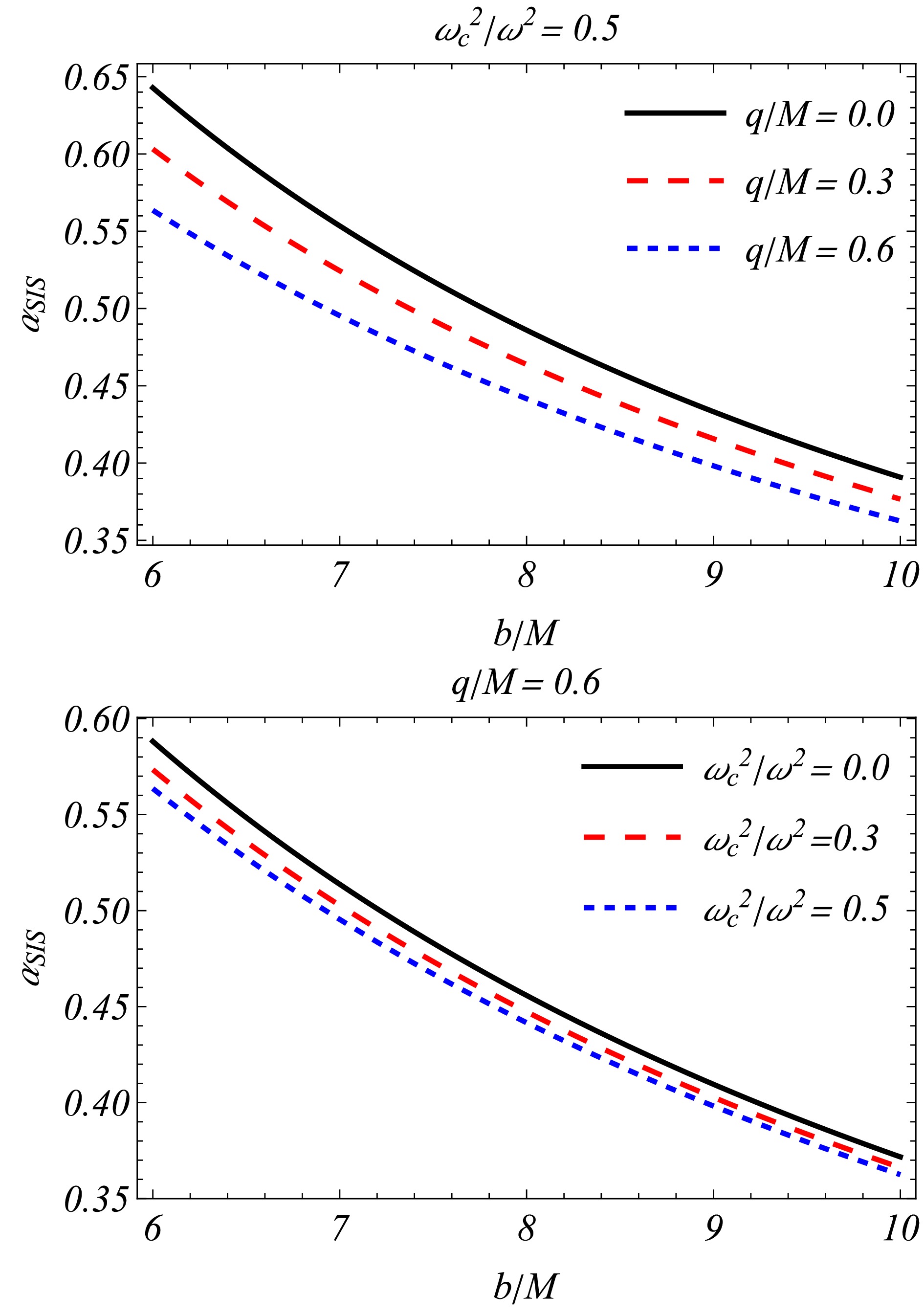
To assimilate the influence of the SIS on the photon trajectory, we plot the deflection angle$\hat{\alpha}_{\rm SIS}$ as a function of the impact parameter b in Fig. 4. Interestingly, we observe that the uniform plasma and SIS medium share common features with respect to b. Fig. 4 shows that the deflection angle $\hat{\alpha}_{\rm SIS}$ decreases because plasma inhomogeneity exerts the opposite effect, and this effect is several times stronger than the vacuum [42, 95]. We observe that $\hat{\alpha}_{\rm SIS}$ decreases as $ \dfrac{\omega^2_c}{\omega^2} $ increases (lower panel) [42, 95], and conversely, $\hat{\alpha}_{\rm SIS}$ decreases as q increases (upper panel). Thus, the presence of the SIS around the black hole has a noticeable impact on the intervening massless particles.

Figure 4.  (color online) Dependence of deflection angle of the light rays in the presence of plasma with non-uniform distribution on the impact parameter for different values of charge (upper panel) and plasma frequency (lower panel).

Now, we proceed to study the motion of photons considering a non-singular isothermal sphere (NSIS), which is a more reasonable and physical setup for the analysis. Unlike the SIS, in this lens model, the singularity is bounded by a finite core at the origin of the gas cloud, whereby the density distribution is defined as

Here, the core radius is represented by $ r_c $.The plasma concentration for the NSIS using Eq. (35) becomes

We compute the plasma frequency from expressions (42) and (43) as follows:

In this case, the deflection angle can be calculated using decomposition expressions (28)–(30) in the following form [48]:

where the first term can automatically be expressed as

Summarizing all terms, we may obtain the expression for the deflection angle in the following form:

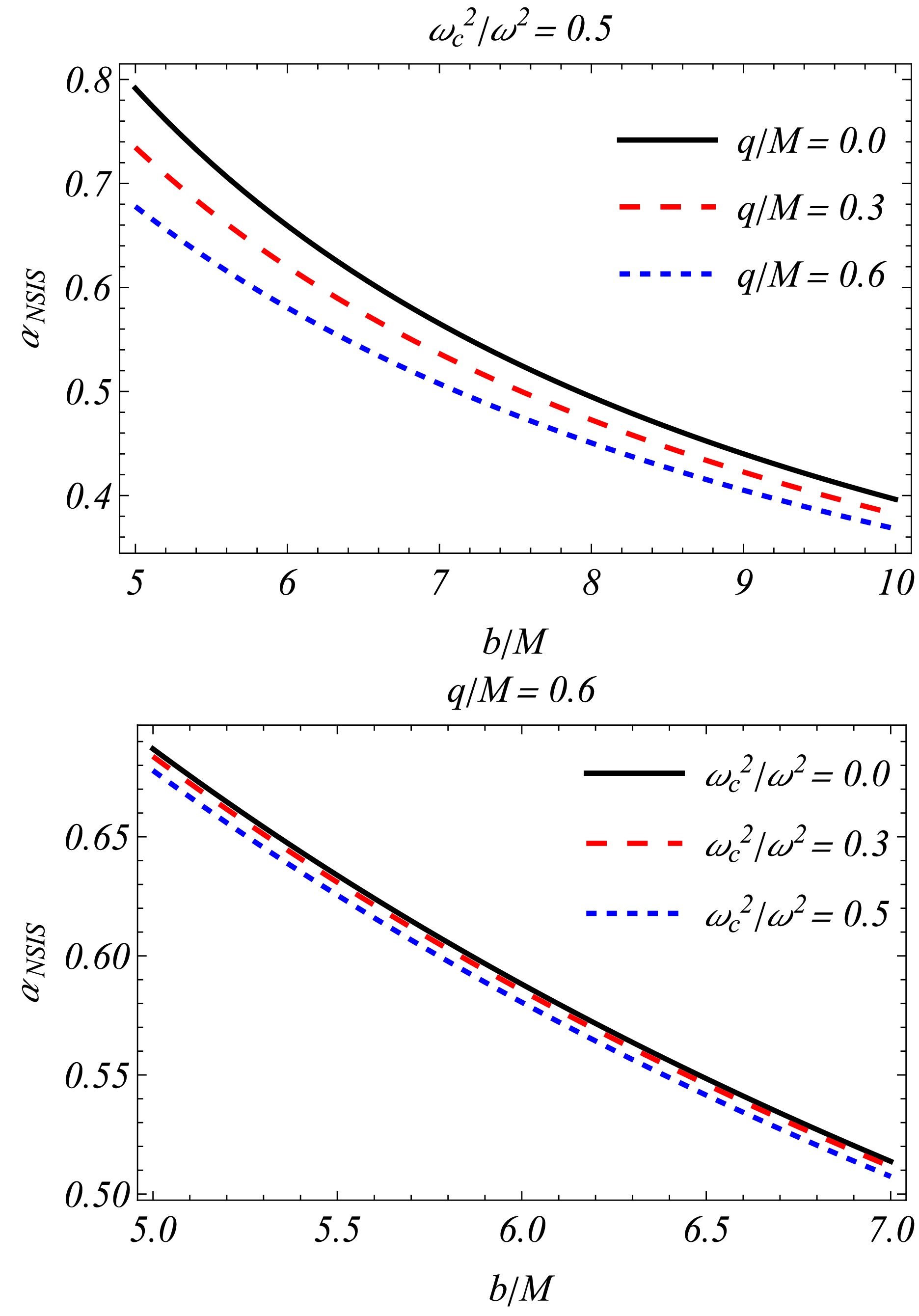
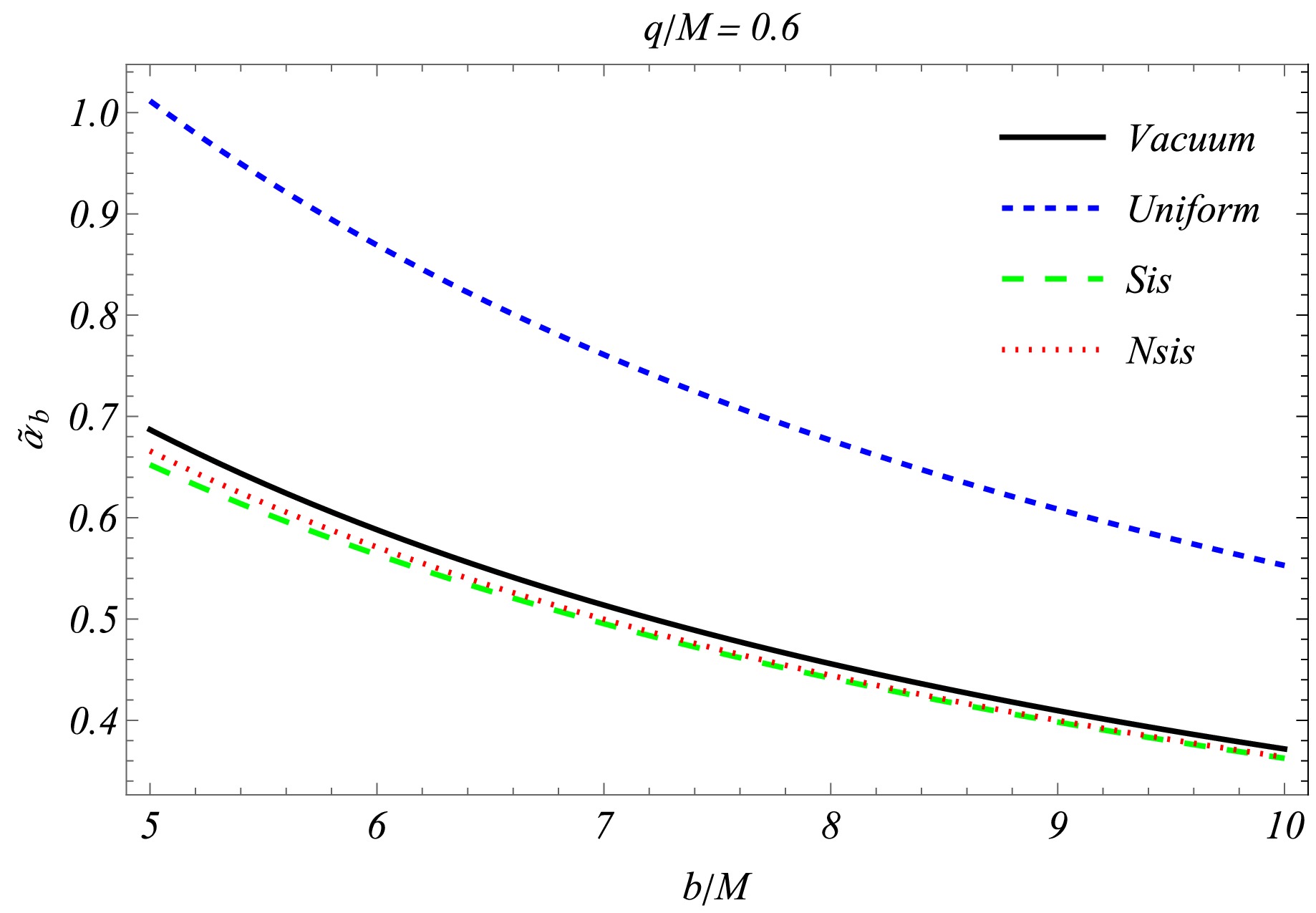
Here, the distribution of the NSIS is associated with the parameter ${\omega^2_c}/{\omega^2}$. Fig. 5 shows that the behaviour of the impact parameter b, the charge of the black hole q, and ${\omega^2_c}/{\omega^2}$ cannot be distinguished from a specific perspective when compared with those in the uniform plasma and SIS case. Nevertheless, Fig. 7 is a visual juxtaposition of $\hat{\alpha}_{\rm uni}, \hat{\alpha}_{\rm vac}, \hat{\alpha}_{\rm NSIS}$, and $\hat{\alpha}_{\rm SIS}$as a function of b and the charge of the black hole. The deflection is maximum when a uniform plasma medium surrounds the black hole. Thus, considering the opposite influence of inhomogeneous plasma, the final result can be expressed in mathematical expressions as [42, 95] $\hat{\alpha}_{\rm uni} > \hat{\alpha}_{\rm vac} > \hat{\alpha}_{\rm NSIS} > \hat{\alpha}_{\rm SIS}$.

Figure 5.  (color online) Dependence of the deflection angle of the light rays in the presence of plasma with non-uniform distribution on the impact parameter for different values of charge (upper panel) and plasma frequency (lower panel).

Figure 7.  (color online) Plot of the deflection angle $ \hat{\alpha}_b $ as function of the impact parameter b. The corresponding fixed parameters are $ \dfrac{\omega^2_0}{\omega^2}=0.5 $, $\dfrac{\omega^2_c}{\omega^2}=0.5,\;r_c=3$.

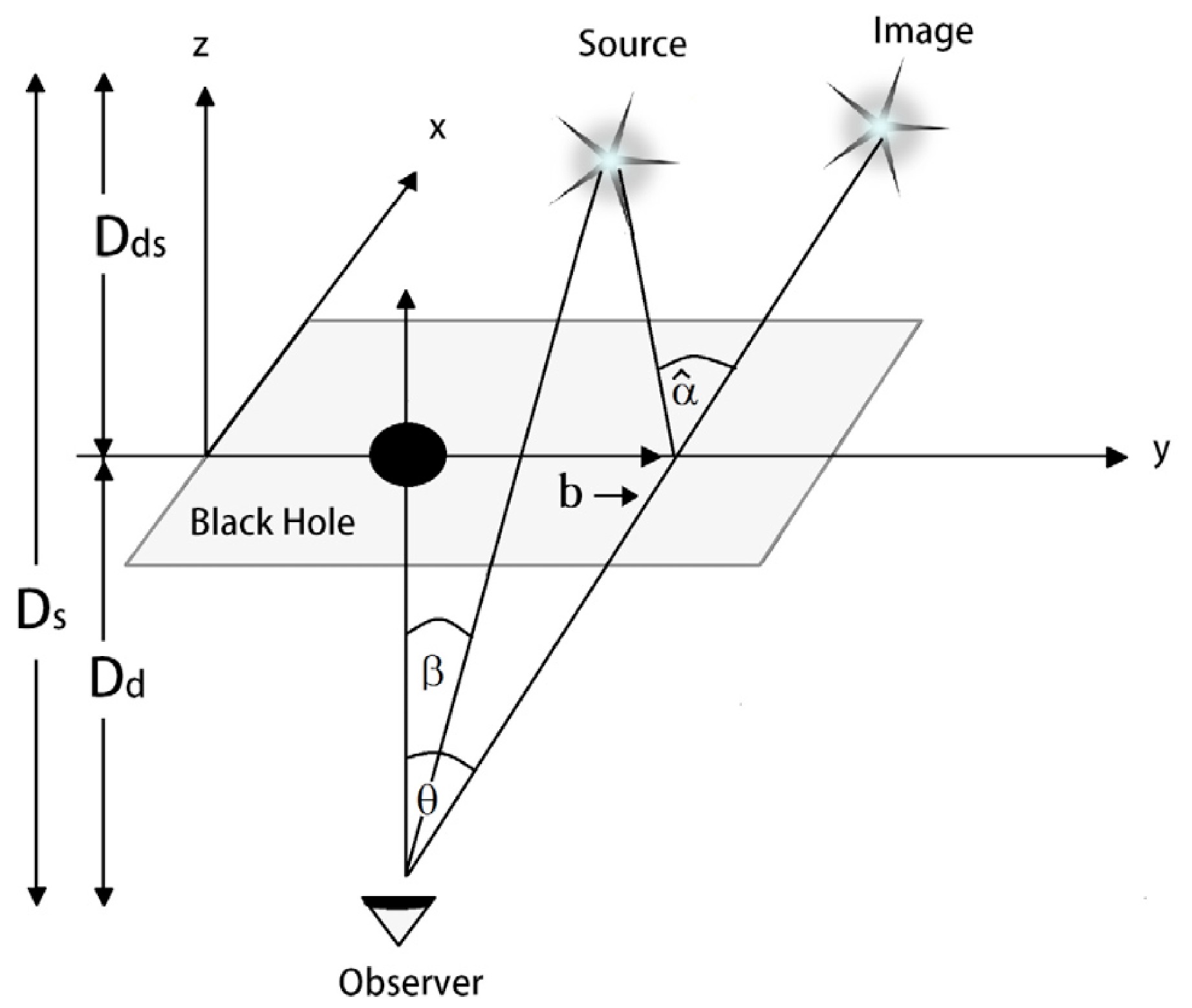
We now focus on observable consequences of gravitational lensing, namely, the magnification of the image source brightness in the presence of plasma performing the angle of deflection $ \hat{\alpha} $discussed in previous sections, particularly for uniform plasma. Figure 8 depicts the gravitational lensing system showing a black hole as a lens, a source, and an observer. To determine the magnification of the image sources, we can use the lens equation, which is related to the angular position of the source β and image θ as well as the distances from the source to the observer $ D_s $ and lens $ D_{ls} $and the deflection angle:

Figure 8.  Schematic view of the gravitational lensing system.

We can use the $ b \thickapprox D_d\theta $ relation in the weak field limit. Thus, we have the following equation:

For uniform plasma, by using Eq. (33) for $ \hat{\alpha} $, we can rewrite Eq. (51) as

By introducing the variable $x=\theta-\dfrac{\beta}{3}$, we can reduce Eq. (52) to the form

where

Hence, the solution of Eq. (53) is given by [96]

where

The total magnification of the images is defined as the ratio of solid angles of the observer to the source, which is then summed up relative to each image. However, in the weak field approximation, the total magnification $ \mu_{\sum} $ of the images is approximated as [97]

where $ \theta_k=x+\beta/3 $. There are three components of the magnification of the images: two ordinary images and relativistic images that appear due to the presence of the q parameter.

Using the above expressions, we can obtain numerical results for the total magnification. Figure 6 depicts the relationship between total magnification and the source position (upper panel), as well as the relative magnifications of individual images. The upper graph shows that the total magnification decreases as the source position angle increases. Additionally, the presence of the plasma environment positively influences the total magnification.

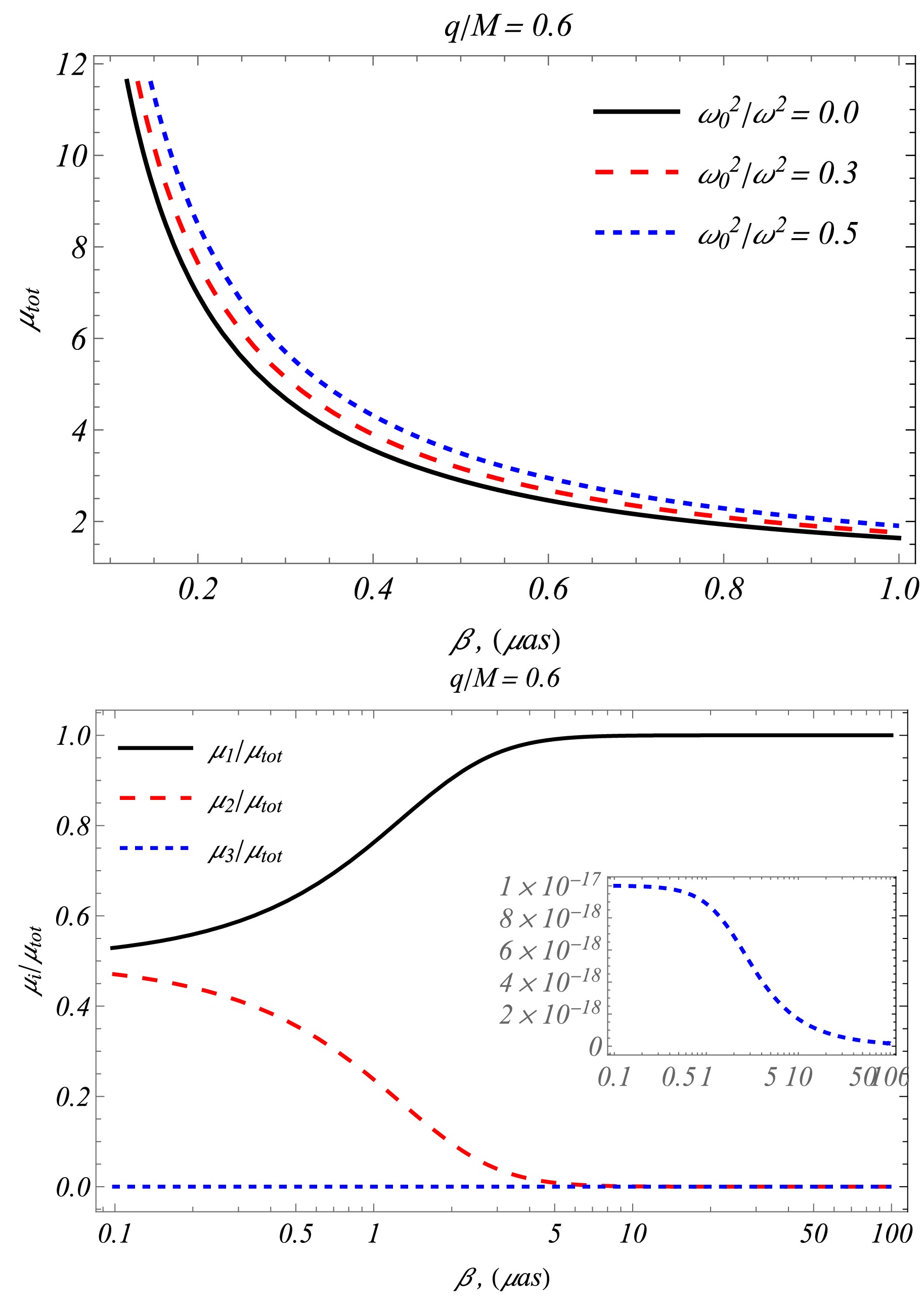
Figure 6.  (color online) (upper panel) Magnification as a function of source position β for$ q/M=0.6 $ and $ M/D_d=22.6\cdot10^{-12} $. (lower panel) Magnification rate of the image source as a function of position of source β for $ \omega^2_0/=\omega^2=0.5 $ and $ M/D_d=22.6 \cdot10^{-11} $. The black thick and red dashed curves represent the magnification rate of primary and secondary images, respectively, and the blue curves represent relativistic images owing to the presence of the charge of the black hole q.

This section introduces the theoretical framework of our study. The time delay of light in a gravitational field is calculated using the geodesic equation [98, 99]

where $ \epsilon=\pm1,0 $is a parameter that is $ 0 $ for a null geodesic, and λ is an affine parameter. In this context, $ V(r)=\dfrac{f(r)}{2}\dfrac{L^2}{r^2} $ defines the effective potential for particles in a spherically symmetric gravitational field, with the impact parameter given by $ b\equiv|L/E| $. Focusing on photon trajectories, we obtain

Using $E=f(r)\dfrac{{\rm d}t}{{\rm d}\lambda}$, the signs $ \pm $ can be interpreted as follows. As a particle moves along its scattering orbit from the source position $ r_S $, the radial coordinate r decreases over time until the particle reaches the closest approach, $ r=r_0 $, to the central black hole. Beyond this turning point $ r=r_0 $, the radial coordinate begins to increase as time advances. Thus, we establish the following relationships:

for a photon traveling from the initial position $ r=r_S $ to the turning point $ r=r_0 $, the radial coordinate behavior is described. Additionally,

where we have considered that the photon moves from the tuning point $ r=r_0 $ to observer position $ r=r_O $. Note that, in gravitational lensing, when the light source is located at $ r=r_S $ and the observer at $ r=r_O $, the time delay of light as it propagates through the gravitational field is formulated as

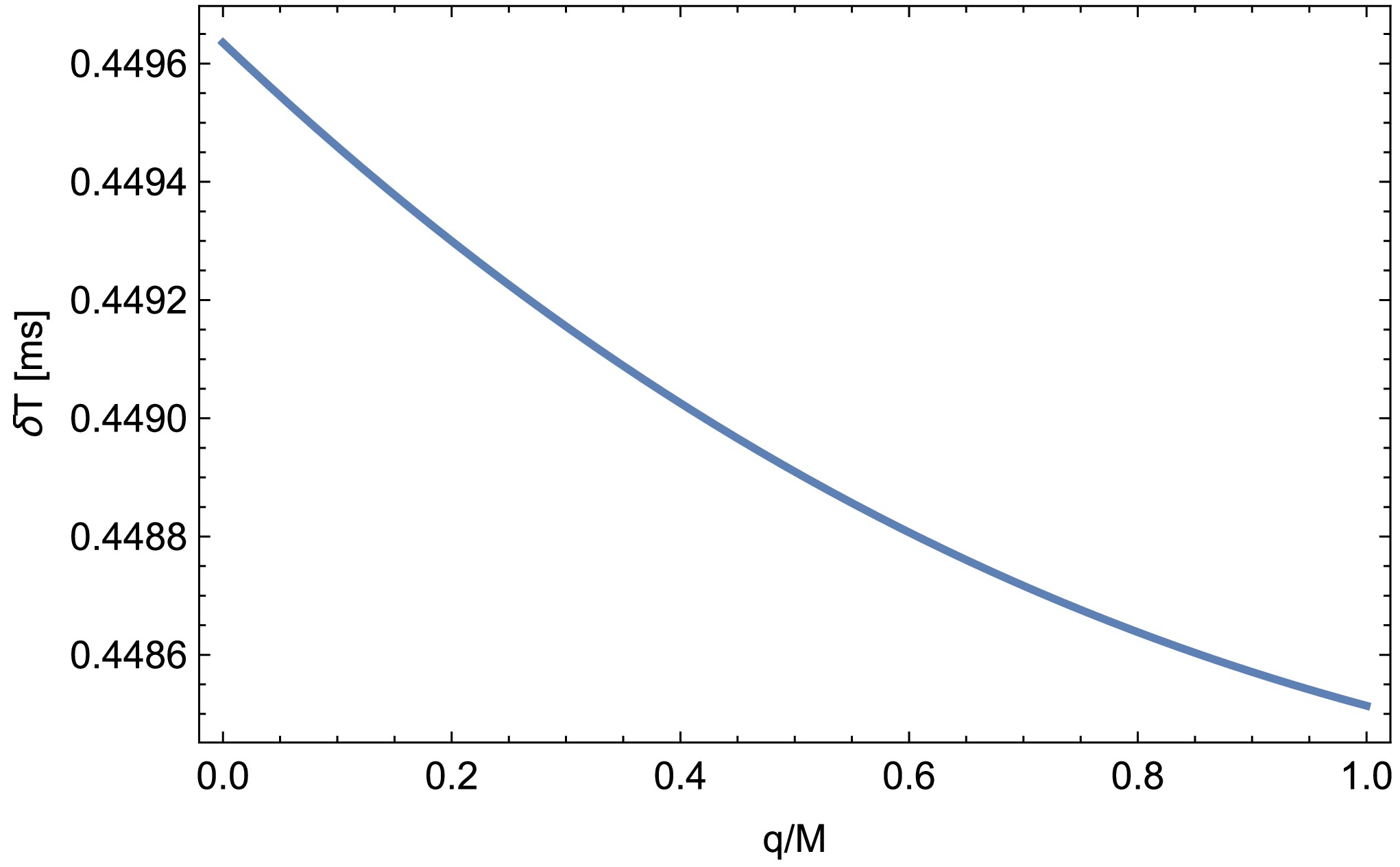
where $ T_0=\sqrt{r^2_S-r_0^2}+\sqrt{r^2_O-r_0^2} $ represents the time taken for light to propagate in the absence of a gravitational field.

For the 2002 superior conjunction of Cassini, the spacecraft was at $ r_O\thickapprox8.43~{\rm AU} $ from the Sun, and the radar grazed near the Sun with an impact parameter $b\thickapprox 1.6R_{\odot}$. The maximum time delay with respect to the flat spacetime is when $r_0 =1.6R_{\odot}$ and $r_S=1.5 \times 10^8$km [100]. Figure 9 clearly shows that, with an increase in the value of $ q/M $for the Sen black hole, the time delay decreases.

Figure 9.  Dependency of the geometrical time delay on the black hole parameter $ q/M $.

We have thoroughly examined the weak gravitational lensing and shadow properties of Sen black holes immersed in a plasma medium, highlighting the significant impact of the black hole's effective charge on these optical phenomena. Our investigation reveals several key findings. The obtained results can be summarized as follows:

$ \bullet $ We find that an increase in the effective charge of a Sen black hole decreases the radius of the photon sphere. This decrease in the photon sphere radius results in a smaller size of the black hole's shadow.

$ \bullet $ The effective charge also influences the bending angle of light rays. Our results indicate that as the effective charge increases, the bending angle diminishes.

$ \bullet $In particular, we have considered a uniform distributed plasma, singular isothermal sphere medium, and non isothermal sphere medium.

$ \bullet $ We also show that the deflection angle increases with increasing plasma frequency, when the plasma is homogeneous, owing to the refractive effect of the medium, the deflection angle decreases when the plasma is inhomogeneous (SIS and NSIS) with increasing plasma frequency.

$ \bullet $An analysis of the angle of deflection of the light beam around the Sen black hole in the plasma medium size and NSIS models shows that the influence of the plasma medium for the SIS model is much less than that for the NSIS model at the same plasma frequency values.

$ \bullet $ By applying the lens equation, we have analyzed the magnification of source brightness, which is influenced by the effective charge of the black hole. Additionally, we study the time delay of light traveling in the presence of a surrounding plasma medium. Our analysis shows that plasma can significantly alter the time delay.

Overall, our study provides new insights into the observational signatures of Sen black holes, emphasizing the role of effective charge and plasma in shaping these signatures. The results enhance our understanding of the effects of these factors on weak gravitational lensing and the black hole shadow, offering new avenues for interpreting astronomical observations and testing theoretical models of black hole physics.