Impact of quadrupole and hexadecapole deformations and associated orientations on a variety of asymmetric nuclear reactions

Significant experimental and theoretical effort has been made in the last few decades to understand the synthesis and decay of the heavy and superheavy nuclei via heavy-ion fusion reactions [1−8]. These studies focus on the influence of various parameters and properties of interacting nuclei on the dynamics of heavy-ion-induced reactions. Numerous methods have been reported in the literature to study the synthesis and decay dynamics of such reactions. For instance, various theoretical models like the dinuclear system (DNS) model [9, 10], diffusion model [11], macro-microscopic model [12], dynamical Langevin model [13, 14], and fluctuation-dissipation model [15] are used as the fusion-ER decay model to study decay by evaporation residue (ER) through fusion reactions. The fusion-ER model considers various processes that lead to the formation of compound nuclei (CN) and their decay via the emission of a cascade of light particles.

Heavy-ion-induced reactions can be studied via three stages [5, 16−18]. In the first stage, the projectile and target (P-T) come in contact after their potential barrier is overcome and the process is quantized via the capture cross-section ($ \sigma_{\rm cap} $). In the second stage, these interacting nuclei fuse to form a compound nucleus (CN). The extent of the formation of CN against the non-compound nucleus (nCN) processes can be determined by the CN formation probability ($P_{\rm CN}$). The formed CN is then studied via the fusion cross-section ($\sigma_{\rm fus}$). When the incident energy of the projectile exceeds the energy required for the production of an intermediate nucleus, the resulting nucleus is called a CN (excited nuclear state). This excited CN becomes stable by decaying to the ground state via the fission channel or emission of light particles like protons, neutrons, $ \alpha $-particles, and gamma radiation. The extent of survival of an excited CN against the fission process and decay via the evaporation of light particles is measured in terms of survival probability ($ W_{\rm sur} $). This process provides a stable residual nucleus in the ground state. Collectively, $ \sigma_{\rm cap} $, $P_{\rm CN}$, and $ W_{\rm sur} $ produce the fusion-ER cross-section ($\sigma_{\rm ER}$).

Ref. [19] demonstrated that the fusion reaction dynamics depend on the properties of the colliding nuclei. Several theoreticians have shown that along with properties like mass and charge number, the deformation and orientation degrees of freedom, angular momentum, and excitation energy of the colliding nuclei significantly influence dynamics of the fusion reaction [20−25]. Additionally, the incorporation of higher order deformations such as octupole $ \beta_3 $ and hexadecapole $ \beta_4 $ deformation induces significant changes in the characteristics of the fusion reaction and better explains experimental results in their compact and elongated configurations [26, 27]. For example, in the reactions of ¹⁶O+^174,176Yb [28, 29] and ^14,15C+²³²Th [30], the authors have found evidence of modification in the fusion barrier after the incorporation of hexadecapole deformations $ \beta_4 $ that significantly enhances capture cross-sections. Moreover, studies in the literature have analyzed fusion cross-sections by incorporating higher-order deformations via microscopic models [31−34]. The optimum orientations of deformed interacting nuclei are determined with respect to the barrier height ($ V_B $) and barrier separation or interaction radius ($ R_B $). For instance, the configuration with the smallest interaction radius and maximum barrier height is called a compact configuration and also known as the belly-to-belly configuration, while the configuration with the largest interaction radius and the minimum barrier height is said to be the elongated configuration or the pole-to-pole configuration [20].

Numerous efforts with different theoretical approaches are used to investigate ER cross-sections via fusion reactions. However, it would be interesting to study the relevance of $ \beta_2 $,$ \beta_4 $ deformations along with their respective 'compact or elongated' orientation degrees of freedom for evaluating fusion-ER cross-sections. Thus, in the present work, the fusion-ER cross-sections are investigated for reactions of the hexadecapole ($ \beta_4 $) deformed targets $ ^{148,150} $Nd, ¹⁶⁵Ho, ¹⁹⁴Pt, $ ^{188,192} $Os, and ¹⁷⁰Er with spherical $ ^{16, 18} $O and $ \beta_4 $-deformed ¹⁹F, ³⁰Si projectile beams for center of mass energies ($E_{\rm c.m.}$) spread across a Coulomb barrier. The fusion-ER cross-sections are calculated for the considered reactions by incorporating the $ \beta_2, \beta_4 $ deformations at their respective compact and elongated configurations. Additionally, cross-sections integrated over all orientations are also calculated to provide more extensive insight. The obtained fusion-ER cross-sections are then compared with available experimental data [18, 35−39].

In the present work, fusion-ER cross-sections for a set of reactions are calculated using the semi-classical approach. In this approach, the fusion-ER cross-sections are determined by using the capture cross-sections ($ \sigma_{\rm cap} $), compound nucleus formation probability ($P_{\rm CN}$), and survival probability ($ W_{\rm sur} $). The capture cross-sections ($ \sigma_{\rm cap} $) are calculated using the extended $ \ell $-summed Wong model incorporating deformations $ \beta_2 $, $ \beta_4 $ at compact, elongated configurations with the proximity potential [40]. The compound nucleus formation probability ($P_{\rm CN}$) dependent on the Coulomb parameter and center of mass energies ($E_{\rm c.m.}$) is determined using the Siwek-Wilczyńska formula [41]. To calculate the survival probability ($ W_{\rm sur} $) of the CN against fission, a statistical model is used [42]. In addition to the deformations and orientations, the influence of the level density parameter ratio between the fission channel to neutron evaporation channel ($ a_f/a_n $) is studied to determine the fusion-ER cross-sections.

The manuscript is organized as follows: Section II provides the formalism for the calculation of the fusion-ER cross-section via the capture cross-section, compound nucleus formation probability, and survival probability. Sections III discusses the results and Section IV summarizes them.

The fusion-ER cross-sections calculated using the semi-classical approach after the emission of x-number of neutrons from the excited compound nucleus is defined by the product of capture cross-section ($ \sigma_{\rm cap} $), compound nucleus (CN) formation probability ($ P_{\rm CN} $), and survival probability of the compound nucleus ($ W_{\rm sur} $) is given by

and the fusion cross-section of the formed CN is determined as

The capture cross-section of deformed and oriented nuclei colliding with the center of mass energies ($E_{\rm c.m.}$) is determined by using the extended $ \ell $-summed Wong Model [43]. This includes the sum of the cross-section corresponding to each $ \ell $-partial wave and is expressed as

where $k=\sqrt{\dfrac{2\mu E_{\rm c.m.}}{\hbar^2}}$ and $ \mu $ is the reduced mass. Here, the sharp cut-off approximation [44, 45] is used to calculate the maximum angular momentum denoted by $\ell_{\rm max}$.

Wong approximated barrier penetration for different $ \ell $-waves using the inverted harmonic oscillator potential with barrier height $ V_{B}^{\ell}(E_{\rm c.m.}) $, interaction radius $ R_{B}^{\ell}(E_{\rm c.m.}) $, and curvature $ \hbar\omega_{B}^{\ell}(E_{\rm c.m.}) $. Thus, the penetration probability $ P_{\ell} $ across the barrier for each '$ \ell $' is given by the Hill-Wheeler approximation [46]:

$V_{B}^{\ell}(E_{\rm c.m.})$, $R_{B}^{\ell}(E_{\rm c.m.})$, and $\hbar\omega_{B}^{\ell}(E_{\rm c.m.})$are obtained from the total interaction potential between the two interacting nuclei, which is the sum of the repulsive Coulomb ($ V_C $) and centrifugal ($ V_{\ell} $) potentials, and attractive nuclear potential ($ V_N $). The total potential $ V_T(R_i,A_i,\beta_{\lambda i},\theta_i) $ is therefore calculated as follows:

The radius vector $ R_i(\alpha_i) $ can be used to express the shape of the deformed nuclear surface, which involves the spherical harmonic wave functions $ Y_{\lambda}^{(0)}(\alpha_i) $ of higher-order deformations $ \beta_{\lambda i} $, where$ \lambda=2,3,4 $ are the orders of quadrupole, octupole, and hexadecapole deformed shapes, respectively [47−50]:

In this case, the projectile and target nuclei are denoted by i = 1 and 2, respectively.

$ R_{0i} = 1.28A^{1/3}_i-0.76+0.8A^{-1/3}_i $, measured in fm [40], represents the radius of the spherical nuclei. The deformation parameter $ \beta_{\lambda i} $ was obtained from the Table of M$ \ddot{o} $ller et al [49]. $ P_{\lambda}(\cos{\alpha_i}) $ is the Legendre polynomial.

The Coulomb potential ($ V_C $) in Eq. (5) is defined as follows for deformed-deformed colliding nuclei [43]:

While for the spherical-deformed cases, $ \beta_{21},\beta_{41}=0.0 $ are considered. The centrifugal potential ($ V_{\ell} $) is represented in the form of rotational kinetic energy and is given as

In Eq. (5), the attractive nuclear potential ($ V_{N} $) between the two interacting nuclei is determined by the generalized theorem for proximity forces discovered by Blocki et al. [40]. According to this theorem, the nuclear potential is the product of $ 4\pi\bar{R}\gamma b $ and $ \Phi(s_0) $. The term $4\pi\bar{R}\gamma b $ depends on the shape and geometry of the colliding nuclei, whereas $\Phi(s_0)$ is a universal function dependent on the shortest distance between the colliding nuclei. Thus, $ V_{N}(R,A_i,\beta_{\lambda i},\theta_i) $, called the 'Proximity potential', is given by [40, 44, 51]

where, 'b' is the surface thickness and considered to be 0.99 fm.

The mean curvature radius ($ \bar{R} $) is calculated in terms of radius vector of curvatures $ R_{i1} $ and $ R_{i2} $ for projectile and target nuclei resp., as follows:

The principal radii of curvature ($ R_{i1} $ and $ R_{i2} $) at the angle of projection w.r.t. the collision axis ($ \alpha_i $) for deformed-deformed or spherical-deformed cases is given [51] by

It is important to note that for spherical projectiles, $ R_{11(\alpha_1)}=R_{12}(\alpha_1)=R_1(\alpha_1) $. In Eq. (9), the surface energy constant $ \gamma $ is expressed in terms of asymmetry terms as

In Eq. (9), the universal function dependent on the shortest distance parameter $ s_0 $ is

Eqs. (5) − (14) outline the total interaction potential and provide valuable information regarding the properties of the interacting nuclei. This includes barrier characteristics such as the barrier height $ V_B $, the barrier position $ R_B $, and the barrier curvature $ \hbar\omega_B $. These parameters are influenced by the degrees of freedom associated with deformation and orientation introduced in the radius vector obtained using Eq. (6). Consequently, these variables are utilized in the calculations of capture cross-sections.

In addition, the integrated or average capture cross-sections are obtained by integrating over the range of orientations $ \theta_i $ of the deformed nuclei having $ \beta_2 \beta_4 $ deformations, which is represented as

The compound nucleus formation probability $ P_{\rm CN} $ provides information about the chances of the formation of a CN, where the fusion cross-section of CN is given by $\sigma_{\rm fus} = \sigma_{\rm cap}\times P_{\rm CN}$. The phenomenological approach for calculating $P_{\rm CN}$ was proposed by Siwek-Wilczyńska [41] and is given by

where $ k $ is taken as 3.0 and $ z $ is the Coulomb parameter,

where $ Z_1 $, $ Z_2 $ represent the atomic number, while $ A_1 $ and $ A_2 $ represent the the mass numbers of the projectile and target, respectively. Parameter $ b $ depends on $ E_{\rm c.m.} $ and mean interaction barrier $ B $ [52, 53]:

where $ B $ is given by

The excited CN is cooled by the emission of neutrons instead of fission. The survival probability ($ W_{\rm sur} $) is used to measure CN's resistance to the fission process and can be obtained using a statistical approach [42, 54]:

where $ \Gamma_n $ and $ \Gamma_f $ are neutron emission and fission decay widths, respectively, and $P_{xn}(E_{\rm CN}^*)$ the 'Jackson factor'[55] is the probability of the emission of $ x $ neutrons from the excited CN at excitation energy $E_{\rm CN}^*$. $ B_{i} $ is the separation energy of the $ i^{th} $ neutron. $ T $ is the temperature (in MeV) obtained using the statistical method [56] as

where $ Q $ is the $ Q $-value and a= $ A $/ 10 is the level density parameter for a CN with mass number $ A $. In terms of $ B_{i} $, $ T $, and $E_{\rm CN}^*$, the $P_{xn} $ is given by

where $ I(\Delta_x, 2x-3) $ is Pearson's incomplete gamma function [57] and $ \Delta_x $ = $ \dfrac{(E_{\rm CN}^*-\sum_{i=1}^{x}B_{i})}{T} $. The classical approach for determining decay width ratios of the $ i^{th} $ neutron to fission $ \frac{\Gamma_n}{\Gamma_f} $ has been suggested by Vandenbosch and Huizenga [58]:

where $ B_f $ is the fission barrier height, which determines the chances of the fission or evaporation of neutrons. The value of the constant $ K_0 $ = $ \hbar^2 $/ $ 2mr_{0}^2 $ is considered to be 10 MeV. The level density parameter of the neutron evaporation channel is $ a_n $ = $ A/10 $ and that of the fission channel is $ a_f $ = $ 1.1a_n $. The values of $ a_f $ are also considered from 1.0 to 1.05 w.r.t $ a_n $. The fission barrier height $ B_f $ before the emission of the $ i^{th} $ neutron is calculated as the sum of the liquid drop fission barrier $ B_f^{LD} $ and shell correction energy $ B_f^{\rm Shell} $[54]:

where the $ B_f^{LD} $ is determined using the approximate analytic method in [59] and the value of $B_f^{\rm shell}$ is obtained from the M$ \ddot{o} $ller and Nix table [49]. $ E_d $ = $ 5.48A^{1/3}/ (1+1.3A^{-1/3}) $ is the damping factor, which characterizes the decrease in shell effects with the increasing excitation energy of CN.

This study focused on analyzing the relevance of higher-order deformations ($ \beta_2, \beta_4 $) on the fusion-ER cross-sections at their respective compact, elongated configurations. To investigate the impact of deformations and orientation degrees of freedom on the fusion-ER cross-section, we considered heavy-ion-induced reactions involving different projectile and target nuclei. For the chosen reactions, the experimental data of ER cross-sections can be obtained from [18, 35−39]. These reactions include the interactions of the hexadecapole ($ \beta_4 $) deformed targets $ ^{148,150} $Nd, ¹⁶⁵Ho, ¹⁹⁴Pt, and ¹⁹²Os with spherical projectiles $ ^{16, 18} $O, and $ \beta_4 $-deformed projectile-target combination ¹⁹F and ¹⁸⁸Os.

The CN formed using these reactions have the mass range $ A $ = $ 150 $ - $ 212 $. The reactions are studied at the center of mass energies ($ E_{\rm c.m.} $) lying across the Coulomb barrier shown in Table 1. The static deformations are taken from the Table of P. M$ \ddot{o} $ller[49].

Reaction	CN	$E_{\rm c.m.}$	$ E_{\rm CN}^* $	$ V_{B} $	$ z $	$ \chi $
18O+148Nd	166Er	55−69	41−56	57.47	60.68	0.581
16O+150Nd	166Er	55−73	42−59	58.061	61.27	0.581
16O+148Nd	164Er	58−72	42−56	58.208	61.46	0.584
16O+165Ho	181Re	66−96	43−73	63.948	66.96	0.644
18O+192Os	210Po	73−113	52−92	69.896	72.46	0.711
18O+194Pt	212Rn	75−97	48−70	71.649	74.20	0.732
16O+194Pt	210Rn	69−96	39−66	72.541	75.101	0.735
19F+188Os	207At	72−95	42−65	79.097	81.45	0.727

Table 1.  Tabulation of the entrance channel properties such as the center of mass energies ($E_{\rm c.m.}$), interaction barrier ($ V_{B} $), Coulomb factor ($ z $), and fissility parameter ($ \chi $) of the formed compound nucleus ($ CN $) at excited energies ($ E_{\rm CN}^* $) for all the considered reactions

Section A discussed the behaviour of the capture cross-section of these reactions as a function of the center of mass energy ($E_{\rm c.m.}$). Section B is dedicated to the fusion cross-sections and Section C covers the analysis of the evaporation residue component.

Past research shown that the deformations and orientations (compact and elongated) associated with the interacting nuclei alter the barrier characteristics $ V_B $, $ R_B $, $ \hbar\omega $, etc., which further influence the capture cross-sections ($ \sigma_{\rm cap} $). We have evaluated $ \sigma_{\rm cap} $ by incorporating the deformations (up to $ \beta_4 $) of the interacting nuclei chronologically (i.e. $ \beta_2 $ and $ \beta_2\beta_4 $) at respective compact, elongated orientations ($ \theta_i $) and integrating over all the orientations of the considered P-T combinations. The $ \sigma_{\rm cap} $ are calculated within the same plane ($ \phi $=0) for the center of mass energies ($E_{\rm c.m.}$) lying across the Coulomb barrier, as depicted in Fig. 1. The $ \ell $-values used to incorporate angular momentum effects are calculated using the sharp cut-off approximation. Fig. 1 shows different cross-section trends for different combinations of deformations at their respective compact/elongated configurations along with the cross-sections integrated over all the orientations in comparison to the spherical system. For example, the presence of $ \beta_{2}^+ $ deformation reduces cross-sections in the compact configuration due to a small interaction radius at the highest barrier height. However, in the elongated configurations of $ \beta_{2}^+ $, the cross-sections are enhanced relative to the spherical case due to the larger interaction radius at the smallest barrier height, as illustrated in Fig. 1(a-h). Further incorporating $ \beta_4^+ $ deformation in $ \beta_2^+ $ elongates the nuclear shape, which increases the interaction radius. Therefore, the cross-sections are further enhanced for both configurations (i.e. compact and elongated) of $ \beta_2^+ $$ \beta_4^+ $ compared to $ \beta_2^+ $ only, which is illustrated in Fig. 1(a-d). For the reactions shown in Fig 1(e-h), the inclusion of $ \beta_4^- $ deformations to the $ \beta_2^+ $ of the target nuclei produces reduced cross-sections in both compact and elongated configurations compared to cross-sections obtained by $ \beta_2^+ $ deformation alone. This suppression is attributed to the compressive effects of $ \beta_4^- $, reducing the interaction radius relative to $ \beta_2^+ $. The integrated cross-sections ($\sigma_{\rm int}$) obtained for the considered $ \beta_2\beta_4 $ deformed nuclei represent the average effect of all orientations. These integrated capture cross-sections ($\sigma_{\rm int}$) are between the cross-sections obtained by compact and elongated configurations, reflecting the combined effects of nuclear shapes and interaction dynamics across all orientations.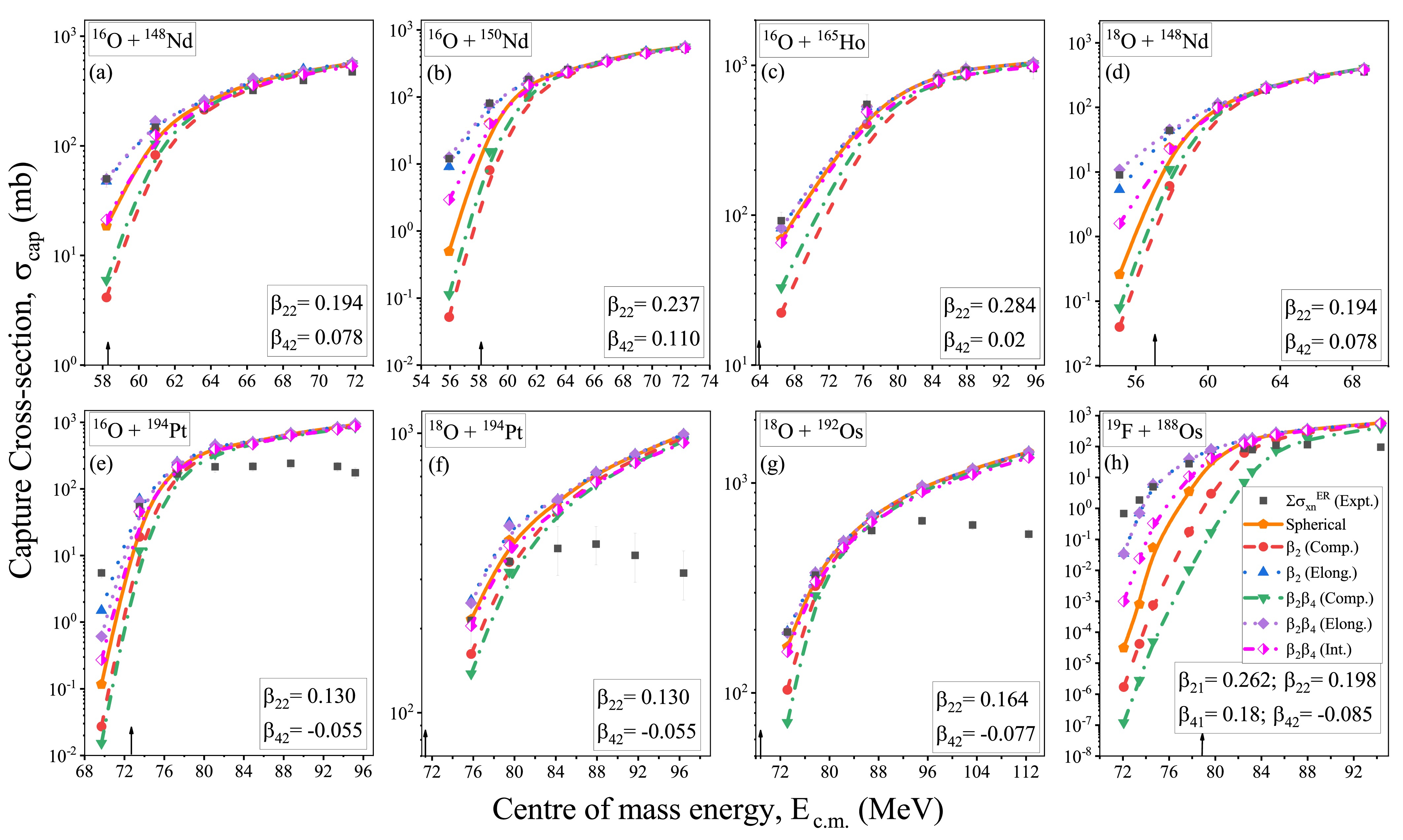

Figure 1.  (color online) Schematic diagram of the capture cross-sections ($ \sigma_{\rm cap} $) obtained by the extended $ \ell $-summed Wong model as a function of $ E_{\rm c.m.} $ with spherical, compact, and elongated configurations along with the cross-sections integrated over all orientations for the considered P-T combinations. The black arrow denotes the Coulomb barrier energy corresponding to each P-T combination.

The obtained capture cross-sections $ \sigma_{\rm cap} $ for the various configurations of the deformed nuclei are then compared with experimental ER cross-sections ($\sum\sigma_{xn}^{\rm ER}$), as shown in Fig. 1. This comparison highlights the significance of nuclear deformation and orientation, which subsequently affect the ER cross-sections. The additional parameters for predicting the ER cross-sections such as the CN formation probability and survival probability are discussed in the subsequent sections.

The previous section emphasizes the importance of incorporating the deformation and orientation degrees of freedom in the capture cross-section, as shown in Fig. 1. At the same time, Fig. 1 provides the idea that the capture cross-sections obtained with the incorporation of $ \beta_4 $ deformation are enhanced. To estimate the fusion-ER cross-section mentioned in Eq. (1), we incorporate the role of the compound nucleus formation probability ($P_{\rm CN}$). This term determines the extent to which the interaction between projectile and target (P-T) can lead to a fusion state and the creation of CN after the capture process. The fusion cross-section, described in Eq. (2), examines the extent of the CN formation. In the present study, we have analyzed $P_{\rm CN}$ using the Siwek-Wilczyńska formula [41] given in Eq. (16). $P_{\rm CN}$ is influenced by the charge and mass number of the entrance channel. These parameters collectively determine the Coulomb parameter '$ z $'. '$ z $' varies the mean interaction barrier for fusion, denoted as '$ B $', which is further used for the calculation of parameter '$ b $' at a given $E_{\rm c.m.}$.

Fig. 2 shows the variation of $P_{\rm CN}$with respect to $E_{\rm c.m.}$. The calculated $P_{\rm CN}$ for the considered reactions is plotted for the same energy range. Further, $P_{\rm CN}$ increases with increasing $E_{\rm c.m.}$, implying the increase in the fusion process for the formation of CN. This value approaches 1 with increasing energy. This variation in $P_{\rm CN}$ for all the considered P-T combinations depends on the Coulomb parameter '$ z $', which hinders the complete formation of CN. For example, the reactions or the P-T combinations with a smaller Coulomb parameter have higher $P_{\rm CN}$ than those with a higher Coulomb parameter. The $ ^{16, 18} $O induced reactions exhibit a higher $P_{\rm CN}$ within the range of 0.7 − 0.9 for the energy range given in Table 1. However, for the ¹⁹F induced reaction, the addition of one proton in ¹⁹F compared to $ ^{16, 18} $O increases the Coulomb parameter, which reduces $P_{\rm CN}$ to values in the range of 0.5 – 0.7. The above discussion makes it evident that the entrance channel plays a crucial role in the formation of CN. This repulsion by the Coulomb parameter is compensated by increasing $E_{\rm c.m.}$, allowing the P-T combination to facilitate the formation of a CN.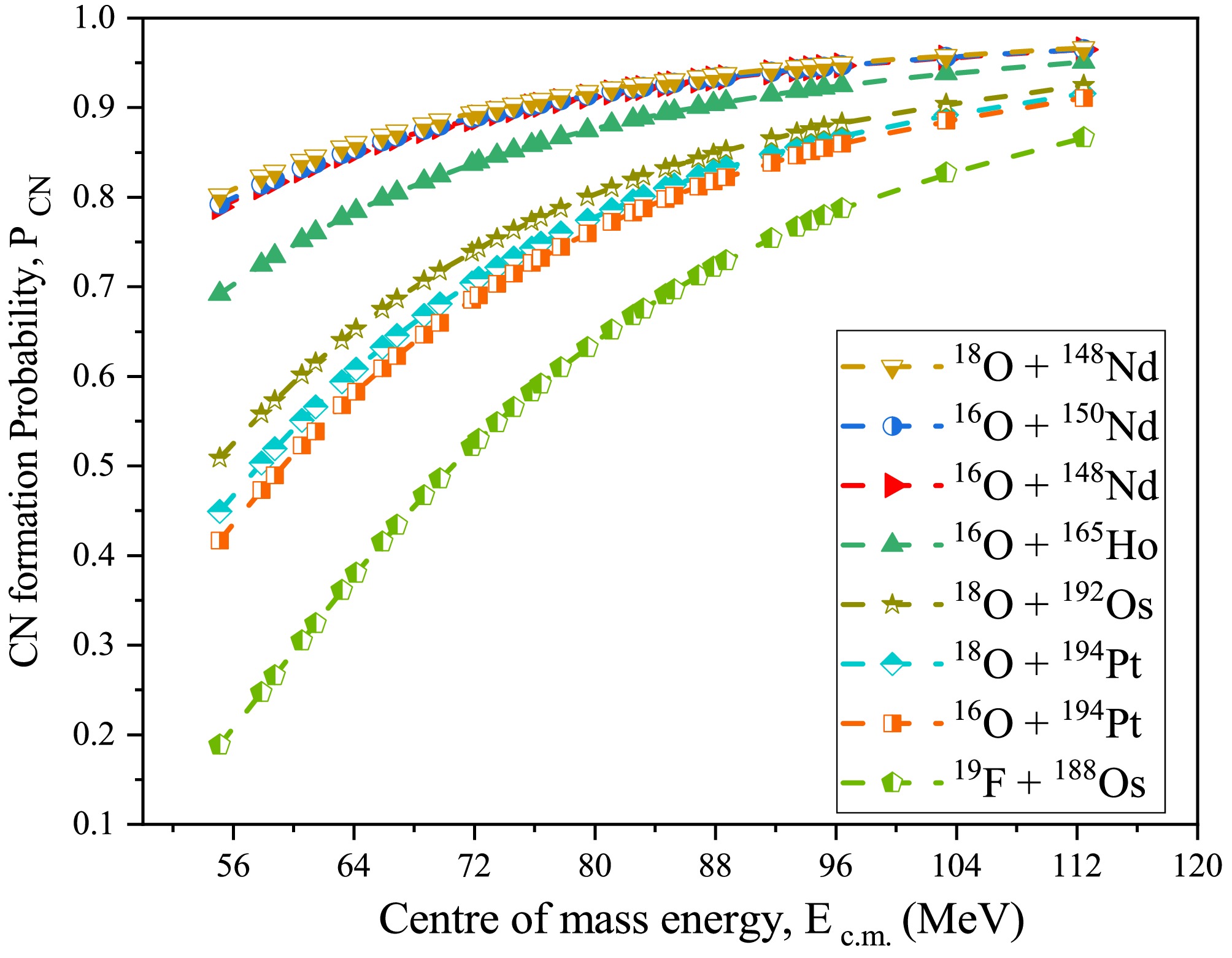

Figure 2.  (color online) Schematic diagram of the variation of the CN formation probability ($P_{\rm CN}$) with the center of mass energies ($E_{\rm c.m.}$) for the considered P-T combinations.

The product of $P_{\rm CN}$ with the capture cross-sections ($ \sigma_{\rm cap} $) gives us the fusion cross-sections ($\sigma_{\rm fus}$). The formation of the CN is investigated by analyzing the ($\sigma_{\rm fus}$), as mentioned in Eq. (2). The $\sigma_{\rm fus}$ values for all the considered reactions are compared to the experimental ER cross-section data depicted in Fig. 3. The figure shows that the fusion component contributes significantly to the capture process, with $ P_{\rm CN} $$ \ge 0.7 $. To achieve an explicit understanding and better explanation of the ER cross-sections, we must introduce the missing term to examine the relevance of the fission process, i.e., the survival probability of the formed compound nucleus ($ W_{\rm sur} $). This part is addressed in the next section.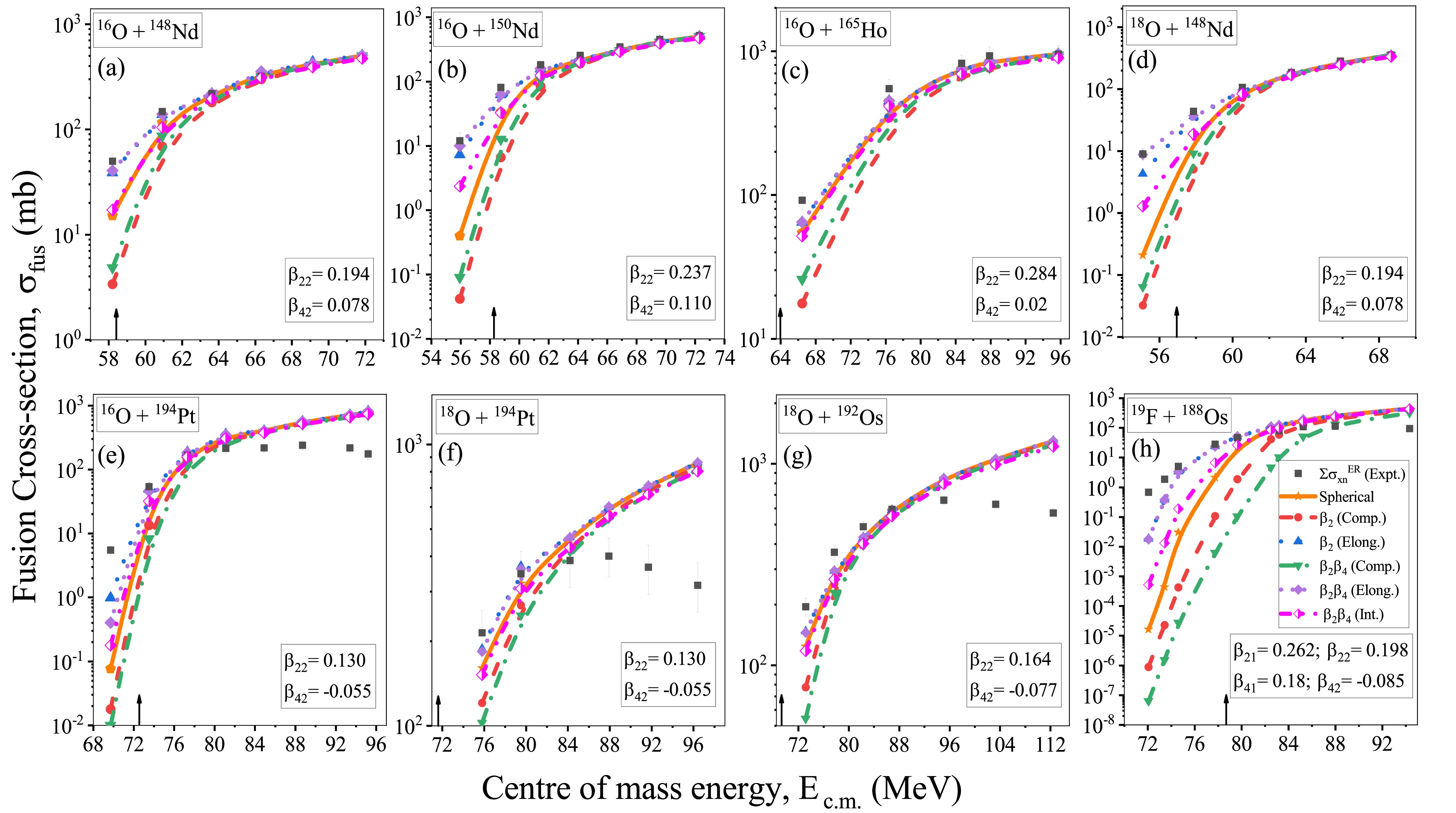

Figure 3.  (color online) Schematic diagram of Fusion cross-sections ($\sigma_{\rm fus}$ = $ \sigma_{\rm cap} $ $ \times $ $P_{\rm CN}$) as functions of $E_{\rm c.m.}$ with spherical, compact, and elongated configurations along with the cross-sections integrated over all orientations for the considered P-T combination. The black arrow denotes the Coulomb barrier energy corresponding to each P-T combination.

The fusion process results in the formation of a CN in an excited nuclear state. The CN stabilizes itself either by emitting light particles or forming fragments through fission. In this study, we examine the possibility of fission by calculating the survival probability $ W_{\rm sur} $ of the formed compound nucleus. The survival probability $ W_{\rm sur} $ in Eq. (1) represents the chances of a CN transitioning to the ground state by emitting neutrons instead of undergoing fission. The survival probability is calculated using the statistical model described in Eq. (20), which takes into account the probability of neutron emission from the excited state $ P_{xn} $ and the ratio of neutron decay width $ \Gamma_n $ to fission decay width $ \Gamma_f $ at a specific excitation energy $ E_{\rm CN}^* $ of the CN. The factor $ P_{xn} $ depends on the temperature ($ T $), excitation energy ($ E_{\rm CN}^* $) of the CN, and separation energies of the neutrons $ B_{i} $ but is independent of the atomic mass of nuclei. However, the ratio of decay widths depends on the mass number $ A $, fission barrier height $ B_{f} $, and neutron separation energy of the CN at a given $ E_{\rm CN}^* $. The survival of the CN against fission is determined by the fission barrier $ B_{f} $ of the CN at that specific $ E_{\rm CN}^* $. The fission barrier $ B_{f} $ is calculated as the sum of the macroscopic part or liquid drop term ($ B_f^{LD} $) and the microscopic shell correction energy ($B_f^{\rm Shell}$), as described in Eq. (23). The $B_f^{\rm Shell}$ decreases exponentially with increasing $ E_{\rm CN}^* $, resulting in a decrease in $ B_{f} $ with increasing $ E_{\rm CN}^* $, enhancing the fission probability. On the contrary, the values of $ B_f^{LD} $ and $B_f^{\rm Shell}$ depend on the mass and atomic number of the formed CN and exhibit different magnitudes of $ B_f^{LD} $ and $B_f^{\rm Shell}$. The $ B_f^{LD} $ component arises from the competition between the Coulomb and surface forces, which is determined by the fissility parameter ($ \chi $). This parameter $ \chi $ depends on the mass number '$ A $' and the charge '$ Z $' of the CN. The magnitudes of $ \chi $ obtained for CN in the considered P-T combinations are provided in Table 1. The fissility parameter decreases as the atomic number decreases, causing an increase in $ B_f^{LD} $. As a result, the fission barrier $ B_{f} $ becomes considerably higher compared to $ B_{i} $ for CN in reactions having high $ B_f^{LD} $ values and very low shell correction energies, such as ¹⁶O+^148,150Nd, ¹⁶⁵Ho, and ¹⁸O+ ¹⁴⁸Nd, leading to a higher likelihood of neutron emissions demonstrated by higher values of $ W_{\rm sur} $. Meanwhile, the fission barrier $ B_{f} $ obtained for compound nuclei having low $ B_f^{LD} $ values and significant shell correction in reactions such as ¹⁶O+ ¹⁹⁴Pt, ¹⁸O+¹⁹⁴Pt, ¹⁹²Os, and ¹⁹F+¹⁸⁸Os is comparable to $ B_i $. Although the higher $B_f^{\rm Shell}$ values of these nuclei having neutron numbers around $ N=126 $ do not have a significant impact on $ B_f $ [18, 60], as $ B_f^{\rm Shell} $ values decrease with increasing $ E_{\rm CN}^* $. Therefore, the decrease in the fission barrier and $ W_{\rm sur} $ implies a higher likelihood of the fission process dominating neutron evaporation channels.

As mentioned in Eq. (1), the fusion-ER cross-section is obtained by multiplying the survival probability $ W_{\rm sur} $ with the fusion cross-section $ \sigma_{fus} $. In the previous discussion, we discussed the various factors affecting both the $ W_{\rm sur} $ and $\sigma_{\rm fus}$ and determined their values for the considered P-T combinations. The total fusion-ER cross-sections calculated by summing all the fusion-ER cross-sections for all the neutron channels are compared with experimental data for the considered reactions in Fig. 4. The calculated fusion-ER cross-sections obtained for the '$ \beta_{2}\beta_{4} $' case for the reactions ¹⁶O+^148,150Nd,¹⁶⁵Ho, and ¹⁸O+ ¹⁴⁸Nd show good agreement with the experimental data presented in Fig. 4(a-d). However, these calculations do not yield satisfactory results for other reactions ¹⁶O+ ¹⁹⁴Pt, ¹⁸O+¹⁹⁴Pt,¹⁹²Os, and ¹⁹F+¹⁸⁸Os shown in Fig. 4(e-h) owing to the presence of a small fission barrier, indicating the dominance of fission.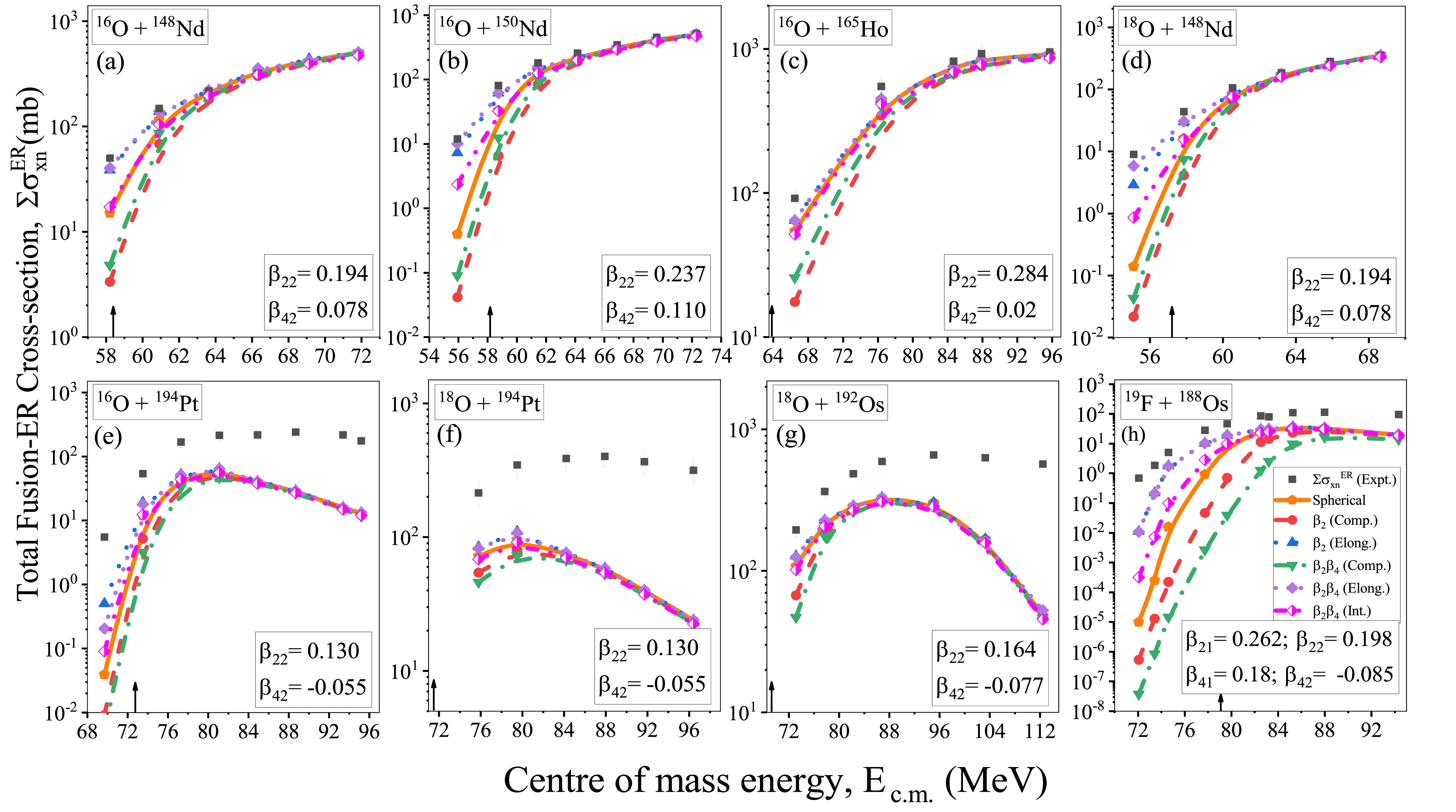

Figure 4.  (color online) Schematic diagram of total fusion-ER cross-sections ($\sum\sigma_{xn}^{\rm ER}$) as a function of $E_{\rm c.m.}$ with spherical, compact, and elongated configurations along with the cross-sections integrated over all the orientations of the considered P-T combinations. The black arrow denotes the Coulomb barrier energy corresponding to each P-T combination.

To obtain the desired cross-sections, it has been observed that, apart from the fission barrier, the $ W_{\rm sur} $ of the nuclei is also affected by the ratio of level density parameters between the fission channel and the neutron evaporation channel ($ a_f/a_n $) [61, 62]. This ratio determines the likelihood of fission in the nuclei. An investigation of $ W_{\rm sur} $ for all the contributing neutron channels is conducted in terms of $ a_f/a_n $ for the compound nuclei (CN) ²¹⁰Po, ²⁰⁷At, and ²¹⁰Rn at a common excitation energy $ E_{\rm CN}^* $. The findings of this analysis are presented in Fig. 5. From the figure, one can observe that as the $ a_f/a_n $ ratio increases, the $ W_{\rm sur} $ of neutrons decreases and the nucleus is likely to undergo the fission process. The variation of $ W_{\rm sur} $ at $ E_{\rm CN}^* $ = 52 MeV is associated with the fission barrier height of the CN, as depicted in Fig. 5(a). While 3n, 4n, and 5n are common neutron decay channels in all of the formed CN, the contribution of neutron channels 6n and 7n is found in ²¹⁰Po, and the contribution of 6n is found in ²¹⁰Rn as the excitation energy increases. This result is depicted in Fig. 5(b-d). Hence, to achieve better agreement with experimental results and gain a deeper understanding of cases with lower fission barriers, the calculation of the survival probability should incorporate lower values for this ratio, as the lower value of the ratio indicates the dominance of decay via neutron evaporation.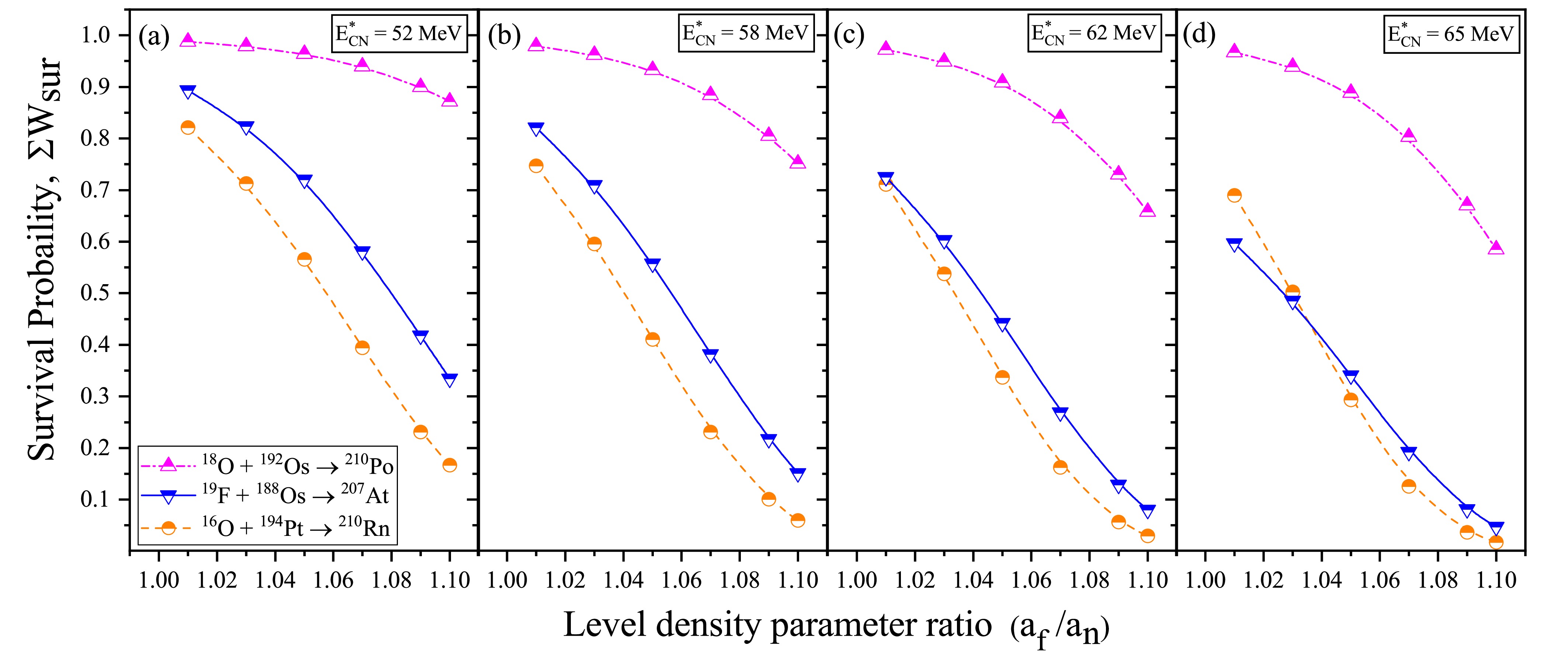

Figure 5.  (color online) Schematic diagram of the survival probability ($\Sigma W_{\rm sur}$) for all the contributing neutron channels corresponding to CN as a function of the level density parameter ratio of the fission to neutron channel ($ a_f/a_n $) at different magnitudes of $ E_{\rm CN}^* $.

For instance, the results represented in Fig. 4 are obtained by considering the ratio $ a_f $/$ a_n $ = 1.1. The sensitivity of the $ a_f $/$ a_n $ ratio in the fusion-ER cross-sections is investigated for the reactions ¹⁶O+¹⁹⁴Pt, ¹⁸O+¹⁹⁴Pt, ¹⁸O+¹⁹²Os and ¹⁹F+¹⁸⁸Os, by varying the value of $ a_f $/$ a_n $ from 1.0 to 1.05 and compared with the cross-sections obtained with $ a_f $/$ a_n $=1.1, as shown in Fig. 6 (a-d) respectively. The figure demonstrates that the fusion-ER cross-sections vary significantly with the change in the value of $ a_f $/$ a_n $ ratio. Based on the graph shown in Fig. 6, it can be observed that the $ a_f/a_{n} $ = 1.03−1.05 provides better agreement with the experimental data for all the considered reactions. On the other hand, the cross-sections for the reactions ¹⁶O+ ^148,150Nd, ¹⁶⁵Ho, ¹⁸O+ ¹⁴⁸Nd persist even when the value of $ a_f $/$ a_n $ varies from 1.0 to 1.1. This can be attributed to the higher $ B_{f} $ of CN. Therefore, the total fusion-ER cross-sections for all the considered reactions are collectively obtained with $ a_f $/$ a_n $ = 1.05 with $ \beta_2\beta_4 $ deformations.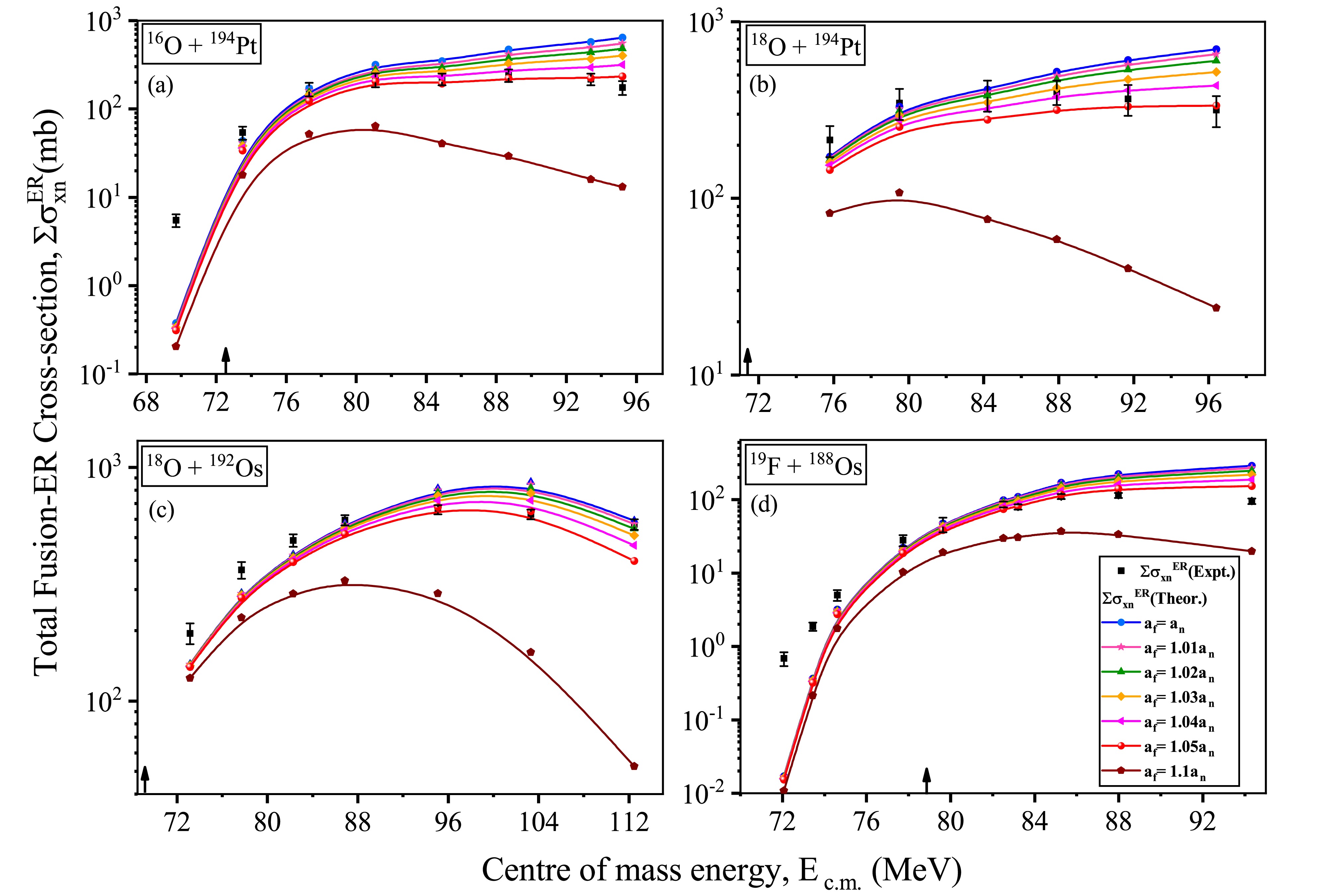

Figure 6.  (color online) Schematic diagram of the total fusion-ER cross-sections ($\sum\sigma_{xn}^{\rm ER}$) as functions of $E_{\rm c.m.}$ with the $ a_f $/$ a_n $ ratio varying from 1.0 to 1.05 and compared with 1.1 for the reactions (a) ¹⁶O+¹⁹⁴Pt, (b) ¹⁸O+¹⁹⁴Pt (c) ¹⁸O+¹⁹²Os, and (d) ¹⁹F+¹⁸⁸Os under the influence of $ \beta_2\beta_4 $ with elongated configuration. The black arrow denotes the Coulomb barrier energy corresponding to each P-T combinations.

The present analysis utilized the parameters $ a_f $/$ a_n $ = 1.05 and $ E_d $ = $ 5.48A^{1/3}/(1+1.3A^{-1/3}) $, in conjunction with the $ \beta_2\beta_4 $ deformation, to calculate the Fusion-ER cross-sections. Along with $ a_f $/$ a_n $, the damping factor ($ E_d $) plays a crucial role in modifying the fission barrier, as shown in Eq. (23). It measures the decrease in shell correction energy that occurs with an increase in the excitation energy of the CN. In Ref. [63], the value of $ E_d $ is considered to be a constant value, that is, $ E_d $=25.65 MeV. To investigate the influence of the $ E_d $ on the cross-sections, we compared the outcomes obtained from a constant $ E_d $ value of 25.65 MeV, and those obtained using the formula-based $ E_d $ expressed as $ 5.48A^{1/3}/(1+1.3A^{-1/3}) $. The calculated ER cross-sections using both approaches facilitate a similar analysis for all the reactions under consideration, as illustrated in Fig. 7.This demonstrates that the formula-based evaluation of $ E_d $ used here aligns well with the fixed value employed in the previous studies, ensuring result consistency. Therefore, the predicted total ER cross-sections associated with $ \beta_2\beta_4 $ along with the observed neutron channels are presented for all reactions at $ a_f $/$ a_n $ = 1.05 and the formula based $ E_d $, as illustrated in Fig. 8.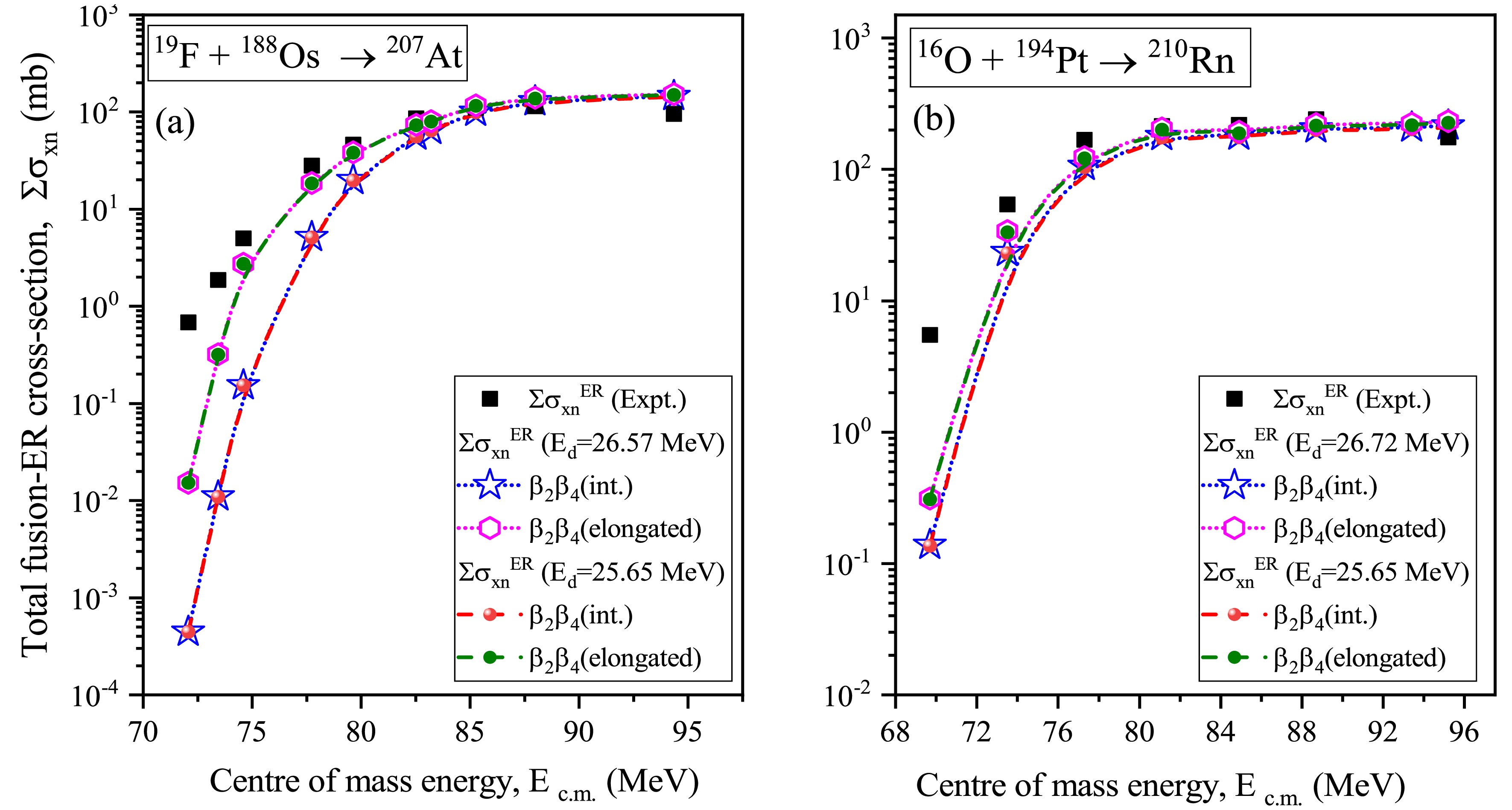

Figure 7.  (color online) Schematic diagram of total fusion-ER cross-sections ($\sum\sigma_{xn}^{\rm ER}$) as a function of $E_{\rm c.m.}$ by considering the ratio $ a_f $/$ a_n $=1.05 for P-T combinations under the influence of average orientations and the elongated configuration of $ \beta_2\beta_4 $ deformed nuclei with different values of $ E_d $.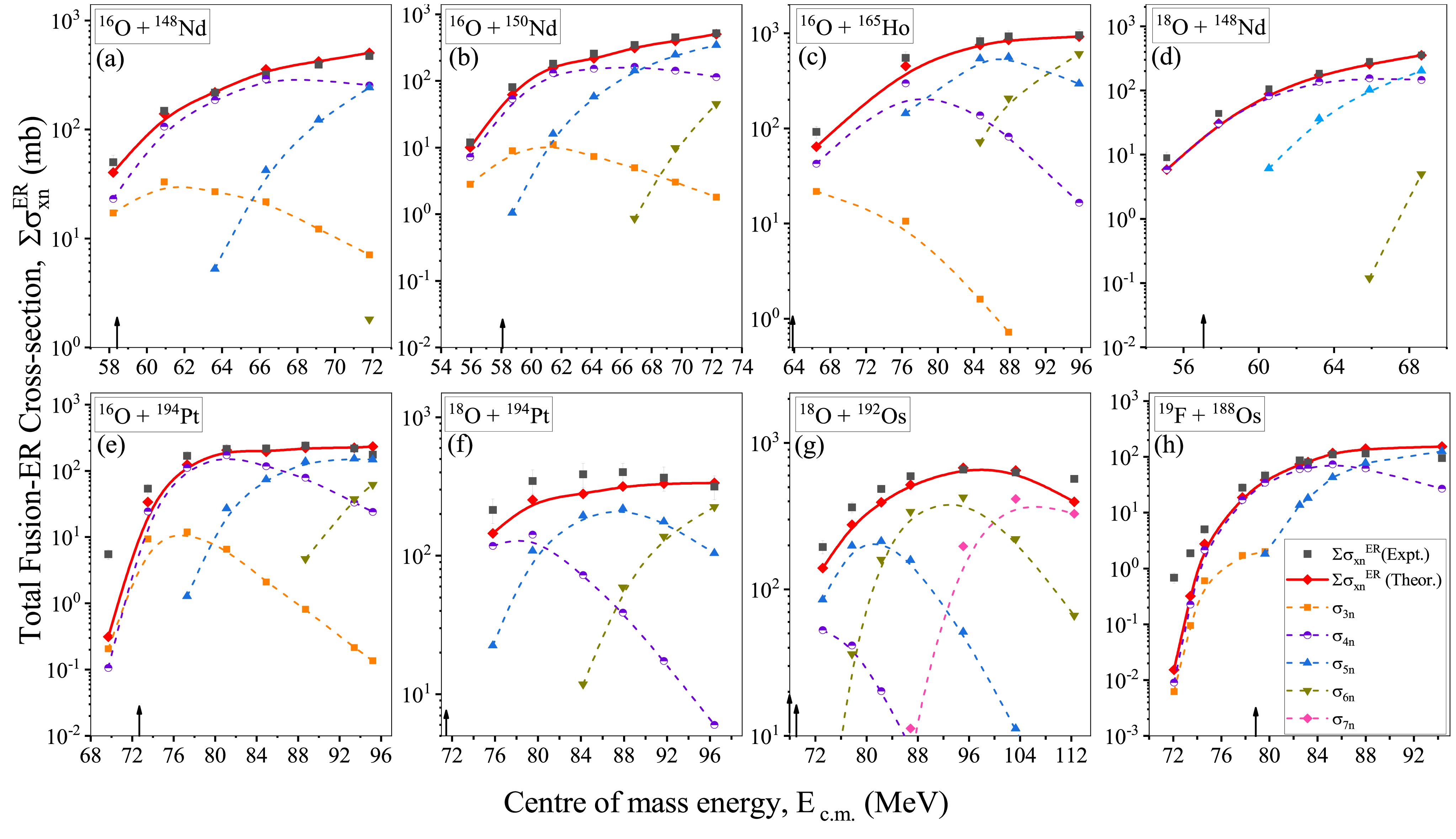

Figure 8.  (color online) Schematic diagram of the total fusion-ER cross-sections ($\sum\sigma_{xn}^{\rm ER}$) with x-neutrons emission channels as a function of $ E_{\rm c.m.} $ at $ a_f $/$ a_n $=1.05 for all the chosen P-T combinations under the influence of $ \beta_2 \beta_4 $ with elongated configuration. The black arrow denotes the Coulomb barrier energy corresponding to each P-T combination.

To validate the results further, we compared the cross-sections obtained from the elongated configuration and cross-sections integrated over all orientations of the $ \beta_2\beta_4 $ deformed nuclei, as shown in Fig. 9. This analysis revealed that, in most cases, the cross-sections from both the elongated configuration and the integrated approach yield comparable outcomes.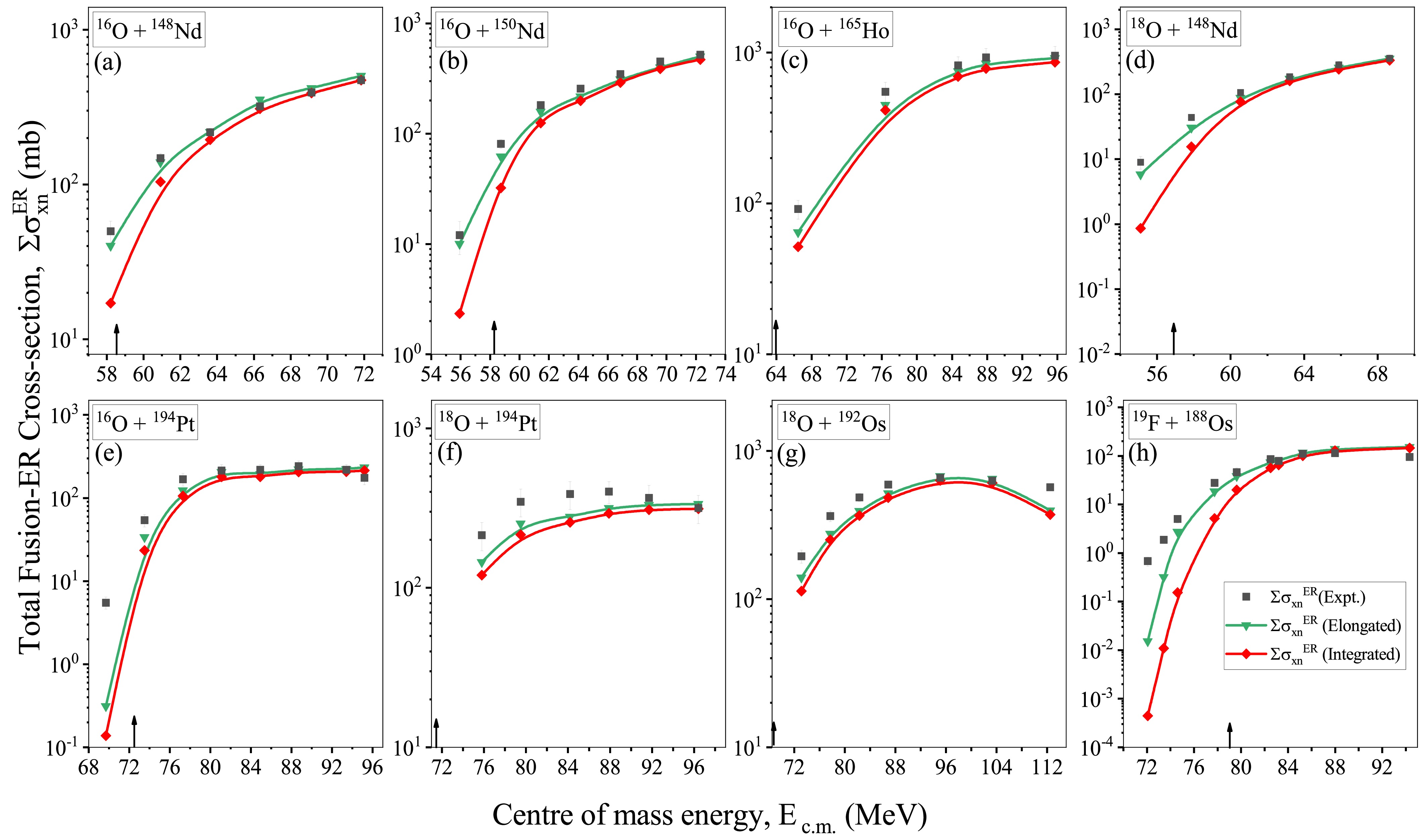

Figure 9.  (color online) Schematic diagram of the total fusion-ER cross-sections ($\sum\sigma_{xn}^{\rm ER}$) as a function of $ E_{\rm c.m.} $ with the ratio $ a_f $/$ a_n $=1.05 for P-T combinations under the influence of average orientations and the elongated configuration of $ \beta_2\beta_4 $ deformed nuclei. The black arrow denotes the Coulomb barrier energy corresponding to each P-T combination.

In addition to the $ O $-induced reactions, we also examined ³⁰Si+¹⁷⁰Er to assess the aforementioned results. For this reaction, the total evaporation residue (ER) cross-sections are calculated by considering the $ \beta_2 $ and $ \beta_2\beta_4 $ deformations of both the projectile and target nuclei in their respective compact and elongated configurations. The cross-sections are also calculated by integrating across all orientations ($ \theta_i $), assuming that $ a_f $/$ a_n $ = 1.05. The calculated results were subsequently compared with experimental data [64] for ER cross-sections, as illustrated in Fig. 10. Similar to previous findings, the $ \beta_2\beta_4 $ deformed nuclei provide better agreement with the experimental data. The results highlight the significant influence of $ \beta_2 $ and $ \beta_4 $ deformations, their corresponding orientations, and the $ a_f $/$ a_n $ parameter in determining the fusion-ER cross-sections in this study.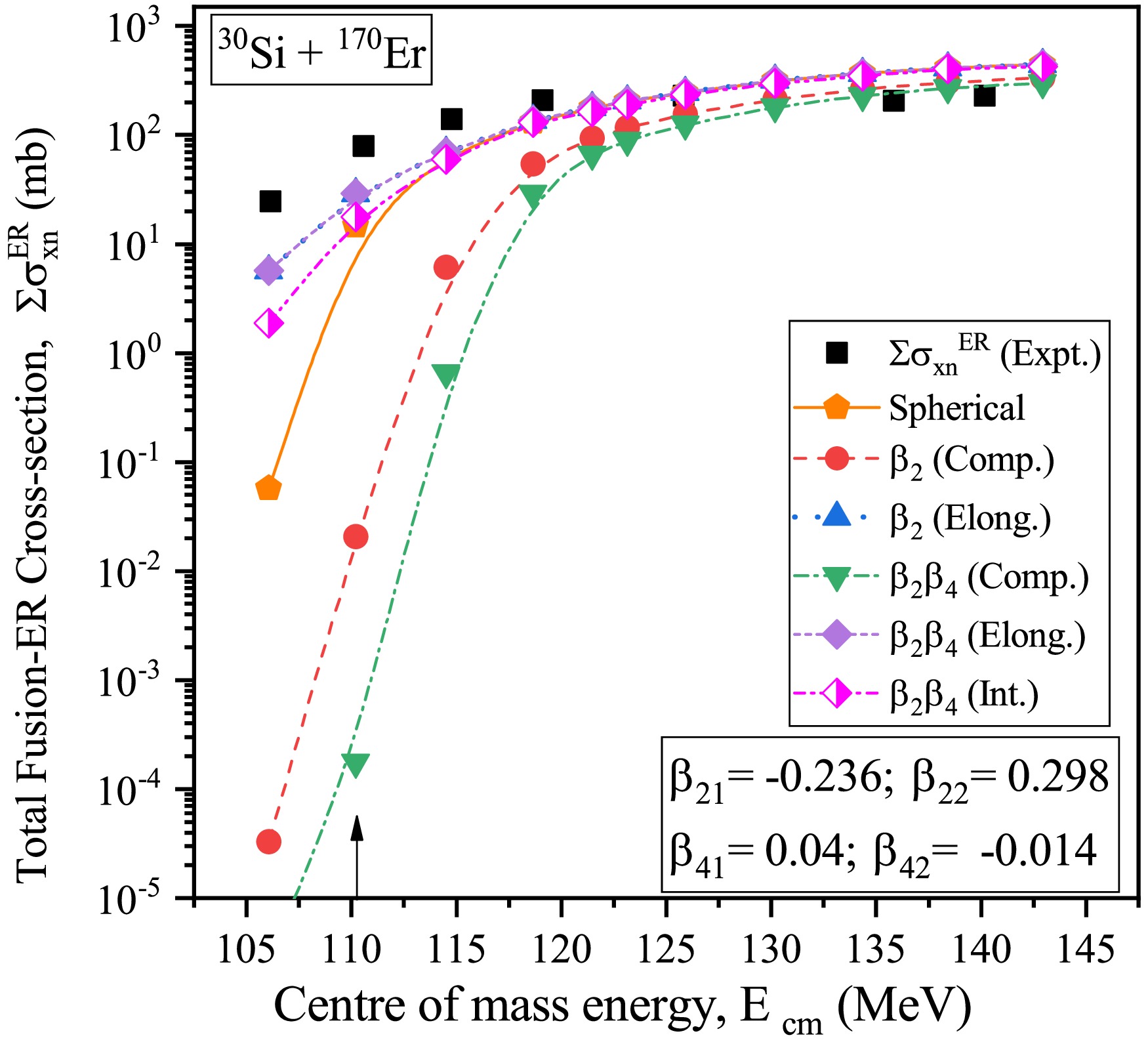

Figure 10.  (color online) Schematic diagram of the total fusion-ER cross-sections ($\sum\sigma_{xn}^{\rm ER}$) of the ³⁰Si+¹⁷⁰Er reaction calculated by incorporating $ \beta_2 $, $ \beta_2\beta_4 $ and the integrated effect of all the orientations of $ \beta_2\beta_4 $ deformations at $ a_f/a_n $ = 1.05 as function of $E_{\rm c.m.}$. The black arrow denotes the Coulomb barrier energy corresponding to P-T combinations.

The analysis focuses on studying the influence of deformations and associated orientations on Fusion-ER cross-sections in ¹⁶O + ^148,150Nd, ¹⁶⁵Ho, ¹⁹⁴Pt, ¹⁸O+ ¹⁴⁸Nd, ¹⁹⁴Pt, ¹⁹²Os, ¹⁹F + ¹⁸⁸Os, and ³⁰Si+¹⁷⁰Er reactions consisting of quadrupole ($ \beta_2 $) and hexadecapole ($ \beta_4 $) deformed target nuclei. The influence of these parameters has been studied in terms of capture cross-section ($ \sigma_{\rm cap} $), CN formation probability ($P_{\rm CN}$), survival probability ($ W_{\rm sur} $), and corresponding fusion-ER cross-sections for the center of mass energies ($E_{\rm c.m.}$) lying across the barrier. The capture cross-sections ($ \sigma_{\rm cap} $) are studied within the $ \ell $-summed Wong model. The $ \beta_2 $ and $ \beta_4 $ deformations within the compact configuration produced hindered cross-sections compared to the spherical, whereas enhanced cross-sections are obtained at the elongated configuration. The extent of the contribution of the fusion component in the capture cross-section is studied using the compound nucleus formation probability ($P_{\rm CN}$). Increasing $E_{\rm c.m.}$ increases $P_{\rm CN}$, enhancing the fusion cross-sections. In addition, the survival probability ($ W_{\rm sur} $) of the compound nucleus is calculated to segregate the contribution of ER and fission components. The observed discrepancy in fusion-ER reactions is attributed to the influence of the fission barrier and neutron separation energy. The survival probability of CN and subsequent ER process are addressed by adopting the appropriate level density ratio ($ a_f/a_n $). The $ a_f/a_n $ ratio plays a dominant role in reactions with a lower fission barrier. The fusion-ER cross-sections are calculated by including $ \beta_2 $$ \beta_4 $ deformations at $ a_f/a_n $ = 1.05 and have a good agreement with experimental data.