Comprehensive constraints on fermionic dark matter-quark tensor interactions in direct detection experiments

I. INTRODUCTION

• I. INTRODUCTION
• II. NONPERTURBATIVE MATCHING OF DM-QUARK INTERACTIONS
• III. XENON1T CONSTRAINTS
•      A DM-nucleus scattering cross section
•      B Constraint from ${\mathrm{NR}}$ signals
•      C Constraint from the Migdal effect
•      D Constraint from ${\mathrm{ER}}$ signals
• IV. CONSTRAINTS FROM OTHER DIRECT DETECTION EXPERIMENTS
• V. CONSTRAINTS FROM NON-DIRECT-DETECTION EXPERIMENTS AND AN EXAMPLE OF UV COMPLETION
• VI. CONCLUSION
• APPENDIX A: SQUARED FORM FACTOR

Although dark matter (DM) constitutes approximately a quarter of the total energy density of the Universe, its particle properties are yet unknown [1, 2]. One of the theoretically motivated candidates is the weakly interacting massive particle (WIMP), which can meet the required properties to explain the DM conundrum and also have a detectable possibility. During the past two decades, although a great amount of theoretical and experimental efforts have been dedicated to searches for WIMPs, DM direct detection (DMDD) experiments have not found any positive signals but have constrained the DM-nucleus cross section to an unprecedented level [3, 4]. However, owing to the kinematic restriction of DM-nucleus elastic scattering, the DM-nucleon interaction remains less constrained below the ${\cal{O}}(1\,{\rm{GeV}})$ DM mass region from direct detection experiments using nuclear recoil (${\mathrm{NR}}$) signals. To address this limitation, inelastic processes are considered, such as bremsstrahlung processes [5] and the Migdal effect [6, 7]. Nevertheless, even with the improvement from inelastic processes, the constraints are still limited up to a mass of approximately 40 MeV [8−13]. For lighter DM particles at the MeV scale, meaningful constraints require considerations such as boosted DM scenarios [14, 15] or novel low-threshold detectors (see review paper [16] and the references therein). In contrast to ${\mathrm{NR}}$ experiments searching for the DM-nucleon interaction, the DM-electron interaction offers a more powerful alternative of probing low-mass DM particles through the electron recoil (${\mathrm{ER}}$) signal [17, 18]. This is due to the significantly smaller mass of the electron compared to a typical nucleus, allowing it to easily gain the recoil energy from a light DM particle. For instance, the single-electron search conducted by XENON1T has the capability of exploring a DM mass as low as approximately 5 MeV [19].

Owing to the small momentum transfer (less than a few MeV) for DMDD experiments, it is preferable to adopt the low energy effective field theory (LEFT) approach, which does not rely on the details of ultraviolet (UV) models, to study the interactions between DM and standard model particles [20−22]. The starting point for DM effective field theory (EFT) is the DM-quark, -lepton, or -photon/gluon interactions at leading order that are color and electric charge neutral. In the Dirac DM case, the leading operators appear at dimension 5 and 6 and take the general forms $\bar \chi \sigma_{\mu\nu}({\rm{i}}\gamma_5) \chi F^{\mu\nu}$ and $(\bar \chi \Gamma \chi)(\bar \psi \Gamma' \psi)$, where χ represents fermionic Dirac-type DM, ψ represents quarks or leptons, and $F^{\mu\nu}$ represents the electromagnetic field strength tensor. For the interest of direct detection, ψ is typically taken to be the up, down, and strange quarks and the electron. For ${\mathrm{NR}}$, the DM-nucleon interaction naturally arises from DM-quark and DM-gluon operators through nonperturbative matching via chiral perturbation theory (χPT) [23].

In this study, we explore the DM-photon interactions induced by nonperturbative QCD effects from DM-quark interactions. This will provide new methods for constraining DM-quark interactions. Similar ideas have previously been used in the study of flavor-violated radiative decays of charged leptons and neutrino electromagnetic (EM) moments [24, 25]. In particular, we consider the two tensor operators $(\bar{\chi} {\rm{i}}\sigma^{\mu\nu} \gamma^5 \chi) (\bar{q} \sigma_{\mu\nu}q)$ and $(\bar{\chi} \sigma^{\mu\nu} \chi)( \bar{q} \sigma_{\mu\nu} q)$, which not only induce the short-distance (SD) DM-nucleon operators covered in most direct detection studies, but also generate the DM electric and magnetic dipole moment operators $(\bar{\chi} {\rm{i}} \sigma_{\mu\nu} \gamma_5 \chi) F^{\mu\nu}$ (edm) and $(\bar{\chi} \sigma_{\mu\nu} \chi) F^{\mu\nu}$ (mdm), which contribute to direct detection via the long-distance (LD) photon mediator.

In previous calculations of the DMDD constraints on the above two tensor operators, only the DM-nucleus scattering induced by the SD operators was considered [11, 20, 21]. In this study, we utilize the XENON1T experiment as a benchmark experiment to comprehensively investigate the constraints from both the SD and LD contributions. We find that there are interesting interference effects between the two in DM-nucleus scattering and the Migdal effect. Owing to the induced dipole interactions, we also investigate the constraints from DM-electron scattering. Remarkably, owing to the excellent sensitivity to low-mass DM, the constraints from ${\mathrm{ER}}$ via this LD effect significantly extend to low-mass (from GeV to MeV) DM. In addition, we collect other existing direct and non-direct-detection constraints on the DM dipole operators and recast them into constraints on the DM-quark tensor operators. In our analysis, we consider the cases in which flavor SU(3) symmetry is imposed and not imposed. For the flavor conserving case, a universal Wilson coefficient is assumed for the operators involving $u,d,s$ quarks (where the corresponding quark mass is attached to the operator as typically practiced in the literature [23]), and for the non-conserving case, the contributions from the three quarks are considered separately.

The paper is organized as follows. Section II is dedicated to nonperturbative chiral matching of the two DM-quark tensor operators to the DM-photon and DM-nucleon interactions. In Section III, we discuss the constraints on these operators from ${\mathrm{NR}}$, the Migdal effect, and ${\mathrm{ER}}$, based on the XENON1T data. The full constraints and comparisons with the literature for direct detection experiments are given in Section IV. In Section V, we further discuss constraints from non-direct-detection experiments and give an example of UV completion for the two DM-quark tensor operators. Our concluding remarks are presented in Section VI. The relevant nuclear form factors are presented in Appendix A.

II. NONPERTURBATIVE MATCHING OF DM-QUARK INTERACTIONS

• I. INTRODUCTION
• II. NONPERTURBATIVE MATCHING OF DM-QUARK INTERACTIONS
• III. XENON1T CONSTRAINTS
•      A DM-nucleus scattering cross section
•      B Constraint from ${\mathrm{NR}}$ signals
•      C Constraint from the Migdal effect
•      D Constraint from ${\mathrm{ER}}$ signals
• IV. CONSTRAINTS FROM OTHER DIRECT DETECTION EXPERIMENTS
• V. CONSTRAINTS FROM NON-DIRECT-DETECTION EXPERIMENTS AND AN EXAMPLE OF UV COMPLETION
• VI. CONCLUSION
• APPENDIX A: SQUARED FORM FACTOR

Because the transferred momentum in DMDD experiments is limited to several hundreds of MeV, we can generically describe the interactions between DM and standard model (SM) light fields within the framework of LEFT. For DMDD, the complete set of operators with fermion and scalar DM particles up to canonical mass dimension 7 have been classified in [23, 26−29]. Here, we are particularly interested in the two tensor operators for the Dirac fermionic DM, which have not received significant attention other than a few studies focusing on ${\mathrm{NR}}$ signals and the Migdal effect induced by SD DM-nucleon interactions [11, 21]. Following the convention in [23], they are parameterized by

where q represents the three light quarks $u,d,s$ of mass $m_q$ relevant to direct detection. For each operator, there is a corresponding unknown Wilson coefficient whose magnitude is parameterized as $|C_{\chi q}^{{\mathrm{T1}}({\mathrm{T2}})}| \equiv 1/ \Lambda^3$ , where Λ is an effective scale related to some unknown UV physics. In the following, we demonstrate that these operators not only contribute to DM-nucleon local interactions but also the DM magnetic and electric dipole moment operators $(\bar{\chi} \sigma_{\mu\nu} \chi) F^{\mu\nu}$ and $(\bar{\chi} {\rm{i}} \sigma_{\mu\nu} \gamma_5 \chi) F^{\mu\nu}$ through nonperturbative QCD effects. These nonperturbative dipole contributions to DMDD will help significantly extend the sensitivity to low mass DM. They can also be systematically extracted through matching within the framework of the (baryon) chiral perturbation theory ((B)$\chi{{\rm{PT}}}$) of QCD at low energy. For applications of (B)$\chi{{\rm{PT}}}$ in the description of DMDD, see, for example, Refs. [23, 30]. Other DM-quark operators involving (pseudo-)scalar or (axial-)vector currents, such as the commonly discussed $\bar{\chi}\chi \bar{q} (\gamma_5) q$ and $\bar{\chi}\gamma^\mu \chi \bar{q} \gamma_\mu (\gamma_5) q$, do not exhibit this unique nonperturbative matching to DM dipole moments but rather generate operators with at least two photon fields owing to QED gauge and parity symmetries. Their contributions to DMDD can be safely ignored because of suppression from the loop factor and additional QED couplings.

Our starting point is the quark level Lagrangian with external sources,

where ${\cal{L}}_{\rm{QCD}}$ is the QCD Lagrangian for the $u,\; d,\; s$ quarks in the chiral limit. The external sources, $l_\mu,\,r_\mu,\,s,\,p$, and $t^{\mu\nu}$, are $3\times 3$ matrices in flavor space, which contain non-strongly interacting fields such as the leptons, photon, and DM that interact with quarks. For the two DM-quark interactions with a tensor quark current in Eq. (1), the corresponding tensor external source is given by

where the first factor on the right-hand side is a tensor chiral projection operator [31] defined as

and $\bar t^{\mu\nu}$ is related to the DM tensor currents and couplings $C_{\chi q}^{{\mathrm{T1}}({\mathrm{T2}})}$and is considered a diagonal matrix in flavor space in our study,

The building blocks of chiral matching of the Lagrangian in Eq. (2) consist of the pseudo Nambu-Goldstone boson (pNGB) matrix U, baryon octet fields B, and external sources. We begin with the pure mesonic chiral Lagrangian that will lead to DM EM moments directly. The leading order Lagrangian appears at ${\cal{O}} (p^2)$ in chiral power counting [32, 33],

where $F_0$ is the pion decay constant in the chiral limit, and U is related to the pNGBs via

and the covariant derivative of U and the combined scalar source χ are

The tensor source first appears at ${\cal{O}} (p^4)$ [31], which yields the DM EM dipole moments. The relevant term is

where $\Lambda_1$ is a low energy constant (LEC), which is typically parameterized in terms of the chiral symmetry breaking scale $\Lambda_\chi$ in the form $\Lambda_1 = c_T \Lambda_\chi/(16\pi^2)$, with $c_T$ as an unknown dimensionless constant. Here, the tensor field matrices in flavor space are given by

with $u^2 = U$. The chiral field strength tensors read as

For our purpose, the vector external sources are recognized as

where $A_\mu$ denotes the photon field, and $Q_q$ is the electric charge of quark q in units of $e \approx 0$.

Expanding Eq. (9) to the lowest order in pNGB fields, the following DM edm and mdm interactions arise:

where the DM mdm and edm are

Assuming the DM EM dipole moments are dominated by these nonperturbative contributions, we can establish the relationship between the scale $\Lambda = |C_{\chi q}^{\mathrm{T1,2}}|^{-1/3}$ for the DM-quark tensor operators and the dipole moments via

where only one flavor quark contribution is assumed. In the above numerical illustration, we use the model estimation of the LEC $c_T = -3.2$ , as found in [34]; other studies provide a smaller magnitude, $c_T\approx -1.0(2)$ [35, 36], which will reduce Λ in Eq. (15) by a factor of 0.7. For the flavor symmetric case with $C_{\chi u}^{\mathrm{T1,2}} = C_{\chi d}^{\mathrm{T1,2}} = C_{\chi s}^{\mathrm{T1,2}}$, $\mu_\chi$ and $d_\chi$ are entirely dominated by the strange quark, whereas the contributions from up and down quarks almost cancel out owing to the approximate mass relation, $Q_um_u+ Q_dm_d\approx 0$.

Now, we consider the matching to DM-nucleon interactions. First, only the single-nucleon currents are present at LO in chiral power counting. Thus, we neglect the subleading contribution from higher chiral power terms and two-nucleon current [37]. The nucleon matrix element of the DM-quark operators can be parameterized in terms of form factors, which are restricted by Lorentz covariance, discrete symmetries, and algebraic identities for Dirac matrices and spinors. For the tensor operator, there are three form factors [38],

where $q^\mu = k_2^\mu-k_1^\mu$, $k_{12}^\mu = k_1^\mu+k_2^\mu$, and $m_N$ is the nucleon mass. ¹ In the BχPT framework, the form factors $F_{T,i}^{q/N}(q^2)$ ($i = 0,1,2$) are calculated order by order in the chiral expansion. Owing to the absence of light pseudoscalar poles as well as the small momentum squared of interest ($|q^2| \sim {\cal{O}} (1\,{\rm{MeV}}^2)$), the form factors can be Taylor-expanded around $q^2 = 0$, with the largest contributions arising from the values evaluated at $q^2 = 0$. For the tensor charges, $F_{T,0}^{q/N}(0) = g_T^{q/N}$, we use the lattice QCD result in [40], ²

whereas for the other two, we adopt a recent result found in [44],

where isospin symmetry is implied, i.e., $F_{T,i}^{u/p} = F_{T,i}^{d/n}$, $F_{T,i}^{d/p} = F_{T,i}^{u/n}$, and $F_{T,i}^{s/p} = F_{T,i}^{s/n}$. An alternative estimation based on hadronic models is given in [45] for the form factors $F_{T,1}^{q/N}$, whose values (including a vanishing central value for $q = s$) are typically employed in the DMDD community [23, 39].

To calculate the DM-nucleus matrix element, nonrelativistic (NR) ³ reduction of the nucleon-level amplitude should be performed to connect with the treatment in nuclear many-body methods. This is achieved by taking both the DM and nucleon spinors to the NR limit and expressing the amplitude as a combination of various NR quantities. The NR amplitude can be equivalently obtained using NR operators. In this operator language, according to Eq. (16), the chiral LO NR expansions of the contact tensor operators are given by

In the NR reduction of ${\cal{O}}_{\chi q}^{\mathrm{T2}}$, we include contributions from the $F_{T,2}^{q/N}$ term, which is spin-independent and potentially comparable to other terms. Including this term is essential for consistency in our analysis, and to the best of our knowledge, it was ignored in previous calculations [39]. For the mdm and edm interactions, the NR expansions read as

where $Q_N$ represents the nucleon electric charge in units of e, and $g_N$ is the nucleon Landé g-factor, with $g_p = 5.59$ and $g_n = -3.83$ for the proton and neutron, respectively. The involved NR operators in Eqs. (19) and (20) are [46−48]

where ${\boldsymbol{q}}$ is the three-momentum transfer, and ${\boldsymbol{S}}_\chi$ and ${\boldsymbol{S}}_N$ are the DM and nucleon spin operators, respectively. Here, the “elastic” transverse velocity is defined by

where ${\boldsymbol{v}}_{\chi}$ is the incoming DM-nucleon relative velocity, and $\mu_{N\chi}$ is the reduced mass for the DM-nucleon system.

III. XENON1T CONSTRAINTS

• I. INTRODUCTION
• II. NONPERTURBATIVE MATCHING OF DM-QUARK INTERACTIONS
• III. XENON1T CONSTRAINTS
•      A DM-nucleus scattering cross section
•      B Constraint from ${\mathrm{NR}}$ signals
•      C Constraint from the Migdal effect
•      D Constraint from ${\mathrm{ER}}$ signals
• IV. CONSTRAINTS FROM OTHER DIRECT DETECTION EXPERIMENTS
• V. CONSTRAINTS FROM NON-DIRECT-DETECTION EXPERIMENTS AND AN EXAMPLE OF UV COMPLETION
• VI. CONCLUSION
• APPENDIX A: SQUARED FORM FACTOR

As mentioned in Section II, ${\cal{O}}_{\chi q}^{\mathrm{T1}}$ and ${\cal{O}}_{\chi q}^{\mathrm{T2}}$ can induce not only 4-fermion DM-nucleon interactions but also the EM dipole moments of DM. Hereafter, we denote their contribution in DMDD experiments as the SD and LD contributions, respectively. In previous calculations of DMDD constraints on ${\cal{O}}_{\chi q}^{\mathrm{T1}}$ and ${\cal{O}}_{\chi q}^{\mathrm{T2}}$ [11, 20, 21], only the DM-nucleus scattering induced by the SD contribution was considered. A consistent calculation must consider both the SD and LD contributions at the amplitude level, where the interference effect between the two is generally expected. In addition to DM-nucleus scattering, the LD dipole operators can also induce DM-electron scattering, as shown in Fig. 1. Owing to the excellent potential of DM-electron scattering in probing low-mass DM [17, 18], significant improvements in the constraints in the low-mass region are possible if we consider the DM-electron scattering induced by the LD dipole contribution. For the operators with vector or axial-vector currents, only the SD contributions to DMDD are induced, and the probed DM mass region is above several GeV from the NR signals and only extends to approximately 0.1 GeV from the Migdal effect [11]. However, we show that the LD contribution from the tensor operators is capable of probing DM as low as 5 MeV.

Figure 1

Figure 1.  (color online) Feynman diagrams for DM-nucleus scattering (the left two diagrams) and DM-electron scattering (the rightmost diagram) induced by ${\cal{O}}_{\chi q}^{\mathrm{T1}}$ and ${\cal{O}}_{\chi q}^{\mathrm{T2}}$.

DownLoad: Full-Size Img PowerPoint

The XENON1T experiment is a DMDD experiment with a dual-phase time projection chamber, in which both DM-electron and DM-nucleus scattering can induce prompt scintillation photons (S1 signal) and drift electrons (S2 signal) [49]. According to the strength ratio between the S1 and S2 signals, the ${\mathrm{NR}}$ and ${\mathrm{ER}}$ signals can be well distinguished [49]. Comprehensive searches for DM particles have been conducted by the XENON1T collaboration, including ${\mathrm{NR}}$ signals for DM-nucleus scattering [49], ${\mathrm{ER}}$ signals for DM-electron scattering [19], and S2-only signals for the Migdal effect [9]. Hereafter, we denote the corresponding constraints from the above three types of signals as the ${\mathrm{NR}}$, ${\mathrm{ER}}$, and Migdal constraints respectively. In this section, we use the XENON1T experiment as a benchmark to recalculate the constraints on ${\cal{O}}_{\chi q}^{\mathrm{T1}}$ and ${\cal{O}}_{\chi q}^{\mathrm{T2}}$ with the data given in [9, 19, 49], in which we consistently consider both the SD and LD contributions.

Our analysis covers the cases in which the flavor SU(3) symmetry is either imposed or not imposed. For the flavor conserving case, a universal Wilson coefficient is assumed for the operators ${\cal{O}}_{\chi q}^{\mathrm{T1}}$ and ${\cal{O}}_{\chi q}^{\mathrm{T2}}$ with all $u,d,s$ quarks. This is the case typically adopted in the literature. We also study the separate contributions from individual quarks without assuming flavor symmetry. We denote the 90% confidence level (C.L.) constraint on Λ as $\Lambda_q$ in the flavor conserving case and $\Lambda_{u,d,s}$ when the three light quarks are treated separately. The effective tensor interactions may also appear without being accompanied by a quark mass; an example of how this occurs in a UV model is shown in Section V, in which case the Wilson coefficients of the dimension-six tensor operators are parameterized by an effective scale $\tilde\Lambda$, and the upper bound on Λ is translated to that on $\tilde\Lambda = \Lambda\sqrt{\Lambda/m_q}$. In Figs. 2 and 3, we show the constraints on both Λ and $\tilde{\Lambda}$ for individual quark contributions.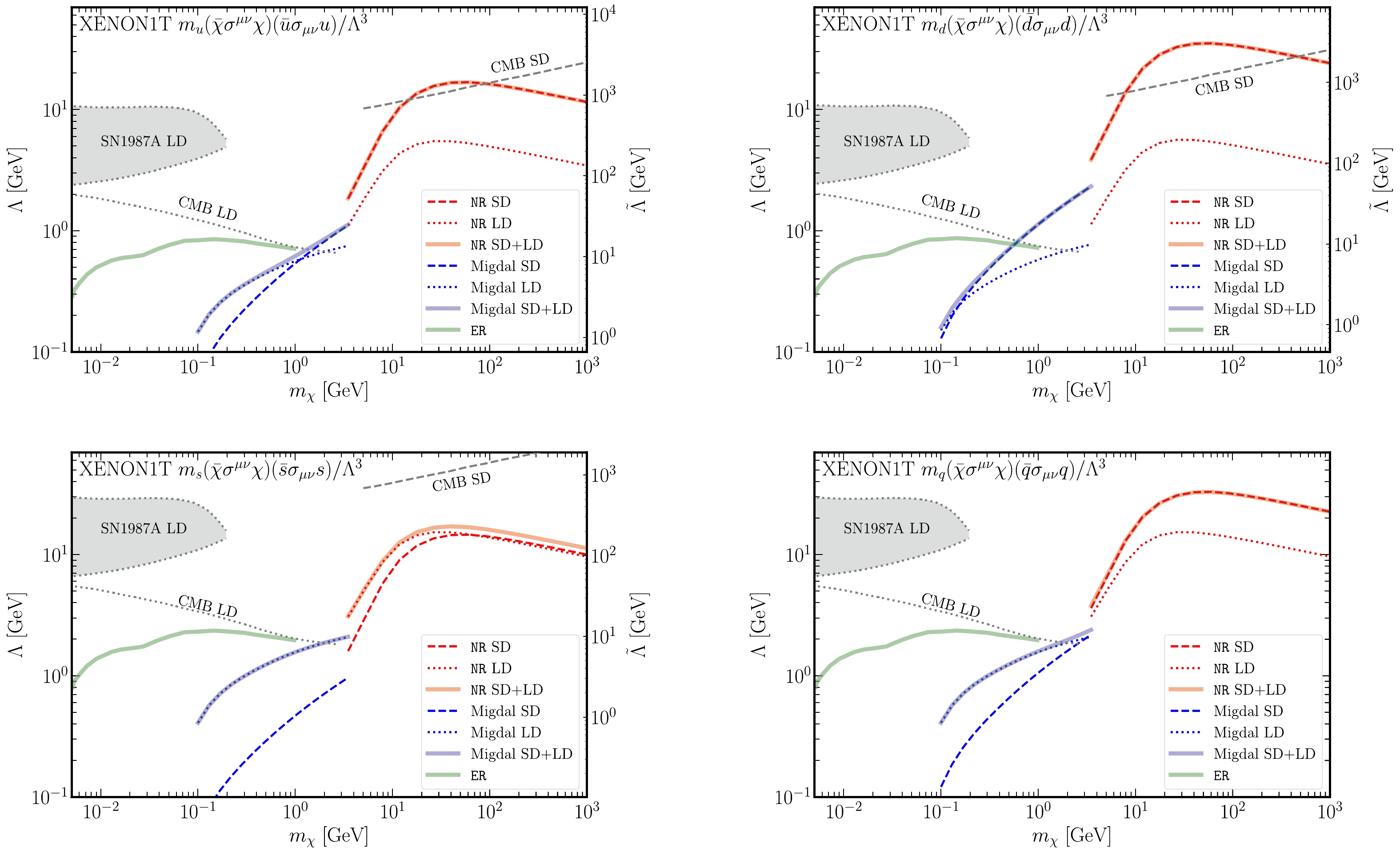

Figure 2

Figure 2.  (color online) XENON1T constraints on ${\cal{O}}_{\chi q}^{\mathrm{T1}}$ from ${\mathrm{NR}}$ signals (red), the Migdal effect (blue), and ${\mathrm{ER}}$ signals (green). Here, Λ denotes the effective scale associated with the dimension-seven ${\cal{O}}_{\chi q}^{\mathrm{T1}}$ and $\tilde\Lambda$ for the corresponding dimension-six operator with the quark mass $m_q$ removed. For the ${\mathrm{NR}}$ and Migdal effect cases, we consider the constraints with SD-only (dashed), LD-only (dotted), and full (solid) contributions. For the ${\mathrm{ER}}$ case, only the LD contribution is included. In all panels excluding the bottom-right one, the individual contributions from the u, d, and s quarks are considered separately. In the bottom-right panel, a flavor universal coupling is assumed for all of the u, d, and s quarks. The constraints from SN1987A and CMB discussed in Section V are also shown here.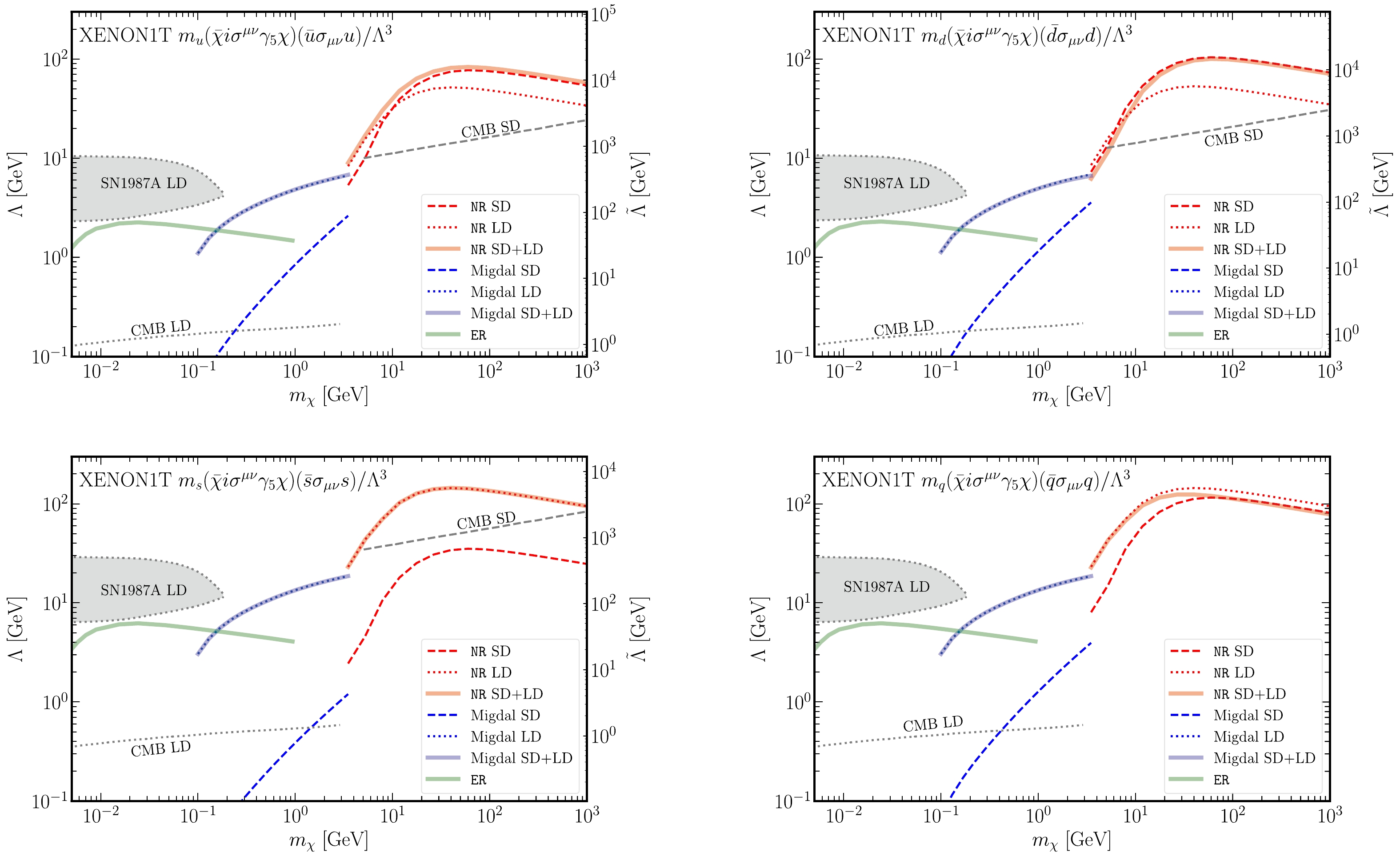

DownLoad: Full-Size Img PowerPoint

Figure 3

Figure 3.  (color online) Same as Fig. 2 but for the operator ${\cal{O}}_{\chi q}^{\mathrm{T2}}$.

DownLoad: Full-Size Img PowerPoint

A DM-nucleus scattering cross section

• I. INTRODUCTION
• II. NONPERTURBATIVE MATCHING OF DM-QUARK INTERACTIONS
• III. XENON1T CONSTRAINTS
•      A DM-nucleus scattering cross section
•      B Constraint from ${\mathrm{NR}}$ signals
•      C Constraint from the Migdal effect
•      D Constraint from ${\mathrm{ER}}$ signals
• IV. CONSTRAINTS FROM OTHER DIRECT DETECTION EXPERIMENTS
• V. CONSTRAINTS FROM NON-DIRECT-DETECTION EXPERIMENTS AND AN EXAMPLE OF UV COMPLETION
• VI. CONCLUSION
• APPENDIX A: SQUARED FORM FACTOR

In this subsection, we provide the differential cross section for DM-nucleus scattering from the two tensor interactions with both the SD and LD contributions included. The distribution with respect to the NR energy $E_R$ ($E_R = {\boldsymbol{q}}^2/2m_A$) in the NR limit is given by [43]

where $m_A$ is the mass of the target nucleus, v is the speed of the incoming DM particle in the lab frame, and $\overline{|{\cal{M}}|^2}$ is the amplitude squared, which is averaged/summed over the initial/final spin states. The DM-nucleus amplitude ${\cal{M}}$ is given by the sum over all protons and neutrons in the nucleus of the single-nucleon amplitude derived in Section II. Furthermore, the corresponding NR operators are decomposed into spherical components with a definite angular momentum, which is suitable for computations of a nucleus in an eigenstate of the total angular momentum. By performing a multipole expansion, the unpolarized amplitude squared can be represented in a compact form [43],

where i and j span the NR operator basis. The squared form factors $F_{i,j} ^{(N,N^\prime)}({\boldsymbol{q}}^2,{\boldsymbol{v}}^{\perp 2}_{T})$ depend on the nuclear responses as well as ${\boldsymbol{q}}^2$ and ${\boldsymbol{v}}^{\perp 2}_{T}\equiv v^2-v_{\rm{min}}^2$, and the relevant ones in our study are presented in Appendix A. Here, $v_{\rm{min}} = \sqrt{E_R m_A}/({\sqrt{2}\mu_{A\chi}})$ is the minimum velocity for DM to induce a NR energy $E_R$, where $\mu_{A\chi}$ is the reduced mass for the DM-nucleus system. Detailed formulations of these squared form factors for various nuclei are provided in [47].

The functions $f_i^N({\boldsymbol{q}}^2)$ are determined by particle physics from the UV down to the chiral scale. In our case, they are contributed by both DM-nucleon and DM dipole interactions induced from the tensor DM-quark operators. For the operator ${\cal{O}}_{\chi q}^{\mathrm{T1}}$, the functions that do not vanish are as follows:

The inclusion of the DM mdm ($\mu_\chi$) results in a new term in $f_4^N$ and a nonvanishing $f_{1,5,6}^N$. The mdm term in $f_{4,5,6}^N$ interferes with the usual SD term in $f_4^N$ in the amplitude squared, whereas $f_1^N$ does not interfere with $f_{4,5,6}^N$, owing to its DM spin independence. Similarly, for the operator ${\cal{O}}_{\chi q}^{\mathrm{T2}}$, the nonvanishing functions are

The DM edm leads to an additional term in $f_{11}^N$, which interferes with the usual SD term in $f_{11}^N$ and $f_{12}^N$ but not with $f_{10}^N$ as the latter is independent of the DM spin.

B Constraint from ${\mathrm{NR}}$ signals

• I. INTRODUCTION
• II. NONPERTURBATIVE MATCHING OF DM-QUARK INTERACTIONS
• III. XENON1T CONSTRAINTS
•      A DM-nucleus scattering cross section
•      B Constraint from ${\mathrm{NR}}$ signals
•      C Constraint from the Migdal effect
•      D Constraint from ${\mathrm{ER}}$ signals
• IV. CONSTRAINTS FROM OTHER DIRECT DETECTION EXPERIMENTS
• V. CONSTRAINTS FROM NON-DIRECT-DETECTION EXPERIMENTS AND AN EXAMPLE OF UV COMPLETION
• VI. CONCLUSION
• APPENDIX A: SQUARED FORM FACTOR

The differential event rate for ${\mathrm{NR}}$ signals is given by

where $\rho_\chi = 0.3\;{{\rm{GeV}} /{\rm{cm}}^3}$ is the local DM energy density near the Earth, and $F(v)$ is the DM velocity distribution in the lab frame. In the actual calculation, the total rate is a sum of contributions from each isotope weighted by its mass fraction in the nuclear target. Note that the angular distribution of the DM velocity is integrated out in $F(v)$, because the target nuclei are considered to be at rest and unpolarized in the lab frame.

In the galaxy rest frame, the DM velocity obeys a normal Maxwell-Boltzmann distribution with the circular velocity $v_0 = 220\;{\rm{km}}/{\rm{s}}$ [50], which leads to [43, 51]

Here, we adopt the averaged Earth relative velocity $v_{\rm E} = 232\;{\rm{km}}/{\rm{s}}$ [52] and escape velocity $v_{\rm{esc}} = 544\;{\rm{km}}/{\rm{s}}$ [50], which leads to the maximal DM velocity in the lab frame $v_{\rm{max}} = v_{\rm{esc}}+v_{\rm E} = 776\;{\rm{km}}/{\rm{s}}$.

We calculate the constraint based on the ${\mathrm{NR}}$ events given in [49] for an exposure of $w =$ 1.0 ton-yr. Considering the SM backgrounds, the 90% C.L. constraint is obtained via the criterion $N_{\mathrm{NR}}^s < 7$ [21], where the number of ${\mathrm{NR}}$ events induced by DM-nucleus scattering is calculated by

Here, we adopt the ${\mathrm{NR}}$ signal efficiency, $\epsilon_{\mathrm{NR}}(E_R)$, given in Fig. (1) in [49].

The XENON1T constraints on ${\cal{O}}_{\chi q}^{\mathrm{T1}}$ and ${\cal{O}}_{\chi q}^{\mathrm{T2}}$ from ${\mathrm{NR}}$ are shown as red curves in Figs. 2 and 3, respectively. The SD contribution (red dashed curves) dominates over the LD contribution in the constraints on ${\cal{O}}_{\chi q}^{\mathrm{T1}}$ for the valence u and d quarks. For the sea s quark, the SD contribution is relatively less important than the LD contribution (red dotted curves) for small $m_\chi$ until $m_\chi \gtrsim 50\;{\rm{GeV}}$ when their constructive interference starts to become significant. Regarding the constraints on ${\cal{O}}_{\chi q}^{\mathrm{T2}}$, the LD contribution dominates overwhelmingly for the s quark, whereas the u and d quarks exhibit comparable but varying contributions from the SD and LD mechanisms. Note that the interference effect is constructive (destructive) in the u (d) quark scenario. This distinct behavior is due to the charge sign difference between the u and d quarks. For both operators ${\cal{O}}_{\chi q}^{\mathrm{T1}}$ and ${\cal{O}}_{\chi q}^{\mathrm{T2}}$ in the flavor conserving case, the SD constraint is dominated by the d quark contribution, whereas the LD constraint is dominated by the s quark contribution. Especially for ${\cal{O}}_{\chi q}^{\mathrm{T2}}$, the LD contribution always dominates; however, it becomes comparable to the SD contribution for a large $m_\chi$ , where a significant destructive interference pattern is evident in the full constraint (red solid curve).

C Constraint from the Migdal effect

• I. INTRODUCTION
• II. NONPERTURBATIVE MATCHING OF DM-QUARK INTERACTIONS
• III. XENON1T CONSTRAINTS
•      A DM-nucleus scattering cross section
•      B Constraint from ${\mathrm{NR}}$ signals
•      C Constraint from the Migdal effect
•      D Constraint from ${\mathrm{ER}}$ signals
• IV. CONSTRAINTS FROM OTHER DIRECT DETECTION EXPERIMENTS
• V. CONSTRAINTS FROM NON-DIRECT-DETECTION EXPERIMENTS AND AN EXAMPLE OF UV COMPLETION
• VI. CONCLUSION
• APPENDIX A: SQUARED FORM FACTOR

In the DM low-mass region (i.e., sub-GeV region) the constraint from ${\mathrm{NR}}$ signals loses sensitivity because the nucleus cannot gain sufficient recoil energy to reach the threshold of a detector. This dilemma can be alleviated by taking advantage of the Migdal effect. In addition to the ${\mathrm{NR}}$ signals from DM-nucleus scattering, the Migdal effect results in additional ionization energy $E_{\rm{EM}}$ deposited in the detector, such that the total detected energy is $E_{\rm{det}} = {\cal{L}} E_R + E_{\rm{EM}}$. Unlike ${\mathrm{ER}}$, a large fraction of ${\mathrm{NR}}$ energy becomes unobservable heat. Here, ${\cal{L}}$ is the quenching factor for the ${\mathrm{NR}}$ signals, which accounts for the fraction of ${\mathrm{NR}}$ energy converting into photoelectric signals. In calculations of the Migdal effect, it has become customary to take a constant value of ${\cal{L}} = 0.15$ [53].

Considering the Migdal effect for DM-nucleus scattering, we must introduce an additional ionization form factor into Eq. (27) to obtain the differential event rate, namely [7],

where $E_R^{\rm{max}} = 2 \mu_{A \chi}^2 v_{\rm{max}}^2/m_A$ , and $E_{\rm{EM}} = E_{\rm{det}}-{\cal{L}}E_R$. Unlike in the ${\mathrm{NR}}$ case, $v_{\rm{min}} = (m_A E_R+ \mu_{A\chi} E_{\rm{EM}})/(\mu_{A\chi} \sqrt{2 m_A E_R })$ depends on not only the ${\mathrm{NR}}$ energy $E_R$ but also the ionization energy $E_{\rm{EM}}$. The ionization factor $|Z_{\rm{ion}}|^2$ also depends on both, which is given by [7]

where $E_e$ is the kinetic energy of the ionized electron given by $E_e = E_{\rm{EM}} - |E_{n \ell}|$, with $|E_{n\ell}|$ as the binding energy of the electron labeled by the principal and orbital quantum numbers $n,\ell$. We adopt the ionization probability $p_{q_e}^c$ of the Xenon atom given in [7].

For the Migdal effect, we calculate the constraint with the S2-only dataset given in [9, 54] for an exposure of $w =$ 22 ton-day. The 90% C.L. constraint is obtained via the criterion $N_{\mathrm{Migdal}}^s < 49$ [11, 53], where the number of signal events induced by the Migdal effect is calculated via

Here, we adopt the signal efficiency of the S2-only data, $\epsilon_{\mathrm{Migdal}} (E_{\rm{det}})$, given in [9, 54].

The XENON1T constraints on ${\cal{O}}_{\chi q}^{\mathrm{T1}}$ and ${\cal{O}}_{\chi q}^{\mathrm{T2}}$ from the Migdal effect are shown as blue curves in Figs. 2 and 3, respectively Upon including the LD contribution, the constraints on ${\cal{O}}_{\chi q}^{\mathrm{T2}}$ achieve a significant enhancement, particularly for $\Lambda_s$, by a factor of up to two orders of magnitude. As for the constraints on ${\cal{O}}_{\chi q}^{\mathrm{T1}}$, there are mass regions in which the SD and LD contributions are comparable for the u and d quarks, where the SD and LD contributions exhibit constructive interference.

D Constraint from ${\mathrm{ER}}$ signals

• I. INTRODUCTION
• II. NONPERTURBATIVE MATCHING OF DM-QUARK INTERACTIONS
• III. XENON1T CONSTRAINTS
•      A DM-nucleus scattering cross section
•      B Constraint from ${\mathrm{NR}}$ signals
•      C Constraint from the Migdal effect
•      D Constraint from ${\mathrm{ER}}$ signals
• IV. CONSTRAINTS FROM OTHER DIRECT DETECTION EXPERIMENTS
• V. CONSTRAINTS FROM NON-DIRECT-DETECTION EXPERIMENTS AND AN EXAMPLE OF UV COMPLETION
• VI. CONCLUSION
• APPENDIX A: SQUARED FORM FACTOR

The constraints on the edm and mdm of DM from ${\mathrm{ER}}$ signals have been obtained by the XENON1T collaboration [19], in which S2-only signals induced by a single electron were used to achieve a lower energy threshold. For the DM-electron scattering induced by ${\cal{O}}_{\chi q}^{\mathrm{T1}}$ and ${\cal{O}}_{\chi q}^{\mathrm{T2}}$, there is only the LD contribution. Hence, we can directly convert the constraints on the DM dipole moments into those on ${\cal{O}}_{\chi q}^{\mathrm{T1}}$ and ${\cal{O}}_{\chi q}^{\mathrm{T2}}$ via Eq. (15).

The XENON1T constraints on ${\cal{O}}_{\chi q}^{\mathrm{T1}}$ and ${\cal{O}}_{\chi q}^{\mathrm{T2}}$ from ${\mathrm{ER}}$ are shown as green curves in Figs. 2 and 3, respectively. These ${\mathrm{ER}}$ constraints effectively probe low-mass DM down to approximately 5 MeV. The small momentum transfer in DM-electron scattering for such low-mass DM results in an enhanced scattering cross section when DM interacts with electrons via edm, leading to a stronger constraint on ${\cal{O}}_{\chi q}^{\mathrm{T2}}$ compared to ${\cal{O}}_{\chi q}^{\mathrm{T1}}$. Moreover, the constraints on $\Lambda_s$ are more stringent than those on $\Lambda_u$ and $\Lambda_d$ owing to the quark mass factor in the definition of ${\cal{O}}_{\chi q}^{\mathrm{T1}}$ (${\cal{O}}_{\chi q}^{\mathrm{T2}}$). For the flavor conserving case, the constraints on both operators from the Migdal effect and ${\mathrm{ER}}$ are similar to those in the single strange quark case because they are dominated by LD contributions, which are further enhanced by the strange mass.

The stronger constraint on ${\cal{O}}_{\chi q}^{\mathrm{T2}}$ can be understood as follows. In the nonrelativistic limit, the spin-averaged and -summed matrix element squared terms of DM-electron scattering for the mdm and edm cases are

Here, q is the momentum transfer in DM-electron scattering and has a typical value of $q \simeq \alpha m_e$ in DMDD experiments. At such a low momentum transfer scale, $\overline{\left|{\cal{M}}_{\chi e}(q)\right|^2}_{\rm{edm}}$ is enhanced by a factor of α, namely, $\overline{\left|{\cal{M}}_{\chi e}(\alpha m_e)\right|^2}_{\rm{edm}} \simeq 64 \pi d_\chi^2 m_\chi^2/\alpha$, which leads to a stronger constraint on the edm of DM compared to that on the mdm of DM.

In summary, owing to the LD contribution from the nonperturbative QCD effects of the tensor operators, the XENON1T experiment extends the sensitivity to MeV-scale DM. In the mass region probed by the Migdal effect ($0.1 \; {{\rm{GeV}}} \lesssim m_\chi \lesssim 3 \; {{\rm{GeV}}}$), the inclusion of the LD contribution results in a sensitivity to the effective scale associated with ${\cal{O}}_{\chi q}^{\mathrm{T2}}$ (${\cal{O}}_{\chi q}^{\mathrm{T1}}$) that is comparable to well-studied operators such as ${\cal{O}} _{\chi q}^{\mathrm{V}}\equiv\bar{\chi}\gamma^\mu\chi \, \bar{q}\gamma_\mu q$ (${\cal{O}} _{\chi q}^{\mathrm{A}}\equiv\bar{\chi}\gamma^\mu\chi \, \bar{q}\gamma_\mu \gamma^5 q$) with $\tilde{\Lambda} \simeq {\cal{O}}(10^2) \; \rm{GeV}$ ($\tilde{\Lambda} \simeq {\cal{O}}(1)\; \rm{GeV}$) [11]. For the NR signal region ($5\,{{\rm{GeV}}} \lesssim m_\chi \lesssim 10^3 \; {\rm{GeV}}$), the constraint on the effective scale associated with ${\cal{O}} _{\chi q}^{\mathrm{V}}$ ($\tilde{\Lambda} \simeq 5 \times 10^4\; \rm{GeV}$) is stronger than those of ${\cal{O}}_{\chi q}^{\mathrm{T1}}$ ($\tilde{\Lambda} \simeq {\cal{O}}(10^3) \; \rm{GeV}$) and ${\cal{O}}_{\chi q}^{\mathrm{T2}}$ ($\tilde{\Lambda} \simeq {\cal{O}}(10^4) \; \rm{GeV}$), which are subsequently stronger than that of ${\cal{O}} _{\chi q}^{\mathrm{A}}$ ($\tilde{\Lambda} \simeq 50 \; \rm{GeV}$) [11].

IV. CONSTRAINTS FROM OTHER DIRECT DETECTION EXPERIMENTS

• I. INTRODUCTION
• II. NONPERTURBATIVE MATCHING OF DM-QUARK INTERACTIONS
• III. XENON1T CONSTRAINTS
•      A DM-nucleus scattering cross section
•      B Constraint from ${\mathrm{NR}}$ signals
•      C Constraint from the Migdal effect
•      D Constraint from ${\mathrm{ER}}$ signals
• IV. CONSTRAINTS FROM OTHER DIRECT DETECTION EXPERIMENTS
• V. CONSTRAINTS FROM NON-DIRECT-DETECTION EXPERIMENTS AND AN EXAMPLE OF UV COMPLETION
• VI. CONCLUSION
• APPENDIX A: SQUARED FORM FACTOR

Besides the XEONON1T experiment [19], constraints on DM EM dipole moments have also been derived in XENON10 and DarkSide50 via ${\mathrm{ER}}$ signals [22] and PandaX via ${\mathrm{NR}}$ signals [55]. Hence, it is instructive to recast these constraints via Eq. (15) to fully constrain the two tensor operators ${\cal{O}}_{\chi q}^{\mathrm{T1}}$ and ${\cal{O}}_{\chi q}^{\mathrm{T2}}$. ⁴ Together with the constraints from XENON1T calculated above, Fig. 4 shows all the available bounds on ${\cal{O}}_{\chi q}^{\mathrm{T1}}$ and ${\cal{O}}_{\chi q}^{\mathrm{T2}}$ obtained in this study as colored curves. Here, we only show the results for the flavor conserving case to facilitate comparison with the results in the literature (represented by dashed gray curves for ${\mathrm{NR}}$ [21] and the Migdal effect [11]), in which only the SD contribution is considered. ⁵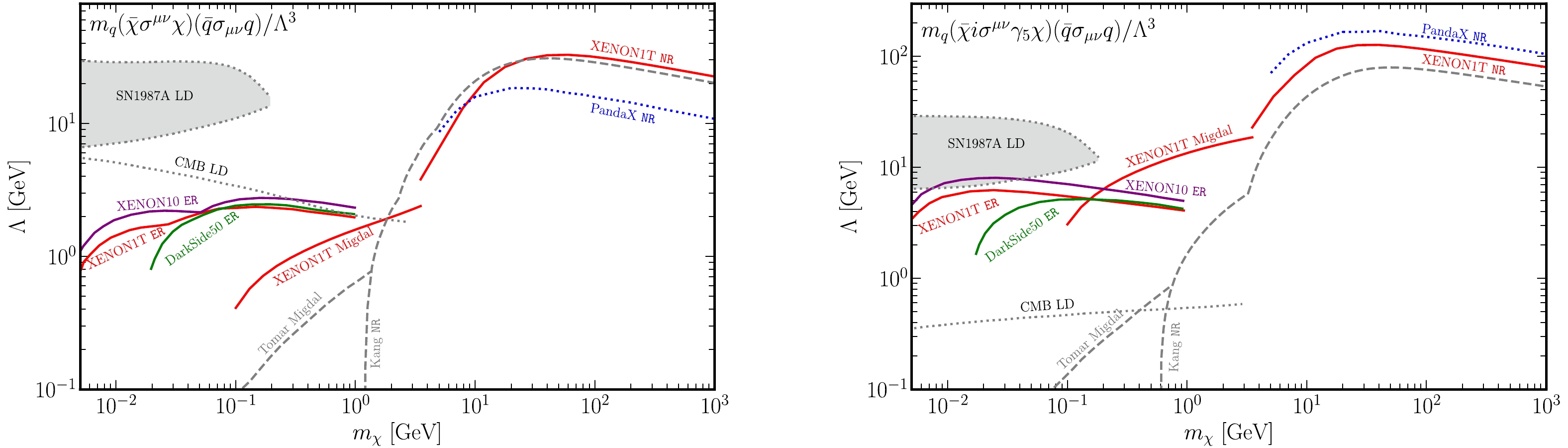

Figure 4

Figure 4.  (color online) Comparison of constraints on ${\cal{O}}_{\chi q}^{\mathrm{T1}}$ (left panel) and ${\cal{O}}_{\chi q}^{\mathrm{T2}}$ (right panel) for the flavor conserving case from current DMDD experiments. The colored lines show the new constraints in this study with the LD contribution included. The two gray dashed curves show previous constraints from ${\mathrm{NR}}$ [21] and the Migdal effect [11], in which only the SD contribution is considered. The two gray dotted lines show constraints from SN1987A and CMB, as discussed in Section V, in which only the LD contribution is considered. The legends follow those in Figs. 2 and 3: the dashed, dotted, and solid curves indicate the constraints with SD-only, LD-only, and full contributions, respectively.

DownLoad: Full-Size Img PowerPoint

By taking advantage of the new LD contribution, ${\cal{O}}_{\chi q}^{\mathrm{T1}}$ and ${\cal{O}}_{\chi q}^{\mathrm{T2}}$ can also be constrained by ${\mathrm{ER}}$, in addition to ${\mathrm{NR}}$ and the Migdal effect. These new ${\mathrm{ER}}$ constraints cover a previously uncovered low-mass region with ${5\; {\rm{MeV}}} \lesssim m_\chi \lesssim {100\; {\rm{MeV}}}$ and surpass the previous constraints from the Migdal effect in the mass region ${100\; {\rm MeV} \lesssim m_\chi \lesssim {1\; {\rm GeV}$. Owing to the enhancement of the LD contribution at the small momentum transfer in the Migdal effect, the newly calculated XENON1T constraint from the Migdal effect is stronger than the previous constraint from the Migdal effect by approximately a factor of three (one order of magnitude) in the ${\cal{O}}_{\chi q}^{\mathrm{T1}}$ (${\cal{O}}_{\chi q}^{\mathrm{T2}}$) case. In particular, for the ${\cal{O}}_{\chi q}^{\mathrm{T2}}$ case, the XENON1T constraint from the Migdal effect can be even stronger than the previous ones from ${\mathrm{NR}}$ in the mass region ${0.7 \; {\rm{GeV}}}\lesssim m_\chi \lesssim {3\; {\rm{GeV}}}$. Owing to the relatively large momentum transfer in ${\mathrm{NR}}$, the improvements in the constraints from the ${\mathrm{NR}}$ are not as evident as those from the Migdal effect. For the ${\cal{O}}_{\chi q}^{\mathrm{T2}}$ case, the PandaX constraint from ${\mathrm{NR}}$ improves in the large mass region ($m_\chi \gtrsim 3\; {\rm{GeV}}$). However, it is expected to become slightly weaker for heavier DM when the SD contribution is also considered, because of the destructive interference between the LD and SD contributions, as shown in Fig. 3.

V. CONSTRAINTS FROM NON-DIRECT-DETECTION EXPERIMENTS AND AN EXAMPLE OF UV COMPLETION

• I. INTRODUCTION
• II. NONPERTURBATIVE MATCHING OF DM-QUARK INTERACTIONS
• III. XENON1T CONSTRAINTS
•      A DM-nucleus scattering cross section
•      B Constraint from ${\mathrm{NR}}$ signals
•      C Constraint from the Migdal effect
•      D Constraint from ${\mathrm{ER}}$ signals
• IV. CONSTRAINTS FROM OTHER DIRECT DETECTION EXPERIMENTS
• V. CONSTRAINTS FROM NON-DIRECT-DETECTION EXPERIMENTS AND AN EXAMPLE OF UV COMPLETION
• VI. CONCLUSION
• APPENDIX A: SQUARED FORM FACTOR

Because the particle properties of DM are completely unknown, it is important to explore DM in various types of observations and experiments to obtain complementary information. In this section, we briefly discuss the constraints originating from collider searches and supernova (SN1987A) and cosmic microwave background (CMB) observations.

The effective operators ${\cal{O}}_{\chi q}^{\mathrm{T1}}$ and ${\cal{O}}_{\chi q}^{\mathrm{T2}}$ can be probed at the LHC via the mono-jet search, in which DM produced via the process $q \bar{q} \to \chi \bar{\chi} +j$ appears as missing energy at collider detectors. Owing to the nature of their four-fermion interactions, the signal cross section is proportional to the center-of-mass energy squared at the parton level and thus gets enhanced at the LHC energy. For the DM mass below hundreds of GeV, one generally obtains a bound $\tilde{\Lambda}\gtrsim 1\; {\rm{TeV}}$ [56]. Nevertheless, direct comparison of the bound with those extracted from DMDD experiments is a delicate issue. First, the bound at high energy colliders is less sensitive to the DM mass as long as the latter is not too close to the parton energy, and it is insensitive to the Lorentz structure of effective interactions. A well-known example is the vastly different bounds on the spin-independent and -dependent interactions extracted in direct detection experiments, which yield similar signals at colliders. Furthermore, the search at colliders cannot distinguish a tensor interaction from other structures. In contrast, direct detection at low energy allows us to examine the tensor structure in a comprehensive manner, that is, only for a tensor structure can an LD interaction be induced from a four-fermion DM-quark interaction, which results in interesting interference between the two and correlates the signal channel in ${\mathrm{NR}}$ and the Migdal effect on one side and the signal channel in ${\mathrm{ER}}$ on the other. The ratio of the signal strengths between the two would help distinguish the tensor DM-quark interactions from other types of interactions and determine the DM mass, if a DM signal is observed. Second, the bounds set at colliders would be modified significantly by a mediator of intermediate mass between ${\cal{O}} (100 \; {\rm{MeV}})$ and ${\cal{O}} (1\; {\rm{TeV}})$, which is common in various portal mechanisms [57]. The constraints from low-energy detection are not flawed with this issue for low-mass DM and are thus more robust.

We next examine the constraints from SN1987A and the CMB. Light DM particles with mass $m_\chi \lesssim 400\; {\rm{MeV}}$ may be generated in pairs within the supernova core and then escape, which would increase the supernova cooling rate and consequently affect the observed supernova neutrino spectrum. Because the generated DM may be reabsorbed by the supernova if its interaction with SM particles is sufficiently sizable, the constraints are two-sided, resulting in an allowed region in parameter space. Regarding the CMB constraint, the extra energy injection from DM annihilation can affect the recombination history leading to modifications in the temperature and polarization power spectra of the CMB. We converted the constraints on the DM edm and mdm in [58, 59] obtained from SN1987A and the CMB to those on ${\cal{O}}_{\chi q}^{\mathrm{T1}}$ and ${\cal{O}}_{\chi q}^{\mathrm{T2}}$ by employing Eq. (15). In addition, the SD ${\cal{O}}_{\chi q}^{\mathrm{T1}}$ and ${\cal{O}}_{\chi q}^{\mathrm{T2}}$ interactions can also be directly constrained by SN1987A and the CMB. Although the supernova constraint with only SD interactions has not been reported in the literature, the case for CMB was achieved in [56]. Note that the CMB constraint becomes significantly weaker for $m_\chi \lesssim m_\pi$ if we include only SD interactions, as there would be no annihilation channel available at the tree level. All of the above constraints from SN1987A and the CMB are also included in Figs. 2, 3, and 4 as gray regions (SN1987A LD), gray dotted lines (CMB LD), and gray dashed lines (CMB SD), respectively. ⁶ In general, the parameter region probed by SN1987A is more strongly constrained but it does not overlap with those probed by DMDD experiments and the CMB. Among the latter two, the DMDD constraint is generally stronger (weaker) for the ${\cal{O}}_{\chi q}^{\mathrm{T2}}$ (${\cal{O}}_{\chi q}^{\mathrm{T1}}$) interaction.

Finally, we show a simple UV model that induces a tensor-type interaction at the tree level without being accompanied by a quark mass. Consider a $\mathbb{Z}_3$ DM model by extending the SM with a vector-like fermion DM $\chi(1,1,0)$ and two colored scalars $S_1(3,1,-1/3)$ and $S_2(3,2,1/6)$, where the numbers in parentheses denote the quantum numbers in the SM gauge group. Under $\mathbb{Z}_3$ symmetry, $\chi\to e^{i 2\pi/3} \chi$ and $S_{1,2} \to e^{- i 2\pi/3}S_{1,2}$, while the SM fields are intact. The relevant Lagrangian terms are

where $y_d$ and $y_Q$ are the dimensionless Yukawa couplings, $\mu_S$ is the dimensionful triple coupling for the scalars, and H is the SM Higgs field with vacuum expectation value v. The Feynman diagram shown in Fig. 5 results in the effective interaction upon integrating out heavy scalars $S_1$ and $S_2$: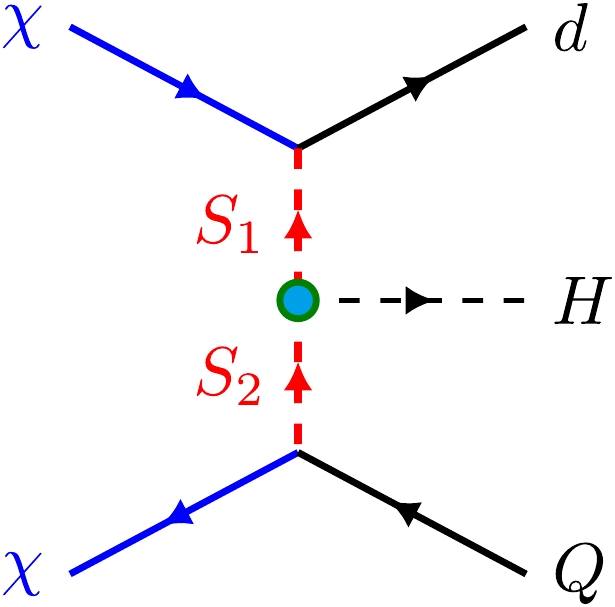

Figure 5

Figure 5.  (color online) Feynman diagram in the $\mathbb{Z}_3$ model that induces a tensor effective interaction.

DownLoad: Full-Size Img PowerPoint

where the Fierz identity is applied. It is natural to assume $m_{S_1}\simeq m_{S_2}\simeq\mu_S = M$ so that the induced tensor operator has a Wilson coefficient $y_d y_Q^* v/(8\sqrt{2} M^3)$ whose magnitude is defined as $\tilde\Lambda^{-2}$ in our discussion.

VI. CONCLUSION

• I. INTRODUCTION
• II. NONPERTURBATIVE MATCHING OF DM-QUARK INTERACTIONS
• III. XENON1T CONSTRAINTS
•      A DM-nucleus scattering cross section
•      B Constraint from ${\mathrm{NR}}$ signals
•      C Constraint from the Migdal effect
•      D Constraint from ${\mathrm{ER}}$ signals
• IV. CONSTRAINTS FROM OTHER DIRECT DETECTION EXPERIMENTS
• V. CONSTRAINTS FROM NON-DIRECT-DETECTION EXPERIMENTS AND AN EXAMPLE OF UV COMPLETION
• VI. CONCLUSION
• APPENDIX A: SQUARED FORM FACTOR

In this study, we conduct a complete investigation of the two DM-quark tensor operators in DMDD experiments in the framework of chiral perturbation theory. We find that DM-quark tensor operators can induce electromagnetic dipole moment operators of DM, in addition to the well-studied DM-nucleon 4-fermion operators. In previous calculations for DMDD experiments, the constraints on DM-quark tensor operators were obtained by calculating the ${\mathrm{NR}}$ and Migdal effect induced by these 4-fermion operators. The DM dipole moment operators give rise to new contributions for both DM-electron and DM-nucleus scatterings. Consequently, a consistent calculation of the constraints from ${\mathrm{NR}}$ and the Migdal effect should include both DM-nucleon and DM dipole moment operators, which may result in interesting interference effects. Remarkably, the DM-quark tensor operators can also be constrained by ${\mathrm{ER}}$ signals caused by the newly studied DM-electron scattering. In this manner, we derive the constraints from ${\mathrm{NR}}$ and the Migdal effect using XENON1T data and recast the existing bounds from the ${\mathrm{ER}}$ (XENON10, XENON1T, DarkSide50) and ${\mathrm{NR}}$ (PandaX) signals to yield comprehensive constraints on the tensor interactions. Our results are significantly improved over the previous results in the literature, especially in the sub-GeV region.

APPENDIX A: SQUARED FORM FACTOR

• I. INTRODUCTION
• II. NONPERTURBATIVE MATCHING OF DM-QUARK INTERACTIONS
• III. XENON1T CONSTRAINTS
•      A DM-nucleus scattering cross section
•      B Constraint from ${\mathrm{NR}}$ signals
•      C Constraint from the Migdal effect
•      D Constraint from ${\mathrm{ER}}$ signals
• IV. CONSTRAINTS FROM OTHER DIRECT DETECTION EXPERIMENTS
• V. CONSTRAINTS FROM NON-DIRECT-DETECTION EXPERIMENTS AND AN EXAMPLE OF UV COMPLETION
• VI. CONCLUSION
• APPENDIX A: SQUARED FORM FACTOR

The squared form factors $F_{i,j} ^{(N,N^\prime)}({\boldsymbol{q}}^2,{\boldsymbol{v}}^{\perp 2}_{T})$ defined in Eq. (24) are related to the basic independent nuclear form factors in the following manner [47]:

1The above parameterization is slightly different from the one used in the package $$\begin{document}$ {\mathrm{DirectDM}}$\end{document}$$ [23, 39], $$\begin{document}$ \langle N(k_2)|m_q \bar q \sigma^{\mu\nu} q|N(k_1)\rangle = \bar{u}_{k_2}\left[F_{T,0}^{q/N}(q^2)\sigma^{\mu\nu} +F_{T,1}^{q/N}(q^2) \frac{i \gamma^{[\mu}q^{\nu]} }{2 m_N} +F_{T,2}^{q/N}(q^2) \frac{{\rm i} q^{[\mu} k^{\nu]}_{12} }{m_N^2} \right] u_{k_1}. $\end{document}$$

2We find different values of $$\begin{document}$ g_T^{s/N} $\end{document}$$ are quoted in the literature. There are two independent lattice calculations yielding consistent results, with $$\begin{document}$ g_T^{s/N} = -0.0027(16) $\end{document}$$ in [40] and $$\begin{document}$ g_T^{s/N} = -3.19 \times 10^{-3}(69)(2)(22) $\end{document}$$ in the erratum to [41] (correcting its first-version value $$\begin{document}$ g_T^{s/N} = -3.2\times 10^{-4}(24)(0) $\end{document}$$ ). Subsequent quotations made typos; e.g., Refs. [42, 43] quoted $$\begin{document}$ g_T^{s/N} = -0.027(16) $\end{document}$$ (see also footnote 5) while Ref. [23] and the package $$\begin{document}$ {\mathrm{DirectDM}}$\end{document}$$ quoted $$\begin{document}$ g_T^{s/N} = (3.2 \pm 8.6)\times 10^{-4} $\end{document}$$ . The tensor charge $$\begin{document}$ g_T^{s/N} $\end{document}$$ is also denoted by $$\begin{document}$ \delta_s^{N} $\end{document}$$ in the literature.

3Note the slight font difference for this abbreviation ''NR'' and the '' $$\begin{document}$ {\mathrm{NR}}$\end{document}$$ '' used for ''nuclear recoil''.

4Note that a consistent calculation on the constraint from PandaX $$\begin{document}$ {\mathrm{NR}}$\end{document}$$ also needs to consider the SD contribution, as we did with XENON1T $$\begin{document}$ {\mathrm{NR}}$\end{document}$$ in the previous section. For simplicity, we restrict our discussion here to the LD contribution only.

5To cross check our calculations, we attempted to reproduce the XENON1T constraints in [11] on the two DM-quark tensor operators from the Migdal effect. We found that we could get results consistent with [11] only when we adopted the mistaken value of $$\begin{document}$ g_T^{s/N} = -0.027 $\end{document}$$ , as discussed in footnote 2.

6The CMB SD curves (gray dashed lines) in Fig. 2 and Fig. 3 represent the CMB constraints with only the SD interaction and are taken from [56]. In [56], the constraints were obtained by parametrizing the two tensor-type interactions as dimension-six operators and taking a universal Wilson coefficient for the three light quarks. Since these constraints cannot be trivially translated into those for the individual quark cases, we just simply take the constraint from [56] as a rough comparison. Note that the actual CMB SD constraints for the individual quark cases would be somewhat weaker due to reduced contributing channels from single quark flavor.

References