-
Compared with the hardon collider, an electron-positron collider is more suitable for precisely studying the Standard Model (SM) of particle physics because of its significantly clearer background. An electron-positron collider with high luminosity, running at the
$ Z^0 $ boson pole, would be a suitable platform for such a precise study because sizable events of interest can be generated in the$ Z^0 $ decays. For example, the Circular Electron-Positron Collider (CEPC) would have$ Z^0 $ yields of$ 7\times10^{11} $ per year in the Z-factory mode [1]. We can precisely measure the parameters of the SM and probe new physics through the decays of the massive$ Z^0 $ events. The future super Z factory will provide not only more yields of the particles but also indirectly enable a supplemental production mechanism.The heavy quarkonium is a bound state system that consists of a pair of a heavy quark and its antiquark. The production of the heavy quarkonium is considered to be a multiscale problem for probing the quantum chromodynamics (QCD) theory. According to the non-relativistic QCD (NRQCD) [2, 3], the heavy quarkonium has three disparate momentum scales: the quark mass
$ \sim m_Q $ , momentum of the heavy quark or antiquark$ \sim m_Q v $ , and kinetic energy of the heavy quark or antiquark$ \sim m_Q v^2 $ . Here, v is the relative velocity between the heavy quark and antiquark in the quarkonium rest frame. According to the NRQCD factorization framework, the production of the heavy quarkonium can be factored into the short-distance coefficients and the long-distance matrix element. The hort-distance coefficients depict the creation of the constituent heavy quark pair$ Q\bar{Q}^\prime $ with definite$ J^{PC} $ quantum numbers that can be calculated perturbatively, whereas the long-distance matrix element expresses the hadronization of$ Q\bar{Q}^\prime $ pair to a physical color-singlet quarkonium non-perturbatively. Thus, the production of the heavy quarkonium has been a popular topic in exploring QCD in both the perturbative and non-perturbative energy regions, which provides rich QCD physics. For more information on the current status of the heavy quarkonium, please refer to Refs. [4−8].The production of the heavy quarkonium has been studied widely. The next-to-leading order (NLO) corrections in QCD to most of the inclusive and exclusive processes of heavy quarkonium at B factories are calculated under the NRQCD factorization framework. Please refer to Refs. [9−17] for some typical examples. For the production of heavy quarkonium at hadron colliders, the NLO calculation for inclusive processes is still challenging. For example, the QCD NLO correction to the
$ p+p \longrightarrow J/\psi + c +\bar{c} $ is still missing. However, significant advances have been made in the NLO calculation for the exclusive production of double heavy quarkonia, such as double$ J/\psi $ production [18, 19] and the very recent$ B_c $ pair production [20]. Recently, QCD next-to-next-to-leading order (NNLO) corrections to the production of double charmonia at B factories have been made [21, 22]. Very recently, significant progress has been achieved in the automated NLO calculation for heavy quarkonium inclusive and associated production processes [23].In our previous paper, we studied the production of double heavy quarkonia at the super Z factory [24]. In this paper, we continue to study the production of the higher excited double heavy quarkonia, i.e., the heavy quarkonia are in the color-singlet state
$ [n^1S_0] $ ,$ [n^3S_1] $ ,$ [n^1P_0] $ , and$ [n^3P_J](J=0,1,2) $ for$ n=1,2,3 $ . The higher excited states would decay into the ground states, and they have a significant influence on the production rates of the ground states. We study the production of higher excited heavy quarkonia in the decay of$ W^\pm $ , top quark,$ Z^0 $ , and Higgs boson [25−29]. The numerical results show that sizable events of these exited$ [nS] $ and$ [nP] $ -wave states ($ n \ge 2 $ ) can be obtained. For example, the contribution of$ 2S $ state would increase the$ 1S $ yield by about 20%$ \sim $ 50%. We must have an estimation of these exited heavy quarkonia before we begin calculating the NLO and even NNLO corrections. This will enable a complete prediction at the leading order (LO).The remainder of this paper is organized as follows. In Sec. II, we introduce the prescription of the production of higher excited heavy quarkonium pairs under the NRQCD framework. In Sec. III, we calculate the total cross sections of
$ e^+e^-\to Z^0 \to |(Q\bar{Q^\prime})[n]\rangle + |(Q^\prime \bar{Q})[n']\rangle $ ($ Q,\; Q^\prime=c $ - or b-quarks) in the color-singlet model and discuss their differential angle distributions and uncertainties. Section IV gives a summary of the paper. -
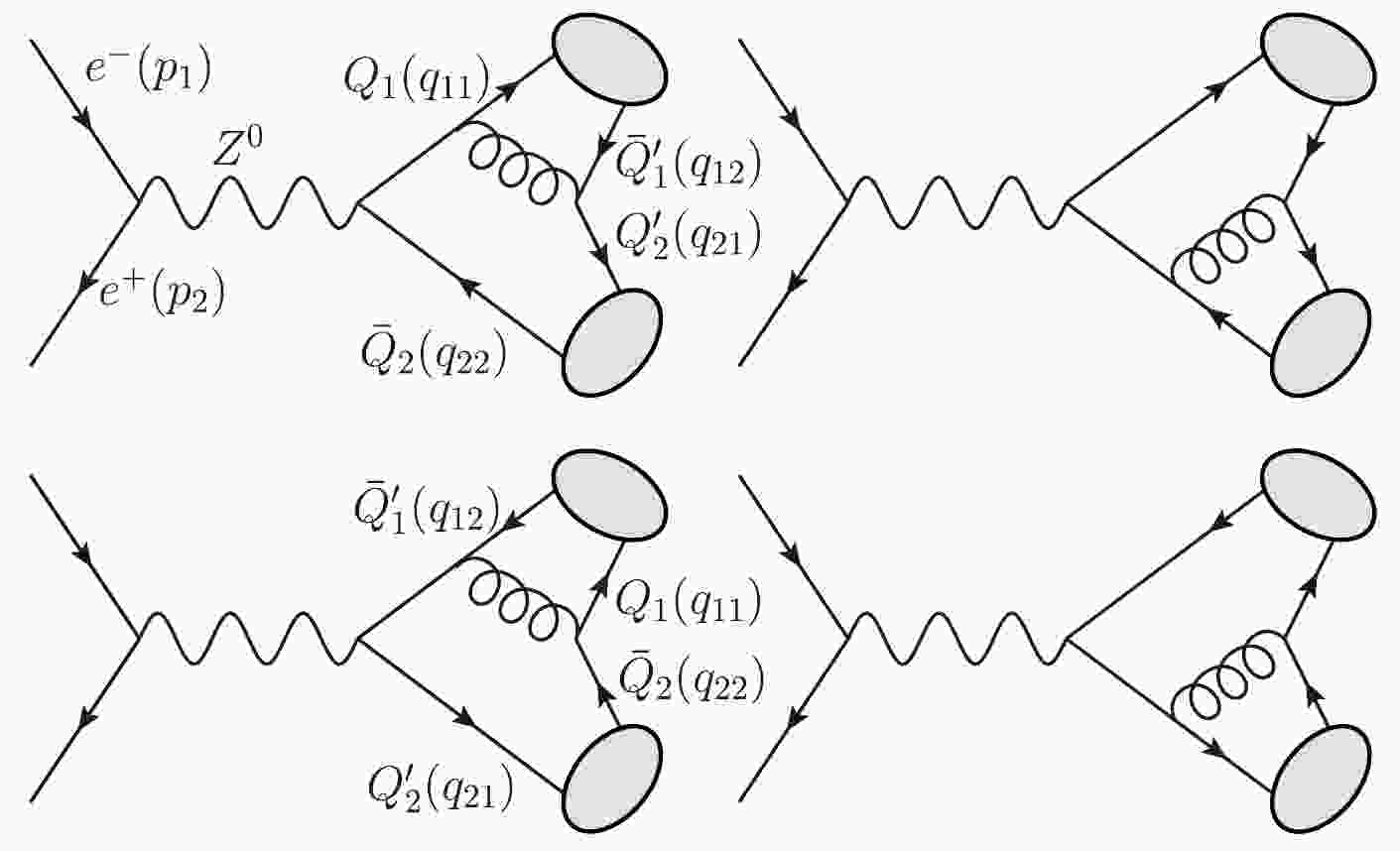
The Feynman diagrams for the production of a pair of higher excited heavy quarkonia via
$ e^-(p_1) e^+(p_2) \to Z^0 \to |(Q\bar{Q}^\prime)[n]\rangle (q_1) + |(Q^\prime\bar{Q})[n^\prime]\rangle (q_2) $ are depicted in Fig. 1. According to the QCD factorization formula, its differential cross sections can be factored into the short-distance coefficients and the long-distance matrix elements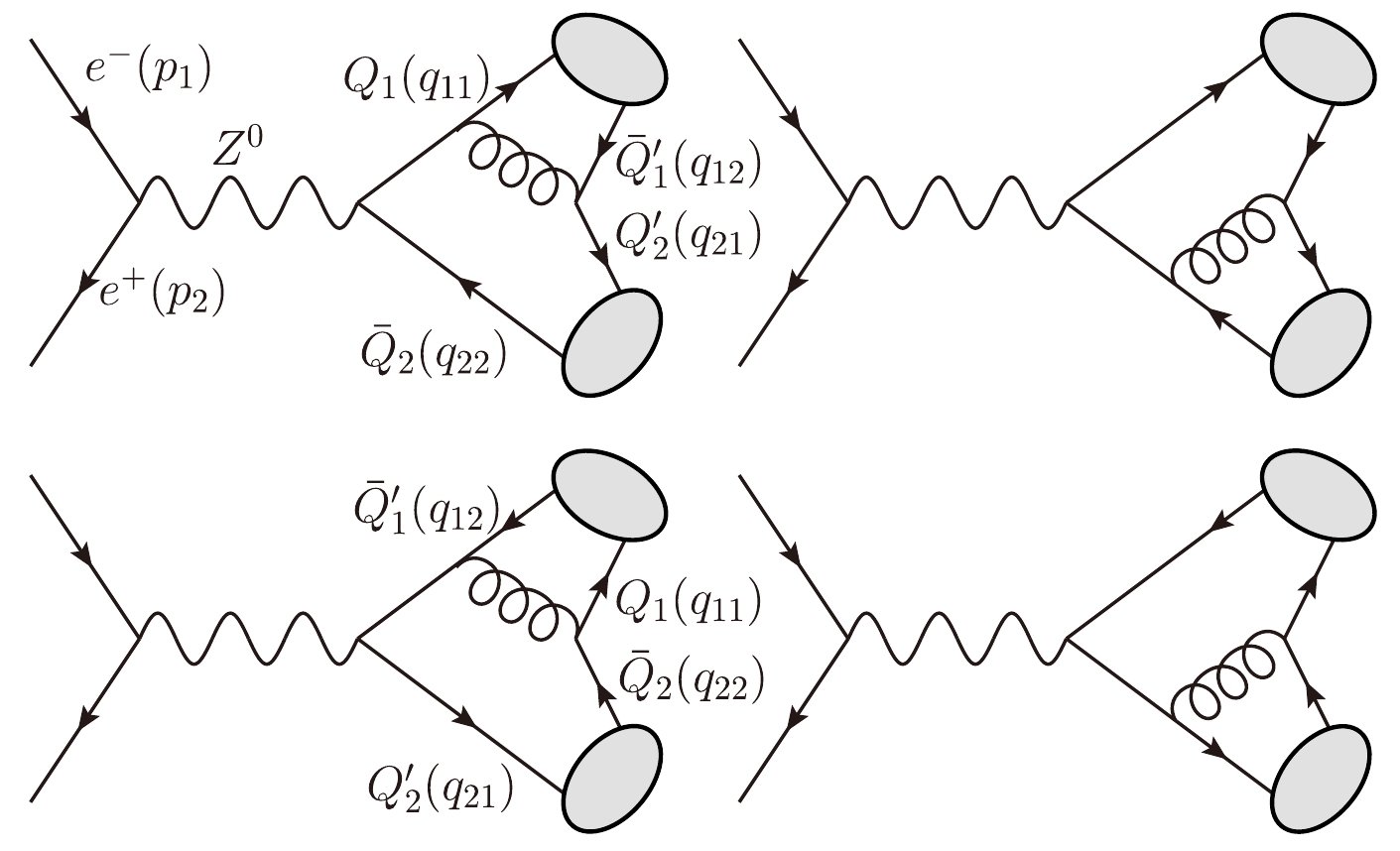
Figure 1. Feynman diagrams for
$ e^-(p_1) e^+(p_2) \to Z^0 \to |(Q\bar{Q}^\prime)[n]\rangle $ $ (q_1) + |(Q^\prime\bar{Q})[n^\prime]\rangle (q_2) $ , where$ Q,\; Q^\prime=c $ -, b-quarks, and$ [n] $ represents the color-singlet$ [n^1S_0], \; [n^3S_1], \; [n^1P_1] $ , and$ [n^3P_J] $ ($ n=1,2,3; J=0,1,2 $ ) heavy quarkonia.$ {\rm d}\sigma=\sum\limits_n {\rm d}\hat\sigma ((Q^\prime\bar{Q})[n]+ (Q\bar{Q^\prime})[n^\prime]) {\langle{\cal O}[n] \rangle} {\langle{\cal O}[n^\prime] \rangle}. $

(1) The short-distance coefficients
$ \hat\sigma((Q^\prime\bar{Q})[n]+ (Q\bar{Q^\prime})[n^\prime]) $ can be calculated perturbatively, which depicts the short-distance production of two Fock states$ (Q^\prime\bar{Q})[n] $ and$ (Q\bar{Q^\prime})[n^\prime] $ ($ Q^{(\prime)} =b $ - or c-quarks) in the spin, color, and angular momentum states$ [n^{(\prime)}] $ . Here,$ [n^{(\prime)}] $ represents the color-singlet states$ [n^{(\prime)1}S_0], \; [n^{(\prime)3}S_1], \; [n^{(\prime)1}P_1] $ , and$ [n^{(\prime)3}P_J] $ ($ n=1,2,3;J=0,1,2 $ ).The long-distance matrix element
$ {\langle{\cal O}[n] \rangle} $ is a non-perturbative parameter that describes the hadronization of the heavy quark pair$ (Q\bar{Q^\prime})[n] $ with quantum number n into the heavy quarkonium$ |(Q\bar{Q^\prime})[n]\rangle $ . In the NRQCD framework, we have contributions from both color-singlet and color-octect states. In this paper, we consider only the color-singlet state, i.e., the intermediate heavy quark pair$ (Q\bar{Q^\prime})[n] $ and the final heavy quarkonium$ |(Q\bar{Q^\prime})[n]\rangle $ have the same n. The color-singlet matrix elements$ \langle{\cal O}([n]) \rangle $ in Eq. (1) can be related to the Schrödinger wave function at the origin$ \Psi_{\mid(Q\bar{Q^\prime})[nS]\rangle}(0) $ for$ nS $ -wave heavy quarkonia or the first derivative of the wave function at the origin$ \Psi^\prime_{\mid(Q\bar{Q^\prime})[nP]\rangle}(0) $ for$ nP $ -wave heavy quarkonia:$ \begin{aligned}[b] \langle{\cal O}([n^1S_0]) \rangle \simeq& \langle{\cal O}([n^3S_1]) \rangle \simeq |\Psi_{\mid(Q\bar{Q^\prime})[nS]\rangle}(0)|^2,\\ \langle{\cal O}([n^1P_0]) \rangle \simeq& \langle{\cal O}([n^3P_J]) \rangle \simeq |\Psi^\prime_{\mid(Q\bar{Q^\prime})[nP]\rangle}(0)|^2. \end{aligned} $

(2) Because the spin-splitting effect at the same n-th level is small, the same values of wave function for both the spin-triplet and spin-singlet Fock states are adopted in our calculation. The Schrödinger wave function at the origin
$ \Psi_{|Q\bar{Q^\prime})[nS]\rangle}(0) $ and its first derivative at the origin$ \Psi^{^\prime}_{|(Q\bar{Q^\prime})[nP]\rangle}(0) $ can be further relevant to the radial wave function at the origin$ R_{|(Q\bar{Q^\prime})[nS]\rangle}(0) $ and its first derivative of the radial wave function at the origin$ R^{^\prime}_{|(Q\bar{Q^\prime})[nP]\rangle}(0) $ , respectively [2]:$ \begin{aligned}[b] \Psi_{|(Q\bar{Q^\prime})[nS]\rangle}(0)&=\sqrt{{1}/{4\pi}}R_{|(Q\bar{Q^\prime})[nS]\rangle}(0),\\ \Psi^\prime_{|(Q\bar{Q^\prime})[nP]\rangle}(0)&=\sqrt{{3}/{4\pi}}R^\prime_{|(Q\bar{Q^\prime})[nP]\rangle}(0). \end{aligned} $

(3) The differential cross section
$ d\hat\sigma $ can be calculated perturbatively, which can be formulated as$ {\rm d}\hat\sigma=\frac{1}{4\sqrt{(p_1\cdot p_2)^2-m^4_{e}}} \overline{\sum} |{\cal M}([n],[n^\prime])|^{2} {\rm d}\Phi_2, $

(4) where
$ \overline{\sum} $ is the average over the spin of the initial positron and electron and sum over the color and spin of the final higher excited heavy quarkonia. The two-body phase space in the$ e^-e^+ $ center-of-momentum (CM) rest frame can be simplified as$ \begin{aligned}[b] {\rm d}{\Phi_2} =\;& (2\pi)^4 \delta^{4}\left(p_1+p_2 - \sum\limits_{f=1}^2 q_{f}\right)\prod\limits_{f=1}^2 \frac{{\rm d}^3{\vec{q}_f}}{(2\pi)^3 2q_f^0} \\ =\;& \frac{{\mid\vec{q}_1}\mid}{8\pi\sqrt{s}}{\rm d}({\rm cos}\theta). \end{aligned} $

(5) Here,
$ s=(p_1+p_2)^2 $ is the squared CM energy. The$ 3 $ -momentum of the heavy quarkonium$ |(Q\bar{Q}^\prime) [n]\rangle $ is${|\vec{q}_1|}= \sqrt{\lambda[s, M^2_{1}, M^2_{2}] }/2\sqrt{s}$ , in which$\lambda[a, b, c]= (a - b - c)^2 - 4 b c$ , and$ M_{1} $ and$ M_{2} $ are the masses of two higher excited heavy quarkonia. θ is the angle between the momentum ($ \vec{p_1} $ ) of the electron and that ($ \vec{q_1} $ ) of the heavy quarkonium$ |(Q\bar{Q}^\prime)[n]\rangle $ .The hard scattering amplitude
$ {\cal M}([n],\; [n^\prime]) $ in Eq. (4) can be read directly from the Feynman diagrams in Fig. 1, which can be expressed as$ {\rm i}{\cal M}([n],[n^\prime])= \sum\limits_{k=1}^4 \bar{v}_{s^\prime} (p_2) {\cal L}^\sigma u_s (p_1) {\cal D}_{\sigma\rho} {\cal A}^\rho_k. $

(6) Here, k is the number of Feynman diagrams, and s and
$ s^\prime $ are the spins of the initial electron and positron, respectively. The vertex$ \cal{L}^\sigma $ and propagator$ \cal{D_{\sigma\rho}} $ for$ Z^0 $ propagated processes have the following forms:$ \begin{aligned}[b] \cal{L}^\sigma =\;&\frac{-{\rm i} g} {4 {\rm cos}\theta_W} \gamma^\sigma (1-4 e_Q {\rm sin}^2 \theta_W-\gamma^5), \\ \cal{D_{\sigma\rho}} =\;&\frac{-{\rm i} g_{\sigma\rho}}{p^2-m^2_Z+{\rm i} m_Z \Gamma_Z}. \end{aligned} $

(7) Here,
$ p=p_1+p_2 $ represents the momentum of the propagator; e denotes the unit of electric charge,$ e_Q=1 $ for the positron and electron,$ e_Q=-1/3 $ for the b-quark and$ e_Q=2/3 $ for the c-quark; g is the weak interaction coupling constant;$ \theta_W $ is the Weinberg angle, and$ \Gamma_Z $ and$ m_Z $ are the total decay width and mass of the$ Z^0 $ boson, respectively.The concrete expressions of the Dirac γ matrix chains
$ {\cal A}^\sigma_k $ in Eq. (6) for the$ nS $ -wave spin-singlet$ n^1S_0 $ and spin-triplet$ n^3S_1 $ ($ n=1,2,3 $ ) can be expressed as$ \begin{aligned}[b] {\cal A}^{\sigma (S,L=0)}_1 &= {\rm i} {\rm Tr} \left[\Pi^{(S,L=0)}_{q_1} \gamma^\alpha \frac{(\not{ q}_1+ \not{ q}_{21})+m_{Q_1}} {[(q_1 + q_{21})^2-m^2_{Q_1}] (q_{12} + q_{21})^2} {\cal L}^{\sigma} \Pi^{(S,L=0)}_{q_2} \gamma^\alpha \right]_{q=0}, \\ {\cal A}^{\sigma (S,L=0)}_2 &= {\rm i} {\rm Tr} \left[\Pi^{(S,L=0)}_{q_1} {\cal L}^{\sigma} \frac{-(\not{ q}_2+ \not{ q}_{12})+m_{{Q}_2}} {[(q_2 + q_{12})^2-m^2_{{Q}_2}] (q_{12} + q_{21})^2} \gamma^\alpha \Pi^{(S,L=0)}_{q_2} \gamma^\alpha \right]_{q=}, \\ {\cal A}^{\sigma (S,L=0)}_3 &= {\rm i} {\rm Tr} \left[\Pi^{(S,L=0)}_{q_1} \gamma^\alpha \Pi^{(S,L=0)}_{q_2} {\cal L}^{\sigma} \frac{-(\not{ q}_1+ \not{ q}_{22})+m_{{Q}_1^\prime}} {[(q_1 + q_{22})^2-m^2_{{Q}_1^\prime}] (q_{11} + q_{22})^2} \gamma^\alpha \right]_{q=0},\\ {\cal A}^{\sigma (S,L=0)}_4 &= {\rm i} {\rm Tr} \left[\Pi^{(S,L=0)}_{q_1} \gamma^\alpha \Pi^{(S,L=0)}_{q_2} \gamma^\alpha \frac{(\not{ q}_2+ \not{ q}_{11})+m_{Q_2^\prime}} {[(q_2 + q_{11})^2-m^2_{Q_2^\prime}] (q_{11} + q_{22})^2} {\cal L}^{\sigma} \right]_{q=0}. \end{aligned} $ 
(8) Here, S and L represent the quantum number of spin and orbit angular momentums of the heavy quarkonium, respectively.
$q_{11}={m_{Q_1}}{q_1}/{M_{1}}$ and$q_{12}={m_{Q_1^\prime}}{q_1}/{M_{1}}$ are the momenta of the two constituent quarks of the heavy quarkonium$ |(Q\bar{Q}^\prime)[n]\rangle (q_1) $ , with$ M_{1}=m_{Q_1}+m_{{Q}_1^\prime} $ .$q_{21}= {m_{Q_2^\prime}}{q_2}/{M_{2}}+q$ and$q_{22}={m_{{Q}_2}}{q_2}/{M_{2}}-q$ are the momenta of the two heavy constituent quarks of the heavy quarkonium$ |(Q^\prime\bar{Q})[n^\prime]\rangle (q_2) $ , with$ M_{2}=m_{Q_2^\prime}+m_{{Q}_2} $ . q respresents the relative momentum between the heavy quarks$ Q_2^\prime $ and$ {Q}_2 $ . We introduce the relative momentum q for the quarkonium$ |(Q^\prime\bar{Q})[n^\prime]\rangle (q_2) $ because it might be either an$ nS $ -wave or$ nP $ -wave state. For an$ nS $ -wave state, the relative momentum q is set to zero directly. For an$ nP $ -wave state, we should first perform the derivative of the amplitude over q and then set$ q=0 $ . The two projectors$ \Pi^{(S,L=0)}_{q_k} $ ($ k=1, 2 $ ) in Eq. (8) have the following forms:$ \begin{aligned}[b] \Pi^{(S,L=0)}_{q_1} = \epsilon_a(q_1) \frac{-\sqrt{M_{1}}}{4 m_{Q_1}m_{Q^\prime_1}}(\not {q}_{12}- m_{Q^\prime_1}) \gamma^a (\not{q}_{11} + m_{Q_1})\otimes\frac{\delta_{ij}} {\sqrt{N_c}}, \end{aligned} $

$ \begin{aligned}[b] \Pi^{(S,L=0)}_{q_2} = \epsilon_a(q_2) \frac{-\sqrt{M_{2}}}{4 m_{Q_2}m_{Q^\prime_2}}(\not {q}_{22}- m_{Q_2}) \gamma^a (\not {q}_{21} + m_{Q^\prime_2})\otimes\frac{\delta_{ij}} {\sqrt{N_c}}. \end{aligned} $

(9) Here,
$ \epsilon_{a}=1 $ and$ \gamma^a=\gamma^5 $ for the spin-singlet$ ^1S_0 $ states ($ S=0,L=0 $ ), and$ \epsilon_{a}=\varepsilon_{\mu} $ and$ \gamma^a=\gamma^\mu $ for spin-triplet$ ^3S_1 $ state ($ S=1,L=0 $ ), where μ is the Lorentz vector index.$ \delta_{ij}/\sqrt{N_c} $ denotes the color operator for a color-singlet projector with$ N_c=3 $ .When
$ |(Q^\prime\bar{Q})[n^\prime]\rangle (q_2) $ is an$ nP $ -wave state, the expressions of$ {\cal A}^\sigma_k\; (k=1,2,3,4) $ for the$ nP $ -wave spin-singlet states$ n^1P_1\; (S=0,L=1) $ and spin-triplet states$n^3P_J (S=1,\;L=1)$ with total angular momentum ($ J=0,1,2 $ ) can be formulated as the first derivative of S-wave amplitudes for the relative momentum q and then we can set$ q=0 $ :$ \begin{aligned}[b] {\cal A}^{\sigma (S=0, L=1)}_k &= \varepsilon_\nu(q_2) \left. \frac{\rm d}{{\rm d} q_\nu} {\cal A}^{\sigma (S=0, L=0)}_k \right|_{q=0}, \\ {\cal A}^{\sigma (S=1, L=1)}_k &= \varepsilon^J_{\mu\nu} (q_2)\left. \frac{\rm d}{{\rm d} q_\nu} {\cal A}^{\sigma (S=1, L=0)}_k \right|_{q=0}. \end{aligned} $

(10) Here,
$ \varepsilon_\nu(q_2) $ denotes the polarization vector of a$ n^1P_1 $ state,$ \varepsilon^{J}_{\mu\nu}(q_2) $ is the polarization tensor for an$ n^3P_J $ state ($ J=0,1,2 $ ). The derivative over the relative momentum$ q_{\nu} $ will result in complicated and lengthy amplitudes. Thus, for$ nP $ -wave states, obtaining the squared amplitudes$ |{\cal M}([n],[n^\prime])|^{2} $ using the traditional method is very time-consuming. We continue using the "improved trace technique" to solve the amplitudes$ {\cal M}([n],[n^\prime]) $ . In this prescription, the compact analytical expressions of the complicated$ nP $ -wave can be obtained, and the efficiency of numerical evaluation can also be improved. To keep this paper short, we do not further describe the "improved trace technique" in details. For complete techniques and typical examples, please refer to Refs. [25, 29−33].When solving the squared amplitudes
$ |{\cal M}([n],[n^\prime])|^{2} $ , we must also sum the polarization vectors or tensors of the heavy quarkonia. The polarization sum for the spin-triplet$ n^3S_1 $ or spin-singlet$ n^1P_1 $ states with momentum p is given by [3]$ \sum\limits_{J_z}\varepsilon_{\mu} \varepsilon_{\mu^\prime} = \Pi_{\mu \mu^\prime} \equiv -g_{\mu \mu^\prime}+\frac{p_{\mu}p_{\mu^\prime}}{p^2}, $

(11) where
$ J_z=S_z $ and$ L_z $ denote$ n^3S_1 $ and$ n^1P_1 $ states, respectively. The sum over the polarization tensors of$ n^3P_J $ states can be obtained by [3]$ \begin{aligned}[b] \varepsilon^{(0)}_{\mu\nu} \varepsilon^{(0)*}_{\mu^\prime\nu^\prime} &= \frac{1}{3} \Pi_{\mu\nu}\Pi_{\mu^\prime\nu^\prime}, \\ \sum\limits_{J_z}\varepsilon^{(1)}_{\mu\nu} \varepsilon^{(1)*}_{\mu^\prime\nu^\prime} &= \frac{1}{2} (\Pi_{\mu\mu^\prime}\Pi_{\nu\nu^\prime}- \Pi_{\mu\nu^\prime}\Pi_{\mu^\prime\nu}) ,\\ \sum\limits_{J_z}\varepsilon^{(2)}_{\mu\nu} \varepsilon^{(2)*}_{\mu^\prime\nu^\prime} &= \frac{1}{2} (\Pi_{\mu\mu^\prime}\Pi_{\nu\nu^\prime}+ \Pi_{\mu\nu^\prime}\Pi_{\mu^\prime\nu})-\frac{1}{3} \Pi_{\mu\nu}\Pi_{\mu^\prime\nu^\prime}. \end{aligned} $

(12) -
For numerical evaluations, the masses of the constituent charm and bottom quarks for the heavy quarkonia
$ |(Q\bar{Q^\prime})[n]\rangle $ and$ |(Q^\prime\bar{Q})[n^\prime]\rangle $ are shown in Table 1. The mass of the higher excited heavy quarkonium is set to be the sum of the masses of its constituent quarks at the same n-th order. This is assured by the gauge invariance of amplitudes within the NRQCD framework. The radial wave functions at the origin$ R_{|(Q\bar{Q^\prime})[nS]\rangle}(0) $ and their first derivatives at the origin$ R^\prime_{|(Q\bar{Q}^\prime)[nP]\rangle}(0) $ for heavy quarkonia$ |(Q\bar{Q^\prime})[n]\rangle $ were calculated under five different potential models in our previous study [26]. Because the Buchmüller and Tye potential (BT-potential) model [34, 35] has the correct two-loop short-distance behavior in the QCD, we adopt the results of the BT-potential in this paper, which are shown in Table 1. The uncertainties of$ R_{|(Q\bar{Q})[nS]\rangle}(0) $ and$ R'_{|(Q\bar{Q})[nP]\rangle}(0) $ are induced by the corresponding varying constituent quark masses. They are considered when we discuss the uncertainties of the total cross sections caused by the varying quark masses in Sec. III.C. The LO running strong coupling constant$ \alpha_s=0.26 $ is adopted for$ |(c\bar{c})[n]\rangle $ and$ |(b\bar{c})[n]\rangle $ , and$ \alpha_s=0.18 $ for$ |(b\bar{b})[n]\rangle $ . Other parameters are derived from the PDG [36].$ m_c $ ,

$ |R_{|(c\bar{c})[nS]\rangle}(0)|^2 $ 

$ m_c $ ,

$ |R'_{|(c\bar{c})[nP]\rangle}(0)|^2 $ 

$ n=1 $ 

1.48 $ \pm $ 0.1,

$ 2.458^{+0.227}_{-0.327} $ 

1.75 $ \pm $ 0.1,

$ 0.322^{+0.077}_{-0.068} $ 

$ n=2 $ 

1.82 $ \pm $ 0.1,

$ 1.671^{+0.115}_{-0.107} $ 

1.96 $ \pm $ 0.1,

$ 0.224^{+0.012}_{-0.012} $ 

$ n=3 $ 

1.92 $ \pm $ 0.1,

$ 0.969^{+0.063}_{-0.057} $ 

2.12 $ \pm $ 0.1,

$ 0.387^{+0.045}_{-0.042} $ 

$ m_b $ ,

$ |R_{|(b\bar{b})[nS]\rangle}(0)|^2 $ 

$ m_b $ ,

$ |R'_{|(b\bar{b})[nP]\rangle}(0)|^2 $ 

$ n=1 $ 

4.71 $ \pm $ 0.2,

$ 16.12^{+1.28}_{-1.23} $ 

4.94 $ \pm $ 0.2,

$ 5.874^{+0.728}_{-0.675} $ 

$ n=2 $ 

5.01 $ \pm $ 0.2,

$ 6.746^{+0.598}_{-0.580} $ 

5.12 $ \pm $ 0.2,

$ 2.827^{+0.492}_{-0.432} $ 

$ n=3 $ 

5.17 $ \pm $ 0.2,

$ 2.172^{+0.178}_{-0.155} $ 

5.20 $ \pm $ 0.2,

$ 2.578^{+0.187}_{-0.186} $ 

$ m_c $ /

$ m_b $ ,

$ |R_{|(c\bar{b})[nS]\rangle}(0)|^2 $ 

$ m_c $ /

$ m_b $ ,

$ |R'_{|(c\bar{b})[nP]\rangle}(0)|^2 $ 

$ n=1 $ 

1.45 $ \pm $ 0.1 /4.85

$ \pm $ 0.2,

$ 3.848^{+0.238}_{-0.225} $ 

1.75 $ \pm $ 0.1 /4.93

$ \pm $ 0.2,

$ 0.518^{+0.122}_{-0.105} $ 

$ n=2 $ 

1.82 $ \pm $ 0.1 /5.03

$ \pm $ 0.2,

$ 1.987^{+0.116}_{-0.118} $ 

1.96 $ \pm $ 0.1 /5.13

$ \pm $ 0.2,

$ 0.500^{+0.036}_{-0.036} $ 

$ n=3 $ 

1.96 $ \pm $ 0.1 /5.15

$ \pm $ 0.2,

$ 1.347^{+0.079}_{-0.082} $ 

2.15 $ \pm $ 0.1 /5.25

$ \pm $ 0.2,

$ 0.729^{+0.080}_{-0.075} $ 

Table 1. Masses (units: GeV) of the constituent heavy quarks, the radial wave functions at the origin
$ |R_{|(Q\bar{Q}^\prime)[nS]\rangle}(0)|^2 $ (units: GeV$ ^3 $ ), and their first derivatives at the origin$ |R'_{|(Q\bar{Q}^\prime)[nP]\rangle}(0)|^2 $ (units: GeV$ ^5 $ ) under the BT-potential model [26]. Note: the uncertainties of$ R_{|(Q\bar{Q})[nS]\rangle}(0) $ and$ R'_{|(Q\bar{Q})[nP]\rangle}(0) $ are induced by the corresponding varying constituent quark masses. -
The total cross sections for the production of the higher excited heavy quarkonium pair in
$ e^-e^+\to Z^0\to |(Q\bar{Q^\prime})[n]\rangle+|(Q^\prime\bar{Q})[n']\rangle $ ($ Q,\; Q^\prime=c $ - or b-quarks) at CM energy$ \sqrt{s}=91.1876 $ GeV are listed in Tables 2−4 for double charmonium, double bottomonium, and$ B_c $ pairs, respectively. The uncertainties are caused by the varying quark masses. The charm quark mass$ m_c $ has the variation$ \pm 0.1 $ GeV, and the bottom quark mass$ m_b $ has the variation$ \pm 0.2 $ GeV. In Tables 2−4, the top three rankings are marked in bold. For the double charmonium channels, we always have$ \sigma_{(|(c\bar{c})[n^3S_1]\rangle+|(c\bar{c})[n'^1P_1]\rangle)} > \sigma_{(|(c\bar{c})[n^1S_0]\rangle+|(c\bar{c})[n'^3P_2]\rangle)} > \sigma_{(|(c\bar{c})[n^1S_0]\rangle+|(c\bar{c})[n'^3P_0]\rangle)} $ at the same nth level. For double bottomonium channels, the largest cross sections can either be$ |(b\bar{b})[n^1S_0]\rangle+ |(b\bar{b})[n'^3S_1]\rangle $ or$ |(b\bar{b})[n^3S_1]\rangle+|(b\bar{b})[n'^3P_2]\rangle $ . For$ B_c $ pair channels, the largest cross section can either be$|(c\bar{b})[n^3S_1]\rangle + |(b\bar{c})[n'^3S_1]\rangle$ or$ |(c\bar{b})[n^3S_1]\rangle+|(b\bar{c})[n'^3P_2]\rangle $ . Note that in Tables 2−4, we have redundant data in the row of$ \sigma_{(|(Q\bar{Q}^\prime)[n^3S_1]\rangle+|(Q\bar{Q}^\prime)[n'^3S_1]\rangle)} $ , i.e., the cross sections are the same when n and$ n^\prime $ are exchanged. This is also a check for our extensive calculations.$ [n]+[n^\prime] $ 

1+1 1+2 1+3 2+1 2+2 2+3 3+1 3+2 3+3 $ \sigma_{([n^1S_0]+[n'^3S_1])} $ 

$ 18.95^{+3.64}_{-4.70} $ 

$ 11.32^{+1.98}_{-2.20} $ 

$ 6.632^{+1.121}_{-1.250} $ 

$ 13.91^{+2.24}_{-2.55 } $ 

$ 8.176^{+1.19}_{-1.04} $ 

$ 4.770^{+0.672}_{-0.579} $ 

$ 8.594^{+1.308}_{-1.506} $ 

$ 5.032^{+0.694}_{-0.598} $ 

$ 2.933^{+0.390}_{-0.332} $ 

$ \sigma_{([n^3S_1]+[n'^3S_1])} $ 

$ 64.16^{+12.29}_{-15.87} $ 

$ 42.55^{+7.09}_{-8.00} $ 

$ 25.63^{+4.08}_{-4.64} $ 

$ 42.55^{+7.09}_{-8.00} $ 

$ 27.62^{+4.01}_{-3.49} $ 

$ 16.55^{+2.29}_{-1.98} $ 

$ 25.63^{+4.08}_{-4.64} $ 

$ 16.55^{+2.29}_{-1.98} $ 

$ 9.900^{+1.308}_{-1.099} $ 

$ \sigma_{([n^1S_0]+[n'^1P_1])} $ 

$ 60.76^{+4.49}_{-7.35} $ 

$ 18.71^{+1.35}_{-0.57} $ 

$ 25.47^{+0.16}_{-1.04} $ 

$ 20.42^{+1.32}_{-1.43} $ 

$ 10.07^{+1.04}_{-0.80} $ 

$ 13.69^{+0.26}_{-0.19} $ 

$ 11.63^{+0.72}_{-0.76} $ 

$ 5.729^{+0.572}_{-0.468} $ 

$ 7.792^{+0.184}_{-0.128} $ 

$ \sigma_{([n^3S_1]+[n'^1P_1])} $ 

$ {454.0}^{+39.1}_{-59.2} $ 

$ {227.1}^{+4.4}_{-14.0} $ 

$ {312.4}^{+1.8}_{-16.2} $ 

$ {247.4}^{+19.0}_{-19.7} $ 

$ {123.8}^{+10.2}_{-8.4} $ 

$ {170.6}^{+0.6}_{-0.2} $ 

$ {141.3}^{+10.4}_{-10.7} $ 

$ {70.77}^{+6.18}_{-5.00} $ 

$ {97.48}^{+1.11}_{-0.41} $ 

$ \sigma_{([n^1S_0]+[n'^3P_0])} $ 

$ {137.0}^{+9.9}_{-16.4} $ 

$ {68.03}^{+2.17}_{-5.01} $ 

$ {93.16}^{+0.70}_{-3.71} $ 

$ {72.27}^{+4.44}_{-4.85} $ 

$ {35.87}^{+3.50}_{-2.93} $ 

$ {49.10}^{+1.04}_{-0.79} $ 

$ {40.87}^{+2.47}_{-2.65} $ 

$ {20.29}^{+2.09}_{-1.71} $ 

$ {27.76}^{+0.73}_{-0.53} $ 

$ \sigma_{([n^1S_0]+[n'^3P_1])} $ 

$ 18.87^{+3.98}_{-4.27} $ 

$ 10.56^{+0.41}_{-0.90} $ 

$ 15.74^{+1.69}_{-2.28} $ 

$ 12.37^{+2.30}_{-2.10} $ 

$ 6.835^{+0.136}_{-0.117} $ 

$ 10.11^{+0.89}_{-0.82} $ 

$ 7.432^{+1.327}_{-1.213} $ 

$ 4.093^{+0.058}_{-0.038} $ 

$ 6.039^{+0.496}_{-0.448} $ 

$ \sigma_{([n^1S_0]+[n'^3P_2])} $ 

$ {284.2}^{+22.2}_{-35.3} $ 

$ {140.9}^{+3.8}_{-9.7} $ 

$ {192.4}^{+0.5}_{-8.5} $ 

$ {153.2}^{+10.5}_{-11.2} $ 

$ {75.96}^{+5.51}_{-6.91} $ 

$ {103.8}^{+1.0}_{-1.6} $ 

$ {87.22}^{+5.69}_{-5.97} $ 

$ {43.26}^{+3.39}_{-4.16} $ 

$ {59.13}^{+0.75}_{-1.18} $ 

$ \sigma_{([n^3S_1]+[n'^3P_0])} $ 

$ 44.03^{+4.60}_{-6.38} $ 

$ 21.89^{+0.95}_{-0.01} $ 

$ 30.20^{+0.80}_{-2.2} $ 

$ 25.92^{+2.31}_{-2.33} $ 

$ 12.76^{+0.85}_{-0.69} $ 

$ 17.50^{+0.27}_{-0.17} $ 

$ 15.15^{+1.28}_{-1.27} $ 

$ 7.437^{+0.542}_{-0.431} $ 

$ 10.18^{+0.12}_{-0.04} $ 

$ \sigma_{([n^3S_1]+[n'^3P_1])} $ 

$ 17.62^{+3.57}_{-3.88} $ 

$ 10.79^{+0.29}_{-0.80} $ 

$ 17.07^{+1.59}_{-2.26} $ 

$ 9.625^{+1.822}_{-1.663} $ 

$ 5.909^{+0.105}_{-0.086} $ 

$ 9.354^{+0.774}_{-0.711} $ 

$ 5.492^{+1.019}_{-0.926} $ 

$ 3.374^{+0.048}_{-0.032} $ 

$ 5.344^{+0.423}_{-0.380} $ 

$ \sigma_{([n^3S_1]+[n'^3P_2])} $ 

$ 57.51^{+8.25}_{-10.02} $ 

$ 24.83^{+0.06}_{-1.18} $ 

$ 38.15^{+2.66}_{-4.20} $ 

$ 22.09^{+3.70}_{-3.42} $ 

$ 13.26^{+0.08}_{-0.01} $ 

$ 20.55^{+1.33}_{-1.19} $ 

$ 12.46^{+2.08}_{-1.92} $ 

$ 7.521^{+0.015}_{-0.069} $ 

$ 11.69^{+0.73}_{-0.64} $ 

Table 2. Total cross sections (units:
$\times 10^{-5}\; {\rm fb}$ ) for the production of higher excited charmonium pairs in$ e^+e^-\to Z^0 \to $ $ |(c\bar{c})[n]\rangle +|(c\bar{c})[n^\prime]\rangle $ at$ \sqrt{s}=91.1876 $ GeV. The uncertainties are caused by the charm quark mass varying by 0.1 GeV, where effects of the uncertainties of the$ R_{|(c\bar{c})[nS]\rangle}(0) $ and$ R'_{|(c\bar{c})[nP]\rangle}(0) $ induced by varying masses are also considered (see Table 1 for explicit values). The top three rankings are marked in bold.$ [n]+[n^\prime] $ 

1+1 1+2 1+3 2+1 2+2 2+3 3+1 3+2 3+3 $ \sigma_{([n^1S_0]+|[n'^3S_1])} $ 

$ {428.6}^{+67.9}_{-60.9} $ 

$ {173.3}^{+29.4}_{-26.9} $ 

$ {54.82}^{+8.92}_{-7.61} $ 

$ {184.3}^{+30.7}_{-27.6} $ 

$ {74.40}^{+13.23}_{-11.87} $ 

$ {23.53}^{+4.03}_{-3.45} $ 

$ {60.18}^{+9.54}_{-8.15} $ 

$ {24.28}^{+4.12}_{-3.53} $ 

$ {7.675}^{+1.25}_{-1.02} $ 

$ \sigma_{([n^3S_1]+[n'^3S_1])} $ 

$ {119.9}^{+18.4}_{-16.6} $ 

$ 49.84^{+8.14}_{-7.08} $ 

$ 16.00^{+2.47}_{-2.16} $ 

$ {49.84}^{+8.14}_{-7.08} $ 

$ 20.69^{+3.58}_{-3.23} $ 

$ 6.634^{+1.097}_{-0.946} $ 

$ 16.00^{+2.47}_{-2.16} $ 

$ 6.634^{+1.097}_{-0.946} $ 

$ 2.127^{+0.336}_{-0.274} $ 

$ \sigma_{([n^1S_0]+[n'^1P_1])} $ 

$ 53.27^{+1.46}_{-1.51} $ 

$ 22.83^{+1.77}_{-1.68} $ 

$ 19.80^{+0.25}_{-0.28} $ 

$ 21.08^{+0.82}_{-0.68} $ 

$ 9.036^{+0.809}_{-0.778} $ 

$ 7.835^{+0.024}_{-0.007} $ 

$ 6.601^{+0.225}_{-0.119} $ 

$ 2.829^{+0.238}_{-0.206} $ 

$ 2.453^{+0.033}_{-0.019} $ 

$ \sigma_{([n^3S_1]+[n'^1P_1])} $ 

$ 61.46^{+4.22}_{-4.05} $ 

$ 26.91^{+3.25}_{-2.95} $ 

$ 23.55^{+0.60}_{-0.63} $ 

$ 24.90^{+1.99}_{-1.72} $ 

$ 10.90^{+1.44}_{-1.32} $ 

$ 9.543^{+0.347}_{-0.374} $ 

$ 7.891^{+0.586}_{-0.434} $ 

$ 3.454^{+0.437}_{-0.373} $ 

$ 3.024^{+0.093}_{-0.075} $ 

$ \sigma_{([n^1S_0]+|([n'^3P_0])} $ 

$ 9.215^{+0.141}_{-0.160} $ 

$ 4.010^{+0.262}_{-0.256} $ 

$ 3.501^{+0.081}_{-0.088} $ 

$ 3.495^{+0.087}_{-0.067} $ 

$ 1.520^{+0.114}_{-0.113} $ 

$ 1.327^{+0.015}_{-0.021} $ 

$ 1.068^{+0.020}_{-0.004} $ 

$ 0.465^{+0.032}_{-0.028} $ 

$ 0.405^{+0.011}_{-0.009} $ 

$ \sigma_{([n^1S_0]+[n'^3P_1])} $ 

$ 14.31^{+1.60}_{-1.60} $ 

$ 6.331^{+1.041}_{-0.925} $ 

$ 5.568^{+0.362}_{-0.368} $ 

$ 6.049^{+0.725}_{-0.635} $ 

$ 2.672^{+0.463}_{-0.412} $ 

$ 2.349^{+0.172}_{-0.176} $ 

$ 1.959^{+0.220}_{-0.176} $ 

$ 0.865^{+0.143}_{-0.121} $ 

$ 0.760^{+0.050}_{-0.045} $ 

$ \sigma_{([n^1S_0]+|[n'^3P_2])} $ 

$ 28.15^{+1.38}_{-1.35} $ 

$ 12.15^{+1.22}_{-1.13} $ 

$ 10.57^{+0.071}_{-0.087} $ 

$ 11.36^{+0.69}_{-0.59} $ 

$ 4.903^{+0.55}_{-0.51} $ 

$ 4.265^{+0.077}_{-0.091} $ 

$ 3.591^{+0.199}_{-0.136} $ 

$ 1.550^{+0.166}_{-0.142} $ 

$ 1.349^{+0.017}_{-0.010} $ 

$ \sigma_{([n^3S_1]+[n'^3P_0])} $ 

$ 68.37^{+6.17}_{-5.83} $ 

$ 30.69^{+4.38}_{-3.92} $ 

$ 27.16^{+1.24}_{-1.26} $ 

$ 27.39^{+2.78}_{-2.41} $ 

$ 12.29^{+1.90}_{-1.70} $ 

$ 10.88^{+0.61}_{-0.63} $ 

$ 8.629^{+0.824}_{-0.639} $ 

$ 3.871^{+0.574}_{-0.486} $ 

$ 3.425^{+0.173}_{-0.150} $ 

$ \sigma_{([n^3S_1]+[n'^3P_1])} $ 

$ 117.5^{+13.6}_{-15.0} $ 

$ {54.03}^{+9.03}_{-7.98} $ 

$ {48.32}^{+3.24}_{-3.25} $ 

$ 46.76^{+5.93}_{-5.16} $ 

$ {21.50}^{+3.85}_{-3.40} $ 

$ {19.23}^{+1.50}_{-1.51} $ 

$ {14.68}^{+1.75}_{-1.44} $ 

$ {6.748}^{+1.166}_{-0.981} $ 

$ {6.034}^{+0.436}_{-0.391} $ 

$ \sigma_{([n^3S_1]+[n'^3P_2])} $ 

$ {230.6}^{+23.6}_{-22.2} $ 

$ {104.8}^{+16.2}_{-14.4} $ 

$ {93.29}^{+5.3}_{-10.5} $ 

$ {91.99}^{+10.5}_{-9.08} $ 

$ {41.81}^{+6.97}_{-6.19} $ 

$ {37.20}^{+2.49}_{-2.53} $ 

$ {28.90}^{+3.12}_{-46} $ 

$ {13.13}^{+2.11}_{-1.78} $ 

$ {11.69}^{+0.72}_{-0.63} $ 

Table 3. Total cross sections (units:
$\times 10^{-4}\; {\rm fb}$ ) for the production of higher excited bottomonium pairs in$ e^+e^-\to Z^0 \to $ $ |(b\bar{b})[n]\rangle +|(b\bar{b})[n^\prime]\rangle $ at$ \sqrt{s}=91.1876 $ GeV. The uncertainties are caused by the bottom quark mass varying by 0.2 GeV, where effects of the uncertainties of the$ R_{|(b\bar{b})[nS]\rangle}(0) $ and$ R'_{|(b\bar{b})[nP]\rangle}(0) $ induced by varying masses are also considered (see Table 1 for explicit values). The top three rankings are marked in bold.$ [n]+[n^\prime] $ 

1+1 1+2 1+3 2+1 2+2 2+3 3+1 3+2 3+3 $ \sigma_{([n^1S_0]+[n'^3S_1])} $ 

$ {634.6}^{+47.8}_{-45.8} $ 

$ 212.9^{+5.7}_{-3.9} $ 

$ 127.9^{+2.3}_{-1.6} $ 

$ {220.3}^{+5.9}_{-41} $ 

$ 72.63^{+0.30}_{-0.29} $ 

$ 43.41^{+0.47}_{-0.57} $ 

$ {133.9}^{+2.4}_{-1.7} $ 

$ 43.89^{+0.47}_{-0.67} $ 

$ 26.19^{+1.34}_{-0.58} $ 

$ \sigma_{([n^3S_1]+[n'^3S_1])} $ 

$ {1150}^{+87}_{-84} $ 

$ {397.2}^{+10.5}_{-7.4} $ 

$ {240.5}^{+4.3}_{-3.1} $ 

$ {397.2}^{+10.5}_{-7.4} $ 

$ {136.3}^{+0.6}_{-0.1} $ 

$ {82.33}^{+0.72}_{-0.94} $ 

$ {240.5}^{+4.3}_{-3.1} $ 

$ {82.33}^{+0.72}_{-0.94} $ 

$ {49.69}^{+0.75}_{-1.00} $ 

$ \sigma_{([n^1S_0]+[n'^1P_1])} $ 

$ 4.810^{+0.399}_{-0.406} $ 

$ 2.134^{+0.154}_{-0.141} $ 

$ 1.405^{+0.033}_{-0.045} $ 

$ 2.747^{+0.021}_{-0.024} $ 

$ 1.357^{+0.148}_{-0.129} $ 

$ 1.042^{+0.035}_{-0.034} $ 

$ 1.840^{+0.016}_{-0.022} $ 

$ 0.926^{+0.100}_{-0.089} $ 

$ 0.729^{+0.027}_{-0.026} $ 

$ \sigma_{([n^3S_1]+[n'^1P_1])} $ 

$ 11.77^{+1.10}_{-1.12} $ 

$ 8.984^{+0.985}_{-0.784} $ 

$ 6.849^{+0.344}_{-0.256} $ 

$ 2.878^{+0.182}_{-0.174} $ 

$ 2.122^{+0.128}_{-0.114} $ 

$ 2.510^{+0.013}_{-0.009} $ 

$ 1.586^{+0.108}_{0.105-} $ 

$ 1.153^{+0.057}_{-0.053} $ 

$ 1.355^{+0.008}_{-0.010} $ 

$ \sigma_{([n^1S_0]+[n'^3P_0])} $ 

$ 15.27^{+1.10}_{-1.12} $ 

$ 12.01^{+1.67}_{-1.35} $ 

$ 14.96^{+1.37}_{-1.12} $ 

$ 4.430^{+0.205}_{-0.226} $ 

$ 3.500^{+0.328}_{-0.300} $ 

$ 4.378^{+0.217}_{-0.204} $ 

$ 2.536^{+0.140}_{-0.157} $ 

$ 2.006^{+0.163}_{-0.155} $ 

$ 2.512^{+0.095}_{-0.097} $ 

$ \sigma_{([n^1S_0]+[n'^3P_1])} $ 

$ 6.162^{+0.701}_{-0.448} $ 

$ 4.751^{+0.443}_{-0.352} $ 

$ 5.659^{+0.242}_{-0.174} $ 

$ 1.451^{+0.151}_{-0.145} $ 

$ 1.161^{+0.041}_{-0.038} $ 

$ 1.419^{+0.014}_{-0.0137} $ 

$ 0.780^{+0.093}_{-0.090} $ 

$ 0.632^{+0.008}_{-0.013} $ 

$ 0.781^{+0.017}_{-0.019} $ 

$ \sigma_{([n^1S_0]+[n'^3P_2])} $ 

$ 3.093^{+0.253}_{-0.236} $ 

$ 1.326^{+0.214}_{-0.163} $ 

$ 1.802^{+0208}_{-0.159} $ 

$ 0.541^{+0.050}_{-0.049} $ 

$ 0.472^{+0.025}_{-0.023} $ 

$ 0.628^{+0.009}_{-0.007} $ 

$ 0.266^{+0.030}_{-0.0296} $ 

$ 0.236^{+0.007}_{-0.007} $ 

$ 0.319^{+0.001}_{-0.002} $ 

$ \sigma_{([n^3S_1]+[n'^3P_0])} $ 

$ 454.2^{+15.7}_{-30.8} $ 

$ {239.3}^{+56.8}_{-42.4} $ 

$ {213.1}^{+33.5}_{-26.1} $ 

$ 153.3^{+12.5}_{-10.78} $ 

$ {79.95}^{+16.38}_{-12.9}0 $ 

$ {70.46}^{+8.89}_{-7.40} $ 

$ 91.71^{+6.72}_{-5.99} $ 

$ {47.74}^{+9.32}_{-7.48} $ 

$ {41.98}^{+4.91}_{-4.20} $ 

$ \sigma_{([n^3S_1]+[n'^3P_1])} $ 

$ 270.1^{+16.2}_{-15.8} $ 

$ 180.1^{+25.2}_{-20.0} $ 

$ 194.7^{+15.7}_{-12.5} $ 

$ 84.10^{+2.73}_{-2.56} $ 

$ 55.80^{+5.52}_{-4.81} $ 

$ 60.11^{+2.53}_{-2.27} $ 

$ 49.46^{+1.83}_{-1.98} $ 

$ 32.77^{+2.88}_{-2.60} $ 

$ 35.27^{+1.11}_{-1.08} $ 

$ \sigma_{([n^3S_1]+[n'^3P_2])} $ 

$ {1133}^{+16}_{-22} $ 

$ {394.1}^{+89.4}_{-67.1} $ 

$ {595.3}^{+80.1}_{-62.6} $ 

$ {376.9}^{+22.5}_{-19.1} $ 

$ {207.9}^{+37.3}_{-29.8} $ 

$ {193.6}^{+19.9}_{-16.7} $ 

$ {224.8}^{+11.5}_{-10.2} $ 

$ {123.7}^{+21.0}_{-17.1} $ 

$ {114.9}^{+20.7}_{-9.3} $ 

Table 4. Total cross sections (units:
$\times 10^{-3}\; {\rm fb}$ ) for the production of higher excited$ B_c $ pairs in$ e^+e^-\to Z^0 \to |(c\bar{b})[n]\rangle +|(b\bar{c})[n^\prime]\rangle $ at$ \sqrt{s}=91.1876 $ GeV. The uncertainties are caused by the charm quark mass varying by 0.1 GeV and bottom quark mass by 0.2 GeV, where effects of the uncertainties of the$ R_{|(c\bar{b})[nS]\rangle}(0) $ and$ R'_{|(c\bar{b})[nP]\rangle}(0) $ caused by varying masses are also considered (see Table 1 for explicit values). The top three rankings are marked in bold.As shown in Tables 2−4, compared with the ''
$ 1+1 $ '' configuration, the cross sections for the production of the higher excited heavy quarkonium pair are sizable. Because most of higher excited heavy quarkonia will decay to ground states for$ n=1 $ , their contribution must be considered carefully when we study the production rates of the ground states.● For the top three double charmonium channels
$ |(c\bar{c})[n^3S_1]\rangle+|(c\bar{c})[n'^1P_1]\rangle $ ,$ |(c\bar{c})[n^1S_0]\rangle+|(c\bar{c})[n'^3P_2]\rangle $ , and$ |(c\bar{c})[n^1S_0]\rangle+|(c\bar{c})[n'^3P_0]\rangle $ , the total cross sections of the$ [1]+[2] $ ,$ [1]+[3] $ ,$ [2]+[1] $ ,$ [2]+[2] $ ,$ [2]+[3] $ ,$ [3]+[1] $ ,$ [3]+[2] $ , and$ [3]+[3] $ configurations are about 50%, 69%, 54%, 27%, 38%, 31%, 16%, and 21% of the cross section of the$ [1]+[1] $ configuration, respectively. An interesting observation is that the top three double charmonium channels for other configurations have very similar ratios to that of the$ [1]+[1] $ configuration.● For the double bottomonium channel
$ |(b\bar{b})[n^1S_0]\rangle+ |(b\bar{b})[n'^3S_1]\rangle $ , the total cross sections of the$ [1]+[2] $ ,$ [1]+[3] $ ,$ [2]+[1] $ ,$ [2]+[2] $ ,$ [2]+[3] $ ,$ [3]+[1] $ ,$ [3]+[2] $ , and$ [3]+[3] $ configurations are about 40%, 13%, 43%, 17%, 5.5%, 14%, 5.7%, and 1.8% of the cross section of the$ [1]+[1] $ configuration, respectively.For the double bottomonium channel
$ |(b\bar{b})[n^3S_1]\rangle+ |(b\bar{b})[n'^3P_1]\rangle $ , the total cross sections of the$ [1]+[2] $ ,$ [1]+[3] $ ,$ [2]+[1] $ ,$ [2]+[2] $ ,$ [2]+[3] $ ,$ [3]+[1] $ ,$ [3]+[2] $ , and$ [3]+[3] $ configurations are about 46%, 41%, 40%, 18%, 16%, 12%, 5.7%, and 5.1% of the cross section of the$ [1]+[1] $ configuration, respectively.For the double bottomonium channel
$ |(b\bar{b})[n^3S_1]\rangle+ |(b\bar{b})[n'^3P_2]\rangle $ , the total cross sections of the$ [1]+[2] $ ,$ [1]+[3] $ ,$ [2]+[1] $ ,$ [2]+[2] $ ,$ [2]+[3] $ ,$ [3]+[1] $ ,$ [3]+[2] $ , and$ [3]+[3] $ configurations are about 45%, 40%, 40%, 18%, 16%, 13%, 5.7%, and 5.1% of the cross section of the$ [1]+[1] $ configuration, respectively.● For the
$ B_c $ pair channel$ |(c\bar{b})[n^1S_0]\rangle+|(b\bar{c})[n'^3S_1]\rangle $ , the total cross sections of the$ [1]+[2] $ ,$ [1]+[3] $ ,$ [2]+[1] $ ,$ [2]+[2] $ ,$ [2]+[3] $ ,$ [3]+[1] $ ,$ [3]+[2] $ , and$ [3]+[3] $ configurations are about 34%, 20%, 35%, 11%, 6.8%, 21%, 6.9%, and 4.1% of the cross section of the$ [1]+[1] $ configuration, respectively.For the
$ B_c $ pair channel$ |(c\bar{b})[n^3S_1]\rangle+|(b\bar{c})[n'^3S_1]\rangle $ , the total cross sections of the$ [1]+[2] $ ,$ [1]+[3] $ ,$ [2]+[1] $ ,$ [2]+[2] $ ,$ [2]+[3] $ ,$ [3]+[1] $ ,$ [3]+[2] $ , and$ [3]+[3] $ configurations are about 35%, 21%, 35%, 18%, 7.2%, 21%, 7.2%, and 4.3% of the cross section of the$ [1]+[1] $ configuration, respectively.For the
$ B_c $ pair channel$ |(c\bar{b})[n^3S_1]\rangle+|(b\bar{c})[n'^3P_2]\rangle $ , the total cross sections of the$ [1]+[2] $ ,$ [1]+[3] $ ,$ [2]+[1] $ ,$ [2]+[2] $ ,$ [2]+[3] $ ,$ [3]+[1] $ ,$ [3]+[2] $ , and$ [3]+[3] $ configurations are about 35%, 53%, 33%, 18%, 17%, 20%, 11%, and 10% of the cross section of the$ [1]+[1] $ configuration, respectively.When CEPC is running in the Z factory operation mode, its designed integrated luminosity with two interaction points can reach as high as
$ 16\; ab^{-1} $ [1]. Thus, we can estimate the events of the production of double higher excited heavy quarkonia. We show the events in Table 5 for the top three channels in Tables 2−4 as an illustration.$ [n]+[n^\prime] $ 

1+1 1+2 1+3 2+1 2+2 2+3 3+1 3+2 3+3 $ |(c\bar{c})[n^3S_1]\rangle+|(c\bar{c})[n'^1P_1]\rangle $ 

73 37 50 40 20 27 23 11 16 $ |(c\bar{c})[n^1S_0]\rangle+|(c\bar{c})[n'^3P_2]\rangle $ 

45 22 30 24 12 16 14 7 9 $ |(c\bar{c})[n^1S_0]\rangle+|(c\bar{c})[n'^3P_0]\rangle $ 

22 11 15 12 6 8 7 3 4 $ |(b\bar{b})[n^1S_0]\rangle+|(b\bar{b})[n'^3S_1]\rangle $ 

686 277 88 295 119 38 96 39 12 $ |(b\bar{b})[n^3S_1]\rangle+|(b\bar{b})[n'^3P_2]\rangle $ 

369 168 149 147 67 60 46 21 19 $ |(b\bar{b})[n^3S_1]\rangle+|(b\bar{b})[n'^3S_1]\rangle $ 

192 80 26 80 33 11 26 11 3 $ |(c\bar{b})[n^3S_1]\rangle+|(b\bar{c})[n'^3S_1]\rangle $ 

$ 1.84\times10^4 $ 

$ 6.36\times10^3 $ 

$ 3.85\times10^3 $ 

$ 6.36\times10^3 $ 

$ 2.18\times10^3 $ 

$ 1.32\times10^3 $ 

$ 3.85\times10^3 $ 

$ 1.32\times10^4 $ 

$ 7.95\times10^2 $ 

$ |(c\bar{b})[n^3S_1]\rangle+|(b\bar{c})[n'^3P_0]\rangle $ 

$ 1.81\times10^4 $ 

$ 6.30\times10^3 $ 

$ 9.51\times 10^3 $ 

$ 6.02\times10^3 $ 

$ 3.32\times10^3 $ 

$ 3.09\times10^3 $ 

$ 3.59\times10^3 $ 

$ 1.98\times10^3 $ 

$ 1.84\times10^3 $ 

$ |(c\bar{b})[n^1S_0]\rangle+|(b\bar{c})[n'^3S_1]\rangle $ 

$ 1.02\times10^4 $ 

$ 3.42\times10^3 $ 

$ 2.06\times 10^3 $ 

$ 3.42\times10^3 $ 

$ 1.17\times10^3 $ 

$ 6.98\times10^2 $ 

$ 2.06\times10^3 $ 

$ 6.98\times10^2 $ 

$ 4.21\times10^2 $ 

In Figs. 2−4, we depict the distribution dσ/dcosθ at
$ \sqrt{s}=91.1876 $ GeV for the production of double higher excited charmonium, double higher excited bottomonium, and higher excited$ B_c $ pairs, respectively. The distribution dσ/dcosθ can be obtained easily using the differential phase space in Eq. (5). Note that θ is the angle between the momentum$ \vec{p_1} $ of the electron and the momentum$ \vec{q_1} $ of the heavy quarkonium. Here, we only show parts of the configurations$ [n]+[n^\prime] $ of top three ranking channels. We show that the largest differential cross section dσ/dcosθ can be obtained at$ \theta=90^\circ $ for the configurations depicted in Fig. 2, and the minimum is achieved at$ \theta=90^\circ $ for the configurations in Fig. 3. In Fig. 4, for double$ B_c $ pair production, we obtain the largest differential cross section dσ/dcosθ near (but not precisely at)$ \theta=90^\circ $ in the left and right plots and obtain the minimum near (but not precisely at)$ \theta=90^\circ $ in the middle plot. The plots, particularly the middle and right ones in Fig. 4, does not indicate the symmetry of θ as those in Figs. 2 and 3.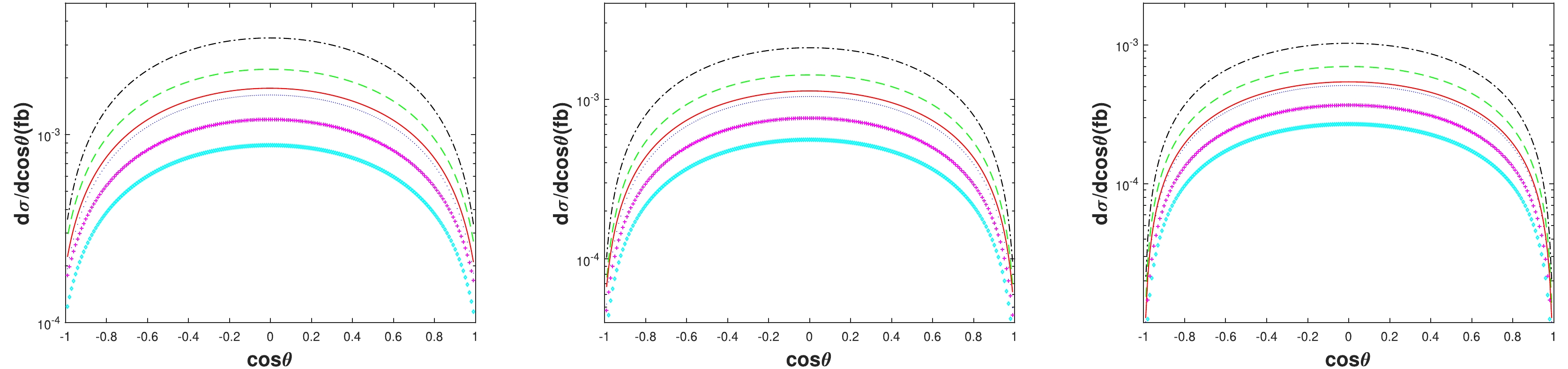
Figure 2. (color online) Differential angle distributions of cross sections dσ/dcosθ at
$ \sqrt{s}=91.1876 $ GeV for$ e^-e^+\to Z^0 \to $ $ |(c\bar{c})[n]\rangle+|(c\bar{c})[n']\rangle $ . The dash-dotted black, dotted blue, dashed green, solid red, diamond cyan, and cross magenta lines are for the$ [1]+[1] $ ,$ [1]+[2] $ ,$ [1]+[3] $ ,$ [2]+[1] $ ,$ [2]+[2] $ ,$ [2]+[3] $ configurations of the$ |(c\bar{c})[n^3S_1]\rangle+|(c\bar{c})[n'^1P_1]\rangle $ channel (left),$|(c\bar{c})[n^1S_0]\rangle + $ $ |(c\bar{c})[n'^3P_2]\rangle$ channel (middle), and$ |(c\bar{c})[n^1S_0]\rangle+|(c\bar{c})[n'^3P_0]\rangle $ channel (right), respectively.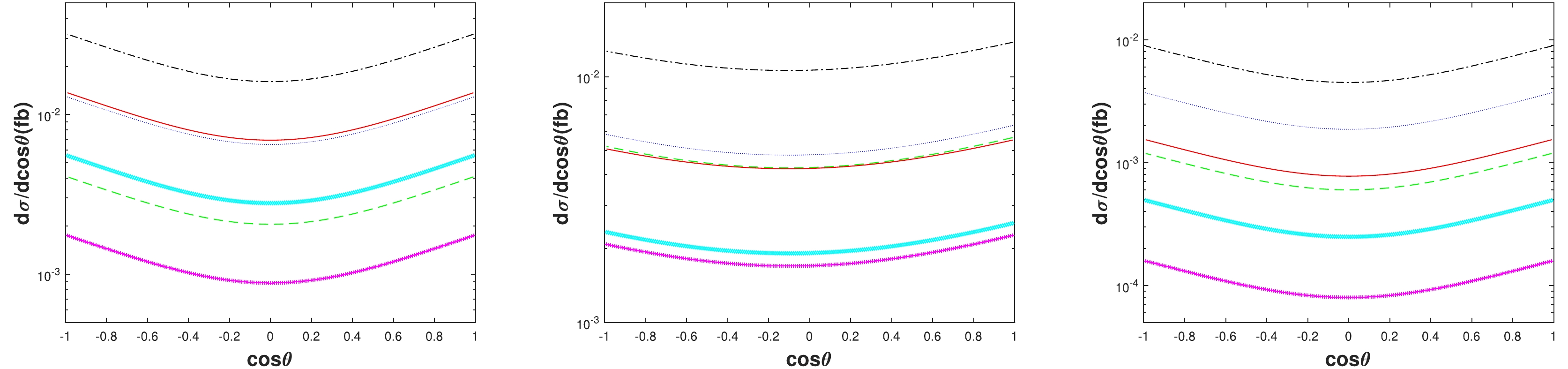
Figure 3. (color online) Differential angle distributions of cross sections dσ/dcosθ at
$ \sqrt{s}=91.1876 $ GeV for the channel$ e^-e^+\to Z^0 \to|(b\bar{b})[n]\rangle+|(b\bar{b})[n']\rangle $ . The dash-dotted black, dotted blue, dashed green, solid red, diamond cyan, and cross magenta lines are for the$ [1]+[1] $ ,$ [1]+[2] $ ,$ [1]+[3] $ ,$ [2]+[1] $ ,$ [2]+[2] $ ,$ [2]+[3] $ configurations of the$ |(b\bar{b})[n^1S_0]\rangle+|(b\bar{b})[n'^3S_1]\rangle $ channel (left) and$ |(b\bar{b})[n^3S_1]\rangle+|(b\bar{b})[n'^3P_2]\rangle $ channel (middle) but for the$ [1]+[1] $ ,$ [1]+[2] $ ,$ [1]+[3] $ ,$ [2]+[2] $ ,$ [2]+[3] $ ,$ [3]+[3] $ configurations of the$ |(b\bar{b})[n^3S_1]\rangle+|(b\bar{b})[n'^3S_1]\rangle $ channel (right), respectively.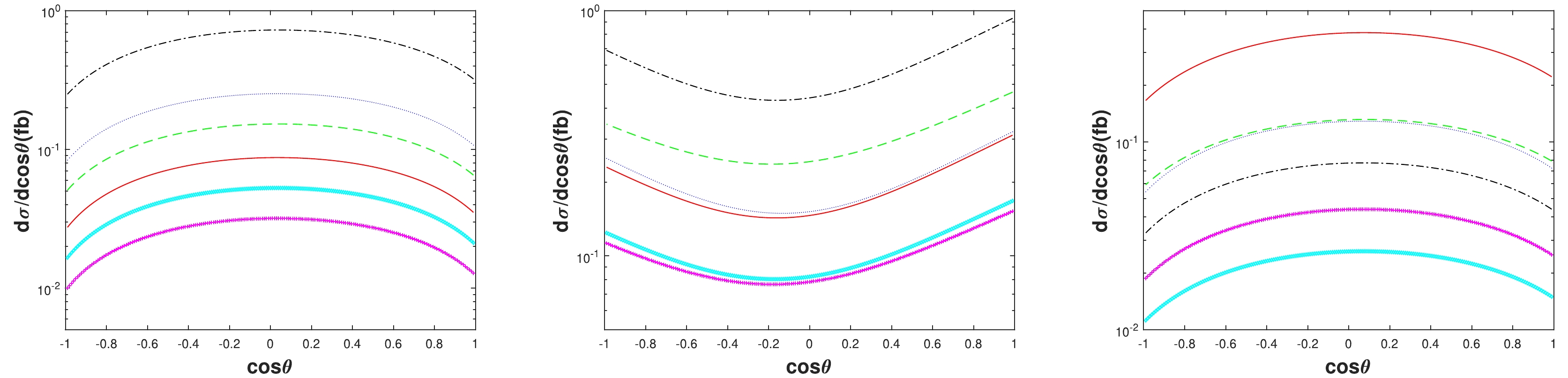
Figure 4. (color online) Differential angle distributions of cross sections dσ/dcosθ at
$ \sqrt{s}=91.1876 $ GeV for the channel$ e^-e^+\to Z^0 \to|(c\bar{b})[n]\rangle+|(b\bar{c})[n']\rangle $ . The dash-dotted black, dotted blue, dashed green, solid red, diamond cyan, and cross magenta lines are for the$ [1]+[1] $ ,$ [1]+[2] $ ,$ [1]+[3] $ ,$ [2]+[2] $ ,$ [2]+[3] $ ,$ [3]+[3] $ configurations of the$ |(c\bar{b})[n^3S_1]\rangle+|(b\bar{c})[n'^3S_1]\rangle $ channel (left) but for the$ [1]+[1] $ ,$ [1]+[2] $ ,$ [1]+[3] $ ,$ [2]+[1] $ ,$ [2]+[2] $ ,$ [2]+[3] $ configurations of the$ |(c\bar{b})[n^3S_1]\rangle+|(b\bar{c})[n'^3P_2]\rangle $ channel (middle) and$ |(c\bar{b})[n^1S_0]\rangle+|(b\bar{c})[n'^3S_1]\rangle $ channel (right), respectively. -
To obtain reliable results in LO calculation, we should consider the main uncertainty sources of the cross sections. For values of the input parameters, the fine-structure constant α, Weinberg angle
$ \theta_W $ , Fermi constant$ G_F $ , and mass and width of the$ Z^0 $ boson are relatively precise. The non-perturbative matrix elements are an overall factor when the quark mass is fixed. In the following, we probe the uncertainties caused by the masses of constituent heavy quarks, and the running coupling constant$ \alpha_s(\mu) $ , which is related to the renormalization scale μ.The uncertainties of total cross sections caused by the varying quark masses are presented in Tables 2−4 for the production of double higher excited charmonium, double higher excited bottomonium, and higher excited
$ B_c $ pairs, respectively. We adopt the mass deviations of 0.1 GeV for$ m_c $ (changing by about 7%) and 0.2 GeV for$ m_b $ (changing by about 4%). Here, the effects of uncertainties of the radial wave function at the origin$ R_{|(Q\bar{Q})[nS]\rangle}(0) $ and its first derivative at the origin$ R'_{|(Q\bar{Q})[nP]\rangle}(0) $ induced by the varying quark masses are also considered. The uncertainties from the radial wave function and its first derivative at the origin induced by varying quark masses were calculated in our previous paper using the BT-potential model [26], which we show explicitly in Table 1. The table shows that a 7% change in the charm quark mass can result in a correction of up to 20% in the total cross section.In Figs. 5−7, we present total cross sections σ as a function of the renormalization scale μ at
$ \sqrt{s}=91.1876 $ GeV for the production of the double higher excited charmonium, double higher excited bottomonium, and higher excited$ B_c $ pairs, respectively. We observe that all the cross sections decrease as the renormalization scale μ increases. The NLO corrections might improve the μ dependence.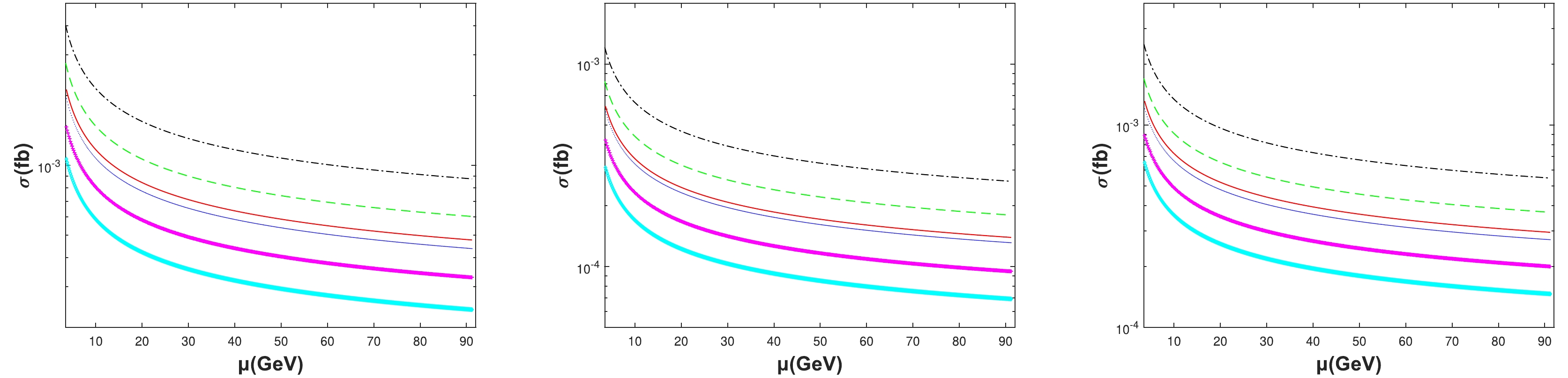
Figure 5. (color online) Total cross sections σ as a function of the renormalization scale μ at
$ \sqrt{s}=91.1876 $ GeV for the channel$ e^-e^+\to Z^0 \to|(c\bar{c})[n]\rangle+|(c\bar{c})[n']\rangle $ . The dash-dotted black, dotted blue, dashed green, solid red, diamond cyan, and cross magenta lines are for the$ [1]+[1] $ ,$ [1]+[2] $ ,$ [1]+[3] $ ,$ [2]+[1] $ ,$ [2]+[2] $ ,$ [2]+[3] $ configurations of the$ |(c\bar{c})[n^3S_1]\rangle+|(c\bar{c})[n'^1P_1]\rangle $ channel (left),$ |(c\bar{c})[n^1S_0]\rangle+|(c\bar{c})[n'^3P_2]\rangle $ channel (middle) and$ |(c\bar{c})[n^1S_0]\rangle+|(c\bar{c})[n'^3P_0]\rangle $ channel (right), respecttively.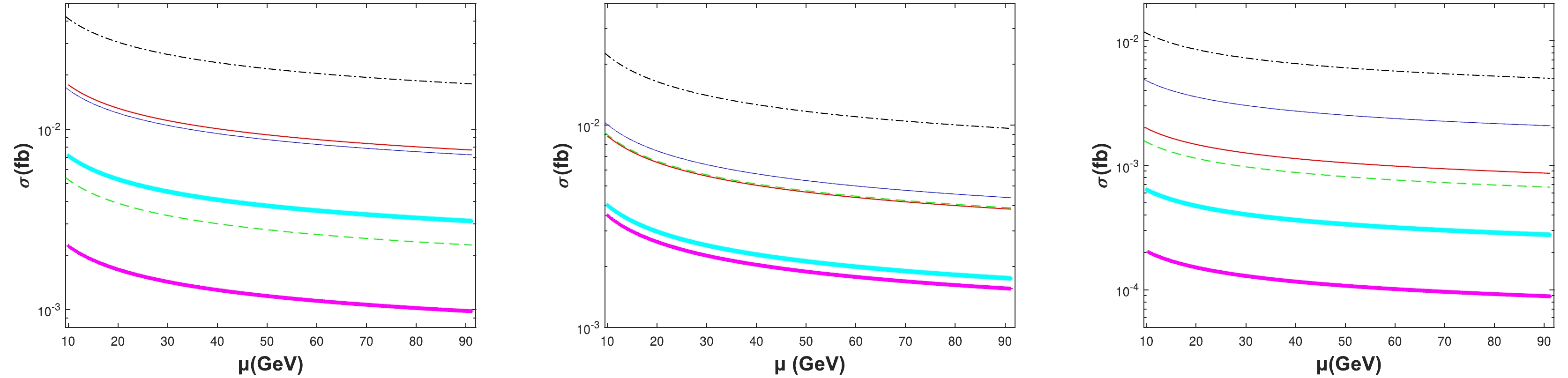
Figure 6. (color online) Total cross sections σ as a function of the renormalization scale μ at
$ \sqrt{s}=91.1876 $ GeV for the channel$ e^-e^+\to Z^0 \to|(b\bar{b})[n]\rangle+|(b\bar{b})[n']\rangle $ . The dash-dotted black, dotted blue, dashed green, solid red, diamond cyan, and cross magenta lines are for the$ [1]+[1] $ ,$ [1]+[2] $ ,$ [1]+[3] $ ,$ [2]+[1] $ ,$ [2]+[2] $ ,$ [2]+[3] $ configurations of the$ |(b\bar{b})[n^1S_0]\rangle+|(b\bar{b})[n'^3S_1]\rangle $ channel (left) and$ |(b\bar{b})[n^3S_1]\rangle+|(b\bar{b})[n'^3P_2]\rangle $ channel (middle), but for the$ [1]+[1] $ ,$ [1]+[2] $ ,$ [1]+[3] $ ,$ [2]+[2] $ ,$ [2]+[3] $ ,$ [3]+[3] $ configurations of the$|(b\bar{b})[n^3S_1]\rangle + |(b\bar{b})[n'^3S_1]\rangle$ channel (right), respectively.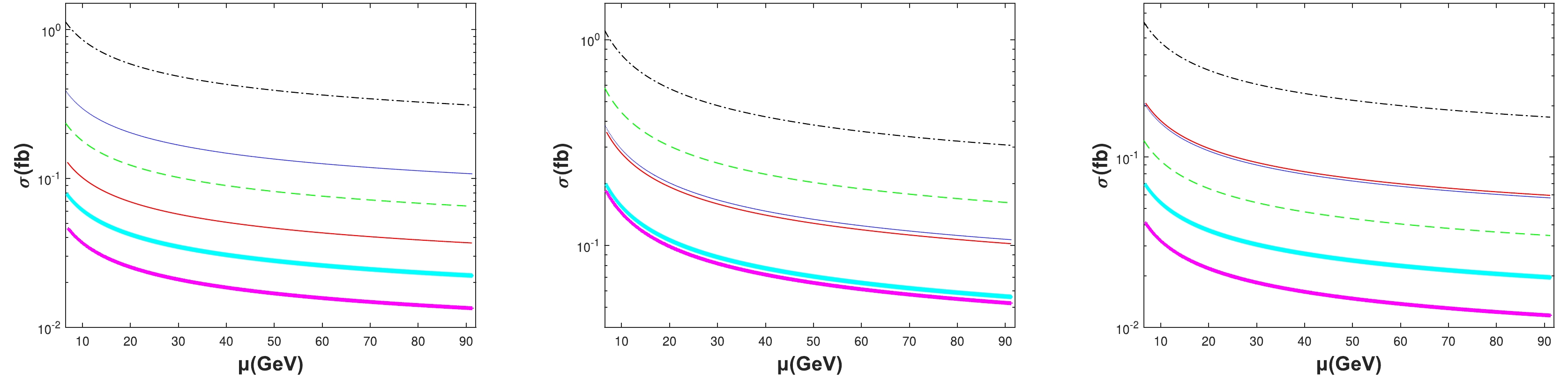
Figure 7. (color online) Total cross sections σ as a function of the renormalization scale μ at
$ \sqrt{s}=91.1876 $ GeV for the channel$ e^-e^+\to Z^0 \to|(c\bar{b})[n]\rangle+|(b\bar{c})[n']\rangle $ . The dash-dotted black, dotted blue, dashed green, solid red, diamond cyan, and cross magenta lines are for the$ [1]+[1] $ ,$ [1]+[2] $ ,$ [1]+[3] $ ,$ [2]+[2] $ ,$ [2]+[3] $ ,$ [3]+[3] $ configurations of the$ |(c\bar{b})[n^3S_1]\rangle+|(b\bar{c})[n'^3S_1]\rangle $ channel (left) but for the$ [1]+[1] $ ,$ [1]+[2] $ ,$ [1]+[3] $ ,$ [2]+[1] $ ,$ [2]+[2] $ ,$ [2]+[3] $ configurations of the$ |(c\bar{b})[n^3S_1]\rangle+|(b\bar{c})[n'^3P_2]\rangle $ channel (middle) and$|(c\bar{b})[n^1S_0]\rangle+ $ $ |(b\bar{c})[n'^3S_1]\rangle$ channel (right), respectively. -
In this paper, we systematically study the production of a pair of higher excited charmonia, a pair of higher excited bottomonia, and the higher excited
$ B_c $ pair in$e^+e^-\to Z^0\to |(Q\bar{Q^\prime})[n]\rangle+ |(Q^\prime\bar{Q})[n']\rangle\; (Q,Q^\prime=c,b\; \; \text{quarks})$ within the NRQCD factorization framework, where$ [n] $ or$ [n'] $ represents the color-singlet Fock states$[n^1S_0], [n^3S_1], \; [n^1P_1]$ , and$ [^3P_J] $ ($n=1,2,3;\;J=0,1,2$ ). The differential angle distributions of the cross sections${\rm d}\sigma/{\rm d}\cos\theta$ are studied for a sound estimation at the future super Z factory, which are shown in Figs. 2−4 for double higher excited charmonia, double higher excited bottomonia, and the higher excited$ B_c $ pair, respectively.In Tables 2−4, we show that the production rates of the higher excited
$ B_c $ pair are approximately two orders of magnitude larger than those of the double higher excited charmonia in the same$ [n]+[n^\prime] $ configuration and approximately one order of magnitude larger than those of the double higher excited bottomonia in the same$ [n]+[n^\prime] $ configuration. The uncertainties caused by the varying quark masses are also shown in Tables 2−4. We show that a 7% change in the charm quark mass can result in a correction of up to 20% in the total cross section. We also present the dependence of total cross sections on the renormalization scale μ in Figs. 5−7. The cross sections always decrease as μ increases.Our calculation shows that the sizable events of the double higher excited heavy quarkonium (principal quantum number
$n=2,\;3$ ) can be produced in the future super Z factory via the process$e^+e^-\to Z^0 \to |(Q\bar{Q^\prime})[n]\rangle+ |(Q^\prime\bar{Q})[n']\rangle\; (Q,Q^\prime=c,\;b\; \text{quarks})$ . The future super Z factory should be a suitable platform to study the exclusive production of the higher excited heavy quarkonium pair. Moreover, because most of these higher excited states would decay into the ground states, we carefully consider these higher excited states for a sound estimation when studying the production of ground states.
Production of higher excited quarkonium pair at the super Z factory
- Received Date: 2023-12-21
- Available Online: 2024-07-15
Abstract: The heavy constituent quark pair of the heavy quarkonium is produced perturbatively and subsequently undergoes hadronization into the bound state non-perturbatively. The production of the heavy quarkonium is essential to testing our understanding of quantum chromodynamics (QCD) in both perturbative and non-perturbative aspects. The electron-positron collider will provide a suitable platform for the precise study of the heavy quarkonium. The higher excited heavy quarkonium may contribute significantly to the ground states, which should be considered for sound estimation. We study the production rates of the higher excited states quarkonium pair in





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: