-
As the first direct detection of a gravitational-wave (GW) and the first observation of a binary black hole merger, GW event GW150914 [1] opened a new window to probe the nature of gravity in the highly dynamical and strong-field regime. Subsequently, other GWs from mergers, such as GW151226 [2], GW170104 [3], and GW170608 [4], have been successfully detected by the same team. These GW events can be used to support Einstein's general relativity (GR) [5−8] and show that the evolution of black hole binary systems is characterized by three stages: the inspiral, merger, and ringdown stages [9, 10]. Generally, we apply numerical-relativity simulations to investigate the evolution of the coalescence of a binary black hole system because these methods can solve the Einstein equation without any approximation up to numerical errors [11]. However, these numerical simulations are costly and take considerable time [12]. Fortunately, there are several powerful approaches to analytically investigate black hole mergers. The first is the light ring/quasinormal mode (QNM) correspondence, which shows that the QNM frequency of the final black hole is associated with the light ring of the spacetime in the eikonal limit [13]. Thus, by studying the light ring from the null geodesics, the ringdown modes of the black hole merger can be obtained, although there is a small deviation from the numerical result [14, 15]. Another approach is the Buonanno-Kidder-Lehner (BKL) recipe [16], which depends on the angular momentum and mass conservations and has successfully been used to estimate the final spins after the merger [17, 18]. In Ref. [19], Wei and Liu used these two approaches to analyze the ringdown modes and final spins of the Kerr-MOG black hole merger in modified gravity and found that the black hole mergers are closely dependent on the scalar field parameter of the gravity. Recently, Siahaan provided some generalities, including the circular geodesics and generalized BKL method, for a black hole merger in the Kerr-Sen case, and obtained the approximate final spins and QNMs of the black hole resulting from the merger process [20].
In this study, we extend the investigation to the so-called degenerate higher-order scalar-tensor (DHOST) theories, which contain the higher order derivative of the scalar field and meet a certain set of degeneracy conditions [21−24]. Recently, the authors of Refs. [25, 26] used the disformal solution-generating method to obtain a disformal rotating black hole solution in quadratic DHOST theories. This disformal Kerr solution was asymptotically flat but no longer Ricci flat, and its disformal parameter could describe the deviation from Kerr geometry [25, 26]. In [27], Long et al. studied the shadow of this disformal Kerr black hole in quadratic DHOST theories and observed that the black hole shadow depended heavily on the deformation parameter. Using the relativistic precession model, Chen et al. investigated the quasi-periodic oscillation frequencies in a disformal Kerr black hole and applied a constraint on the disformal parameter with the observation data of GRO J1655-40 [28]. In [29], Anson et al. analyzed the post-Newtonian orbits of stars around a deformed Kerr black hole and compared the effects to those predicted by the Kerr metric. Furthermore, Takamori et al. tested the non-circularity of the spacetime around Sagittarius A
$ ^{*} $ (Sgr A$ ^{*} $ ) with orbiting pulsars and argued that the Square Kilometer Array (SKA) can distinguish a disformal Kerr black hole from a Kerr black hole through the non-circularity of the spacetime around Sgr A$ ^{*} $ [30]. More recently, Zhou et al. studied the effect of noncircularity on the dynamic behaviors of particles in a disformal rotating black-hole spacetime and noted that the dynamic behavior of timelike particles in the disformal Kerr black-hole spacetime with noncircularity becomes richer than that in the usual Kerr black-hole case [31]. To go a step further, in this study, we consider the disformal Kerr black hole merger, give a more complete picture of the effects of the disformal parameter on the ringdown modes and final black hole spin, and compare the results with those given for the Kerr-MOG black hole merger [19], because the Kerr-MOG solution can also describe the modification from the Kerr solution [32, 33].This paper is organized as follows. In Sec. II, we briefly review the disformal Kerr black hole in quadratic DHOST theories. In Sec. III, we give the geodesics of a test particle in this disformal Kerr background. In Sec. IV, we use the light ring/QNM correspondence to calculate the QNMs in the ringdown stage. In Sec. V, we use the BKL recipe to estimate the final black hole spins. We conclude in the final section with our main results.
-
We begin with the most general action of the quadratic DHOST theories [21]:
$ \begin{aligned}[b] S=\;&\int {\rm d}^4x\sqrt{-g}\bigg[P( X,\varphi)+Q(X,\varphi)\Box\varphi\\&+F(X,\varphi)R+\sum_{i=1}^5A_i(X,\varphi)L_i\bigg], \end{aligned} $

(1) where we define
$ \begin{aligned}[b]& L_1\equiv\varphi_{\mu\nu}\varphi^{\mu\nu},\;\; \; L_2\equiv(\Box\varphi)^2,\; \; \; L_3\equiv\varphi^\mu\varphi_{\mu\nu}\varphi^{\nu}\Box\varphi,\; \;\\& L_4\equiv\varphi^\mu\varphi_{\mu\nu}\varphi^{\nu\rho}\varphi_\rho,\; \;\; L_5\equiv(\varphi^\mu\varphi_{\mu\nu}\varphi^\nu)^2, \end{aligned} $

(2) with the usual Ricci scalar R, scalar field φ, covariant derivative of the scalar field
$ \varphi_\mu=\nabla_\mu\varphi $ , second covariant derivatives of the scalar field$ \varphi_{\mu\nu}=\nabla_{\nu}\nabla_{\mu}\varphi $ , and kinetic term$ X=\varphi_\mu\varphi^\mu $ . For the quadratic DHOST theories, the functions F and$ A_i $ must meet the degeneracy conditions given in [22, 34], whereas P and Q are completely free, ensuring that there is only an extra scalar degree of freedom besides the usual tensor modes of gravity. By performing a disformal transformation of the metric, a new solution from a known "seed" solution can be obtained in DHOST Ia theory. In general, by introducing the disformal transformation of the metric [22]$ \begin{array}{*{20}{l}} g_{\mu\nu}=A(X,\varphi)\tilde{g}_{\mu\nu}-B(X,\varphi)\varphi_\mu\varphi_\nu, \end{array} $

(3) we can relate the "disformed" metric
$ g_{\mu\nu} $ to the original "seed" metric$ \tilde{g}_{\mu\nu} $ . To obtain a new solution, the conformal and disformal factors$ A(X, \varphi) $ and$ B(X, \varphi) $ , respectively, should satisfy the condition that the two metrics$ g_{\mu\nu} $ and$ \tilde{g}_{\mu\nu} $ are not degenerate. Considering the factor$ A(X,\varphi)=1 $ , which can avoid a global physically irrelevant constant conformal factor in the metric, and$ B(X,\varphi)=B_{0} $ ($ B_{0} $ is a constant), from the Kerr metric in GR, we can express the disformal Kerr metric as [25, 26]$ \begin{aligned}[b] {\rm d}s^2=\;&-\frac{\Delta}{\rho}\bigg({\rm d}t-a\sin^2\theta {\rm d}\phi\bigg)^2+\dfrac{\rho}{\Delta} {\rm d} r^2+ \rho {\rm d}\theta^2\\&+ \frac{\sin^2\theta}{\rho}\bigg[a{\rm d}t-(r^2+a^2){\rm d}\phi\bigg]^2\\&+\alpha\bigg[{\rm d}t+\frac{\sqrt{2Mr(r^2+a^2)}}{\Delta} {\rm d}r\bigg]^2, \end{aligned} $

(4) and the scalar field is only a function of the coordinates t and r [25, 26],
$ \phi(t, r)=-m t-\int \frac{\sqrt{\mathcal{R}}}{\Delta} {\rm d} r, $

(5) with
$ \begin{array}{*{20}{l}} \rho=r^2+a^2\cos\theta^2,\; \; \Delta=r^2+a^2-2Mr,\; \; \mathcal{R}=2 M m^{2} r\left(r^{2}+a^{2}\right), \end{array} $

(6) where the parameter α=
$ -B_0 m^2 $ , which is related to the rest mass m of the scalar field. Obviously, this disformal Kerr black hole with an extra disformal parameter belongs to non-stealth rotating solutions in the quadratic DHOST theories [25, 26].Because the disformal Kerr metric (4) is not Ricci flat, i.e.,
$ R_{\mu\nu}\neq0 $ , its asymptotical behavior is not entirely the same as that of the Kerr metric. In addition, for the disformal Kerr spacetime, the presence of the${\rm d}r{\rm d}t$ term results in a lack of circularity, which changes the structure of the black hole horizons such that the horizons depend on the polar angle θ and cannot be given by$ r=const $ in Boyer-Lindquist coordinates; hence, the corresponding surface gravity is no longer a constant [25, 26]. Because none of the coefficients of metric (4) depend on t and φ, the disformal geometry admits the two Killing vectors$ \xi_t=\partial_t $ and$ \xi_\varphi=\partial_\varphi $ , similar to the usual Kerr black hole case. Thus, we can observe at the positions of the ergospheres$ \begin{array}{*{20}{l}} \xi_{t} \cdot \xi_{t}=g_{t t}=0, \end{array} $

(7) i.e.,
$ \begin{array}{*{20}{l}} r^{2}-2 M_{1} r+a^{2} \cos ^{2} \theta=0, \end{array} $

(8) with
$ M_1=M/(1-\alpha) $ . Consequently, similar to the Kerr metric, the disformal Kerr metric has outer and inner ergospheres denoted by$ \varepsilon _+ $ and$ \varepsilon_- $ , respectively, and their positions are$ \begin{array}{*{20}{l}} r_{\mathcal{E}_{ \pm}}(\theta)=M_{1} \pm \sqrt{M_{1}^{2}-a^{2} \cos ^{2} \theta}, \end{array} $

(9) which are closely related to θ. To satisfy the inequality
$ {M_1}^2-a^2\cos^2\theta\geq0 $ for all cases, we should have$ \frac{a_{\max }}{M}=\frac{1}{1-\alpha}. $

(10) -
For the disformal Kerr black hole in quadratic DHOST theories, the corresponding Lagrangian of a test particle is given by
$ \mathcal{L}=\frac{\mu_{0}}{2} g_{\mu \nu} \dot{x}^{\mu} \dot{x}^{\nu}, $

(11) where
$ \mu_{0} $ is the mass of the massive particle. Note that the value$ \mu_{0}=0 $ corresponds to the photon. The conserved quantities in this axially symmetric and stationary spacetime are$ \frac{\partial \mathcal{L}}{{\rm d}\dot{t}}=g_{t t} \dot{t}+g_{tr} \dot{r}+g_{t \phi} \dot{\phi} \equiv-E, $

(12) $ \frac{\partial \mathcal{L}}{{\rm d}\dot{\phi}}=g_{t \phi} \dot{t}+g_{\phi \phi} \dot{\phi} \equiv L, $

(13) which give us
$ \dot{t}=\frac{g_{\phi \phi} E+g_{t \phi} L+g_{t r} g_{\phi \phi} \dot{r}}{g_{t \phi}^{2}-g_{t t} g_{\phi \phi}}, $

(14) $ \dot{\phi}=\frac{g_{t \phi} E+g_{t t} L+g_{t r} g_{t \phi} \dot{r}}{g_{t t} g_{\phi \phi}-g_{t \phi}^{2}}. $

(15) Thus, we can express the geodesics in general as
$ \begin{array}{*{20}{l}} g_{t t} \dot{t}^{2}+2 g_{tr} \dot{t} \dot{r}+g_{r r} \dot{r}^{2}+g_{\theta\theta} \dot{\theta}^{2}+2 g_{t \phi} \dot{t} \dot{\phi}+g_{\phi \phi} \dot{\phi}^{2}=-\delta \text {, } \end{array} $

(16) where
$ \delta=\mu_0^2 $ corresponds to a timelike particle, and$ \delta=0 $ represents a null object. The timelike effective potential$ V_{\mathrm{eff}}\left(r, \theta; E, L\right)=\left(g_{r r}+\frac{g_{t r}^{2} g_{\phi \phi}}{g_{t \phi}^{2}-g_{t t} g_{\phi \phi}}\right)\dot{r}^{2}+g_{\theta \theta} \dot{\theta}^{2}, $

(17) on the equatorial plane can be rewritten as
$ V_{\mathrm{eff}}\left(r, \theta ; E, L\right)=\frac{g_{\phi \phi}E^{2}+2 g_{t \phi} E L+g_{t t} L^{2}}{g_{t \phi}^{2}-g_{t t} g_{\phi \phi}}-\mu_0^2. $

(18) Here,
$ \mu_0=0 $ represents the effective potential of a null object. -
As the final stage of a black hole merger, the ringdown stage is characterized by the QNMs, which are associated with the light ring of spacetime in the eikonal limit [13]. According to the light ring/QNM correspondence for an asymptotically flat spacetime, we can express the QNM frequency using the angular velocity
$ \varOmega_c $ and Lyapunov exponent of the light ring λ as [13, 35, 36]$ \omega_{\mathrm{QNM}}=m \Omega_{c}-{\rm i}\bigg(n+\frac{1}{2}\bigg)|\lambda|, $

(19) with
$ \Omega_{c}=\left.\frac{\dot{\phi}}{\dot{t}}\right|_{r_{c}}, \quad \lambda=\left.\sqrt{-\frac{V_{\mathrm{eff}}^{\prime \prime}}{2\dot{t}^{2}}}\right|_{r_{c}}, $

(20) where the prime denotes the derivative with respect to r, and m, n, and
$ r_c $ are the angular momentum of the perturbation, the overtone number, and the radius of the light ring, respectively. Note that the characteristic parameters of the light rings,$ \mu_0=0 $ in Eq. (18), can be obtained using the conditions$ \begin{array}{*{20}{l}} V_{\mathrm{eff}}=0, \quad V^{\prime}_{\mathrm{eff}}=0, \quad V^{\prime \prime}_{\mathrm{eff}}<0, \end{array} $

(21) which lead to the radius
$ r_c $ and minimum impact parameter$ u_c $ of the light rings. In the case of$ a=0 $ , i.e., a nonrotating black hole, we obtain$ \dfrac{r_{c}}{M}=\frac{3}{1-\alpha},\quad u_{\mathrm{c}}=\frac{L}{EM}=\frac{3 \sqrt{3}}{\sqrt{1-3 \alpha+3 \alpha^{2}-\alpha^{3}}}, $

(22) which reduce to the case of the Schwarzschild black hole with
$ \alpha=0 $ $ \dfrac{r_{c}}{M}=3,\quad u_{\mathrm{c}}=\frac{L}{EM}=3 \sqrt{3}. $

(23) In the case of
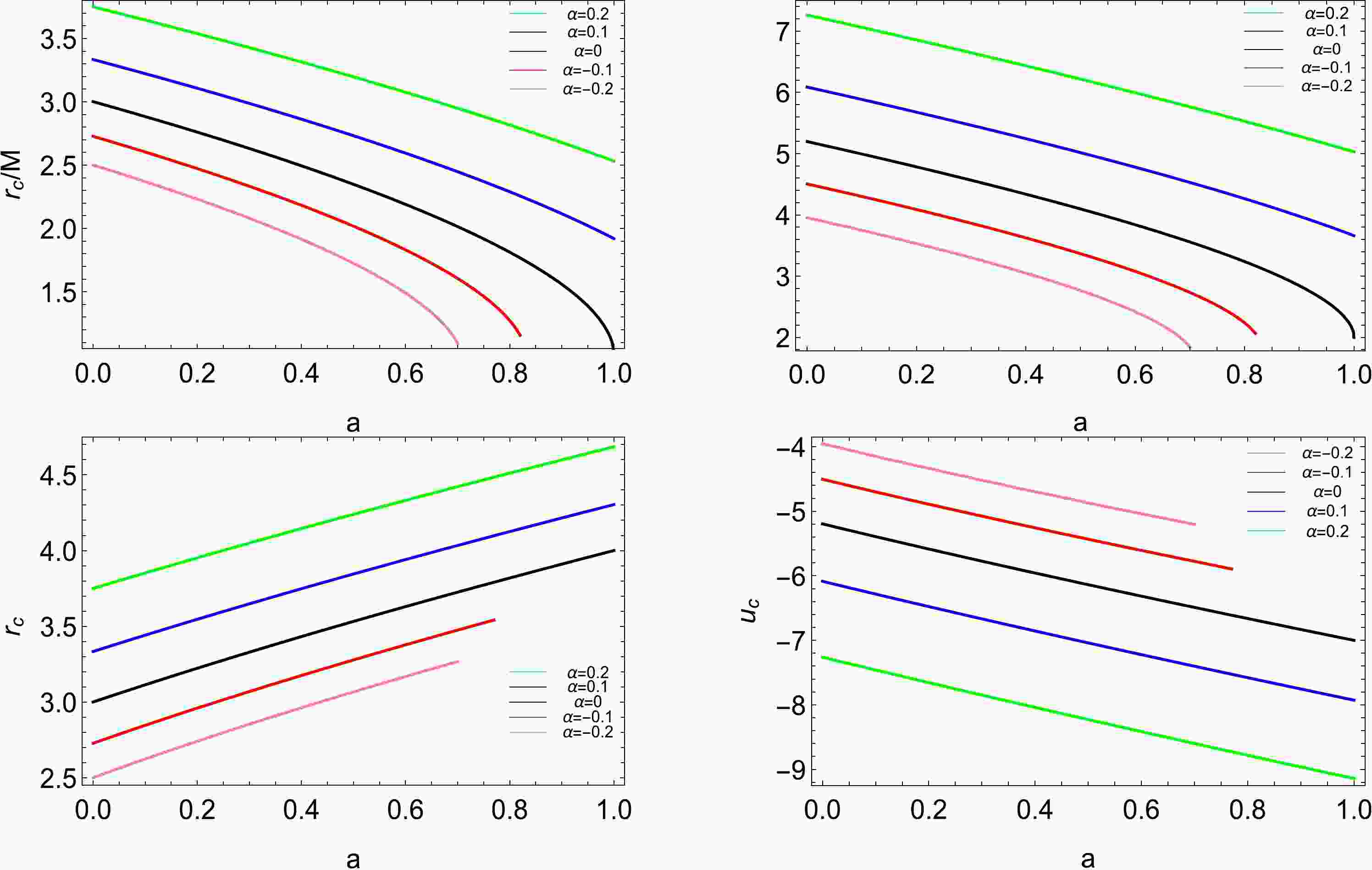
$ a\neq0 $ , i.e., a rotating black hole, the light rings will be different for prograde and retrograde cases because of the dragging effect. Because it is impossible to provide the analytical formula, we numerically solve the conditions (21) and present the results in Fig. 1 for the prograde and retrograde orbits. As shown in this figure, both the radius$ r_c $ and minimum impact parameter$ u_c $ decrease with increasing spin a but increase with the parameter α for the prograde orbit in the top two panels, and$ r_c $ increases with a or α but$ u_c $ decreases with a or α for the retrograde orbit in the bottom two panels. This behavior of the disformal parameter α is reminiscent of that observed in Ref. [19], where$ r_c $ and$ u_c $ decrease with an increase in the MOG parameter for the prograde orbit, whereas$ r_c $ decreases and$ u_c $ increases with the MOG parameter for the retrograde orbit. Therefore, we conclude that the disformal parameter in the disformal Kerr metric and the MOG parameter in the Kerr-MOG case have completely different effects on the radius$ r_c $ and minimum impact parameter$ u_c $ of the light rings.
Figure 1. (color online) Radius
$ r_c $ and minimum impact parameter$ u_c $ versus the spin a for the prograde (top) and retrograde (bottom) light rings with different disformal parameters α. In the first three panels, the five lines from top to bottom correspond to decreasing disformal parameters, i.e.,$ \alpha=0.2 $ (green),$ 0.1 $ (blue),$ 0 $ (black),$ -0.1 $ (red), and$ -0.2 $ (pink), which are opposite to those in the final panel.To obtain the QNM frequency, we should calculate the angular velocity and Lyapunov exponent of the unstable null geodesics. For the nonrotating black hole with
$ a=0 $ , we have$ \Omega_c M=\frac{\sqrt{(1-\alpha)^{3}}}{3 \sqrt{3}}, \quad \lambda M=\frac{\sqrt{2(\alpha-1)^{3}(2\alpha+1)^{2}}}{3\sqrt{3\alpha^{2}-24\alpha-6}}. $

(24) For the rotating black hole with
$ a\neq0 $ , we show the results in Fig. 2. For both the prograde orbit in the top two panels and the retrograde orbit in the bottom two panels, there is a noticeable increase in the angular velocity$ \Omega_c $ as the spin parameter a increases. However,$ \Omega_c $ decreases with α for the prograde orbit, whereas it increases with α for the retrograde orbit. On the other hand, the combination of the disformal parameter α and spin parameter a has a more subtle effect on the Lyapunov exponent λ. For the prograde orbit, λ decreases with increasing a in the case of$ \alpha=0 $ , which is different from the case of$ \alpha\neq0 $ . For example, λ increases with increasing a in the case of$ \alpha=-0.1 $ , and λ decreases with increasing α, except in the Kerr case for a large spin parameter a. However, for the retrograde orbit, λ decreases with increasing a or α. Comparing the results with those given in [19] for the Kerr-MOG background, where$ \Omega_c $ increases with the MOG parameter for the prograde orbit but decreases for the retrograde orbit, and λ increases with the MOG parameter for the retrograde orbit but increases and decreases with it for small a and large a, respectively, for the prograde orbit, we find that the disformal parameter in the disformal Kerr black hole and the MOG parameter in the Kerr-MOG case have obviously different effects on the QNM frequency.
Figure 2. (color online) Angular velocity
$ \Omega_c $ and Lyapunov exponent λ with respect to the spin a for prograde (top) and retrograde (bottom) light rings with different disformal parameters α. In each panel, the five lines correspond to different disformal parameters, i.e.,$ \alpha=-0.2 $ (pink),$ -0.1 $ (red),$ 0 $ (black),$ 0.1 $ (blue), and$ 0.2 $ (green).Although our calculations rely on the geodesics, i.e., the point particle approximation, this method still holds even for equal mass black hole collisions [37−39]. Thus, the combination of the disformal and spin parameters provides richer physics in the ringdown stage of the black hole merger.
-
To estimate the final spin of the black hole, we employ an approximate method based on the BKL recipe [16]. Following the BKL recipe, we use the first ansatz: the mass of the system is conserved to the first order, which results in the total mass of the final black hole
$ M=M_1+M_2 $ because the total radiated energy remains very small [1−3]. Next, the individual spins of the black holes remain constant; hence, the initial spins determine the contribution to the final total angular momentum due to the individual black-hole spins. Moreover, the contribution of the orbital angular momentum to the final angular momentum is estimated by adopting the orbital angular momentum of a test-particle orbiting in the innermost stable circular orbit (ISCO) of the final black hole. Thus, we can obtain the dimensionless final spin$ a_f $ of the black hole as [16]$ a_{f}=\frac{\tilde{L}\left(r_{\mathrm{ISCO}}, a_{f}\right)}{M}+\frac{M_{1} a_{1}}{M}+\frac{M_{2} a_{2}}{M}, $

(25) where
$ \tilde{L}\left(r_{\mathrm{ISCO}}, a_{f}\right) $ is the orbital angular momentum of a test particle (of the reduced mass$ \mu_{0}=M_1M_2/M $ ) in the ISCO of the final black hole. By assuming$ M_1\geq M_2 $ without loss of generality, we can express the final spin as [16]$ \begin{aligned}[b] a_{f}=\;&{L}\left(r_{\mathrm{ISCO}}, a_{f}\right) \nu+\frac{\chi_{1} M}{4}\bigg(1+\sqrt{1-4 \nu}\bigg)^{2}\\&+\frac{\chi_{2} M}{4}\bigg(1-\sqrt{1-4 \nu}\bigg)^{2}, \end{aligned} $

(26) where
$ \chi_{i}=a_{i} / M_{i} $ are the dimensionless spins of the initial black holes with the range$ -1\leq\chi_{i}\leq1 $ , and$ \nu=\mu_{0}/M $ is the mass parameter with the range$ 0\leq\nu\leq1/4 $ . Here,$ {L}\left(r_{\mathrm{ISCO}}, a_{f}\right) $ denotes the angular momentum of a unit mass test particle.We can determine the ISCO from the geodesics, i.e., the conditions to solve the ISCO are given by
$ \begin{array}{*{20}{l}} V_{\mathrm{eff}}=0, \quad V^{\prime}_{\mathrm{eff}}=0, \quad V^{\prime \prime}_{\mathrm{eff}}=0, \end{array} $

(27) where the effective potential
$ V_{\mathrm{eff}} $ is introduced in (18). For the nonrotating black hole, we can analytically obtain the ISCO, angular momentum, and energy:$ \frac{r_{\mathrm{ISCO}}}{M}=\frac{6}{1-\alpha}, \quad \frac{L}{\mu_0 M}=\pm\frac{2 \sqrt{3}}{\sqrt{1-2 \alpha+\alpha^{2}}}, \quad \frac{E}{\mu_{0}}=\frac{2 \sqrt{2(1-\alpha)}}{3}. $

(28) When
$ \alpha=0 $ , the above results reduce to the case of the Schwarzschild black hole$ \frac{r_{\mathrm{ISCO}}}{M}=6, \quad \frac{L} {\mu_0M}=2\sqrt{3}, \quad\frac{E}{\mu_0}=\frac{2\sqrt{2}}{3}. $

(29) For the rotating black hole, we can recover the case of the Kerr black hole in the limit
$ \alpha=0 $ in Eq. (27), just as in Ref. [40]. However, in the case of$ a\neq 0 $ and$ \alpha\neq 0 $ , we must rely on the numerical method to solve Eq. (27) and plot the radius$ r_{\mathrm{ISCO}} $ and angular momentum L as functions of the black hole spin a with various disformal parameters α for the prograde orbit (top two panels) and retrograde orbit (bottom two panels), as shown in Fig. 3. For the prograde orbit, we clearly find that both the radius$ r_{\mathrm{ISCO}} $ and angular momentum L decrease with increasing a but increase with increasing α. Interestingly, for the retrograde orbit, the radius$ r_{\mathrm{ISCO}} $ increases with a or α but the angular momentum L decreases with a or α.
Figure 3. (color online) Radius
$ r_{\mathrm{ISCO}} $ and angular momentum L with respect to the spin a for the prograde (top) and retrograde (bottom) light rings with different disformal parameters α. In the first three panels, the five lines from top to bottom correspond to decreasing disformal parameters, i.e.,$ \alpha=0.2 $ (green),$ 0.1 $ (blue),$ 0 $ (black),$ -0.1 $ (red), and$ -0.2 $ (pink), which are opposite to those in the final panel.Now, we can estimate the final spin of the merger. First, we study the equal spin case, i.e., the two black holes have equal spin,
$ \chi_{1}=\chi_{2}=\chi $ , which leads to the final spin$ \begin{array}{*{20}{l}} a_{f}={L}\left(r_{\mathrm{ISCO}}, a_{f}\right) \nu+M(1-2 \nu)\chi. \end{array} $

(30) Solving the above equation numerically, we show the final spin
$ a_f $ as a function of the mass parameter ν for the fixed spin parameter$ \chi=0 $ ,$ 0.4 $ ,$ 0.7 $ , and$ 0.9 $ in Fig. 4. For the case of$ \chi=0 $ , which describes a merger of two nonrotating black holes, the final spin$ a_f $ increases as the mass parameter ν or disformal parameter α increases. Obviously, if the values of the initial spin χ are small, the results are similar. If two black holes have a large initial spin, for example,$ \chi=0.7 $ with$ \alpha=-0.2 $ and$ \chi=0.9 $ with$ \alpha=-0.2 $ and$ -0.1 $ , it is interesting to note that the final spin$ a_f $ decreases as the mass parameter ν increases. Comparing the results with the findings shown in Refs. [16−20], we note that although the underlying mechanism remains unknown, the smaller disformal parameter α or the larger initial spin χ makes the emergence of this novel phenomenon easier.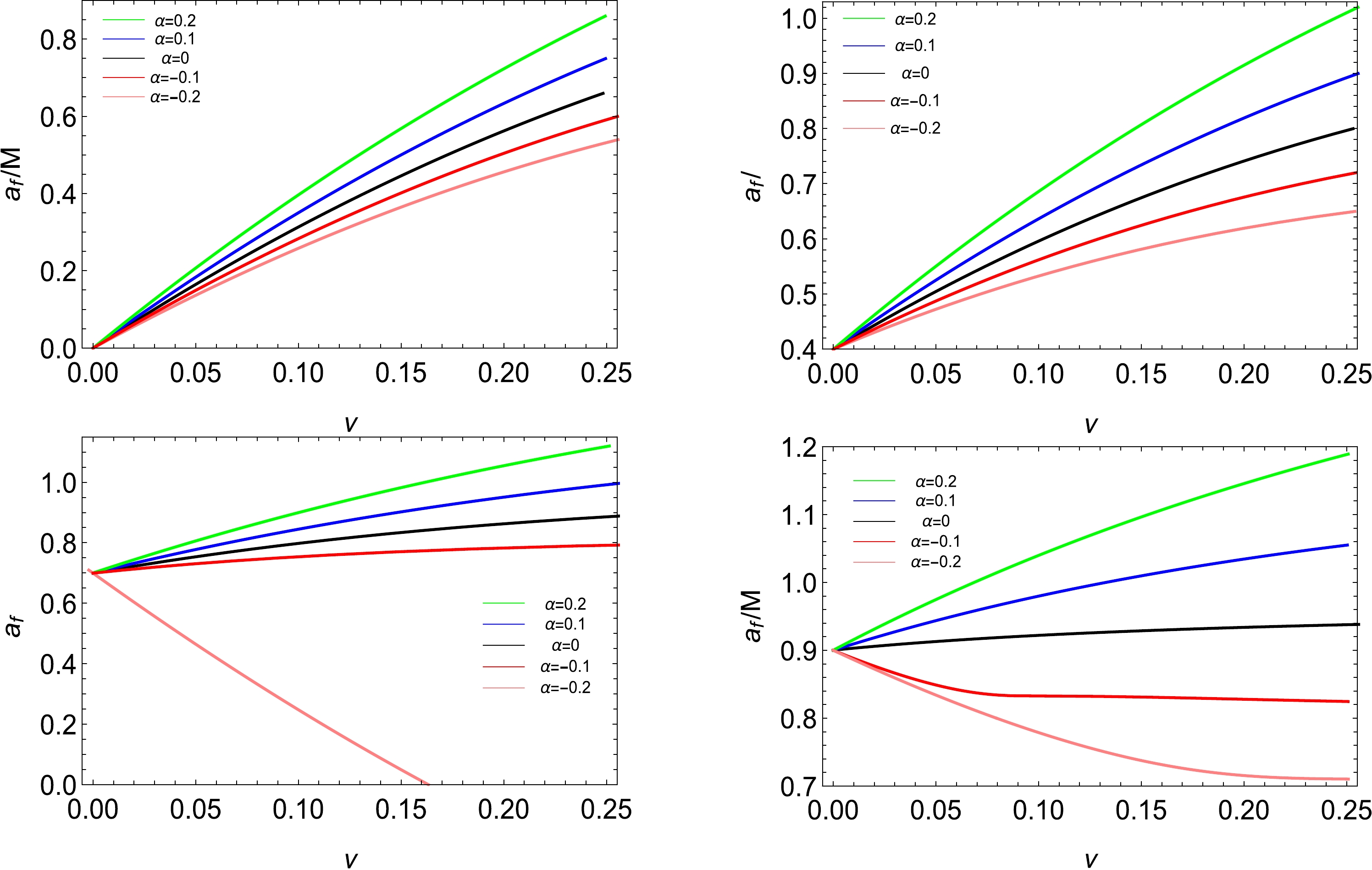
Figure 4. (color online) Final spin
$ a_f $ with respect to the mass parameter ν with different disformal parameters α for the fixed spin parameter$ \chi=0 $ (top-left),$ 0.4 $ (top-right),$ 0.7 $ (bottom-left), and$ 0.9 $ (bottom-right). In each panel, the five lines from top to bottom correspond to decreasing disformal parameters, i.e.,$ \alpha=0.2 $ (green),$ 0.1 $ (blue),$ 0 $ (black),$ -0.1 $ (red), and$ -0.2 $ (pink).Next, we consider an unequal spin merger, in particular, an unequal spin case but with equal mass. Without loss of generality, we set
$ \chi_2=\beta\chi,\; \chi_1=\chi $ with the unequal spin parameter$ \beta\in[-1, 1] $ and fix$ \nu=0.25 $ , which results in the final spin$ a_{f}=\frac{1}{4}\left[{L}{(r_{\mathrm{ISCO}}, a_{f})}+(1+\beta)M\chi\right]. $

(31) Fixing one of the black hole spins at
$ 0.5 $ and considering that it is aligned or antialigned with respect to the initial orbital angular momentum, in Fig. 5 , we present the final spin as a function of the unequal spin parameter β with different disformal parameters α for equal mass black holes. We observe that regardless of the disformal parameter, the final spin increases or decreases with increasing β in the aligned or antialigned case, which agrees well with the results in Ref. [19]. However, for both cases, the final spin increases with increasing α for a fixed parameter β.
Figure 5. (color online) Final spin
$ a_f $ with respect to the unequal spin parameter β with different disformal parameters α for the fixed spin parameter$ \chi=0.5 $ (left) and$ -0.5 $ (right). In each panel, the five lines from top to bottom correspond to decreasing disformal parameters, i.e.,$ \alpha=0.2 $ (green),$ 0.1 $ (blue),$ 0 $ (black),$ -0.1 $ (red), and$ -0.2 $ (pink).Finally, we investigate a generic spin configuration merger, where the orbit plane of the ISCO is inclined with respect to the final total angular momentum. To calculate the orbital contribution to the total angular momentum, we use the fit formula shown in [41]; therefore, the orbital angular momentum of the inclined orbit is in the form [16, 41]
$ \begin{aligned}[b] L\left(\vartheta, a_{f}\right) =\;& \frac{1}{2}\bigg(1+\cos \vartheta\bigg) L^{\mathrm{pro}}\left(r_{\mathrm{ISCO}}^{\mathrm{pro}}, a_{f}\right) \\& +\frac{1}{2}\bigg(1-\cos \vartheta\bigg)\left|L^{\mathrm{ret}}\left(r_{\mathrm{ISCO}}^{\mathrm{ret}}, a_{f}\right)\right|, \end{aligned} $

(32) with the inclination angle ϑ between the final spin
$ a_f $ and the orbital angular momentum. For simplicity, we consider the case in which two merged black holes have the same masses and spins. Therefore, we can express the final spin$ a_f $ as$ a_{f}=\frac{1}{8}\bigg[L^{\mathrm{pro}}+\left|L^{\mathrm{ret}}\right|+4 M \chi+\left(L^{\mathrm{pro}}-\left|L^{\mathrm{ret}}\right|\right) \cos \vartheta\bigg]. $

(33) In Fig. 6, we plot the final spin
$ a_f $ as a function of the spin parameter χ with different inclination angles ϑ for the fixed disformal parameter$ \alpha=-0.2 $ ,$ 0 $ , and$ 0.2 $ . We clearly observe that for a fixed disformal parameter α, the final spin$ a_f $ increases as ϑ or χ increases, which is in good agreement with the numerical results in [19]. For the fixed inclination angle ϑ and spin parameter χ, note that the final spin$ a_f $ increases as α increases, which is consistent with the findings in Figs. 4 and 5.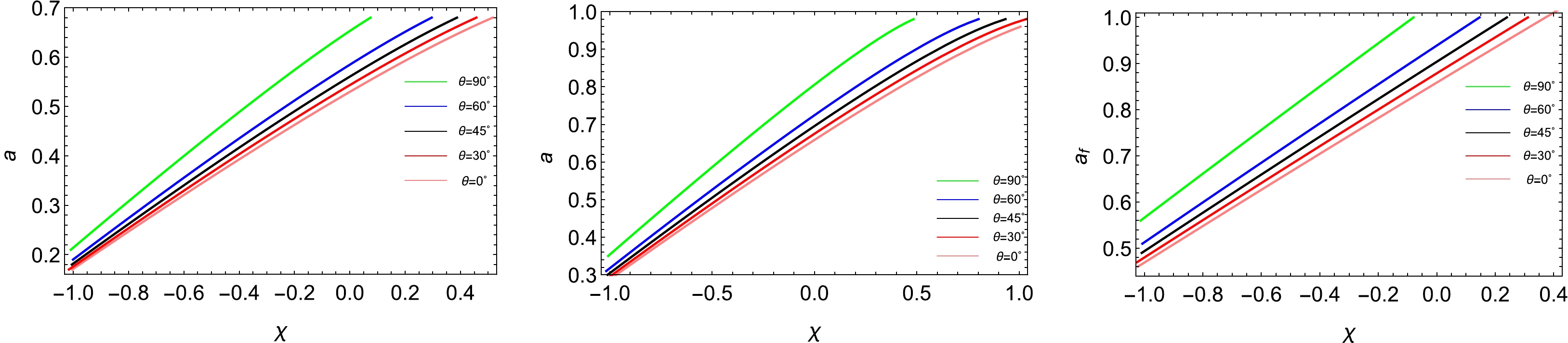
Figure 6. (color online) Final spin
$ a_f $ with respect to the spin parameter χ with different inclination angles ϑ for the fixed disformal parameter$ \alpha=-0.2 $ (left),$ 0 $ (middle), and$ 0.2 $ (right). In each panel, the five lines from top to bottom correspond to decreasing inclination angles, i.e.,$ \vartheta=90^{\circ} $ (green),$ 60^{\circ} $ (blue),$ 45^{ \circ} $ (black),$ 30^{\circ} $ (red), and$ 0^{\circ} $ (pink).Before we finish, we would like to make a comment. As shown in Figs. 4, 5, and 6, the final spin
$ a_f $ always increases with an increase in the disformal parameter α, regardless of an equal spin, unequal spin, or generic spin configuration merger. This is different from the MOG parameter in the Kerr-MOG background [19], where the final spin$ a_f $ always decreases with an increase in the MOG parameter. Thus, we argue that the disformal parameter in the disformal Kerr background and the MOG parameter in the Kerr-MOG case have completely different effects on the final spins of the merged black holes, which suggests the differences between these two spacetime structures. -
We investigate the signatures of a disformal Kerr black hole merger in quadratic DHOST theories, which reveals that the disformal parameter α provides richer physics in the black hole merger. We also compare the results with those given for the Kerr-MOG black hole merger [19] because the disformal Kerr and Kerr-MOG solutions both describe the modification from the Kerr solution. Using the null geodesics, we analyze the ringdown stage of the black hole merger, where the real and imaginary parts of the QNMs are described by the angular velocity
$ \varOmega_c $ and Lyapunov exponent of the light ring λ, respectively. We observe that for the prograde orbit,$ \Omega_c $ decreases with increasing α, and λ also decreases with it, except in the Kerr case ($ \alpha=0 $ ) for a large spin parameter a. For the retrograde orbit,$ \Omega_c $ increases with α, whereas λ decreases. This behavior of the disformal parameter α is obviously different from that of the MOG parameter in the Kerr-MOG background observed in Ref. [19], where for the prograde orbit,$ \Omega_c $ increases with the MOG parameter and λ increases with it for small a but decreases for large a, and for the retrograde orbit,$ \Omega_c $ decreases with the MOG parameter, whereas λ increases. Moreover, adopting the BKL recipe, we estimate the final black hole spin$ a_f $ . We find that$ a_f $ always increases with increasing α, regardless of an equal spin, unequal spin, or generic spin configuration merger, which is different from the case of the MOG parameter in the Kerr-MOG background [19], where$ a_f $ always decreases with an increase in the MOG parameter. Thus, we conclude that the disformal parameter in the disformal Kerr background and the MOG parameter in the Kerr-MOG case have completely different effects on the final spins of the merged black holes, which suggests the differences between these two spacetime structures.
Merger estimates for a disformal Kerr black hole in quadratic degenerate higher-order scalar-tensor theories
- Received Date: 2024-01-18
- Available Online: 2024-05-15
Abstract: We investigate the main features of a disformal Kerr black hole merger in quadratic degenerate higher-order scalar-tensor theories. In the ringdown stage of the black hole merger, for the prograde orbit, the real part of the quasinormal modes decreases with an increase in the disformal parameter, and the imaginary part also decreases, except in the Kerr case for a large spin parameter. However, for the retrograde orbit, the real part increases with an increase in the disformal parameter, and the imaginary part always decreases with it. For the approximate final spin, regardless of an equal spin, unequal spin, or generic spin configuration merger, the final black hole spin always increases with an increase in the disformal parameter. Our results show that the disformal parameter in the disformal Kerr solution and the MOG parameter in the Kerr-MOG case have obviously different effects on the black hole merger, which suggests the differences between these two spacetime structures.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: