Dark energy and matter interacting scenario to relieve H₀ and S₈ tensions

In the framework of the $\tilde\Lambda$CDM model in standard cosmology, particles are created in the neighborhood of the Friedmann universe horizon. Such dynamics is effectively described by the particle production rate $\Gamma_m= -(\chi/4\pi)(\dot H/H^2)$ and energy density $\rho_{m}^H=2 \chi m^2H^2$ of produced particles. Here, m represents the particle mass, and χ characterizes the width $\chi/m$ of the particle-production layer on the horizon. The interplay between vacuum energy and matter (radiation) is delineated through the particle production rate $\Gamma_m$ and density $\rho_{m}^H$, explicated in Refs. [63, 64] as

The matter density $\rho_{{m}}$ is for non-relativistic particles, and the radiation density $\rho_{{r}}$ for relativistic particles. Equations (1) and (2) are Friedmann equations for the time-varying cosmological term $\rho_{\Lambda}(t)$, and we have $p_{\Lambda}=-\rho_{\Lambda}$. Vacuum energy and matter (radiation) interact via the right-handed sides of the energy conservation equations (3) and (4). With initial values at either the reheating end or today, four dynamic equations form a closed set, providing the unique solutions $\rho_{{m, r, \Lambda}}$ and H.

The numerical solutions are too complex to proceed with data analysis. Nevertheless, the model accommodates scaling solutions, consistent with the principles of asymptotic safety in gravitational theories [59, 61]. That is, the $\tilde\Lambda$CDM quantities $\rho_{{m, r, \Lambda}}$ receive scaling factor $(1+z)^\delta$ (with $|\delta|\ll 1$) corrections to $\Lambda {{\rm{CDM}}}$ counterparts when the redshift z becomes small (late times). Thus, we produce ansatz solutions $\rho_{{m, r}}\propto (1+z)^{3(1+w_{m, r})-\delta^{M, R}_G}$ deviating from normal matter with $w_m=0$ and normal radiation with $w_r= 1/3$, and $\rho_{\Lambda}\propto (1+z)^{3(1+w_{\Lambda})+\delta_{\Lambda}}$ deviating from normal vacuum energy with $w_{\Lambda}=-1$.

Therefore, in late times, the $\tilde\Lambda$CDM model parameterizes the Friedmann equation as

where $E(z)=H(z)/H_0$, and the three scaling indexes $\delta^{M, R}_{G}$ and $\delta_{\Lambda}$ are considerably smaller than unity. The generalized conservation law yields

At the leading order of $\delta^{M, R}_{G}$ and $\delta_{\Lambda}$ and for low redshifts, we find the relation

Two independent parameters $\delta^{M, R}_{G}$ can be constrained by observational data. Their negative (positive) values indicate the process of radiation and matter conversion into dark energy (the inverse process). For a comparative analysis, we also introduce the simplified $\tilde\Lambda$CDM model from our previous study [40], characterized by $\delta_G\equiv \delta_{_G}^M= \delta_{_G}^R$ and $\delta_\Lambda=\delta_G(\Omega_{m}+\Omega_{r})/\Omega_\Lambda$.

In this study, we employ CMB, BAO, SN, $H_0$, and $S_8$ data. For CMB data, we use the Planck 2018 full-mission TT, TE, and EE + lowE + lensing power spectrum [3]. For BAO data, we utilize five points from three observations (the 6dF Galaxy Survey, SDSS DR7 Main Galaxy Sample, and DR12 galaxy sample) [5–7]. For SN data, we use 1048 data points from the Pantheon compilation [67]. In addition, we also consider two Gaussian priors, that is, $S_8= 0.766^{+0.020}_{-0.014}$ (here, $S_8\equiv\sigma_8(\Omega_{{\rm{m}}}/0.3)^{0.5}$), which originated from the combination of the KiDS/Viking and SDSS data [14], $H_0=73.04 \pm 1.04 \; {\rm{km\; s}}^{-1} {\rm{Mpc}}^{-1}$, which was determined from the distance ladder by the SH0ES team [4].

To conduct the Markov-chain Monte Carlo (MCMC) analysis, we use the $\mathtt{MontePython}$ code [68]. To assess how well the various models fit the data, we use the Akaike information criterion (AIC) [69–71], ${{\rm{AIC}}}\equiv \chi^2 +2d$, where d is the number of free parameters. We use $\Delta {{\rm{AIC}}}=\Delta\chi^2+2\Delta d$ to compare a model with ΛCDM.

To evaluate the $\tilde\Lambda$CDM model, we use the ΛCDM model as a reference. First, we constrain the ΛCDM and $\tilde\Lambda$CDM models using the joint CBS data. The results are shown in Table 1 and Fig. 1. In the $\tilde\Lambda$CDM model, we obtain fit values of $H_0=69.5\pm 1.8\; {\rm{km\; s}}^{-1} {\rm{Mpc}}^{-1}$ and $S_8=0.822\pm 0.011$; thus, the $H_0$ and $S_8$ tensions are relieved to be at the $2.87\sigma$ and $2.77\sigma$ levels, respectively. We find that, in this case, the $H_0$ tension is greatly alleviated, and the $S_8$ tension is also slightly alleviated, which is difficult to realize in other cosmological models.

Model	ΛCDM	$\tilde\Lambda$CDM
$\delta^M_{G}$	-	$-0.00052\pm 0.00088$
$\delta^R_{G}$	-	$-0.0061\pm 0.0059$
$\delta_{\Lambda}$	-	$-0.00022\pm 0.00038$
$\Omega_{m}$	$0.3097\pm 0.0055$	$0.3060\pm 0.0081$
$H_0 [{ {\rm{km} } \;{\rm s^{-1} \;Mpc^{-1} }}]$	$67.66\pm 0.41$	$69.5\pm 1.8$
$\sigma_8$	$0.8107\pm 0.0059$	$0.814\pm 0.010$
$S_8$	$0.824\pm 0.010$	$0.822\pm 0.011$
${H_0} ~{ {\rm{tension} } }$	$4.81\sigma$	$2.87\sigma$
${S_8} ~{ {\rm{tension} } }$	$2.94\sigma$	$2.77\sigma$
$\chi_{{\rm{min}}}^{2}$	1907.55	1907.34
$\Delta {{\rm{AIC}}}$	0	3.79

Table 1.  Constraint results of parameters in the ΛCDM and $\tilde\Lambda$CDM models with the CBS data. Here, $H_0$ is in units of ${\rm{km\; s}}^{-1}\; {\rm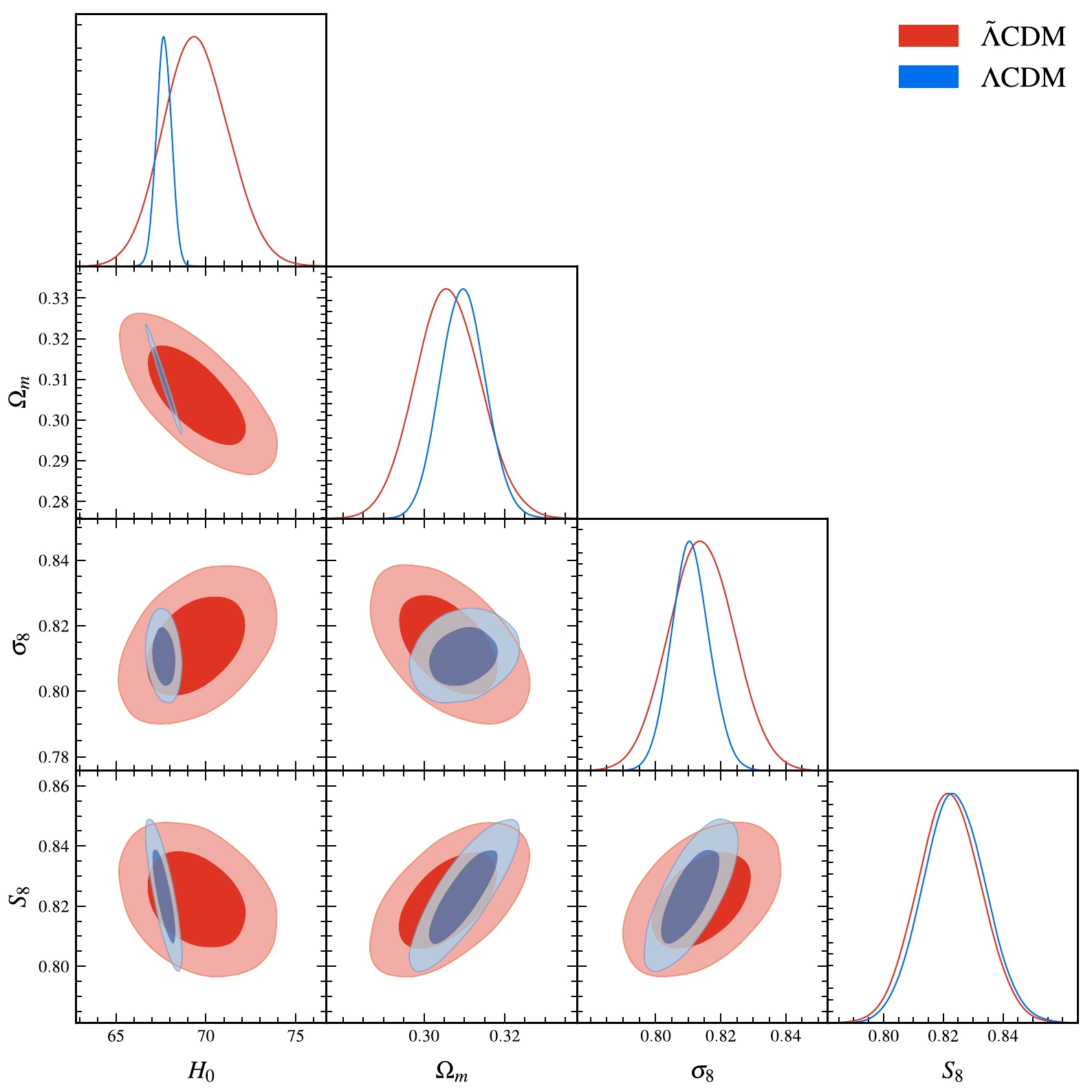{Mpc}}^{-1}$.

Figure 1.  (color online) Constraints (68.3% and 95.4% confidence levels) on $H_0$, $\Omega_{m}$, $\sigma_8$, and $S_8$ in the ΛCDM and $\tilde\Lambda$CDM models using the CBS data. Here, $H_0$ is in units of ${\rm{km\; s}}^{-1}\; {\rm{Mpc}}^{-1}$.

Although the $\tilde\Lambda$CDM model demonstrates potential in concurrently mitigating the $H_0$ and $S_8$ discrepancies, it leads to a larger AIC value compared to the ΛCDM model. This indicates that compared to ΛCDM, the $\tilde\Lambda$CDM model's capability in fitting observational data is weaker for the CBS case.

To ascertain the $\tilde\Lambda$CDM model's potential in reducing both the $H_0$ and $S_8$ tensions, we present the correlation coefficients between the cosmological parameters of the ΛCDM and $\tilde\Lambda$CDM models in the CBS case in Fig. 2. Our findings reveal that within the $\tilde\Lambda$CDM model, the correlation coefficients of $\delta_G^M$ and $\delta_G^R$ with $H_0$ are negative, and the current constraints give negative $\delta_G^M$ and $\delta_G^R$ values. Consequently, the $\tilde\Lambda$CDM model significantly alleviates the $H_0$ tension. Additionally, the extra free parameters exhibit weak correlations with $S_8$, suggesting that mitigating the $S_8$ tension presents considerable challenges.

Figure 2.  (color online) Correlation coefficients between cosmological parameters in the ΛCDM and $\tilde\Lambda$CDM models using the CBS data.

The evolution of $\Omega_{m, r, \Lambda}$ with redshift z in the $\tilde\Lambda$CDM model exhibits similarities to the ΛCDM counterparts. To delineate the distinct characteristics between the $\tilde\Lambda$CDM and ΛCDM models, we define the differences as follows:

Employing the constrained results from the CBS dataset, as delineated in Table 1 and Fig. 1, we graphically represent the differences in Fig. 3. As shown in Fig. 3, the proportion of dark energy was nearly zero in the early universe, which is consistent with the result of the ΛCDM model. However, in the late universe, when dark energy begins to dominate cosmic evolution, its proportion is somewhat larger than that predicted by the ΛCDM model. Correspondingly, the proportion of matter density in the late universe is slightly less than that in the standard model. This characteristic means that in this model, the accelerated expansion of the late universe begins earlier and is more intense. Consequently, the age of the universe is younger than that predicted by the standard model, resulting in a larger Hubble constant.

Figure 3.  (color online) Differences $\delta\Omega_{m, r, \Lambda}(z)$ between the $\tilde\Lambda$CDM and ΛCDM models in the CBS case. Shown here is the best-fit result.

As shown in Table 1 and Fig. 1, the CBS data constrain the $\tilde\Lambda$CDM $H_0$ and $\sigma_8$ ($\Omega_m$), with the best-fit values larger (smaller) than their ΛCDM counterparts. Nonetheless, it is evident that the confidence ranges of these parameters are more broad in the $\tilde\Lambda$CDM model compared to those in the ΛCDM model. As a result, the $H_0$ tension relieves to $2.87\sigma$ in the $\tilde\Lambda$CDM model. $S_8= \sigma_8(\Omega_{m}/0.3)^{0.5}$ depends on both $\sigma_8$ and $\Omega_{m}$. The $\tilde\Lambda$CDM $\Omega_m$ ($\sigma_8$) best-fit value decreases (increases) and its spreading increases, resulting in a decrease in the $\tilde\Lambda$CDM $S_8$ tension to $2.77\sigma$, in contrast with the increasing $S_8$ tension found in many other models. Consequently, the interaction dynamics between dark energy and matter, as illustrated in Fig. 3, are pivotal in substantially mitigating both the $H_0$ and $S_8$ tensions.

Finally, we constrain the $\tilde\Lambda$CDM model using the three data combinations, CBS+$H_0$, CBS+$S_8$, and CBS+ $H_0$+$S_8$. The constraint results are shown in Table 2 and Fig. 4. We also compute the AIC values for the $\tilde\Lambda$CDM model using various data combinations to enable a systematic comparison between the $\tilde\Lambda$CDM and ΛCDM models across different datasets. In the previous case (the CBS case), although the $H_0$ tension is greatly relieved and the $S_8$ tension is also slightly alleviated, the $\tilde\Lambda$CDM model is not favored by the CBS data because its ΔAIC value is greater than 0 ($\Delta{{\rm{AIC}}}=3.79$). However, when the $H_0$ and $S_8$ data are added to the data combination, we find that the situation is significantly improved both in relieving the tensions and fitting the observations.

Data	CBS+$H_0$	CBS+$S_8$	CBS+$H_0$+$S_8$
$\delta^M_{G}$	$-0.00140\pm 0.00075$	$0.00038^{+0.00072}_{-0.00098}$	$-0.00046\pm 0.00069$
$\delta^R_{ G }$	$-0.0146\pm 0.0040$	$-0.0053^{+0.0055}_{-0.0068}$	$-0.0147\pm 0.0040$
$\delta_{\Lambda}$	$-0.00059\pm 0.00030$	$0.00018^{+0.00031}_{-0.00046}$	$-0.00020\pm 0.00029$
$\Omega_{m}$	$0.2974\pm 0.0066$	$0.3108^{+0.0077}_{-0.0091}$	$0.3018\pm 0.0066$
$H_0$	$72.3\pm 1.2$	$68.8^{+2.1}_{-1.7}$	$71.9\pm 1.2$
$\sigma_8$	$0.8203\pm 0.0095$	$0.8000^{+0.0093}_{-0.0079}$	$0.8050\pm 0.0081$
$S_8$	$0.817\pm 0.010$	$0.814\pm 0.010$	$0.8074\pm 0.0098$
${H_0}~ { {\rm{tension} } }$	$0.47\sigma$	$1.96\sigma$	$0.72\sigma$
${S_8} ~{ {\rm{tension} } }$	$2.59\sigma$	$2.43\sigma$	$2.11\sigma$
$\chi_{{\rm{min}}}^{2}$	$1909.53$	$1912.46$	$1914.76$
$\Delta {{\rm{AIC}}}$	$-2.07$	$5.02$	$-2.29$

Table 2.  Constraint results of parameters in the $\tilde\Lambda$CDM model with CBS+$H_0$, CBS+$S_8$, and CBS+$H_0$+$S_8$ data.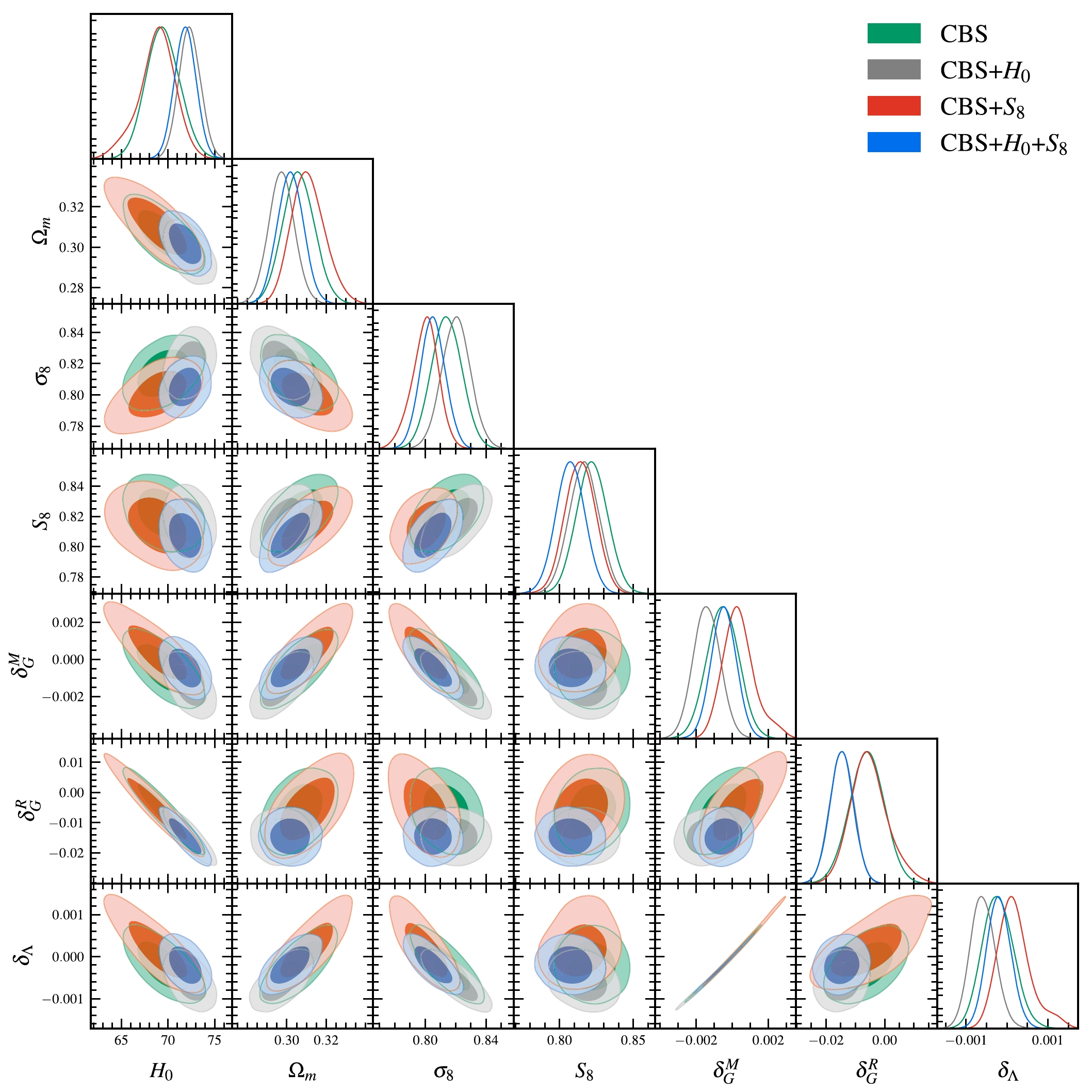

Figure 4.  (color online) Constraints (68.3% and 95.4% confidence levels) on the $\tilde\Lambda$CDM model using CBS, CBS+$H_0$, CBS+$S_8$, and CBS+$H_0$+$S_8$ data. $H_0$ is in units of ${\rm{km\; s}}^{-1}\; {\rm{Mpc}}^{-1}$.

In the CBS+$H_0$ case, we have $H_0=72.3\pm 1.2$ ${\rm{km\; s}}^{-1}\; {\rm{Mpc}}^{-1}$ and $S_8=0.817\pm 0.010$. Therefore, the $H_0$ and $S_8$ tensions are further relieved, and the $H_0$ tension is greatly relieved to $0.47\sigma$. Furthermore, in this case, $\Delta{{\rm{AIC}}}=-2.07$, indicating that the $\tilde\Lambda$CDM model is favored by the data over ΛCDM. However, the $\tilde\Lambda$CDM model is not favored by the CBS+$S_8$ data, in which though the $S_8$ tension is slightly improved (to $2.43\sigma$), the $H_0$ tension is slightly relieved (to $1.96\sigma$), and the fit gives $\Delta{{\rm{AIC}}}=5.02$. Consequently, incorporating $H_0$ and $S_8$ priors into the data combination effectively mitigates the tensions. Therefore, employing the CBS+$H_0$+$S_8$ dataset fosters an optimally synthesized scenario, for which we obtain $H_0=71.9\pm 1.2$ ${\rm{km\; s}}^{-1}\; {\rm{Mpc}}^{-1}$ and $S_8=0.8074\pm 0.00998$, consequently reducing the $H_0$ and $S_8$ tensions to $0.72\sigma$ and $2.11\sigma$, respectively. Furthermore, under these conditions, the model exhibits the highest degree of concordance with the data, as indicated by $\Delta{{\rm{AIC}}}=-2.29$.

We compare our findings with those derived from the simplified $\tilde\Lambda$CDM model [40], wherein it is postulated that $\delta_{G}^M$ and $\delta_{G}^R$ are identical in Eqs. (5) and (7), that is, $\delta_{G}^M=\delta_{G}^R=\delta_G$ and $\delta_\Lambda=\delta_G(\Omega_{m}+\Omega_{{\rm{r}}})/\Omega_\Lambda$. Employing the CBS dataset, the $H_0$ tension can be relieved to $3.59\sigma$ (with the best fit $H_0= 67.71 \;{\rm{km\; s}}^{-1}\; {\rm{Mpc}}^{-1}$), and in this case, the $S_8$ tension is exacerbated (with the best fit $S_8=$ 0.8252). Additionally, within the simplified $\tilde\Lambda$CDM model constrained by the CBS + $H_0$ dataset, we obtain the best-fit values $\sigma_8=0.8720$ and $S_8=0.8310$, and the $\sigma_8$ and $S_8$ tensions significantly increase while alleviating the $H_0$ tension.

We extend our comparison to the $\Lambda(t)$CDM model, an interacting vacuum energy model that posits an energy exchange between vacuum energy and cold dark matter, as detailed by the specific equations $\dot{\rho}_{\Lambda} = \beta H \rho_c$ and $\dot{\rho}_c+3H\rho_c = - \beta H \rho_c$ (here, the dimensionless parameter β describes the interaction strength). In Ref. [38], the same CBS+$H_0$ dataset is used to constrain the $\Lambda(t)$CDM model to obtain $H_0 = 69.36\; {\rm{km\; s}}^{-1}\; {\rm{Mpc}}^{-1}$ and $\sigma_8=0.844$. In contrast, as illustrated in Table 2, the current findings explicitly show that the $\tilde\Lambda$CDM model exhibits distinct advantages over the $\Lambda(t)$CDM model.

In this study, we propose a new cosmological model, in which the vacuum energy interacts with matter and radiation, which is considered to originate from the asymptotic safety and particle production of gravitational quantum field theory. We test this model using the current cosmological observations and discuss its capability for relieving the $H_0$ and $S_8$ tensions.

To elucidate the mechanisms by which the ${\tilde\Lambda}$CDM model relieves tensions, we analyze the differences $\delta\Omega_{{{\rm{m}}, r}, \Lambda}(z)$ between the ${\tilde\Lambda}$CDM and ${\Lambda}$CDM models. The alleviation of the $H_0$ tension is attributed to the ${\tilde\Lambda}$CDM model's enhanced dark energy proportion and reduced matter fraction at low redshifts relative to the ${\Lambda}$CDM model, which stem from the conversion of matter into dark energy. The findings of $\delta_G^{M, R}<0$ and $\delta_\Lambda<0$ corroborate the $\tilde\Lambda$CDM hypothesis in which in the late universe radiation and matter decay into dark energy [64, 65].

We find that this cosmological model can significantly relieve the $H_0$ tension and simultaneously slightly reduce the $S_8$ tension, which cannot be easily observed in other cosmological models. When using the CBS data to constrain the model, we find that the $H_0$ tension is relieved to $2.87\sigma$, and meanwhile, the $S_8$ tension is also improved to $2.77\sigma$. However, in this case, the $S_8$ tension is only slightly reduced, and the model is not favored by the CBS data (because $\Delta{{\rm{AIC}}}=3.79$).

When the $H_0$ and $S_8$ data are added to the data combination, the situation is significantly improved. In the CBS+$H_0$ case, we obtain the result $H_0=72.3\pm 1.2$ ${\rm{km\; s}}^{-1}\; {\rm{Mpc}}^{-1}$, indicating that the $H_0$ tension is relieved to $0.47\sigma$, and in this case, the model is favored over ΛCDM ($\Delta{{\rm{AIC}}}=-2.07$). In the CBS+$H_0$+$S_8$ case, we obtain a synthetically best situation, in which $H_0=71.9\pm 1.2$ ${\rm{km\; s}}^{-1}\; {\rm{Mpc}}^{-1}$ and $S_8=0.8074\pm 0.0098$; thus, the $H_0$ and $S_8$ tensions are relieved to $0.72\sigma$ and $2.11\sigma$, respectively. In this case, the model is most favored by the data ($\Delta{{\rm{AIC}}}=-2.29$).

Therefore, we find that such a cosmological model can greatly relieve the $H_0$ tension and simultaneously alleviate the $S_8$ tension.

Undoubtedly, this model requires further in-depth research in many aspects. Such an interaction between vacuum energy and matter is likely to introduce many additional observational effects. For example, we are not certain whether this model will lead to a significant integrated Sachs-Wolfe effect. Research on this issue requires further related theoretical study and analysis using full CMB angular power spectrum data. Moreover, this additional interaction may also lead to modifications in the middle-scale clustering patterns of large-scale structures, which will potentially affect the clustering strength at various scales. Therefore, such modifications may also affect the mass function and profile of dark matter halos, the statistical properties of galaxy clusters, the alignments of galaxies, the structure of the cosmic web, and so on. The study of these effects is a complicated issue, requires the use of N-body simulations, and also relies on assumptions about the nature of dark matter (such as cold or fuzzy dark matter). All these aspects deserve further in-depth discussion.