-
The structure of hadrons, the bound states of strong interactions, is conveniently probed by exploring the other fundamental forces, namely, the electromagnetic, weak, and gravitational interactions. For the proton's overall properties, both electromagnetic and weak form factors can be effectively determined, whereas our understanding of gravitational form factors (GFFs) is inadequate. Because gravity couples to matter via the energy-momentum tensor (EMT), the distributions of energy, angular momentum, and various mechanical properties can be obtained from the matrix elements of the EMT [1, 2]. These properties are encoded in the GFFs. Specifically, the GFFs provide critical information about the fundamental properties (mass M, spin J, and the Druck term (D term)) and offer direct access to the proton's internal structure [3−5]. The sum GFFs, which are divided into quark and gluon contributions, are measurable quantities defined purely for the total system, providing information on the quantum origin of mass and the internal dynamics of the proton.
The mass and pressure distributions in the proton are constructed from the A- and D-term GFFs. However, despite the precise measurement of the proton mass and quark D-term extracted from deeply virtual Compton scattering (DVCS) experiments [6], complete information on the proton GFFs is lacking. Recently, one study obtained the D-term under the assumption that the quark and gluon D-term are the same, because there is no information on the gluon D-term from experiments [6]. However, the quark and gluon contributions to the D-term have been researched using lattice quantum chromodynamics (LQCD) [7−10], enhancing our understanding of the proton GFFs. To date, the exact value of the D-term, which varies with the squared momentum transfer t, remains a subject of ongoing research.
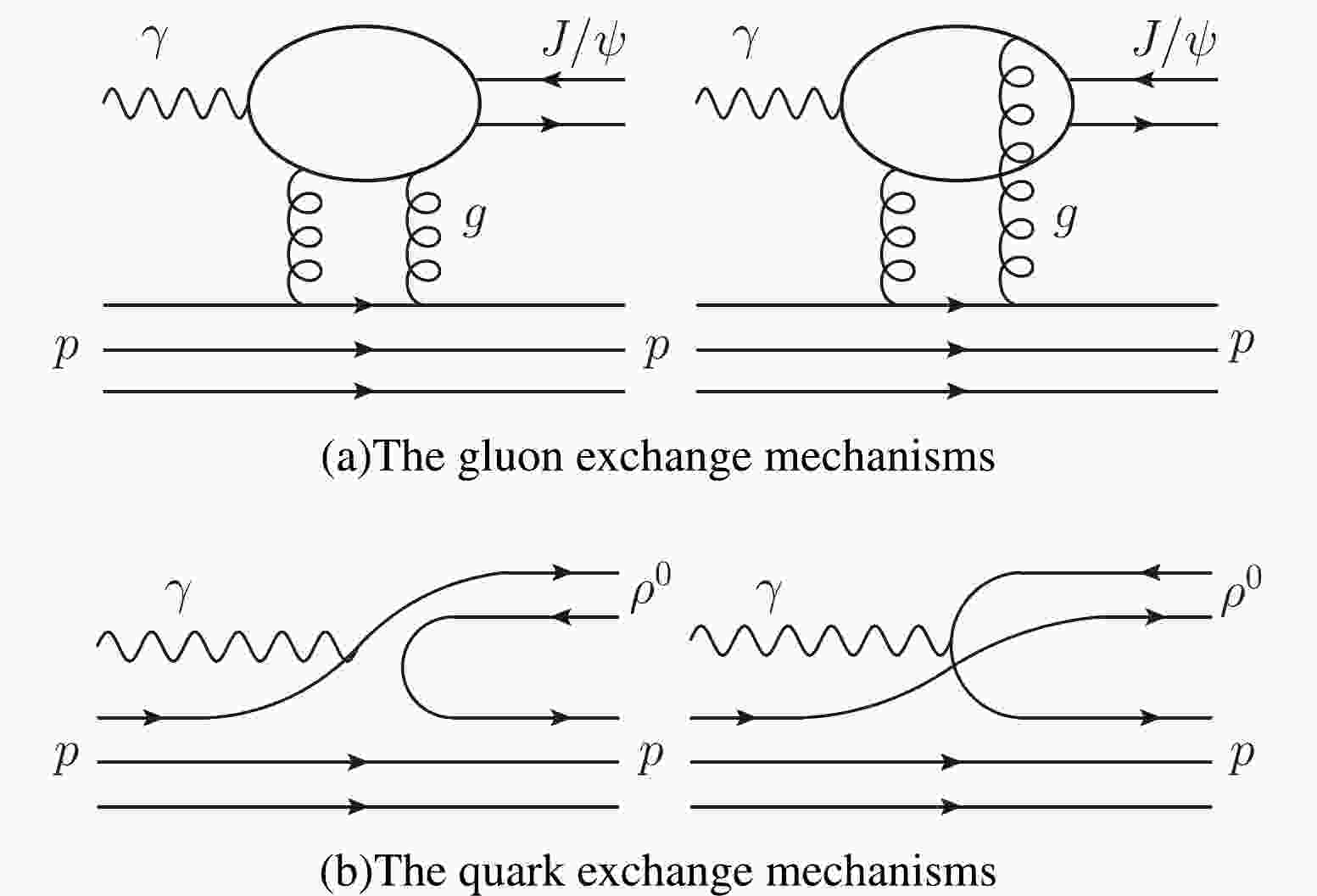
To address this problem, the near-threshold vector meson photoproduction (NTVMP) process should be considered as a indispensable method. This is because in the indirect measurement of GFFs in exclusive processes, besides DVCS,
$ \gamma \gamma^* $ reaction, time-like Compton scattering, and double DVCS [11], vector meson production experiments are regarded as advantageous, and abundant experiment data have been collected by comparison. The internal nature of the proton can be explored using a photon as a probe in the$ \gamma p\to V p $ process, with the same vector quantum numbers as a photon and a vector meson, which is$ J^{PC}=1^{--} $ , such as the proton mass radius [5, 12, 13], the trace anomaly contribution to the proton mass [14−17], and the quarkonium–proton scattering length [18−22]. Moreover, near-threshold heavy quarkonium photoproduction offers a superior path to access the gluon GFFs [5, 23−30]. One main reason is that the scalar gluon operator is dominant in the production amplitude of a heavy quarkonium (such as$ J/\psi $ ) and sensitive to the gluonic structure of the proton [5]. In fact, light vector meson (such as$ \rho^0 $ ) photoproduction mainly reflects the quark part of the GFFs [13] because the exchange of a scalar quark-antiquark pair is not suppressed and far exceeds the contribution of scalar gluon exchange [13, 31]. Currently, systematic research on proton GFFs is scarce and challenging. The separate quark and gluon EMT operators are not conserved because additional form factors appear in the decompositions of their matrix elements. Moreover, the individual quark and gluon GFFs acquire scale- and scheme-dependence. Therefore, we find it promising to obtain complete information on proton GFFs from the light and heavy NTVMP process, which is essential to extract the related properties inside the proton.Although DVCS experiments are almost insensitive to the gluon D-term, future experiments are cruical to gain insight into the proton's remaining GFFs, for instance, at Jefferson Lab (JLab) [32] and electron-ion colliders (EICs) [33−35]. This study will set important benchmarks for revealing the internal characteristics of the proton in future experiments at JLab and EICs.
-
The expression for the GFFs is analogous to the electric charge distribution, which can be mapped out via electron scattering experiments [36]. Similarly, scattering off gravitons would allow information on the spatial distribution of the energy inside a proton to be accessed. The physical content of the information encoded in the EMT form factors is revealed in the so-called Breit frame [4]. Here, the
$ (00) $ component of the EMT donates the isotropous energy density inside the proton, which can be expressed as [4]$ T_{00} (r)= \int \frac{{\rm d}^{3} {\bf\Delta}}{(2 \pi)^{3}} {\rm e}^{-{\rm i} r {\bf\Delta} } G(t), $

(1) where
$ t=-{\bf\Delta}^2 $ is the squared momentum transfer, and the GFFs$ G(t) $ can be written as [4, 16, 23]$ G(t)= M A(t) - \frac{t}{4M} \left( A(t) -2J(t)+ D(t) \right), $

(2) where M is the proton mass. The form factors
$ A (t) $ ,$ J (t) $ , and$ D (t) $ can be used to derive the proton mass distribution, angular momentum distribution, and mechanical properties, respectively. Here,$ A(0)=1 $ ,$ J(0)=\dfrac{1}{2} $ , and the form factor$ B(t)=2J (t)-A (t) $ is essentially consistent with zero [8, 27, 37]. The proton GFFs are the sum contributions of the quark and gluon GFFs, which are given as [4]$ G_{q/g}(t) = M A_{q/g}(t)- \frac{ t}{4 M }\left( -B_{q/g}(t)+D_{q/g}(t) \right) +M\bar{C}_{q/g}(t), $

(3) where the
$ \bar{C}_{ g}(t) $ form factor can be written as [23, 38]$ \bar{C}_{ g}(t)=-\frac{A_{ g}(t)}{4} + \frac{- t}{16 M^2 }\left( B_{ g}(t)-3 D_{ g}(t) \right) $

(4) and the
$ \bar{C} $ -GFFs satisfy the constraint$ \bar{C}_q(t) +\bar{C}_g(t) =0 $ owing to EMT conservation [4]. Note that the expression of$ \bar{C}_{ g}(t) $ in Eq. (4) has a potential inaccuracy for our evolution, because Eq. (4) works well in the large momentum transfer region, where$ |t| $ exceeds the square of the proton mass [39, 38], which requires further study to obtain a more viable solution. As the contribution of the$B_{g}(t)+ D_{g}(t)$ is negligible [23, 38−41], the component of the gluon GFF part becomes [23]$ \begin{aligned}[b] G_{g}(t) =\; & \frac{3}{4}M A_{g}(t) - \frac{ t}{4 M } D_{g}(t) +\frac{3t}{16M}\left(B_{g}(t)+D_{g}(t)\right) \\ \approx \;& \frac{3}{4}M A_{g}(t) - \frac{ t}{4 M } D_{g}(t) . \end{aligned} $

(5) The quark GFFs are obtained as follows:
$ \begin{aligned}[b] G_{q}(t) =\; & M A_{q}(t)- \frac{ t}{4 M }\left( -B_{q }(t)+D_{q }(t) \right) -M\bar{C}_{g}(t) \\ \approx \;& M A_{q}(t)+ \frac{1}{4}M A_{g}(t) - \frac{ t}{4 M } D_{q}(t) -\frac{3t}{16M}\left( B_{g}(t)+D_{g}(t)\right) \\ \approx \;& M A_{q}(t)+ \frac{1}{4}M A_{g}(t) - \frac{ t}{4 M } D_{q}(t) \\[-18pt] \end{aligned} $

(6) as the form factor
$ B(t)=B_q(t)+B_g(t)\approx 0 $ .For A-GFFs, the mass distribution of the proton is encoded in the A-term, which can be expressed under the dipole form parameterization as
$ A(t)=\frac{A_{q}(0)}{(1- t/m_q^{ 2} )^2}+\frac{A_{g }(0)}{(1- t/m_g^2 )^2} , $

(7) where the constraint
$ A_{q}(0)+A_{g }(0)=1 $ is the consequence of momentum conservation [4, 42], and$ m_q $ and$ m_g $ are free parameters. The gluon contribution$ A_g(0)=0.414 $ was obtained from global QCD analysis [43] and agrees with other LQCD results [9, 44, 45]. In this study, to mirror the mass distribution inside the proton, the mean square radius of the mass distribution (A-term mass radius) is defined as$ \left<R_{ A -term}^2\right>=\frac{\displaystyle\int {\rm d}^{3} r r^{2} A(r)}{\displaystyle\int {\rm d}^{3} r A(r)} = 12 \left(\frac{A_q(0)}{m_q^2} + \frac{ A_g(0)}{m_g^2} \right), $

(8) where
$A (r)= \int \dfrac{{\rm d}^{3} {\bf\Delta} }{(2 \pi)^{3}} {\rm e}^{-{\rm i} r {\bf\Delta} } A(t)$ . In a previous study [5], the expression for$ G(t) $ , shown in Eq. (2), is considered as a mass distribution when$ |t| $ is as sufficiently small as$ G(t) \approx MA(t) $ . Through the extraction of the form factor from$ J/\psi $ photoproduction at small$ |t| $ [5, 12, 28], the gluon radius of the proton can be derived by considering the gluon contribution, whereas the radius derived from the$ \rho^0 $ differential cross section can be regarded as the quark contribution without the gluon part [13]. In fact,$ A(t)=A_q(t)+A_g(t) $ denotes the sum contribution inside the proton, which allows us to define the proton mass radius from the A-term as Eq. (8).The D-term in GFFs is an area of significant interest and can define pressure and shear force distributions inside the proton. The D-term is typically parameterized in the tripole form as [7, 46, 47]
$ D (t)=\frac{D_q(0)}{(1- t/ d_q^2 )^{3}}+\frac{D_g(0)}{(1-t/d_g^2)^{3}}, $

(9) where
$D_q(0),\;d_q$ and$D_g(0),\,d_g$ correspond to the quark and gluon parameters, respectively.Because gravity couples to matter via the EMT, the proton GFFs offer direct access to the proton's mechanical structure from the matrix elements of the EMT [1, 2]. Specifically, the pressure
$ p(r) $ and shear forces$ s(r) $ are “good observables” for reporting the pressure and shear force distributions inside the proton, which can be expressed as [3, 4]$ s(r)= - \frac{1}{2} r\frac{\rm d}{{\rm d}r} \frac{1 }{ r} \frac{{\rm d}}{{\rm d}r} \widetilde{D} (r), \; \; \; \; \; \; p(r)= \frac{1}{3} \frac{1 }{ r^2} \frac{{\rm d}}{{\rm d}r} r^2 \frac{{\rm d}}{{\rm d}r} \widetilde{D} (r), $

(10) where
$ \widetilde{D} (r) $ is the Fourier transform of$ D(t) $ [3, 4],$ \widetilde{D} (r) =\int \frac{\text{d}^3 {\bf\Delta} }{2 M (2\pi)^3 } {\rm e}^{-{\rm i} {\bf\Delta} r}\left( D_{g}(- {\bf\Delta}^2) +D_{q}(- {\bf\Delta}^2) \right). $

(11) The positive combination
$F_n(r)=\dfrac{2}{3} s(r)+p(r)$ represents the normal force distribution in the composed particle system [4]. We can define the mechanical radius of the proton in terms of the normal force distribution in the system, which can be described as [4]$ \left<R^2_{\rm mech}\right> = \frac{\displaystyle\int \text{d}^3r \; r^2 \left[F_n^{ q+ g }(r) \right] }{\displaystyle\int \text{d}^3r \left[F_n^{q+ g }(r) \right] } = \frac{ 12 \left( \dfrac{ D_q(0) }{ d_q}+ \dfrac{D_g(0)}{ d_g} \right) }{ D_q(0) d_q + D_g(0) d_g }. $

(12) The energy density
$ T_{00} (r) $ in Eq. (1) can only be defined for the total system, which can be written as [4]$ \begin{aligned}[b] T_{00}(r)=\;& \int \frac{{\rm d}^{3} {\bf\Delta} }{(2 \pi)^{3}} {\rm e}^{-{\rm i} r {\bf\Delta} } \left( G_q(t)+G_g(t) \right) \\ =\;&\sum_{a=q,g}\frac{ 16 M^2 A_a(0) m_a^3 e^{-m_a r} - (-3 + d_a r) D_a(0 ) d_a^5 e^{-d_a r} }{ 128 \pi M} . \end{aligned} $

(13) Moreover, the energy density satisfies
$ T_{00}(r)>0 $ in a mechanical system, which allows us to introduce the mean square radius of the energy density (energy radius) as [4]$ \langle R_{E}^{2}\rangle =\frac{\displaystyle\int {\rm d}^{3} r r^{2} T_{00}(r)}{\displaystyle\int {\rm d}^{3} r T_{00}(r)} =\left<R_{ A -term}^2\right> -\frac{3\left(D_q(0)+D_g(0)\right)}{2M^2}. $

(14) The proton energy radius can be associated with the slope of
$ A(t) $ in Eq. (8) and the D-term GFFs while covering the proton A-term mass radius. -
Next, we conduct a complete analysis of the gluon and quark GFFs from near-threshold heavy quarkonium and light vector meson photoproduction, respectively. For gluon GFFs, a recent study achieved great success [28] with the help of the pure nature of
$ J/\psi $ photoproduction, where the quark exchange is strongly suppressed by the Okubo-Zweig-Izuki (OZI) rule. Thus heavy quarkonium photoproduction is a promising path to accessing the gluon GFFs owing to the dominant gluon exchange (Fig. 1(a)). Conversely, the quark GFFs can be naturally associated with$ \rho^0 $ photoproduction because the exchange between the proton and meson states is occupied by valence quarks (Fig. 1(b)) and the gluon exchange is meager when$ |t| $ is small [13, 31, 48].Typically, the photoproduction cross section of the vector meson is given by [49]
$ \frac{{\rm d}\sigma_{\gamma p\to V p}}{{\rm d}t}=\frac{1}{64 \pi W^2} \frac{1}{|{\bf p}_{\gamma}|^2} \left| \mathcal{M}_{\gamma p\to V p} \right|^2 , $

(15) where
$ {\bf p}_{\gamma } $ and W are the center of mass (c.m.) photon momentum and c.m. energy in the$ \gamma p\to V p $ process, respectively. As an assumption, in this study, the amplitudes of light and heavy quarkonia are primarily attributed to the quark and gluon parts of the EMT of QCD, respectively, which can be written as [5]$ \begin{array}{*{20}{l}} \mathcal{M}_{\gamma p\to V p} =-Q _e c_2 2 M g^2 \left< P^{\prime}| T^{q(g)}_{00} |P \right > ,\end{array} $

(16) where
$ Q_e $ represents the coupling of the photon to the electric charge of the quarks in the vector meson,$ c_2 $ is the short-distance coefficient, and$ g^2=4 $ is the QCD coupling with$ \alpha_s \approx 0.32 $ [30]. Combining Eqs. (5) and (6), the components of the quark and gluon EMT form factors become$ \begin{aligned}[b] &\left< P^{\prime}|T^{g }_{00}|P \right> =\bar{u} (P^{\prime}) u(P) \left(\frac{3}{4} M A_{g }(t) - \frac{ t}{4 M } D_{ g }(t) \right) \\ & \left< P^{\prime}|T^{q}_{00}|P \right> =\bar{u} (P^{\prime}) u(P) \left( M A_{q}(t)+ \frac{1}{4}M A_{g}(t) - \frac{ t}{4 M } D_{q}(t) \right) \end{aligned} $

(17) where the spinor normalization
$ \bar{u} (P^{\prime}) u(P)=2M $ . By integrating the differential cross section (Eq. (15)) over the allowed kinematical range from$ t_{\min} $ to$ t_{\max} $ , the total cross section is computed and expressed as$ \sigma=\int_{t_{\min}}^{t_{\max}} {\rm d}t \left(\frac{{\rm d} \sigma}{{\rm d} t} \right) , $

(18) The form factor
$ G_{q/g}(t) $ in Eqs. (5) and (6) is found to satisfy$ \begin{aligned}[b] G_q(0)=\;& MA_q(0)+\frac{1}{4}MA_g(0)\; \; \text{and } \\ G_g(0)=\;&\frac{3}{4}MA_g(0) \end{aligned} $

(19) and the coefficient
$ c_2 $ in Eq. (16) can be determined by extrapolating the near-threshold differential cross section at$ t=0 $ . So far, we have established the relationship between the complete GFFs and the NTVMP, including the differential and total cross sections in Eqs. (15) and (18).As discussed in Ref. [23], the parameters
$ m_g $ ,$ D_g(0) $ , and$ d_g $ in the gluon GFFs are attained by global fitting near-threshold$ J/\psi $ photoproduction data, including the differential and total cross sections [28, 50−54]. The quark GFF calculation resembles that of the gluon GFFs (as described in Ref. [23]). We consider the squared momentum transfer t of the differential cross section to be in the range$ |t|<1 $ GeV$ ^2 $ . A meticulous global fitting of the$ \rho^0 $ photoproduction experimental data is employed [55] to extract the parameters$ m_q $ ,$ D_q(0) $ , and$ d_q $ in the quark GFFs (Eqs. (15)). These obtained parameters as presented in Table 1. A comparison of the differential cross section of$ \rho^0 $ photoproduction and the experimental measurements is shown in Fig. 2, exhibiting a good agreement. To check the fitting accuracy of the differential cross sections, we compare these integral values via Eq. (18) with the total cross section experimental data [55], as depicted in Fig. 3. Our results demonstrate agreement with the values and trends of the experimental data, proving reliable fitting.quark GFFs (this study) $ m_q $ /GeV

$ D_q(0) $ 

$ d_q $ /GeV

$ 0.85\pm 0.05 $ 

$ -1.76\pm 0.30 $ 

$ 0.88\pm 0.05 $ 

gluon GFFs [23] $ m_g $ /GeV

$ D_g(0) $ 

$ d_g $ /GeV

$ 1.43\pm 0.10 $ 

$ -2.08 \pm 0.25 $ 

$ 0.90 \pm 0.07 $ 

Table 1. Top: Obtained values of the parameters
$ m_q $ ,$ D_q(0) $ , and$ d_q $ in the quark GFFs via a global fitting of the$ \rho^0 $ differential cross section experimental data [55]. Bottom: Parameters$ m_g $ ,$ D_g(0) $ , and$ d_g $ in the gluon GFFs achieved from global fitting of the$ J/\psi $ photoproduction data [28, 50−54].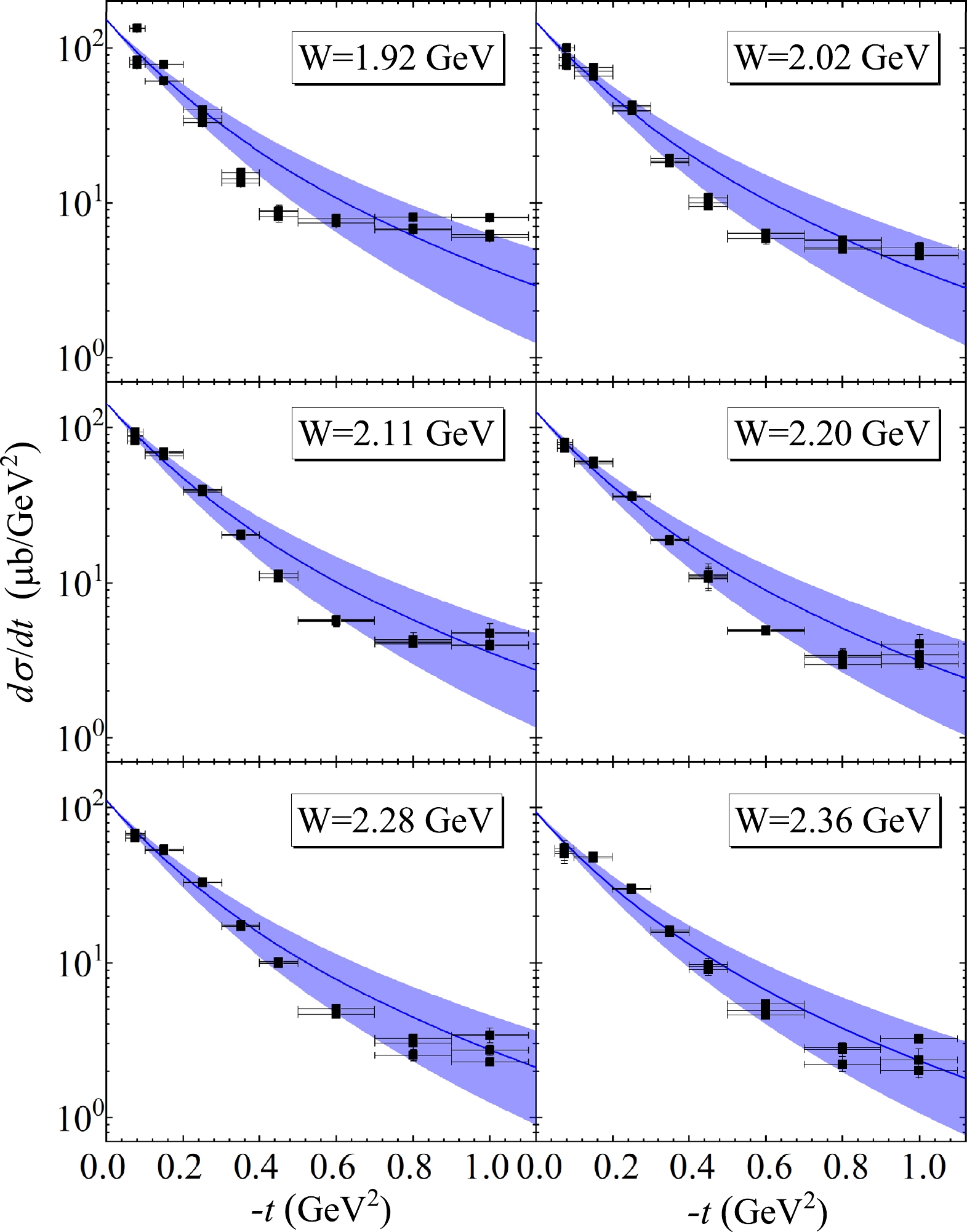
Figure 2. (color online) Global fitting result of the
$ \gamma p \to \rho^0 p $ differential cross section as a function of$ -t $ at c.m. energies of 1.92, 2.02, 2.11, 2.20, 2.28, and$ 2.36\text{ GeV} $ . The blue bands reflect the statistical errors of$ m_q $ ,$ D_q(0) $ , and$ d_q $ . References for the data can be found in [55].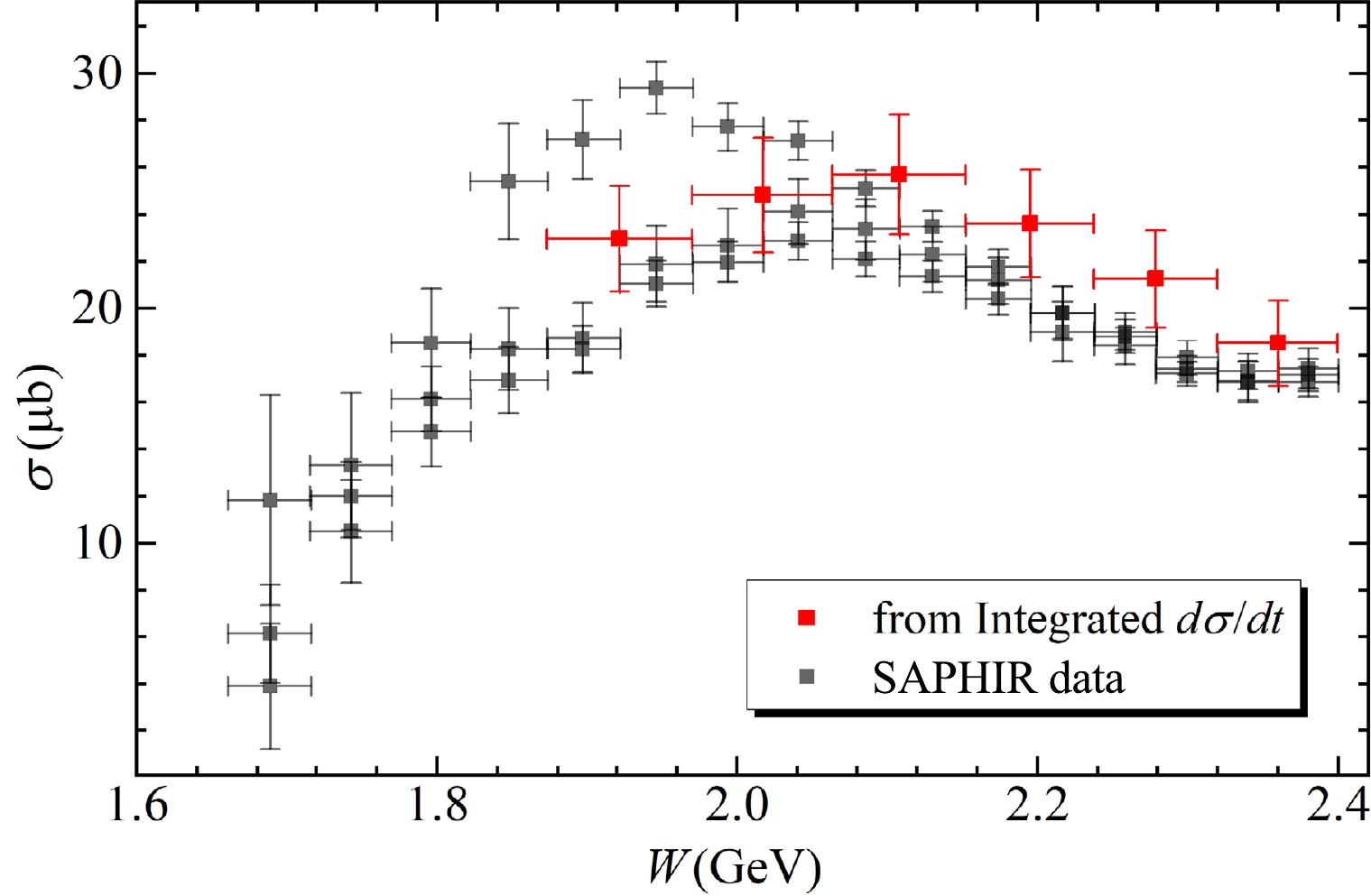
Figure 3. (color online) Total cross sections calculated by integrating the functions fitted to the differential cross sections for the six beam energy regions, with the statistical uncertainties of
$ m_q $ ,$ D_q(0) $ , and$ d_q $ shown, and compared with the experimental results (black squares) [55].As shown in Fig. 4, the values of the quark and gluon A- and D-terms are compared with the DVCS experiment data and LQCD determinations [10]. Here, the parameter errors include all uncertainties of the GFFs. For the quark GFFs, the quark D-term exhibits a notable agreement with the DVCS experiment data and LQCD determinations, whereas our A-term is approximately half that of the LQCD results [10]. The converse gluon A- and D-terms are displayed in Fig. 4 to avoid overlapping data points. Notably, the gluon D-term contributes slightly more than the quark D-term, and our gluon A and D-terms are approximately comparable with the LQCD results [10]. The total GFFs are shown in Fig. 5 and compared with the LQCD results [10]. For
$ D(t) $ , our result is found to be consistent with the LQCD result, whereas both$ A(t),J(t) $ are slightly smaller. The deviation of$ A(t) $ can be attributed to the absence of the s quark contribution in our calculations, and then$ J(t)=\dfrac{1}{2}A(t) $ can be derived. Therefore, further research is necessary.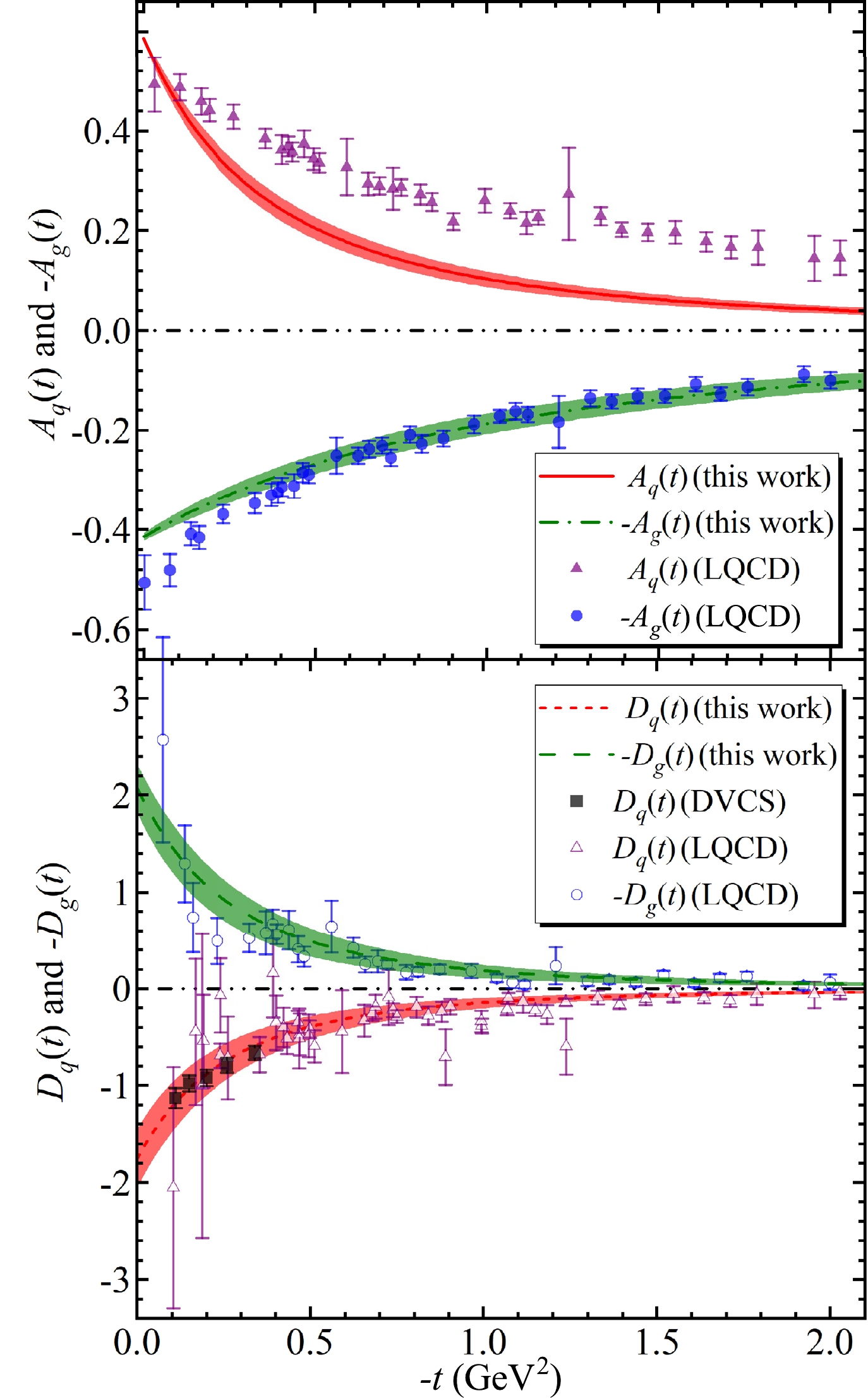
Figure 4. (color online) Top panel:
$ A_{q}(t) $ (red solid curve) and converse$ A_{g}(t) $ (green dash-dotted curve) compared with LQCD results [10]. Bottom panel:$ D_{q}(t) $ (red dotted curve) and converse$ D_{g}(t) $ (green dashed curve) compared with LQCD results [10] and the result extracted from DVCS experiments [6].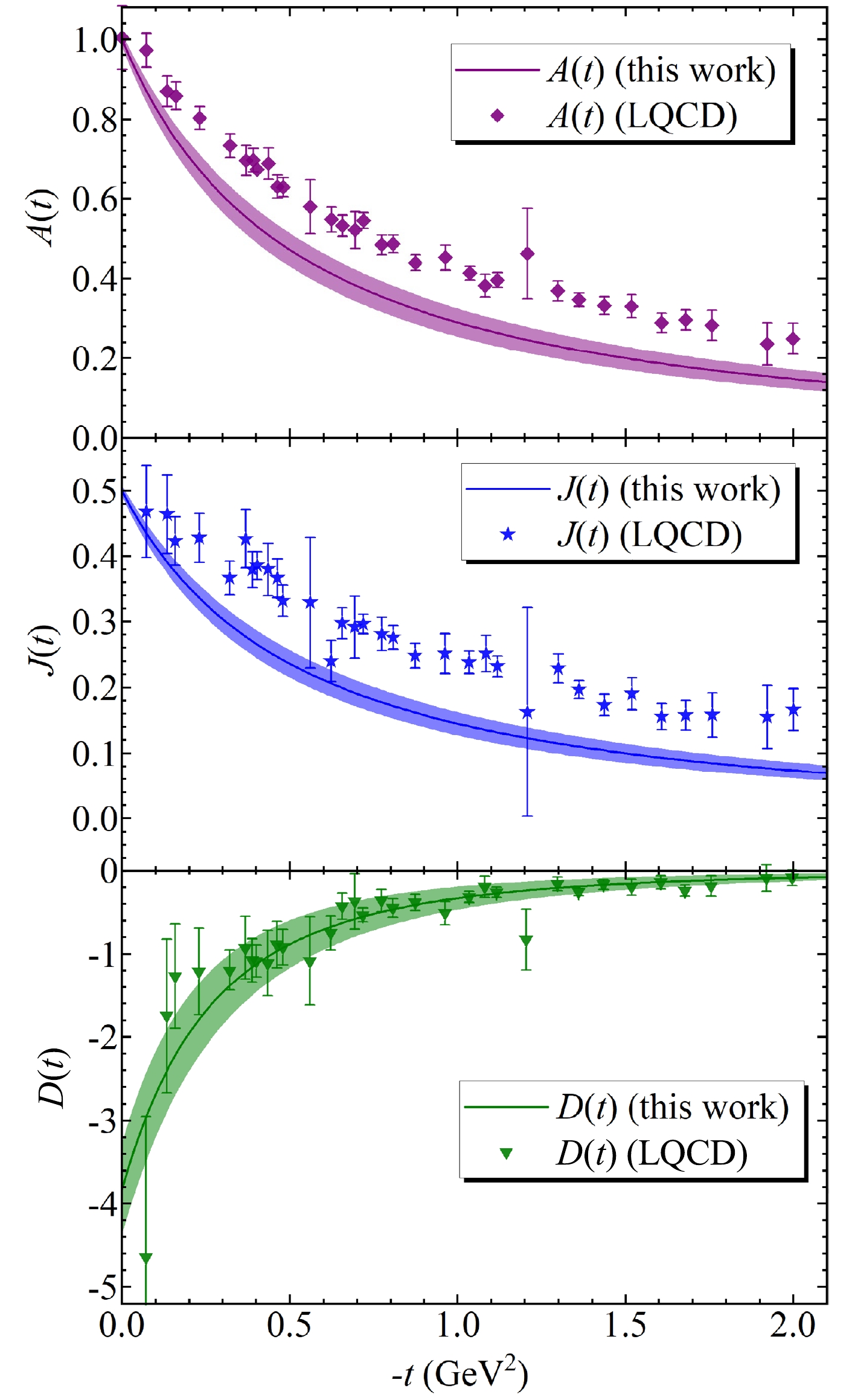
Figure 5. (color online) Three GFFs of the proton, including
$ A(t) $ ,$ J(t) $ , and$ D(t) $ , as functions of t are compared with LQCD results [10].The proton A-term mass radius, mechanical radius, and energy radius in Eqs. (8), (12), and (14) are computed, as listed in Table 2. Two important mechanical quantities, the pressure and energy density at the center of the proton, are also revealed. Surprisingly, the obtained proton A-term mass radius is a notable achievement in that the corresponding ratio of the radius derived from the mass and electromagnetic form factor is
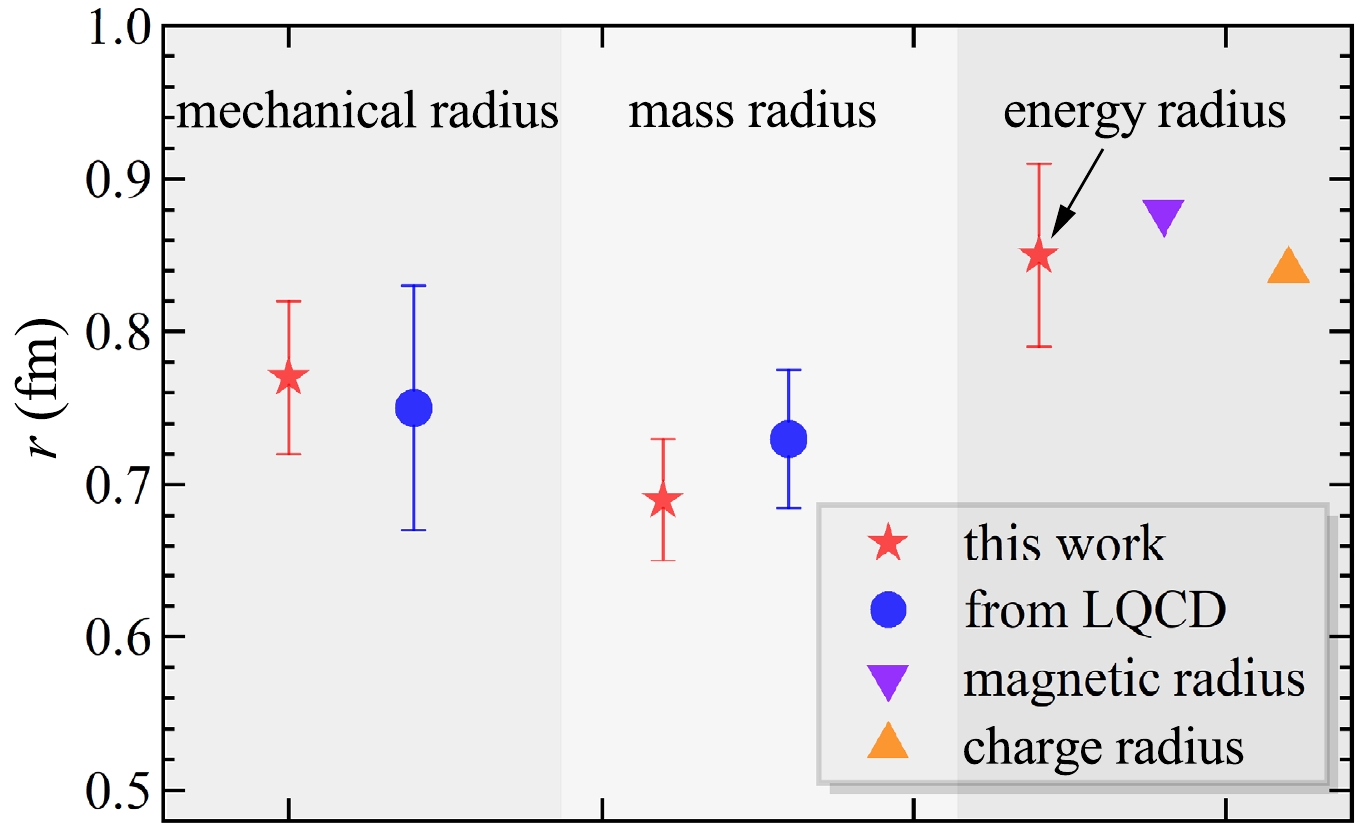
$ 0.82\pm0.05 $ , which approaches the π meson's determination of 0.79(3) [56]. The ratios of the mass and charge radii of different hadrons appear to be consistent.A-term mass radius/fm mechanical radius/fm energy radius/fm $ 0.69 \pm 0.04 $ 

$ 0.77\pm 0.05 $ 

$ 0.85\pm 0.06 $ 

$ p(0) $ (GeV/fm

$ ^3 $ )

$ T_{00}(0) $ (GeV/fm

$ ^3 $ )

− $ 1.49^{+0.87}_{-0.60} $ 

$ 5.40^{+2.54}_{-2.76} $ 

− Table 2. Extracted internal nature of the proton from the GFFs: A-term mass radius
$\sqrt{\left < R_{ A\text{-}\rm term}^2\right > }$ , mechanical radius$\sqrt{\left < R^2_{\rm mech}\right > }$ , energy radius$ \sqrt{\langle R_{E}^{2}\rangle } $ , and the pressure and energy density at the center of the proton.Notably, the energy radius derived from the GFFs in Eq. (14) can also be written as
$ \langle R_{E}^{2}\rangle=\frac{\displaystyle\int {\rm d}^{3} r r^{2} T_{00}(r)}{\displaystyle\int {\rm d}^{3} r T_{00}(r)}=\left.-\frac{6}{G(0)} \frac{{\rm d} G(t)}{{\rm d} t}\right|_{t=0}\, , $

(20) which resembles the proton charge and magnetic radius defined from the electric and magnetic form factors [58]. Surprisingly, the proton energy radius
$ 0.85\pm 0.06 \text{ fm} $ is similar in size to its charge and magnetic radii, as shown in Fig. 6. The proton A-term mass radius and mechanical radius are also compared. An intriguing pattern emerges in that the electric, magnetic, and GFFs are homologous and delicately govern the enigmatic properties of the proton. Therefore, the accurate measurement of the proton energy radius deserves the same attention as the charge and magnetic radii in future studies.The pressure and shear force distributions inside the proton are obtained and displayed in Fig. 7. Here, the positive sign indicates repulsion toward the outside, and the negative sign indicates attraction directed toward the inside. The total pressure and shear force distributions of the sum of the quark and gluon contributions are represented as the blue-solid curve in Fig. 7. The pressure is positive in the inner region and negative in the outer region, with a zero crossing near
$r= 0.63 \text{ fm} $ , which reveals that the repulsive and binding pressures dominating in the proton are separated in radial space. Moreover, the shear forces reach their distribution peak at approximately r = 0.66 fm based on our observation.
Figure 7. (color online) Left panel: Pressure distribution
$ r^2p(r) $ of the proton. Right panel: Shear force distribution$ r^2s(r) $ of the proton. The blue solid curve corresponds to the total pressure and shear force distributions, whereas the red dotted and green dashed curves denote the quark and gluon contributions to the total, respectively. -
In our previous study, we provided
$ D_q(t) $ results for the NTVMP process. However, a comparison with the results of other models, conducted in Ref. [4], revealed that there are large differences between different models. Therefore, we introduce a generalized model-independent algorithm for further validation, known as the resonance via Padé (RVP) method based on the Schlessinger point method (SPM) [59−61]. This method is essentially an interpolation approximation that relies only on experimental data points. When given a finite dataset$ \{(x_i,y_i)|_{i=1,2,\cdots,N}\} $ with a data volume of N, the function$ y(x) $ can be accurately reconstructed by constructing the interpolating continuous partition$ C_N(x) $ via the SPM.$ C_{N}(x)=\frac{y_{1}}{1+\dfrac{a_{1}\left(x-x_{1}\right)}{1+\dfrac{a_{2}\left(x-x_{2}\right)}{\vdots_{a_{N-1}\left(x-x_{N-1}\right)}}}} $

(21) where the coefficients
$ \{a_i|i=1,2,\cdots,N-1\} $ can be constructed recursively via Eq. (22), and$ y(x_i)=C_N(x_i) $ can be ensured.$ \begin{aligned}[b] &a_{1}=\frac{y_{1} / y_{2}-1}{x_{2}-x_{1}} \\ &a_{i}=\frac{1}{x_{i}-x_{i+1}}\left[1+\frac{a_{i-1}\left(x_{i+1}-x_{i-1}\right)}{1+} \cdots \frac{a_{1}\left(x_{i+1}-x_{1}\right)}{1-y_{1} / y_{i+1}}\right]. \end{aligned} $

(22) For GFFs, only experimental data from DVCS are available. Therefore, the form of
$ D_q(t) $ under the RVP method can be obtained by inserting the experimental data points from DVCS into Eqs. (21) and (22), which is simplified as$ D_q^{\text{RVP}}(Q)=\frac{0.061913 - 0.346966 Q - 0.004908 Q^2}{-0.033875 + 0.010085 Q + Q^2}, $

(23) where
$ Q=-t $ .Our calculated results using the RVP method are displayed in Fig. 8. Compared with our results from the NTVMP method, the results of
$ D_q(t) $ from this model-independent algorithm are in good agreement within the small$ |t| $ range. In addition, compared with those of other models in Ref. [4], the results of these methods appear to conform better with the experimental data and LQCD determinations. This further confirms our NTVMP method calculation. However, there are several issues that must be clarified regarding the results obtained using the RVP method:
Figure 8. (color online) Blue solid line: Quark D-term results obtained by reconstructing the DVCS experimental data points using the RVP method based on the SPM. Red dashed line: Quark D-term in the NTMVP process. Comparison with LQCD results.
● Feasibility of interpolation and extrapolation : The RVP method based on the SPM is a type of Padé approximation, which can accurately reconstruct an underlying function from data points. Its radius of convergence is determined by a branch point of the function, which is located near the real-axis domain of the data sample. Moreover, the discrete nature of the method ensures that its results can be reasonably extended over a wider range. For example,
$ |t|\in [0.1 \;\; \text{GeV}^2 $ , 0.4$ \text{GeV}^2 $ ] in the experimental data of DVCS, whereas we finally extrapolate our results to$ |t| $ = 2$ \text{GeV}^2 $ , which are in good agreement with both the NTVMP process results and LQCD determinations. In addition, other hadron physics related problems are accurately calculated and their feasibility is illustrated in Refs. [61−64] using this method.● Identification of threshold energies and poles: As shown in Fig. 8, the results of the RVP method exhibit a pole at
$ |t| = 0.178 \text{ GeV}^2 $ and the point also corresponds to the result with the largest error in LQCD. This may be a coincidence; however, it was noted in Refs. [61, 62] that the RVP method has the ability to identify threshold energies and poles. Because the underlying function reconstructed using this method exhibits non-canonicality as it approaches the poles, and this non-canonical behavior provides a clear indication of the region where the poles are located, we believe that there may an interesting physics phenomenon at$ |t| = 0.178 \text{ GeV}^2 $ , which we will investigate in our subsequent research. -
In this study, based on current light vector meson
$ \rho^0 $ and heavy quarkonium$ J/\psi $ photoproduction data, a groundbreaking analysis of the complete proton GFFs connecting the energy-momentum tensor and NTVMP is conducted. The obtained GFFs are compared with the DVCS experimental results and LQCD determinations [10], and we find that the quark D-term is comparable with the current result, whereas differences persist between our quark A-term and LQCD results [10]. For the gluon GFFs, the values of the gluon A- and D-terms are approximately consistent with the LQCD results [10]. The results of this study illustrate the remarkable revelation that the NTVMP process offers tremendous potential for obtaining complete proton GFFs. Conversely, the connection between heavy quarkonium photoproduction and gluon GFFs faces challenges. One study revealed that this process is light-cone dominated and has no direct connection with the gluon GFFs [57]. Therefore, further exploration of the physical mechanisms is imperative.This study employs a first-ever definition pattern on the mean square radius of the mass distribution, comprising the sum contributions of quarks and gluons inside the proton. This definition pattern in Eq. (8) differs from that of previous studies. From our perspective, the previous direct extraction from vector meson photoproduction [5, 12, 13, 28] reflects the energy distribution (see Eqs. (14) and (20)) instead of the mass distribution inside the proton because these studies assumed that
$ G(t) $ can be considered a mass distribution when$ |t| $ is sufficiently small that$ G(t) \approx MA(t) $ . This study tries to clarify this point and develops the specific values of the A-term mass radius and energy radius from the mass and energy distributions. Moreover, the total D-form factor is helpful for investigating their applications in describing the mechanical properties. Correspondingly, the pressure and shear force distributions inside the proton are obtained. We realize the internal nature of the proton, including the proton A-term mass, mechanical, and energy radii, normal forces, and energy density distribution in the proton system.Considering that there are differences in the distributions of proton GFFs given by different theoretical models [4], to reduce the influence of parameters and models on physical results, we use the RVP method to compute the quark D-term based on DVCS experimental data. The results demonstrate that this model-independent generalized algorithm is more supportive of the NTVMP process in this study. Subsequently, we will consider other computational methods, such as machine learning [61−65], to conduct further research targeting other GFF contributions.
In this study, the NTVMP process offers significant information for the study of proton GFFs. Therefore, high-precision photo/electroproduction data on light and heavy vector mesons (including
$ \rho^0, \omega $ ,$ \phi, J/\psi, $ and Υ) are highly required, which can be realized at JLab [32] and EICs [33−35]. Moreover, this study offers theoretical reference for GFF measurement in future DVCS experiments and other indirect measurement in exclusive processes.
Gravitational form factors of the proton from near-threshold vector meson photoproduction
- Received Date: 2024-01-15
- Available Online: 2024-05-15
Abstract: We systematically analyze the quark and gluon gravitational form factors (GFFs) of the proton by connecting the energy-momentum tensor and near-threshold vector meson photoproduction (NTVMP). Specifically, the quark contributions of GFFs are determined by applying global fitting to the cross section of the lightest vector meson






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: