-
As a result of a nuclear reaction, the final nucleus appears in an excited state. The lifetime of such states is of the order of nuclear time. In some cases, long-lived excited states of the nuclei are formed, which are associated with a high degree of forbidden transitions between excited levels or low energy of the excitation level. Such states are called isomeric or metastable states and have half-lives in a wide range of times [1].
There are nuclei with two unstable states, metastable (m) and ground (g) states, which may aid in determining the population of the metastable state of a given nucleus relative to its ground state or obtaining an isomeric ratio (IR). This value is defined as the ratio of the cross-sections for the nucleus formation in the metastable state to the ground state [2–4]. Moreover, in literature, the value of the IR is given as the ratio of the cross-sections for the nucleus formation in the high-spin and low-spin states. In experiments with bremsstrahlung flux, the IR of the products of the studied reactions is measured [4–7] as the ratio of flux-averaged cross-sections or reaction yields.
The study of IR values using photonuclear reactions has the advantage that the gamma quantum introduces a small angular momentum and does not change the nucleon composition of the compound nucleus. The data on the IR values of the reaction products facilitate the resolution of questions related to nuclear reactions and nuclear structure: the spin dependence of the nuclear level density, angular momentum transfer, nucleon pairing, and shell effects. These findings allow us to refine the theory of gamma transitions and test theoretical nuclear models [8–12].
The experimental results in the energy range above the giant dipole resonance (GDR) and up to the pion production threshold are of interest because the mechanism of the nuclear reaction changes. As shown in Ref. [13], in the energy range of 30–145 MeV, the reaction mechanism changes from the dominant giant dipole resonance to the quasideuteron mechanism and direct reactions. For a detailed study of this process, one needs to use the values of experimental cross-sections and IR values of multiparticle photonuclear reactions in a wide range of atomic mass and energies. However, there is still a lack of such experimental data [14, 15].
Experiments on the photodisintegration of stable isotopes of the Mo nucleus and determination of the IR values of the nuclide products
$ ^{95{{m,g}}}{\rm{Nb}} $ from the${^{\rm{nat}}{\rm{Mo}}}(\gamma,x{{\rm{np}}})$ reaction were described in previous literature [16–23], using beams of bremsstrahlung photons and the residual γ-activity method.In the energy region of GDR, the formation of isomeric pair
$ ^{95{{m,g}}}{\rm{Nb}} $ in photonuclear reaction on$ {^{\rm{nat}}{\rm{Mo}}} $ has been studied [16–20]. Thus, in Refs. [16, 17], the experimental result for$IR = Y_{{m}}(E_{\rm{\gamma max}}) / (Y_{{g}}(E_{\rm{\gamma max}}) + Y_{{m}}(E_{\rm{\gamma max}}))$ was obtained at an energy of 30 MeV. The authors of Ref. [18] defined the values of IR as the ratio of$ Y_{{m}}(E_{\rm{\gamma max}}) / Y_{{g}}(E_{\rm{\gamma max}}) $ at energies of 25 and 30 MeV. In Refs. [19, 20], the range of investigated energies was extended to 14–24 MeV, and the IR values of the reaction products of the natMo$ (\gamma,x{{{np}}})^{95{{m,g}}}{\rm{Nb}} $ reaction were also obtained by the γ-activation method. However, the results of Refs. [19, 20] contradict each other. It should be noted that, in the obtained experimental results [16–20], for the formation of the isomeric pair$^{95{{m,g}}}{\rm{Nb}} $ from${^{\rm{nat}}{\rm{Mo}}}(\gamma,x{{{np}}})$ reaction, the 96Mo isotope plays a main role.At an intermediate energy region, the natMo
$ (\gamma, x{{{np}}})^{95{{m,g}}}{\rm{Nb}} $ reaction was investigated [21–23]. In Ref. [21], the values of$ IR = Y_{\rm{H}}(E_{\rm{\gamma max}}) / Y_{\rm{L}}(E_{\rm{\gamma max}}) $ were obtained based on 96Mo$ (\gamma,{{p}}) $ , 97Mo$ (\gamma,{{{np}}}) $ , and 98Mo$ (\gamma,{{2np}}) $ reactions, which was the first measurement with natMo targets at$ E_{\rm{\gamma max}} $ = 50, 60, and 70 MeV. In Ref. [22], the authors extended the range of the study up to 45–70 MeV and attempted to compare the independent IR values of$ ^{95{{m,g }}} {\rm{Nb}}$ for different reactions: natMo$ (\gamma,x{{{np}}}) $ , natMo$({{p}}, \alpha x{{n}})$ , and natZr$ ({{p}},x{{n}}) $ .In Ref. [23], experimental and theoretical investigations of the photodisintegration of molybdenum isotopes are described. The yields of various photonuclear reactions on stable molybdenum isotopes were determined by the γ-activation method for the bremsstrahlung end-point energies of 19.5, 29.1, and 67.7 MeV. For the energy of 67.7 MeV, the authors were able to determine the yields
$Y_{{g}}(E_{\rm{\gamma max}})$ and$Y_{{m}}(E_{\rm{\gamma max}})$ for the formation of the$^{95{{m,g}}}{\rm{Nb}} $ nucleus in the ground and metastable states, respectively, whose ratio is 5.1/5.5.The experimental results from Refs. [21–23] agree with each other, while the data from Refs. [16–20] obtained in different representations of the value IR contradict each other. This does not allow estimation of the energy dependence of IR in the wide region
$ E_{\rm{\gamma max}} $ = 14–70 MeV.The present work is devoted to the study of the formation of the isomeric pair
$^{95{{m,g}}}{\rm{Nb}} $ in photonuclear reactions on natMo at the bremsstrahlung end-point energy range of$ E_{\rm{\gamma max}} $ = 38–93 MeV. This will extend the range of previously known experimental IR values and improve the reliability of these data. -
An experimental study of the
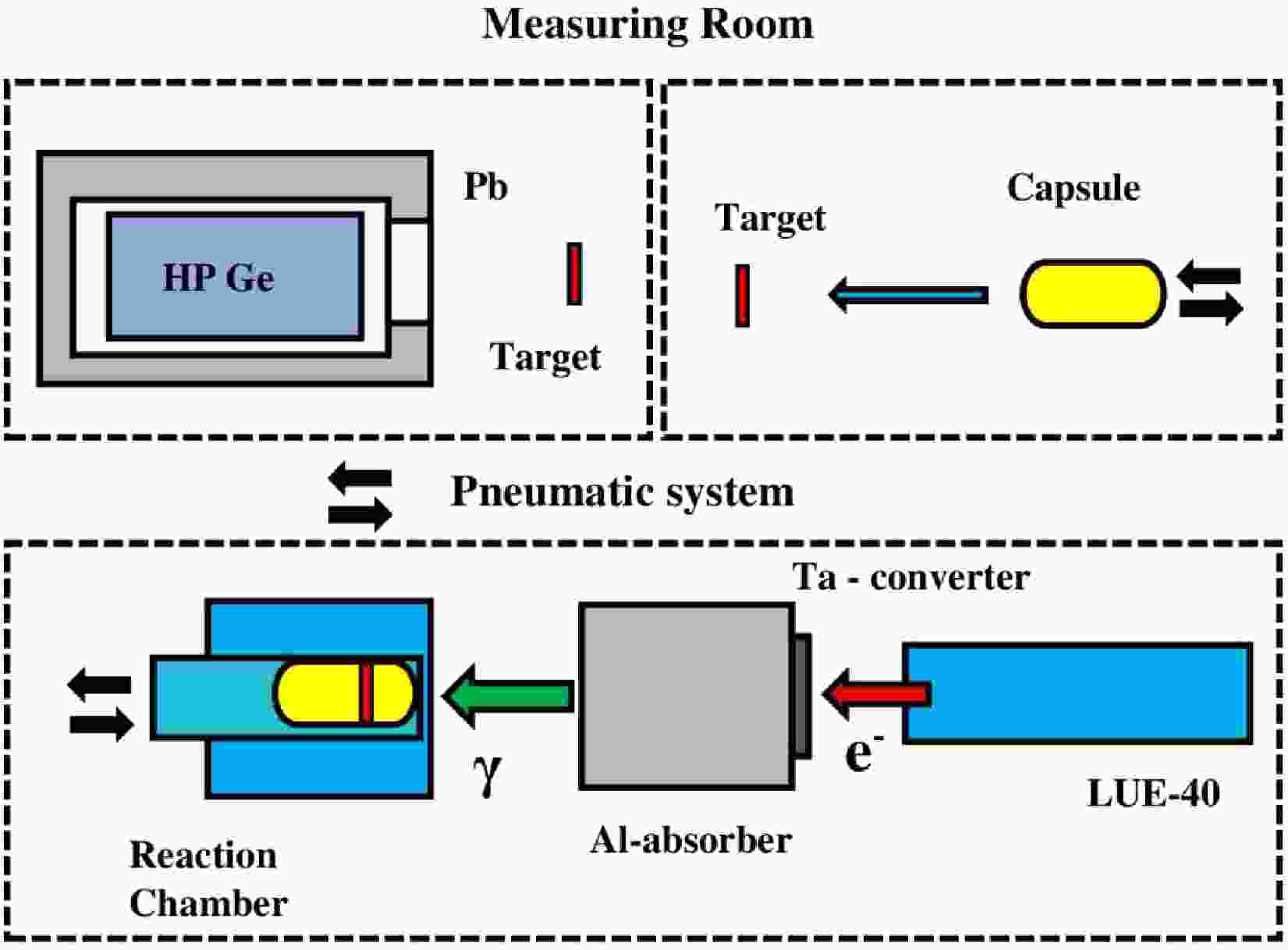
$^{95{{m,g}}}{\rm{Nb}} $ isomeric pair formation in the photonuclear reactions on natMo was performed using the electron beam of the linac LUE-40 at the National Science Center "Kharkov Institute of Physics and Technology" with the activation and off-line γ-ray spectrometric technique. The experimental procedure is described in detail in Refs. [24–27].The experimental complex for the study of photonuclear reactions is presented as a block diagram in Fig. 1. The linac LUE-40 provides an electron beam with an average current
$ I_{\rm{e}} \approx 3\; \mu {\rm{A}}$ and an energy spectrum with a full width at half maximum (FWHM) of$\Delta E_{\rm e}/E_{\rm e} \approx 1$ %. The range of initial energies of electrons is$ E_{\rm{e}} $ = 30–100 MeV. A detailed description and parameters of the LUE-40 linac are given in literature [28–31].
Figure 1. (color online) Schematic block diagram of the experiment. The upper part shows the measuring room, where the irradiated target is extracted from the capsule and is arranged before the HPGe detector for γ-activity measurements. The lower part shows the linac LUE-40, Ta converter, Al absorber, and exposure reaction chamber.
On the axis of the electron beam, there are a converter, an absorber, and a reaction chamber. The converter, made of natural tantalum, is a
$ 20\times20 $ mm plate with thickness l = 1.05 mm and is attached to an aluminum absorber, shaped as a cylinder, with dimensions$ \oslash 100 $ mm and a thickness of 150 mm. The thickness of the aluminum absorber was calculated to clean the beam of γ-quanta from electrons with energies up to 100 MeV.In this experiment, targets were made of natural molybdenum, which were thin discs with a diameter of 8 mm and a thickness of ≈ 0.11 mm, which corresponded to a mass of
$ \approx $ 57–60 mg. Natural molybdenum consists of 7 stable isotopes, with isotope abundance (%) as follows: 92Mo – 14.84, 94Mo – 9.25, 95Mo – 15.92, 96Mo – 16.68, 97Mo – 9.55, 98Mo – 24.13, and 100Mo – 9.63 (according to Refs. [32, 33]).The targets were placed in an aluminum capsule and taken to the reaction chamber using a pneumatic transport system for irradiation and back to the measurement room to record the induced γ-activity of reaction products in the target substance.
The γ-quanta of the reaction products were detected using a Canberra GC-2018 semiconductor HPGe detector. At
$ E_\gamma $ = 1332 keV, its total efficiency was 20% relative to the NaI(Tl) scintillator with dimensions 3 inches in diameter and 3 inches in thickness. The resolution FWHM is 1.8 keV for energy$ E_\gamma $ = 1332 keV and 0.8 keV for$ E_\gamma $ = 122 keV. The dead time for γ-quanta detection varied between 0.1 and 5%. The absolute detection efficiency$ \varepsilon(E_\gamma) $ was obtained using a standard set of γ-ray sources: 22Na, 60Co, 133Ba, 137Cs, 152Eu, and 241Am. The analytical curve in the form$ {{\rm{ln}}} \varepsilon (E_{\gamma}) = \sum_{i=1}^{n} a_i ({{\rm{ln}}} E_{\gamma})^i $ , proposed in Ref. [34], was used to determine the value of$ \varepsilon(E_\gamma) $ for various energies of γ-quanta.The electron bremsstrahlung spectra were calculated using the open-source software code GEANT4.9.2, PhysList G4LowEnergy [33]. The real geometry of the experiment was used in calculations, and the space and energy distributions of the electron beam were taken into account.
The bremsstrahlung flux was monitored by the yield of the
$ ^{100}{\rm{Mo}}(\gamma,n)^{99}{\rm{Mo}} $ reaction (the half-life$ T_{1/2} $ of the$ ^{99}{\rm{Mo}} $ nucleus is$ 65.94 \pm 0.01 $ h) by comparing the experimentally obtained average cross-section values$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{{\rm{exp}}} $ with the computation data$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{{\rm{th}}} $ . To determine the experimental$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{{\rm{exp}}} $ values, the yield for the γ-line of energy$ E_{\gamma} $ = 739.50 keV and intensity$ I_{\gamma} $ =$ 12.13 \pm 0.12 $ % is used. The average cross-section$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{{\rm{th}}} $ values were computed with the cross-sections$ \sigma(E) $ from the TALYS1.95 code. Thus, we find the transition coefficient from calculated to experimental flux. Details of the monitoring procedure can be found in Refs. [24–27].The γ-radiation spectrum of a natMo target irradiated by a beam of bremsstrahlung γ-quanta with high end-point energy has a complex pattern. There are emission γ-lines of the nuclei product of the natMo
$ (\gamma,x{{n}}y{{p}}) $ reactions located on a background substrate, formed owing to the Compton scattering of photons. As an example, the γ-radiation spectrum of a natMo target with a mass of 57.862 mg after irradiation with$ E_{\rm{\gamma max}} $ = 92.50 MeV is shown in Fig. 2.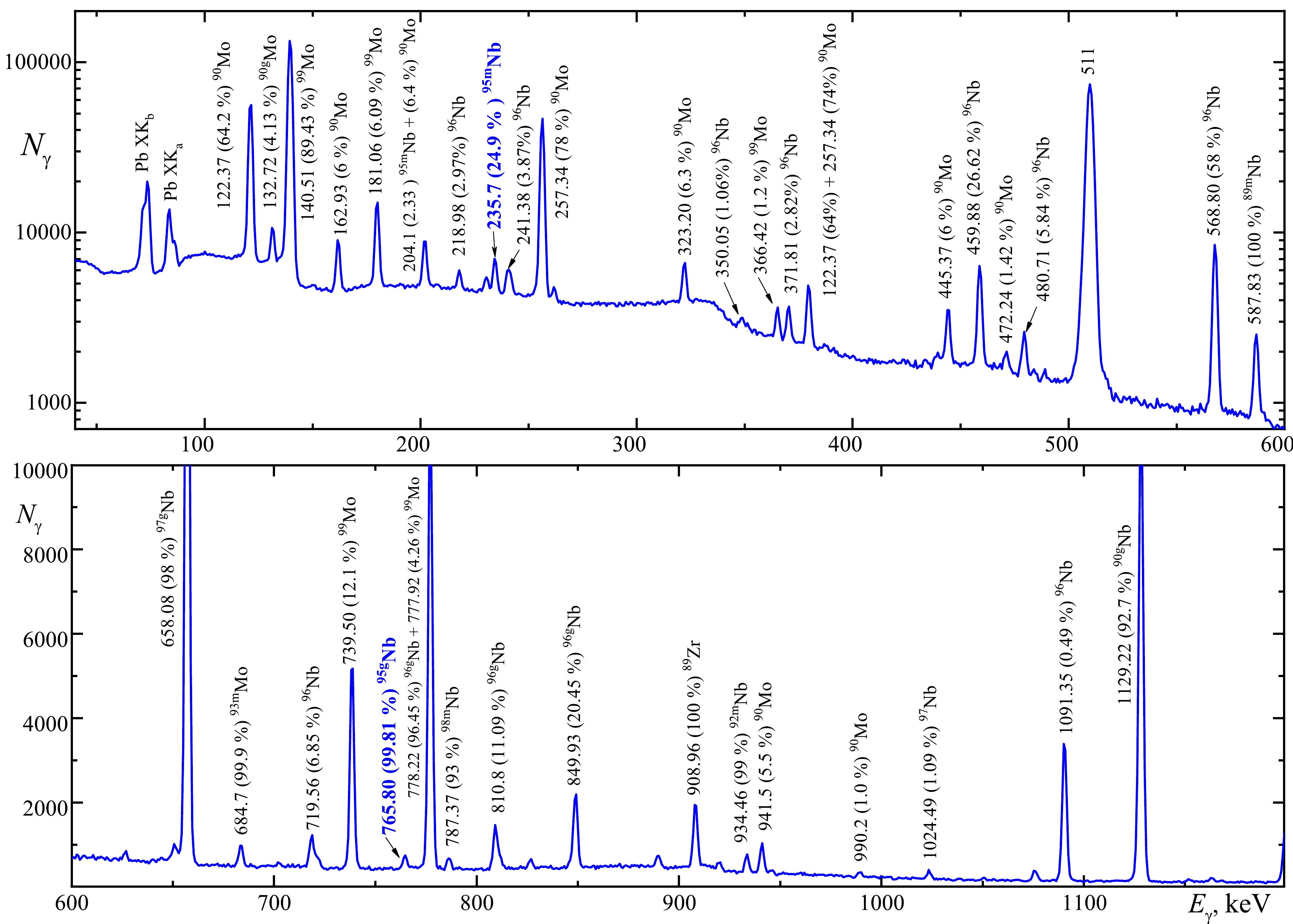
Figure 2. (color online) Fragments of γ-ray spectrum in the energy ranges
$ 40 \leq E_{\rm{\gamma}} \leq 600 $ keV and$ 600 \leq E_{\rm{\gamma}} \leq 1200 $ keV from the natMo target of mass 57.862 mg after irradiation of the bremsstrahlung γ-flux at the end-point energy$ E_{\rm{\gamma max}} $ = 92.50 MeV. The irradiation$ t_{\rm{irr}} $ and measurement$ t_{\rm{meas}} $ times were both 3600 s. -
The 95Nb nucleus in the metastable and ground states can be formed in photonuclear reactions natMo
$ (\gamma,x{{{{np}}}}) $ . Natural molybdenum consists of 7 stable isotopes, but only four isotopes contribute to the formation of the 95Nb nucleus; there are four reactions with the following thresholds:96Mo
$(\gamma,{{p}})^{95{{g}}} {\rm{Nb}}$ –$ E_{\rm{thr}} $ = 9.30 MeV;97Mo
$(\gamma,{{{np}}})^{95{{g}}} {\rm{Nb}}$ –$ E_{\rm{thr}} $ = 16.12 MeV;98Mo
$(\gamma,{{2np}})^{95{{g}}} {\rm{Nb}}$ –$ E_{\rm{thr}} $ = 24.76 MeV;100Mo
$(\gamma,{{4np}})^{95{{g}}} {\rm{Nb}}$ –$ E_{\rm{thr}} $ = 38.98 MeV.The thresholds for the formation of the
$ ^{95{{m}}} {\rm{Nb}} $ nucleus in the metastable state are higher than in the ground state, with an excess excitation energy of 235.7 keV.The calculation of theoretical cross-sections
$ \sigma(E) $ of studied reactions for monochromatic photons was performed using the TALYS1.95 code [32], which is installed on Linux Ubuntu-20.04, for different level density models LD 1-6. There are three phenomenological level density models and three options for microscopic level densities:$ LD 1 $ : Constant temperature + Fermi gas model, introduced by Gilbert and Cameron [35].$ LD 2 $ : Back-shifted Fermi gas model [36].$ LD 3 $ : Generalized superfluid model (GSM) [37, 38].$ LD 4 $ : Microscopic level densities (Skyrme force) from Goriely’s tables [39].$ LD 5 $ : Microscopic level densities (Skyrme force) from Hilaire’s combinatorial tables [40].$ LD 6 $ : Microscopic level densities based on temperature-dependent Hartree-Fock-Bogoliubov calculations using the Gogny force from Hilaire’s combinatorial tables [41].Figure 3 lists the total (metastable + ground) cross-sections
$ \sigma(E) $ for the formation of the 95Nb nucleus on 4 stable isotopes of molybdenum calculated in the TALYS1.95 code, LD1. The cross-sections for the 96,97,98,100Mo nuclei are given considering the abundance of isotopes. The cross-section of the natMo$ (\gamma,x{{{np}}})^{95} {\rm{Nb}} $ reaction is their algebraic sum. As can be seen, in the energy range above 35 MeV, the cross-section of the 98Mo$ (\gamma,{{2np}})^{95} {\rm{Nb}} $ reaction has the highest values. This is due to both the 98Mo isotopic abundance of 24.13% and insignificant differences in the cross-sections for the formation of the 95Nb nucleus on different molybdenum isotopes.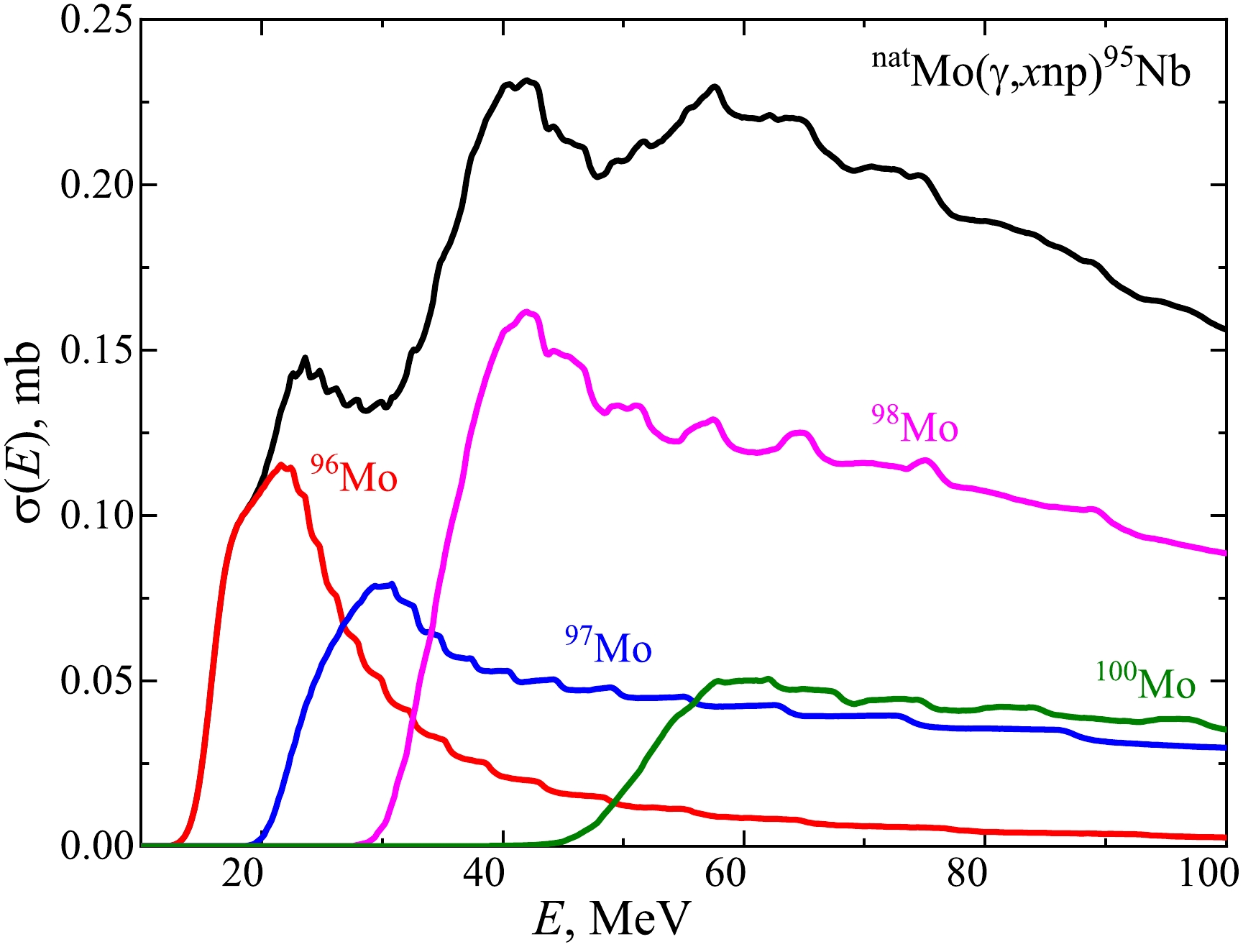
Figure 3. (color online) Theoretical total (metastable + ground) cross-sections
$ \sigma(E) $ for the formation of the 95Nb nucleus on stable isotopes of molybdenum 96,97,98,100Mo, considering isotopic abundance (color curves), and on natMo (black curve). The calculations were performed for the level density model LD1.Figure 4 shows the cross-sections
$ \sigma(E) $ for the formation of the 95Nb nucleus in the metastable and ground states in the natMo$ (\gamma,x{{{np}}}) $ reactions and the total cross-section calculated using the TALYS1.95 code, LD1. The cross-section for natMo$ (\gamma,x{{{np}}})^{95{{g}}} {\rm{Nb}} $ is the algebraic sum of the cross-sections of the formation of$ ^{95{{g}}} {\rm{Nb}} $ on each of the 4 isotopes multiplied by the isotopic abundance. Similarly, it needs to take sum in the case of the cross-section for the natMo(γ, xnp)$^{95{m}}{\rm{Nb}} $ reaction. The total cross-section is calculated as the sum of cross-sections for the ground and metastable states. As can be seen from the figure, the contribution of the metastable state to the total cross-section does not exceed 20% at energies above 30 MeV.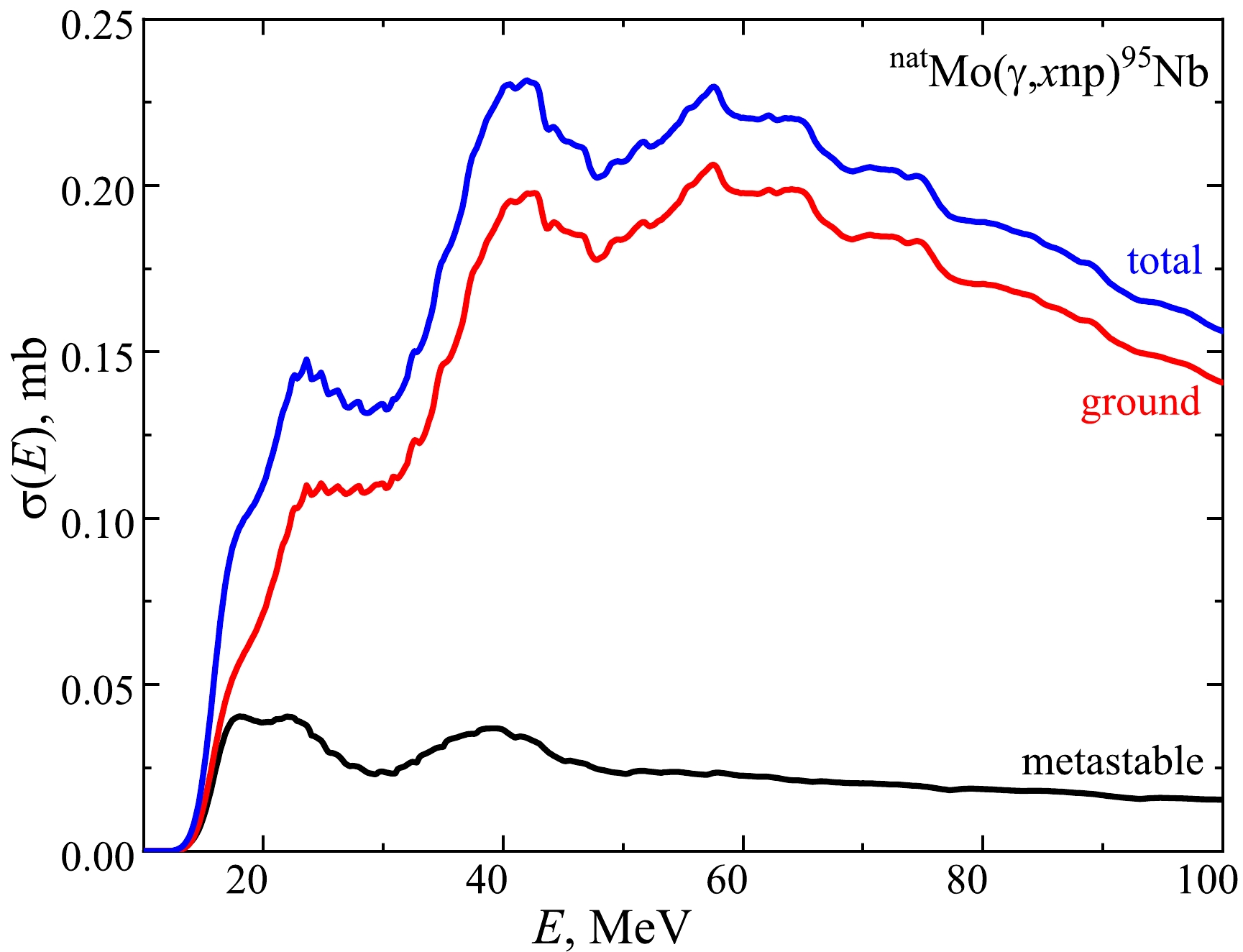
Figure 4. (color online) Theoretical cross-sections
$ \sigma(E) $ of the natMo$(\gamma,x{{{np}}})^{95{{m,g}}}{\rm{Nb}}$ reactions. The calculations were performed for the level density model LD1.Using the theoretical cross-section
$ \sigma(E) $ , one can obtain the reaction yield, which is determined by the formula$ Y(E_{\rm{\gamma max}}) = N_n \int\nolimits_{E_{{\rm{thr}}}}^{E_{\rm{\gamma max}}}\sigma(E)\cdot W(E,E_{\rm{\gamma max}}){\rm d}E, $

(1) where
$ N_n $ is the number of atoms of the element under study,$ W(E,E_{\rm{\gamma max}}) $ is the bremsstrahlung γ-flux,$ E_{\rm{thr}} $ is an energy of the reaction threshold, and$ E_{\rm{\gamma max}} $ is the bremsstrahlung end-point energy.To estimate the i-th reaction contribution in the total production of a studied nuclide (for example, the 96Mo
$ (\gamma,p) $ reaction in the production of the 95Nb nucleus on natMo), the relative reaction yield$ Y_{\rm{i}}(E_{\rm{\gamma max}}) $ was used. To calculate$ Y_{\rm{i}}(E_{\rm{\gamma max}}) $ , we used the cross-sections from the TALYS1.95 code and the following expression:$ Y_{\rm{i}}(E_{\rm{\gamma max}}) = \frac {A_i \displaystyle\int\nolimits_{E^i_{{\rm{thr}}}}^{E_{\rm{\gamma max}}}\sigma_i(E)\cdot W(E,E_{\rm{\gamma max}}){\rm d}E} {\sum^4_{k=1} A_k \displaystyle\int\nolimits_{E^k_{{\rm{thr}}}}^{E_{\rm{\gamma max}}}\sigma_k(E)\cdot W(E,E_{\rm{\gamma max}}){\rm d}E}, $

(2) where
$ \sigma_k(E) $ is the cross-section for the formation of the 95Nb nucleus on the k-th isotope with isotopic abundance$ A_k $ . Summation over k was performed for 4 stable molybdenum isotopes 96,97,98,100Mo. The relative reaction yield on a given isotope is affected by the cross-section, reaction threshold, and isotope abundance.As a rule, in the presence of several isotopes, there is one whose contribution to the reaction yield dominates (> 90%); see Refs. [42, 43] for examples. In the case of the reaction under study at energies up to 20 MeV, the contribution from the reaction on 96Mo is 100%. However, at the bremsstrahlung end-point energy above 30 MeV, it is difficult to determine the dominant reaction (see Fig. 5). Thus, for natural molybdenum, it is necessary to consider the contribution of all stable isotopes to the yield of the natMo
$ (\gamma,x{{{np}}})^{95} {\rm{Nb}} $ reaction.
Figure 5. (color online) Theoretical reaction yields of the 95Nb formation on various molybdenum isotopes relative to the total yield on natMo according to Eq. (2). The sum of the relative yield is equal to 1.0. The calculations were performed for the level density model LD1.
In this study, the values of the IR are calculated as the ratio of the yield
$ Y_{\rm{H}}(E_{\rm{\gamma max}}) $ of the formation of the nucleus in the high-spin state to the yield$ Y_{\rm{L}}(E_{\rm{\gamma max}}) $ of the formation of the nucleus in the low-spin state:$ IR = Y_{\rm{H}}(E_{\rm{\gamma max}}) / Y_{\rm{L}}(E_{\rm{\gamma max}}). $

(3) Figure 6 shows the theoretical prediction of the IR calculated using the cross-sections from the TALYS1.95 code with the LD1 model. As can be seen, the calculated IR values differ for different isotopes (96,97,98,100Mo). The IR value calculated for natural Mo is within the range of these varying values.
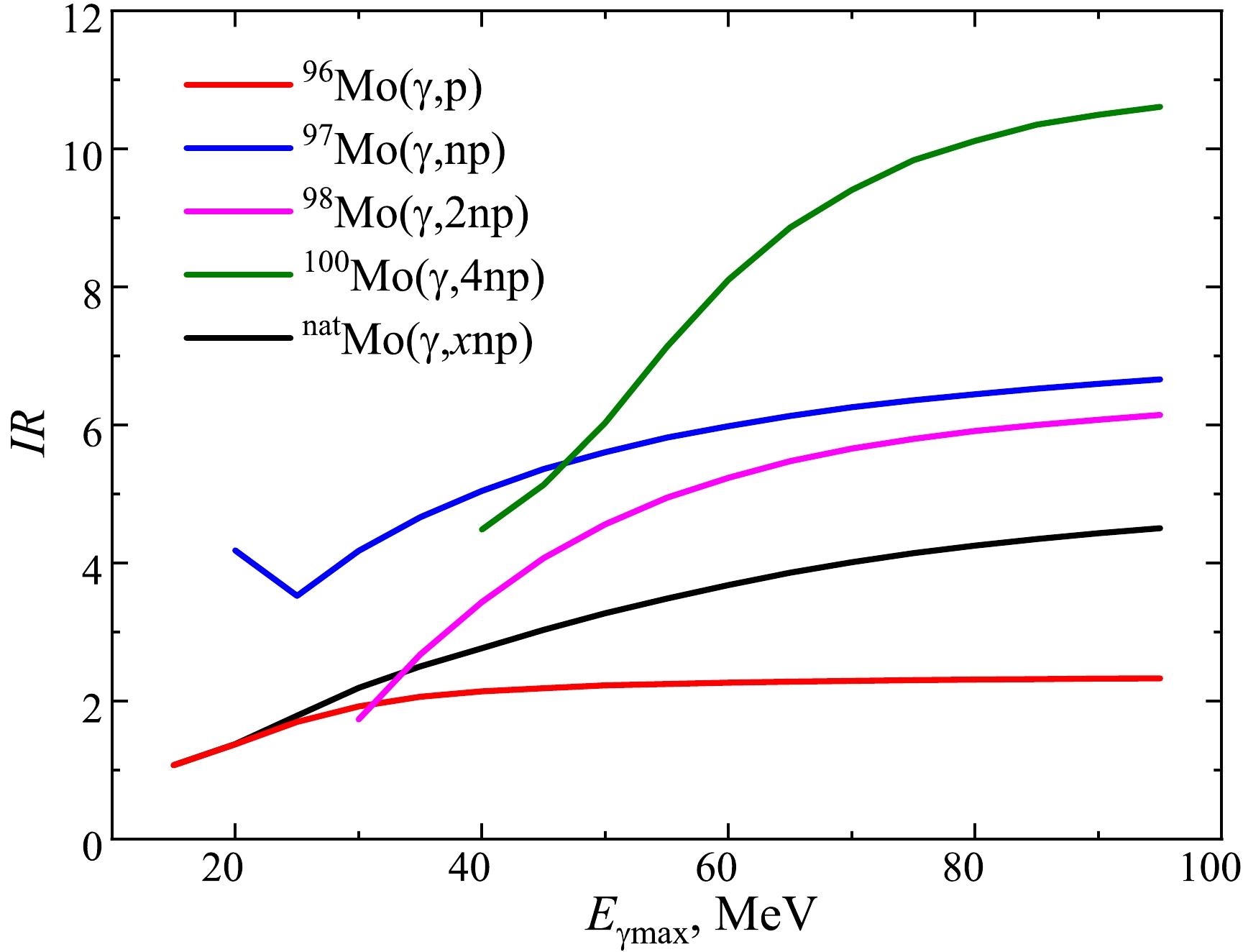
Figure 6. (color online) Theoretical IR values for the reaction products
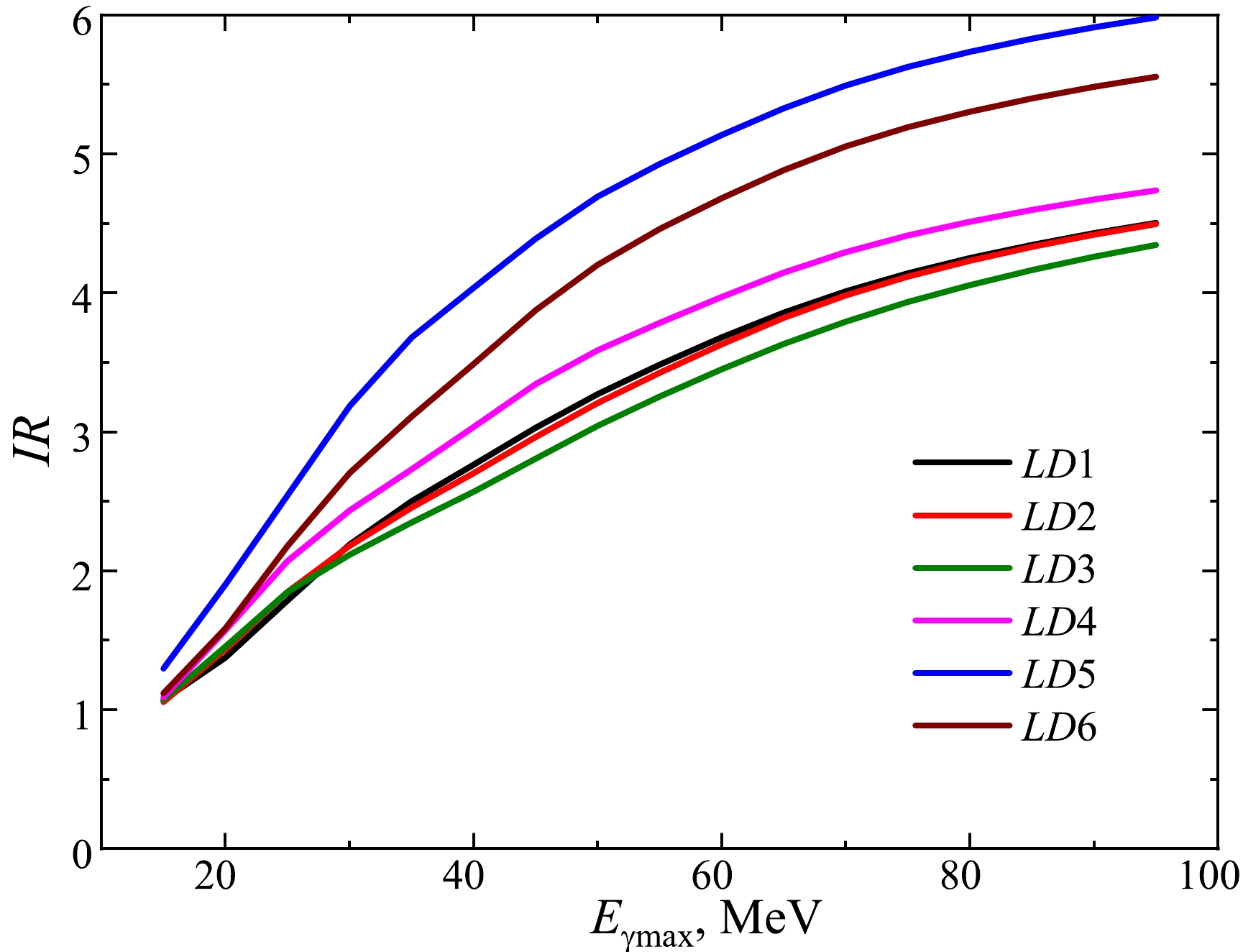
$^{95{{m,g}}}{\rm{Nb}} $ on different molybdenum isotopes and natMo. The calculations were performed for the level density model LD1.The theoretical estimations of the IR values were calculated using the cross-sections from the TALYS1.95 code for six level density models LD and are shown in Fig. 7. As can be seen, the theoretical IR values differ by 17%–36% in the range of
$ E_{\rm{\gamma max}} $ = 35–95 MeV. The IR calculated for the LD3 model has the lowest value in this energy range. -
A simplified diagram of the decay of the niobium nucleus from the ground
$^{95{{g}}} {\rm{Nb}}$ and metastable$^{95{{m}}} {\rm{Nb}}$ states is shown in Fig. 8, according to Ref. [1].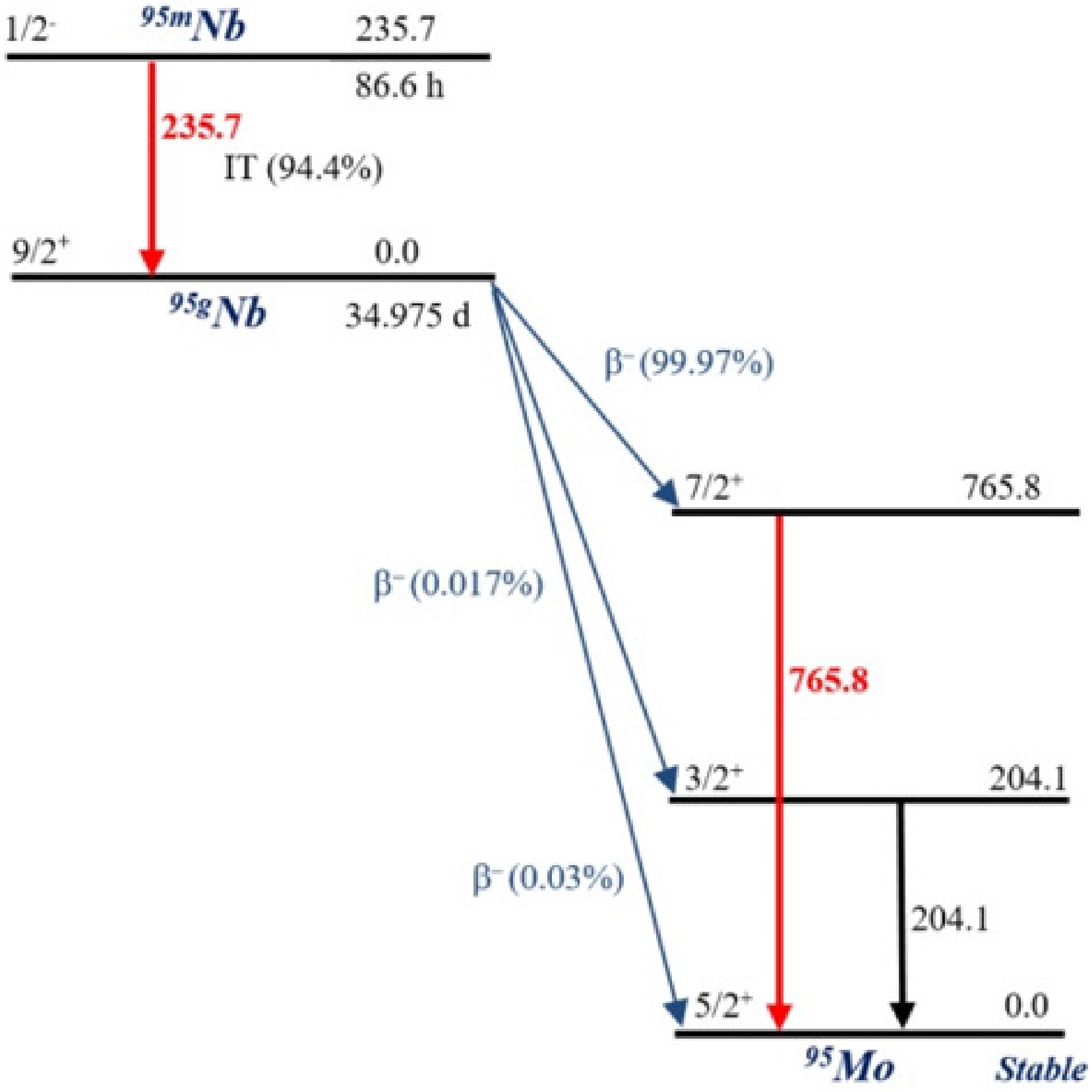
Figure 8. (color online) Simplified representation of the formation and decay scheme of the isomeric pair 95m,gNb. The nuclear level energies are in keV. The red color shows the emission γ-lines that were used in this study for the analysis.
The metastable state
$^{95{{m}}} {\rm{Nb}}$ ($ J^\pi = 1/2^{-} $ ) with a half-life$ T_{1/2} $ of$ 86.6 \pm 0.08 $ h decays to the unstable ground state$^{95{{g}}} {\rm{Nb}}$ ($ J^\pi = 9/2^{+} $ ) by emitting γ-quanta with an energy of 235.7 keV ($ I_\gamma = 24.9 \pm 0.8 $ %) through an internal transition with a branching ratio p of$ 94.4 \pm 0.6 $ %. Meanwhile, 5.6% of the metastable state decays to the various energy levels of stable 95Mo via a$ \beta^- $ -process. The unstable ground state$^{95{{g}}} {\rm{Nb}}$ with a half-life$ T_{1/2} $ of$ 34.975 \pm 0.007 $ d decays to the 765.8 keV ($ I_\gamma$ = 100%) energy level of 95Mo via a$ \beta^- $ -process (99.97%).This decay pattern leads to the ground state radionuclide
$^{95{{g}}} {\rm{Nb}}$ , which can be formed in two ways: directly from the target nuclide and/or indirectly through the decay of the metastable radionuclide.As a result, to find the experimental values of the IR, it is necessary to solve the system of equations describing the radioactive decay of the metastable state and decay with accumulation for the ground state. The solution of such a system of equations is described in several works [4, 44, 45], with different analytical representations.
In this study, to determine the experimental values of the IR, the following expression is used according to Ref. [44]:
$ \begin{aligned}[b] IR =& Y_{{H}}(E_{\rm{\gamma max}}) / Y_{{L}}(E_{\rm{\gamma max}}) = \\& \left[ \frac{\lambda_{{g}} F_{{m}}(t)}{\lambda_{{m}} F_{{g}}(t)} \left(\frac{\Delta A_{{g}} I_{{m}} \varepsilon_{{m}}}{\Delta A_{{m}} I_{{g}} \varepsilon_{{g}}} - p\frac{\lambda_{{g}}}{\lambda_{{g}} - \lambda_{{m}}}\right) + p\frac{\lambda_{{m}}}{\lambda_{{g}} - \lambda_{{m}}} \right], \end{aligned} $

(4) $ F_{{m}}(t) = (1-{\rm e}^{-\lambda_{{m}} t_{\rm{irr}}}){\rm e}^{-\lambda_{{m}} t_{\rm{cool}}}(1-{\rm e}^{-\lambda_{{m}} t_{\rm{meas}}}), $

(5) $ F_{{g}}(t) = (1-{\rm e}^{-\lambda_{{g}} t_{\rm{irr}}}){\rm e}^{-\lambda_{{g}} t_{\rm{cool}}}(1-{\rm e}^{-\lambda_{{g}} t_{\rm{meas}}}), $

(6) where
$\lambda_{{g}}$ and$\lambda_{{m}}$ are the decay constants for the ground and metastable states, respectively;$\Delta A_{{g}}$ and$\Delta A_{{m}}$ are the number of counts under the peaks at the energies of γ-quanta corresponding to the decays of the ground and metastable states, respectively;$\varepsilon_{{g}}$ and$I_{{g}}$ ($\varepsilon_{{m}}$ and$I_{{m}}$ ) are the detector efficiency and absolute intensity of a γ-quantum with an energy corresponding to the decay of the ground state (metastable state); p is the branching ratio for the decay of the metastable to the ground state (94.4%); and$ t_{\rm{irr}} $ ,$ t_{\rm{cool}} $ , and$ t_{\rm{meas}} $ are the irradiation time, cooling time, and measurement time, respectively.In natural molybdenum targets, as a result of the natMo
$ (\gamma,x{{n2p}}) $ reaction, the 95Zr nucleus can also be formed. In the decay scheme of 95Zr ($ T_{1/2} = 65.02 \pm 0.05 $ d), there is a γ-transition with an energy$ E_\gamma $ = 235.7 keV and intensity$ I_\gamma = 0.294 \pm 0.016 $ %. The decay of the 95Zr nucleus can contribute to the observed value of$\Delta A_{{m}}$ . Considering this contribution, calculations were performed in the TALYS1.95 code with level density model LD1. It was found that the activity of 95Zr estimated using the γ-linewith 235.7 keV is negligible. The contribution of 95Zr was also experimentally verified by the γ-lines corresponding to the decay of the 95Zr nucleus, namely,$ E_\gamma $ = 724.2 keV ($ I_\gamma = 44.17 \pm 0.13 $ %) and$ E_\gamma $ = 756.7 keV ($ I_\gamma $ = 54%). No such peaks were found in the measured spectra of the induced γ-activity of the targets.For the γ-quanta with an energy of 235.7 keV and the thicknesses of the molybdenum targets used, the self-absorption coefficients were calculated using the GEANT4.9.2 code. It was found that the value of the self-absorption coefficient did not exceed 0.8%, which was considered when processing the experimental results.
The experimental values of the IR of the nuclei products from the natMo
$ (\gamma,x{{{np}}})^{95{{m,g}}}{\rm{Nb}} $ reaction were determined at the bremsstrahlung end-point energy of 38–93 MeV (see Fig. 9 and Table 1).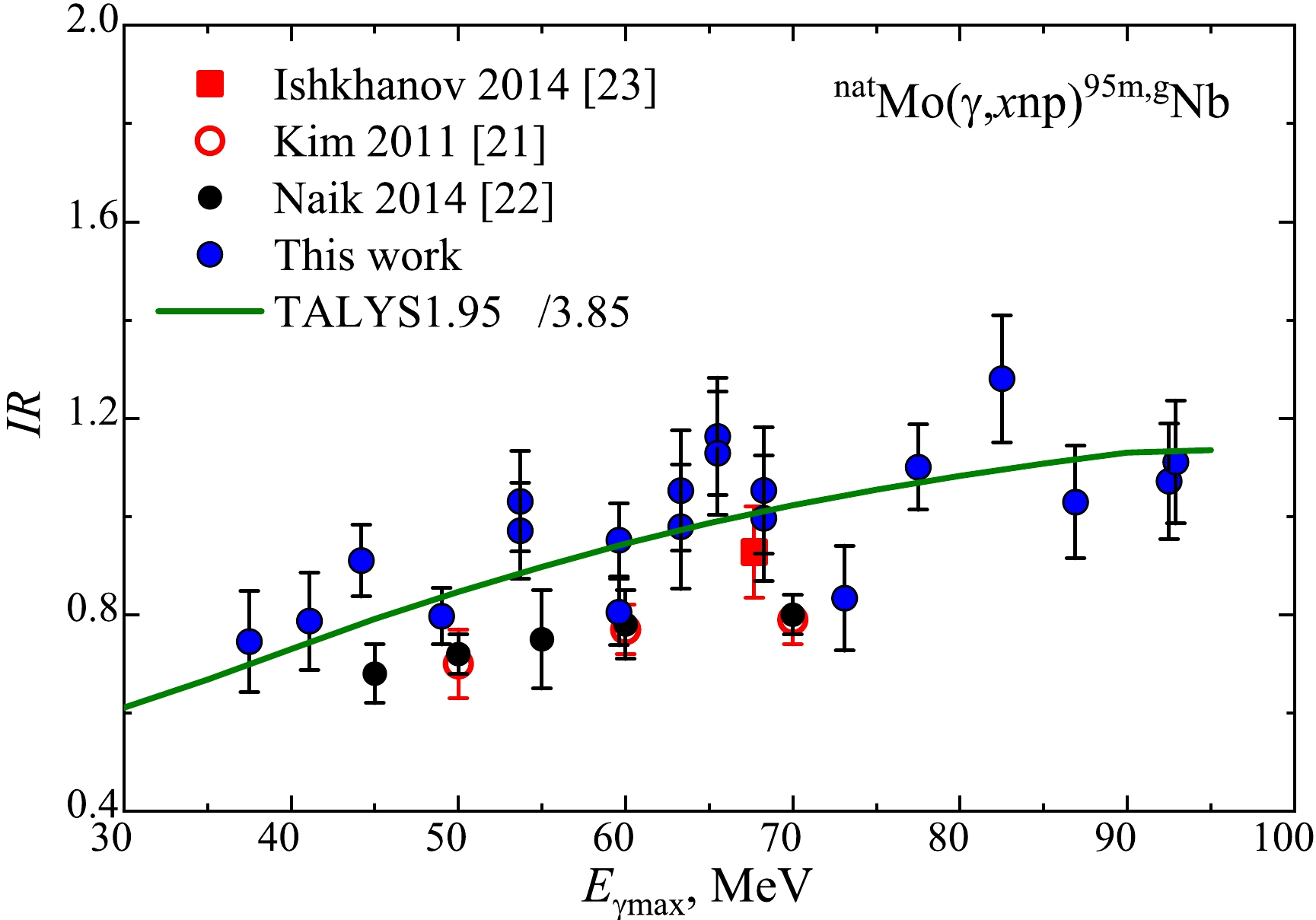
Figure 9. (color online) IR for the reaction products from the natMo
$(\gamma,x{{{np}}})^{95{{m,g}}}{\rm{Nb}}$ reaction. Experimental results of this study are indicated using blue circles. The data of other studies are indicated as follows: square – [23], red empty circles – [21], and black circles – [22]. The curve indicates the calculation using the code TALYS1.95, LD3, divided by a factor of 3.85.$ E_{\rm{\gamma max}} $ /MeV

$IR \pm \Delta IR $ 

37.50 0.75 ± 0.10 41.10 0.79 ± 0.10 44.20 0.91 ± 0.07 49.00 0.80 ± 0.06 53.70 0.97 ± 0.10 53.70* 1.03 ± 0.10 59.60 0.95 ± 0.07 59.60* 0.81 ± 0.07 63.30 1.05 ± 0.12 63.30* 0.98 ± 0.13 65.50 1.16 ± 0.12 65.50* 1.13 ± 0.13 68.25 1.05 ± 0.13 68.25* 1.00 ± 0.13 73.10 0.83 ± 0.11 77.50 1.10 ± 0.09 82.50 1.28 ± 0.13 86.90 1.03 ± 0.11 92.50 1.07 ± 0.12 92.90 1.11 ± 0.13 Table 1. IR for the nuclei products
$^{95{{m,g}}}{\rm{Nb}}$ from the$ {^{\rm{nat}}{\rm{Mo}}}(\gamma,x{{{np}}}) $ reaction.The calculation of the experimental error of the IR values was performed considering statistical and systematic errors, the description of which can be found, for example, in [24, 25]. The uncertainties related to IR were calculated from Eq. (4) using the error propagation principle, which indicates the maximum uncertainty of the measured values in Fig. 9 and Table 1.
-
Two main representations of the IR are used in literature. One of them is defined as the ratio of the yields of states,
$Y_{{m}}(E_{\rm{\gamma max}})$ and$Y_{{g}}(E_{\rm{\gamma max}})$ :$IR = Y_{{m}}(E_{\rm{\gamma max}}) / Y_{{g}}(E_{\rm{\gamma max}})$ (for example, see Ref. [18]). The IR values can also be found as the ratio of the yield for the formation of a product nucleus in the high-spin state$ Y_{\rm{H}}(E_{\rm{\gamma max}}) $ to the yield for the low-spin state$ Y_{\rm{L}}(E_{\rm{\gamma max}}) $ :$ IR = Y_{\rm{H}}(E_{\rm{\gamma max}}) / Y_{\rm{L}}(E_{\rm{\gamma max}}) $ [21, 22]. These values will be equal to each other if the nucleus in the metastable state has a larger spin. However, the ground state of the 95Nb nucleus has a high spin$ J^\pi = 9/2^{+} $ , while the spin of the$^{95{{m}}} {\rm{Nb}}$ metastable state is$ J^\pi = 1/2^{-} $ . This means that the values of IR described above are inversely proportional to each other and are presented differently in different works.In this study, the experimental IR values of the pair
$^{95{{m,g}}}{\rm{Nb}} $ were obtained by Eq. (4). A comparison of our results with the data of other studies [21, 22] shows satisfactory agreement within the experimental error. The estimate of the value of IR, obtained using the yield values from Ref. [23], is in agreement with both our results and the data from Refs. [21, 22].The IR values (in
$ Y_{\rm{H}} / Y_{\rm{L}} $ presentation) for most photonuclear reactions increase rapidly as the bremsstrahlung energies increase from the reaction threshold up to the end of the GDR region. The fast-increasing IR values can be explained by a compound nuclear reaction mechanism, in which the increased momentum was transferred to the compound nuclei. After ~30 MeV, the IR increases slowly in all energy ranges, which has been shown in Refs. [22, 46]. At higher incident energies, the direct channel of the$ (\gamma,x{{n}}) $ or$ (\gamma,x{{{np}}}) $ reactions also occurs. The directly emitted particles carry away a relatively large angular momentum, and only fractions of the energy and angular momentum of the incident quanta are transformed into the target nucleus. The direct reactions largely suppress the population of states with higher spins, and the yield ratio of high to low-spin states might not continue their rapidly increasing trend. These patterns are discussed in Refs. [46, 47].The saturation of IR for each isotope occurs at different excitation energies of the compound nucleus, the value of which is related to the form of the energy dependence of the reaction cross-section and a reaction threshold on a given isotope. We present our data from the bremsstrahlung end-point energy. The observed dependence of IR on
$ E_{\rm{\gamma max}} $ for natMo is a weighted combination of IR for 4 stable isotopes.The range of changes in the experimental values of IR indicates that the yield for the formation of the
$^{95{{g}}} {\rm{Nb}}$ nucleus on natMo differs from the production yield of$^{95{{m}}} {\rm{Nb}}$ by 0.7–1.2 times. At the same time, the experimental results obtained in this study and literature data [21–23] are significantly lower than the theoretical predictions obtained with the cross-sections from the TALYS1.95 code with level density models LD 1–6. The difference between the theoretical and experimental values is 3.85 to 5.80 times. These factors were obtained by the$ \chi^2 $ method using all experimental values shown in Fig. 9. The result of the theoretical calculation of IR, obtained using the level density model LD3, is the closest to the experimental data.The observed difference may be due to the underestimation of the calculation for the cross-section of the formation of the nucleus in the metastable state. Alternatively, it may be the result of incorrect calculation of both
$\sigma_{{m}}(E)$ and$\sigma_{{g}}(E)$ . However, the theoretical prediction of the energy dependence of IR describes well the gradual increase in the measured values with increasing$ E_{\rm{\gamma max}} $ in the energy range under study. -
In the present study, the experiment was performed using the beam from the NSC KIPT linear accelerator LUE-40 and the activation and off-line γ-ray spectrometric technique. The IR values of the
$^{95{{m,g}}}{\rm{Nb}} $ reaction products from photonuclear reactions on natural Mo were determined. The region of bremsstrahlung γ-quanta spectra had the end-point energy of$ E_{\rm{\gamma max}} $ = 38–93 MeV. Within experimental errors, the present data are in satisfactory agreement with the available literature data [21–23].The calculations of IR were performed using the cross-sections
$ \sigma(E) $ for the studied reaction from the TALYS1.95 code for the six level density models LD 1–6.The comparison of the experimental and calculated values of IR for the isomeric pair
$^{95{{m,g}}}{\rm{Nb}}$ from the$ {^{\rm{nat}}{\rm{Mo}}}(\gamma,x{{{np}}}) $ reaction showed a significant excess of the theoretical predictions over the experimental values. The result of the theoretical calculation of IR, obtained using the level density model LD3, is the closest to the experimental data. For the investigated range of$ E_{\rm{\gamma max}} $ , the theoretical dependence of IR on energy was confirmed – the IR smoothly increases with increasing energy. -
The authors would like to thank the staff of the linear electron accelerator LUE-40 NSC KIPT, Kharkiv, Ukraine, for their cooperation in the realization of the experiment.
-
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Isomeric pair 95m,g Nb in the photonuclear reactions on natMo at the bremsstrahlung end-point energy of 38–93 MeV
- Received Date: 2023-07-09
- Available Online: 2023-12-15
Abstract: The





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: