-
The observations of neutrino oscillations have thus far prompted several puzzles about neutrinos in the Standard Model (SM), including their tiny mass origin, Dirac or Majorana nature, and distinctive Pontecorvo–Maki–Nakagawa–Sakata (PMNS) mixing pattern from that of the quark Cabibbo–Kobayashi–Maskawa mixing matrix. Any attempt towards these problems has catalyzed a host of investigations from theoretical constructions to experimental searches, and from low-energy particle physics to high-temperature early Universe. Despite the leading interests in the Majorana neutrinos, the Dirac neutrino scenarios on their own right can help to explain some fundamental problems encountered in the SM, such as the baryon asymmetry of the Universe (BAU) [1, 2] and its connection to the dark matter origin [3–5]. In addition, the Dirac neutrino scenarios could generate promising experimental signals especially in the lepton-flavor-violating (LFV) processes [6–8] and in the cosmic detection via the effective neutrino number shift,
$ \Delta N_{\rm eff} $ , at the big-bang nucleosynthesis (BBN) [9–12] and cosmic microwave background (CMB) epochs [13–17].A simple and testable scenario for generating the Dirac neutrino masses is obtained by introducing a new Higgs doublet with a much smaller vacuum than the electroweak one and an exclusive interaction to the neutrinos, i.e., the neutrinophilic two-Higgs-doublet model (2HDM) [18, 19] (for Majorana neutrinos in the 2HDM, see, e.g., Refs. [20–24]). In most previous investigations [6–8], however, an eV-scale Higgs vacuum was often invoked to embrace the
$ \mathcal{O}(1) $ neutrino Yukawa couplings. Detailed phenomenological analyses of such an eV-vacuum Dirac neutrino model have also been performed in Refs. [6–8], pointing out especially that the LFV process$ \mu\to e \gamma $ can reach the future MEG sensitivities [25, 26]. However, the$ \mathcal{O}(1) $ Yukawa couplings for three right-handed Dirac neutrinos can delay their decoupling in the early Universe via the effective four-fermion interactions mediated by the new scalar [27], and thus can readily violate the bound of$ \Delta N_{\rm eff} $ extracted from the BBN and CMB measurements [13]. If the new scalar doublet has a higher-scale vacuum instead, it could be expected that the resulting LFV rates of$ \ell_\alpha \to \ell_\beta \gamma $ ,$ \ell_\alpha \to 3\ell_\beta $ ,$ Z\to \ell_\alpha \ell_\beta $ ,$ h\to \ell_\alpha \ell_\beta $ , or$ \mu-e $ conversion in nuclei would quickly drop below the future sensitivities.When the vacuum reaches the keV scale, a purely thermal Dirac leptogenesis mechanism [28, 29] can be at work to explain the BAU problem and further help to predict the Dirac CP-violating phase in neutrino oscillation experiments [30]. The generation of leptonic CP asymmetry considered in Refs. [28, 29] is a purely finite-temperature effect, which requires fewer lepton Yukawa matrices to participate in the BAU generation, and consequently renders a direct link between the low-energy leptonic CP violation and the BAU via some simple basis transformations. As detailed in Ref. [29], there are two possible candidates to realize such a purely thermal Dirac leptogenesis, which can be either triggered by the lightest Dirac neutrino or by the two lighter ones. However, given the current neutrino mass spectrum inferred from the oscillation experiments and cosmological constraints, the baryogenesis via the lightest Dirac neutrino can be the most natural candidate for the BAU resolution, as will be demonstrated in this work.
In addition to providing a simple framework to explain the Dirac neutrino mass origin and the matter-antimatter asymmetry in the early Universe, the keV-vacuum neutrinophilic 2HDM can manifest itself via a significant contribution to the
$ \Delta N_{\rm eff} $ shift. The prediction of$ \Delta N_{\rm eff} $ can then be correlated to the purely thermal Dirac leptogenesis, providing consequently a compelling test of the keV-vacuum desert considered here. In particular, such a keV-vacuum scenario predicts$ 0.097\leqslant \Delta N_{\rm eff}\leqslant 0.112 $ , in which the upper bound can be tested in the future Simons Observatory (SO) [31, 32] survey, while the lower limit can be fully falsified by the forecast sensitivities from, e.g., the CMB Stage-IV (CMB-S4) experiments [33, 34], the Large Scale Structure (LLS) surveys [35, 36], and their combinations. Therefore, any observation of the LFV processes in the future experiments will rule out this keV-vacuum desert in the neutrinophilic 2HDM. Even if no LFV signal is observed, the$ \Delta N_{\rm eff} $ shift can still serve as a complementary and promising observable to test such a Dirac neutrino scenario that bridges the BAU and neutrino mass origins.The purpose of this work is, therefore, to explore the desert where the vacuum in the neutrinophilic 2HDM populates in the keV scale by focusing on its potential effects in the cosmological regime. We will assume that the new scalar mass is determined by the electroweak vacuum such that the perturbative unitarity condition sets the mass bounded from above. It will be shown that this scenario is more realistic and also more predictable than the one considered in Ref. [29], because the scalar vacuum is confined within a narrow keV range and the lightest neutrino mass is predicted to be lighter than
$ 0.004 $ eV.In Sec. II, we revisit briefly the keV-vacuum neutrinophilic 2HDM with a quasi-degenerate scalar mass spectrum. Then, in Sec. III, we show the inert property of the scenario in the low-energy flavor physics with typical examples from the severely constrained LFV transitions. In Sec. IV, we illustrate the
$ \nu_1 $ -leptogenesis mechanism as a natural BAU resolution, and the resulting$ \Delta N_{\rm eff} $ phenomenology is analyzed in Sec. V. Finally, our conclusion is presented in Sec. VI. -
The Dirac neutrino masses could be simply generated by coupling the right-handed Dirac neutrinos
$ \nu_R $ to a new Higgs doublet Φ via$ \begin{array}{*{20}{l}} -\mathcal{L}_\nu= Y_\nu \bar L \tilde{\Phi} \nu_R+\rm h.c., \end{array} $

(1) in addition to the SM content. A global
$ U(1) $ symmetry can be imposed to forbid$ \nu_R $ from interacting with the SM-like Higgs doublet$ \Phi_{\rm SM} $ that is responsible for all the charged fermion masses. In addition, the classical lepton-number symmetry is invoked to forbid the Majorana mass term$ \overline{\nu_R^c}\nu_R $ , such that the right-handed Dirac neutrinos also carry lepton numbers to realize the Dirac leptogenesis [1]. The global$ U(1) $ symmetry is explicitly and softly broken in the scalar potential via [19]$ \begin{aligned}[b] V(\Phi_{\rm SM},\Phi)=&m_{11}^2 \Phi_{\rm SM}^\dagger \Phi_{\rm SM}+m_{22}^2 \Phi^\dagger \Phi -\left[\mu^2 \Phi_{\rm SM}^\dagger \Phi+ \text{h.c.}\right]\\&+\frac{\lambda_1}{2}(\Phi_{\rm SM}^\dagger \Phi_{\rm SM})^2 +\frac{\lambda_2}{2}(\Phi^\dagger \Phi)^2\\&+\lambda_3(\Phi_{\rm SM}^\dagger\Phi_{\rm SM})(\Phi^\dagger \Phi) +\lambda_4 (\Phi_{\rm SM}^\dagger \Phi)(\Phi^\dagger \Phi_{\rm SM}). \end{aligned} $

(2) After the spontaneously electroweak symmetry breaking specified by
$ \langle 0\vert \Phi_{\rm SM}^T\vert 0 \rangle=(0,v_{\Phi_{\rm SM}}/\sqrt{2}) $ and$ \langle 0\vert \Phi^T\vert 0 \rangle= (0,v_{\Phi}/\sqrt{2}) $ , the soft$ U(1) $ breaking induced by the$ \mu^2 $ term seeds a seesaw-like suppression of the new scalar vacuum, leading to [18, 19]$ v_{\Phi_{\rm SM}} \simeq v_{\rm EW}, \qquad v_\Phi\simeq \frac{\mu^2 }{m_{22}^2+\bar\lambda v_{\rm EW}^2}v_{\rm EW}, $

(3) where
$ (v_{\Phi_{\rm SM}}^2+v_\Phi^2)^{1/2}\simeq v_{\rm EW}\simeq 246 $ GeV and$ \bar\lambda\equiv (\lambda_3+\lambda_4)/2 $ . As we are concerned with a keV-scale vacuum$ v_\Phi\simeq \mathcal{O}(\rm keV) $ to generate the tiny Dirac neutrino masses via Eq. (1) and with an electroweak-scale doublet Φ, Eq. (3) would point out that the soft scale is at$ \mu\simeq \mathcal{O}(10^{-2}) $ GeV if$ m_{22}^2+\bar\lambda v_{\rm EW}^2\simeq \mathcal{O}(10^2) $ GeV. Note that$ m_{22} $ is a free parameter in Eq. (2). However, if$ m_{22}\ll \bar\lambda v_{\rm EW}^2 $ , the new Higgs doublet can still live in the electroweak regime and, at the same time, the masses of the new Higgs scalars will be independent of$ m_{22} $ , as we shall see below.The resulting hierarchy
$ v_{\rm EW}\gg v_\Phi $ makes the$ \Phi_{\rm SM}–\Phi $ mass mixing suppressed at the order of$ v_\Phi/v_{ \rm EW}\simeq 10^{-8} $ , guaranteeing therefore$ \Phi_{\rm SM} $ the SM-like Higgs. The corresponding physical scalar mass spectrum from the new Higgs doublet then reads$ m_{H^+}^2=m_{22}^2+\frac{\lambda_3}{2}v_{\rm EW}^2,\quad m_{H^0}^2=m_A^2=m_{H^+}^2+\frac{\lambda_4}{2}v_{\rm EW}^2, $

(4) where
$ H^+ $ is the charged Higgs boson,$ H^0 $ the neutral scalar, and A the neutral pseudoscalar in the CP-conserving limit. An interesting mass spectrum to be considered in this work is the quasi-degenerate limit,$m_S\equiv m_{H^0}= m_A\approx m_{H^+}$ , achieved in the small$ \lambda_4 $ regime. Under the quasi-degenerate circumstance, such a simple framework is characterized by only two free parameters, the scalar mass$ m_S $ and the vacuum scale$ v_\Phi $ . When the neutrino masses and PMNS matrix are pinpointed from the experimental measurements, the framework is already able to provide a very predictable and correlative phenomenology, as will be exploited in this work. We will further consider an interesting situation where$m_{22}\ll \lambda_3 v_{\rm EW}$ . In this case, the new scalar mass is approximated by$ m_S\approx \sqrt{\lambda_3/2} v_{\rm EW}, $

(5) and will be bounded from above owing to the perturbative unitarity condition [37, 38]. For example, taking
$ |\lambda_3|<4\pi $ , the upper limit of the scalar mass is given approximately by$ m_S\approx 617 $ GeV. Such an upper limit can be in turn used to constrain the vacuum as well as the lightest neutrino mass, as will be detailed in Sec. IV. -
Most previous studies on the neutrinophilic 2HDM focused on a vacuum
$ v_\Phi $ at eV or even lower scales [6–8, 18, 19]. It can be observed from Eq. (1) that sub-eV neutrino masses indicate$ \mathcal{O}(1) $ Yukawa couplings$ Y_\nu $ . Such large couplings will contribute to the tree-level$ H^+ $ -mediated lepton decays$ \ell_\alpha \to \ell_\beta \nu\bar \nu $ as well as the loop-induced LFV processes, such as$ \ell_\alpha \to \ell_\beta \gamma $ ,$ \ell_\alpha \to 3\ell_\beta $ ,$ Z\to \ell_\alpha \ell_\beta $ , and$ h\to \ell_\alpha \ell_\beta $ . However, due to the vacuum hierarchy$ v_{\rm EW}\gg v_\Phi $ , the quark couplings to the new scalars are strongly suppressed and their effects in the quark sector, e.g., in the flavor-changing neutral-current processes$ b\to s\gamma $ ,$ b\to s \ell \bar\ell $ and in the$ B_q-\bar B_q $ mixing systems, are all negligible. In this section, we will show with two stringently constrained processes$ \ell_\alpha \to \ell_\beta \gamma $ and$ \ell_\alpha \to 3\ell_\beta $ that the neutrinophilic 2HDM with a keV-scale vacuum is nearly secluded from the low-energy flavor physics.As investigated already in Ref. [8], owing to the current and future experimental sensitivities, the most prominent signatures of the neutrinophilic 2HDM are expected to be observed in the LFV transitions. For the
$ \ell_\alpha \to \ell_\beta \gamma $ decays, the contribution comes from the$ H^+– H^-–\nu_R $ loop, with the resulting branching ratios given by$ \mathcal{B}(\ell_\alpha \to \ell_\beta \gamma)\equiv \frac{\Gamma(\ell_\alpha\to \ell_\beta \gamma)}{\Gamma(\ell_\alpha\to e \nu \bar \nu)}=\frac{\alpha_{\rm EM}}{96\pi} \left(\frac{v_{\rm EW}}{m_S v_\Phi}\right)^4 \Big| U_{\alpha i} m_{i}^2 U^\dagger_{i\beta}\Big|^2. $

(6) Here, U is the PMNS matrix, and we have replaced the diagonal neutrino Yukawa matrix
$ \hat{Y}_{\nu}\equiv U Y_\nu $ by the physical neutrino masses$ m_{i} $ , with$ \hat{Y}_{\nu,i}=\sqrt{2}m_{i}/v_\Phi $ .① As the differences from both the neutrino masses and the PMNS matrix elements [39] are not significantly large, the branching ratios$ \mathcal{B}(\ell_\alpha \to \ell_\beta \gamma) $ for different lepton flavors are governed by the overall factor$ v_{\rm EW}m_i/m_S v_\Phi $ . Therefore, the most severe bound from the current MEG experiment [25],$ \mathcal{B}(\mu\to e\gamma)<4.2\times 10^{-13} $ , controls the largest allowed rate for a generic process$ \ell_\alpha \to \ell_\beta \gamma $ . Nevertheless, an order-of-magnitude estimate shows that, for the largest neutrino mass scale$ 0.05 $ eV (see Fig. 1) and$ |U|\simeq \mathcal{O}(0.1) $ ,$ \mathcal{B}(\ell_\alpha \to \ell_\beta \gamma)\lesssim \mathcal{O}(10^{-26}) $ is predicted for$ v_\Phi\gtrsim 1 $ keV and$ m_S\gtrsim v_{\rm EW} $ , which is far below the future MEG sensitivity of$ \mathcal{B}(\mu\to e\gamma)<6\times 10^{-14} $ [26].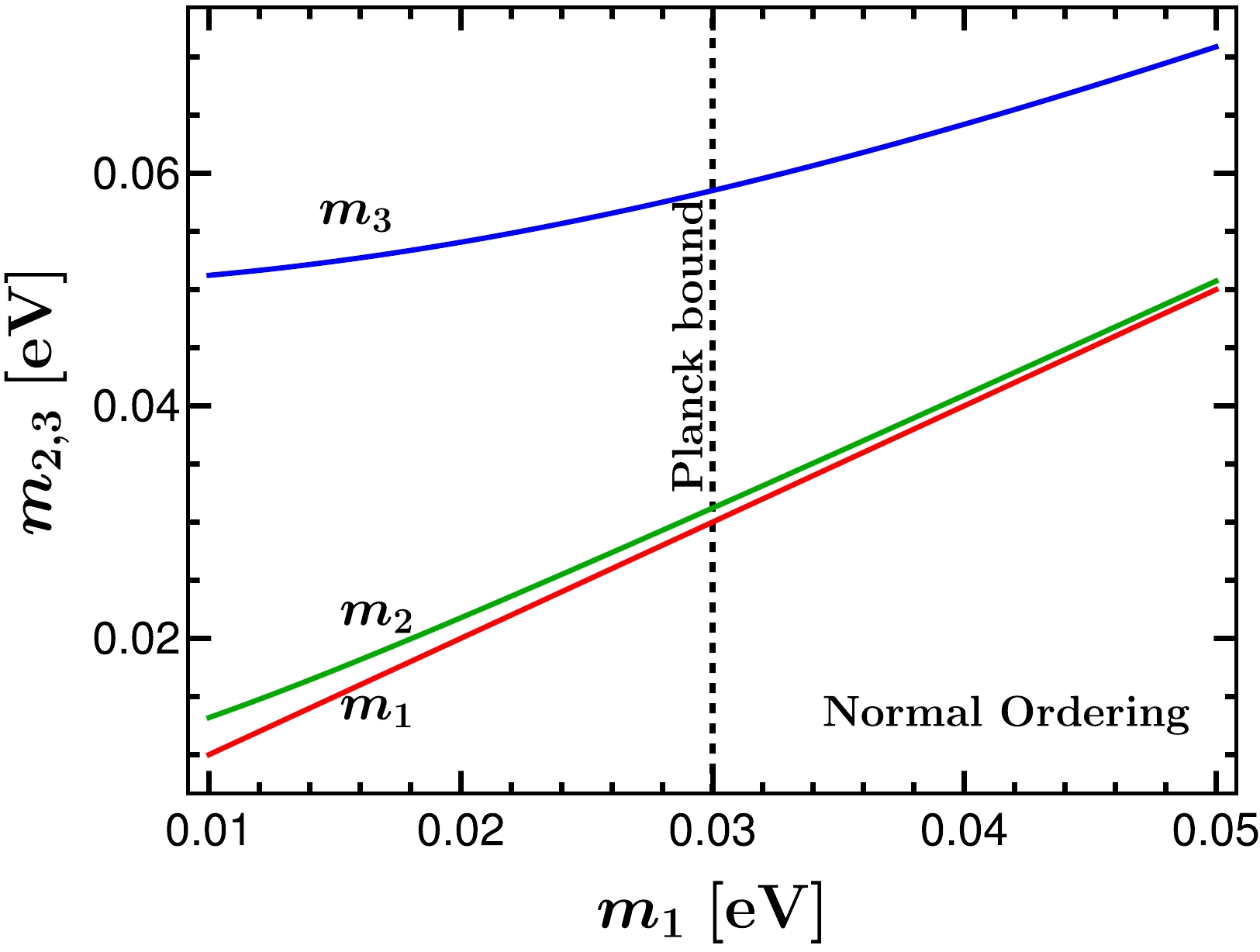
Figure 1. (color online) Current neutrino mass spectrum in the normal ordering. The lightest neutrino mass has a maximum value
$ m_1\simeq 0.030 $ eV after saturating the Planck mass bound$ \sum_i m_{\nu_i}<0.12 $ eV (vertical dashed line) [13]. We also depict the lightest neutrino mass (red) to have a clear comparison with the two heavier ones (green and blue).For the LFV
$ \ell_\alpha \to 3\ell_\beta $ processes, the dominant contribution in the higher$ v_\Phi $ region comes from the γ-penguin diagram with the$ H^+ – H^-–\nu_R $ loop, leading to [8]$ \begin{aligned}[b] \mathcal{B}(\ell_\alpha \to 3\ell_\beta)\equiv& \frac{\Gamma(\ell_\alpha \to 3\ell_\beta)}{\Gamma(\ell_\alpha \to e \nu \bar \nu)} \simeq \frac{\alpha_{\rm EM}^2}{3456\pi^2}\left(\frac{v_{\rm EW}}{m_S v_\Phi}\right)^4\\&\times\left(24\ln\left(\frac{m_{\ell,\alpha}}{m_{\ell,\beta}}\right)-43\right)\Big| U_{\alpha i} m_{i}^2 U^\dagger_{i\beta}\Big|^2. \end{aligned} $

(7) Similar to that observed for the
$ \ell_\alpha\to \ell_\beta \gamma $ decays, the$ \ell_\alpha \to 3\ell_\beta $ rates are governed by the common scale ratio$ v_{\rm EW}m_i/m_S v_\Phi $ . An order-of-magnitude estimate tells us that$ \mathcal{B}(\ell_\alpha \to 3\ell_\beta)\lesssim 10^{-28} $ , which is far below the future Mu3e sensitivity of$ \mathcal{B}(\mu\to 3e)\simeq 10^{-16} $ [40].While we have only demonstrated above that the keV-vacuum neutrinophilic 2HDM has negligible effects on the
$ \ell_\alpha\to \ell_\beta \gamma $ and$ \ell_\alpha \to 3\ell_\beta $ decays, similar conclusions can also be made for other LFV processes, such as the$ \mu\to e $ conversion in nuclei as well as the$ Z\to \ell_\alpha \ell_\beta $ and$ h\to \ell_\alpha \ell_\beta $ decays. Here, the key ingredient comes from the fact that these LFV processes have a quartic dependence on the neutrino Yukawa couplings. When$ v_\Phi\gtrsim 1 $ keV, the neutrino Yukawa couplings populate below$ 10^{-5} $ , rendering the LFV rates negligibly small even though they are severely constrained by the current and future experimental sensitivities. A particularly important observation is that, owing to the common dependence on the neutrino Yukawa couplings, it is hopeless within the keV-vacuum neutrinophilic 2HDM framework to observe the$ Z\to \ell_\alpha \ell_\beta $ and$ h\to \ell_\alpha \ell_\beta $ decays even in the future forecast experiments (see, e.g., Ref. [41]) without violating the$ \mu\to e\gamma $ bound. We can, therefore, conclude that the keV-vacuum neutrinophilic 2HDM becomes nearly secluded from the low-energy flavor physics.In fact, similar inert effects are also expected in electroweak precision observables, such as the invisible Z decay
$ Z\to \nu\bar\nu $ . The corresponding decay width receives a leading contribution of$ \mathcal{O}(Y_\nu^4) $ as well, which is similar to the LFV processes discussed above. Meanwhile, as a quasi-degenerate mass spectrum of scalars is assumed, the new physics contributions to the oblique parameters S, T and U [42] are also suppressed. However, it is worth mentioning that the breakdown of mass degeneracy between neutral and charged Higgs bosons could provide a possibility to accommodate the W-mass anomaly observed recently by the CDF collaboration [43]. If this anomaly is confirmed in the future, it would be quite interesting to consider the case with significant mass splitting between$ H^0/A $ and$ H^+ $ in the keV-vacuum neutrinophilic 2HDM. Nevertheless, this work is restricted to the illustration of stringent LFV constraints discussed above and to the cosmological imprints of Dirac neutrinos in the following sections.Finally, let us make a brief comment on the LHC phenomenology. The current LHC constraints on the keV-vacuum neutrinophilic 2HDM are weak. For instance, the
$ tb $ -associated production studied widely at the LHC [44, 45] is closed owing to the strongly suppressed quark-scalar couplings within the framework. Furthermore, the dominant decay products of$ H^0, A $ and$ H^+ $ are neither quarks nor leptons, especially given that the lepton-scalar interaction is suppressed by the neutrino Yukawa couplings. In addition, the quasi-degenerate scalar mass spectrum forbids the transitions between the charged and neutral Higgs bosons, e.g.,$ H^0/A\to H^\pm W^\mp $ . These observations indicate that the new scalars are basically produced from and decay into the SM gauge bosons, e.g., through the vector-boson fusion production and di-boson decay chain,$ W^+ Z\to H^+\to W^+ Z $ [46], which is nevertheless a loop-induced process. On the other hand, the loop corrections to the SM Higgs signals are expected to be suppressed as well. A particular case is the di-photon decay$ h\to 2\gamma $ , which receives loop correction from the charged Higgs. Applying the general formula for the SM Higgs decay width [47], we find that the ratio$ \Gamma(h\to 2\gamma)/ \Gamma(h\to 2\gamma)_{\rm SM} $ is corrected at$ \mathcal{O}(10^{-3}) $ , which is smaller than the current experimental uncertainty of$ \mathcal{O}(10^{-2}) $ [39]. Therefore, we can safely conclude that the framework considered here is also secluded from the current LHC phenomenology. -
From the discussion in the last section, any observation of the LFV processes with the future forecast experimental sensitivities can rule out the neutrinophilic 2HDM with a keV-scale vacuum in explaining the Dirac neutrino masses. While being nearly secluded from the low-energy flavor physics, such a minimal framework with a keV-scale vacuum can successfully realize a purely thermal Dirac leptogenesis to explain the BAU problem, as detailed in our recent sequential studies [28, 29]. The currently observed baryon asymmetry as inferred from Planck 2018 reads [13]
$ Y_B=\frac{n_B-\bar n_B}{s_{\rm SM}}\approx\frac{n_B}{s_{\rm SM}}=(8.68\pm0.08)\times 10^{-11}, $

(8) where
$ n_{B}\,(\bar n_B) $ denotes the baryon (antibaryon) density, and the SM entropy density is given by$ s_{\rm SM}=\frac{g_*^s 2\pi^2}{45} T^3, $

(9) with
$ g_*^s $ denoting the relativistic degrees of freedom (d.o.f) for the entropy.The purely thermal Dirac leptogenesis applies, for the first time, the finite-temperature effect to the leptogenesis scenarios where the SM neutrinos are of Dirac type [28, 29] (similar applications but based on the Majorana neutrinos have been considered in Refs. [48, 49]). Here, the scalar decay rate
$ \Gamma(\Phi\to \bar L \nu_R) $ is suppressed owing to the small neutrino Yukawa couplings, providing therefore an out-of-equilibrium condition in the early Universe. In addition, the leptonic CP asymmetry generated from the scalar decay has an imaginary interference term between the tree- and loop-level amplitudes, in which the coupling phase is provided by the complex Yukawa matrix and the kinetic phase by a thermal Cutkosky cut in the finite-temperature quantum field theory [50]. The generated lepton-number asymmetry can be maintained in the right-handed Dirac neutrino sector, but it is reprocessed by the thermal sphaleron transitions [51] in the left-handed lepton sector, leading finally to a net baryon asymmetry in the early Universe after the sphaleron processes decouple.It is especially interesting to note that, after some simple basis transformations, the coupling phase is entirely provided by the Dirac CP-violating phase in the PMNS matrix, rendering therefore a direct link between the low-energy CP violation and the high-temperature CP asymmetry [29]. However, to produce significant CP asymmetry at finite temperatures and, at the same time, to ensure the out-of-equilibrium condition, only two of the three Dirac neutrinos are at most allowed to establish a left-right equilibration after the sphaleron processes freeze out at
$ T_{\rm sph}\approx 132 $ GeV [52]. Under this circumstance, we are left with two possibilities in realizing such a purely thermal Dirac leptogenesis: one is that two of the three Dirac neutrinos have much lighter masses than the third one, and the other requires the Yukawa coupling of the lightest neutrino to be much smaller than that of the other two heavier neutrinos. As an illustrating example, we have considered in Ref. [29] the second possibility, dubbed$ \nu_1 $ -leptogenesis, in which the baryon asymmetry can be formulated in terms of the (unknown) lightest neutrino mass$ m_1 $ , the vacuum$ v_\Phi $ , and the thermal scalar mass parameter parameterized by$ m_{\Phi}\simeq 0.3 $ T. In particular, the sign of the baryon asymmetry is determined by the Dirac CP-violating phase via$ Y_B\propto \sin\delta_{\rm CP} $ . As a consequence, such a phase dependence disfavors the inverted ordering of the neutrino mass spectrum because$ \sin\delta_{\rm CP}>0 $ only appears in the normal ordering [39] (see also Ref. [30]).Concerning the first possibility that has not been discussed in Ref. [29], we will see that the current neutrino masses as inferred from the oscillation measurements and cosmological constraints already disfavors it as a realization of the purely thermal Dirac leptogenesis. To this end, we depict in Fig. 1 the neutrino mass spectrum in light of the current oscillation data [39] and under the Planck mass bound
$ \sum_i m_{i}<0.12 $ eV [13]. It can be observed that at least two neutrinos are expected to reside at$ 0.01-0.05 $ eV. Specific to the neutrinophilic 2HDM, such a neutrino mass spectrum indicates a striking property when we consider the evolution of the right-handed Dirac neutrinos in the early Universe. Let us consider the first possibility that only the heaviest neutrino$ \nu_{3R} $ in the normal ordering establishes thermal equilibrium before$ T_{\rm sph} $ , and make an order-of-magnitude estimate about the neutrino decoupling. The thermal decay rate at high temperatures is given by②$ \Gamma_{\Phi\to \bar L \nu_{jR}}=\frac{m_\Phi}{8\pi v_\Phi^2}\left(1-\frac{m_{Li}^2}{m_\Phi^2}\right)^2\Big|U_{i1}m_{j}\Big|^2, $

(10) with the summed index
$ i=1,2,3 $ . The decoupling temperature of$ \nu_R $ can be estimated via$ \Gamma_{\Phi\to \bar L \nu_{jR}}\sim H $ , where the Hubble parameter at the radiation-dominated epoch is given by$ \begin{equation} H (T) = \sqrt{\frac{4\pi^3 g_\ast^\rho}{45M_{P}^2}}\,T^2, \end{equation} $

(11) with
$ g_\ast^\rho $ representing the relativistic d.o.f for the energy density and$ M_{P} =1.22\times 10^{19} $ GeV the Planck mass. One can then find that the thermalization of$ \nu_{3R} $ occurs approximately at$ T_3\sim 10^6 $ GeV for$ v_\Phi\sim 1 $ keV. Until the temperature drops below the scalar mass,$ T<m_S $ , the$ \nu_{3R} $ production via decay will be quickly closed owing to the exponential Boltzmann suppression of the scalar number density, and it signifies the frozen-out epoch of$ \nu_{3R} $ .③ Because$ m_2/m_3\gtrsim 0.2 $ , as inferred from Fig. 1, the thermalization of$ \nu_{2R} $ occurring at$ T_2\sim T_3 m_2^2/m_3^2\gtrsim 10^4 $ GeV implies that both the two heavier neutrinos in the normal ordering have established thermal equilibrium well above$ T_{\rm sph}\approx 132 $ GeV. This obviously contradicts our starting assumption that only$ \nu_{3R} $ establishes thermal equilibrium before$ T_{\rm sph} $ , and thus rules out the first possibility in terms of the current neutrino mass ordering.With respect to the second possibility, as the lightest neutrino
$ \nu_{1R} $ has an upper rather than a lower mass bound, the situation where$ \nu_{1R} $ is much lighter and undergoes a distinguishable evolution from that of the two heavier ones is easier to occur. Furthermore, the quasi-degeneracy between the neutral and charged scalars,$ m_{H^0}= m_A\approx m_{H^+} $ , can make a strongly first-order phase transition less feasible [53–55] to trigger the electroweak baryogenesis [56]. In addition, the lack of physical phase in the scalar potential (see Eq. (2)) cannot provide additional CP violation in the electroweak baryogenesis. As a consequence, the$ \nu_1 $ -leptogenesis candidate is more feasible to resolve the BAU problem within the minimal keV-vacuum neutrinophilic 2HDM.Let us now proceed to compute the baryon asymmetry within the framework outlined in Sec. II. Our starting point is the general formula of the baryon asymmetry [29],
$ \begin{aligned}[b] Y_B=&\frac{8}{23} Y_{\nu_{1R}}=\frac{8}{23} \int_{T_{\rm c}}^{\infty} {\rm d}T\,\frac{g_\Phi m_{\Phi}^2}{\pi^2s_{\rm SM} H } \epsilon_{\rm CP} K_1 \left(\frac{m_{\Phi}}{T}\right) \Gamma_{\Phi\to \bar L \nu_{1R}}, \end{aligned}$

(12) where the factor
$ 8/23 $ comes from the sphaleron transition coefficient,$ Y_{\nu_{1R}}\equiv (n_{\nu_{1R}}-n_{\bar\nu_{1R}})/s_{\rm SM} $ denotes the asymmetry yield of the lightest right-handed Dirac neutrino,$ g_\Phi=2 $ takes into account the two gauge d.o.f in the scalar doublet, and$ K_1(m_\Phi/T) $ is the modified Bessel function. The CP asymmetry in the$ \nu_1 $ -leptogenesis mechanism is generated by the interference between the tree-level and the one-loop amplitudes with self-energy correction in the left-handed leptons. With the thermal Cutkosky cut on the loop, the result reads$ \begin{aligned}[b] \epsilon_{\rm CP}\equiv \frac{\Gamma(\Phi\to \bar L \nu_{1R})-\Gamma(\bar\Phi\to L \bar\nu_{1R})}{\Gamma(\Phi\to \bar L \nu_{1R})+\Gamma(\bar\Phi\to L \bar\nu_{1R})} \end{aligned} $

$ \begin{aligned}[b] \quad =&\frac{1}{2\pi}\frac{m_{\nu,j}^2}{v_\Phi^2}\frac{ \text{Im}[U^*_{i1}U_{k1}U_{ij}U^*_{kj}] }{ |U_{n1}|^2 (m_\Phi^2-m_{L,n}^2)} \int_{{m_\Phi (m_{L,i}^2-m_\Phi^2)/2m_{L,i}^2} }^{(m_{L,i}^2-m_\Phi^2)/2m_\Phi}{\rm d}\omega \\ & \times \frac{m_\Phi^2\left[f_F(-\omega)+f_B(E_i-\omega)\right]}{(m_\Phi^2-m_{L,i}^2)(m_{L,i}^2-m_{L,k}^2)}\Big [ (m_{L,i}^2-m_\Phi^2)m_\Phi-2m_{L,i}^2\omega \Big], \end{aligned} $

(13) where the indices
$ i\neq k $ and$ j,n $ are summed over the three lepton flavors, and$ f_{B/F}(E) $ denotes the boson/fermion phase-space distribution function, with$ f_{B/F}(E)=\frac{1}{e^{E/T}\mp 1}. $

(14) Note that the temperature integration in Eq. (12) is performed within the range
$[T_{\rm c}, \infty)$ . Here, the lower limit corresponds to the critical temperature$T_{\rm c}\simeq 160$ GeV [57] when electroweak symmetry breaking occurs and, afterwards, the production of CP asymmetry is quickly closed as the scalar obtains a vacuum mass$ m_S \gg T $ , which results in the Boltzmann suppression via the phase-space distribution function$f_{B/F}(\omega)\sim f_{B/F}(m_S)\simeq {\rm e}^{-m_S/T}$ . The initial temperature is, taken at infinity, and such a choice does not cause significant numerical difference since the integrand in Eq. (12) is basically suppressed by$ 1/T^2 $ at higher temperatures.Before electroweak symmetry breaking, the decay rate with a final state
$ \nu_{R} $ is given by Eq. (10), where the PMNS matrix appears in the neutrino Yukawa sector. Therefore, the coupling phase in$ \epsilon_{\rm CP} $ defined by Eq. (13) is entirely attributed to the Dirac CP-violating phase from the PMNS matrix U, which is parameterized in the standard form as [39]$ \begin{array}{*{20}{l}} U=\left( \begin{array}{ccc} c_{{12}}c_{{13}} \, & s_{{12}} c_{{13}} \, & {\rm e}^{-{\rm i} \delta_{\rm CP}} s_{{13}} \\[0.15cm] -s_{{12}}c_{{23}}-{\rm e}^{{\rm i} \delta_{\rm CP}}c_{{12}} s_{{13}} s_{_{23}} \, & c_{{12}}c_{{23}}-{\rm e}^{{\rm i} \delta_{\rm CP}}s_{{12}} s_{{13}} s_{{23}}\,& c_{{13}} s_{{23}} \\[0.15cm] s_{{12}}s_{{23}}-{\rm e}^{{\rm i} \delta_{\rm CP}}c_{{12}} s_{{13}} c_{{23}} \, & -c_{{12}}s_{{23}}-{\rm e}^{{\rm i} \delta_{\rm CP}}s_{{12}} s_{{13}} c_{{23}}\, & c_{{13}}c_{{23}}\\ \end{array} \right). \end{array} $ 
(15) Here
$ s_{ij}\equiv \sin\theta_{ij} $ ,$ c_{ij}\equiv \cos\theta_{ij} $ , and$\delta_{\rm CP}$ is the Dirac CP-violating phase.In the finite-temperature regime, the thermal lepton mass
$ m_L $ comes from the one-loop self-energy diagrams with gauged$S U(2)_L$ ,$ U(1)_Y $ , and Yukawa interactions, leading to$ m_L^2(T)=\left(\frac{3}{32}g_2^2+\frac{1}{32}g_1^2 +\frac{1}{8}\frac{m_\ell^2}{v_{\rm EW}^2}\right)T^2, $

(16) where
$ g_{2,1} $ are the$S U(2)_L$ and$ U(1)_Y $ gauge couplings respectively, and$ m_\ell $ the charged lepton mass. Concerning the thermal scalar mass parameter participating in the baryon asymmetry generation, the approximation$ m_\Phi\approx 0.3 T $ was selected in the original$ \nu_1 $ -leptogenesis [29], which was motivated by the small bare mass parameter$ m_{22} $ and the only thermal corrections from$S U(2)_L$ and$ U(1)_Y $ gauge couplings [58]. However, to have an electroweak-scale$ m_S $ , Eq. (5) indicates that$ \lambda_3\simeq \mathcal{O}(1) $ , which will contribute significantly to the thermal scalar mass. With this$ \lambda_3 $ correction taken into account, the thermal mass parameter$ m_\Phi(T) $ is now given by [58, 59]$ m_\Phi^2(T)= \left(\frac{3}{16}g_2^2+\frac{1}{16}g_1^2+\frac{1}{6}\lambda_3 \right) T^2. $

(17) Within the temperature range considered in Eq. (12), we can approximately simulate the mass parameter
$ m_\Phi $ via Eq. (17), which implies that$ m_\Phi(T)\simeq T $ for a large$ \lambda_3 $ .To evaluate the baryon asymmetry numerically, we use the central values of the PMNS mixing angles
$ \theta_{ij} $ and the neutrino mass-squared differences$ \Delta m_{21}^2\equiv m_2^2-m_1^2 $ ,$ \Delta m_{31}^2\equiv m_3^2-m_1^2 $ [39]. Furthermore, we particularly apply a benchmark point of the Dirac CP-violating phase$ \delta_{\rm CP}=5\pi/6 $ , which is the lower limit that predicts an atmospheric mixing angle$ \theta_{23}>45^\circ $ as found in Ref. [30]. It should be mentioned, however, that because the baryon asymmetry depends on the phase trigonometrically,$ Y_B\propto \sin\delta_{\rm CP} $ [29], the variation of$ \delta_{\rm CP} $ within the current fitting range$ 0.78\pi<\delta_{\rm CP}<\pi $ in the normal ordering [39] causes only a small numerical difference, unless the leptonic CP violation is frustratingly small$ \delta_{\rm CP}\simeq \pi $ . Within our numerical setup, the final baryon asymmetry is evaluated to be$ Y_B=\frac{8}{23}\left(\frac{\rm keV}{v_\Phi}\right)^4\left(\frac{m_1}{\rm meV}\right)^2 \left[\frac{\mathcal{G}(\lambda_3)}{10^4}\right], $

(18) where
$ \mathcal{G}(\lambda_3) $ is an analytic but involved function of$ \lambda_3 $ . The dependence of$ \mathcal{G}(\lambda_3) $ on the scalar mass$ m_S $ is shown in Fig. 2, which suggests that, when the scalar populates in the electroweak scale, the size of the baryon asymmetry is predominantly determined by the lightest neutrino mass and the vacuum. -
To realize a successful
$ \nu_1 $ -leptogenesis with the generated baryon asymmetry$ Y_B $ matched to the observed value and, at the same time, the right-handed Dirac neutrinos meeting the necessary out-of-equilibrium condition, we must properly choose the neutrino Yukawa couplings. This in turn implies that the neutrinophilic vacuum will become bounded. Let us first outline the evolution of the three right-handed Dirac neutrinos. In the early Universe, the scalar doublet Φ establishes thermal contact with the SM plasma via gauge interactions. In the high-temperature regime$ T>m_S $ , the production of right-handed Dirac neutrinos mainly comes from the scalar decay, because the production via the scattering process$ \text{SM}+\text{SM} \to \nu_R+\bar\nu_R $ is suppressed by the higher-order neutrino Yukawa couplings. If the decay rate is much larger than the Hubble expansion, the right-handed Dirac neutrinos produced can then establish thermal equilibrium. When the temperature drops below the scalar mass, the production rate would exhibit an exponential Boltzmann suppression from the scalar number density. When the decay rate can no longer compete with the expansion of the Universe, the thermal right-handed Dirac neutrinos will freeze out from the plasma. If the neutrino Yukawa couplings are much smaller, the production rate may never compete with the expansion of the Universe and, in this case, the right-handed Dirac neutrinos would be out of equilibrium.The out-of-equilibrium condition for realizing the
$ \nu_1 $ -leptogenesis formally requires that the lightest right-handed Dirac neutrino cannot establish thermal equilibrium before the sphaleron transitions decouple at$ T_{\rm sph}\approx 132 $ GeV, while the two heavier right-handed Dirac neutrinos should be at least maintained in thermal equilibrium until$ T_{\rm sph}\approx 132 $ GeV. These conditions can be approximately estimated by comparing the Hubble friction term$ 3Hn_{\nu_R} $ with the production rate in the right-hand side of the Boltzmann equation, i.e.,$ \begin{aligned}[b]& \int \frac{{\rm d}^3p_{\Phi}}{(2\pi)^32E_{\Phi}} f_{\Phi} \frac{{\rm d}^3p_L}{(2\pi)^32E_L} \frac{{\rm d}^3p_{\nu_{R}}}{(2\pi)^32E_{\nu_{R}}} \\&\quad (2\pi)^4\delta^4(p_{\Phi}-p_L-p_{\nu_{R}})\vert \mathcal{M}_{{\Phi}\to \bar{L} \nu_{R}} \vert^2, \end{aligned} $

(19) leading therefore to
$ \frac{n_\Phi}{n_{\nu_{1R}} }\Gamma_{\Phi\to \bar L \nu_{1R}} \lesssim 3 H\lesssim \frac{n_\Phi}{n_{\nu_{2R}}}\Gamma_{\Phi\to \bar L \nu_{2R}}\Big|_{T=T_{\rm sph}}. $

(20) Notice that, because
$ m_3\gtrsim m_2 $ in the normal ordering, it turns out that$ \Gamma_{\Phi\to \bar L \nu_{2R}}<\Gamma_{\Phi\to \bar L \nu_{3R}} $ , and thus the upper limit of the neutrinophilic vacuum$ v_\Phi $ will be determined by the$ \nu_{2R} $ production rate. In addition, for the case of$ T_{\rm sph}<T_{\rm c} $ , the decay rate after electroweak symmetry breaking is given as a sum of three channels, i.e., one charged and two neutral decay channels for the$ \nu_R $ production. Neglecting the charged lepton and neutrino vacuum masses in the final states, we can then approximate the total decay rate as$ \Gamma_{\Phi\to \bar L\nu_{iR}}\approx \frac{m_{i}^2}{4\pi v_\Phi^2}m_S, $

(21) where we have replaced the Yukawa couplings
$ \hat{Y}_{\nu} $ by the neutrino mass$ m_{i} $ , and$ m_S\approx \sqrt{\lambda_3/2}v_{\rm EW}>T_{\rm sph} $ has been assumed such that the thermal mass correction$ m_\Phi(T) $ at$ T_{\rm sph} $ can be neglected in the above decay rate. Finally, applying the distributions of relativistic$ \nu_R $ and nonrelativistic Φ at equilibrium, which are given respectively by$ n_{\nu_R}=\frac{3\zeta(3)}{4\pi^2} T^3, \qquad n_\Phi\approx \left(\frac{m_S T}{2\pi}\right)^{3/2}{\rm e}^{-m_S/T}, $

(22) we can estimate Eq. (20) as
$ 23.3 \left(\frac{m_{1}}{\text{meV}}\right)\mathcal{R}_S\lesssim \left(\frac{v_\Phi}{\text{keV}}\right)\lesssim 23.3 \left[\left(\frac{m_1 }{\text{meV}}\right)^2+73.9\right]^{1/2}\mathcal{R}_S, $

(23) where
$\mathcal{R}_S\equiv(m_S/2 T_{\rm sph})^{5/4}{\rm e}^{-m_S/2T_{\rm sph}}$ . Note that the above condition does not set any upper limit on the lightest neutrino mass. However, as discussed in the first possibility of the$ \nu_1 $ -leptogenesis, if there is no strong hierarchy between$ m_1 $ and$ m_2 $ , the lightest$ \nu_R $ may have established the left-right equilibration above$ T_{\rm sph} $ . In this case, the production rate of$ \nu_{1R} $ below$ T_{\rm sph} $ can still be sufficiently small owing to the Boltzmann suppression. To ensure that$ \nu_{1R} $ does not thermalize above$ m_S $ , we can further set$ \frac{n_\Phi}{n_{\nu_{1R}} }\Gamma_{\Phi\to \bar L \nu_{1R}} \lesssim 3 H\lesssim \frac{n_\Phi}{n_{\nu_{2R}}}\Gamma_{\Phi\to \bar L \nu_{2R}}\Big|_{T\geqslant m_S}, $

(24) with the relativistic scalar distribution
$ n_\Phi=\zeta(3) T^3/\pi^2 $ . It can then be found that$ 21.1\left(\frac{m_1}{\rm meV}\right)\lesssim\left(\frac{v_\Phi}{\rm keV}\right)\lesssim 21.1\left[\left(\frac{m_1}{\rm meV}\right)^2+73.9\right]^{1/2}, $

(25) which indicates that the left-hand (right-hand) side of the above condition is stronger (weaker) than that of Eq. (23). This is because
$ \mathcal{R}_S $ can only reach a maximal value of$ \mathcal{R}_S(m_S=330\; \rm GeV)\approx 0.4 $ . Therefore, the vacuum bound under the out-of-equilibrium condition of the$ \nu_1 $ -leptogenesis is given by$ 21.1\left(\frac{m_1}{\rm meV}\right)\lesssim\left(\frac{v_\Phi}{\rm keV}\right)\lesssim 23.3 \left[\left(\frac{m_1 }{\text{meV}}\right)^2+73.9\right]^{1/2}\mathcal{R}_S. $

(26) The above condition now implies an upper bound of
$ m_1 $ in terms of the scalar mass$ m_S $ , the maximum of which gives$ m_1\approx 3.9 $ meV for$ m_S=330 $ GeV, as shown in Fig. 3. Moreover, by matching the predicted with the observed$ Y_B $ , we can replace$ m_1 $ in terms of$ v_\Phi $ ,$ m_S $ and then insert the result into the condition (26), leading consequently to an upper bound of the vacuum in terms of the scalar mass. As shown in Fig. 3, in the perturbative regime$ |\lambda_3|<4\pi $ , the vacuum has an upper bound$ v_\Phi\approx 55.8 $ keV, and the upper bound decreases for a lighter scalar mass, reaching$ v_\Phi\approx 14.8 $ keV for$ m_S=200 $ GeV.
Figure 3. (color online) Upper bounds on the lightest neutrino mass
$ m_1 $ (dark red) and the vacuum$ v_{\Phi,10}\equiv 0.1 v_{\Phi} $ (dark green) in terms of the scalar mass$ m_S $ .Finally, we would like to make a comparison between the analysis presented above and that in Ref. [29]. Both analyses considered the regime with
$ m_{22}\ll v_{\rm EW} $ and a keV-scale vacuum$ v_\Phi $ . As mentioned before, the range of$ v_\Phi $ in Ref. [29] used a thermal mass$ m_\Phi(T)\approx 0.3 T $ for the new Higgs doublet Φ. This numerical setup in fact assumed$ m_{22}\ll v_{\rm EW} $ and very light scalars. Nevertheless, very light scalars can readily generate large contributions to some precision observables in the low-energy regime. For$ m_S\gg 100 $ GeV, however the new physics effects would be diluted by their large masses. Thus, it is phenomenologically more viable and realistic to consider a heavier Φ. In this case, Eq. (5) dictates that$ \lambda_3\simeq \mathcal{O}(1) $ and$ m_\Phi(T)\approx 0.3 T $ would not be realistic given that a large thermal contribution arising from the$ \lambda_3 $ coupling cannot be ignored, as can be observed from Eq. (17). In fact, using$ m_\Phi(T_{\rm sph})\approx 0.3 T_{\rm sph}\approx 40 $ GeV in Eq. (20) is justified only when the vacuum mass$ m_S $ is light. From this point of view, the present analysis can provide a more realistic vacuum range without neglecting the significant dependence on$ m_S $ . -
As discussed in Sec. III, there is rare hope to see the LFV signals in neutrinophilic 2HDM with a keV-scale vacuum. Nevertheless, the expected sensitivity is dramatically different in the cosmic regime, especially given the fact that the current precision of astrophysical and cosmological observations is now making the probes of feeble couplings and light species strikingly possible [60]. In this section, we will determine the evolution of the three hierarchical right-handed Dirac neutrinos, and then calculate the
$ \Delta N_{\rm eff} $ shift. It will be shown that$ 0.097\leqslant \Delta N_{\rm eff}\leqslant 0.112 $ is predicted under the natural$ \nu_1 $ -leptogenesis, which can be tested by the future experiments with forecast sensitivities of$0.01- 0.1$ , and, in particular, the minimal value can be readily falsified by the CMB-S4, LSS, and their combinations. -
Owing to the feeble Yukawa coupling, the lightest right-handed Dirac neutrino is essentially produced via the freeze-in mechanism [61, 62]. Defining the energy yield
$ Y_{\nu_R}^{\rho}\equiv \rho_{\nu_R}/s_{\rm SM}^{4/3} $ , we can write the Boltzmann equation for$ \nu_{1R} $ as$ \frac{{\rm d}Y_{\nu_{1}}^\rho}{{\rm d}T}=-\frac{2N_{\nu_1}\mathcal{C}_{\nu_{1}}^\rho}{s_{\rm SM}^{4/3}H T}, $

(27) where the d.o.f
$ N_{\nu_{1}}=2 $ counts the energy densities from the lightest$ \nu_{1R} $ as well as from its antiparticle, and the factor$ 2 $ amounts to the two gauge components of the doublet Φ;that is, we treat both Φ and L as single thermal species with two d.o.f.④ Such a treatment is justified by the fact that the freeze-in production essentially occurs at the gauge symmetric phase and quickly shuts off due to the Boltzmann suppression when temperature drops below $T_{\rm c}$ . The collision term$ \mathcal{C}_{\nu_{1}}^\rho $ is given by$ \begin{aligned}[b] \mathcal{C}_{\nu_{1}}^\rho =&\int \frac{{\rm d}^3p_{\Phi}}{(2\pi)^32E_{\Phi}} f_{\Phi} \frac{{\rm d}^3p_L}{(2\pi)^32E_L} \frac{{\rm d}^3p_{\nu}}{(2\pi)^32E_{\nu}} (2\pi)^4\delta^4\\&\times(p_{\Phi}-p_L-p_{\nu}) E_{\nu}\vert \mathcal{M}_{{\Phi}\to \bar{L} \nu_1} \vert^2. \end{aligned} $

(28) where we have neglected the inverse decay and the Pauli-blocking effects, that is,
$ 1-f_{\nu_{1R},L}\approx 1 $ .The phase-space integral of Eq. (28) can be calculated following Ref. [63]. Making use of the identity,
$ \delta^3 (\boldsymbol{p_\Phi-p_L-p_\nu})=\int \frac{{\rm d}^3 \lambda}{(2\pi)^3}{\rm e}^{{\rm i}(\boldsymbol{p_\Phi-p_L-p_\nu})\cdot \boldsymbol{\lambda}}, $

(29) we can rewrite Eq. (28) as
$ \begin{aligned}[b] \mathcal{C}_{\nu_{1}}^\rho =&\frac{1}{8(2\pi)^8}\int f_\Phi {\rm d}E_\Phi {\rm d}E_L E_{\nu} {\rm d}E_{\nu} \delta(E_\Phi-E_L-E_{\nu}) \\ & \times \int {\rm d}\Omega_\lambda \lambda^2 {\rm d}\lambda \vert \mathcal{M}_{\Phi\to \bar{L} \nu_1} \vert^2 \; \prod\limits_{i=\Phi,L,\nu_1} \end{aligned} $

$ \begin{aligned}[b] \quad\quad &\times\left( p_i \int {\rm d}\cos\theta_i {\rm d}\varphi_i {\rm e}^{{\rm i} p_i \lambda \cos\theta_i}\right), \end{aligned} $

(30) where
${\rm d}^3\lambda={\rm d}\Omega_\lambda \lambda^2 {\rm d}\lambda$ ,${\rm d}\Omega_i={\rm d}\cos\theta_i {\rm d}\varphi_i$ , and the angles$ \theta_i $ are defined as$ \cos\theta_i\equiv \boldsymbol{p_i}\cdot \boldsymbol{\lambda}/ p_i \lambda $ , with i running over the scalar, the left-handed leptons, and the lightest right-handed Dirac neutrino, respectively. The amplitude-squared is calculated at the gauge symmetric phase, with the result given by$ \vert \mathcal{M}_{\Phi\to \bar{L} \nu_1} \vert^2=\frac{2m_\Phi^2}{v_\Phi^2}\left(1-\frac{m_{L,i}^2}{m_\Phi^2}\right)\left|U_{i1} m_1\right|^2, $

(31) summing over the three lepton flavors. Integrating Eq. (30) first over
$ \cos\theta_i $ ,$ \varphi_i $ and then over$ \Omega_\lambda $ , λ, together with$ \delta(E_\Phi-E_L-E_\nu) $ to integrate over$ E_\nu $ , we finally arrive at$ \begin{aligned}[b] \frac{\mathcal{C}_{\nu_{1}}^\rho}{\vert \mathcal{M}_{\Phi\to \bar{L} \nu_1} \vert^2} =&\frac{1}{32\pi^3}\int_{m_\Phi}^\infty f_\Phi {\rm d}E_\Phi \int_{E_{\rm min}}^{E_{\rm max}}(E_\Phi-E_L){\rm d}E_L \\=& \frac{1}{64\pi^3}\left(1-\frac{m_L^2}{m_\Phi^2}\right)^2 m_\Phi^2 T K_2(m_\Phi/T), \end{aligned} $

(32) where the Boltzmann distribution
$f_\Phi={\rm e}^{-E_\Phi/T}$ has been applied, and the upper (lower) integration limit is given by$ E_{\rm max(min)} =\frac{ E_\Phi(m_\Phi^2+m_L^2) \pm p_\Phi(m_\Phi^2-m_L^2)}{2m_\Phi^2}. $

(33) Note that the integration with a full Bose-Einstein statistics can also be performed analytically, which, nevertheless, does not cause significant numerical difference with respect to the Boltzmann distribution. This is expected because the potential Bose-Einstein enhancement at the soft momentum regime is now suppressed by the thermal mass correction, which can reach
$ m_{\Phi}(T)\sim T $ for a large value of$ \lambda_3 $ .The energy density at the frozen-in temperature
$ T_{1,\rm dec} $ of the lightest right-handed Dirac neutrino is then given by$ \rho_{\nu_{1R}, \rm dec}= s_{\rm SM}^{4/3}(T_{1, \rm dec})\int_{T_c}^{\infty}\frac{2N_{\nu_1}\mathcal{C}_{\nu_{1}}^\rho}{s_{\rm SM}^{4/3}H T}{\rm d}T, $

(34) where we have taken the approximation
$g_{1, \rm dec}\equiv g_*^\rho (T_{1, \rm dec})\approx g_*^s(T_{1, \rm dec})$ . After$ \nu_{1R} $ freezes in, the energy exchange between the SM plasma and$ \nu_{1R} $ ceases, and the energy density$ \rho_{\nu_{1R},\rm ref} $ at a late-time reference temperature$ T_{\rm ref} $ can be simply rescaled by$ \frac{\rho_{\nu_{1R}, \rm ref}}{\rho_{\nu_{1R}, \rm dec}}=\frac{\rho_{\text{SM}, \rm ref}}{\rho_{\text{SM}, \rm dec}}, $

(35) where the SM energy density is given by
$ \rho_{\text{SM}}=g_*^\rho \frac{\pi^2}{30} T^4. $

(36) For the two thermalized right-handed Dirac neutrinos, their energy densities have the thermal spectrum
$ \rho_{\nu_{2R}}= \rho_{\nu_{3R}}=\frac{7\pi^2}{120}T^4, $

(37) where the energy density from the antiparticle has been taken into account. After the two heavier right-handed Dirac neutrinos freeze out, the energy densities at late times will be determined by Eq. (35).
-
The extra radiation contributing to the SM plasma in the early Universe can be parameterized by a shift of the effective neutrino number via
$ \Delta N_{\rm eff}\equiv \frac{\rho_{\rm rad}}{\rho_{\nu_L}}, $

(38) where
$ \rho_{\nu_L} $ is the energy density of a left-handed neutrino. In the SM,$ N_{\rm eff}^{\rm SM}=3 $ just prior to the BBN and$N_{\rm eff}^{\rm SM} = 3.044-3.045$ after taking into account the non-instantaneous decoupling of active neutrinos below$ T=\mathcal{O}(1) $ MeV [64–70]. The extra radiation contribution to$ \Delta N_{\rm eff} $ can also be expressed in terms of the SM energy density via [17, 71]$ \Delta N_{\rm eff} = \frac{4}{7} \left[\frac{g_{*}^s(T_{\gamma e \nu})}{g_{*}^s(T_{\rm ref})}\right]^{4/3} g_*^\rho (T_{\rm ref})\, \frac{\rho_{\rm rad}(T_{\rm ref})}{\rho_{\text{SM}}(T_{\rm ref})}, $

(39) where
$ g_{*}^s(T_{\gamma e \nu})=10.75 $ corresponds to the epoch when the relativistic SM plasma contains photons, electrons, positrons, and neutrinos.Applying the above equations, we find that the
$ \Delta N_{1,\rm eff} $ shift from$ \nu_{1R} $ depends quadratically on$ m_1/v_\Phi $ and nontrivially on$ m_S $ . The frozen-in temperature of$ \nu_{1R} $ is simply fixed at$T_{\rm c}$ , when both the CP asymmetry$ \epsilon_{\rm CP} $ and the$ \nu_{1R} $ production from scalar decay essentially cease. The$ \Delta N_{2,\rm eff} $ shift from$ \nu_{2R} $ depends on the frozen-out temperature$ T_{2,\rm dec} $ mildly via the d.o.f$ g_{2,\rm dec} $ , while the$ \Delta N_{3,\rm eff} $ shift from$ \nu_{3R} $ can be simply obtained by replacing the frozen-out temperature$ T_{2,\rm dec} $ with$ T_{3,\rm dec}= m_3^2 T_{2,\rm dec}/ m_2^2 \approx 25 T_{2,\rm dec} $ . We show in the left panel of Fig. 4 the contributions from the two thermalized$ \nu_R $ as a function of$ T_{2,\rm dec} $ . It can be observed that$ \Delta N_{3,\rm eff} $ becomes nearly constant after$ T_{2,\rm dec}>10 $ GeV, because the decoupling$ T_{3,\rm dec} $ is pushed up to$ \mathcal{O}(10^2) $ GeV where$ g_{3,\rm dec} $ has become a constant.
Figure 4. (color online) Left:
$ \Delta N_{\rm eff} $ from the two thermalized$ \nu_R $ , where$ T_{3,\rm dec}\approx 25 T_{2,\rm dec} $ has been used. Right: The frozen-out temperature$ T_{2,\rm dec} $ as a function of the vacuum$ v_\Phi $ . The upper limit of$ v_\Phi $ is imposed from Fig. 3 with different scalar masses. The dotted curves are obtained by applying the temperature dependence of the d.o.f [72], while the solid curves result from the nonlinear fits.Note that
$ T_{2,\rm dec} $ can be estimated by the instantaneous frozen-out condition$ \frac{n_\Phi}{n_{\nu_{2R}}}\Gamma_{\Phi\to \bar L \nu_{2R}}\simeq 3H\Big|_{T=T_{2, \rm dec}}, $

(40) with a nonrelativistic
$ n_\Phi $ distribution and a decay rate given by Eq. (21). The above condition can be numerically solved after applying the temperature dependence of the d.o.f [72]. The resulting$ T_{2,\rm dec} $ is then a function of$ m_1 $ ,$ v_\Phi $ , and$ m_S $ . For the later analytical determination of the corresponding$ \Delta N_{\rm eff} $ , we make a nonlinear fit of$ T_{2,\rm dec} $ in terms of$ v_\Phi $ , as shown in the right panel of Fig. 4, where the scalar mass varies within the perturbative range$200–600$ GeV, and the quadratic dependence on$ m_1 $ has been removed by matching Eq. (8) with Eq. (12). The total theoretical prediction of$ \Delta N_{\rm eff} $ is then given by the sum of the three hierarchical right-handed Dirac neutrinos$ \begin{array}{*{20}{l}} \Delta N_{\rm eff}=\Delta N_{1,\rm eff}(v_\Phi,m_S)+\Delta N_{2,\rm eff}(v_\Phi,m_S)+\Delta N_{3,\rm eff}(v_\Phi,m_S), \end{array} $

(41) with
$ T_{3,\rm dec}\approx 25 T_{2,\rm dec} $ applied in the third term.Currently, a combined constraint from BBN and CMB, and, in particular,
$ \text{CMB}+\text{BBN}+Y_p+\text{D} $ , gives$ N_{\rm eff}= 2.843\pm 0.154 $ , setting an upper limit$\Delta N_{\rm eff}=N_{\rm eff}-3 < 0.151$ at the$ 2\sigma $ level [12], while the bound from the Planck 2018 results is given by$ N_{\rm eff}=2.99\pm 0.17 $ , limiting$ \Delta N_{\rm eff}=N_{\rm eff}-3.045<0.285 $ at the$ 95\ $ % confidence level [13]. The future forecast$ 2\sigma $ sensitivity from the SPT-3G is expected to be$ 2\sigma(N_{\rm eff})=0.116 $ [73], and the SO experiment is forecast to have$ 2\sigma(N_{\rm eff})=0.1 $ [31, 32]. Moreover, the CMB-S4 experiment can reach a$ 2\sigma $ uncertainty of$ 2\sigma(N_{\rm eff})=0.06 $ [33, 34]. In addition, when combining the CMB-S4 with the LSS data, e.g., with the 21 cm survey [74], the forecast sensitivity can further reach$ 2\sigma(N_{\rm eff})=0.036 $ [36]. The sensitivity can even be increased to lower values when more datasets from LSS and CMB are combined in the fits (see also Ref. [75] and references therein).We show in Fig. 5 the
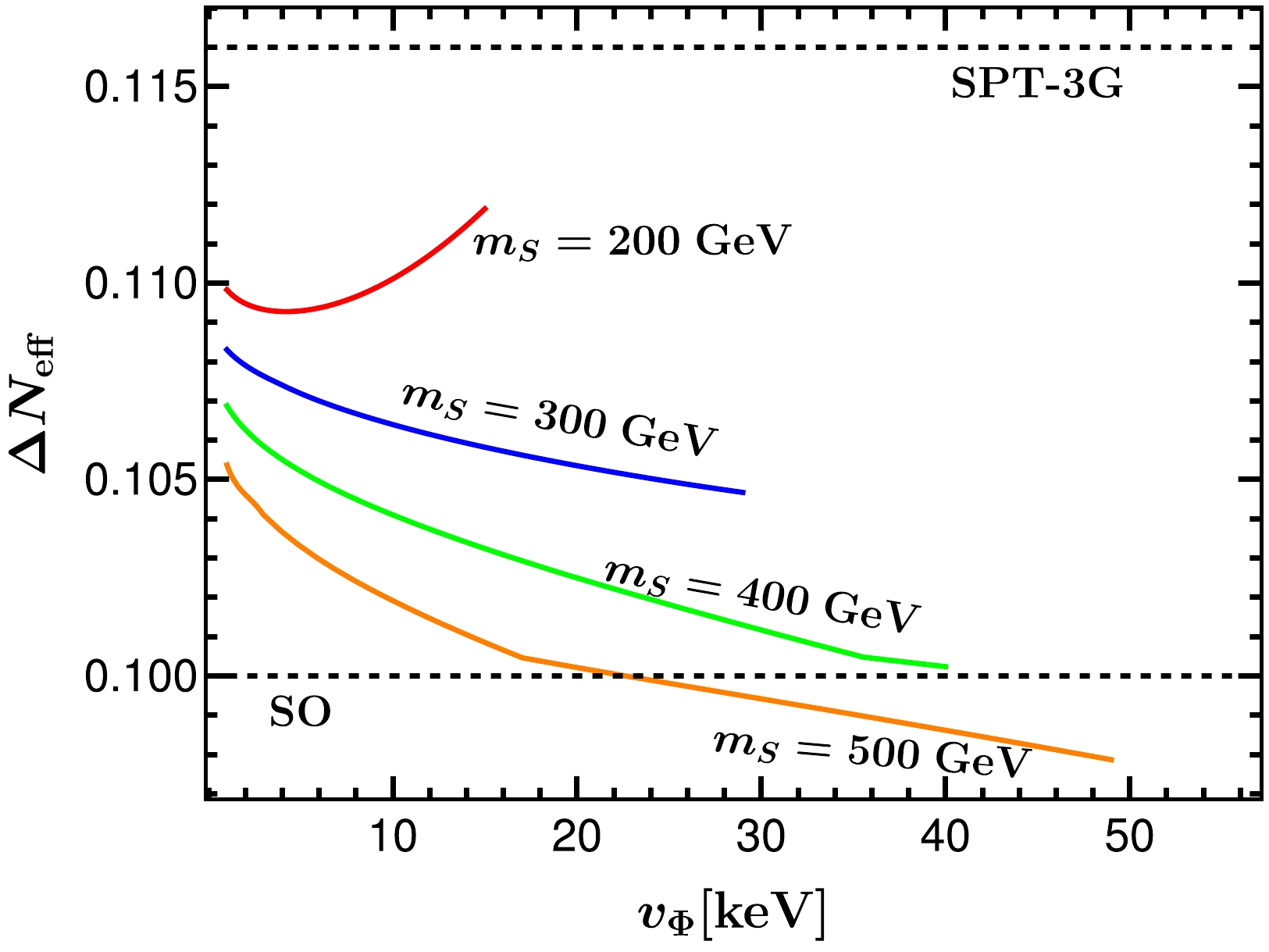
$ \Delta N_{\rm eff} $ shift as a function of the vacuum$ v_\Phi $ , in which the scalar mass varies below the perturbative limit and the decoupling temperature$ T_{2, \rm dec} $ in terms of$ v_\Phi $ is taken from the fit in the right panel of Fig. 4. It can be observed that a maximal shift$ \Delta N_{\rm eff}\approx $ 0.112 can be reached when$ m_S=200 $ GeV. In this case, the vacuum is bounded from above with$ v_\Phi \lesssim 14.8 $ keV, and$ m_1\lesssim 3.4 $ meV. It can also be observed that, with$ m_S=500 $ GeV, the minimal shift reads$ \Delta N_{\rm eff}\approx 0.098 $ ,⑤ which corresponds to a maximally allowed vacuum$ v_\Phi \approx $ 48.9 keV and a maximally allowed$ m_1\approx 3.4 $ meV, as can be observed from Fig. 3. Note that we do not consider here the scalar with mass below$ 200 $ GeV, because for smaller masses, on the one hand, the evaluation of the baryon asymmetry$ Y_B $ and the decay rate should be modified by taking the thermal mass corrections at lower temperatures and, on the other hand, the collider constraints will come into play, with a general lower bound$ m_{H^+}>80 $ GeV as obtained previously by the LEP experiment [76]. -
The fact that there is no observation as yet of Dirac neutrino related signals in both direct collider detection and indirect low-energy flavor physics could just hint towards a feeble Dirac neutrino Yukawa regime. This motivates us to consider in this work the neutrinophilic 2HDM with a keV-scale vacuum. We have shown that, while the framework is inert in the low-energy flavor physics such that any observation of the LFV processes is not expected in the future experiments, the promising sensitivities from the cosmological regime can probe such an LFV-inert model. Besides being distinguishable from the lighter-vacuum cases with observable LFV processes, the scenario considered can also provide a correlative explanation of the BAU problem, the Dirac neutrino mass origin, and an observable
$ \Delta N_{\rm eff} $ shift with only two free parameters, namely, the new vacuum scale$ v_\Phi $ and the quasi-degenerate scalar mass$ m_S $ , provided that the unknown lightest neutrino mass and Dirac CP-violating phase are pinpointed by the upcoming experiments. In particular, the theoretical prediction of$ \Delta N_{\rm eff} $ populates in the forecast sensitivities from many future experiments, including the SO, CMB-S4, and LLS. This provides therefore another remarkable avenue to fully test the Dirac neutrino model proposed here.
Cosmological imprints of Dirac neutrinos in a keV-vacuum 2HDM
- Received Date: 2022-10-08
- Available Online: 2023-04-15
Abstract: The Dirac neutrino masses could be simply generated by a neutrinophilic scalar doublet with a vacuum being dramatically different from the electroweak one. While the case with an eV-scale vacuum has been widely explored previously, we exploit in this work the desert where the scalar vacuum is of






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: