-
Quark-gluon plasma (QGP) is a state of matter in which quarks and gluons are deconfined instead of being bounded inside hadrons [1–3]. Relativistic heavy-ion collisions provide a unique laboratory to study the properties of QGP [1], and jet quenching is among the major signatures of the creation of QGP in these energetic collisions [4–6]. The observed suppression of the high transverse momentum (
$ p_{T} $ ) hadron and reconstructed jet spectra is considered a consequence of both elastic and inelastic scatterings between the energetic partons produced via initial hard collisions and the color-deconfined QGP medium [7–20]. The amount of energy transferred between jet partons and QGP is governed by a set of transport coefficients, such as the strong coupling parameter$ \alpha_\mathrm{s} $ and jet quenching parameter$ \hat{q} $ [21, 22]. Efforts are underway to extract these parameters from jet quenching data, such as the nuclear modification factor [23–25], which helps quantify the transport properties or opacity of the QGP medium.With tremendous efforts on systematical experimental measurements and ever more sophisticated theoretical calculations, studies on jet-medium interactions have been extended from nuclear modification of high
$ p_{T} $ hadrons [26–33] and jets [34–46], to the intra-structures of jets [47–59] as well as jet-related correlations [60–69]. In most of these studies, jet production in heavy-ion collisions is usually divided into three stages: parton production and shower in vacuum (or proton-proton collisions), interaction with QGP, and hadronization. However, different assumptions have been adopted for the starting time of jet-medium interactions. This could introduce uncertainties in evaluating the nuclear modification on jets and has driven several recent investigations [70, 71]. For instance, this starting time has shown to affect the azimuthal dependence of jet quenching [70]. Moreover, with a time reclustering algorithm, jets with longer formation time exhibit a weaker quenching [71].In this study, we comprehensively analyzed the effects of the jet formation time on jet energy loss. The initial jets prior to the interaction with QGP were generated from Pythia 8 simulation [72, 73]. Owing to the lack of information on the jet formation time from Pythia, we designed three different evaluations on the production time of each parton within jets, varying from zero formation time to an estimation based on a single splitting before formation, and a more elaborate estimation for a sequence of multiple splittings generated in Pythia. Interactions between these jet partons and QGP were then simulated using a linear Boltzmann transport (LBT) model [32, 74] that describes both elastic and inelastic scatterings between jet partons and thermal partons from QGP. Within this framework, we investigated how different estimations of the jet parton formation time affects the nuclear modification of fully reconstructed jets at RHIC energy, and found that different models of this formation time impact not only the overall magnitude but also the
$ p_{T} $ dependence of the nuclear modification factor of jets. The goal of the present study was to explore the sensitivity of jet quenching to the starting time of parton-medium interactions. For a more comprehensive discussion on the LBT model and its comparison with various experimental data, one may refer to Refs. [26, 32, 36, 45, 47, 54, 61, 63, 74, 75].The remainder of this paper is organized as follows. In Sec. II, we discuss how the parton shower generated by Pythia was used to estimate the formation time of each parton and study the dependence of the formation time on the parton energy. In Sec. III, we investigate effects of formation time on the nuclear modification factor (
$ R_{AA} $ ) and central-to-peripheral ratio ($ R_\mathrm{cp} $ ) of jets in heavy-ion collisions using the LBT model. The paper is summarized in Sec. IV. -
We used the Pythia 8 event generator to simulate jet parton production and its vacuum shower. Given that initial parton production processes – e.g., multi-parton interaction (MPI) – other than the hardest scattering are also essential in describing jet observables, especially those related to soft particles [61, 76], we fed full Pythia events of final-state partons into the LBT model for their subsequent interactions with QGP. In hard scatterings, a pair of highly virtual partons are first created that continue splitting until the virtuality of each daughter is sufficiently low – close to its mass shell or approaching the scale of hadronization. We used the mother-daughter tree provided by the Pythia shower to evaluate the time required by each splitting, thereby obtaining the formation time of each parton.
For a
$ 1\rightarrow 2 $ process, the splitting time can be estimated using the uncertainty principle as [77]$ \tau_\mathrm{form}=\frac{2Ex(1-x)}{k_\perp^2}, $

(1) in which E represents the energy of the mother parton, x and
$ (1-x) $ are the energy fractions taken by the two daughters, and$ k_\perp $ is the transverse momentum of the daughters with respect to their mother. Here, the rest masses of both mother and daughters are neglected. Given that$ k_\perp^2/[x(1-x)] $ provides the virtuality ($ Q^2 $ ) of the mother parton, the formation time can also be written as$ \tau_\mathrm{form}=2E/Q^2 $ . Given that the uncertainty principle$ \Delta x \Delta p \sim 1 $ has been used to obtain Eq. (1), one should treat this relation as an approximation of the same order. Therefore, it is necessary to understand the sensitivity of jet energy loss to the exact values applied for the formation time. In the literature,$ \tau_\mathrm{form}\sim2E/k_\perp^2 $ is also frequently used by assuming that$ k_\perp^2 $ and$ Q^2 $ are of the same order.To study the effects of parton formation time on jet quenching, we compared our calculations for three different estimations of this formation time.
● Setup 1: zero formation time – the vacuum shower is assumed to occur instantaneously (
$ \tau_1=0 $ ) and jet partons start to interact with QGP when the hydrodynamic evolution of QGP commences (at$ \tau_0 $ ).● Setup 2: formation time from single splitting – each parton is assumed to be formed from one splitting, which requires a time expressed as
$ \tau_2=2Ex(1-x)/k_\perp^2 $ , where E represents the energy of the ancestor parton (directly produced by the initial hard scattering) at the top of the mother-daughter tree generated by Pythia shower, and x and$ k_\perp $ are respectively the fractional energy and transverse momentum of the given final-state parton with respect to its ancestor; thus, this jet parton starts to interact with QGP at$ t_\mathrm{init}=\max (\tau_0,\tau_2) $ .● Setup 3: formation time from multiple splittings – the full sequence of splittings from the very first ancestor to each final-state parton in Pythia is tracked, and the parton formation time is calculated as
$\tau_3=\sum_i 2E_i x_i(1-x_i)/ k_{\perp i}^2$ , where$ E_i $ represents the energy of the mother parton in the i-th splitting, and$ x_i $ and$ k_{\perp i} $ are respectively the fractional energy and transverse momentum of a daughter with respect to the mother; thus, this jet parton starts to interact with QGP at$ t_\mathrm{init}=\max (\tau_0,\tau_3) $ .These setups are well defined for partons originating from the initial hard scattering process. For those from other sources in Pythia simulation, such as the initial state radiation, we set their formation time as zero in the present study. Theoretically, we consider that setup-3 is a better choice than setup-2. However, given that setup-2 is widely applied in the literature as a quick estimation of the hard parton formation time from jet vacuum showers, it is worth investigating their difference on jet observables within the same framework.
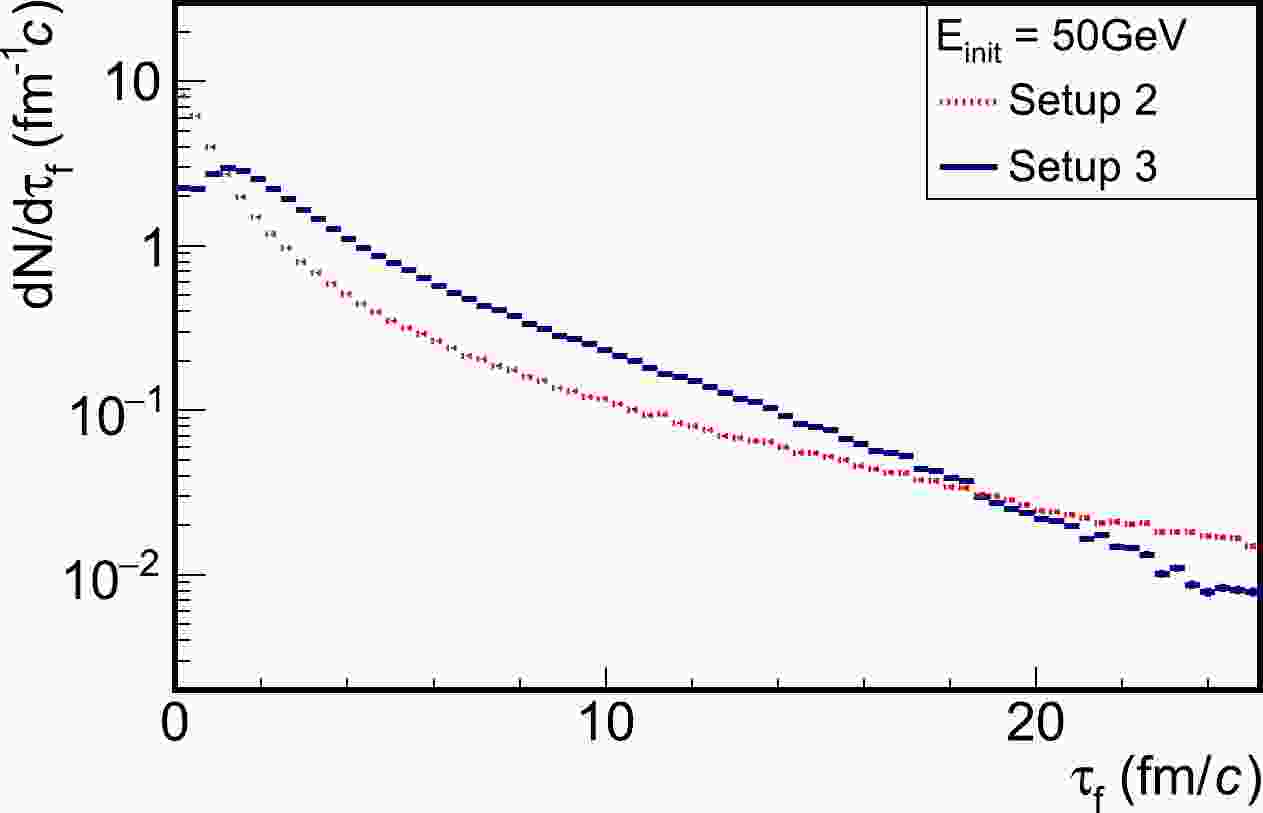
In Fig. 1, we show the formation time distribution of the final-state Pythia partons developed from a single quark at a fixed energy of 50 GeV and maximum possible virtuality scale of 50 GeV; besides, setup-2 (single splitting) and setup-3 (sequential splittings) are compared. One would expect a δ-function at zero formation time for setup-1 (instantaneous formation). Compared to setup-1, one observes that a large number of partons from setup-2 and 3 are formed during the QGP phase: there are only approximately 50% partons for setup-2 and 20% partons for setup-3 formed before
$ \sim 1 $ fm/c (the scale of the initial time of QGP); these percentages increase to approximately 83% and 76%, respectively, at the time around 5 fm/c, and approaches approximately 90% and 92%, respectively, around 10 fm/c (the QGP lifetime). The remaining amount is formed out of dense nuclear matter. Therefore, the consideration of the parton formation time significantly delays the jet-medium interaction and affects the jet quenching observables.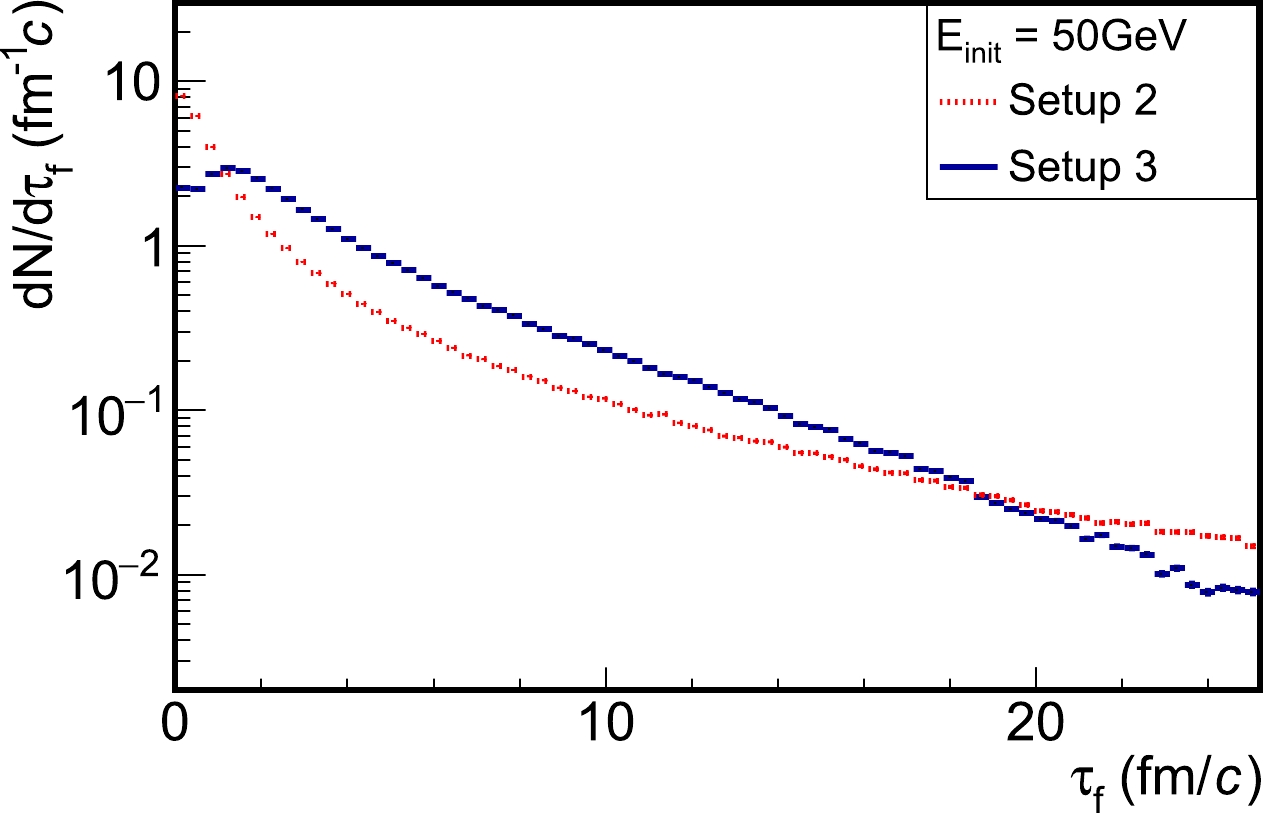
Figure 1. (color online) Distribution of final-state partons from Pythia emanating from a 50 GeV quark as a function of the formation time; comparison between different setups.
The difference in the formation time between setup-2 and 3 originates from two competing effects. The addition of time for a sequence of splittings (setup-3) can lead to a longer formation time than that of a single splitting (setup-2). By contrast, given that both the energy E and virtuality
$ Q^2 $ (or$ k_\perp^2 $ ) in Eq. (1) decrease after each splitting, a longer formation time may be estimated from setup-2 than from setup-3. In general, the parton distributions are comparable (of the same order) over a wide range of formation time, as shown in Fig. 1. This can be understood from the dominating contribution to the total formation time from the last (softest) splitting. However, a closer comparison suggests that, within the QGP lifetime ($ 1\sim 10 $ fm/c), partons from setup-3 tend to form later than those from setup-2.To further investigate the dependence of the formation time on the parton energy scale, Fig. 2 presents the average formation time of partons as a function of their final state
$ p_{T} $ generated by Pythia. Here, we simulated proton-proton (p+p) collisions$ \sqrt{s}=200 $ GeV and used setup-3 for sequential splittings to calculate the parton formation time. Inside the figure, results from different$ \hat{p}_{T} $ bins are compared; govern the amount of momentum exchange for the initial hard scatterings in Pythia and were set around the initial$ p_{T} $ of partons directly produced from the hard splittings. Note from Fig. 2 that for a given$ \hat{p}_{T} $ bin, the formation time first increases and then decreases as the final-state parton$ p_{T} $ increases. Given that the hardest final-state partons are most likely produced via few unbalanced splittings (or even no splitting at all) from the initial hard parton, they exhibit a short formation time. By contrast, medium$ p_{T} $ partons that approach mass shells after multiple splittings show a longer formation time. Note also that the longest formation time comes from splittings where daughter partons are almost collinear ($ k_\perp\rightarrow 0 $ ). The peak value of the formation time becomes larger as one increases the initial$ \hat{p}_{T} $ bin. This is because partons produced from more energetic collisions usually possess higher virtualities and therefore require a longer time to shower towards their mass shells.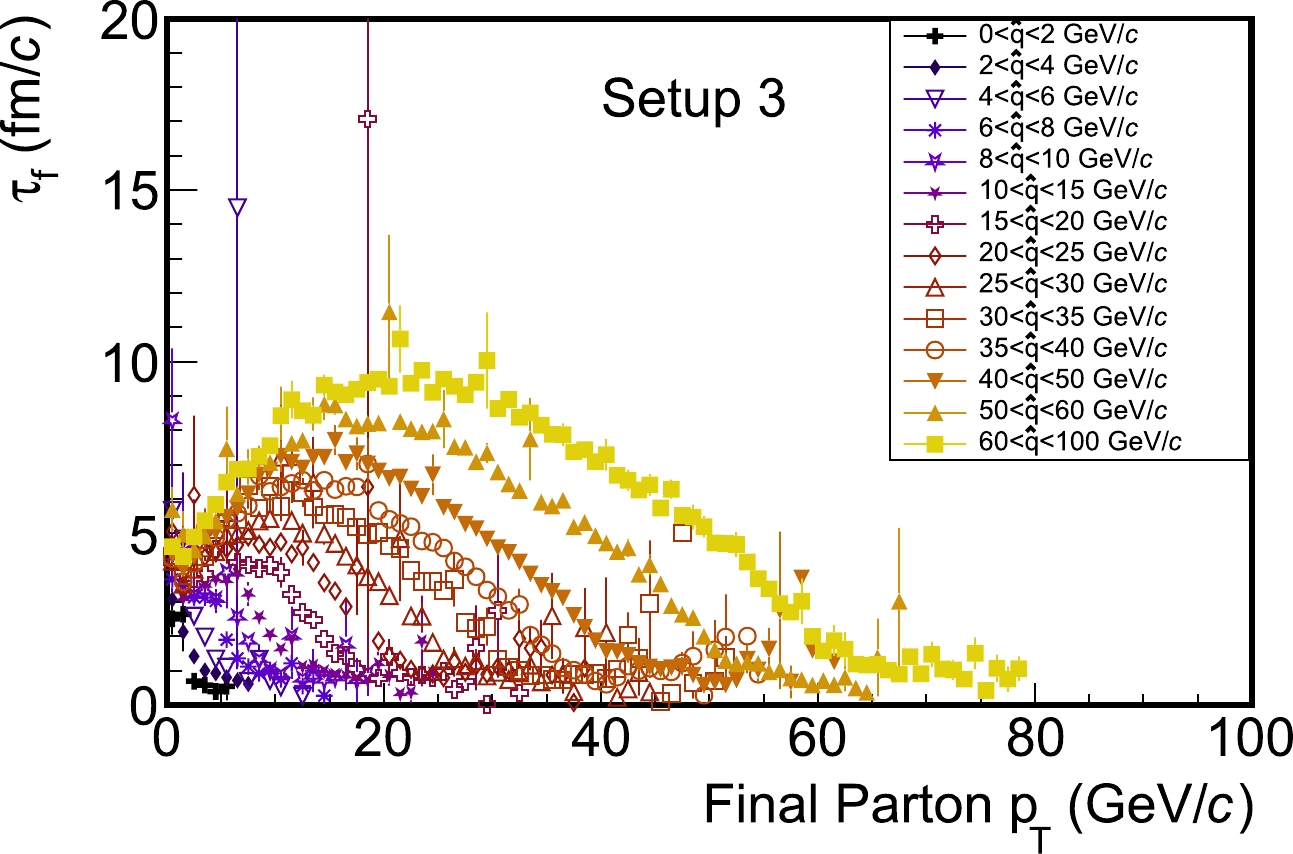
Figure 2. (color online) Dependence of the average formation time from sequential splittings (setup-3) on the final-state parton
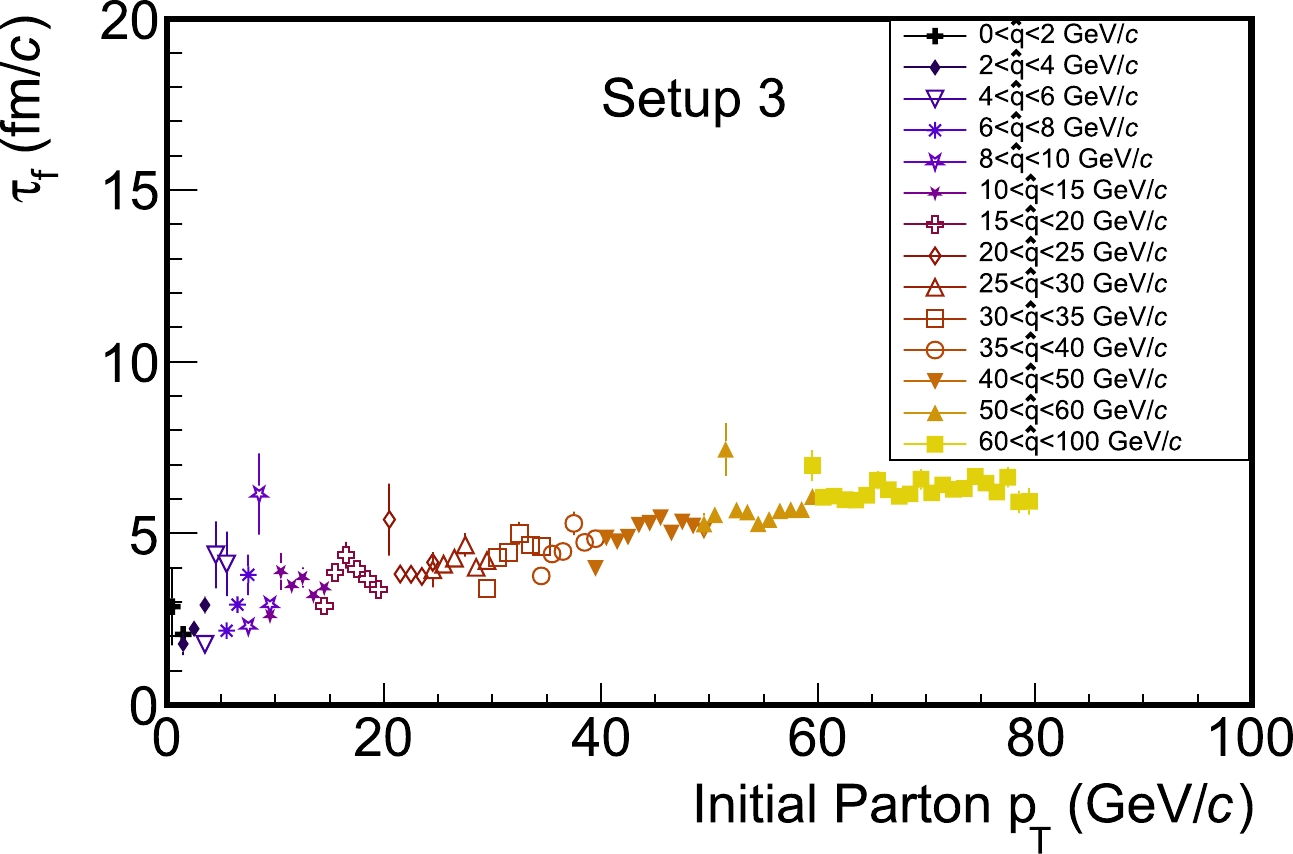
$p_{T}$ ; different$\hat{p}_{T}$ regions in Pythia are compared for p+p collisions at$ \sqrt{s}=200 $ GeV.The same conclusions can also be drawn from Fig. 3, where we present the average formation time as a function of the
$ p_{T} $ of the ancestor partons directly produced from hard collisions in Pythia. In this figure, one can clearly observe the mapping between the$ \hat{p}_{T} $ bins and the ranges of the ancestor parton$ p_{T} $ . With the increase of this initial$ p_{T} $ , the average time for shower partons to approach their mass shells becomes longer. An approximately linear relation can be seen between the average formation time of the shower partons and the initial$ p_{T} $ of the ancestor partons. We confirmed that the parton formation time estimated using setup-2 (single splitting scenario) shares dependences on the initial and final state partons$ p_{T} $ similar to those resulting from setup-3. -
The final-state partons generated by Pythia were fed into the linear Boltzmann transport (LBT) model [32, 74] for their subsequent interactions with the QGP medium. In LBT, the phase space distribution of jet partons (denoted by "a" here) evolves according to the Boltzmann equation
$ \begin{array}{*{20}{l}} p_a \cdot \partial f_a= E_a (\mathcal{C}_\mathrm{el}+\mathcal{C}_\mathrm{inel}), \end{array} $

(2) where the collision term on the right hand side includes contributions from both elastic and inelastic processes. From the collision term, one may extract the elastic scattering rate as
$ \begin{aligned}[b] \Gamma_a^\mathrm{el}(\vec{p}_a,T)=&\sum_{b,(cd)}\frac{\gamma_b}{2E_a}\int \prod_{i=b,c,d}\frac{{\rm d}p_i^3}{E_i(2\pi)^3} f_b S_2(\hat{s},\hat{t},\hat{u})\\ &\times (2\pi)^4\delta^{(4)}(p_a+p_b-p_c-p_d)|\mathcal{M}_{ab\rightarrow cd}|^2, \end{aligned} $

(3) in which we sum over all possible
$ ab\rightarrow cd $ channels;$ \gamma_b $ and$ f_b $ represent the color-spin degrees of freedom and the distribution of thermal partons inside QGP, respectively, and the function$ S_2(\hat{s},\hat{t},\hat{u})=\theta(\hat{s}\ge 2\mu_\mathrm{D}^2)\theta(-\hat{s}+ \mu^2_\mathrm{D}\le \hat{t} \le -\mu_\mathrm{D}^2) $ is introduced [78] to avoid the collinear divergence in the leading-order (LO) scattering matrices$ \mathcal{M}_{ab\rightarrow cd} $ , with$ \hat{s} $ ,$ \hat{t} $ , and$ \hat{u} $ denoting the Mandelstam variables, and$ \mu_\mathrm{D} $ denoting the Debye screening mass. Meanwhile, the inelastic scattering rate is related to the average number of medium-induced gluons per unit time as$ \Gamma_a^\mathrm{inel} (E_a,T,t) = \int {\rm d}x{\rm d}k_\perp^2 \frac{{\rm d}N_g^a}{{\rm d}x {\rm d}k_\perp^2 {\rm d}t}, $

(4) where the gluon spectrum is taken from the higher-twist energy loss calculation [11, 17, 79]:
$ \frac{{\rm d}N_g^a}{{\rm d}x {\rm d}k_\perp^2 {\rm d}t}=\frac{2C_A\alpha_\mathrm{s} P^\mathrm{vac}_a(x)}{\pi C_2(a) k_\perp^4}\,\hat{q}_a\, {\sin}^2\left(\frac{t-t_i}{2\tau_f}\right). $

(5) In the above equation, x and
$ k_\perp $ are the fractional energy and transverse momentum of the emitted gluon with respect to its parent parton,$ P^\mathrm{vac}_a(x) $ is the vacuum splitting function of a with the color factor$ C_2(a) $ included,$ \hat{q}_a $ is the parton transport coefficient that characterizes the transverse momentum broadening square per unit time due to elastic scatterings,$ t_i $ represents the production time of parton a, and$ \tau_f={2E_a x(1-x)}/k_\perp^2 $ denotes the formation time of the emitted gluon in LBT. The formation time (or production time) of jet partons discussed in the previous section directly determines when they start these elastic and inelastic scatterings with the QGP medium. The only parameter we adjusted for LBT in this study is the strong coupling constant$ \alpha_\mathrm{s} $ , which directly affects the interaction strength in elastic scatterings and controls the rate of medium-induced gluon through the jet transport coefficient$ \hat{q}_a $ .For realistic heavy-ion collisions, the spatial distribution of initial jets was calculated according to the binary collision vertices from the Monte-Carlo (MC) Glauber model. QGP was simulated using a viscous hydrodynamic model (VISHNew [80–82] in this study) whose entropy density distribution was initialized using the MC Glauber model. The initial time of the hydrodynamic evolution was set as
$ \tau_0=0.6 $ fm/c, whereas the specific shear viscosity was set as$ \eta/s=0.08 $ for a reasonable description of the soft hadron observables at RHIC and LHC. This hydrodynamic model provides the spacetime information of the local temperature and flow velocity of the QGP medium, based on which we obtained the momentum distribution of thermal partons that entered the collision term on the right hand side of Eq. (2).In the LBT model, we tracked the phase space evolution of the jet partons and their emitted gluons. In addition, we tracked the thermal partons that scattered out of the QGP background. The latter is denoted as "recoil" partons. Generation of these recoil partons leaves particle holes inside the QGP that are denoted as back-reaction or "negative" partons. Thus, we also tracked inside LBT to guarantee the energy-momentum conservation of the parton system. Recoil and negative partons constitute the "jet-induced medium excitation" and have demonstrated to be essential in understanding observables related to fully reconstructed jets [44, 45]. At the chemical freezeout hypersurface (
$ T_\mathrm{c}=165 $ MeV), all partons discussed above were collected for jet reconstruction and observable analysis. Their further interaction with the hadron gas was neglected, considering its much more dilute density with respect to the QGP medium.For jet reconstruction, we fed all partons from Pythia (for p+p collisions) or Pythia+LBT (for heavy-ion, or A+A, collisions) into the Fastjet package with the anti-
$ k_\perp $ algorithm selected [83, 84]. In this study, particles in the mid-rapidity$ |\eta|<1 $ and$ p_{T}>0.2 $ GeV/c were used for constructing jets. For a given jet cone size R, the reconstructed jet$ \eta_\mathrm{jet} $ was required to be at R distance from the acceptance edge as$ |\eta_\mathrm{jet}|<1-R $ , so that the full jet became located inside the acceptance coverage. Note that the energy-momentum of the negative partons produced by LBT is subtracted from the reconstructed jets, similar to subtracting the medium background.Figure 4 shows the nuclear modification factor
$ R_{AA} $ of full jets with a cone size$ R=0.2 $ in the top 10% Au-Au collisions at$\sqrt{s_{NN}}=200$ GeV. We compare the three proposed setups of parton formation time using different panels: the upper panel for instantaneous formation (setup-1), middle panel for single splitting (setup-2), and lower panel for sequential splittings (setup-3). In each panel, results from different$ \alpha_\mathrm{s} $ values are compared. For a given setup of formation time, the jet$ R_{AA} $ becomes smaller with an increasing value of$ \alpha_\mathrm{s} $ due to stronger jet-medium interactions. Meanwhile, with the same$ \alpha_\mathrm{s} $ value, an increasing$ R_{AA} $ can be observed from top to bottom panels, because a longer formation time ($ t_\mathrm{init}^\mathrm{setup-3} >t_\mathrm{init}^\mathrm{setup-2}>t_\mathrm{init}^\mathrm{setup-1} $ ) delays the medium modification on jets. A similar trend of larger$ R_{AA} $ with later jet formation time was also observed in Ref. [70]. In addition to the overall magnitude of jet quenching, note also that the$ p_{T} $ dependence of the jet$ R_{AA} $ can be affected by different assumptions regarding the parton formation time. At RHIC energy, the jet$R_{AA}$ would decrease with$ p_{T} $ if instantaneous formation is assumed (upper panel). However, by adopting a more realistic modeling of formation time, a slightly rising trend of$ R_{AA} $ with respect to$ p_{T} $ is observed. This can be understood from the longer formation time for higher$ p_{T} $ partons, as previously discussed in Figs. 2 and 3. This effect on the$ p_{T} $ dependence of the jet$ R_{AA} $ does not depend on the$ \alpha_\mathrm{s} $ value we used here. Note that the STAR data [85] of$ R_{AA}^\mathrm{Pythia} $ (ratio of jet spectra between measurement in A+A collisions and Pythia simulation) are also included in Fig. 4 as a reference. However, as discussed earlier, we did not aim to precisely constrain the formation time from data in this study, given that our current model calculation is still incomplete. For instance, jet partons at high virtuality (before arriving at their mass shells) can also lose energy inside the QGP [86, 87], this was not considered in this study. Therefore, results from setup-3 in the lower panel of Fig. 4 do not lead to conclude that the coupling strength should be as strong as$ \alpha_\mathrm{s}=0.5 $ . In addition, owing to the remaining challenge concerning hadronizing jet partons in heavy-ion collisions, uncertainties exist when it comes to comparing the partonic jets in the present study to the charged jets with a high$ p_{T} $ hadron trigger measured by STAR. These will be addressed in future studies.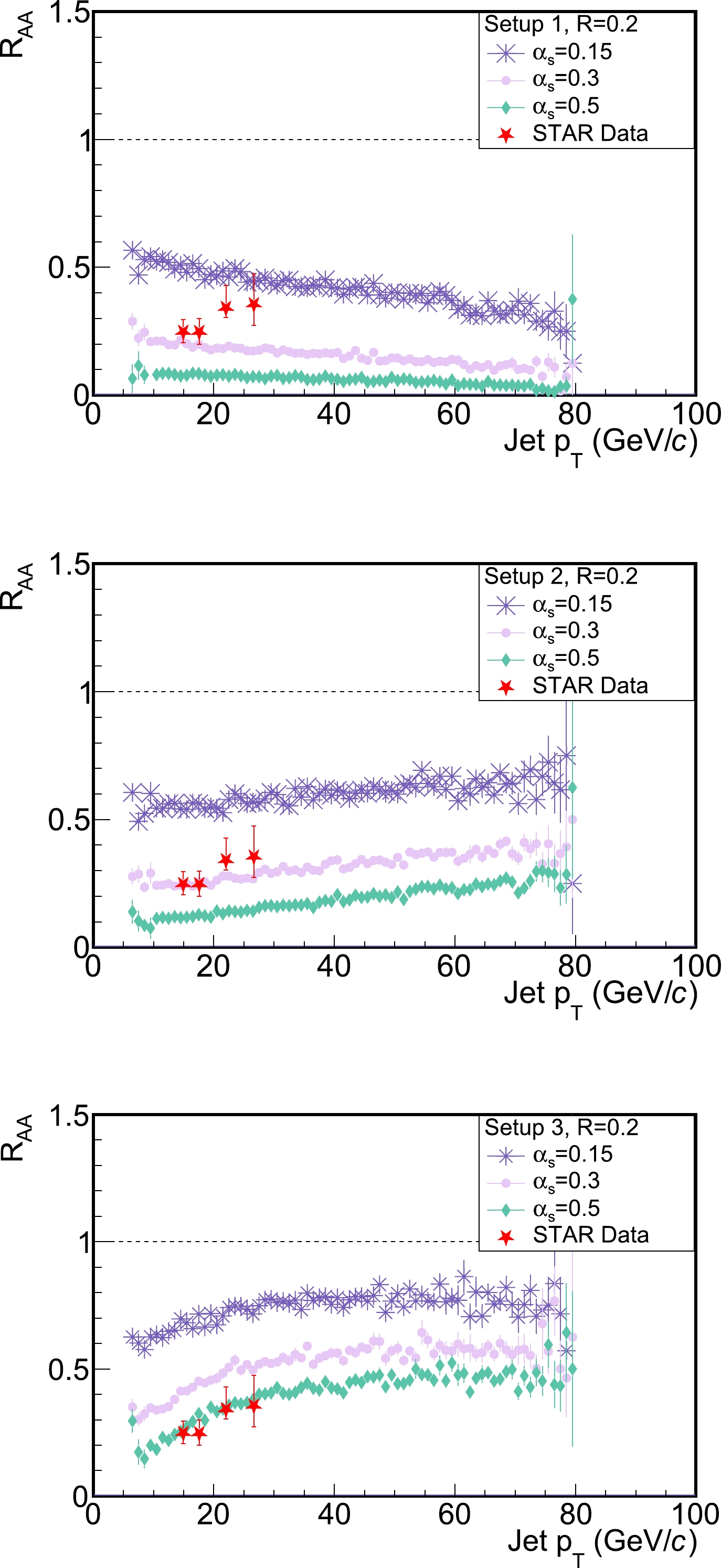
Figure 4. (color online) Nuclear modification factor
$ R_{AA} $ of jets in 0–10% Au+Au collisions at$\sqrt{s_{NN}}=200$ GeV; different$ \alpha_\mathrm{s} $ values and setups of the parton formation time are employed for comparison – upper panel for setup-1, middle panel for setup-2, and lower panel for setup-3.To avoid uncertainties introduced by lacking the p+p baseline of jet measurement, one may also quantify the nuclear modification effect using the central-to-peripheral ratio (
$ R_\mathrm{cp} $ ) of the jet spectra in A+A collisions. Figure 5 shows our calculation on this$ R_\mathrm{cp} $ between 0–10% and 60%–80% centrality bins, compared to the STAR data [85]. From the top to bottom panels, we present results for different jet cone sizes –$ R=0.2 $ , 0.3, and 0.4 respectively. In each panel, we compare the three proposed setups of formation time estimation. Similar to the jet$ R_\mathrm{AA} $ previously presented in Fig. 4, we found that different models of the parton formation time affect not only the overall magnitude, but also the$ p_{T} $ dependence of the jet$ R_\mathrm{cp} $ . Setup-1, that is, instantaneous parton formation, leads to a decreasing jet$ R_\mathrm{cp} $ with respect to its$ p_{T} $ , which is disfavored by the STAR data. By contrast, the increasing trend of$ R_\mathrm{cp} $ with jet$ p_{T} $ from more realistic evaluations of the formation time (setup-2 and 3) appear qualitatively consistent with the experimental observation. Given that the formation time increases with the virtuality scale of the initial hard partons, its impact on jet quenching is expected to be even stronger in more energetic collisions at the LHC.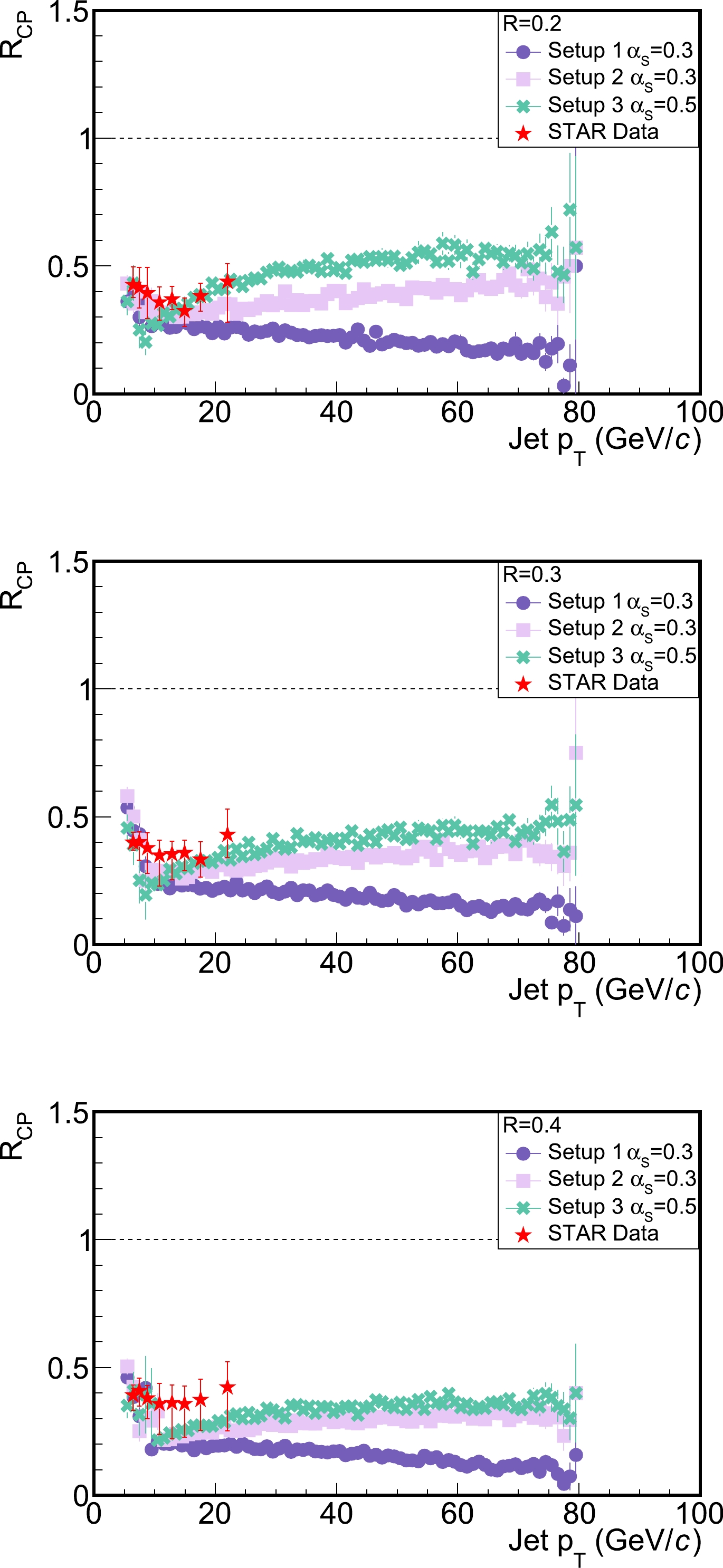
Figure 5. (color online) Central (0–10%) to peripheral (60%–80%) ratio (
$ R_\mathrm{cp} $ ) of jets in Au+Au collisions at$\sqrt{s_{NN}}=200$ GeV; different setups of the parton formation time at different jet cone sizes are employed for comparison: upper panel for$ R=0.2 $ , middle panel for$ R=0.3 $ , and lower panel for$ R=0.4 $ . -
In this study, we explored the impact of the parton shower formation time on jet quenching in relativistic heavy-ion collisions. The Pythia event generator was used to obtain parton showers in vacuum, based on which three different models were set up to estimate the formation time of each parton, including instantaneous formation (setup-1), formation from single splitting (setup-2), and sequential splittings (setup-3). The final-state partons from Pythia were then fed into the LBT model for their subsequent interactions with the QGP medium.
Within this framework, we found that after considering the time required by realistic splittings (for both setup-2 and 3), only a limited number of partons within jets form prior to the QGP formation, while a large number form inside and even after the QGP stage. The formation time becomes longer as the scale of the momentum exchange in the initial hard scatterings increases. Within the lifetime of QGP produced at RHIC energy, we found that the average parton formation time follows the hierarchy
$ t_\mathrm{init}^\mathrm{setup-3}>t_\mathrm{init}^\mathrm{setup-2}>t_\mathrm{init}^\mathrm{setup-1} $ , which leads to an inverse hierarchy of parton energy loss inside the QGP. Remarkable effects were observed on both the overall magnitude and transverse momentum dependence of the nuclear modification factor of jets. For a given value of$ \alpha_\mathrm{s} $ , a smaller$ R_{AA} $ was observed for a shorter formation time. The jet$ R_{AA} $ decreased with$ p_{T} $ for setup-1 and increased with$ p_{T} $ for setup-2 and 3 owing to a longer average parton formation time from a more energetic jet. Consistent results were observed across different$ \alpha_\mathrm{s} $ values, as well as for the central-to-peripheral ratio of the jet spectra ($ R_\mathrm{cp} $ ).While this study provides a detailed demonstration on the sensitivity of jet quenching observables to the formation time of parton showers, further improvements are required in several directions to achieve quantitative constraints on the parton formation time from the jet quenching data. For instance, instead of the free-streaming assumption, it is necessary to introduce a medium modification on jet partons during their high virtuality stage to avoid possible underestimation of jet quenching, especially when the parton formation time is long. This would narrow the differences resulting from introducing various assumptions of the formation time, although different
$ p_{T} $ dependences of jet observables are still expected due to different jet energy loss mechanisms occurring at different virtuality scales. A solid hadronization scheme should also be introduced for a more direct comparison between our current model calculation at the parton level and experimental measurements on the charged hadron jets. Finally, more jet observables, such as the anisotropic flow coefficients of jets and the jet shape, should be included to establish a stronger constraint on the formation time. -
We thank Yayun He, Tan Luo, Weiyao Ke, Maowu Nie, and Xin-Nian Wang for helpful discussions.
Effects of the formation time of parton shower on jet quenching in heavy-ion collisions
- Received Date: 2022-08-30
- Available Online: 2023-02-15
Abstract: Jet quenching has successfully served as a hard probe to study the properties of Quark-Gluon Plasma (QGP). As a multi-particle system, jets require time to develop from a highly virtual parton to a group of partons close to mass shells. In this study, we present a systematical analysis on the effects of this formation time on jet quenching in relativistic nuclear collisions. Jets from initial hard scatterings were simulated with Pythia, and their interactions with QGP were described using a Linear Boltzmann Transport (LBT) model that incorporates both elastic and inelastic scatterings between jet partons and the thermal medium. Three different estimations of the jet formation time were implemented and compared, including instantaneous formation, formation from single splitting, and formation from sequential splittings, before which no jet-medium interaction was assumed. We found that deferring the jet-medium interaction with a longer formation time not only affects the overall magnitude of the nuclear modification factor of jets but also its dependence on the jet transverse momentum.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: