-
Renormalization [1–5] is an important subject in quantum field theory, which was developed to deal with ultraviolet divergences. After renormalization, physical observables shall be finite and independent of the cutoff, i.e., renormalization-group (RG) invariant. Traditionally, it has been thought that a theory is renormalizable if all of its coupling constants in the Lagrangian have nonnegative mass dimensionality; otherwise, it is nonrenormalizable and thus not that useful. However, the modern view of renormalizability is different [6–9], and it is based on the idea of effective field theory (EFT).
Quantum chromodynamics (QCD) is regarded as a correct theory of strong interaction, which is part of the Standard Model of particle physics. QCD can be solved perturbatively at high energies because of asymptotic freedom. However, QCD is nonperturbative at low energies, where most of the nuclear interactions happen. One way to solve the problems in the low energy range is using lattice QCD, another way is using effective theories. Chiral effective field theory (χEFT) is an effective theory of QCD at low energies, where the degrees of freedom are no longer quarks and gluons but baryons and pions. χEFT applies when the characteristic momentum Q in a process is well below the QCD nonperturbative scale
$ M_{\rm QCD}\sim 1 $ GeV. From the point of view of an effective theory, one can add as many terms as one wants in an effective Lagrangian as long as they obey the required symmetries. Of course, these terms must be ordered in a proper way based on some power counting. For an effective theory at low energies, the details of its high energy physics are not shown explicitly or are unknown, and the effects are embedded in interaction strengths or "low-energy constants" (LECs). Once the Lagrangian is obtained, physical observables can be calculated in a systematic expansion in powers of$ Q/M_{\rm QCD} $ (abbreviated as Q hereafter if there is no confusion) [10]. This way is obviously model independent. Ultraviolet divergences can be absorbed by the LECs via order-by-order renormalization.Weinberg's seminal articles [11, 12] have inspired numerous applications of EFTs to a variety of nuclear, hypernuclear, and antinuclear systems. Since the first implementation [13–15] in this direction, significant improvements have been made, which are reviewed for instance in Refs. [16–19]. In Refs. [20, 21], Weinberg's proposal was extended to antinucleon-nucleon (
$ \overline{N} N $ ) systems. Here, we discuss the renormalization of one-pion exchange (OPE) in χEFT for$ \overline{N} N $ scattering at low energies, which is an extension of Ref. [22].Renormalization has been extensively studied (most in the framework of EFTs) for the
$ N N $ system [23–55], and there are still some disagreements. It was known that there are inconsistencies in Weinberg's power counting (WPC), i.e., the observables obtained with Weinberg's approach are not RG invariant [23, 25, 31, 34, 56–58]. For different views, see for instance Refs. [49–53, 55]. The reason for this is that WPC is based on naive dimensional analysis (NDA) [59], which has its origin in the application of naturalness [60, 61] to perturbative series [62], while$ N N $ has a nonperturbative character at LO. It is well known that nonperturbative renormalization can be very different from the perturbative one [63]. Once a channel contains an attractive OPE tensor force with a$ \sim -r^{-3} $ singular part, an additional counterterm is needed compared to that expected by the NDA when the OPE is treated nonperturbatively [31, 64, 65]. In other words, the LECs are in fact promoted by the nonperturbative RG running.In this work, we extend our previous study on the renormalization of the
$ \overline{N} N $ scattering amplitudes [22] to other higher partial waves with total angular momentum$ J\leq 3 $ . The OPE will be treated nonperturbatively as before. Again, we use the results of the Groningen energy-dependent partial-wave analysis (PWA) [66] as a kind of base. The Groningen PWA provides a very good description of the data for elastic$ \overline{p}p\rightarrow \overline{p}p $ and charge-exchange$ \overline{p}p\rightarrow \overline{n}n $ scattering below 925 MeV/c antiproton laboratory momentum. In our previous paper [22], we studied the renormalization of OPE in the uncoupled S, P, and the coupled S-D and P-F partial waves. Here, we focus on the uncoupled D, F, and the coupled D-G partial waves. The analysis is similar to those of Refs. [22, 31], and we use the same the boundary conditions as in the Groningen PWA, with a coordinate-space regulator [25, 64, 67]. At a certain energy, the LEC is fitted to the phase shift and inelasticity of the PWA, with phase shifts and inelasticities at other energies and mixing angles being postdictions of the EFT at LO. We work in the isospin basis because isospin breaking is a higher-order effect. In future studies, we will try to treat the OPE perturbatively in some$ \overline{N} N $ partial waves [68, 69] and include other higher order interactions.The organization of this paper is the following. In Sec. II, we describe the OPE potential and the contact interactions, and identify the partial waves, which have attractive singular tensor forces and thus need more counterterms than those expected by NDA. In Sec. III, the renormalization strategy is explained and the results are shown. The conclusions and outlooks are presented in Sec. IV.
-
Since χEFT is a low energy EFT of QCD, the degrees of freedom are nucleon (N) and antinucleon (
$ N^c $ ) now in an antinuclear system, and for processes involving momenta Q on the order of the pion mass, the three pions ($ \pi^a $ , with$ a=1,\,2,\,3 $ ) must also be included explicitly as pseudo-Goldstone bosons from the spontaneous breaking of chiral symmetry. The interactions are constrained by the approximate chiral symmetry and other symmetries of the QCD. OPE arises from the first few terms in the nonrelativistic chiral Lagrangian density [70]$ \begin{aligned}[b] \mathcal{L}_{\overline{N} N} =& N^\dagger \left({\rm i} \partial_0+\frac{\nabla^2}{2m_N}\right) N + {N^c}^\dagger\left({\rm i} \partial_0+\frac{\nabla^2}{2m_N}\right)N^c \\&-\frac{1}{2}\pi^a\left(\partial^2+m_\pi^2\right)\pi^a \\ & + \,\frac{g_A}{2 f_\pi}\left({N^\dagger}\vec{\sigma}\tau^a N + {{N^c}^\dagger}{\vec\sigma}\tau^{aT} N^c\right)\cdot\vec{\nabla}\pi^a +\dots\,, \end{aligned} $

(1) where
$ m_N\simeq 940 $ MeV is the (anti)nucleon mass,$ m_\pi\simeq 138 $ MeV is the pion mass,$ g_A\simeq 1.29 $ is the axial-vector coupling constant,$ f_\pi\simeq 92.4 $ MeV is the pion decay constant, and$ \tau^a $ ($ \vec{\sigma} $ ) are the Pauli matrices for isospin (spin). The contact interactions are buried in the dots. The electromagnetic terms are not included because we are studying the strong interaction here.The energy transfer between (anti)nucleons is of order
$ Q^2/m_N $ after renormalization, and thus the pion propagator can be taken as approximately static. At LO, i.e., at the order of$ Q^0 $ , the OPE potential in the coordinate space for the$ \overline{N} N $ system can be obtained from the Eq. (1):$ \begin{equation} V_\pi = -\frac{g_A^2 m_\pi^3}{16\pi f_\pi^2} \,\boldsymbol{\tau}_1\cdot\boldsymbol{\tau}_2\, \bigl[v_S(m_\pi r) \,\vec{\sigma}_{1}\cdot\vec{\sigma}_{2} + v_T(m_\pi r)\,S_{12}\bigr] \, , \end{equation} $

(2) where
$ S_{12}=3\,\vec{\sigma}_{1}\cdot\hat{r}\,\vec{\sigma}_{2}\cdot\hat{r} -\vec{\sigma}_{1}\cdot\vec{\sigma}_{2} $ is the tensor operator, and$ v_S(x) = \frac{{\rm e}^{-x}}{3x}\; , \tag{3a}$

$ v_T(x) = \left(1+x+\frac{x^2}{3}\right) \frac{{\rm e}^{-x}}{x^3} \ . \tag{3b} $

At next-to-leading order (NLO), i.e., at the order of Q, there is no correction because of Lorentz invariance and parity invariance [12, 13]. At next-to-next-to-leading order (
$ {\text N}^2 $ LO), i.e., at the order of$ Q^2 $ , chiral-symmetry-breaking corrections represent the Goldberger-Treiman discrepancy, which increases the strength of the static OPE [71, 72], while chiral-symmetric corrections to the pion-(anti)nucleon interaction account for recoil [13]. Two-pion-exchange (TPE) also appears at this order [13]. Equation (2) has the opposite sign as the OPE for$ N N $ (cf., for example, Ref. [31]), because the G parity of the pions is$ -1 $ .For higher partial waves, the perturbative treatment of the OPE potential may be proper and sufficient at low energies, but as there is yet no clear boundary between nonperturbation and perturbation [63], we will leave this for further study, and will continue to treat the OPE potential nonperturbatively in this work, as we have done in Ref. [22]. The nonperturbative results presented here can also be used as a comparison for the future perturbative results, which may also be helpful in identifying the boundary between nonperturbation and perturbation if it exists.
As one can see in Eq. (2), the OPE potential is singular and it diverges as
$ r^{-3} $ and thus needs to be regularized. The regulator we use here is the same as the one used in the Groningen PWA [66], which follows the procedure of the Nijmegen PWAs of Refs. [73–75], and the short-range and long-range interactions are separated at a boundary$ b=1.2 $ fm. The long-range potential consists of the electromagnetic interaction, OPE, and TPE [76, 77]. At$ r=b $ a boundary condition is chosen that, for convenience, corresponds to a complex spherical well, which is independent of energy and depends on the spin and isospin of the partial wave. The partial-wave Schrödinger equation is solved for the coupled$ \overline{p}p $ and$ \overline{n}n $ channels with a long-range potential with$ r>b $ . In this paper, the long-range potential only contains the OPE and the partial-wave Schrödinger equation can be solved in a similar way as that in Ref. [66]. Solving the Schrödinger equation with the OPE potential is equivalent to iterating the OPE to all orders. The boundary radius b, however, is not fixed at$ 1.2 $ fm and can vary now. The relation between the ultraviolet cutoff Λ and the boundary radius b is$ \Lambda\equiv 1/b $ .In χEFT, the short-range QCD are embedded in the contact interactions. For
$ \overline{N} N $ , they are complex instead of real in the$ N N $ case. The complex character is responsible for the complicated annihilation processes. Mesons generated in these processes with energies on the order of$ 2m_N $ cannot be accounted for as explicit degrees of freedom in the EFT. One example is the annihilation diagram into one pion, related to OPE by crossing, which would be present in a relativistic theory. There are also annihilation states containing soft pions, which give rise to long-range effects, but their contributions to elastic scattering are suppressed by a factor of$ (Q/4\pi f_\pi)^2 $ , as for other irreducible loops. Annihilation also generates contributions to the real parts of the LECs in addition to their imaginary parts, which makes the LECs of$ \overline{N} N $ different from those of$ N N $ . Like any other EFT LECs, these contact interactions must appear at orders no higher than where they are needed to remove the arbitrary regulator dependence. The actual values of the real and imaginary parts will be determined by fitting to the empirical PWA "data."The contact interactions, which are (derivatives of) Dirac delta functions in the coordinate space, are smeared with a spherical well [25, 64, 67] resembling the one used in Ref. [66]. Schematically, for a channel c,
$ C_{c} \, \mathcal{O}_{c}\delta^{(3)}(r) \rightarrow \frac{3C_{c}}{4\pi b^3}\,\theta(b-r)\,\mathcal{P}_{c} \equiv \left(V_c+{\rm i} W_c\right)\, \theta(b-r) \, \mathcal{P}_{c} \ , $

(4) where
$ C_c $ is a complex LEC,$ \mathcal{O}_{c} $ is a combination of derivatives,$ \mathcal{P}_c $ is the projection operator on channel c, and the real short-range parameters$ V_c $ and$ W_c $ from different channels are independent. Therefore, the regulator is proportional to the Heaviside function. For a different way of defining the counterterms of the annihilation, see Refs. [20, 21].As we are considering uncoupled D, F and coupled D-G partial waves here, the short-range interactions are expected by NDA to appear at even higher orders than those of the lower partial waves considered in Ref. [22]. However, whether a short-range interaction is needed at LO in a certain channel hinges on the tensor part of the OPE being attractive, as has been discussed for the
$ N N $ case in Refs. [31, 34] and for the$ \overline{N} N $ case in Ref. [22]. Therefore, here, the short-range interactions in the partial waves whose tensor part of the OPE is attractive need to be promoted to LO as well, and we will check this.A partial wave is denoted by
$ ^{2I+1\;2S+1}L_J $ , where I (S) is the total isospin (spin) and L (J) is the orbital (total) angular momentum. Because the Pauli principle does not apply to the$ \overline{N} N $ system, the total isospin is independent from other quantum numbers, which is unlike in the$ N N $ system where$ I+S+L $ must be odd. Moreover, due to annihilation, there are four times as many phase parameters (phase shifts, inelasticities, and mixing angles) compared to$ np $ scattering, viz., 20 phase parameters for each value of$ J\neq0 $ [75, 78]. For uncoupled partial waves, the S matrix is just a complex number with two real parameters,$ \begin{equation} S = \eta\,{\rm e}^{2{\rm i}\delta} \ , \end{equation} $

(5) where δ is the phase shift and η (
$ 0\leq\eta\leq1 $ ) is the inelasticity due to annihilation. For the coupled spin-triplet partial waves with$ L=J\mp1 $ ($ J\ge1 $ ) the$ 2\times 2 $ S matrix is parameterized as [66, 74]$ \begin{equation} S^J = \exp({\rm i}\bar{\delta}) \, \exp({\rm i}\varepsilon_{J}\sigma_x) \,\, H^J \, \exp({\rm i}\varepsilon_{J}\sigma_x) \, \exp({\rm i}\bar{\delta})\; , \end{equation} $

(6) where
$ \bar{\delta} $ is a diagonal matrix with real entries$ \delta_{J-1,J} $ and$ \delta_{J+1,J} $ , and$ \varepsilon_{J} $ is the mixing angle. The matrix$ H^J $ parameterizes the inelasticities. It is written as$ \begin{equation} H^J = \exp(-{\rm i}\omega_J\sigma_y) \, \left( \begin{array}{cc} \eta_{J-1,J} & 0 \\ 0 & \eta_{J+1,J} \end{array} \right) \, \exp({\rm i}\omega_J\sigma_y)\; , \end{equation} $

(7) where
$ \eta_{J-1,J} $ and$ \eta_{J+1,J} $ are the inelasticities ($ 0 \leq \eta_{J\mp1,J}\leq 1 $ ) and$ \omega_J $ is the mixing angle for inelasticity. The S matrix for the coupled partial waves is thus written in terms of six real parameters.Because the sign of the singular tensor force is a crucial point for the renormalization property of a certain partial wave, let us figure them out. The matrix elements of the tensor force have similar properties to those for
$ N N $ . From Eq. (2), one can see that the sign of the singular tensor force depends on the matrix elements of$ \boldsymbol{\tau}_1\cdot\boldsymbol{\tau}_2 $ and$ S_{12} $ . The spin-singlet channels do not have singular long-range forces as the matrix elements of$ S_{12} $ between those channels vanish. These spin-singlet channels are$ ^1D_2 $ and$ ^1F_3 $ waves in this paper. For the spin-triplet channels, the matrix elements of$ S_{12} $ do not vanish. The operator$ \boldsymbol{\tau}_1\cdot\boldsymbol{\tau}_2=2I(I+1)-3=-3,\,+1 $ for$ I=0,\,1 $ , respectively. Therefore, the spin-triplet uncoupled channels always make one channel attractive and its isospin partner repulsive. These spin-triplet uncoupled channels are$ ^3D_2 $ and$ ^3F_3 $ waves in this paper. We tabulate in Table 1 the values of the matrix element of$ -\boldsymbol{\tau}_1\cdot\boldsymbol{\tau}_2 \,S_{12} $ in these partial waves. The eigenvalues of$ S_{12} $ are$ 2 $ and$ -4 $ , regardless of J. Therefore, for the spin-triplet coupled channels, one eigenchannel is always attractive and the other repulsive. These spin-triplet coupled channels are$ ^3D_3 $ -$ ^3G_3 $ waves in this paper. On account of$ \boldsymbol{\tau}_1\cdot\boldsymbol{\tau}_2 $ , the isoscalar eigenchannel is the most attractive.Partial wave $ ^{13}D_2 $ 

$ ^{33}D_2 $ 

$ ^{13}F_3 $ 

$ ^{33}F_3 $ 

$ -\langle\boldsymbol{\tau}_1\cdot\boldsymbol{\tau}_2 \,S_{12}\rangle $ 

$ +6 $ 

$ -2 $ 

$ +6 $ 

$ -2 $ 

Table 1. Values of
$ -\boldsymbol{\tau}_1\cdot\boldsymbol{\tau}_2 \,S_{12} $ in the spin-triplet uncoupled D and F waves.In summary, we have the partial waves
$ ^{11}D_2 $ ,$ ^{31}D_2 $ ,$ ^{11}F_3 $ , and$ ^{31}F_3 $ , which have no tensor force; the partial waves$ ^{13}D_2 $ and$ ^{13}F_3 $ , which have repulsive tensor force; the partial waves$ ^{33}D_2 $ and$ ^{33}F_3 $ , which have attractive tensor force; and the partial waves$ ^{13}D_3 $ -$ ^{13}G_3 $ and$ ^{33}D_3 $ -$ ^{33}G_3 $ , in which always one eigenchannel is attractive and the other repulsive. In the next section, we confirm numerically that partial waves having an attractive tensor force need more LECs than those expected by NDA, whereas the others do not need them. Further, we compare the phase shifts, inelasticities, and mixing angles they yield with the empirical PWA values. -
The strategy is the same as that in Ref. [22], where the renormalization of the OPE for the lower partial waves was discussed. First, we check the cutoff dependence of the phase shifts and mixing angles before renormalization. This can be done by solving the partial-wave Schrödinger equation with
$ V_c=W_c=0\; {\rm fm}^{-1} $ because the other parameters of the OPE are known (When$ W_c=0\; {\rm fm}^{-1} $ , the inelasticities are trivial, i.e.,$ \eta_{J\mp 1,J}=1 $ and hence, their mixing angles$ \omega_J $ are not well determined by Eq. (7); thus, none of them are shown before renormalization). We show the results at various representative laboratory energies ($ T_{\rm lab} = $ 10, 50, 100 MeV). Second, we adjust the strength of the short-range spherical well as function of b for each partial wave where cutoff dependence is found. Here,$ V_c $ and$ W_c $ play the role of counterterms, whose cutoff dependence ensures that physical observables be cutoff independent within error bars. We determine$ V_c $ and$ W_c $ by fitting to the phase shift and inelasticity of the Groningen PWA [66] at some energy. The fit results are not significantly sensitive to the choice of fitting energy, which is taken to be$ T_{\rm lab}=20 $ MeV. Third, after verifying that cutoff independence is achieved, we take a cutoff value$ \Lambda \sim M_{\rm QCD} $ (specifically,$ \Lambda= 5 $ fm$ ^{-1} $ ) and compare phase shifts, inelasticities, and mixing angles as functions of the laboratory momentum$ p_{\rm lab} $ (between$ 0 $ and$ 450 $ MeV/c) with the PWA. The PWA values we show here contain more points but are consistent with the values in Tables VIII and IX of Ref. [66], which assume isospin symmetry.In the following, we split the analysis between spin-singlet and triplet channels because the former ones have no tensor force and the latter ones have, and the tensor force is the determining factor for the renormalization of OPE.
-
The spin-singlet channels have
$ ^{11}D_2 $ ,$ ^{31}D_2 $ ,$ ^{11}F_3 $ , and$ ^{31}F_3 $ partial waves. According to the NDA, the counterterms of the$ ^{1}D_2 $ waves start to appear on the order of$ Q^4 $ , and the counterterms of the$ ^{1}F_3 $ waves start to appear on the order of$ Q^6 $ . They do not need to be promoted to LO because the OPE potential has no tensor forces in these channels. As can be observed in Fig. 1, the phase shifts are obviously cutoff independent in the cutoff range between$ 2 $ $ {\rm fm}^{-1} $ and$ 8 $ $ {\rm fm}^{-1} $ . All phase shifts approach finite values as the cutoff increases. The isospin-singlet phase shifts are attractive and relatively large, whereas the isospin-triplet ones are repulsive and relatively small due to the factor$ -\boldsymbol{\tau}_1 \cdot \boldsymbol{\tau}_2\,\vec{\sigma}_{1} \cdot \vec{\sigma}_{2} $ . The ηs are all equal to$ 1 $ because$ W_c=0\; {\rm fm}^{-1} $ here, and thus, they are not shown in the plots. Figure 2 shows the phase shifts and inelasticities against laboratory momentum and the comparison with the PWA values, where$ V_c $ and$ W_c $ are from Table 2. The results agree with the PWA values well in the energy range considered except for the phase shift of$ ^{31}D_2 $ , which means that in this wave high order contributions might be needed to make a better agreement with the PWA. These agreements with the PWA are comparable with those obtained in the$ N N $ case [31]. Thus, a satisfactory description of the spin-singlet channels is obtained at low energies with a LO consisting of iterated OPE and no contact interaction.
Figure 1. (color online) Cutoff dependence of the phase shifts in the spin-singlet D and F waves at the laboratory energies of 10 MeV (black solid line), 50 MeV (red dashed line), and 100 MeV (green dotted line) for
$ V_c=W_c=0\; \text{fm}^{-1} $ .
Figure 2. (color online) Phase shifts (left panels) and inelasticities (right panels) of the spin-singlet D and F waves against laboratory momentum. The (red) dashed lines denote the iterated one-pion exchange for
$ b=0.2 $ fm and$ V_c=W_c=0\; \text{fm}^{-1} $ , whereas the (black) solid lines indicate the results of the PWA [66].Partial wave $ ^{11}D_2 $ 

$ ^{31}D_2 $ 

$ ^{11}F_3 $ 

$ ^{31}F_3 $ 

$ ^{13}D_2 $ 

$ ^{33}D_2 $ 

$ ^{13}F_3 $ 

$ ^{33}F_3 $ 

$ V_c $ (fm

$ ^{-1} $ )

0 0 0 0 0 −86.96 0 −162.73 $ W_c $ (fm

$ ^{-1} $ )

0 0 0 0 0 −0.05 0 −0.00 Table 2. Values of the real (
$ V_c $ ) and imaginary ($ W_c $ ) components of the short-range potential at$ b=0.2 $ fm for the uncoupled D and F partial waves. These of$ ^{33}D_2 $ and$ ^{33}F_3 $ waves are obtained by fitting to the PWA "data" [66] at$ T_{\rm lab}=20 $ MeV, whereas these of the other waves are set to be$ 0\; {\rm fm}^{-1} $ by hand. -
Now, we turn to the spin-triplet channels. First, we focus on the uncoupled partial waves, and the signs of the tensor forces of these waves are indicated in Table 1. In Fig. 3, the cutoff dependence of the phase shifts of these D and F waves are shown. The phase shifts of the
$ ^{13}D_2 $ and$ ^{13}F_3 $ waves are obviously cutoff independent and they converge to finite values as the cutoff increases because these channels have no attractive singular tensor force. One can find that the phase shift of the$ ^{33}D_2 $ wave is obviously cutoff dependent, although only in some limited ranges, when the cutoff is sufficiently high because this channel has an attractive singular tensor force. The$ ^{33}F_3 $ wave also has an attractive singular tensor force. However, the phase shift of the$ ^{33}F_3 $ wave only shows very tiny cutoff dependence at the laboratory kinetic energy$ T_{\rm lab}=100 $ MeV and when the cutoff is sufficiently high. This occurs because the contact interaction of this wave starts to appear on the order of$ Q^6 $ according to the NDA. It should be expected that the cutoff dependence in this wave would be more obvious when it moves to higher energies. The different strengths of cutoff dependence of these two waves are also due to their centrifugal barriers via orbital angular momenta. In Fig. 3, the cutoff ranges of the isospin-singlet and the isospin-triplet waves are different because we want to observe the cutoff dependence in the isospin-triplet waves, which is expected from the experience in the lower partial waves of the$ \overline{N} N $ system [22].
Figure 3. (color online) Cutoff dependence of the phase shifts in the spin-triplet uncoupled D and F waves at the laboratory energies of 10 MeV (black solid line), 50 MeV (red dashed line), and 100 MeV (green dotted line) for
$ V_c=W_c=0\; \text{fm}^{-1} $ .We have observed that the phase shifts of the
$ ^{13}D_2 $ and$ ^{13}F_3 $ waves are cutoff independent because these waves have repulsive tensor forces, and thus they do not need counterterms at LO, which is expected in the NDA, and therefore we set$ V_c=W_c=0\; {\rm fm}^{-1} $ in these channels. In Fig. 4, the phase shifts and inelasticities against laboratory momentum of the$ ^{13}D_2 $ and$ ^{13}F_3 $ waves are shown, and where the cutoff of the iterated OPE is taken to be$ b=0.2\; {\rm fm} $ or$ \Lambda=5\; {\rm fm}^{-1} $ . The results agree with the PWA values in the energy range considered. Again, these agreements with the PWA values are comparable with those obtained in the$ N N $ case [31]. The ηs are almost$ 1 $ in these two waves, which means that there are almost no annihilation in these channels.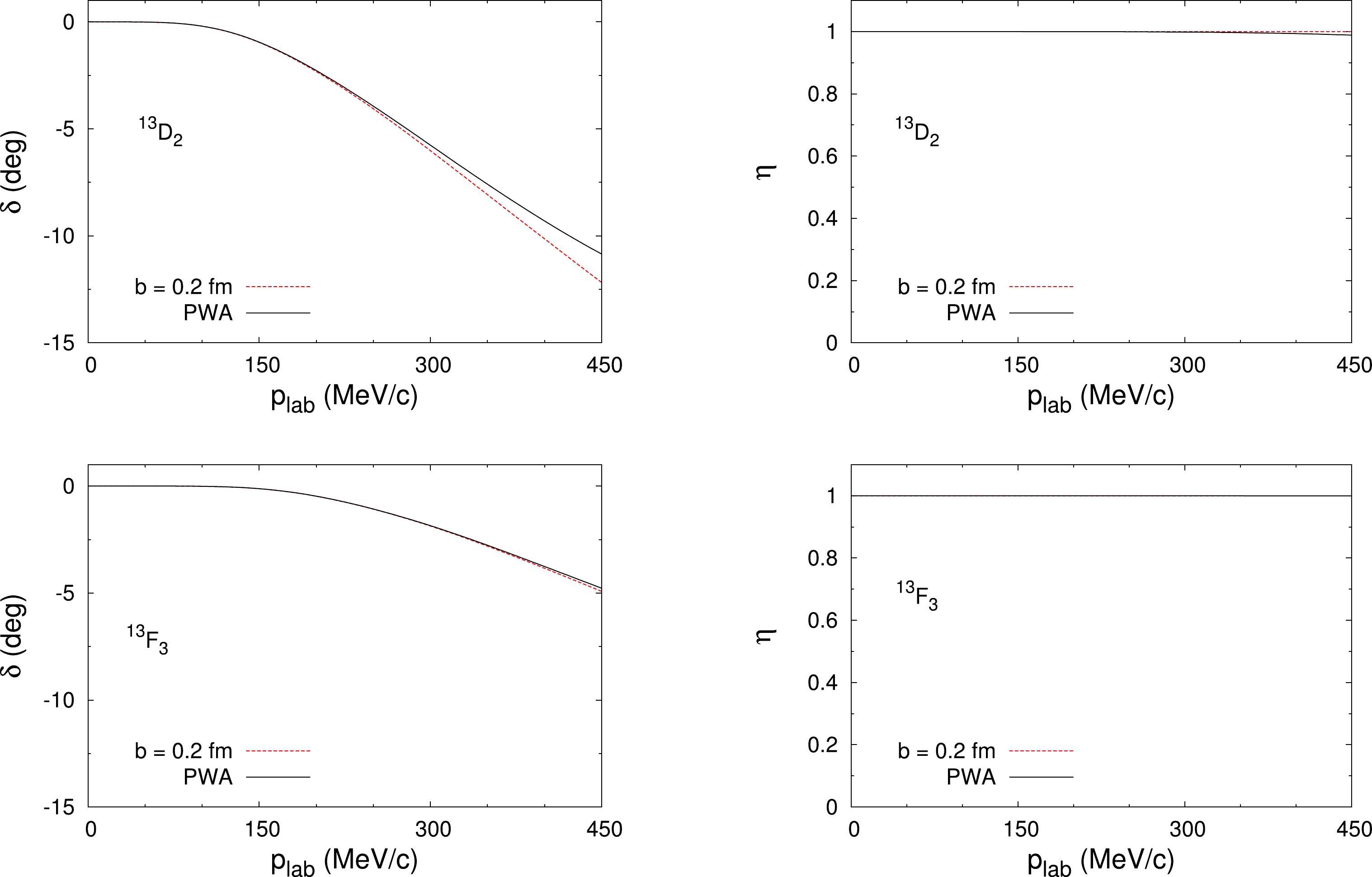
Figure 4. (color online) Phase shifts (left panels) and inelasticities (right panels) of the spin-triplet uncoupled
$ ^{13}D_2 $ and$ ^{13}F_3 $ waves against laboratory momentum. The (red) dashed lines denote the iterated one-pion exchange for$ b=0.2 $ fm and$ V_c=W_c=0\; \text{fm}^{-1} $ , whereas the (black) solid lines indicate the results of the PWA [66].In the other two spin-triplet uncoupled waves,
$ ^{33}D_2 $ and$ ^{33}F_3 $ , where the OPE tensor force is singular and attractive, the counterterms are expected, even though the cutoff dependence is not very obvious in the$ ^{33}F_3 $ channel at the energies considered here. In Fig. 5, the running of the corresponding LECs$ V_c $ and$ W_c $ is shown for the$ ^{33}D_2 $ and$ ^{33}F_3 $ waves. The values of these LECs are obtained by fitting to the corresponding phase shifts and inelasticities of the PWA at the laboratory kinetic energy$ T_{\rm lab}=20 $ MeV. The magnitudes of$ V_c $ are much greater than the magnitudes of$ W_c $ , which is also observed in the other partial waves in Ref. [22], and the relative difference between$ V_c $ and$ W_c $ becomes larger as the orbital angular momentum L increases. The tiny "ripples" on the tail part of the curve in the plot of$ W_c $ of the$ ^{33}F_3 $ wave occur because there the values of$ W_c $ are too small, and thus the quality of fitting is not as good as those in the lower cutoff range, say$ \Lambda<7\; {\rm fm}^{-1} $ . The residual cutoff dependence of the phase shifts and inelasticities of the$ ^{33}D_2 $ and$ ^{33}F_3 $ waves is shown in Fig. 6. We see that, after renormalization, the phase shifts and inelasticities are cutoff independent and converge to finite values with increasing cutoff. Their phase shifts and inelasticities as functions of the laboratory momentum are plotted in Fig. 7 for$ b = 0.2 $ fm, where the LECs take the values given in Table 2. The results of the$ ^{33}F_3 $ wave agree with the PWA values in the energy range considered. The results of the$ ^{33}D_2 $ wave agree with the PWA values when$ p_{\rm lab}\lesssim230 $ MeV/c. However, there are dents in both the curves of phase shift and inelasticity in the$ ^{33}D_2 $ wave when$ p_{\rm lab}\simeq250 $ MeV/c, which might need higher order contributions to compensate, or which might be due to an unnecessary iteration of OPE. The dents will move to the right as the cutoff Λ decreases. Of course, the actual reason for the dents need further investigation. This type of dent has not been found in the$ N N $ case [31] or in the lower partial waves in the$ \overline{N} N $ case [22].
Figure 5. (color online) Cutoff dependence of
$ m_N V_c $ (left panels) and$ m_N W_c $ (right panels) for the spin-triplet uncoupled$ ^{33}D_2 $ and$ ^{33}F_3 $ waves. The PWA phase shifts and inelasticities are fitted at$ T_{\rm lab}=20 $ MeV.
Figure 6. (color online) Residual cutoff dependence of the phase shifts and inelasticities in the spin-triplet uncoupled
$ ^{33}D_2 $ and$ ^{33}F_3 $ waves at the laboratory energies of 10 MeV (black solid line), 50 MeV (red dashed line), and 100 MeV (green dotted line) for$ V_c $ and$ W_c $ in Fig. 5.
Figure 7. (color online) Phase shifts (left panels) and inelasticities (right panels) of the spin-triplet uncoupled
$ ^{33}D_2 $ and$ ^{33}F_3 $ waves against laboratory momentum. The (red) dashed lines denote the iterated one-pion exchange for$ b=0.2 $ fm and$ V_c $ ,$ W_c $ from Table 2, whereas the (black) solid lines indicate the results of the PWA [66].Now, let us look at the spin-triplet coupled partial waves, which are the
$ ^{13}D_3 $ -$ ^{13}G_3 $ and$ ^{33}D_3 $ -$ ^{33}G_3 $ waves in this paper. The cutoff dependence of the phase shifts and their mixing angles$ \varepsilon_J $ before renormalization are shown in Fig. 8. Again the inelasticities ηs are not shown because they all equal$ 1 $ as$ W_c=0\; {\rm fm}^{-1} $ here. The mixing angles$ \omega_J $ are not shown either, because they are not well determined in this case, as one can see from Eq. (7). One can find that those of the$ ^{13}D_3 $ -$ ^{13}G_3 $ wave are obviously cutoff dependent at higher energies, whereas those of the$ ^{33}D_3 $ -$ ^{33}G_3 $ wave are almost cutoff independent except for the phase shift of$ ^{33}D_3 $ at$ T_{\rm lab}=100 $ MeV. Although both of these coupled waves have one eigenchannel, which contains the attractive singular tensor force, the cutoff-dependence behaviours are different for these two coupled waves. The difference shall be due to the different isospin factors. In any case, these two coupled waves need contact interactions at LO to remove the cutoff dependence, i.e., the contact interactions shall be promoted to LO although they are not there according to the NDA. Again, in Fig. 8, the cutoff ranges of the isospin-singlet and the isospin-triplet waves are different because we also want to see the cutoff dependence in the isospin-triplet waves, which is expected from the experience in the lower partial waves of the$ \overline{N} N $ system [22].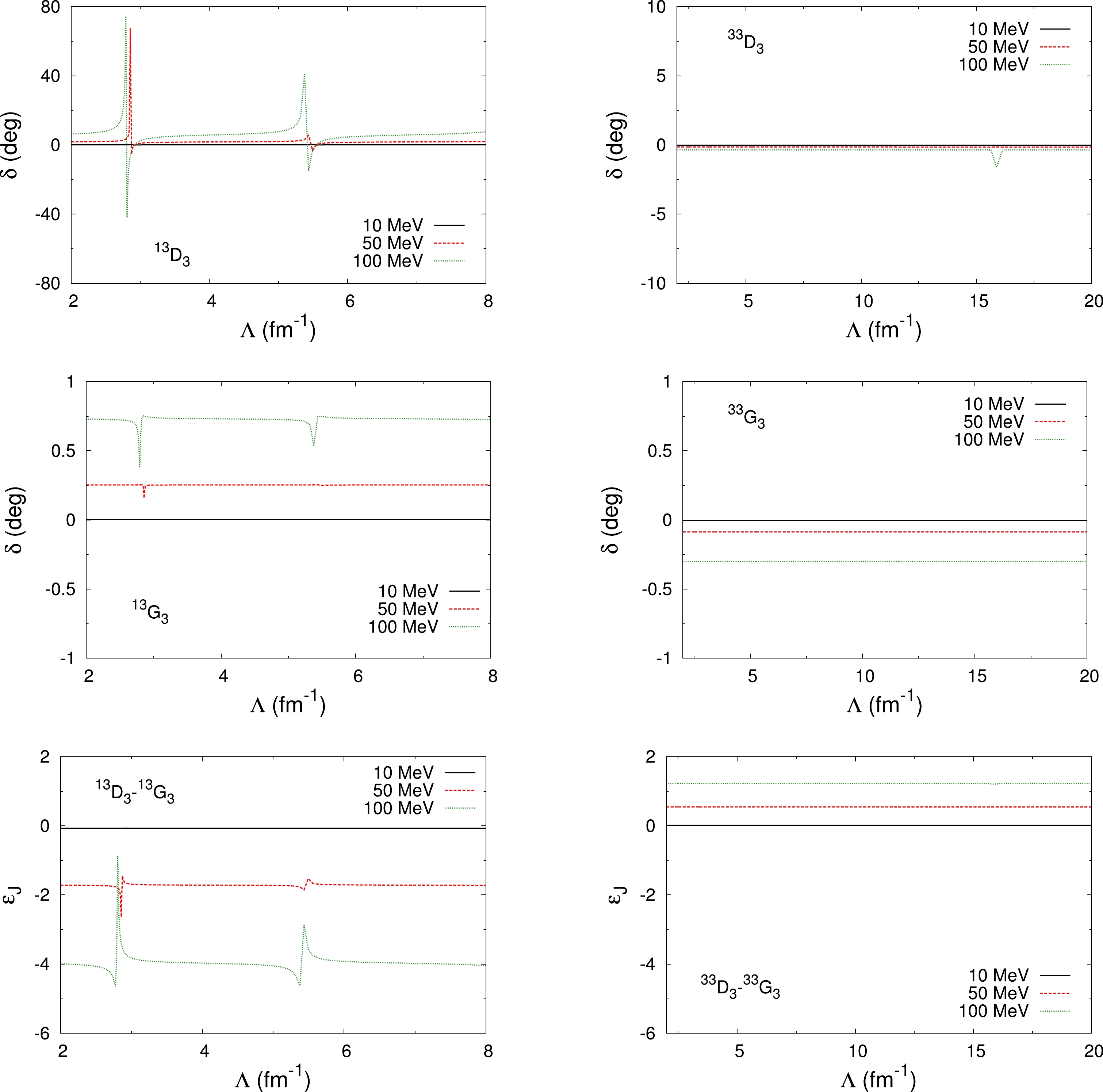
Figure 8. (color online) Cutoff dependence of the phase shifts and mixing angles
$ \varepsilon_{J} $ in the spin-triplet coupled D-G waves at the laboratory energies of 10 MeV (black solid line), 50 MeV (red dashed line), and 100 MeV (green dotted line) for$ V_c=W_c=0\; \text{fm}^{-1} $ .The cutoff dependence of the LECs
$ V_c $ and$ W_c $ of the$ ^{13}D_3 $ and$ ^{33}D_3 $ waves are shown in Fig. 9. Again, the values of these LECs are obtained by fitting to the corresponding phase shifts and inelasticities of the PWA at the laboratory kinetic energy$ T_{\rm lab}=20 $ MeV. In general, the magnitude of$ V_c $ is larger than the magnitude of the corresponding$ W_c $ . One can also see that the curves of$ V_c $ and$ W_c $ in the$ ^{13}D_3 $ wave have more structures than those in the$ ^{33}D_3 $ wave, which are the reflections of Fig. 8. The residual cutoff dependence of the phase shifts, inelasticities, and mixing angles are shown in Figs. 10 and 11. There are some "ripples" in the plots of the$ ^{13}D_3 $ phase shift and inelasticity, which are due to the difficulty of fitting in this wave when b becomes smaller or equivalently Λ becomes larger. It looks like there is a weird oscillatory behaviour of the mixing angle$ \omega_J $ for$ ^{33}D_3 $ -$ ^{33}G_3 $ at$T_{\rm lab}=10$ MeV in Fig. 11. However, this is not a problem because the inelasticities of$ ^{33}D_3 $ and$ ^{33}G_3 $ are both equal to$ 1 $ in the cutoff range and thus$ \omega_J $ can take any values in this case, as can be seen from Eq. (7). Therefore, one can see that the observables are cutoff independent after renormalization. The values of$ V_c $ and$ W_c $ at$ b=0.2 $ fm for the coupled D-G waves are indicated in Table 3, which will be used later on.
Figure 9. (color online) Cutoff dependence of
$ m_N V_c $ (left panels) and$ m_N W_c $ (right panels) for the spin-triplet coupled$ ^{13}D_3 $ and$ ^{33}D_3 $ waves. The PWA phase shifts and inelasticities are fitted at$ T_{\rm lab}=20 $ MeV.
Figure 10. (color online) Residual cutoff dependence of the phase shifts, inelasticities, and mixing angles in the spin-triplet coupled
$ ^{13}D_3 $ -$ ^{13}G_3 $ waves at the laboratory energies of 10 MeV (black solid line), 50 MeV (red dashed line), and 100 MeV (green dotted line) for$ V_c $ and$ W_c $ in Fig. 9.
Figure 11. (color online) Residual cutoff dependence of the phase shifts, inelasticities, and mixing angles in the spin-triplet coupled
$ ^{33}D_3 $ -$ ^{33}G_3 $ waves at the laboratory energies of 10 MeV (black solid line), 50 MeV (red dashed line), and 100 MeV (green dotted line) for$ V_c $ and$ W_c $ in Fig. 9.Partial wave $ ^{13}D_3 $ 

$ ^{13}G_3 $ 

$ ^{33}D_3 $ 

$ ^{33}G_3 $ 

$ V_c $ (fm

$ ^{-1} $ )

–33336.83 0 –105.36 0 $ W_c $ (fm

$ ^{-1} $ )

–31.18 0 –0.00 0 Table 3. Values of the real (
$ V_c $ ) and imaginary ($ W_c $ ) components of the short-range potential at$ b=0.2 $ fm for the coupled D-G partial waves. The values of$ ^{3}D_3 $ waves are obtained by fitting to the PWA "data" [66] at$ T_{\rm lab}=20 $ MeV, while these of$ ^{3}G_3 $ waves are set to be$ 0\; {\rm fm}^{-1} $ by hand.After renormalization, the phase shifts, inelasticities, mixing angles against laboratory momentum, and the comparison with the PWA values are shown in Figs. 12 and 13. The values of
$ V_c $ and$ W_c $ for the iterated OPE are taken from Table 3. The results agree with the PWA except for the phase shift and inelasticity of$ ^{13}D_3 $ when$ p_{\rm lab} \gtrsim300 $ MeV/c, and the phase shift of$ ^{33}D_3 $ when$ p_{\rm lab} \gtrsim200 $ MeV/c. There is also a dip-bump structure in the (red) dashed phase-shift curve of$ ^{33}D_3 $ around$ p_{\rm lab}=200 $ MeV/c in Fig. 13. All of these discrepancies might be hints that we should treat the OPE perturbatively in these waves. Of course, this need further investigation. It seems that the (red) dashed lines in Figs. 12 and 13 of the mixing angles$ \omega_J $ have weird behaviours in the low energy range. Again, these are not important. This occurs because the inelasticities are very close or equal to$ 1 $ at these energies, and thus$ \omega_J $ is not well determined as can be seen from Eq. (7). In other words,$ \omega_J $ can take any values in this case. The very small dip-bump structures of the PWA curves of$ \omega_J $ in Figs. 12 and 13 may also be due to the same reason. The quality of the agreement with the PWA of the coupled D-G waves is comparable with that in the$ N N $ system [31].
Figure 12. (color online) Phase shifts and mixing angle (left panels) and inelasticities and their mixing angle (right panels) of the spin-triplet coupled
$ ^{13}D_3 $ -$ ^{13}G_3 $ waves against laboratory momentum. The (red) dashed lines denote the iterated one-pion exchange for$ b=0.2 $ fm and$ V_c $ ,$ W_c $ from Table 3, whereas the (black) solid lines indicate the results of the PWA [66].
Figure 13. (color online) Phase shifts and mixing angle (left panels) and inelasticities and their mixing angle (right panels) of the spin-triplet coupled
$ ^{33}D_3 $ -$ ^{33}G_3 $ waves against laboratory momentum. The (red) dashed lines denote the iterated one-pion exchange for$ b=0.2 $ fm and$ V_c $ ,$ W_c $ from Table 3, whereas the (black) solid lines are the results of the PWA [66]. -
In summary, as an extension of the previous work [22], we have adapted the framework of the partial-wave analysis for
$ \overline{N} N $ scattering [66] to study the renormalization of the iterated static OPE potential in the other partial waves with total angular momentum$ J\le3 $ , which are the uncoupled D, F and coupled D-G waves.The spin-singlet channels
$ ^{11}D_2 $ ,$ ^{31}D_2 $ ,$ ^{11}F_3 $ , and$ ^{31}F_3 $ have no tensor forces. We have seen that their phase shifts are cutoff independent when$V_c=W_c= 0\; {\rm fm}^{-1}$ , and therefore no counterterms are needed in these spin-singlet channels. For the spin-triplet uncoupled channels, we have confirmed that the renormalization of the iterated OPE requires counterterms in the$ ^{33}D_2 $ and$ ^{33}F_3 $ channels, which have attractive singular tensor forces, while the$ ^{13}D_2 $ ,$ ^{13}F_3 $ channels do not need counterterms because they have repulsive singular tensor forces. For the spin-triplet coupled channels, we have confirmed that$ ^{13}D_3 $ and$ ^{33}D_3 $ need counterterms whereas$ ^{13}G_3 $ and$ ^{33}G_3 $ do not, because one eigenchannel is attractive and the other is repulsive.According to the NDA, the counterterms start to appear on the order of
$ Q^4 $ for the$ ^{33}D_2 $ channel, and start to appear on the order of$ Q^6 $ for the$ ^{33}F_3 $ and$ ^{3}D_3 $ -$ ^{3}G_3 $ channels. The RG invariant requires that these counterterms need to be promoted to LO as we have seen. After renormalization, most of the observables agree with the PWA values in the energy range considered, except that some of them agree with the PWA values well in some lower energy ranges. The discrepancies between the iterated OPE results and the PWA values might be reduced when high order contributions, such as TPE, are included. Of course, this need further investigation, because TPE is treated perturbatively as required by renormalization. Further, it is claimed in Ref. [55] that a cutoff independent scattering amplitude can in general not be obtained in the infinite-cutoff (RG-invariant) scheme beyond the leading order in spite of the perturbative treatment of subleading contributions.The magnitudes of
$ V_c $ are much greater than those of the corresponding$ W_c $ , as can be observed from Figs. 5 and 9. This is already the case in the lower partial waves of the$ \overline{N} N $ system [22], but it is even more evident here. The$ W_c $ in the$ ^{33}D_2 $ ,$ ^{33}F_3 $ , and$ ^{33}D_3 $ waves might even be set to be$ 0\; {\rm fm}^{-1} $ , because they are relatively very small compared to the corresponding$ V_c $ . In the plot of$ W_c $ for the$ ^{13}D_3 $ wave, there are some sharp spikes in the very limited cutoff ranges. The magnitudes of these spikes are comparable with the magnitude of the corresponding$ V_c $ . Therefore, it seems that in some higher partial waves, the imaginary part of an LEC is not on the same order as the corresponding real part lies. We leave this issue for a future study.As we have seen, the results are satisfactory when OPE is treated nonperturbatively. However, it might be unnecessary to treat OPE nonperturbatively in some high partial waves. In most of these high partial waves, the perturbative results should be similar to the nonperturbative ones owing to the smallness of the phase shifts. In a future investigation, we will study the renormalization in the
$ \overline{N} N $ system with OPE treated perturbatively and attempt to identify the boundary between nonperturbation and perturbation in OPE. -
The author thank R. G. E. Timmermans, U. van Kolck, and B. Long for useful discussions and suggestions.
Renormalization of one-pion exchange in higher partial waves in chiral effective field theory for antinucleon-nucleon system
- Received Date: 2022-10-22
- Available Online: 2023-03-15
Abstract: The renormalization of the iterated one-pion exchange (OPE) has been studied in chiral effective field theory (χEFT) for the antinucleon-nucleon (





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: