-
In 2013, the BESIII and Belle collaborations explored the
$ e^+e^- \to \pi^+\pi^-J/\psi $ process and observed a$ Z_c^\pm(3900) $ structure in the$ \pi^\pm J/\psi $ mass spectrum [1, 2]. In the same year, the BESIII collaboration also investigated the$ e^+e^- \to \pi D \bar{D}^* $ process and observed a$ Z_c^\pm(3885) $ structure in the$ (D \bar{D}^*)^{\pm} $ mass spectrum [3].$ Z_c(3900/3885) $ have the spin-parity$ J^P=1^+ $ [3, 4].In 2020, the BESIII collaboration observed a
$ Z_{cs}^-(3985) $ structure in the$ K^{+} $ recoil-mass spectrum of the$ e^+e^-\to K^+ (D_s^- D^{*0} + D^{*-}_s D^0) $ process [5] and found the Breit-Wigner mass and width to be$ 3985.2^{+2.1}_{-2.0}\pm1.7\,{\rm{MeV}} $ and$ 13.8^{+8.1}_{-5.2}\pm4.9\,{\rm{MeV}} $ , respectively [5].In 2021, the LHCb collaboration observed two new exotic states,
$ Z_{cs}^+(4000) $ and$ Z_{cs}^+(4220) $ , in the$ J/\psi K^+ $ mass spectrum of the$ B^+ \to J/\psi \phi K^+ $ process [6]. The most significant state,$ Z_{cs}^+(4000) $ , had a Breit-Wigner mass and width of$ 4003 \pm 6 {}^{+4}_{-14}\,{\rm{MeV}} $ and$ 131 \pm 15 \pm 26\,{\rm{MeV}} $ , respectively, and the spin-parity$ J^P =1^+ $ [6].$ Z_c(3900/3885) $ and$ Z_{cs}(3985/4000) $ have analogous decay modes,$ Z^{\pm}_c(3900) \to J/\psi \pi^\pm \, , \quad Z^+_{cs}(4000) \to J/\psi K^+ \, , $

(1) $ \begin{array}{*{20}{l}} Z_c^{\pm}(3885)\to (D\bar{D}^*)^\pm \, , \\ Z_{cs}^-(3985) \to D_s^- D^{*0}\, , \, D^{*-}_s D^0 \, , \end{array} $

(2) which leads to the possibility that they have analogous quark structures. Although the Particle Data Group assumes that
$ Z_c(3900) $ and$ Z_c(3885) $ are the same particle according to the analogous masses and widths [7], it is difficult to explain the ratio [3],$ R_{\rm exp}=\frac{\Gamma(Z_c(3885)\to D\bar{D}^*)}{\Gamma(Z_c(3900)\to J/\psi \pi)} =6.2 \pm 1.1 \pm 2.7 \, , $

(3) in a satisfactory manner. In contrast, the widths of
$ Z^-_{cs}(3985) $ and$ Z_{cs}^+(4000) $ are inconsistent.$ Z_c(3900/3885) $ and$ Z_{cs}(3985/4000) $ may indeed be four distinguished particles.The exotic states
$ Z_{cs}(3985/4000) $ lie above the$ D_s^- D^{*0} $ and$ D^{*-}_s D^0 $ thresholds$ 3975.2 $ and$ 3977.0\;{\rm{MeV}} $ , respectively, and if they are molecular states, we should introduce coupled-channel effects to account for the mass gaps and decay widths [8–12] or just re-scattering effects [13, 14]. It is more natural to reproduce their masses in the diquark-antidiquark type tetraquark pictures than the color-singlet-color-singlet type tetraquark pictures if we choose the theoretical framework of potential quark models [15, 16].In QCD sum rules, we typically choose color antitriplet-triplet type and singlet-singlet type four-quark currents to interpolate hidden-charm exotic states and reproduce the masses of
$ Z_{cs}(3985/4000) $ in the pictures of both the tetraquark [17–21] and molecular states [17, 21–25]. There may be two$ Z_{cs} $ states, an antitriplet-triplet type tetraquark state and singlet-singlet type molecular state, or only one$ Z_{cs} $ state, which has both antitriplet-triplet type and singlet-singlet type components. We must explore two-body strong decays to diagnose their nature.In Ref. [26], we assigned
$ Z^\pm_c(3900) $ as the diquark-antidiquark type tetraquark state with the quantum numbers$ J^{PC}=1^{+-} $ , calculated the hadronic coupling constants$ G_{ZJ/\psi\pi} $ ,$ G_{Z\eta_c\rho} $ , and$ G_{ZD \bar{D}^{*}} $ using three-point QCD sum rules based on rigorous duality for the first time, and obtained partial decay widths to diagnose the nature of$ Z_c^\pm(3900) $ . Thereafter, rigorous duality was successfully applied to study the strong decays of the exotic states$ X(4140) $ ,$ X(4274) $ ,$ X(4660) $ ,$ Z_c(4600) $ , and$ P_c(4312) $ [27–32].In this study, we extend our previous research on the masses of hidden-charm tetraquark states and molecular states with strangeness [19, 25] to explore the two-body strong decays of
$ Z_{cs}(3985/4000) $ with possible assignments of$ J^{PC}=1^{+-} $ and hence diagnose their nature.This paper is organized as follows: In Sec. II, we acquire QCD sum rules for the hadronic coupling constants
$ G_{ZJ/\psi K} $ ,$ G_{Z\eta_cK^*} $ , and$ G_{ZD^* \bar{D}_s} $ . In Sec. III, we present the numerical results and discussions. Finally, Sec. IV is reserved for our conclusion. -
We investigate the two-body strong decays
$ Z_{cs}^-(3985/4000)\to J/\psi K^- $ ,$ \eta_cK^{*-} $ , and$ D^{*0} \bar{D}_s^{-} $ and$ D^0 \bar{D}_s^{*-} $ using the three-point correlation functions$ \Pi_{\mu\nu}^{1}(p,q) $ ,$ \Pi_{\mu\nu}^{2}(p,q) $ , and$ \Pi_{\mu\nu}^{3}(p,q) $ ,$ \begin{aligned}[b] \Pi_{\mu\nu}^{1}(p,q)= {\rm i}^2\int {\rm d}^4x{\rm d}^4y \, {\rm e}^{{\rm i}px}{\rm e}^{{\rm i}qy}\, \langle 0|T\left\{J_\mu^{J/\psi}(x)J_5^{K}(y)J^\dagger_{\nu}(0)\right\}|0\rangle\, , \end{aligned} $

$ \begin{aligned}[b] \Pi_{\mu\nu}^{2}(p,q)=& {\rm i}^2\int {\rm d}^4x {\rm d}^4y\, {\rm e}^{{\rm i}px}{\rm e}^{{\rm i}qy}\, \langle 0|T\left\{J_5^{\eta_c}(x)J_\mu^{K^*}(y)J^\dagger_{\nu}(0)\right\}|0\rangle \, , \\ \Pi_{\mu\nu}^{3}(p,q)=& {\rm i}^2\int {\rm d}^4x {\rm d}^4y \, {\rm e}^{{\rm i}px}{\rm e}^{{\rm i}qy}\, \langle 0|T\left\{J_\mu^{D^*}(x)J_5^{D_s}(y)J^\dagger_{\nu}(0)\right\}|0\rangle \, , \end{aligned} $

(4) where the currents
$ \begin{aligned}[b] J_\mu^{J/\psi}(x)=&\bar{c}(x)\gamma_\mu c(x) \, , \qquad J_5^{K}(y)=\bar{u}(y){\rm i}\gamma_5 s(y) \, , \\ J_5^{\eta_c}(x)=&\bar{c}(x){\rm i}\gamma_5 c(x) \, , \qquad J_\mu^{K^*}(y)=\bar{u}(y)\gamma_\mu s(y) \, , \\ J_\mu^{D^*}(x)=&\bar{u}(x)\gamma_\mu c(x) \, , \qquad J_5^{D_s}(y)=\bar{c}(y){\rm i}\gamma_5 s(y) \, , \\ J^\dagger_\nu(0)=&J_\nu^{T\dagger}(0)\, , \, J_\nu^{M\dagger}(0)\, , \end{aligned} $

(5) $ \begin{aligned}[b] J_\nu^{T\dagger}(0)=&\frac{\varepsilon^{ijk}\varepsilon^{imn}}{\sqrt{2}}\Big\{c^{Tn}(0)C\gamma_\nu u^m(0)\, \bar{c}^k(0)\gamma_5 C \bar{s}^{Tj}(0)\\&-c^{Tn}(0)C\gamma_5 u^m(0)\, \bar{c}^k(0)\gamma_\nu C \bar{s}^{Tj}(0) \Big\} \, , \\ J_\nu^{M\dagger}(0)=& \frac{1}{\sqrt{2}}\Big\{\bar{s}(0)\gamma_\nu c(0)\, \bar{c}(0){\rm i}\gamma_5 u(0)\\&+\bar{s}(0){\rm i}\gamma_5 c(0)\, \bar{c}(0) \gamma_\nu u(0)\Big\}\, , \end{aligned} $

(6) interpolate the mesons
$ J/\psi $ , K,$ \eta_c $ ,$ K^* $ ,$ D^* $ ,$ D_s $ ,$ Z^T_{cs} $ , and$ Z^M_{cs} $ , respectively, and the superscripts T and M denote tetraquark-type and molecule-type four-quark currents/tetraquarks, respectively [19, 25].We insert a complete set of intermediate hadronic states with the same quantum numbers as the currents into the three-point correlation functions and isolate the ground state contributions.
$ \begin{aligned}[b] \Pi_{\mu\nu}^{T,1} (p,q)=&\left\{ \frac{f_{K}M_{K}^2f_{J/\psi}M_{J/\psi}\lambda_{Z}^T G^T_{ZJ/\psi K}}{m_u+m_s} \frac{\rm i}{(M_{Z}^2-p^{\prime2})(M_{J/\psi}^2-p^2)(M_{K}^2-q^2)} \right. +\frac{\rm i}{(M_{Z}^2-p^{\prime2})(M_{J/\psi}^2-p^2)}\int_{s^0_K}^{\infty} {\rm d} u\frac{\rho_{Z K^\prime}(p^{\prime2},p^2,u)}{u-q^2}\\ &+\frac{\rm i}{(M_{Z}^2-p^{\prime2})(M_{K}^2-q^2)}\int_{s^0_{J/\psi}}^{\infty} {\rm d}s\frac{\rho_{Z \psi^\prime}(p^{\prime2},s,q^2)}{s-p^2}\\ &\left.+\frac{\rm i}{(M_{J/\psi}^2-p^2)(M_{K}^2-q^2)}\int_{s^0_Z}^{\infty} {\rm d} s^\prime \frac{\rho_{Z^\prime J/\psi}(s^\prime,p^2,q^2)+\rho_{Z^\prime K}(s^\prime,p^2,q^2)}{s^\prime-p^{\prime2}}+\cdots \right\} g_{\mu\nu}+\cdots \\ =& {\rm i}\,\Pi_T^1(p^{\prime2},p^2,q^2)\,g_{\mu\nu}+\cdots\, , \end{aligned} $ 
(7) $ \begin{aligned}[b] \Pi_{\mu\nu}^{M,1}(p,q)= \left\{\frac{f_{K}M_{K}^2f_{J/\psi}M_{J/\psi}\lambda_{Z}^M G^M_{ZJ/\psi K}}{m_u+m_s} \frac{1}{(M_{Z}^2-p^{\prime2})(M_{J/\psi}^2-p^2)(M_{K}^2-q^2)} +\cdots \right\}g_{\mu\nu}+\cdots = \Pi^1_M(p^{\prime2},p^2,q^2)\,g_{\mu\nu}+\cdots\, , \end{aligned} $

(8) $ \Pi_{\mu\nu}^{T,2}(p,q)= \left\{\frac{f_{\eta_c}M_{\eta_c}^2f_{K^*}M_{K^*}\lambda_{Z}^TG_{Z\eta_c K^*}^T}{2m_c} \frac{\rm i}{(M_{Z}^2-p^{\prime2})(M_{\eta_c}^2-p^2)(M_{K^*}^2-q^2)}+\cdots \right\} g_{\mu\nu}+\cdots = {\rm i}\, \Pi_T^2(p^{\prime2},p^2,q^2)\,g_{\mu\nu}+\cdots\, , $

(9) $ \Pi_{\mu\nu}^{M,2}(p,q)=\left\{ \frac{f_{\eta_c}M_{\eta_c}^2f_{K^*}M_{K^*}\lambda_{Z}^MG_{Z\eta_c K^*}^M}{2m_c} \frac{1}{(M_{Z}^2-p^{\prime2})(M_{\eta_c}^2-p^2)(M_{K^*}^2-q^2)} +\cdots \right\}g_{\mu\nu}+\cdots = \Pi_M^2(p^{\prime2},p^2,q^2)\,g_{\mu\nu}+\cdots\, , $

(10) $ \Pi_{\mu\nu}^{T,3}(p,q)=\left\{ \frac{f_{D_s}M_{D_s}^2f_{D^*}M_{D^*}\lambda_{Z}^TG^T_{Z D^*\bar{D}_s}}{m_c+m_s} \frac{\rm i}{(M_{Z}^2-p^{\prime2})(M_{D^*}^2-p^2)(M_{D_s}^2-q^2)} +\cdots \right\}g_{\mu\nu}+\cdots ={\rm i}\, \Pi_T^3(p^{\prime2},p^2,q^2)\,g_{\mu\nu}+\cdots \, , $

(11) $ \Pi_{\mu\nu}^{M,3}(p,q)=\left\{ \frac{f_{D_s}M_{D_s}^2f_{D^*}M_{D^*}\lambda_{Z}^M G^M_{Z D^*\bar{D}_s}}{m_c+m_s} \frac{1}{(M_{Z}^2-p^{\prime2})(M_{D^*}^2-p^2)(M_{D_s}^2-q^2)}+\cdots\right\} g_{\mu\nu}+\cdots = \Pi_M^3(p^{\prime2},p^2,q^2)\,g_{\mu\nu}+\cdots \, , $

(12) where
$ p^\prime=p+q $ ,$ f_{J/\psi} $ ,$ f_{K} $ ,$ f_{\eta_c} $ ,$ f_{K^*} $ ,$ f_{D^*} $ ,$ f_{D_s} $ ,$ \lambda_Z^T $ , and$ \lambda_{Z}^M $ are the decay constants of the mesons$ J/\psi $ , K,$ \eta_c $ ,$ K^* $ ,$ D^* $ ,$ D_s $ ,$ Z_{cs}^T $ , and$ Z_{cs}^M $ , respectively,$ \begin{aligned}[b] \langle0|J_{\mu}^{J/\psi}(0)|J/\psi(p)\rangle=&f_{J/\psi}M_{J/\psi}\,\xi_\mu \,\, , \\ \langle0|J_{\mu}^{K^*}(0)|K^*(q)\rangle=&f_{K^*}M_{K^*}\,\varepsilon_\mu \,\, , \\ \langle0|J_{\mu}^{D^*}(0)|D^*(p)\rangle=&f_{D^*}M_{D^*}\,\varsigma_\mu \,\, , \\ \langle0|J_{5}^{K}(0)|K(q)\rangle=&\frac{f_{K}M_{K}^2}{m_u+m_s} \,\, , \\ \langle0|J_{5}^{\eta_c}(0)|\eta_c(p)\rangle=&\frac{f_{\eta_c}M_{\eta_c}^2}{2m_c} \,\, , \\ \langle0|J_{5}^{D_s}(0)|D_s(q)\rangle=&\frac{f_{D_s}M_{D_s}^2}{m_c+m_s} \,\, , \\ \langle 0|J^{T/M}_\nu(0)|Z_{cs}^{T/M}(p^\prime)\rangle=&\lambda_{Z}^{T/M}\,\zeta_\nu\,\, , \end{aligned} $

(13) and ξ, ε, ς, and ζ are the polarization vectors of
$ J/\psi $ ,$ K^* $ ,$ D^* $ , and$ Z_{cs}^{T/M} $ , respectively. The hadronic coupling constants$ G^T_{ZJ/\psi K} $ ,$ G^M_{ZJ/\psi K} $ ,$ G^T_{Z\eta_cK^*} $ ,$ G^M_{Z\eta_cK^*} $ ,$ G_{Z D^*\bar{D}_s}^T $ , and$ G_{Z D^*\bar{D}_s}^M $ are defined by$ \begin{aligned}[b] \langle J/\psi(p)K(q)|Z^T_{cs}(p^{\prime})\rangle=&-\xi^*(p)\cdot\zeta(p^{\prime})\, G^T_{ZJ/\psi K} \, , \\ \langle\eta_c(p)K^*(q)|Z_{cs}^T(p^{\prime})\rangle=&-\varepsilon^*(q)\cdot\zeta(p^{\prime})\, G^T_{Z\eta_cK^*} \, , \\ \langle D^*(p)D_s(q)|Z^T_{cs}(p^{\prime})\rangle=&-\varsigma^*(p)\cdot\zeta(p^{\prime})\, G^T_{Z D^*\bar{D}_s} \, , \\ \langle J/\psi(p)K(q)|Z^M_{cs}(p^{\prime})\rangle=& {\rm i}\xi^*(p)\cdot\zeta(p^{\prime})\, G^M_{ZJ/\psi K} \, , \\ \langle\eta_c(p)K^*(q)|Z_{cs}^M(p^{\prime})\rangle=& {\rm i}\varepsilon^*(q)\cdot\zeta(p^{\prime})\, G^M_{Z\eta_cK^*} \, , \\ \langle D^*(p)D_s(q)|Z^M_{cs}(p^{\prime})\rangle=& {\rm i}\varsigma^*(p)\cdot\zeta(p^{\prime})\, G^M_{Z D^*\bar{D}_s} \, . \end{aligned} $

(14) The hadronic spectral densities
$ \rho_{Z K^\prime}(p^{\prime2},p^2,u) $ ,$ \rho_{Z \psi^\prime}(p^{\prime2},s,q^2) $ ,$ \rho_{Z^\prime J/\psi}(s^\prime,p^2,q^2) $ ,$ \rho_{Z^\prime K}(s^\prime,p^2,q^2) $ in the component$ \Pi_T^1(p^{\prime2},p^2,q^2) $ represent the transitions between the ground states and continuum states (including the first radial excited states). In fact, such hadronic spectral densities also exist in the large$\{ \; \}$ in the components$ \Pi_T^2(p^{\prime2},p^2,q^2) $ ,$ \Pi_T^3(p^{\prime2},p^2,q^2) $ ,$ \Pi_M^1(p^{\prime2},p^2,q^2) $ ,$\Pi_M^2(p^{\prime2}, p^2,q^2)$ , and$ \Pi_M^3(p^{\prime2},p^2,q^2) $ ; however, we neglect them for simplicity. In this study, we choose the tensor structure$ g_{\mu\nu} $ to explore the hadronic coupling constants$ G^{T/M}_{ZJ/\psi K} $ ,$ G^{T/M}_{Z\eta_cK^*} $ , and$ G^{T/M}_{Z D^* \bar{D}_s} $ and neglect other tensor structures for simplicity.We accomplish operator product expansion up to the vacuum condensates of dimension five and neglect the tiny gluon condensate contributions, as in our previous studies [26–30]. Then, we obtain the QCD spectral densities
$\rho_{\rm QCD}(p^{\prime2},s,u)$ through the double dispersion relation and express the correlation functions on the QCD side in the form$ \Pi_{\rm QCD}(p^{\prime2},p^2,q^2)= \int_{\Delta_s^2}^\infty {\rm d}s \int_{\Delta_u^2}^\infty {\rm d}u \frac{\rho_{\rm QCD}(p^{\prime2},s,u)}{(s-p^2)(u-q^2)}\, , $

(15) where
$ \Delta_s^2 $ and$ \Delta_u^2 $ are the thresholds. On the hadron side, we obtain the hadron spectral densities$ \rho_H(s^\prime,s,u) $ through the triple dispersion relation and express the correlation functions in the form$ \begin{aligned}[b] \Pi_{H}(p^{\prime2},p^2,q^2)=&\int_{\Delta_s^{\prime2}}^\infty {\rm d} s^{\prime} \int_{\Delta_s^2}^\infty {\rm d} s \int_{\Delta_u^2}^\infty {\rm d} u\\&\times \frac{\rho_{H}(s^\prime,s,u)}{(s^\prime-p^{\prime2})(s-p^2)(u-q^2)}\, , \end{aligned}$

(16) according to Eqs. (7) – (12), where
$ \Delta_{s}^{\prime2} $ are the thresholds. We match the hadron side with the QCD side of the correlation functions below the continuum thresholds using the dispersion relation at the QCD side to warrant rigorous quark-hadron duality.$ \begin{aligned}[b]& \int_{\Delta_s^2}^{s_{0}}{\rm d}s \int_{\Delta_u^2}^{u_0}{\rm d}u \frac{\rho_{\rm QCD}(p^{\prime2},s,u)}{(s-p^2)(u-q^2)}\\=& \int_{\Delta_s^2}^{s_0}{\rm d}s \int_{\Delta_u^2}^{u_0}{\rm d}u \left[ \int_{\Delta_{s}^{\prime2}}^{\infty}{\rm d}s^\prime \frac{\rho_H(s^\prime,s,u)}{(s^\prime-p^{\prime2})(s-p^2)(u-q^2)} \right]\, , \end{aligned} $

(17) where
$ s_0 $ and$ u_0 $ are the continuum thresholds. We first integrate over${\rm d} s^\prime$ and introduce several unknown parameters to parameterize the contributions involving higher resonances and continuum states in the$ s^\prime $ channel [26, 27]. Note that we consider the higher resonances and continuum states rather than neglecting them. For example, using Eq. (7), we explicitly write the correlation function on the hadron side as$ \begin{aligned}[b]& \int_{\Delta_s^2}^{s_{0}}{\rm d}s \int_{\Delta_u^2}^{u_0}{\rm d}u \frac{\rho_{\rm QCD}(p^{\prime2},s,u)}{(s-p^2)(u-q^2)}\\=& \frac{A_{ZJ/\psi K}}{(M_{Z}^2-p^{\prime2})(M_{J/\psi}^2-p^2)(M_{K}^2-q^2)}\\&+\frac{C^T_{J/\psi K}}{(M_{J/\psi}^2-p^2)(M_{K}^2-q^2)}\, , \end{aligned} $

(18) where
$ \begin{aligned}[b] A_{ZJ/\psi K}=& \frac{f_{K}M_{K}^2f_{J/\psi}M_{J/\psi}\lambda_{Z}^T G^T_{ZJ/\psi K}}{m_u+m_s}\, , \\ C^T_{J/\psi K}=&\int_{s^0_Z}^{\infty} {\rm d}s^\prime \frac{\rho_{Z^\prime J/\psi}(s^\prime,p^2,q^2)+\rho_{Z^\prime K}(s^\prime,p^2,q^2)}{s^\prime-p^{\prime2}} \, , \end{aligned} $

(19) where the unknown parameter
$ C_{J/\psi K}^T $ parameterizes the contributions involving higher resonances and continuum states with the same quantum numbers as$ Z_{cs} $ (in the$ s^\prime $ channel). The unknown parameters$ C_{J/\psi K}^M $ ,$ C_{\eta_c K^*}^T $ ,$ C_{\eta_c K^*}^M $ ,$ C_{D^* \bar{D}_s}^T $ , and$ C_{D^* \bar{D}_s}^M $ in Eqs. (21)–(25) are implied in the same manner.Next, we integrate over the variable
${\rm d} s^\prime$ . We do not require the continuum threshold parameters$ s^{\prime }_0 $ , and the duality is rigorous in the sense that we do not set$ s_0=s^{\prime}_0=s^0_Z $ approximately [33]. If we set$ s_0=s_0^{\prime}=s^0_Z $ in the present case,$ \sqrt{s_0}> M_Z>\psi^\prime> \eta_c^\prime>M_{D_s^{*\prime}}>M_{D_s^\prime} $ , and the contaminations from the excited states are out of control. Without first integrating over the variable${\rm d}s^\prime$ , the representations on the QCD and hadron sides will not match, and to date, no researcher has agreed that they match without merging the s and$ s^\prime $ channels,$ s_0=s^{\prime}_0=s^0_Z $ , on the hadron side by hand. In fact, approximations such as$ s_0=s^{\prime}_0 $ are incorrect because the s and$ s^\prime $ channels are different.In the s and u channels, we deal with conventional mesons and choose standard vector and pseudoscalar currents to interpolate them. Direct calculations indicate that we can reproduce their masses satisfactorily with the two-point QCD sum rules below the continuum thresholds
$ s_0 $ and$ u_0 $ , respectively. The quark-hadron duality is hence reliable.We set
$ p^{\prime2}=p^2 $ and$ p^{\prime2}=4p^2 $ in the correlation functions$ \Pi^{1/2}_{T/M}(p^{\prime 2},p^2,q^2) $ and$ \Pi^{3}_{T/M}(p^{\prime 2},p^2,q^2) $ , respectively, and accomplish the double Borel transform in regard to the variables$ P^2=-p^2 $ and$ Q^2=-q^2 $ , respectively. Then, we set the Borel parameters$ T_1^2=T_2^2=T^2 $ to obtain the six QCD sum rules,$ \begin{aligned}[b] \\[-5pt] &\frac{f_{K}M_{K}^2f_{J/\psi}M_{J/\psi}\lambda_{Z}^TG^T_{ZJ/\psi K}}{m_u+m_s}\frac{1}{M_{Z}^2-M_{J/\psi}^2} \left[ \exp\left(-\frac{M_{J/\psi}^2}{T^2} \right)-\exp\left(-\frac{M_{Z}^2}{T^2} \right)\right]\exp\left(-\frac{M_{K}^2}{T^2} \right) +C^T_{J/\psi K} \exp\left(-\frac{M_{J/\psi}^2+M_{K}^2}{T^2} \right)\\=&\frac{1}{64\sqrt{2}\pi^4}\int_{4m_c^2}^{s^0_{J/\psi}} {\rm d}s \int_{0}^{u^0_{K}} {\rm d}u \sqrt{1-\frac{4m_c^2}{s}} u\left(2s+4m_c^2-3m_s m_c\right)\exp\left(-\frac{s+u}{T^2} \right)-\frac{m_s\left[2\langle\bar{q}q\rangle+\langle\bar{s}s\rangle\right]}{24\sqrt{2}\pi^2}\int_{4m_c^2}^{s^0_{J/\psi}} {\rm d}s \sqrt{1-\frac{4m_c^2}{s}}\left(s+2m_c^2\right)\\ &\times\exp\left(-\frac{s}{T^2}\right) -\frac{m_s\langle\bar{q}g_s\sigma Gq\rangle}{288\sqrt{2}\pi^2}\int_{4m_c^2}^{s^0_{J/\psi}} {\rm d}s \frac{s+20m_c^2}{\sqrt{s\left(s-4m_c^2\right)}} \exp\left(-\frac{s}{T^2}\right)-\frac{m_s\langle\bar{q}g_s\sigma Gq\rangle}{24\sqrt{2}\pi^2T^2}\int_{4m_c^2}^{s^0_{J/\psi}} {\rm d}s \sqrt{1-\frac{4m_c^2}{s}}\left(s+2m_c^2\right) \exp\left(-\frac{s}{T^2}\right) \, , \end{aligned} $ 
(20) $ \begin{aligned}[b] &\frac{f_{K}M_{K}^2f_{J/\psi}M_{J/\psi}\lambda_{Z}^MG^M_{ZJ/\psi K}}{m_u+m_s}\frac{1}{M_{Z}^2-M_{J/\psi}^2} \left[ \exp\left(-\frac{M_{J/\psi}^2}{T^2} \right)-\exp\left(-\frac{M_{Z}^2}{T^2} \right)\right]\exp\left(-\frac{M_{K}^2}{T^2} \right) +C^M_{J/\psi K} \exp\left(-\frac{M_{J/\psi}^2+M_{K}^2}{T^2} \right)\\=&\frac{1}{128\sqrt{2}\pi^4}\int_{4m_c^2}^{s^0_{J/\psi}} {\rm d}s \int_{0}^{u^0_{K}} {\rm d}u \sqrt{1-\frac{4m_c^2}{s}} u\left(2s+4m_c^2-3m_s m_c\right)\exp\left(-\frac{s+u}{T^2} \right)-\frac{m_s\left[2\langle\bar{q}q\rangle+\langle\bar{s}s\rangle\right]}{48\sqrt{2}\pi^2}\int_{4m_c^2}^{s^0_{J/\psi}} {\rm d}s \sqrt{1-\frac{4m_c^2}{s}}\left(s+2m_c^2\right)\\ &\times\exp\left(-\frac{s}{T^2}\right)-\frac{m_s\langle\bar{q}g_s\sigma Gq\rangle}{288\sqrt{2}\pi^2}\int_{4m_c^2}^{s^0_{J/\psi}} {\rm d}s \frac{s+20m_c^2}{\sqrt{s\left(s-4m_c^2\right)}} \exp\left(-\frac{s}{T^2}\right)-\frac{m_s\langle\bar{q}g_s\sigma Gq\rangle}{48\sqrt{2}\pi^2T^2}\int_{4m_c^2}^{s^0_{J/\psi}} {\rm d}s \sqrt{1-\frac{4m_c^2}{s}}\left(s+2m_c^2\right)\exp\left(-\frac{s}{T^2}\right) \, , \end{aligned} $

(21) $ \begin{aligned}[b] &\frac{f_{\eta_c}M_{\eta_c}^2f_{K^*}M_{K^*}\lambda_{Z}^TG^T_{Z\eta_c K^*}}{2m_c } \frac{1}{M_{Z}^2-M_{\eta_c}^2}\left[ \exp\left(-\frac{M_{\eta_c}^2}{T^2} \right)-\exp\left(-\frac{M_{Z}^2}{T^2} \right)\right]\exp\left(-\frac{M_{K^*}^2}{T^2} \right) +C^T_{\eta_c K^*} \exp\left(-\frac{M_{\eta_c}^2+M_{K^*}^2}{T^2} \right)\\=&-\frac{1}{64\sqrt{2}\pi^4}\int_{4m_c^2}^{s^0_{\eta_c}} {\rm d}s \int_{0}^{u^0_{K^*}} {\rm d}u \sqrt{1-\frac{4m_c^2}{s}} u\left(2s-3m_sm_c \right)\exp\left(-\frac{s+u}{T^2} \right)+\frac{m_s\langle\bar{q}q\rangle}{8\sqrt{2}\pi^2}\int_{4m_c^2}^{s^0_{\eta_c}} {\rm d}s \sqrt{1-\frac{4m_c^2}{s}}\, s\, \\&\times\exp\left(-\frac{s}{T^2}\right)+\frac{m_s\langle\bar{s}g_s\sigma Gs\rangle}{96\sqrt{2}\pi^2T^2}\int_{4m_c^2}^{s^0_{\eta_c}} {\rm d}s \sqrt{1-\frac{4m_c^2}{s}}\, s\, \exp\left(-\frac{s}{T^2}\right)+\frac{m_s\langle\bar{q}g_s\sigma Gq\rangle}{72\sqrt{2}\pi^2}\int_{4m_c^2}^{s^0_{\eta_c}} {\rm d}s \frac{s+2m_c^2}{\sqrt{s\left(s-4m_c^2\right)}}\exp\left(-\frac{s}{T^2}\right)\\ &-\frac{m_c\left[\langle\bar{q}g_s\sigma Gq\rangle+\langle\bar{s}g_s\sigma Gs\rangle\right]}{24\sqrt{2}\pi^2} \int_{4m_c^2}^{s^0_{\eta_c}} {\rm d}s \sqrt{1-\frac{4m_c^2}{s}}\exp\left(-\frac{s}{T^2}\right) \, , \end{aligned} $

(22) $ \begin{aligned}[b] &\frac{f_{\eta_c}M_{\eta_c}^2f_{K^*}M_{K^*}\lambda_{Z}^MG^M_{Z\eta_c K^*}}{2m_c } \frac{1}{M_{Z}^2-M_{\eta_c}^2}\left[ \exp\left(-\frac{M_{\eta_c}^2}{T^2} \right)-\exp\left(-\frac{M_{Z}^2}{T^2} \right)\right]\exp\left(-\frac{M_{K^*}^2}{T^2} \right) +C^M_{\eta_c K^*} \exp\left(-\frac{M_{\eta_c}^2+M_{K^*}^2}{T^2} \right)\\=&\frac{1}{128\sqrt{2}\pi^4}\int_{4m_c^2}^{s^0_{\eta_c}} {\rm d}s \int_{0}^{u^0_{K^*}} {\rm d}u \sqrt{1-\frac{4m_c^2}{s}} u\left(2s-3m_sm_c \right)\exp\left(-\frac{s+u}{T^2} \right)-\frac{m_s\langle\bar{q}q\rangle}{16\sqrt{2}\pi^2}\int_{4m_c^2}^{s^0_{\eta_c}} {\rm d}s \sqrt{1-\frac{4m_c^2}{s}} s \exp\left(-\frac{s}{T^2}\right)\\ &-\frac{m_s\langle\bar{s}g_s\sigma Gs\rangle}{192\sqrt{2}\pi^2T^2}\int_{4m_c^2}^{s^0_{\eta_c}} {\rm d}s \sqrt{1-\frac{4m_c^2}{s}}\,s\,\exp\left(-\frac{s}{T^2}\right)-\frac{m_s\langle\bar{q}g_s\sigma Gq\rangle}{72\sqrt{2}\pi^2} \int_{4m_c^2}^{s^0_{\eta_c}} {\rm d}s \frac{s+2m_c^2}{\sqrt{s\left(s-4m_c^2\right)}} \exp\left(-\frac{s}{T^2}\right)\\ &+\frac{m_c\left[\langle\bar{q}g_s\sigma Gq\rangle+\langle\bar{s}g_s\sigma Gs\rangle\right]}{48\sqrt{2}\pi^2}\int_{4m_c^2}^{s^0_{\eta_c}} {\rm d}s \sqrt{1-\frac{4m_c^2}{s}}\exp\left(-\frac{s}{T^2}\right) \, , \end{aligned} $

(23) $ \begin{aligned}[b] &\frac{f_{D_s}M_{D_s}^2f_{D^*}M_{D^*}\lambda_{Z}^TG^T_{Z D^*\bar{D}_s}}{4(m_c+m_s) } \frac{1}{\widetilde{M}_{Z}^2-M_{D^*}^2}\left[ \exp\left(-\frac{M_{D^*}^2}{T^2} \right)-\exp\left(-\frac{\widetilde{M}_{Z}^2}{T^2} \right)\right]\exp\left(-\frac{M_{D_s}^2}{T^2} \right)+ C^T_{ D^*\bar{D}_s} \exp\left(-\frac{M_{D^*}^2+M_{D_s}^2}{T^2} \right)\\=&-\frac{m_c\langle\bar{s}g_s\sigma Gs\rangle}{96\sqrt{2}\pi^2}\int_{m_c^2}^{s^0_{D^*}} {\rm d}s \left( \frac{9}{2}-\frac{10m_c^2}{s}+\frac{3m_c^4}{2s^2}\right)\exp\left(-\frac{s+m_c^2}{T^2}\right)+\frac{m_s\langle\bar{q}g_s\sigma Gq\rangle}{96\sqrt{2}\pi^2}\int_{m_c^2}^{u^0_{D_s}} {\rm d}u \left(2+\frac{3m_c^2}{u}\right) \frac{m_c^2}{u}\exp\left(-\frac{u+m_c^2}{T^2}\right)\\&+\frac{m_c\langle\bar{q}g_s\sigma Gq\rangle}{96\sqrt{2}\pi^2}\int_{m_c^2}^{u^0_{D_s}} {\rm d}u \left( \frac{3}{2}+\frac{4m_c^2}{u}-\frac{3m_c^4}{2u^2}\right)\exp\left(-\frac{u+m_c^2}{T^2}\right)-\frac{m_s\langle\bar{q}g_s\sigma Gq\rangle}{192\sqrt{2}\pi^2}\int_{m_c^2}^{u^0_{D_s}} {\rm d}u \frac{1}{u-m_c^2}\left(u-9m_c^2-\frac{5m_c^4}{u}-\frac{3m_c^6}{u^2}\right)\\&\times\exp\left(-\frac{u+m_c^2}{T^2}\right)\, , \end{aligned} $

(24) $ \begin{aligned}[b] &\frac{f_{D_s}M_{D_s}^2f_{D^*}M_{D^*}\lambda_{Z}^MG^M_{Z D^*\bar{D}_s}}{4(m_c+m_s) } \frac{1}{\widetilde{M}_{Z}^2-M_{D^*}^2}\left[ \exp\left(-\frac{M_{D^*}^2}{T^2} \right)-\exp\left(-\frac{\widetilde{M}_{Z}^2}{T^2} \right)\right]\exp\left(-\frac{M_{D_s}^2}{T^2} \right) + C^M_{ D^*\bar{D}_s} \exp\left(-\frac{M_{D^*}^2+M_{D_s}^2}{T^2} \right)\\=&-\frac{3}{64\sqrt{2}\pi^4}\int_{m_c^2}^{s^0_{D^*}} {\rm d}s \int_{m_c^2}^{u^0_{D_s}} {\rm d}u \left(1-\frac{m_c^2}{s}\right)\left(1-\frac{m_c^2}{u}\right)\left(2s-m_c^2-\frac{m_c^4}{s}\right)\left(u-m_c^2+2m_s m_c\right)\exp\left(-\frac{s+u}{T^2}\right)+\frac{m_c\langle\bar{s}s\rangle}{8\sqrt{2}\pi^2}\int_{m_c^2}^{s^0_{D^*}} {\rm d}s\\ &\times \left(1-\frac{m_c^2}{s}\right)\left(2s-m_c^2-\frac{m_c^4}{s}\right)\exp\left(-\frac{s+m_c^2}{T^2}\right)+\frac{3m_c\langle\bar{q}q\rangle}{8\sqrt{2}\pi^2}\int_{m_c^2}^{u^0_{D_s}} {\rm d}u \left(1-\frac{m_c^2}{u}\right)\left(u-m_c^2+2m_s m_c\right) \exp\left(-\frac{u+m_c^2}{T^2}\right)\\ &+\frac{m_s\langle\bar{s}s\rangle}{16\sqrt{2}\pi^2}\left(1+\frac{m_c^2}{T^2}\right)\int_{m_c^2}^{s^0_{D^*}} {\rm d}s \left(1-\frac{m_c^2}{s}\right)\left(2s-m_c^2-\frac{m_c^4}{s}\right)\exp\left(-\frac{s+m_c^2}{T^2}\right)-\frac{3m_c^3\langle\bar{q}g_s\sigma Gq\rangle}{32\sqrt{2}\pi^2T^4}\int_{m_c^2}^{u^0_{D_s}} {\rm d}u \left(1-\frac{m_c^2}{u}\right)\left(u-m_c^2+2m_s m_c\right) \\ &\times\exp\left(-\frac{u+m_c^2}{T^2}\right)-\frac{m_sm_c^4\langle\bar{s}g_s\sigma Gs\rangle}{96\sqrt{2}\pi^2T^6}\int_{m_c^2}^{s^0_{D^*}} {\rm d}s \left(1-\frac{m_c^2}{s}\right) \left(2s-m_c^2-\frac{m_c^4}{s}\right)\exp\left(-\frac{s+m_c^2}{T^2}\right) \\ &+\frac{m_c\langle\bar{s}g_s\sigma Gs\rangle}{16\sqrt{2}\pi^2T^2}\left(1-\frac{m_c^2}{2T^2} \right)\int_{m_c^2}^{s^0_{D^*}} {\rm d}s\left(1-\frac{m_c^2}{s}\right) \left(2s-m_c^2-\frac{m_c^4}{s}\right)\exp\left(-\frac{s+m_c^2}{T^2}\right) \, ,\\[-10pt] \end{aligned} $

(25) where
$ \widetilde{M}_{Z}^2=\dfrac{M_{Z}^2}{4} $ , and$ s^0_{J/\psi} $ ,$ u^0_{K} $ ,$ s^0_{\eta_c} $ ,$ u^0_{K^*} $ ,$ s^0_{D^*} $ , and$ u^0_{D_s} $ are the continuum threshold parameters. There are end-divergences at the endpoints$ s=4m_c^2 $ and$ u=m_c^2 $ , which we regularize using the simple replacements$ \begin{aligned}[b]& \dfrac{1}{\sqrt{s-4m_c^2}} \to \dfrac{1}{\sqrt{s-4m_c^2+4m_s^2}}\\& \dfrac{1}{u-m_c^2} \to \dfrac{1}{u-m_c^2+4m_s^2}\end{aligned} $

by adding a small squared s-quark mass
$ 4m_s^2 $ [26–30].Now, we take a short digression to illustrate the end-point divergences. We often encounter the typical integral
$ I_{21}= \int {\rm d}^4k_1 \frac{1}{(k_1^2-m_c^2)^2}\frac{1}{((p-k_1)^2-m_c^2)}\, , $

(26) which is calculated using Cutkosky's rules,
$ \begin{aligned}[b] I_{21}=&\frac{\partial}{\partial A } \int {\rm d}^4k_1\frac{1}{k_1^2-A}\frac{1}{(p-k_1)^2-m_c^2}\bigg|_{A\to m_c^2}\\ =&\frac{\partial}{\partial A } \frac{(-2\pi {\rm i})^2}{2\pi {\rm i}}\int_{(\sqrt{A}+m_c)^2}^{\infty}{\rm d}t\frac{1}{t-p^2}\int {\rm d}^4k_1d^4k_2\delta^4\\&\times(k_1+k_2-p)\delta(k_1^2-A)\delta(k_2^2-m_c^2)\\ =&\frac{\partial}{\partial A }\frac{(-2\pi {\rm i})^2}{2\pi {\rm i}}\int_{(\sqrt{A}+m_c)^2}^{\infty} {\rm d} t\frac{1}{t-p^2}\frac{\pi}{2}\frac{\sqrt{\lambda(t,A,m_c^2)}}{t}\bigg|_{A\to m_c^2}\\ =&\frac{(-2\pi {\rm i})^2}{2\pi {\rm i}}\int_{4m_c^2}^{\infty}{\rm d}t\frac{1}{t-p^2}\frac{\pi}{2} \frac{-1}{\sqrt{t(t-4m_c^2)}}\, , \end{aligned} $

(27) for which a divergence appears at the end-point
$ t=4m_c^2 $ . Such terms are accompanied by the small s-quark mass$ m_s $ and play a minor yet important role. We regularize the endpoint divergences by empirically adding a small squared s-quark mass$ 4m_s^2 $ , as in previous studies [26–30]. If we vary$ 4m_s^2 $ by adding a small uncertainty$ 4m_s^2\pm\delta $ , we can obtain almost invariant numerical results.Furthermore, we smear the dependencies of the parameters
$ C_{J/\psi K}^T $ ,$ C_{J/\psi K}^M $ ,$ C_{\eta_c K^*}^T $ ,$ C_{\eta_c K^*}^M $ ,$ C_{D^* \bar{D}_s}^T $ , and$ C_{D^* \bar{D}_s}^M $ on the Lorentz invariants$ p^{\prime2} $ ,$ p^2 $ , and$ q^2 $ and take them as free parameters. Then, we search for the best values to remove contaminations from the high resonances and continuum states to acquire stable QCD sum rules with variations in the Borel parameter$ T^2 $ . -
On the QCD side, we take the standard values
$\langle \bar{q}q \rangle= -(0.24\pm 0.01\, {\rm{GeV}})^3$ ,$ \langle\bar{s}s\rangle=(0.8\pm0.1)\langle\bar{q}q\rangle $ ,$ \langle\bar{q}g_s\sigma G q \rangle= m_0^2\langle \bar{q}q \rangle $ ,$ \langle\bar{s}g_s\sigma G s \rangle=m_0^2\langle \bar{s}s \rangle $ , and$ m_0^2=(0.8 \pm 0.1)\,{\rm{GeV}}^2 $ at the energy scale$ \mu=1\, {\rm{GeV}} $ [34–36] and take the$ \overline{MS} $ quark masses$ m_{c}(m_c)=(1.275\pm0.025)\,{\rm{GeV}} $ and$m_s(\mu= 2\,{\rm{GeV}})=(0.095\pm0.005)\,{\rm{GeV}}$ from the Particle Data Group [7]. We set$ m_u=m_d=0 $ and take account of the energy-scale dependence of the input parameters,$ \begin{aligned}[b] \langle\bar{q}q \rangle(\mu)=&\langle\bar{q}q \rangle({{\rm{1GeV}}})\left[\frac{\alpha_{s}({{\rm{1GeV}}})}{\alpha_{s}(\mu)}\right]^{\frac{12}{33-2n_f}}\, , \\ \langle\bar{s}s \rangle(\mu)=&\langle\bar{s}s \rangle({{\rm{1GeV}}})\left[\frac{\alpha_{s}({{\rm{1GeV}}})}{\alpha_{s}(\mu)}\right]^{\frac{12}{33-2n_f}}\, , \\ \langle\bar{q}g_s \sigma Gq \rangle(\mu)=&\langle\bar{q}g_s \sigma Gq \rangle({{\rm{1GeV}}})\left[\frac{\alpha_{s}({{\rm{1GeV}}})}{\alpha_{s}(\mu)}\right]^{\frac{2}{33-2n_f}}\, , \\ \langle\bar{s}g_s \sigma Gs \rangle(\mu)=&\langle\bar{s}g_s \sigma Gs \rangle({{\rm{1GeV}}})\left[\frac{\alpha_{s}({{\rm{1GeV}}})}{\alpha_{s}(\mu)}\right]^{\frac{2}{33-2n_f}}\, , \\ m_c(\mu)=&m_c(m_c)\left[\frac{\alpha_{s}(\mu)}{\alpha_{s}(m_c)}\right]^{\frac{12}{33-2n_f}} \, ,\\ m_s(\mu)=&m_s({{\rm{2GeV}}})\left[\frac{\alpha_{s}(\mu)}{\alpha_{s}({{\rm{2GeV}}})}\right]^{\frac{12}{33-2n_f}} \, ,\\ \alpha_s(\mu)=&\frac{1}{b_0t}\left[1-\frac{b_1}{b_0^2}\frac{\log t}{t} +\frac{b_1^2(\log^2{t}-\log{t}-1)+b_0b_2}{b_0^4t^2}\right]\, , \end{aligned} $

(28) from the renormalization group equations
$ \begin{aligned}[b]t=&\log \frac{\mu^2}{\Lambda_{\rm QCD}^2},\quad b_0=\frac{33-2n_f}{12\pi},\\ b_1=&\frac{153-19n_f}{24\pi^2},\quad b_2=\frac{2857-\dfrac{5033}{9}n_f+\dfrac{325}{27}n_f^2}{128\pi^3}\end{aligned} $

$\Lambda_{\rm QCD}=210\,{\rm{MeV}}$ ,$ 292\,{\rm{MeV}} $ , and$ 332\,{\rm{MeV}} $ for the flavors$ n_f=5 $ ,$ 4 $ , and$ 3 $ , respectively [7, 37], and all input parameters are evolved to the typical energy scale$\mu= m_c(m_c)\approx$ 1.3 GeV to extract hadronic coupling constants [19, 25, 38].On the hadron side, we take the parameters as
$ M_{K}= $ 0.4937 GeV,$ M_{K^*}= $ 0.8917 GeV,$ M_{J/\psi}= $ 3.0969 GeV,$ M_{\eta_c}= $ 2.9834 GeV,$ M_{D^*}= $ 2.007 GeV and$ D_{s}= $ 1.969 GeV [7],$ f_{K}= $ 0.156 GeV [7],$ f_{K^*}= $ 0.220 GeV,$ \sqrt{u^0_{K}}= $ 1.0 GeV,$ \sqrt{u^0_{K^*}}= $ 1.3 GeV [39],$ f_{D_s}= $ 240 MeV,$ \sqrt{u^0_{D_s}}= $ 2.6 GeV,$ f_{D^*}= $ 263 MeV,$ \sqrt{s^0_{D^*}}= $ 2.5 GeV [40],$ f_{J/\psi}= $ 0.418 GeV,$ f_{\eta_c}= $ 0.387 GeV [41],$ \sqrt{s^0_{J/\psi}}= $ 3.6 GeV,$ \sqrt{s^0_{\eta_c}}= $ 3.5 GeV [7],$ M_{Z}= $ 3.99 GeV,$\lambda_{Z}^T=2.85\times 10^{-2} {\rm{GeV}}^5$ [19],$ \lambda_{Z}^M=1.96\times 10^{-2}\,{\rm{GeV}}^5 $ [25], and$\dfrac{f_{K}M^2_{K}}{m_u+m_s}= -\dfrac{\langle \bar{q}q\rangle+\langle \bar{s}s\rangle}{f_{K}(1-\delta_K)}$ from the Gell-Mann-Oakes-Renner relation$ \delta_K=0.50 $ [42].In calculations, we fit the unknown parameters to be
$ \begin{aligned}[b] C^T_{J/\psi K}=&0.00045+0.00038\times T^2\,{\rm{GeV}}^8 \\ C_{\eta_c K^*}^T=&-0.00184-0.00068\times T^2\,{\rm{GeV}}^8 \\ C^T_{D^* \bar{D}_s}=&0+0\times T^2\,{\rm{GeV}}^8\\ C^M_{J/\psi K}=&0.0004+0.00017\times T^2\,{\rm{GeV}}^8\\C^M_{\eta_c K^*}=&0.00094+0.00033\times T^2\,{\rm{GeV}}^8\\ C^M_{D^* \bar{D}_s}=&-0.023-0.00405\times T^2\,{\rm{GeV}}^8\end{aligned} $

to acquire the flat Borel platforms
$T^2_{\max}-T^2_{\min}=1\,{\rm{GeV}}^2$ , where max and min represent the maximum and minimum values, respectively (see Fig. 1 for an example). In the picture of tetraquark states, the Borel parameters are$ T^2_{J/\psi K}=(2.7-3.7)\,{\rm{GeV}}^2 $ ,$ T^2_{\eta_c K^*}=(2.5-3.5)\,{\rm{GeV}}^2 $ , and$ T^2_{D^*\bar{D}_s}=(3.1-4.1)\,{\rm{GeV}}^2 $ for the hadronic coupling constants$ G_{ZJ/\psi K}^T $ ,$ G^T_{Z\eta_cK^*} $ , and$ G^T_{ZD^*\bar{D}_s} $ , respectively, whereas in the picture of molecular states, the Borel parameters are$ T^2_{J/\psi K}=(2.7-3.7)\,{\rm{GeV}}^2 $ ,$ T^2_{\eta_c K^*}=(2.3-3.3)\,{\rm{GeV}}^2 $ , and$ T^2_{D^* \bar{D}_s}=(2.3-3.3)\,{\rm{GeV}}^2 $ for the hadronic coupling constants$ G_{ZJ/\psi K}^M $ ,$ G^M_{Z\eta_cK^*} $ , and$ G^M_{ZD^*\bar{D}_s} $ , respectively, where we add the subscripts$ J/\psi K $ ,$ \eta_c K^* $ , and$ D^*\bar{D}_s $ to denote the corresponding channels. The uncertainties originate from the uncertainties on the input parameters on the QCD side, which, in general, can be absorbed together into the decay and coupling constants. For example,$ f_{J/\psi} $ ,$ f_{K} $ ,$ \lambda_Z^T $ , and$ G^T_{ZJ/\psi K} $ in the QCD sum rules of Eq. (20).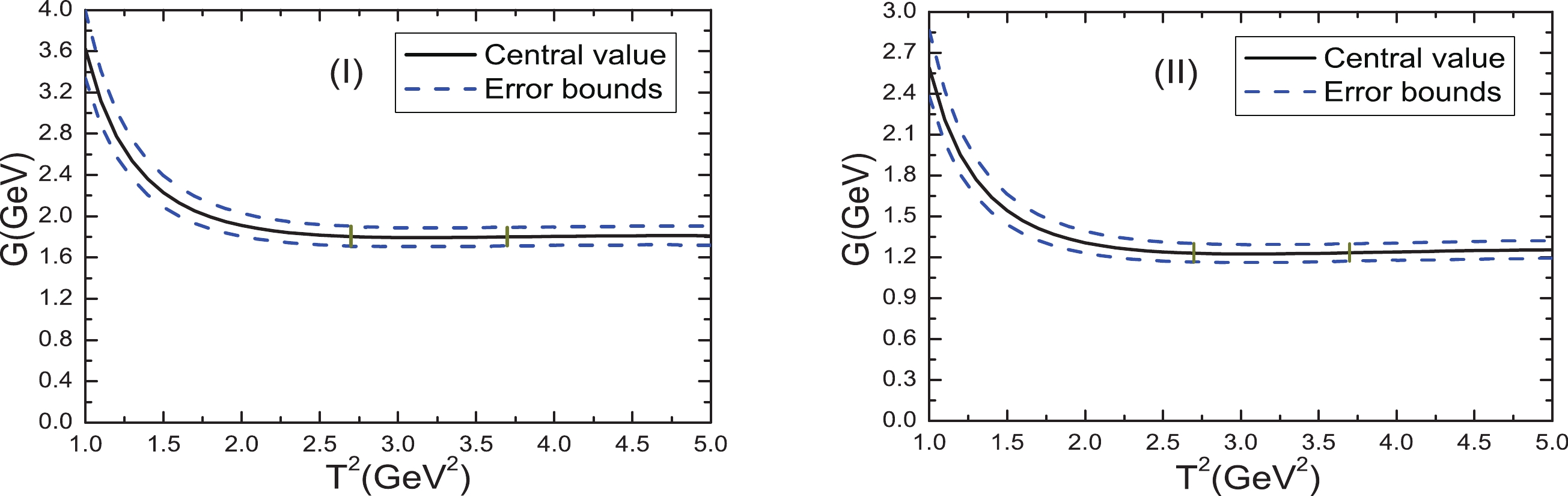
Figure 1. (color online) Hadronic coupling constants
$ G^T_{ZJ/\psi K} $ (I) and$ G^M_{ZJ/\psi K} $ (II) with variations in the Borel parameter$ T^2 $ , where the regions between the two vertical lines are the Borel windows.If we use the symbol ξ to represent the input parameters on the QCD side, the uncertainties
$ \xi \to \xi +\delta \xi $ lead to the uncertainties$ f_{J/\psi}f_{K}\lambda^T_{Z}G^T_{ZJ/\psi K} \to f_{J/\psi}f_{K}\lambda^T_{Z}G^T_{ZJ/\psi K}+ \delta\,f_{J/\psi}f_{K}\lambda^T_{Z}G^T_{ZJ/\psi K} $ and$ C^T_{J/\psi K} \to C^T_{J/\psi K}+\delta C^T_{J/\psi K} $ , where$ \begin{aligned}[b]& \delta\,f_{J/\psi}f_{K}\lambda^T_{Z}G^T_{ZJ/\psi K} \\=&f_{J/\psi}f_{K}\lambda^T_{Z}G^T_{ZJ/\psi K}\left( \frac{\delta f_{J/\psi}}{f_{J/\psi}} +\frac{\delta f_{K}}{f_{K}}+\frac{\delta \lambda^T_{Z}}{\lambda^T_{Z}}+\frac{\delta G^T_{ZJ/\psi K}}{G^T_{ZJ/\psi K}}\right)\, , \end{aligned} $

(29) and we can approximately set
$\dfrac{\delta f_{J/\psi}}{f_{J/\psi}} = \dfrac{\delta f_{K}}{f_{K}}= \dfrac{\delta \lambda^T_{Z}}{\lambda^T_{Z}}=\dfrac{\delta G^T_{ZJ/\psi K}}{G^T_{ZJ/\psi K}}$ ,$ \delta\,f_{J/\psi}f_{K}\lambda^T_{Z}G^T_{ZJ/\psi K} =f_{J/\psi}f_{K}\lambda^T_{Z}G^T_{ZJ/\psi K} \frac{4\delta G^T_{ZJ/\psi K}}{G^T_{ZJ/\psi K}} \, , $

(30) to avoid overestimating the uncertainty on the hadronic coupling constant. In calculations, we analogously estimate the uncertainties according to Eq. (30) and neglect uncertainties on the unknown parameters
$ C^T_{J/\psi K} $ ,$ C_{\eta_c K^*}^T $ ,$ C^T_{D^* \bar{D}_s} $ ,$ C^M_{J/\psi K} $ ,$ C^M_{\eta_c K^*} $ , and$ C^M_{D^* \bar{D}_s} $ , except in the case of$ \delta m_c(m_c) $ for$ C^M_{D^* \bar{D}_s} $ , for which we must consider the uncertainty to acquire a flat Borel platform.Now, we obtain the values of the hadronic coupling constants routinely.
$ \begin{aligned}[b] G^T_{ZJ/\psi K} =&1.79\pm0.10\,{\rm{GeV}}\, , \\ |G^T_{Z\eta_cK^*}|=&2.97\pm 0.22\;{\rm{GeV}}\, , \\ |G^T_{ZD^*\bar{D}_s}|=&0.71\pm0.04\;{\rm{GeV}}\, , \\ G^M_{ZJ/\psi K} =&1.23\pm0.07\;{\rm{GeV}}\, , \\ G^M_{Z\eta_c K^*}=&2.20\pm 0.16\;{\rm{GeV}}\, , \\ |G^M_{ZD^*\bar{D}_s}|=&9.60\pm1.27\;{\rm{GeV}}\, . \end{aligned} $

(31) Then, we choose the masses
$M_{K^-}=0.4937\;{\rm{GeV}}$ ,$M_{K^{*+}}=0.8917\;{\rm{GeV}}$ ,$M_{J/\psi}=3.0969\;{\rm{GeV}}$ ,$M_{\eta_c}=2.9834\;{\rm{GeV}}$ ,$M_{D^{*0}}=2.0069 \;{\rm{GeV}}$ ,$M_{D^{-}_s}=1.9690\;{\rm{GeV}}$ ,$M_{D^0}=1.8648 \;{\rm{GeV}}$ ,$M_{D^{*-}_s}=2.1122 \;{\rm{GeV}}$ [7], and$M_{Z_c}=3.99\;{\rm{GeV}}$ [19, 25] and obtain the partial decay widths$ \begin{aligned}[b] \Gamma(Z_{cs}^T\to J/\psi K^-)=&5.36\pm 0.60\;{\rm{MeV}} \, ,\\ \Gamma(Z_{cs}^T\to\eta_c K^{*-})=&9.54\pm 1.41\;{\rm{MeV}} \, , \\ \Gamma(Z_{cs}^T\to D^{*0} \bar{D}^-_s)=&0.21\pm 0.02\;{\rm{MeV}} \, ,\\ \Gamma(Z_{cs}^T\to D^0 \bar{D}^{*-}_s)=&0.20\pm 0.02\;{\rm{MeV}} \, , \end{aligned} $

(32) $ \begin{aligned}[b] \Gamma(Z_{cs}^M\to J/\psi K^-)=&2.53\pm 0.29\;{\rm{MeV}} \, ,\\ \Gamma(Z_{cs}^M\to\eta_c K^{*-})=&5.23\pm 0.76 \;{\rm{MeV}} \, , \\ \Gamma(Z_{cs}^M\to D^{*0} \bar{D}^-_s)=&38.69\pm 10.24\;{\rm{MeV}} \, ,\\ \Gamma(Z_{cs}^M\to D^0 \bar{D}^{*-}_s)=&37.06\pm 9.81\;{\rm{MeV}} \, , \end{aligned} $

(33) and total widths
$ \begin{aligned}[b] \Gamma_{Z_{cs}}^T =&15.31\pm 2.06\;{\rm{MeV}}\, ,\\ \Gamma_{Z_{cs}}^M =& 83.51\pm21.09\;{\rm{MeV}}\, , \end{aligned} $

(34) which are consistent with the experimental values from the BESIII collaboration,
$ 13.8^{+8.1}_{-5.2}\pm4.9\,{\rm{MeV}} $ [5], and LHCb collaboration,$ 131 \pm 15 \pm 26\,{\rm{MeV}} $ [6], respectively. There are two$ Z_{cs} $ states with analogous masses, as in the case of the$ Z_c^{\pm} $ states, and there is a tetraquark candidate$ Z_c(3900) $ and molecule candidate$ Z_c(3885) $ [26].The physical
$ Z_{cs} $ states may have both diquark-antidiquark type and color-singlet-color-singlet type tetraquark Fock components, and it is better to choose the mixing currents or more physical currents to interpolate them.$ J_\nu(x)=J^T_\nu(x)\,\cos\theta+J^M_\nu(x)\,\sin\theta\, , $

(35) where θ is the mixing angle. Both the currents
$ J^T_\nu(x) $ and$ J^M_\nu(x) $ can lead to a mass of approximately$ 3.99\pm 0.09\;{\rm{GeV}} $ if choosing the same constraints [19, 25]. The additional parameter θ does not significantly affect the predicted mass but can have a considerable effect on the predicted width. We can estimate the hadronic coupling constant G using the simple replacement$ G\to G^T\,\cos\theta+G^M\,\sin\theta\, , $

(36) and in the future, we may compare the predicted total widths and branching fractions with precise experimental data to estimate the mixing angle θ since the branching fractions have not yet been measured. The significance of
$ Z^{-}_{cs}(3985) $ is approximately$ 5.3 \, \sigma $ [5], whereas the significance of$ Z^{+}_{cs}(4000) $ is approximately$ 15\,\sigma $ [6]. Such large significances only suggest the existence of these resonance structures, and more experimental data are required even to unambiguously distinguish (and confirm)$ Z_{cs}(3985) $ and$ Z_{cs}(4000) $ . In this study, we can at least tentatively conclude that a larger color-singlet-color-singlet component in the$ Z_{cs} $ state leads to a larger decay width, and the$ Z_{cs}(3985) $ may have a large diquark-antidiquark type Fock component, whereas$ Z_{cs}(4000) $ may have a large color-singlet-color-singlet type Fock component. -
In this study, we explore the hadronic coupling constants
$ G_{ZJ/\psi K} $ ,$ G_{Z\eta_c K^*} $ , and$ G_{ZD^* \bar{D}_s} $ of the exotic states$ Z_{cs}(3985/4000) $ in the pictures of both the tetraquark and molecular states with the tentative assignments$ J^{PC}=1^{+-} $ based on rigorous quark-hadron duality. We present the three-point correlation functions and achieve operator product expansion up to the vacuum condensates of dimension-five, neglecting the tiny gluon condensate contributions, as in our previous studies. We obtain spectral densities through the dispersion relation and acquire rigorous quark-hadron duality below the continuum thresholds$ s_0 $ and$ u_0 $ by integrating over the variable$ ds^\prime $ to obtain six QCD sum rules for the hadronic coupling constants. We investigate the two-body strong decays of the axialvector tetraquark and molecular states, respectively, and obtain total widths of$\Gamma_{Z_{cs}}^T =15.31\pm 2.06\;{\rm{MeV}}$ and$\Gamma_{Z_{cs}}^M=83.51\pm21.09\;{\rm{MeV}}$ , which are consistent with the experimental values from the BESIII collaboration,$13.8^{+8.1}_{-5.2}\pm4.9\;{\rm{MeV}}$ , and LHCb collaboration,$131 \pm 15 \pm 26\;{\rm{MeV}}$ , respectively. The present calculations support assigning$ Z_{cs}(3985) $ and$ Z_{cs}(4000) $ as the hidden-charm tetraquark and molecular states with$ J^{PC}=1^{+-} $ , respectively. Alternatively, we may at least conclude that$ Z_{cs}(3985) $ has a large diquark-antidiquark type Fock component, whereas$ Z_{cs}(4000) $ has a large color-singlet-color-singlet type Fock component.
Decay widths of Zcs(3985/4000) based on rigorous quark-hadron duality
- Received Date: 2022-05-09
- Available Online: 2022-10-15
Abstract: In this study, we explore the hadronic coupling constants





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

























 DownLoad:
DownLoad: