-
The 2.8-second pulsar J0737-3039B is the companion of the 23-millisecond pulsar J0737-3039A. The two pulsars form a highly relativistic binary neutron star (NS) system [1], and the mass of the NS J0737-3039A should be related to the mass and metallicity of its companion [2]. The NS J0737-3039A has a mass M=1.34 M
$ _{\odot} $ , which is typical for NSs [1, 3, 4].Morrison et al. constructed a numerical model of the binary pulsar J0737-3039A using its measured mass, spin, and moment of inertia to determine the optimal model for different equations of state (EoS) so as to determine the radius of the pulsar. The NS they used, PSR J0737-3039A, has a gravitational mass M=1.337 M
$ _{\odot} $ [5]. In 2006, Kramer et al. more accurately determined the mass of the NS PSR J0737-3039A to be M = 1.3381±0.0007 M$ _{\odot} $ [6].In 2008, Worley et al. placed special emphasis on the PSR J0737-3039A component of the extremely relativistic double NS system PSR J0737-3039. They found its moment of inertia to be between 1.30
$ \times $ 10$ ^{45} $ $\rm g\cdot cm^{2} $ and 1.63$ \times $ 10$ ^{45} $ $\rm g\cdot cm^{2} $ [7]. Using well-known universal relations between NS observables, Landry et al. translated the reported 90%-credible bounds on tidal deformability into a direct constraint on the moment of inertia of PSR J0737-3039A [8].In 2020, Avdeev et al. developed a parameterized post-Keplerian formalism for hybrid metric-Palatini
$ f(R) $ -gravity and obtained the mass ratio$ M_{A}/M_{B} $ =1.0714. On this basis, they predicted the mass of the NS PSR J0737-3039A as 1.3374 M$ _{\odot}< $ $ M< $ 1.3440 M$ _{\odot} $ in the framework of hybrid$ f(R) $ -gravity [9].An NS has a high density, strong magnetic field, and high rotation speed [10–16]. Several massive NSs, PSR J1614-2230 [17, 18], PSR J0348+0432 [19], and PSR J0740+6620 [20], have been observed in recent years. Although the NS PSR J0737-3039A has a significantly smaller mass than these, its mass is typical, and it is a member of a binary NS system. Therefore, theoretical research on this NS is important.
NSs are formed by the neutrino radiation cooling of proto neutron stars (PNSs) [21]. Studying PNSs is vital for understanding the evolution of stars. Therefore, we are very interested in the PNS PSR J0737-3039A.
In this study, we investigate the properties of the PNS PSR J0737-3039A with relativistic mean field (RMF) theory [22] considering a baryon octet.
-
The mesons
$ f_{0}(975) $ (denoted as$ \sigma^{*} $ ) and$ \phi(1020) $ (denoted as ϕ) represent the interactions between nucleons and hyperons [23]. The Lagrangian density of hadronic matter containing the mesons$ \sigma^{*} $ and ϕ is expressed as follows [24]:$ \begin{aligned}[b] {\cal{L}}=&\sum\limits_{B}\overline{\Psi}_{ B}({\rm i}\gamma_{\mu}\partial^{\mu}-{m}_{B}+g_{\sigma B}\sigma+g_{\sigma^{*}B}\sigma^{*} \\ &-g_{\omega B}\gamma^{0}\omega-g_{\phi B}\gamma^{0}\phi-g_{\rho B}\gamma^{0}\tau_{3}\rho)\Psi_{ B} \\ &-\frac{1}{2}m_{\sigma}^{2}\sigma^{2}-\frac{1}{3}g_{2}\sigma^{3}-\frac{1}{4}g_{3}\sigma^{4}\\&+\frac{1}{2}m_{\omega}^{2}\omega^{2}+\frac{1}{2}m_{\rho}^{2}\rho^{2} -\frac{1}{2}m_{\sigma^{*}}^{2}\sigma^{*2}+\frac{1}{2}m_{\phi}^{2}\phi^{2} \\ &+\sum\limits_{\lambda=e,\mu}\overline{\Psi}_{ \lambda}\left({\rm i}\gamma_{\mu}\partial^{\mu} -m_{\lambda}\right)\Psi_{ \lambda} . \end{aligned} $

(1) Considering neutrino binding, the baryon partition function of PNS matter is [25, 26]
$ {\rm ln}Z_{B}=\frac{V}{T}\langle{\cal{L}}\rangle+\sum\limits_{B}\frac{2J_{B}+1}{2\pi^{2}}\int_{0}^{\infty}k^{2}{\rm d}k \left\{{\rm ln}\left[1+{\rm e}^{-(\varepsilon_{B}(k)-\mu_{B})/T}\right]\right\}. $

(2) From the above, the total baryon number density is obtained as follows:
$ \rho=\sum\limits_{B}\frac{2J_{B}+1}{2\pi^{2}}b_{B}\int_{0}^{\infty}k^{2}n_{B}(k){\rm d}k. $

(3) The energy density and pressure are respectively
$ \begin{aligned}[b] \varepsilon=&\frac{1}{2} m_{\sigma}^{2}\sigma^{2}+\frac{1}{2} m_{\sigma^{*}}^{2}\sigma^{*2}+\frac{1}{3}g_{2}\sigma^{3}\\&+\frac{1}{4}g_{3}\sigma^{4}+\frac{1}{2}m_{\omega}^{2}\omega_{0}^{2}+\frac{1}{2}m_{\phi}^{2}\phi^{2} +\frac{1}{2}m_{\rho}^{2}\rho_{03}^{2} \\ &+\sum\limits_{B}\frac{2J_{B}+1}{2\pi^{2}}\int_{0}^{\infty}k^{2}n_{B}(k)\mathrm {\rm d}k\sqrt{k^{2}+m_{B}^{*2}}, \end{aligned} $

(4) $ \begin{aligned}[b] p=&-\frac{1}{2}m_{\sigma}^{2}\sigma^{2}-\frac{1}{2}m_{\sigma^{*}}^{2}\sigma^{*2}-\frac{1}{3}g_{2}\sigma^{3} \\&-\frac{1}{4}g_{3}\sigma^{4}+\frac{1}{2}m_{\omega}^{2}\omega_{0}^{2}+\frac{1}{2}m_{\phi}^{2}\phi^{2} +\frac{1}{2}m_{\rho}^{2}\rho_{03}^{2} \\ &+\frac{1}{3}\sum\limits_{B}\frac{2J_{B}+1}{2\pi^{2}}\int_{0}^{\infty}\frac{k^{4}}{\sqrt{k^{2} +m_{B}^{*2}}}n_{B}(k){\rm d}k. \end{aligned} $

(5) Here,
$ n_{B}(k) $ is the Fermi-Dirac partition function of baryons,$ n_{B}(k)=\frac{1}{1+{\rm exp}\left[\left(\varepsilon_{B}(k)-\mu_{B}\right)/T\right]}, $

(6) and
$ m_{B}^{*} $ is the effective mass of baryons,$ \begin{array}{*{20}{l}} m_{B}^{*}=m_{B}-g_{\sigma B}\sigma-g_{\sigma^{*} B}\sigma^{*}. \end{array} $

(7) Ignoring the interactions of leptons at finite temperature, we express their partition function as
$ \begin{aligned}[b] {\rm ln}Z_{L}=&\frac{V}{T}\sum\limits_{i}\frac{\mu_{i}^{4}}{24\pi^{2}}\left[1+2\left(\frac{\pi T}{\mu_{i}}\right)^{2}+\frac{7}{15}\left(\frac{\pi T}{\mu_{i}}\right)^{4}\right] \\ &+V\sum\limits_{\lambda}\frac{1}{\pi^{2}}\int_{0}^{\infty}k^{2}{\rm d}k \left\{{\rm ln}\left[1+{\rm e}^{-(\varepsilon_{\lambda}(k)-\mu_{\lambda})/T}\right]\right\}, \end{aligned} $

(8) where the first line represents the contribution of massless neutrinos, and the second line represents the contribution of electrons and μs.
The lepton number density is
$ \rho_{l}=\frac{1}{\pi^{2}}\int_{0}^{\infty}k^{2}n_{l}(k){\rm d}k, $

(9) $ \rho_{\nu}=\frac{\pi^{2}T^{2}\mu_{\nu}+\mu_{\nu}^{3}}{6\pi^{2}} $

(10) and the contributions of leptons to the energy density and pressure are respectively
$ \begin{aligned}[b] \varepsilon=&\sum\limits_{l}\frac{1}{\pi^{2}}\int_{0}^{\infty}k^{2}n_{l}(k)\mathrm dk\sqrt{k^{2}+m_{l}^{2}}\\&+\sum\limits_{\nu}\left(\frac{7\pi^{2}T^{4}}{120}+\frac{T^{2}\mu^{2}_{\nu}}{4}+ \frac{\mu_{\nu}^{4}}{8\pi^{2}}\right), \end{aligned} $

(11) $ \begin{aligned}[b] p=&\frac{1}{3}\sum\limits_{l}\frac{1}{\pi^{2}}\int_{0}^{\infty}\frac{k^{4}}{\sqrt{k^{2} +m_{l}^{2}}}n_{l}(k){\rm d}k \\ &+\sum\limits_{\nu}\frac{1}{360}\left(7\pi^{2}T^{4}+30T^{2}\mu^{2}_{\nu}+ \frac{15\mu_{\nu}^{4}}{\pi^{2}}\right). \end{aligned} $

(12) The chemical potentials of baryons are
$ \begin{array}{*{20}{l}} \mu_{i}=\mu_{n}-q_{i}\left(\mu_{e}-\mu_{\nu e}\right). \end{array} $

(13) To describe neutrino trapping, the content of leptons in a PNS is defined as
$ Y_{l \nu}=Y_{l}+Y_{\nu l}=\frac{\rho_{l}+\rho_{\nu l}}{\rho}. $

(14) We can calculate the mass and radius of a PNS using the Tolman-Oppenheimer-Volkoff (TOV) equations [27, 28]
$ \frac{\mathrm dp}{\mathrm dr}=-\frac{\left(p+\varepsilon\right)\left(M+4\pi r^{3}p\right)}{r \left(r-2M \right)} , $

(15) $ M=4\pi\int_{0}^{R}\varepsilon r^{2}\mathrm dr . $

(16) -
Here, we calculate the parameters of the PNS PSR J0737-3039A with five sets of nucleon coupling constants (DD-MEI [29], GL85 [30], GL97 [24], GM1 [31], and NL2 [32]). For the outer crust with
$ 4.73\times 10^{-15} $ $ <\rho<8.907\times 10^{-3} $ fm$ ^{-3} $ , we use the EoS of a BPS [24], and for the region of$ \rho>8.907\times 10^{-3} $ fm$ ^{-3} $ , we use the EoS for PNS matter corresponding to the nuclear properties above.The ratios of the hyperon coupling constant to nucleon coupling constant are defined as
$x_{\sigma h}={g_{\sigma h}}/{g_{\sigma}}$ ,$x_{\omega h}= {g_{\omega h}}/{g_{\omega}}$ , and$x_{\rho h}={g_{\rho h}}/{g_{\rho}}$ , with h denoting the hyperons$ \Lambda, \Sigma $ , and Ξ.$ x_{\rho h} $ and$ x_{\omega h} $ are chosen using SU(6) symmetry [33, 34]. Then,$ x_{\sigma h} $ is obtained using [24]$ U_{h}^{(N)}=m_{n}\left(\frac{m_{n}^{*}}{m_{n}}-1\right)x_{\sigma h}+\left(\frac{g_{\omega}}{m_{\omega}}\right)^{2}\rho_{0}x_{\omega h} . $

(17) In this study, the hyperon-potentials are chosen as
$ U_{\Lambda}^{(N)}=-30 $ MeV [34, 35, 36],$ U_{\Sigma}^{(N)} $ =30 MeV [34, 35, 36, 37], and$ U_{\Xi}^{(N)}=-14 $ MeV [38].The coupling constants of the mesons
$ \sigma^{*} $ and ϕ can be chosen as [23]$ \begin{array}{*{20}{l}} g_{\phi \Xi}=2g_{\phi \Lambda}=2g_{\phi \Sigma}=-2\sqrt{2}g_{\omega}/3 , \end{array} $

(18) $\quad\quad \;\;\;\begin{array}{*{20}{l}} \ g_{\sigma^{*} \Lambda}/g_{\sigma}=g_{\sigma^{*} \Sigma}/g_{\sigma}=0.69 , \end{array} $

(19) $ \quad\quad \;\;\;\begin{array}{*{20}{l}} \ g_{\sigma^{*} \Xi}/g_{\sigma}=1.25 . \end{array} $

(20) Temperatures in the interiors of PNSs can reach up to 30 MeV. After that, they can be cooled by neutrino radiation [21]. In this study, the temperature of the PNS PSR J0737-3039A is taken as T=20 MeV.
-
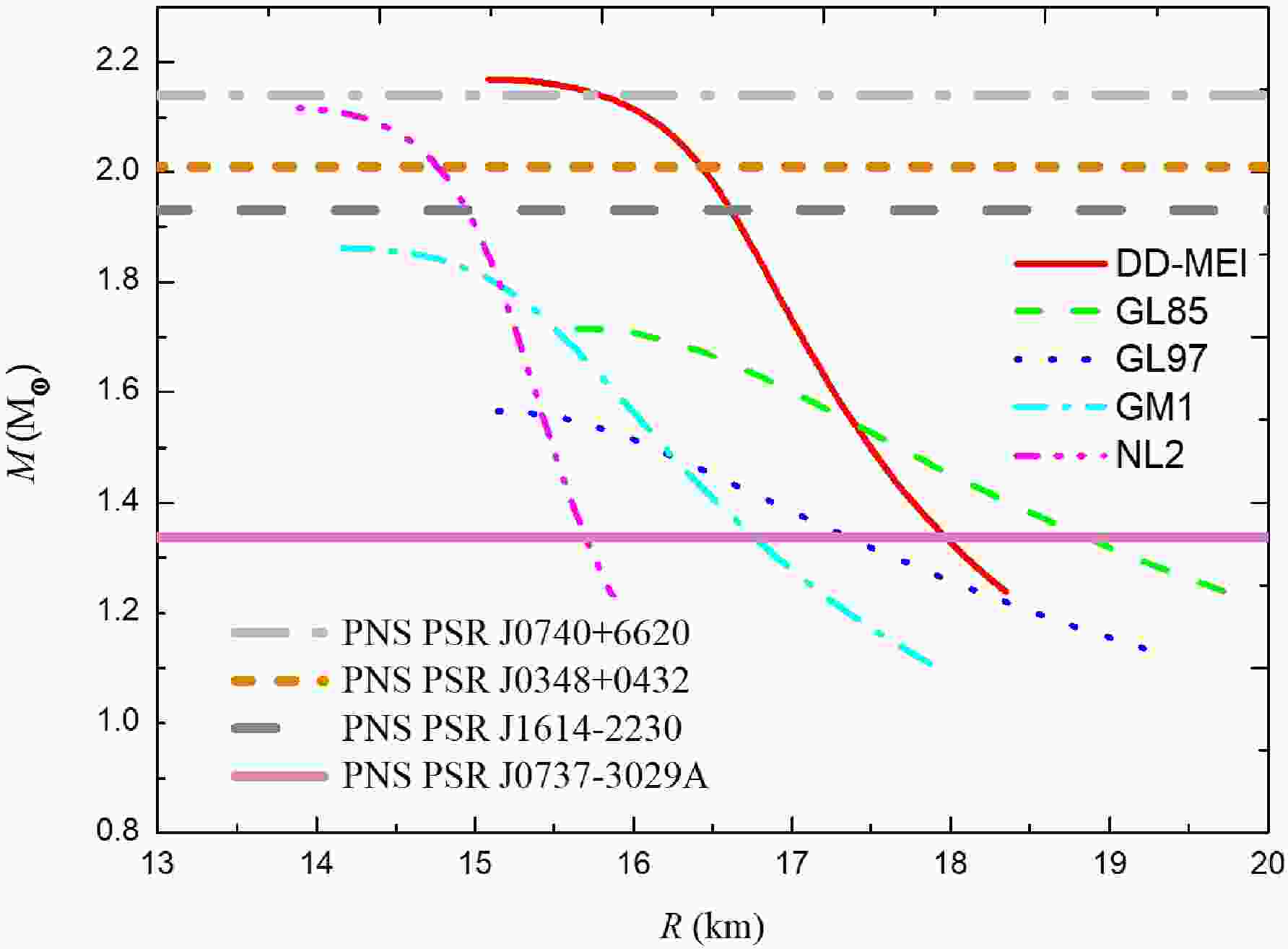
The mass M of the PNS is calculated as a function of the radius R. In Fig. 1, the coarse curves indicate the masses of the PNSs PSR J0740+6620, PSR J0348+0432, PSR J1614-2230, and PSR J0737-3039A, and the five fine curves represent the results of the five nucleon coupling constants DD-MEI, GL85, GL97, GM1, and NL2. We find that only the nucleon coupling constant DD-MEI can give the masses of the PNSs PSR J0740+6620, PSR J0348+0432, PSR J1614-2230, and PSR J0737-3039A. NL2 cannot give the mass of the PNS PSR J0740+6620; however, it can give the mass of the PNSs PSR J0348+0432, PSR J1614-2230, and PSR J0737-3039A. GL85, GL97, and GM1 cannot give the masses of the PNSs PSR J0740+6620, PSR J0348+0432, and PSR J1614-2230; however, they can give the masses of the PNS PSR J0737-3039A. All five sets of nucleon coupling constants give the masses of the PNS PSR J0737-3039A.
As shown in Fig. 1 and Table 1, the radii of the PNS PSR J0737-3039A given by the five sets of nucleon coupling constants are different. NL2 gives the smallest radius, R=15.693 km, and GL85 gives the largest radius, R=18.846 km. In other words, the radius of the PNS PSR J0737–3039A calculated using these five sets of nucleon coupling constants is R=15.693–18.846 km. The NS PSR J0030+0451 has a mass similar to that of the PNS PSR J0737-3039A; hence, it is logical to compare their radii. The mass and radius of the NS PSR J0030+0451 given by Riley et al. are in the ranges M=1.18–1.49 M
$ _{\odot} $ and R=11.52–13.85 km [39], respectively, and those given by Miller et al. are M=1.30–1.59 M$ _{\odot} $ and R=11.96–14.26 km, respectively [40]. The PNS radius calculated in this study is larger than that calculated by Riley et al. and Miller et al., which is reasonable because the radius of a PNS is larger than that of an NS of the same mass [41].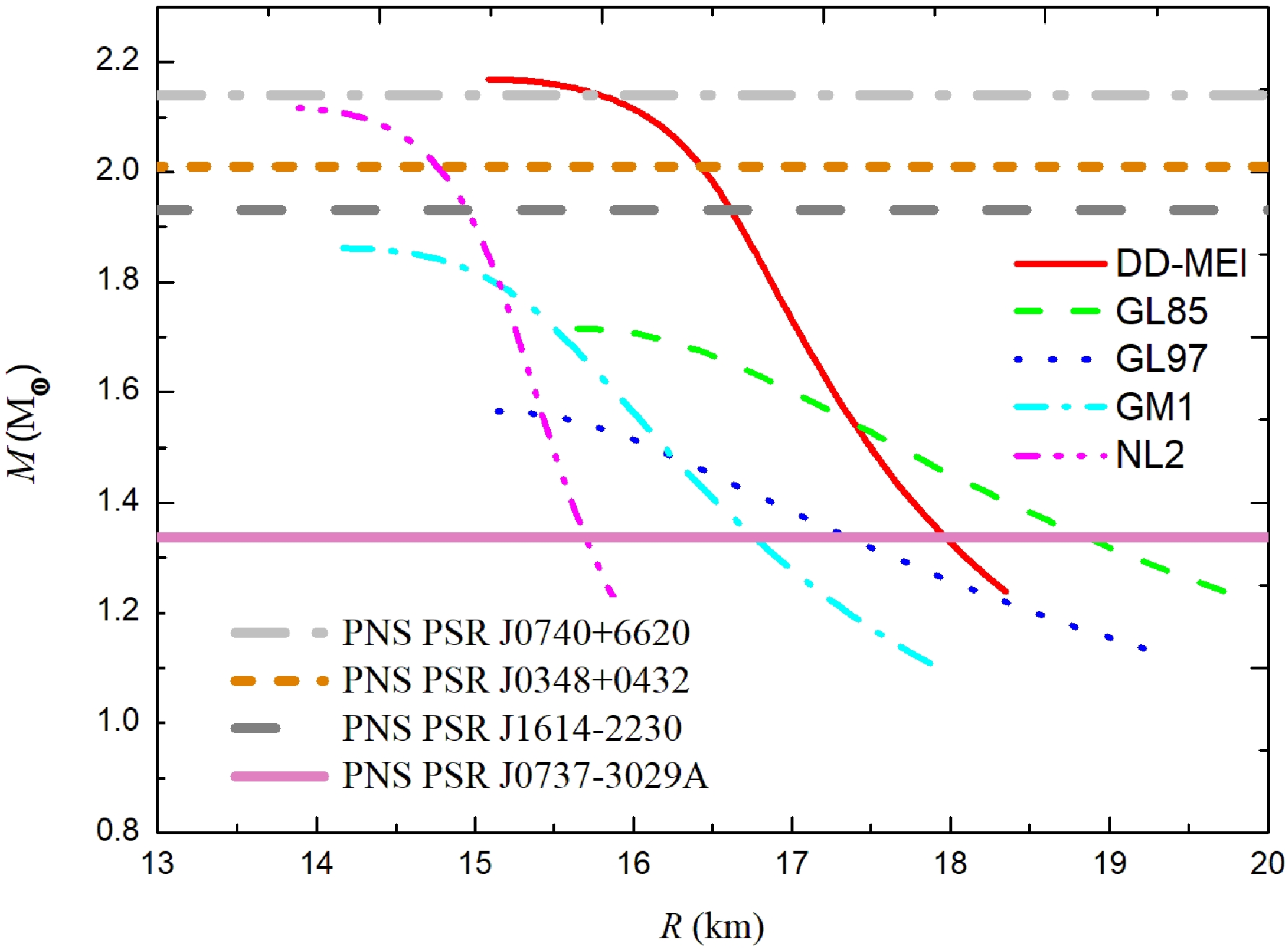
Figure 1. (color online) Mass M of the PNS calculated as a function of the radius R. The coarse curves indicate the masses of the PNSs PSR J0740+6620, PSR J0348+0432, PSR J1614-2230, and PSR J0737-3039A. The five fine curves represent the results of the five nucleon coupling constants DD-MEI, GL85, GL97, GM1, and NL2.
Parameter R/km $\rho_{\rm c}/{\rm{fm} }^{-3}$ 

$\varepsilon_{\rm c}\times 10^{15}/({\rm g}\cdot {\rm{cm} })^{-3}$ 

$ p_{\rm c} \times 10^{35} /({\rm{dyne}}\cdot {\rm{cm}})^{-2} $ 

DD-MEI 18.006 0.247 0.430 0.379 GL85 18.846 0.290 0.519 0.427 GL97 17.353 0.359 0.649 0.585 GM1 16.798 0.310 0.545 0.506 NL2 15.693 0.293 0.508 0.506 Table 1. Results calculated in this study. The mass of the PNS PSR J0737-3039A is M=1.338 M
$ _{\odot} $ . R,$ \rho_{\rm c} $ ,$ \varepsilon_{\rm c} $ , and$ p_{\rm c} $ are the radius, central baryon density, central energy density, and central pressure of the PNS PSR J0737-3039A, respectively.The central baryon densities
$ \rho_{\rm c} $ of the PNS PSR J0737-3039A calculated with different nucleon coupling constants are different.$ \rho_{\rm c} $ of the PNS PSR J0737-3039A calculated using GL97 is the largest,$ \rho_{\rm c} $ =0.359 fm$ ^{-3} $ , whereas$ \rho_{\rm c} $ calculated using DD-MEI is the smallest,$ \rho_{\rm c} $ =0.247 fm$ ^{-3} $ . That is, the central baryon density calculated using the five nucleon coupling constants is$ \rho_{\rm c} $ =0.247–0.359 fm$ ^{-3} $ . -
The effective mass of nucleons, Λ, Σ, and Ξ as a function of the baryon density ρ are shown in Fig. 2. We denote the center effective mass of nucleons, Λ, Σ, and Ξ as
$ m^{*}_{N c} $ ,$ m^{*}_{\Lambda c} $ ,$ m^{*}_{\Sigma c} $ , and$ m^{*}_{\Xi c} $ , respectively. As shown in Fig. 2, the effective masses of nucleons, Λ, Σ, and Ξ all decrease with increasing baryon density ρ. At the center of the PNS, the effective mass of the baryon reaches a minimum. Corresponding to the same baryon density ρ, the effective mass calculated using DD-MEI is the smallest, whereas that calculated using GL97 is the largest. As shown in Table 2, the center effective masses of nucleons, Λ, Σ, and Ξ calculated using the above five groups of nucleon coupling constants are$ m^{*}_{N c} $ =384.521–606.324 MeV,$ m^{*}_{\Lambda c} $ =778.280–911.405 MeV,$ m^{*}_{\Sigma c} $ =939.187–1080.822 MeV, and$ m^{*}_{\Xi c} $ =1152.637–1218.964 MeV, respectively.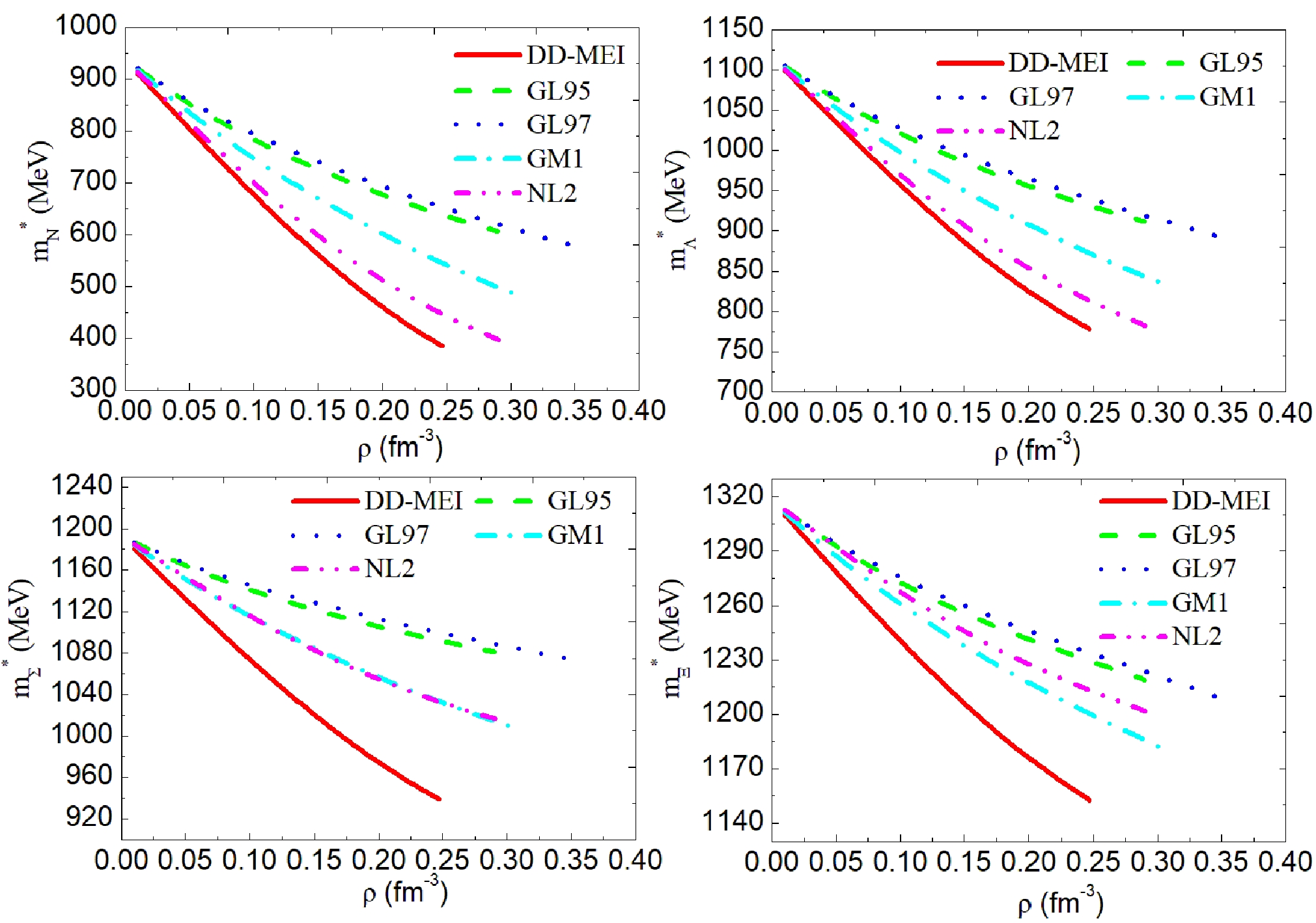
Figure 2. (color online) Effective mass of baryons in the PNS PSR J0737-3039A as a function of baryon density. The five curves represent the results of the five nucleon coupling constants DD-MEI, GL85, GL97, GM1, and NL2.
Parameter $ m^{*}_{N c}/{\rm{MeV}} $ 

$ m^{*}_{\Lambda c}/{\rm{MeV}} $ 

$ m^{*}_{\Sigma c}/{\rm{MeV}} $ 

$ m^{*}_{\Xi c}/{\rm{MeV}} $ 

$ \mu_{nc}/{\rm{fm}}^{-1} $ 

$ \mu_{ec} /{\rm{fm}}^{-1}$ 

DD-MEI 384.521 778.280 939.187 1152.637 5.340 0.721 GL85 606.324 911.405 1080.822 1218.964 5.421 0.943 GL97 573.011 888.351 1071.635 1206.096 5.516 0.989 GM1 478.656 831.015 1006.070 1179.389 5.418 0.763 NL2 394.604 780.860 1015.662 1200.968 5.367 0.829 Table 2. Effective mass of baryons and the chemical potentials of n and e in the PNS PSR J0737-3039A calculated in this study.
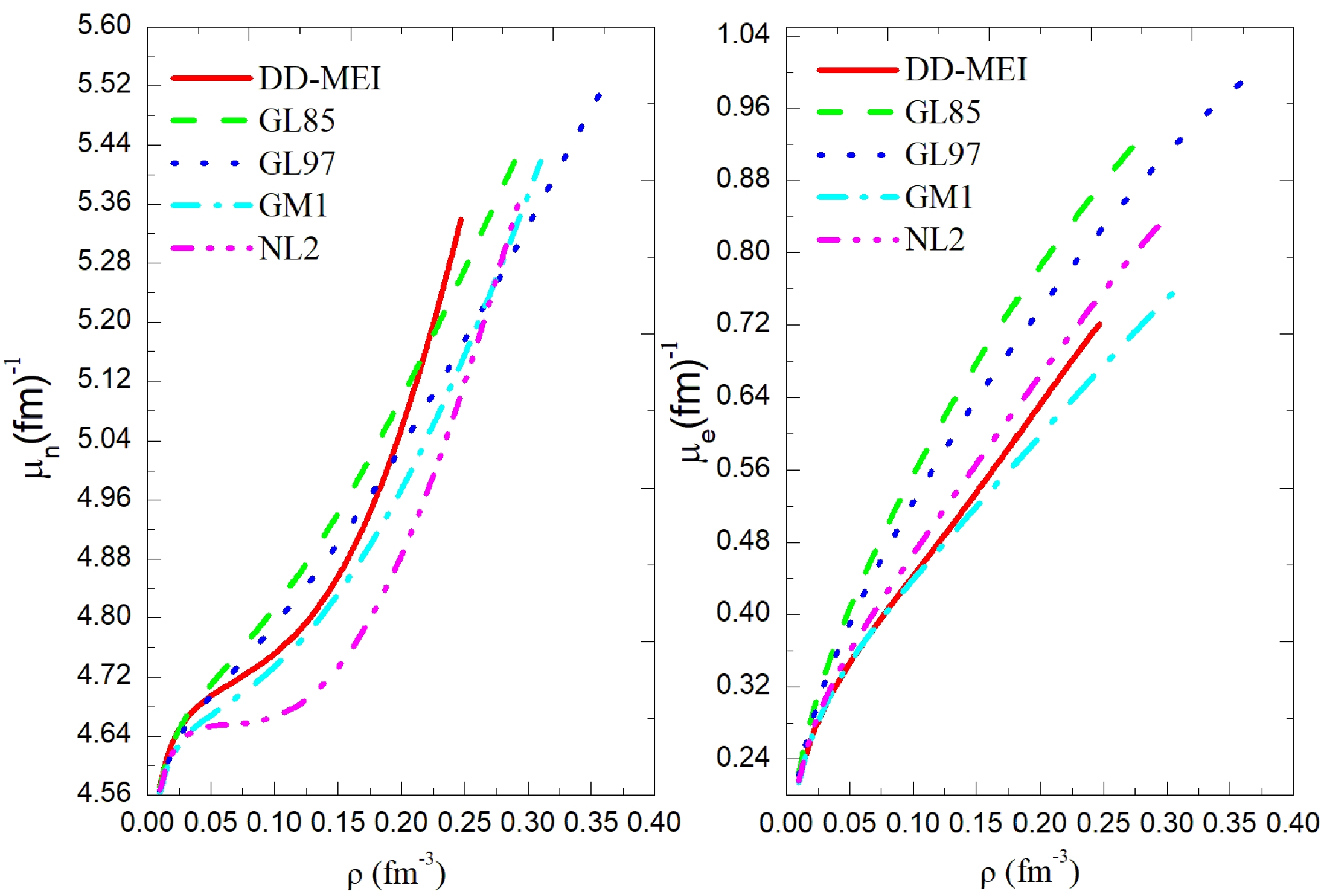
$ m^{*}_{N c} $ ,$ m^{*}_{\Lambda c} $ ,$ m^{*}_{\Sigma c} $ , and$ m^{*}_{\Xi c} $ are the center effective masses of nucleons N, Λ, Σ, and Ξ, respectively.$ \mu_{nc} $ and$ \mu_{ec} $ are central chemical potentials of n and e, respectively.The chemical potentials of neutrons and electrons are shown in Fig. 3. The chemical potentials of neutrons
$ \mu_{n} $ and electrons$ \mu_{e} $ increase with increasing baryon density ρ. Different nucleon coupling constants result in different chemical potentials relative to the same baryon density ρ. The central neutron chemical potential of the five nucleon coupling constants is calculated as$ \mu_{nc} $ =5.340–5.516 fm$ ^{-1} $ , and the central electron chemical potential is calculated as$ \mu_{ec} $ =0.721–0.989 fm$ ^{-1} $ . -
The energy density ε and pressure p in the PNS PSR J0737-3039A as a function of the baryon density ρ are shown in Fig. 4. Both the energy density ε and pressure p increase with increasing baryon density ρ. Corresponding to the same baryon density ρ, the energy densities calculated using different nucleon coupling constants have little difference; however, the calculated pressures differ greatly. The central energy density and central pressure calculated for the five sets of nucleon coupling constants are different. GL97 results in the maximum center energy density and center pressure.
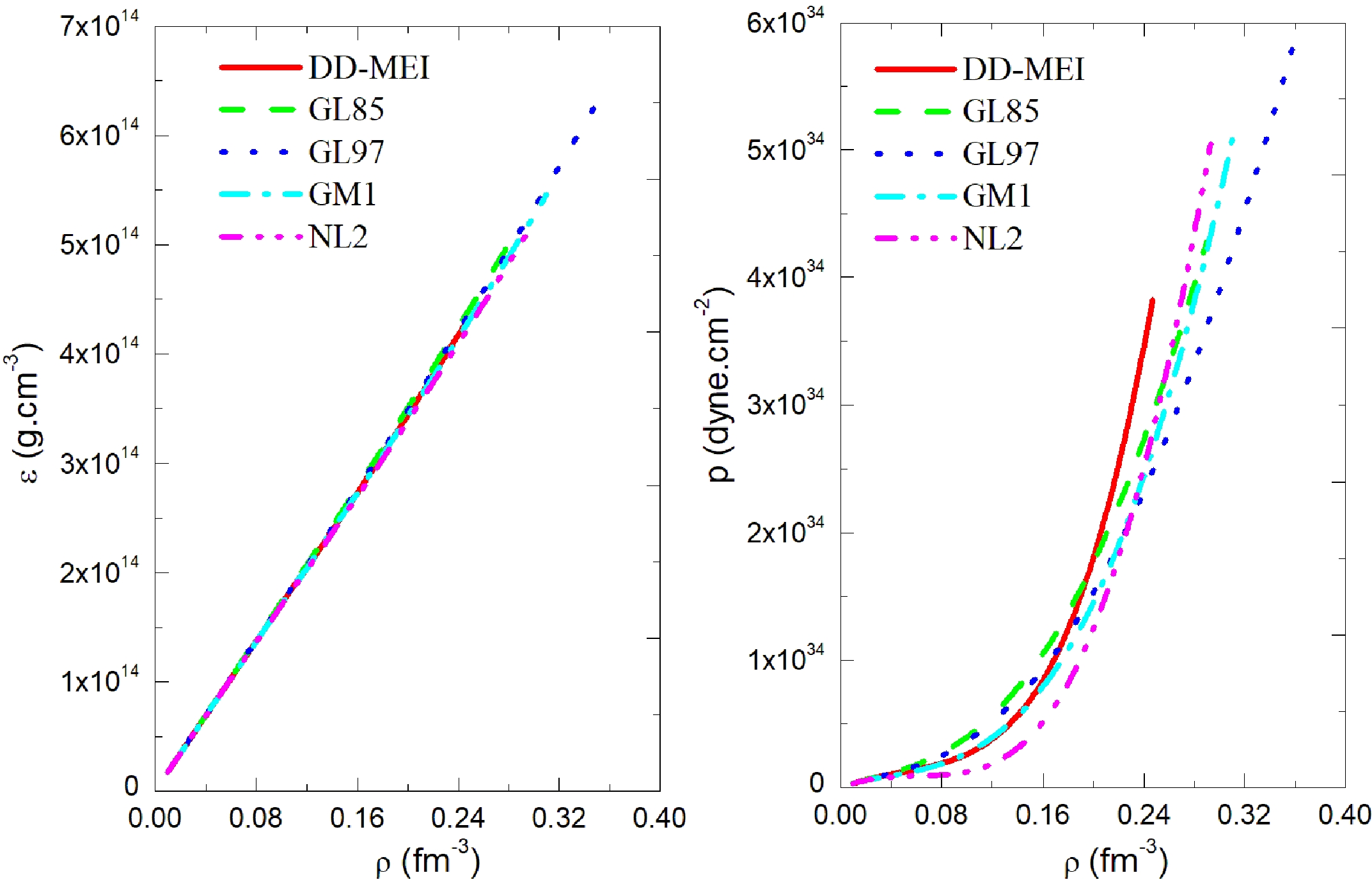
Figure 4. (color online) Energy density and pressure in the PNS PSR J0737-3039A as a function of baryon density. The five curves represent the results of the five nucleon coupling constants DD-MEI, GL85, GL97, GM1, and NL2.
As shown in Table 1, the minimum central energy density given with DD-MEI is
$ \varepsilon_{\rm c} $ =4.30$ \times $ 10$ ^{14} $ $\rm g\cdot cm^{-3} $ . GL97 gives the largest central energy density,$ \varepsilon_{\rm c} $ =6.49$ \times $ 10$ ^{14} $ $ \rm g\cdot cm^{-3} $ . The central energy density calculated from the five nucleon coupling constants is$ \varepsilon_{\rm c} $ =4.30$ \times $ 10$ ^{14} $ –6.49$ \times $ 10$ ^{14} $ $\rm g\cdot cm^{-3} $ . Similarly, the central pressure calculated using the five nucleon coupling constants is$ p_{\rm c} $ =3.79$ \times $ 10$ ^{34} $ –5.85$ \times $ 10$ ^{34} $ $\rm dyne\cdot cm^{-2} $ . -
Figure 5 shows the relative particle density
$ \rho_{i}/\rho $ in the PNS PSR J0737-3039A as a function of the baryon density ρ.
Figure 5. (color online) Relative particle density in the PNS PSR J0737-3039A as a function of baryon density. The five curves represent the results of the five nucleon coupling constants DD-MEI, GL85, GL97, GM1, and NL2.
As shown in Fig. 5 and Table 3, baryons n, p, Λ,
$ \Sigma^{+} $ ,$ \Sigma^{0} $ ,$ \Sigma^{-} $ ,$ \Xi^{0} $ and$ \Xi^{-} $ all appear in the PNS PSR J0737-3039A when using the nucleon coupling constants DD-MEI, GL85, GL97, and GM1. However, with NL2, only baryons n, p, Λ,$ \Sigma^{0} $ ,$ \Sigma^{-} $ ,$ \Xi^{0} $ , and$ \Xi^{-} $ are present, while baryon$ \Sigma^{+} $ is absent.Parameter $ \rho_{nc}/\rho \;{\text%}$ 

$ \rho_{pc}/\rho \;{\text%}$ 

$ \rho_{\Lambda c}/\rho \;{\text%}$ 

$ \rho_{\Sigma^{+}c}/\rho \;{\text%}$ 

$ \rho_{\Sigma^{0}c}/\rho \;{\text%}$ 

$ \rho_{\Sigma^{-}c}/\rho \;{\text%}$ 

$ \rho_{\Xi^{0}c}/\rho \;{\text%}$ 

$ \rho_{\Xi^{-}c}/\rho \;{\text%}$ 

DD-MEI 90.7 8.8 0.5 1E-6 2.0E-4 0.04 5.1E-5 0.02 GL85 81.0 17.5 1.5 2.9E-3 4.0E-4 5.7E-5 1.3E-3 0.05 GL97 80.5 16.5 2.8 1.3E-3 4.1E-4 1.3E-4 2.4E-3 0.18 GM1 90.7 8.4 0.8 2E-6 1.8E-4 0.02 1.07E-4 0.05 NL2 87.5 11.5 1.0 0 1.3E-5 5.2E-4 1.5E-5 5.8E-3 Table 3. Central relative particle densities in the PNS PSR J0737-3039A.
$ \rho_{nc}/\rho $ ,$ \rho_{pc}/\rho $ ,$ \rho_{\Lambda c}/\rho $ ,$ \rho_{\Sigma^{+} c}/\rho $ ,$ \rho_{\Sigma^{0}c}/\rho $ ,$ \rho_{\Sigma^{-}c}/\rho $ ,$ \rho_{\Xi^{0}c}/\rho $ , and$ \rho_{\Xi^{-}c}/\rho $ are the central relative particle densities of n, p, Λ,$ \Sigma^{+} $ ,$ \Sigma^{0} $ ,$ \Sigma^{-} $ ,$ \Xi^{0} $ , and$ \Xi^{-} $ , respectively, in the PNS PSR J0737-3039A.As shown in Fig. 5, corresponding to the same baryon density, the relative particle densities of the same baryon in the PNS PSR J0737-3039A calculated using different nucleon coupling constants differ greatly. As shown in Table 3, the central relative baryon densities of the PNS PSR J0737-3039A calculated using different nucleon coupling constants also differ greatly. For example, for hyperon Λ, the minimum central relative baryon density given using DD-MEI is
$ \rho_{\Lambda c}/\rho $ =0.5%, whereas GL97 gives the largest central baryon density,$ \rho_{\Lambda c}/\rho $ =2.8%. In other words, the central baryon density of the Λ-hyperon calculated using the five nucleon coupling constants is$ \rho_{\Lambda c}/\rho $ =0.5%–2.8%. Similarly, the central baryon density of n calculated using five groups of nucleon coupling constants is$ \rho_{nc}/\rho $ =80.5%–90.7%, the central baryon density of p is$ \rho_{pc}/\rho $ =8.4%–17.5%, the central baryon density of the$ \Sigma^{0} $ hyperon is$ \rho_{\Sigma^{0}c}/\rho $ =1.3$\times$ 10$ ^{-3} $ %–4.1$ \times $ 10$ ^{-4} $ %, the central baryon density of the$ \Sigma^{-} $ hyperon is$ \rho_{\Sigma^{-}c}/\rho $ =5.7$ \times $ 10$ ^{- 5} $ %–0.04%, the central baryon density of the$ \Xi^{0} $ hyperon is$ \rho_{\Xi^{0}c}/\rho $ =1.5$ \times $ 10$ ^{- 5} $ %–2.4$ \times $ 10$ ^{-3} $ %, and the central baryon density of the$ \Xi^{-} $ hyperon is$ \rho_{\Xi^{-}c}/\rho $ =5.8×10$ ^{-3} $ %–0.18%. The hyperon$ \Sigma^{+} $ in the PNS PSR J0737-3039A calculated using NL2 does not appear, whereas the central baryon density of$ \Sigma^{+} $ calculated using DD-MEI, GL85, GL97, and GM1 is$ \rho_{\Sigma^{+}c}/\rho $ =1.0$ \times $ 10$ ^{-6} $ %–2.9$ \times $ 10$ ^{-3} $ %. -
In this study, the influence of nucleon coupling constants on the properties of the PNS PSR J0737-3039A is investigated using RMF theory. Here, five sets of nucleon coupling constants (DD-MEI, GL85, GL97, GM1, and NL2) are used, and the temperature of the PNS PSR J0737-3039A is chosen as T=20 MeV.
The radius R, central baryon density
$ \rho_{\rm c} $ , central energy density$ \varepsilon_{\rm c} $ , and central pressure$ p_{\rm c} $ of the PNS PSR J0737-3039A calculated using different nucleon coupling constants are different. Using these five sets of nucleon coupling constants, we find that the radius of the PNS PSR J0737-3039A is R=15.693–18.846 km, the central baryon density is$ \rho_{\rm c} $ =0.247–0.359 fm$ ^{-3} $ , the central energy density is$ \varepsilon_{\rm c} $ =4.30$ \times $ 10$ ^{14} $ –6.49$ \times $ 10$ ^{14} $ $\rm g\cdot cm^{-3} $ , and the central pressure is$ p_{\rm c} $ =3.79$ \times $ 10$ ^{34} $ –5.85$ \times $ 10$ ^{34} $ $\rm dyne\cdot cm^{-2} $ . Although the PNS radius should be larger than that of an NS of the same mass, it should not be significantly larger. As shown in Table 1, the radius of the PNS PSR J0737-3039A calculated using the nucleon coupling constant NL2 is the smallest, R=15.693 km, and is closest to the radius calculated by Riley et al. and Miller et al. Therefore, NL2 seems to be the most reasonable coupling constant.For four sets of nucleon coupling constants (DD-MEI, GL85, GL97 and GM1), baryons n, p, Λ,
$ \Sigma^{+} $ ,$ \Sigma^{0} $ ,$ \Sigma^{-} $ ,$ \Xi^{0} $ , and$ \Xi^{-} $ all appear in the PNS PSR J0737-3039A. However, using NL2, only baryons n, p, Λ,$ \Sigma^{0} $ ,$ \Sigma^{-} $ ,$ \Xi^{0} $ , and$ \Xi^{-} $ are present, while baryon$ \Sigma^{+} $ does not appear.Corresponding to the same baryon density, the relative densities of the same baryon in the PNS PSR J0737-3039A calculated using different nucleon coupling constants differ greatly. The central relative baryon densities of the PNS PSR J0737-3039A calculated using different nucleon coupling constants also differ greatly. The central baryon density of n calculated using the five groups of nucleon coupling constants is
$ \rho_{nc}/\rho $ =80.5%–90.7%, the central baryon density of p is$ \rho_{pc}/\rho $ =8.4%–17.5%, the central baryon density of Λ is$ \rho_{\Lambda c}/\rho $ =0.5%–2.8%, the central baryon density of the$ \Sigma^{0} $ hyperon is$ \rho_{\Sigma^{0}c}/\rho $ =1.3$ \times $ 10$ ^{-3} $ %–4.1$ \times $ 10$ ^{-4} $ %, the central baryon density of the$ \Sigma^{-} $ hyperon is$ \rho_{\Sigma^{-}c}/\rho $ =5.7$ \times $ 10$ ^{- 5} $ %–0.04%, the central baryon density of the$ \Xi^{0} $ hyperon is$ \rho_{\Xi^{0}c}/\rho $ =1.5$ \times $ 10$ ^{- 5} $ %–2.4$ \times $ 10$ ^{-3} $ %, and the central baryon density of the$ \Xi^{-} $ hyperons is$ \rho_{\Xi^{-}c}/\rho $ =5.8$ \times $ 10$ ^{-3} $ %–0.18%. The hyperon$ \Sigma^{+} $ does not appear with NL2, whereas the central baryon density of hyperon$ \Sigma^{+} $ calculated using DD-MEI, GL85, GL97, and GM1 is$ \rho_{\Sigma^{+}c}/\rho $ =1.0$ \times $ 10$ ^{-6} $ %–2.9$ \times $ 10$ ^{-3} $ %.
Properties of proto neutron star PSR J0737-3039A
- Received Date: 2022-04-30
- Available Online: 2022-10-15
Abstract: Using five sets of nucleon coupling constants (DD-MEI, GL85, GL97, GM1, and NL2), we find that the radius of the PNS PSR J0737-3039A is R=15.693–18.846 km, the central baryon density is





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



























 DownLoad:
DownLoad: