Proton-neutron symplectic model description of ²⁰Ne

The microscopic description of the properties of atomic nuclei is a longstanding challenge in nuclear structure physics. A general microscopic framework for the study of nuclear collective motion is provided by the nuclear shell model, which includes all many-particle fermion degrees of freedom. Unfortunately, the dimension of the model space grows rapidly with the increase in the number of the nucleons or/and the available single particle states included in the model calculation, even when the valence shell is solely considered. Accordingly, several submodels of the shell model have been constructed to reduce the number of states as well as the computational difficulty. In particular, the algebraic models formulated in terms of spectrum generating algebras and dynamical groups, are remarkable. These shell-model submodels describe more of the physical structure of states in terms of well-defined quantum numbers.

The corner-stone of the spherical harmonic oscillator shell model is provided by the $SU(3)$ algebraic structure of the three-dimensional harmonic oscillator, first proposed in nuclear physics by Elliott [1] in 1958, which is present as a building block in all sophisticated algebraic models proposed during the time for the description of the nuclear structure. The $SU(3)$ classification scheme of the many-particle nuclear states allows us to answer whether these states are indeed eigenfunctions of a realistic Hamiltonian for a given real nucleus.

Various shell-model classification schemes are most easily applied to the light nuclei, where the size of the model space is considerably smaller than in the case of intermediate and heavy mass nuclei. From the light nuclei, ²⁰Ne is a typical example of a well-deformed (prolate) nucleus from the $ds$ shell, exhibiting rotational bands with enhanced quadrupole collectivity. Despite the well-pronounced collective character, the different microscopic shell-model calculations indicate the complicated structure of the observed rotational bands in ²⁰Ne. Hence, this nucleus serves as a good example that can be used to test the different collective models of nuclear structure.

The first microscopic approach that demonstrated how collective properties can emerge from the underlying shell-model structure was provided by the Elliott $SU(3)$ model [1] applied to the light $ds$ nuclei. Since then, various shell-model calculations have been performed to establish the microscopic structure of the low-lying states in this nucleus. From the early studies (refer to a review paper by Harvey [2]), we mention a study by Akiyama, Arima, and Sebe [3], in which the shell-model calculations have been performed for some $ds$-shell nuclei using a phenomenological effective interaction of the central Yukawa type. It has been demonstrated that the $SU(3)$ multiplets $(8,0)$ and $(6,1)$, with corresponding space symmetry [4] and [31], and exhaust up to 95% of the ground state band structure. The dominant $SU(3)$ component is given by the $(8,0)$ multiplet and is approximately 80%-90% for different angular momentum states within the ground band.

From the more recent shell-model calculations, we point out the calculations performed by Rosensteel and Rowe [4], which explore the competition between the $SU(3)$ and pair shell-model coupling schemes in the $ds$ nuclear shell model. They considered a model Hamiltonian consisting of $\widetilde{Q}\cdot \widetilde{Q}$ interactions and an $L = 0$ $SO(6)$ pairing term that breaks the $SU(3)$ symmetry. The $SO(6)$ term actually introduces a horizontal mixing of different $SU(3)$ multiplets within the $sd$ shell. They considered the rotational states of the ground and first two β bands in ²⁰Ne. The results indicated that the $6^{+}_{1}$ and $8^{+}_{1}$ states of the ground state band have a pure $SU(3)$ symmetry determined by the $(8,0)$ representation. The three remaining lowest $0^{+}_{1}, 2^{+}_{1}, 4^{+}_{1}$ states exhibit a significant $SU(3)$ mixing of the $(8,0)$, $(4,2)$, and $(0,4)$ irreps, which in contrast to the pure $SU(3)$ case produces nonzero interband electric quadrupole transitions. Among the six observed interband $B(E2)$ transition probabilities [4, 5], four were found in qualitative agreementwith the usage of an effective charge. This supports the used physical picture of the $SU(3)$ mixing created by the $SO(6)$ Casimir operator, which is qualitatively correct. The results obtained in [4] demonstrate that the low-energy rotational states in the three lowest positive-parity bands in ²⁰Ne lie close to the critical point of a quantum phase transition, where the pairing and quadrupole interactions compete with each other, thereby confirming its complex rotational character.

The Elliott $SU(3)$ shell model [1, 2] has clearly demonstrated that the rotational bands of states is obtained by using the in-shell quadrupole-quadrupole interaction $\widetilde{Q}\cdot \widetilde{Q}$, which is actually expressed using the second-order Casimir operators of the $SU(3)$ and $SO(3)$ groups. Because Elliott's (truncated) quadrupole operator $\widetilde{Q}_{2M}$ has vanishing matrix elements between the shell-model states from different major shells, an effective charge should be used in the calculations. Hence, the $SU(3)$ shell model can be considered as a projected in-shell image of the rigid rotor model [6], which includes the full major-shell-mixing quadrupole operator $Q_{2M}$ among its generators. Therefore, if the latter is included to the set of angular momentum operators, i.e. replacing $\widetilde{Q}_{2M}$ by $Q_{2M}$, the so-called (one-component) symplectic $Sp(6,R)$ model [7] can be obtained, which is a multi-major-shell extension of the Elliott $SU(3)$ model, that contains the latter as a submodel. The advantage of the $Sp(6,R)$ model, owing to the mixing of various shell-model states from different major shells (vertical mixing), is that it allows the observed enhanced quadrupole collectivity to be achieved without the introduction of an effective charge.

The first $Sp(6,R)$ model calculation for the rotational states of low-lying states of the ground state band in ²⁰Ne has already been given in [8], using a phenomenological Hamiltonian comprising a harmonic oscillator and collective potential, which is expressed as a polynomial, up to the fourth degree in the mass quadrupole moment operators. The shell-model calculations within the framework of the $Sp(6,R)$ model indicated that the dominant contribution to the microscopic structure of the ground band states is provided by the so-called stretched states, which are $SU(3)$ states of the type $(\lambda_{0}+2n,\mu_{0})$ with $n = 0,1,2,\ldots$ [9]. In particular, 90% of the $^{20}{\rm Ne}$ ground state originates from the $(8,0)$, $(10,0)$, and $(12,0)$ stretched states [8]. The results exhibited excessive collectivity compared to the experimental data.

A more realistic Hamiltonian with a pairing and single-particle energy symplectic symmetry-breaking interactions was subsequently adopted for the same nucleus to obtain a better agreement [10]. A good description of the intraband $B(E2)$ transition strengths between the states of the ground band was obtained. The degree of horizontal and vertical mixing was determined to be approximately 20% in the ground state and up to as much as 50% for the $8^{+}_{1}$ level. A contracted version of the symplectic model [11] has also been applied [12] for the description of the ground band in ²⁰Ne, using a hamiltonian that generates the shell structure and includes the full major-shell-mixing quadrupole-quadrupole interaction $Q\cdot Q$, plus a residual rotor term. The results of these shell-model calculations for the eigenstates of the ground band in ²⁰Ne exhibit a considerable shell mixing in which the $0 \hbar\omega$ contribution increases from approximately 50% for $L = 0$ to approximately 80% for $L = 8$. In Refs. [10, 12] only the ground band was considered; hence, only the ground state intraband $B(E2)$ transition probabilities have been provided with no interband transition strengths.

More recent shell-model calculations for the structure of the ground band and the first few resonance-excited bands in ²⁰Ne have been performed within the framework of the one-component $Sp(6,R)$ symplectic model in [13], using a fermionic Hamiltonian with partial $SU(3)$ dynamical symmetry, and a symplectic Hamiltonian comprising a harmonic oscillator term, $Q\cdot Q$ interaction, and residual rotor part. The microscopic structure of the ground band states exhibits a strong $0 \hbar\omega$ component $(8,0)$ $(\geq 60 {\text {\%}})$ with a restriction of the model space up to $8 \hbar\omega$. States of the first resonance band ($K = 0^{+}_{2}$) contain significant contributions from all, except the highest $8 \hbar\omega$, shells. States are found to be dominated by one representation $(10,0)$ for the $K = 0^{+}_{2}$ band, $(8,1)$ for $K = 1^{+}_{1}$, $(6,2) \kappa = 2$ for $K = 2^{+}_{1}$, and $(6,2) \kappa = 1$ for $K = 0^{+}_{3}$, while the other irreps contribute only a few percent. The resonance bands resulting from the calculations of [13] within the framework of the $Sp(6,R)$ symplectic model within a single $Sp(6,R)$ irrep lie high in energy, in the region of giant resonances (i.e., there are no low-lying vibrations). To obtain other low-lying excited bands (e.g., β bands) within the one-component $Sp(6,R)$ symplectic model, the symplectic-breaking interactions need to be considered, such as the pairing or spin-orbit forces, which mix different $Sp(6,R)$ representations.

Finally, ab initio large-scale multi-shell calculations within the framework of the symmetry-adapted no-core shell model [14], in which the $U(3)\otimes SU(2)_{S_{p}}\otimes SU(2)_{S_{n}}$ coupled basis is adopted with no a priori symmetry constraints, have been applied to the description of low-energy nuclear structure in some light nuclei, including ²⁰Ne, using various QCD-inspired realistic interactions. Unfortunately, only the ground band in ²⁰Ne was considered with the intraband $B(E2)$ transition strengths up to $L = 4$, in which the structure is dominated by a single deformed shape that results from the leading $SU(3)$ irrep $(8,0)$.

Recently, a fully microscopic proton-neutron symplectic model (PNSM) of a nuclear collective motion with an $Sp(12,R)$ dynamical algebra was introduced by considering the symplectic geometry and possible collective flows in the two-component many-particle nuclear system [15]. Via its more general motion group $GL(6,R) \subset$$Sp(12,R)$, which allows for the separate treatment of the collective dynamics of proton and neutron subsystems, as well as the combined proton-neutron collective excitations, the PNSM generalizes the $Sp(6,R)$ model [7, 8] for the case of two-component proton-neutron many-particle nuclear systems. The collective states in the PNSM were initially classified by the basis states of the six-dimensional harmonic oscillator by considering the following dynamical symmetry reduction chain: $Sp(12,R) \supset U(6) \supset SU_{p}(3) \otimes SU_{n}(3) \supset SU(3) \supset SO(3)$. Using this chain, the PNSM has been applied for the simultaneous description of the microscopic structure of the lowest ground, β, and γ bands in $^{166}$Er [16], $^{152}$Sm [17], $^{154}$Sm [18], and $^{238}$U [19]. The results for the microscopic structure of negative-parity states of the lowest $K^{\pi} = 0^{-}_{1}$ and $K^{\pi} = 1^{-}_{1}$ bands in $^{152}$Sm, $^{154}$Sm, and $^{238}$U were also reported [17, 20, 21], including the low-energy $B(E1)$ interband transition strengths between the states of the ground band and $K^{\pi} = 0^{-}_{1}$ band [17, 21] for these three nuclei. A significant achievement of the presented approach is the simultaneous description of low-lying $B(E2)$ and $B(E1)$ transition strengths without the introduction of an effective charge.

The objective of this study is to test the validity of PNSM in its application to the light nuclei, particularly for the case of ²⁰Ne. For this purpose, we apply a different version of the PNSM, in which the shell-model many-particle nuclear states are classified by the following dynamical symmetry chain $Sp(12,R) \supset SU(1,1) \otimes SO(6) \supset$$U(1) \otimes SU_{pn}(3) \otimes SO(2) \supset SO(3)$. The latter was recently demonstrated to correspond to a microscopic shell-model counterpart [22] of the Bohr-Mottelson [23] collective model. Preliminary results along this shell-model classification scheme, applied to the excitation spectra of the first few collective bands in $^{158}$Gd, $^{106}$Ru, $^{150}$Nd and $^{148}$Nd, and the ground intraband $B(E2)$ quadrupole collectivity in these nuclei, have been presented in Refs. [24, 25]. In this study, we consider the collective states of the ground and first two $K^{\pi} = 0^{+}$ excited bands only in ²⁰Ne, including also the observed interband $B(E2)$ transition probabilities for the low-lying collective states.

The PNSM dynamical group $Sp(12,R)$ has several subgroup chains, which can be divided into two types of chains: the collective-model and shell-model chains. The first chain-type reveals the dynamical content of the symplectic symmetry. For more details regarding the dynamical content of the PNSM, refer to Ref. [15]. From another perspective, the shell-model chains of $Sp(12,R)$ relate the PNSM to the shell-model nuclear theory, and thus provide a connection to the microscopic many-fermion physics. They also provide a shell-model coupling scheme and a basis for detailed microscopic shell-model calculations.

A given shell-model chain is naturally expressed in terms of the harmonic oscillator creation and annihilation operators

Then, the many-particle realization of the $Sp(12,R)$ algebra is given by all bilinear combinations of these harmonic oscillator operators, which are $O(m)$ invariant [26]:

where $i,j = 1,2,3$; $\alpha,\beta = p,n$ and $s = 1,\ldots,m = A-1$. In Eq. (1), $x_{is}(\alpha)$ and $p_{is}(\alpha)$ denote the coordinates and corresponding momenta of the translationally-invariant Jacobi vectors of the $m$-quasiparticle two-component nuclear system, respectively, while $A$ denotes the number of protons and neutrons.

We classify the shell-model nuclear states by the following reduction chain [22]:

where to different subgroups are assigned the quantum numbers that characterize their irreducible representations. The chain (5) defines a shell-model coupling scheme for the PNSM.

The $SU(1,1)$ Lie algebra, related to the radial dynamics, is generated by the shell-model operators [22]:

which are obtained from (2)-(4) by contraction with respect to both indices i and α. The group $SO(6)$ can be expressed using the number-preserving $U(6)$ generators $A^{LM}(\alpha,\beta)$ (4) in the standard way by taking their antisymmetric combination [22]:

This group introduces $L$-pairing correlations, and its irreps are labelled by the $SO(6)$ seniority υ. The generators of different $SO(6)$ subgroups along the chain (5) are given by the following operators

and

which generate the $SU_{pn}(3)$ and $SO(2)$ groups, respectively. Evidently, by construction, the ($SO(3)$) scalar operator $M$ of $SO(2)$ commutes with the non-scalar generators (10)-(11) of $SU_{pn}(3)$. The two groups $SU_{pn}(3)$ and $SO(2)$ are therefore mutually complementary [27] within the fully symmetric $SO(6)$ irreps $\upsilon \equiv (\upsilon,0,0)_{6}$ and form a direct product subgroup $SU_{pn}(3) \otimes SO(2) \subset SO(6)$. Hence, the $SU_{pn}(3)$ irrep labels $(\lambda,\mu)$ are in one-to-one correspondence with the $SO(6)$ and $SO(2)$ quantum numbers υ and ν, given by the following expression [22]:

The reduction rules for $SU_{pn}(3) \supset SO(3)$ are given in terms of a multiplicity index $q$, which distinguishes the same $L$ values in the $SU_{pn}(3)$ multiplet $(\lambda,\mu)$ [1]:

An $Sp(12,R)$ unitary irreducible representation $\langle \sigma \rangle =$$\langle \sigma_{1}+\dfrac{m}{2}, \dots, \sigma_{6}+\dfrac{m}{2} \rangle$ is generated by acting on the lowest-weight state $|\sigma \rangle$, defined by the following equations

with raising symplectic generators (2), as schematically presented in Fig. 1. We have used the following notations for the indices $a \equiv i\alpha$ and $b \equiv j\beta$, taking the values $1,\ldots,6$. The symplectic bandhead $\langle \sigma \rangle$ is defined by the lowest-grade $U(6)$ irreducible representation $\sigma = [\sigma_{1},\ldots,\sigma_{6}]$. The structure of the $Sp(12,R)$ irreps is that of the coupled product of a 21-dimensional oscillator, related to the giant resonance vibrational degrees of freedom, and an intrinsic symplectic bandhead structure $\langle \sigma \rangle$, related to the valence shell proton-neutron degrees of freedom. The symplectic bandhead $\langle \sigma \rangle$ contains several $SU(3)$ multiplets that are appropriate for the description of different low-lying collective bands. The structure of the symplectic $Sp(12,R)$ irreducible representations is schematically presented in Fig. 2. If the symplectic bandhead is represented by the scalar $\langle \sigma \rangle = 0$ $Sp(12,R)$ representation, corresponding to the physically unimportant case of doubly-closed shell nuclei, then one obtains the irreducible collective space of the two-fluid irrotational-flow collective model of Bohr-Mottelson type. This is a characteristic feature of all phenomenological models of the nuclear structure. Therefore, the main difference of the present symplectic-based shell-model approach from the phenomenological models is that the combined proton-neutron collective dynamics is governed by the non-scalar $Sp(12,R)$ symplectic bandhead structure $\langle \sigma \rangle \neq 0$. If we allow the mixing of different $SU(3)$ multiplets within the symplectic bandhead (horizontal mixing), we will obtain a distribution over λ and μ. Using their relationship to the Bohr-Mottelson deformation parameters β and γ [9, 28, 29], we will obtain a distribution over β and γ. In other words, in contrast to the $Sp(6,R)$ symplectic model, here, we obtain low-lying shape vibrations. The $SU(3)$ states of the symplecic bandhead can also be mixed with the $SU(3)$ shell-model configurations from the higher major shells (vertical mixing). Accordingly, we see that the PNSM naturally incorporates rotational, low-lying, and high-lying vibrational collective degrees of freedom into nuclear dynamics.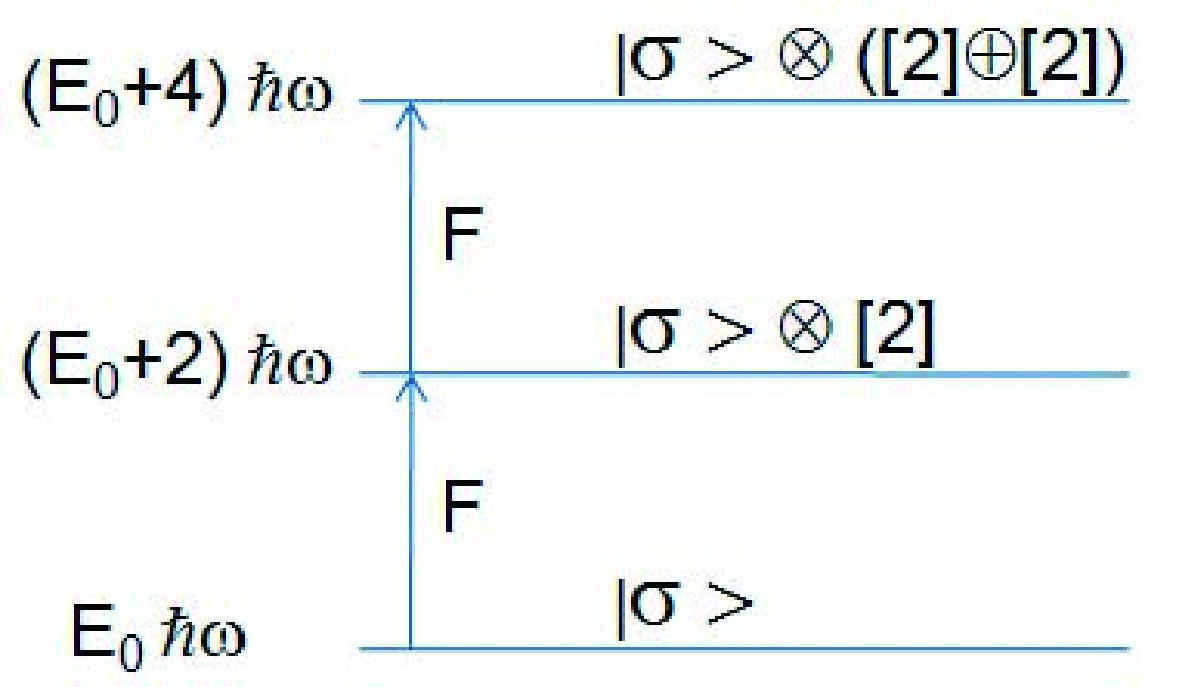

Figure 1.  (color online) Construction of the symplectic basis by acting with the symplectic raising generators (2) on the lowest-weight state $|\sigma \rangle.$

Figure 2.  (color online) Structure of the $Sp(12,R)$ irreducible representations that can be represented as a coupled product of a 21-dimensional oscillator, related to the giant resonance vibrational degrees of freedom, and an intrinsic symplectic bandhead structure $\langle \sigma \rangle$, related to the valence shell proton-neutron degrees of freedom, which contains several $SU(3)$ multiplets appropriate for the description of different low-lying collective bands.

The relevant $Sp(12,R)$ symplectic irreducible representation for ²⁰Ne is obtained by filling pairwise the $ds$ shell by two valence protons and two valence neutrons, which first gives the identical $SU(3)$ irreducible representation $(4,0)$ for both the proton and neutron subsystem, respectively. These two identical irreps are then strongly coupled to produce the leading $SU(3)$ irreducible representation $(8,0)$, i.e. $(4,0)\otimes(4,0) \rightarrow (8,0)$. The $Sp(12,R)$ irrep is therefore determined by the lowest-weight $U(6)$ state $|\sigma \rangle$, which is fixed by the requirement to contain the leading $SU(3)$ multiplet $(8,0)$ as a subrepresentation. Then, the shell-model considerations based on the real $SU(3)$ scheme, originally proposed by Elliott [1] (in contrast to the so-called "pseudo-$SU(3)$ scheme" [30] used for the case of heavy nuclei), gives the following $Sp(12,R)$ irreducible representation $\langle\sigma\rangle = \langle 10+ \dfrac{19}{2},2+\dfrac{19}{2},$$2+\dfrac{19}{2}, 2+ \dfrac{19}{2}, 2+\dfrac{19}{2},2+\dfrac{19}{2}\rangle$ of ²⁰Ne with the lowest $U(6)$ irrep $\sigma = [10, 2, 2, 2, 2, 2]_{6} \equiv [8]_{6}$, which we denote as $0 \hbar\omega \ [8]_{6}$, for simplicity. The $U(6)$ irrep $[8]_{6}$ in turn decomposes to the following $SO(6)$ irreps: $\upsilon = 8, 6, 4, 2,$ and 0, each containing the corresponding $SU_{pn}(3)$ subrepresentations. The lowest-weight $U(6)$ irrep is the symplectic bandhead, from which the set of remaining basis states for the considered $Sp(12,R)$ irreducible representation is obtained via the repeated actions on it by the raising symplectic generators, which increase the harmonic oscillator energy by two quanta. In Table 1, we present the relevant model space for performing the shell-model calculations in ²⁰Ne. From Eq. (15), it follows that the minimum number of oscillator quanta (eigenvalue of the number operator $N = \sum_{a}A_{aa}$) is $N'_{0} = (\sigma_{1} + \ldots + \sigma_{6}) + \dfrac{6}{2}m$, counting all filled levels and including the factor $\dfrac{6}{2}m$ for the zero-point motion of the $m = A-1$ Jacobi quasiparticles. However, because the protons and neutrons are actually physically present in the real three-dimensional potential well, half of the zero-point degrees of freedom are redundant. The proper value of the minimum Pauli allowed number of oscillator quanta will then be given by $N_{0} = (\sigma_{1} + \ldots + \sigma_{6}) + \dfrac{3}{2}m$, which for ²⁰Ne gives $N_{0} = 20+\dfrac{3}{2}.19 = 48.5$.

$N$	$\upsilon \backslash \nu$	$\cdots$	10	8	6	4	2	0	−2	−4	−6	−8	−10	$\cdots$
$\vdots$	$\vdots$	$\ddots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	${\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}}$
$N_{0}+2$	10	(10, 0)		(9, 1)	(8, 2)	(7, 3)	(6, 4)	(5, 5)	(4, 6)	(3, 7)	(2, 8)	(1, 9)	(0, 10)
	8			(8, 0)	(7, 1)	(6, 2)	(5, 3)	(4, 4)	(3, 5)	(2, 6)	(1, 7)	(0, 8)
	6				(6, 0)	(5, 1)	(4, 2)	(3, 3)	(2, 4)	(1, 5)	(0, 6)
	4					(4, 0)	(3, 1)	(2, 2)	(1, 3)	(0, 4)
	2						(2, 0)	(1, 1)	(0, 2)
	0	..		.	.	.	.	(0, 0)	.	.	.	.
$N_{0}$	8			(8, 0)	(7, 1)	(6, 2)	(5, 3)	(4, 4)	(3, 5)	(2, 6)	(1, 7)	(0, 8)
	6				(6, 0)	(5, 1)	(4, 2)	(3, 3)	(2, 4)	(1, 5)	(0, 6)
	4					(4, 0)	(3, 1)	(2, 2)	(1, 3)	(0, 4)
	2						(2, 0)	(1, 1)	(0, 2)
	0			.	.	.	.	(0, 0)	.	.	.	.

Table 1.  Relevant $SO(6)$ and $SU_{pn}(3)$ irreducible representations, which are contained in the $Sp(12,R)$ irreducible collective space $0 \hbar\omega \ [8]_{6}$ and obtained according to Eq. (13).

The basis functions along the chain (5) can thus be written in the form [22]:

where $Y^{\upsilon}_{\nu qLM}(\Omega_{5})$ represents the $SO(6)$ Dragt's spherical harmonics [31, 32]. The $SU(1,1)$ group describes the radial motion, while the $SO(6)$ group is associated with orbital excitations. Accordingly, the nuclear collective dynamics splits into radial and orbital motions. The full many-particle Hilbert space of the nucleus can therefore be represented as a direct sum

of Hilbert spaces labeled by a seniority quantum number υ, each of which carries an irrep of the direct product group $SU(1,1) \otimes SO(6)$. For the harmonic oscillator series $\lambda_{\upsilon} = \upsilon + 6/2$.

The starting point of the present application is the following dynamical symmetry Hamiltonian

in which the first term $2S^{(\lambda)}_{0} = H_{0}$ represents the harmonic oscillator mean field that defines the shell structure. Because the second-order Casimir operator $C_{2}[SU_{pn}(3)]$ of $SU_{pn}(3)$ is proportional to the in-shell quadrupole-quadrupole interaction $\widetilde{q}\cdot \widetilde{q}$, its role, together with the fourth term, is to reduce the energy of the $SU(3)$ multiplet with the maximal eigenvalue of this operator, i.e. the most deformed one $(8,0)$, within the valence shell with $N_{0} = 48.5$ and maximal seniority $\upsilon_{0} = 8$. All terms in the Hamiltonian (18) are $SU(3)$ scalars; hence, they do not mix different $SU(3)$ irreps. The eigenvalues of the Hamiltonian (18) with respect to the shell-model coupling scheme (5) are therefore given by

where $\langle C_{2}[SU_{pn}(3)]\rangle = \dfrac{2}{3}(\lambda^{2}+\mu^{2}+\lambda\mu+3\lambda+3\mu)$ represents the eigenvalue of the $SU_{pn}(3)$ second-order Casimir operator.

For the calculation of the $B(E2)$ transition strengths, we adopt the $E2$ transition operator $T^{E2} = (eZ/(A-1)) \widetilde{q}^{2m}$, where the in-shell quadrupole moment operator $\widetilde{q}^{2m}$ is given by Eq. (10). Because $\widetilde{q}^{2m}$ is a generator of the $SU_{pn}(3)$ group, one obtains the well-known result for the $B(E2)$ transition probabilities [24]:

where $\langle (\lambda,\mu)qL_{i}; (1,1)2|| (\lambda,\mu)q'L_{f} \rangle$ denotes the $SU(3) \supset SO(3)$ isoscalar factor. In the present shell-model calculations, as in other symplectic model applications, no effective charge is used, i.e. $e = 1$. Using Eq. (20), $B(E2;2^{+}_{1}\rightarrow 0^{+}_{1}) = 19.5$ W.u. is obtained for the leading $SU(3)$ irrep $(8,0)$, to be compared with the experimental value 20.3 [5]. This indicates that the $SU(3)$ symmetry already provides a very good approximation to the first $B(E2)$ transition probability of the ground band; however, it slightly underestimates the experimental value. Furthermore, we point out that in the pure $SU(3)$ limit, there are no non-zero interband $B(E2)$ transition probabilities.

In the present application, we use the Hamiltonian (18) plus the mixing Hamiltonian

consisting of horizontal and vertical mixing terms lying in the enveloping algebra of $Sp(12,R)$ dynamical group and given by the following expressions

The $a$ and $b$ operators are expressed by the proton and neutron raising operators of the harmonic oscillator quanta using $a^{\dagger}_{j} = \dfrac{1}{\sqrt{2}}\Big(-{\rm i}B^{\dagger}_{j}(p)+B^{\dagger}_{j}(n)\Big)$, $b^{\dagger}_{j} = \dfrac{1}{\sqrt{2}}$$\Big({\rm i}B^{\dagger}_{j}(p)+B^{\dagger}_{j}(n)\Big)$ and their conjugate counterparts [24]. $H_{\rm hmix}$ mixes different $SU_{pn}(3)$ multiplets within a given $SO(6)$ representation υ, whereas $H_{\rm vmix}$ mixes the $SU(3)$ multiplets of the $(\lambda,\mu)$ and $(\lambda\pm2,\mu)$ types from the adjacent oscillator shells. Hence, we diagonalize the model Hamiltonian consisting of Eqs. (18) and (21) within the $Sp(12,R)$ irreducible collective space $0 \hbar\omega \ [8]_{6}$ of ²⁰Ne given in Table 1, and restricted up to energy $20 \hbar\omega$ above the valence shell given by the minimal Pauli allowed number of oscillator quanta $N_{0} = 48.5$. In addition, due to the prolate-oblate symmetry of the $SU_{pn}(3)$ multiplets related with the conjugate $SU_{pn}(3)$ multiplets $(\lambda,\mu)$ and $(\mu,\lambda)$ contained within the corresponding $SO(6)$ irreducible representations, we use only the $SU(3)$ multiplets $(\lambda,\mu)$ with $\lambda \geqslant \mu$. Practically, the model space in which the Hamiltonian is diagonalized contains the $SU_{pn}(3)$ multiplets $(\lambda,\mu)$ with $\lambda \geqslant \mu$ within the maximal seniority $SO(6)$ irrep $\upsilon_{0} = 8$ (cf. Table 1) and the so-called stretched $SU(3)$ states of the type $(\lambda+2k,\mu)$ [9] with $k = 0, 1, 2, \ldots$ built on them up to the energy $20 \hbar\omega$.

The results of diagonalization for the low-lying excitation spectrum in ²⁰Ne together with the experimental data are presented in Fig. 3, while the intraband $B(E2)$ transition strengths between the states of the ground band for this nucleus are given in Fig. 4. In the calculations for the corresponding $B(E2)$ values, no effective charge is used. The values of the model parameters (in MeV), obtained by a fit to both the energy levels and $B(E2)$ transition probabilities, are as follows: $B = 0$, $C = -1.756$, $D = 0.0098$, $a = 0.15$, $\xi_{1} = -0.143$, and $\xi_{2} = -0.099$. The major shell separation energy $\hbar\omega$ is determined by the standard formula $41A^{-1/3}$ MeV. From Fig. 3, it is observed that the structure of the three lowest bands in ²⁰Ne is reasonably well described by the theory, especially for the ground band. For the two β bands, the model calculations give rotational bands with smaller moments of inertia than those observed in the experiment. Generally, the agreement can be improved by introducing deformation- or/and energy-dependent moments of inertia (see, e.g., [33, 34]). The position of the $0^{+}_{2}$ bandhead is obtained at much low energy then observed in an experiment, a situation encountered also in Ref. [4], and in less extended, in Ref. [3]. The position of this and other excited bands depends first on the third and fourth terms of the Hamiltonian (18). However, more importantly, the result of the calculations depends on the amount of the horizontal and vertical mixings of the $SU(3)$ states from the corresponding irreducible collective space, which in turn crucially affects the transition strengths. In this regard, an L pairing interaction can be introduced to improve the agreement on the position of the β excited bands, which at the same time does not affect the $SU(3)$ structure of the wave functions. Fig. 4 demonstrates that the ground state intraband $B(E2)$ quadrupole collectivity is well described within the error bars. Furthermore, in Table 2 we compare the values of the experimentally known interband $B(E2)$ transition probabilities with the theoretical predictions for the lowest states. Among the six observed interband $B(E2)$ transition probabilities, five were found in qualitative agreement and only the $2^{+}_{2} \rightarrow 2^{+}_{1}$ transition was approximately an order of magnitude smaller than the experimental value. We point out that, in contrast to the results of Ref. [4], here, the intraband and interband $B(E2)$ values are obtained without involving an effective charge. The interband $B(E2)$ transition probabilities strongly depend on the amount of the $SU(3)$ mixing and their relative values are a result of the delicate balance of the horizontal and vertical mixing of the $SU(3)$ shell-model configurations. We calculated the quadrupole moments of the corresponding $2^{+}$ excited states for the three bands under consideration. The obtained theoretical values are $-0.17$, $-0.19$, and $-0.15 \ {\rm eb}$, respectively for the ground, $\beta_{1}$, and $\beta_{2}$ bands, to be compared with the known experimental value $Q(2^{+}_{1}) =$$-0.23(\pm0.03) \ {\rm eb}$ for the $2^{+}$ state of the ground band. In general, from the presented results, a good overall description of the experimental data can be observed for the excitation energies and $B(E2)$ transition probabilities.

Figure 3.  (color online) Comparison of the experimental energy levels with the theory for the low-lying ground, $\beta_{1}$, and $\beta_{2}$ bands in ²⁰Ne.

Figure 4.  (color online) Comparison of the experimental and theoretical intraband $B(E2)$ values in Weisskopf units between the states of the ground band in ²⁰Ne. No effective charge is used.

${\rm initial}$	${\rm final}$	$B(E2;L_{i}\rightarrow L_{f})_{\rm th}$	$B(E2;L_{i}\rightarrow L_{f})_{\exp }$
$0_{2}$	$2_{1}$	$\qquad 4.63$	$\qquad\quad 3.6$
$0_{3}$	$2_{1}$	$\qquad 0.26$	$\qquad\quad 0.31$
$2_{2}$	$2_{1}$	$\qquad 0.19$	$\qquad\quad 1.7$
$4_{2}$	$2_{1}$	$\qquad 1.73$	$\qquad\quad 5.8$
$2_{3}$	$0_{1}$	$\qquad 0.52$	$\qquad\quad 0.73$
$4_{3}$	$2_{1}$	$\qquad 2.04$	$\qquad\quad 8.3$

Table 2.  Theoretical and experimental values in Weisskopf units of the interband $B(E2)$ transition probabilities. No effective charge is used.

In Fig. 5, we provide the $SU(3)$ decomposition of the wave functions for the collective states of the ground and first two excited β bands in ²⁰Ne. From the figure, it can be observed that the $SU(3)$ symmetry of the states under consideration is severely broken. For the states of the ground band, it can be observed that the microscopic structure is predominated by the $0 \hbar\omega$ component of the leading $(8,0)$ irreducible representation of the symplectic bandhead, in accordance with Refs. [3, 10, 12, 13]. For the low angular-momentum states of the three considered bands, one observes a significant amount of both the vertical and horizontal mixing of different $SU(3)$ shell-model configurations to the structure of the collective states.

Figure 5.  (color online) $SU(3)$ decomposition of the wave functions for the states of the ground, $\beta_{1}$, and $\beta_{2}$ bands in ²⁰Ne.

In this study, we studied the microscopic structure of low-lying positive-parity rotational states in the ground and first two excited β bands in ²⁰Ne within the framework of the symplectic-based shell-model approach provided by the proton-neutron symplectic model of collective motions in atomic nuclei. This is the first application of PNSM to light nuclei. The shell-model states are classified by the following dynamical symmetry chain $Sp(12,R)\, \supset \,SU(1,1) \otimes \,SO(6) \,\supset \,U(1)\, \otimes \, SU_{pn}(3) \otimes SO(2) \supset$$SO(3)$, which was demonstrated recently to correspond to a microscopic version of the Bohr-Mottelson model [22]. The PNSM dynamics naturally incorporates the low-lying rotations, high-lying vibrations associated with the giant resonance degrees of freedom, and (in contrast to the one-component $Sp(6,R)$ symplectic model) low-lying vibrations [15, 26].

To determine the microscopic shell-model structure of the collective states in ²⁰Ne, we adopt a dynamical symmetry Hamiltonian, including a simple algebraic interaction, lying in the enveloping algebra of the $Sp(12,R)$ dynamical group of PNSM, which introduces both the horizontal and vertical mixings of the $SU(3)$ multiplets within the $Sp(12,R)$ irreducible collective space $0 \hbar\omega \ [8]_{6}$ of ²⁰Ne, including the shell-model configurations from the major shells up to energy $20 \hbar\omega$. A good overall description is obtained for the excitation energies of the three bands considered, as well as for the ground state intraband $B(E2)$ quadrupole collectivity and the known interband $B(E2)$ transition probabilities between the low-lying collective states. The results for the $B(E2)$ transition strengths are obtained without the use of an effective charge, inherent to the symplectic-based shell-model approach to nuclear structure.

The results of this study indicate that the PNSM, which was initially proposed for the description of the collective motion in heavy mass nuclei, can also be applied successfully to light nuclei.