-
The discovery of neutrino oscillations [1-3] confirmed that neutrinos have sub-eV masses; however, the underlying mechanism behind such tiny neutrino masses is still open to question. Regarding the standard model (SM) as a low energy effective field theory, the simplest pathway to generate neutrino mass is via the Weinberg operator
$ LL\Phi\Phi/\Lambda $ [4]. There are three potential methods for realizing this operator at tree level [5], which correspond to the canonical type-I [6, 7], type-II [8-13], and type-III [14] seesaw. To verify whether these scenarios are realized in nature, the signatures of seesaw models have been extensively studied at colliders [15-18]. Because the conventional type-I seesaw requires heavy right-hand neutrinos$ N_R $ ($ \gtrsim10^{14} $ GeV with the corresponding Yukawa coupling$ \sim{\cal{O}} $ (1)), this method is far beyond the ability of current and planned colliders. Therefore, we consider the type-II seesaw in this study. Other possible low scale approaches to generating a tiny neutrino mass are summarized in Refs. [19, 20].The type-II seesaw introduces a scalar triplet ∆ with a hypercharge
$ Y = +2 $ , where neutrino mass is generated by the Yukawa interaction between the lepton doublets and scalar triplet. After the spontaneous symmetry breaking of the SM Higgs doublet Φ, the trilinear term$ \mu \Phi^T i\tau_{2}\Delta^\dagger\Phi $ induces a vacuum expectation value for the neutral component of the scalar triplet with$ v_\Delta\sim \mu v^2/M_\Delta^2 $ . As the scalar triplet ∆ also carries the lepton number$ +2 $ , the µ-term breaks the lepton number by two units. This trilinear term is the only source of lepton number violation; thus, it should be naturally small according to 't Hooft's naturalness principle [21]. Then, for$ \mu\sim v_\Delta $ , we can naturally have$ M_\Delta\sim v $ , i.e., the mass of the scalar triplet is at the electroweak scale [22].A distinct feature of this model is the presence of the doubly charged Higgs
$ H^{\pm\pm} $ . Assuming a degenerate mass spectrum for the scalar triplet, the typical channels used to hunt for$ H^{\pm\pm} $ are the same-sign dilepton channel$ H^{\pm\pm}\to\ell^\pm\ell^\pm $ and the same-sign diboson channel$ H^{\pm\pm}\to W^\pm W^\pm $ [23]. For a non-degenerate case, the cascade decay channel$ H^{\pm\pm} \to H^\pm W^\pm $ is also possible [24-27]. Corresponding signatures have been extensively studied at the LHC [28-34], HE-LHC [35-39],$ e^+e^- $ collider [40, 41], and$ ep $ colliders [42, 43]. When$ v_\Delta<10^{-4} $ GeV,$ H^{\pm\pm}\to \ell^\pm \ell^\pm $ is the dominant decay mode; a direct search at the LHC has already excluded the region$ M_{H^{\pm\pm}}<870 $ GeV [44]. In this case, the branching ratios of$ H^{\pm\pm}\to\ell^\pm\ell^\pm $ are only correlated with neutrino oscillation parameters [45]. When$ v_\Delta>10^{-4} $ GeV, the$ H^{\pm\pm}\to W^\pm W^\pm $ mode becomes dominant; searches for the pair production of$ H^{\pm\pm} $ in this diboson channel have excluded$ M_{H^{\pm\pm}}<350 $ GeV [46, 47].Among the various potential collider signatures of the type-II seesaw, the same-sign tetralepton signature is unique [48, 49] and arises from the mixing of neutral Higgs bosons and their cascade decays to singly and doubly charged Higgs bosons. Previous studies [48, 49] focused on the hadron colliders as the LHC and FCC-hh with
$ \sqrt{s} = 100 $ TeV; however, in this study, we analyze this signature at future lepton colliders. Considering the current lower bound on the doubly charged Higgs$ M_{H^{\pm\pm}}>350 $ GeV, this signature is beyond the reach of the CEPC [50]. To pair produce$ H^{\pm\pm} $ , the collision energy should at least be higher than 700 GeV. Therefore, we take the following four benchmark scenarios to illustrate:$ M_{H^{\pm\pm}}\lesssim M_{A^0} = 400 $ GeV at the$ \sqrt{s} = 1 $ TeV ILC [51, 52],$ M_{H^{\pm\pm}}\lesssim M_{A^0} = 600 $ GeV at the$ \sqrt{s} = 1.5 $ TeV CLIC,$ M_{H^{\pm\pm}}\lesssim M_{A^0} = 1000 $ GeV at the$ \sqrt{s} = 3 $ TeV CLIC [53, 54], and$ M_{H^{\pm\pm}}\lesssim M_{A^0} = 1500 $ GeV at the$ \sqrt{s} = 6 $ TeV Muon Collider (MuC) [55, 56]. As will shown later, the cross section of the triplet scalars$ H^0A^0 $ at lepton colliders can be much larger than that at the LHC. Especially, for large$ v_\Delta >10^{-4} $ GeV, the resulting promising region of the same-sign tetralepton signature at lepton colliders is even larger than that in the direct search for$ H^{\pm\pm}\to W^\pm W^\pm $ at the HL-LHC; this signal heavily depends on the parameters$ \lambda_4 $ and$ v_\Delta $ . Hence, observation of this signal provides an appealing method of probing these two parameters.In this paper, Sec. II contains a brief introduction of the type-II seesaw model and a discussion on the branching ratios of the scalar triplet components and corresponding constraints. The same-sign tetralepton signals at the ILC, CLIC, and MuC are analyzed in Sec. III, and the conclusion is presented in Sec. IV.
-
We concisely review the type-II seesaw in this section. Besides the SM Higgs doublet Φ, a scalar triplet ∆ is also employed, which can be denoted as
$ \Phi = \left( {\begin{array}{*{20}{c}} {{\phi ^ + }}\\ {{\Phi ^0}} \end{array}} \right),\qquad \Delta = \left( {\begin{array}{*{20}{c}} {\dfrac{{{\Delta ^ + }}}{{\sqrt 2 }}}&{{\Delta ^{ + + }}}\\ {{\Delta ^0}}&{ - \dfrac{{{\Delta ^ + }}}{{\sqrt 2 }}} \end{array}} \right), $

(1) where the neutral components can be further written as
$\Phi^{0} = \dfrac{1}{\sqrt{2}} \left(v+\phi^{0}+ $ $ {\rm i} \chi^{0}\right)$ and$ \Delta^{0} = \dfrac{1}{\sqrt{2}}\left(v_\Delta+\delta^{0}+{\rm i} \eta^{0}\right) $ , respectively, after spontaneous symmetry breaking. The Yukawa interaction that generates the tiny neutrino mass is given by$ {\cal{L}}_{Y} = Y_{\Delta} \overline{L_{L}^{c}} {\rm i} \tau_{2} \Delta L_{L}+\text { h.c. }, $

(2) where
$ \tau_{2} $ is the second Pauli matrix. The scalar potential involving Φ and ∆ is$\begin{aligned}[b] V(\Phi, \Delta) =& m_{\Phi}^{2} \Phi^{\dagger} \Phi+M^{2} {\rm{Tr}}\left(\Delta^{\dagger} \Delta\right)+\left(\mu \Phi^{{T}} {i}\tau_{2} \Delta^{\dagger} \Phi+\mathrm{h.c.}\right)\\&+\frac{\lambda_0}{4}\left(\Phi^{\dagger} \Phi\right)^{2} +\lambda_{1}\left(\Phi^{\dagger} \Phi\right) {\rm{Tr}}\left(\Delta^{\dagger} \Delta\right)+\lambda_{2}\left[{\rm{Tr}}\left(\Delta^{\dagger} \Delta\right)\right]^{2}\\&+\lambda_{3} {\rm{Tr}}\left[\left(\Delta^{\dagger} \Delta\right)^{2}\right]+\lambda_{4} \Phi^{\dagger} \Delta \Delta^{\dagger} \Phi. \end{aligned}$

(3) Mixing between the doublet and triplet scalars leads to seven physical scalars, i.e., a doubly charged Higgs
$ H^{\pm\pm} $ , singly charged Higgs$ H^\pm $ , CP-even Higgs bosons h and$ H^0 $ , and CP-odd Higgs$ A^0 $ , with the mixing angles specified by$ \begin{aligned}[b]& \tan \beta_{\pm} = \frac{\sqrt{2} v_{\Delta}}{v}, \qquad \tan \beta_{0} = \frac{2 v_{\Delta}}{v}, \\&\tan 2 \alpha = \frac{4 v_{\Delta}}{v} \frac{v^{2}\left(\lambda_{1}+\lambda_{4}\right)-2 M_{\Delta}^{2}}{v^{2} \lambda-2 M_{\Delta}^{2}-4 v_{\Delta}^{2}\left(\lambda_{2}+\lambda_{3}\right)},\end{aligned} $

(4) where
$ M^2_\Delta = \mu v^2/(\sqrt{2}v_\Delta) $ . The masses of the doubly and singly charged Higgs bosons$ H^{++} $ and$ H^{+} $ are given by$ M_{H^{++}}^{2} = M_{\Delta}^{2}-v_{\Delta}^{2} \lambda_{3}-\frac{\lambda_{4}}{2} v^{2}, \quad M_{H^+}^{2} = \left(M_{\Delta}^{2}-\frac{\lambda_{4}}{4} v^{2}\right)\left(1+\frac{2 v_{\Delta}^{2}}{v^{2}}\right). $

(5) The masses of CP-even Higgs bosons h and
$ H^0 $ can be written as$ M_{h}^{2} = {\cal{T}}_{11}^{2} \cos ^{2} \alpha+{\cal{T}}_{22}^{2} \sin ^{2} \alpha-{\cal{T}}_{12}^{2} \sin 2 \alpha, $

(6) $ M_{H^{0}}^{2} = {\cal{T}}_{11}^{2} \sin ^{2} \alpha+{\cal{T}}_{22}^{2} \cos ^{2} \alpha+{\cal{T}}_{12}^{2} \sin 2 \alpha, $

(7) where
$ {\cal{T}}_{11} $ ,$ {\cal{T}}_{22} $ , and$ {\cal{T}}_{12} $ are of the form$ \begin{aligned}[b]& {\cal{T}}_{11}^{2} = \frac{\lambda_0}{2} v^{2} , \quad {\cal{T}}_{22}^{2} = M_{\Delta}^{2}+2 v_{\Delta}^{2}\left(\lambda_{2}+\lambda_{3}\right), \\&{\cal{T}}_{12}^{2} = -\frac{2 v_{\Delta}}{v} M_{\Delta}^{2}+ v_{\Delta}v\left(\lambda_{1}+\lambda_{4}\right). \end{aligned}$

(8) Finally, the CP-odd Higgs
$ A^0 $ has the following mass$ M_{A^0}^{2} = M_{\Delta}^{2}\left(1+\frac{4 v_{\Delta}^{2}}{v^{2}}\right). $

(9) Constrained by the ρ parameter,
$ v_\Delta\lesssim 1 $ GeV should be satisfied. Neglecting the contributions from$ v_\Delta $ , masses of triplet scalars have the relation$ M_{H^{++}}^2-M_{H^+}^2\approx M_{H^+}^2-M_{H^0,A^0}^2\approx -\frac{1}{4}\lambda_4v^2. $

(10) In this paper, we consider the scenario with
$ \lambda_4>0 $ , which leads to the mass spectrum$ M_{H^{++}}<M_{H^+}< M_{H^0}\simeq $ $ M_{A^0} $ . The mass difference between$ H^0 $ and$ A^0 $ plays a vital role in the production of the same-sign trilepton signature, which is controlled by$ v_\Delta $ as$ M_{H^0}^2-M_{A^0}^2\sim 2(\lambda_2+\lambda_3)v_\Delta^2-4\frac{M_\Delta^2}{v^2}v_\Delta^2. $

(11) Here, we briefly discuss the decay properties of triplet scalars with the mass spectrum
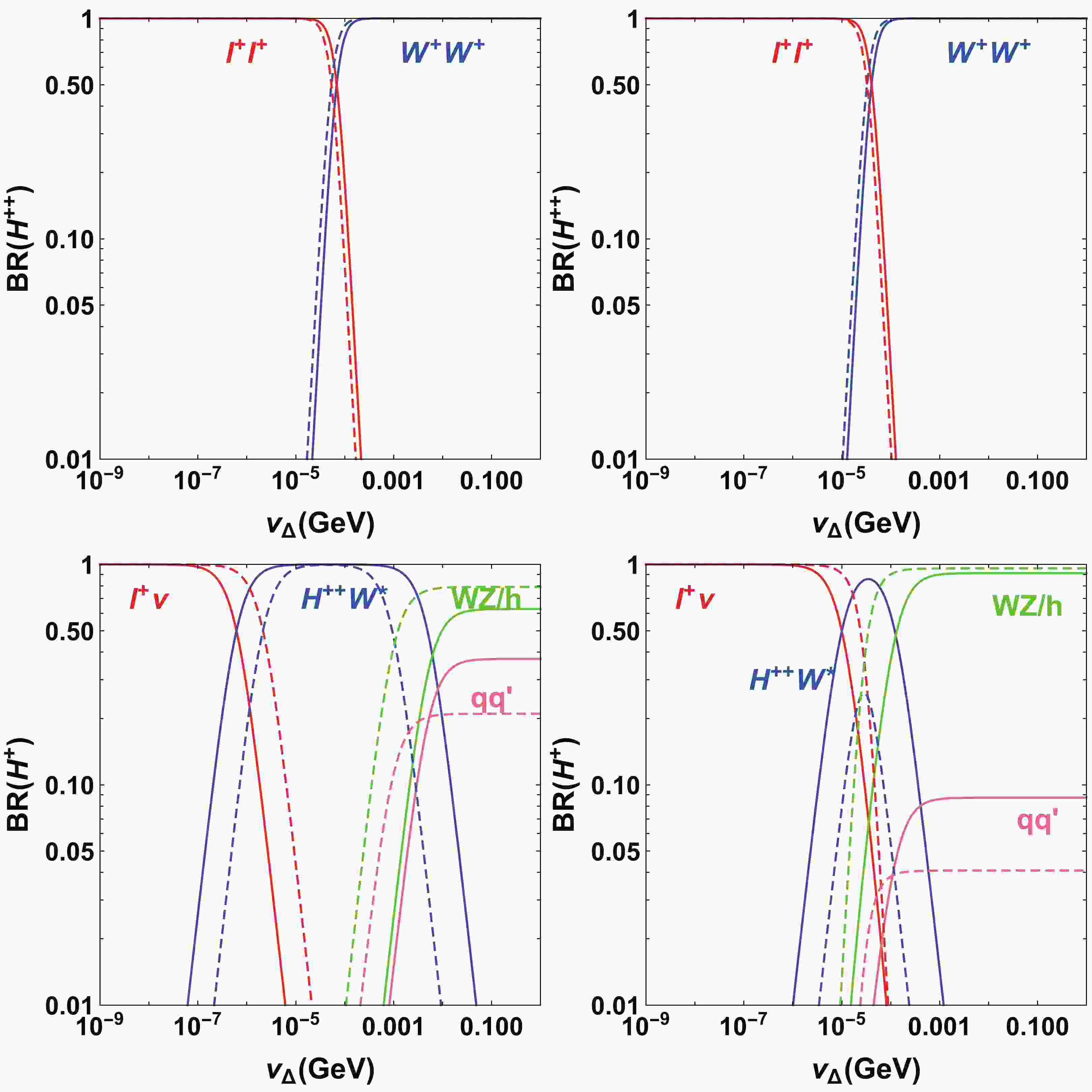
$ M_{H^{++}}<M_{H^+}<M_{H^0}\simeq M_{A^0} $ . Expressions for the partial decay widths of triplet scalars can be found in Ref. [25]. In this scenario, the doubly charged Higgs$ H^{\pm\pm} $ is the lightest. The possible decay channels are same-sign dilepton$ H^{\pm\pm}\to \ell^\pm\ell^\pm $ and same-sign diboson$ H^{\pm\pm}\to W^\pm W^\pm $ . The branching ratios are plotted in Fig. 1 for the four benchmark cases with$ M_{A^0} = $ 400, 600, 1000, and 1500 GeV. The decay widths of the dilepton$ H^{\pm\pm}\to \ell^\pm\ell^\pm $ channel is proportional to$ 1/v_{\Delta}^2 $ , while that of the diboson$ H^{\pm\pm}\to W^\pm W^\pm $ channel is proportional to$ v_\Delta^2 $ . Therefore, we have BR($ H^{\pm\pm}\to $ $ \ell^\pm\ell^\pm)\simeq 1 $ for$ v_\Delta\lesssim 10^{-5} $ GeV and BR($ H^\pm\to H^{\pm\pm}W^*)\simeq1 $ for$ v_\Delta\gtrsim10^{-3} $ GeV. Increasing the mass of$ H^{\pm\pm} $ does not have a large impact on the results of BR($ H^{\pm\pm} $ ). As for the singly charged Higgs$ H^\pm $ , possible decay channels are leptonic$ H^\pm \to \ell^\pm \nu $ , bosonic$ H^\pm \to W^\pm Z/W^\pm h $ , quarks$ H^\pm \to tb/cs $ , and cascade$ H^\pm\to H^{\pm\pm}W^* $ . Here, we focus on the same-sign tetralepton signature related channel, i.e., the cascade decay$ H^\pm\to H^{\pm\pm}W^* $ . This channel is dominant in the range of$ 10^{-6}\lesssim v_\Delta\lesssim 10^{-3} $ GeV ($ 10^{-5}\lesssim v_\Delta\lesssim 10^{-4} $ GeV) when$ M_{A^0} = 400(600) $ GeV. As the mass of the triplet scalars increase to approximately 1000 GeV, the dominant range of this channel shrinks to$ v_\Delta\sim5\times10^{-5} $ GeV and the corresponding branching ratio never reaches one. Meanwhile, this channel cannot become dominant when$ M_{A^0} = 1500 $ GeV because, as the triplet scalar masses increase, the phase space of cascade decay is suppressed. It has been shown that the dominant range of cascade decays$ H^0\to H^\pm W^* $ and$ A^0\to H^\pm W^* $ are similar to the channel$ H^\pm\to H^{\pm\pm}W^* $ [26].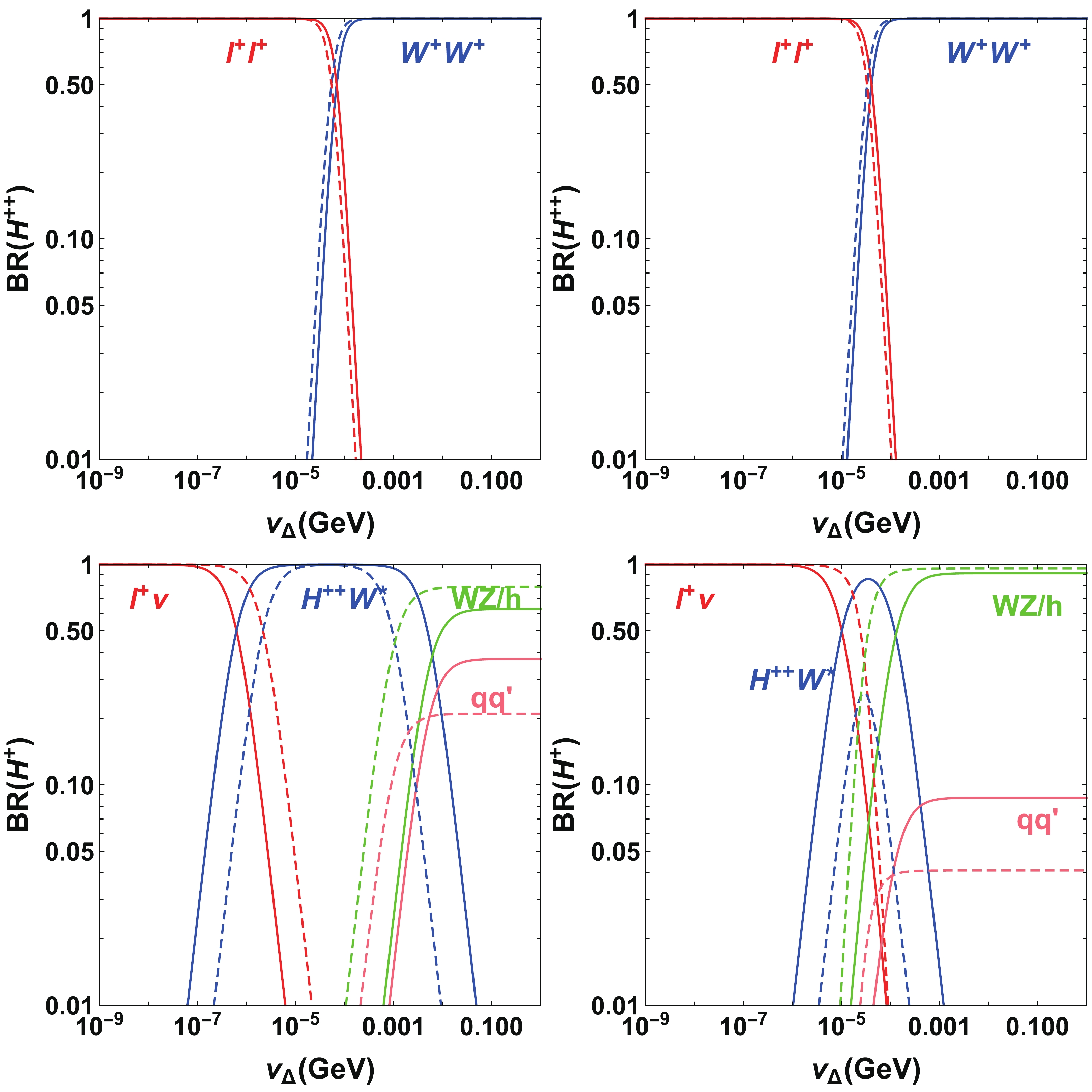
Figure 1. (color online) The branching ratios of
$H^{++}$ (upper panels) and$H^+$ (lower panels). In the left panels, the solid (dashed) lines indicate the results for$M_{A^0}=400 (600)$ GeV. In the right panels, the solid (dashed) lines indicate the results for$M_{A^0}=1000 (1500)$ GeV. Other relevant parameters are fixed as$\lambda_0=0.52$ ,$\lambda_{1,2,3}=0.01$ , and$\lambda_4=0.3$ . -
In this part, we briefly summarize the constraints on the type-II seesaw model. The vacuum stability requires the following bounded-from-below conditions [22, 34]:
$\begin{aligned}[b]& \lambda_0,\lambda_2\geqslant0,\quad \lambda_2+\frac{\lambda_3}{2}\geq0, \quad \lambda_1+\sqrt{\lambda_0(\lambda_2+\lambda_3)}\geqslant0, \\ & \lambda_1+\lambda_4+\sqrt{\lambda_0(\lambda_2+\lambda_3)}\geqslant0, \quad |\lambda_4|\sqrt{\lambda_2+\lambda_3}-\lambda_3\sqrt{\lambda_0}\geqslant0. \end{aligned}$

(12) In addition, the unitarity of the S-matrix from tree-level scattering processes produces 10 further constraints on the quartic couplings [34]. However, only the following is nontrivial:
$ \begin{aligned}[b]& \Big |(3\lambda_0+16\lambda_2+12\lambda_3)\\&\pm\sqrt{(3\lambda_0-16\lambda_2-12\lambda_3)^2+24(2\lambda_1+\lambda_4)^2}\Big |\leqslant 64\pi. \end{aligned} $

(13) For the study of the same-sign tetralepton signature, the quartic couplings are
$ \lambda_0 = 0.52,\;\lambda_{1,2,3} = 0.01 $ , and$\lambda_4\in $ $ [0.1,1]$ , which satisfy the above stability and unitarity constraints.Furthermore, a nondegenerate mass spectrum is required to produce this signal, which contributes to the electroweak oblique parameters as
$\begin{aligned}[b] S =& -\frac{1}{32\pi}\ln\frac{M^2_{H^{\pm\pm}}}{M_{H^0}^2}-\frac{2}{\pi}\left[(1-2s_W^2)^2\xi\left(\frac{M_{H^{\pm\pm}}^2}{M_Z^2}\right)\right.\\&\left.+s_W^4\xi\left(\frac{M_{H^{\pm}}^2}{M_Z^2}\right)+\xi\left(\frac{M_{H^{0}}^2}{M_Z^2}\right)\right], \end{aligned} $

(14) $ T = \frac{1}{8\pi c_W^2 s_W^2}\left[\eta\left(\frac{M_{H^{\pm\pm}}^2}{M_Z^2},\frac{M_{H^{\pm}}^2}{M_Z^2}\right)+\eta\left(\frac{M_{H^{\pm}}^2}{M_Z^2},\frac{M_{H^{0}}^2}{M_Z^2}\right)\right], $

(15) where the functions
$ \xi(x) $ and$ \eta(x,y) $ can be found in Ref. [34]. The best fit values for the S and T parameters are$ S = 0.06\pm0.09 $ and$ T = \pm0.10\pm 0.07 $ with a correlation coefficient of +0.91 [57]. For instance,$ M_{A^0} = $ $ 400\; \text{GeV}, \; \lambda_4 = 1 $ predicts$ S = 0.021 $ and$ T = 0.029 $ , which is allowed by the fit value.The charged scalars also contribute to the decay
$ h\to\gamma\gamma $ . The corresponding decay width is [58, 59]$ \begin{aligned}[b] \Gamma(h\to \gamma\gamma) = & \frac{G_{\rm F} \alpha^2 M_h^3}{128\sqrt{2}\pi^3}\Big|\sum\limits_{f} N_c^f Q_f^2 g_f A_{1/2}(\tau_f) +g_W A_1(\tau_W) \\ &+\tilde{g}_{H^{\pm}}A_0(\tau_{H^\pm})+4\tilde{g}_{H^{\pm\pm}}A_0(\tau_{H^{\pm\pm}})\Big|^2. \end{aligned} $

(16) where
$ N_c^f = 3(1) $ for quarks(leptons),$ Q_f $ is the charge of particle f,$ \tau_i = M_h^2/4M_i^2 $ , and the loop functions are presented in Refs. [60-62]. In the limit$ v_\Delta\ll v $ , the Higgs couplings are$ g_f\simeq1, \;\;\; g_W\simeq1, \;\;\; \tilde{g}_{H^\pm}\simeq \lambda_1 \frac{v M_W}{g M^2_{H^\pm}}, \;\;\; \tilde{g}_{H^{\pm\pm}}\simeq \left(\lambda_1+\frac{\lambda_4}{2}\right) \frac{v M_W}{g M^2_{H^{\pm\pm}}}. $

(17) Provided the production cross section of h is the same as that of the SM Higgs, the signal strength is
$ R_{\gamma\gamma} = \frac{\text{BR}(h\to\gamma\gamma)_\text{Type II}}{\text{BR}(h\to\gamma\gamma)_\text{SM}}. $

(18) For
$ M_{A^0} = 400 $ GeV,$ \lambda_1 = 0.01, \; \lambda_4 = 1 $ , the predicted signal strength$ R_{\gamma\gamma} $ is 0.99, which is within the experimental range$ R_{\gamma\gamma} = 1.12\pm0.09 $ [63].Finally, the sensitivity to doubly charged scalars at the High-Luminosity (HL) LHC is considered. According to the results in Ref. [37], the HL-LHC can probe
$ M_{H^{\pm\pm}} $ up to approximately 2200 GeV with$ {\cal{L}} = 3000\; \text{fb}^{-1} $ in the dilepton channel$ H^{\pm\pm}\to \ell^\pm\ell^\pm $ . Assuming the same selection efficiency, we simply project the diboson channel$ H^{\pm\pm}\to W^\pm W^\pm $ result in Ref. [47] with$ 139\; \text{fb}^{-1} $ into$ 3000\; \text{fb}^{-1} $ and find that the HL-LHC can probe$ M_{H^{\pm\pm}}\lesssim 490 $ GeV. -
In this section, we explore the same-sign tetralepton signature resulting from the neutral Higgs decay. First, the production cross section of
$ H^0A^0 $ is considered. The results are shown in Fig. 2, where the cross section$ \sigma(H^0A^0) $ at the 14 TeV LHC and 100 TeV FCC-hh are also illustrated for comparison. All the results are computed using Madgraph5_aMC@NLO [64] with the UFO [65, 66] model file provided by Ref. [39]. For lepton colliders, the neutral Higgs pair$ H^0A^0 $ can be produced when$ M_{A^0}<\sqrt{s}/2 $ . At the 1 TeV ILC, the cross section$ \sigma(H^0A^0) $ is larger than that at the 14 TeV LHC in the range of$ 300\lesssim M_{A^0}\lesssim 470 $ GeV. For$ 380\lesssim M_{A^0}\lesssim 610 $ GeV ($ 610\lesssim M_{A^0}\lesssim 1200 $ GeV), the 1.5 TeV (3 TeV) CLIC generates the largest cross section among lepton colliders. Notably,$ \sigma(H^0A^0) $ at the 3 TeV CLIC can be two orders of magnitude larger than that at the LHC for$ M_{A^0}\sim 1000 $ GeV. When$ M_{A^0}\gtrsim 1200 $ GeV, the 6 TeV MuC becomes one of the best options; in the range of$ 1700\lesssim M_{A^0}\lesssim2700 $ GeV,$ \sigma(H^0A^0) $ at the 6 TeV MuC is even larger than that at the 100 TeV FCC-hh.
Figure 2. (color online) Production cross section of
$H^0A^0$ at various colliders. The solid red, black, green, and blue lines are the results from the 1 TeV ILC, 1.5 TeV CLIC, 3 TeV CLIC, and 6 TeV MuC, respectively. The dashed cyan and pink lines are the results from the 14 TeV LHC and 100 TeV FCC-hh.At the 1 TeV ILC with
$ M_{A^0} = 400 $ GeV, this signal is generated via the tetraboson process$ \begin{aligned}[b] e^+e^- &\to H^0A^0 \to H^\pm W^{ *}H^\pm W^{ *} \to H^{\pm\pm} W^{ *} H^{\pm\pm} W^{ *}+ W^{ *} W^{ *}\\&\to 4 W^\pm + X, \end{aligned}$

(19) with the leptonic decay
$ W^\pm\to \ell^\pm \nu \; (\ell = e,\mu) $ . Note that the dilepton decay$ H^{\pm\pm}\to \ell^\pm\ell^\pm $ has already been excluded by a direct search at the LHC. Because the typical mass splitting between triplet scalars for the same-sign tetralepton signature is of the order of$ {\cal{O}}(\text{GeV}) $ , the final states from off-shell W decay are difficult to detect. Such a signature occurs owing to the interference effect between$ H^0 $ and$ A^0 $ , which is sizable when$ \delta M = M_{H^0}-M_{A^0}\sim \Gamma_{H^0/A^0} $ . The cross section for this signal is calculated by [48]$ \begin{aligned}[b] \sigma_W(4\ell^\pm+X) =& \sigma\left(e^+ e^- \rightarrow H^{0} A^{0}\right) \times \left(\frac{2+x^2}{1+x^2}\frac{x^2}{1+x^2}\right)\\& \times \text{BR}\left(H^{0} / A^{0} \rightarrow H^{\pm} W^{*}\right)^{2} \times \text{BR}\left(H^{\pm} \rightarrow H^{\pm \pm} W^{*}\right)^{2} \\ & \times \text{BR}\left(H^{\pm \pm} \rightarrow W^{\pm} W^{\pm}\right)^{2} \times \text{BR}(W^\pm\to \ell^\pm\nu)^4, \end{aligned} $

(20) where
$ x = \delta M/\Gamma_{H^0/A^0} $ . The initial cross section$\sigma(e^+e^-\to $ $ H^0A^0)$ is approximately 10 fb at the 1 TeV ILC with$ M_{A^0} = 400 $ GeV. In the left panel of Fig. 3, we show the product of the BRs in the above process. As shown in Fig. 1, BR$ (H^{\pm\pm}\to W^\pm W^\pm) $ is quickly suppressed for$ v_\Delta <10^{-4} $ GeV, which corresponds to the left boundary; the right one is determined by the cascade decay branching ratios BR$ (H^\pm\to H^{\pm\pm}W^*) $ . Therefore, a larger$ \lambda_4 $ leads to a larger mass splitting and hence a wider range of$ v_\Delta $ [27].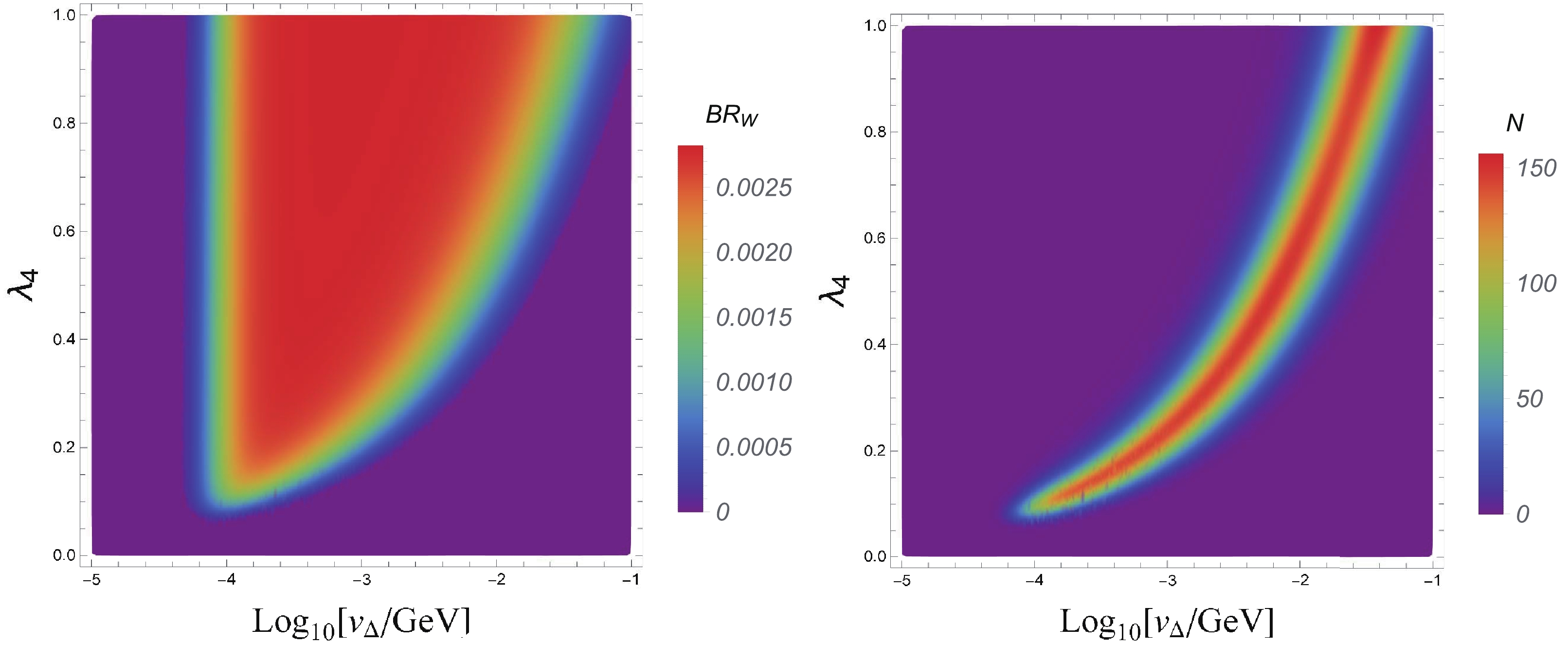
Figure 3. (color online) (left panel) Product of the branching ratios
$\text{BR}_W\equiv{\rm{BR}}\left(H^{0}/A^0 \rightarrow H^{\pm} W^{-*}\right)^2 \times {\rm{BR}}\left(H^{\pm} \rightarrow H^{\pm \pm} W^{-*}\right)^{2} \times $ $ {\rm{BR}}\left(H^{\pm \pm} \rightarrow W^{\pm} W^{\pm}\right)^{2} \times {\rm{BR}}\left(W^{\pm} \rightarrow \ell \nu\right)^{4}$ for the process$e^+e^- \rightarrow H^0 A^0$ with a mass of$A^0$ fixed as$M_{A^0}=400~ \mathrm{GeV}$ . (right panel) Event number N of the same-sign tetralepton signature$4\ell^{\pm} +X$ for the mass$M_{A^{0}}= 400 ~\mathrm{GeV}$ from$e^+e^- \to H^0 A^0$ and subsequent decays at the$\sqrt{s}=1~ \mathrm{TeV}$ ILC with$\mathcal{L}=8~ \mathrm{ab}^{-1}$ .In the right panel of Fig. 3, we show the expected event number for the same-sign tetralepton signature at the 1 TeV ILC with an integrated luminosity
$ {\cal{L}} = 8\; \text{ab}^{-1} $ . A detector level simulation with Delphes [67] is also performed, where only$ p_T(\ell^\pm)>10 $ GeV and$ |\eta(\ell^\pm)|<2.5 $ are required. The total cut efficiency applied is$ c_{\rm eff} = 0.6 $ for$ M_{A^0} = 400 $ GeV. The promising region in the$ \lambda_4-v_\Delta $ plane fills a narrow band, where the maximum event number can reach approximately 160. Such a narrow band is formed mainly owing to the interference effect between$ H^0 $ and$ A^0 $ . For a fixed value of$ v_\Delta $ , the mass splitting$ \delta M $ is then determined. A certain value of$ \lambda_4^M $ resulting in a suitable cascade decay width, i.e.,$ x = \delta M/\Gamma_{H^0/A^0}\sim1 $ , leads to the maximum event number. If$ \lambda_4>\lambda_4^M $ ,$ \Gamma_{H^0/A^0} $ will increase; thus, x will decrease, and the final event number will also decrease. Considering that, for a small mass splitting of the triplet scalars$\Delta M \sim $ $ \lambda_4 v^2/(8 M_{A^0})$ , the cascade decay's dominant width$ \Gamma_{H^0/A^0}\propto \Delta M^5 $ and$ \delta M\propto v_\Delta^2 $ , it is easy to derive the relation$ \lambda_4\propto v_\Delta^{2/5} $ by taking$ \delta M\sim \Gamma_{H^0/A^0} $ .Furthermore, we consider
$ M_{H^0}\sim M_{A^0} = 600 $ GeV at the$ \sqrt{s} = 1.5 $ TeV CLIC. In this scenario,$ H^{\pm\pm}\to W^\pm W^\pm $ is again the only allowed decay mode; therefore, the tetralepton signal is also generated via the process in Eq. (19). The product of the BRs and corresponding event number are shown in Fig. 4. Compared to the previous scenario with$ M_{A^0} = 400 $ GeV, the dominant region of BR$ _W $ decreases for$ M_{A^0} = 600 $ GeV, e.g.,$10^{-4}\lesssim v_\Delta\lesssim $ $ 10^{-2}\; \text{GeV}$ . With an integrated luminosity of$ 2.5\; \text{ab}^{-1} $ , approximately 10 signal events occur at the 1.5 TeV CLIC with$ M_{A^0} = 600 $ GeV at best. Therefore, this scenario is marginally promising.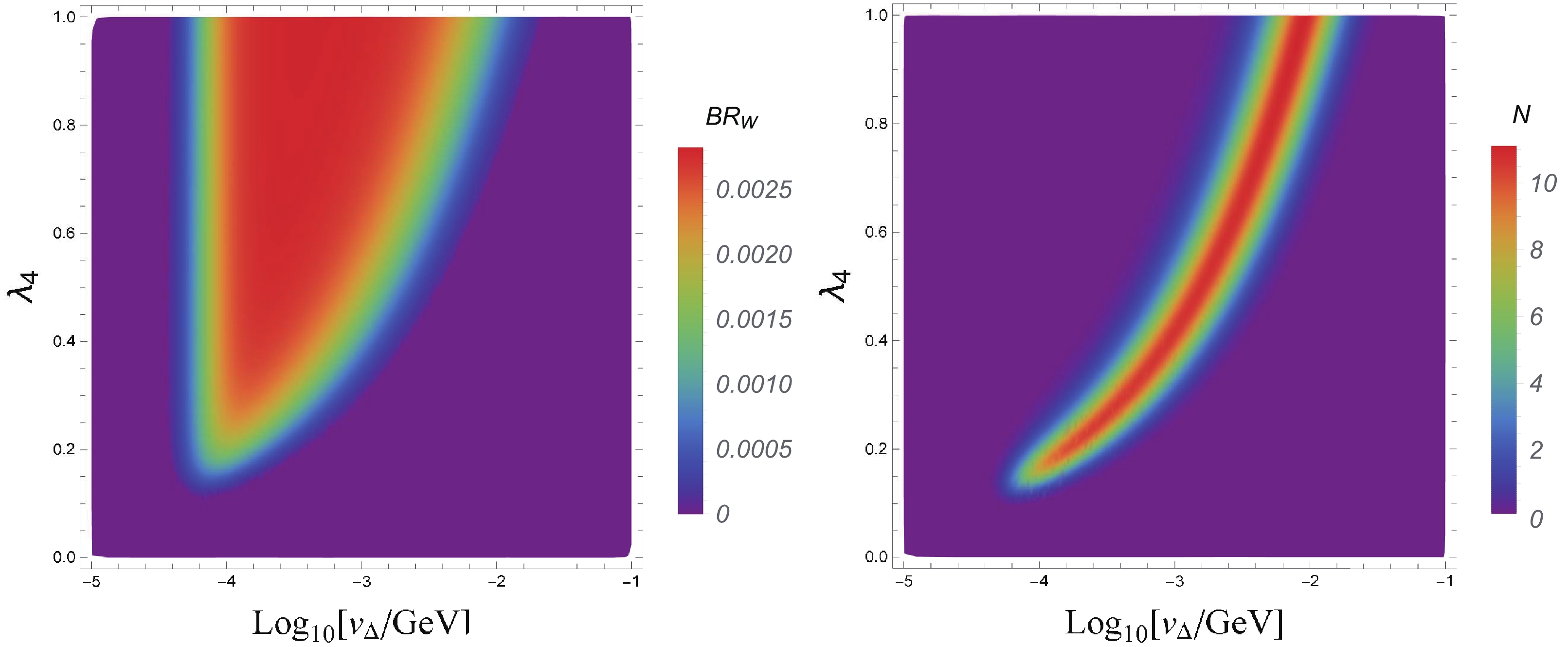
Figure 4. (color online) Same as Fig. 3 but for
$M_{H^0}\sim M_{A^0}=600$ GeV at the$\sqrt{s}=1.5$ TeV CLIC with luminosity$\mathcal{L}=2.5~\text{ab}^{-1}$ .Now, the same-sign tetralepton signature at the 3 TeV CLIC is considered. In this scenario, we set
$M_{A^0} = 1000$ GeV, and the same-sign dilepton decay$ H^{\pm}\to \ell^\pm \ell^\pm $ is allowed. Therefore, in addition to the tetraboson process in Eq. (19), we also have the direct tetralepton channel$ \begin{aligned}[b] e^+e^-& \to H^0A^0 \to H^\pm W^{ *}H^\pm W^{ *} \to H^{\pm\pm} W^{ *} H^{\pm\pm} W^{ *}\\&+ W^{ *} W^{ *}\to 4 \ell^\pm + X. \end{aligned}$

(21) The corresponding cross section is then calculated as
$ \begin{aligned}[b] \sigma_\ell(4\ell^\pm+X) = & \sigma\left(e^+ e^- \rightarrow H^{0} A^{0}\right) \times \left(\frac{2+x^2}{1+x^2}\frac{x^2}{1+x^2}\right) \\&\times \text{BR}\left(H^{0} / A^{0} \rightarrow H^{\pm} W^{*}\right)^{2} \end{aligned}$

$ \begin{aligned}[b] \quad\times \text{BR}\left(H^{\pm} \rightarrow H^{\pm \pm} W^{*}\right)^{2} \times \text{BR}\left(H^{\pm \pm} \rightarrow \ell^{\pm} \ell^{\pm}\right)^{2}. \end{aligned}$

(22) In the upper left panel of Fig. 5, we show the product of the BRs in the direct tetralepton decay process BR
$ _\ell $ . As shown in Fig. 1, the cascade decays are suppressed for$ v_\Delta\lesssim 10^{-5} $ GeV with$ M_{A^0} = 1000 $ GeV; hence, we do not show the region$ v_\Delta<10^{-5} $ GeV. The right boundary corresponds to the area where BR($ H^{\pm\pm}\to\ell^\pm\ell^\pm $ ) is suppressed. For$ \lambda_4>0.5 $ , there is a large parameter space where the product of the BRs reaches its maximum: 0.25. In the upper right panel of Fig. 5, the product of the BRs in the diboson process BR$ _W $ is also shown. Comparing with the region of$ M_{A^0} = 400 $ GeV in Fig. 3, the region of$M_{A^0} = 1000$ GeV is much smaller. For instance, when the product of the BRs is larger than 0.002,$ \lambda_4\gtrsim 0.5 $ and$ 10^{-4}\lesssim v_\Delta\lesssim10^{-3} $ GeV are required. This is because, for a heavier scalar triplet, the branching ratios of cascade decays are suppressed.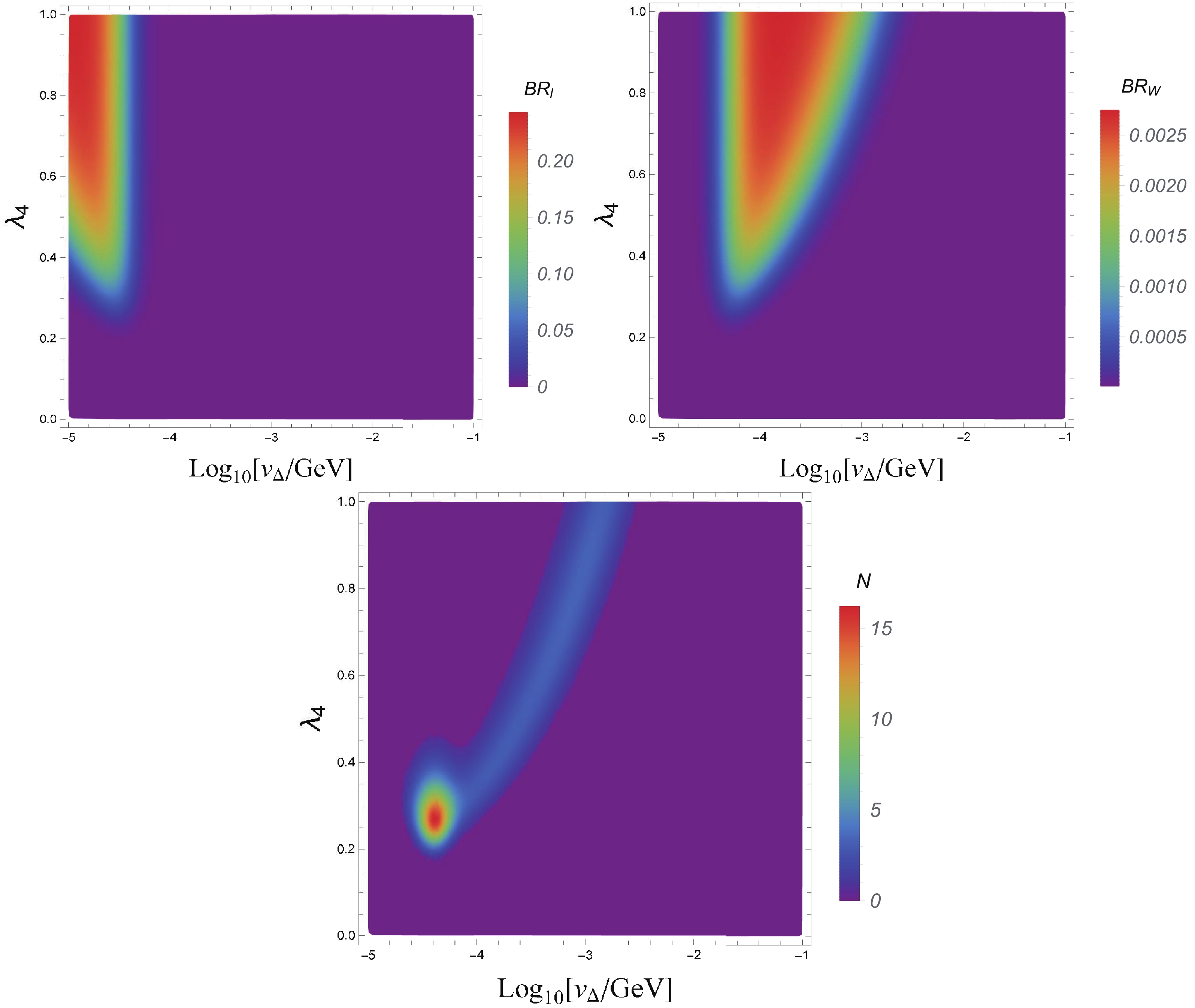
Figure 5. (color online) (upper left panel) Product of the branching ratios
$\text{BR}_\ell\equiv{\rm{BR}}\left(H^{0}/A^0 \rightarrow H^{\pm} W^{-*}\right)^2 \times {\rm{BR}}\left(H^{\pm} \rightarrow H^{\pm \pm} W^{-*}\right)^{2} \times $ $ {\rm{BR}}\left(H^{\pm \pm} \rightarrow \ell^{\pm} \ell^{\pm}\right)^{2}$ for the process$e^+e^- \rightarrow H^0 A^0$ with$M_{A^0}=1000 \;\mathrm{GeV}$ . (upper right panel) Product of the branching ratios$\text{BR}_W\equiv{\rm{BR}}\left(H^{0}/A^0 \rightarrow H^{\pm} W^{-*}\right)^2 \times {\rm{BR}}\left(H^{\pm} \rightarrow H^{\pm \pm} W^{-*}\right)^{2} \times {\rm{BR}}\left(H^{\pm \pm} \rightarrow W^{\pm} W^{\pm}\right)^{2} \times {\rm{BR}}\left(W^{\pm} \rightarrow \ell \nu\right)^{4}$ . (lower panel) Event number N of the same-sign tetralepton signature$4\ell^{\pm}+X$ for the mass$M_{H^{0}} \sim M_{A^{0}}= 1000 \;\mathrm{GeV}$ from$e^+e^- \to H^0 A^0$ and subsequent decays at the$\sqrt{s}=3 ~\mathrm{TeV}$ CLIC with luminosity$\mathcal{L}=5~ \mathrm{ab}^{-1}$ .In the lower panel of Fig. 5, we show the expected event number for the same-sign tetralepton signature at the 3 TeV CLIC with an integrated luminosity
$ {\cal{L}} = 5\; \text{ab}^{-1} $ . Here, the expected event number is the sum of the diboson decay process in Eq. (20) and the dilepton decay process in Eq. (22). In a small area at approximately$ v_\Delta\sim4\times10^{-4} $ GeV and$ \lambda_4\sim0.26 $ , we have the maximum number$ \sim 16 $ , where the dominant contribution is from$ H^{\pm\pm}\to \ell^\pm\ell^\pm $ . Meanwhile, the$ H^{\pm\pm}\to W^\pm W^\pm $ dominant tail region with$ 10^{-4}\lesssim v_\Delta\lesssim 10^{-3} $ GeV only predicts a total event number of less than three; thus, this long tail region is not promising.Finally, we consider the same-sign tetralepton signature at the 6 TeV MuC. The corresponding production processes at the muon collider are
$\begin{aligned}[b] \mu^+\mu^- &\to H^0A^0 \to H^\pm W^{ *}H^\pm W^{ *} \to H^{\pm\pm} W^{ *} H^{\pm\pm} W^{ *}\\&+ W^{ *} W^{ *}\to 4 W^\pm(\to \ell^\pm\nu) + X, \end{aligned} $

(23) $ \begin{aligned}[b] \mu^+\mu^- &\to H^0A^0 \to H^\pm W^{ *}H^\pm W^{ *} \to H^{\pm\pm} W^{ *} H^{\pm\pm} W^{ *}\\&+ W^{ *} W^{ *}\to 4 \ell^\pm + X. \end{aligned} $

(24) The production cross section is obtained by simply replacing
$ \sigma(e^+e^-\to H^0A^0) $ in Eq. (20) and Eq. (22) with$ \sigma(\mu^+\mu^-\to H^0A^0) $ . In the upper panels of Fig. 6, we show the product of the BRs in the direct tetralepton and tetraboson decay processes with$ M_{A^0} = 1500 $ GeV. To realize a relatively large BR value,$ \lambda_4 $ must be larger than$ 0.8 $ . However, such a large$ \lambda_4 $ leads to an excessively large mass splitting of the triplet scalars; hence, the interference factor x is suppressed. In the lower panel of Fig. 6, we show the total event number for the same-sign tetralepton signature at the 6 TeV MuC with an integrated luminosity$ {\cal{L}} = 10\; \text{ab}^{-1} $ . It is clear that the event number is always smaller than three. Therefore, the same-sign tetralepton signature is not promising at the MuC for$ M_{A^0} = 1500 $ GeV.
Figure 6. (color online) Same as Fig. 5, but for
$M_{H^{0}} \sim M_{A^{0}}= 1500 \;\mathrm{GeV}$ from the process$\mu^+\mu^-\to H^0A^0$ at the$\sqrt{s}=6 ~\mathrm{TeV}$ MuC with luminosity$\mathcal{L}=10~ \mathrm{ab}^{-1}$ .Based on the above benchmarks, we discuss the significance of the same-sign tetralepton signature at various lepton colliders. Notably, as the discovery channel for type-II seesaw, the direct production of the doubly charged scalar pair
$ H^{++}H^{--} $ is the best option. The same-sign tetralepton signature is a promising channel for probing the other scalars for a certain parameter space with$ M_{H^{\pm\pm}}<M_{H^\pm}<M_{H^0}\simeq M_{A^0} $ . To estimate the observability of this signal at lepton colliders, we calculate the maximum event number$ N_\text{Max} $ and corresponding significance$ S_\text{Max} $ . The significance S is calculated as [68, 69]$ S = \sqrt{2\left((N+B)\log\left(1+\frac{N}{B}\right)-N\right)}, $

(25) where we assume
$ B = 1 $ for the background event. The dominant background arises from the electron charge-flip in the opposite-sign four electron signature$ e^+e^-e^+e^-(4e) $ . The cross section of$ 4e $ at the 1 TeV ILC is 3.6 fb. According to Ref. [70], the charge misidentification probabilities vary between 0.01% and 0.8% with the BDT method. Taking 0.4% as the average value, the background event is approximately 0.46 with$ 8\; \text{ab}^{-1} $ at the 1 TeV ILC. For higher collision energies, the cross section of$ 4e $ decreases, but the misidentification rate increases for higher electron transverse energies. Therefore, taking the background event to be approximately$ B = 1 $ is a conservative estimation.The results are shown in Fig. 7. It is clear that, with an increase in
$ M_{A^0} $ , the maximum event number rapidly decreases. For the same-sign tetralepton originating from the tetraboson$ 4W^\pm $ , the discovery regions for the 1 TeV ILC, 1.5 TeV CLIC, 3 TeV CLIC, and 6 TeV MuC are$ M_{A^0}\lesssim $ 480, 620, 800, 710 GeV, respectively. Even in the future, when the HL-LHC will not observe$ H^{\pm\pm} $ in the diboson decay mode, the possibility to observe this signature in the mass range$ M_{A^0}\in [490,800] $ GeV at the CLIC remains. Moreover, if we consider an additional contribution from the direct teralepton channel$ 4\ell^\pm $ , the 3 TeV CLIC and 6 TeV MuC can probe$ M_{A^0}\lesssim $ 1100, 1160 GeV, respectively. However, taking into account the future results from the HL-LHC, if no clear observation of$ H^{\pm\pm} $ is obtained, the 1 TeV ILC will have no signature; also, there will be no direct tetralepton signal$ 4\ell^\pm $ at the 3 TeV CLIC and 6 TeV MuC.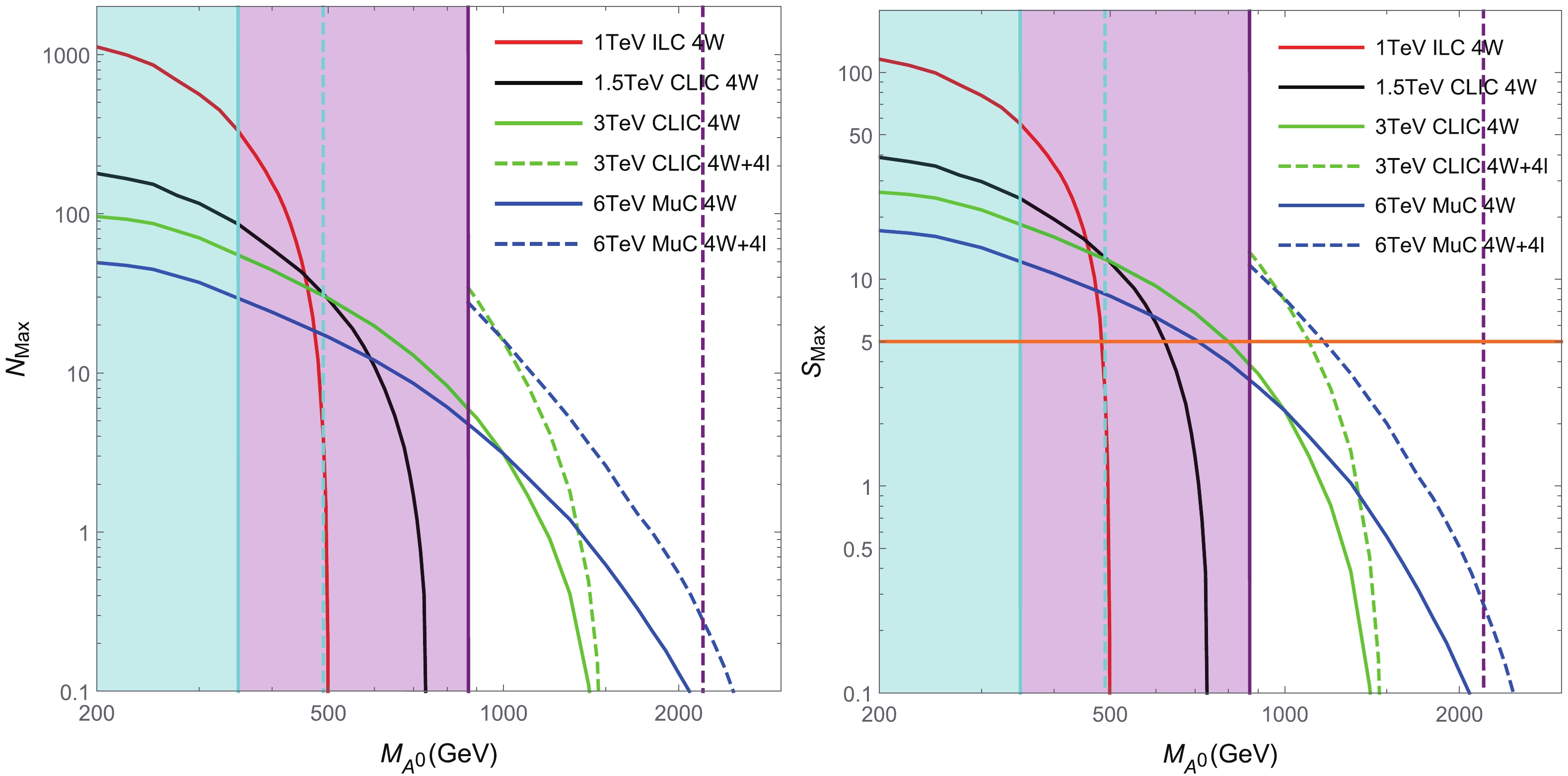
Figure 7. (color online) The maximum event number
$N_\text{Max}$ (left) and corresponding significance$S_\text{Max}$ of the same-sign tetralepton signature. The cyan and purple regions are excluded by the$H^{\pm}\to W^\pm W^\pm$ and$H^{\pm\pm}\to \ell^\pm\ell^\pm$ search at present, and the future exclusion limits at the HL-LHC are indicated by the dashed cyan and purple lines.The implication of the above bounds are now considered. The most promising scenario is the observation of
$ H^{\pm\pm} $ with$ M_{H^{++}}\sim $ 1 TeV in upcoming experiments. Then, the observation of the same-sign tetralepton signature at the 3 TeV CLIC will determine the coupling$ \lambda_4 $ and triplet VEV$ v_\Delta $ according to Fig. 5. In contrast, if this signal is observed in the$ 4W^\pm $ channel, we obtain a strong relation between$ \lambda_4 $ and$ v_\Delta $ , as shown in Fig. 3. In this scenario, the VEV$ v_\Delta $ could be further fixed when$ \lambda_4 $ is determined by the measurement of mass splitting between$ H^{\pm\pm} $ and$ H^\pm $ . In the worst case, i.e., if no same-sign tetralepton signal is observed at future lepton colliders,$ H^\pm\pm $ should be heavier than 800 GeV under certain relations between$ \lambda_4 $ and$ v_\Delta $ . -
In this study, we investigate the novel same-sign tetra-lepton signature in type-II seesaw at future lepton colliders (including the 1 TeV ILC, 3 TeV CLIC, and 6 TeV MuC). The signature arises from the mixing of the associated production of Higgs fields
$ H^0 A^0 $ followed by the cascade decays$ H^{0} / A^{0} \rightarrow H^{\pm} W^{*} $ ,$ H^{\pm} \rightarrow H^{\pm \pm} W^{*} $ , and$ H^{\pm\pm}\to \ell^\pm\ell^\pm/W^\pm W^\pm $ with$ W^\pm\to \ell^\pm\nu $ . There are two important parameters$ \lambda_4 $ and$ v_\Delta $ closely related to this signature, where$ \lambda_4 $ controls the mass splitting of the triplet scalars and$ v_\Delta $ determines the decay mode of$ H^{\pm\pm} $ .First, we consider a low mass benchmark scenario with
$ M_{A^0} = 400 $ GeV at the 1 TeV ILC. In this case,$ H^{\pm\pm}\to W^\pm W^\pm $ is the only viable decay mode. The production cross section of the process$ e^+ e^- \to H^0 A^0 $ varies around 10 fb. The promising region corresponds to a narrow band in the range$ 10^{-4}\lesssim v_\Delta \lesssim10^{-2} $ GeV. With an integrated luminosity$ {\cal{L}} = 8\; \mathrm{ab}^{-1} $ , we find that a neutral Higgs with a mass of approximately$ 400 \; \mathrm{GeV} $ can lead to roughly$ 150 $ events at the ILC. Then, we study the scenario$ M_{A^0} = 600 $ GeV at the 1.5 TeV ILC, where approximately 10 events can be produced with$ {\cal{L}} = 2.5\; \text{ab}^{-1} $ . For heavier triplet scalars, we consider$ M_{A^0} = 1000 $ GeV at the 3 TeV CLIC, where the cross section$ \sigma(e^+ e^- \to H^0 A^0) $ is approximately 2 fb. Although this value is roughly two orders of magnitude larger than that at the 14 TeV LHC, the cascade decay branching ratios are suppressed for small$ \lambda_4 $ values. This leads to a mismatch between the cascade decays and the interference effect. A maximum event number$ \sim 16 $ can be obtained at approximately$ v_\Delta\sim4\times10^{-4} $ GeV and$ \lambda_4\sim0.26 $ with an integrated luminosity$ {\cal{L}} = 5\; \mathrm{ab}^{-1} $ at the CLIC. In this high mass scenario, the$ H^{\pm\pm}\to \ell^\pm\ell^\pm $ decay mode is the dominant contribution to the same-sign tetralepton signature. If the triplet scalars are even heavier than 1 TeV (e.g.,$ M_{A^0} = 1500 $ GeV), the cascade decays will be heavily suppressed. With an integrated luminosity$ {\cal{L}} = 10\; \mathrm{ab}^{-1} $ at the 6 TeV MuC, there are three signal events at best. Therefore, this signature is not promising at the MuC.Based on the above benchmarks, we consider the significance of this signature. In the
$ H^{\pm\pm}\to W^\pm W^\pm $ decay mode, the promising region of the tetraboson$ 4W^\pm $ is$ 350\lesssim M_{A^0}\lesssim800 $ GeV at lepton colliders. Meanwhile, in the$ H^{\pm\pm}\to \ell^\pm \ell^\pm $ decay mode, the promising region of the direct tetralepton$ 4\ell^\pm $ is$ 870\lesssim M_{A^0}\lesssim1160 $ GeV. If no doubly charged scalar$ H^{\pm\pm} $ is observed at future HL-LHCs, the direct$ 4\ell^\pm $ channel will not be examined at lepton colliders. However, one can still probe this signal in the mass range$ M_{A^0}\in $ [490, 800] GeV in the$ 4W^\pm $ channel at the CLIC.
Same-sign tetralepton signature in type-II seesaw at lepton colliders
- Received Date: 2021-09-01
- Available Online: 2022-01-15
Abstract: The same-sign tetralepton signature via the mixing of neutral Higgs bosons and their cascade decays to charged Higgs bosons is a unique signal in the type-II seesaw model with the mass spectrum






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF






































 DownLoad:
DownLoad: