-
Primary tasks at the Large Hadron Collider (LHC) include the precision test of the standard model (SM) and the search for new physics beyond the SM (BSM). Since the discovery of the
125GeV Higgs boson by both ATLAS and CMS collaborations at the LHC in 2012 [1, 2], the SM has become the most successful theory in describing the interactions of fundamental particles. However, the discovery of this SM-like Higgs boson is merely one step toward fully investigating the electroweak symmetry breaking (EWSB). As is well known, the theoretical predictions of the SM are not always compatible with experimental observations, such as the dark matter in the universe, the oscillation of neutrinos, the huge hierarchy between electroweak and Planck scales, and the fine-tuning problem of Higgs mass. These conceptional and experimental difficulties encountered by the SM imply the existence of new physics beyond the SM.We may extend the SM by enlarging its gauge symmetry and/or introducing much more gauge multiplets to construct a new physics model. Among all the BSM theories, the two-Higgs-doublet model (2HDM) [3] is one of the simplest extensions of the SM. The Higgs sector responsible for the EWSB consists of two complex scalar isospin doublets, and the minimal supersymmetric standard model is a particular realization of the 2HDM. After EWSB, the three Goldstone modes
G± andG0 in the Higgs sector of the 2HDM are absorbed by the weak gauge bosonsW± andZ0 , respectively, providing the longitudinal polarizations ofW± andZ0 . The remaining five mass eigenstates of the Higgs sector are the so-calledCP -even Higgs bosonsh0 andH0 ,CP -odd Higgs bosonA0 , and charged Higgs bosonsH± .Clearly, any discovery of a BSM Higgs boson will be an evidence for the existence of a new Higgs sector. At the LHC, the neutral Higgs bosons of the 2HDM can be produced both singly and in identical or mixed pairs. The dominant mechanism for single production of neutral Higgs bosons is gluon-gluon fusion. Concerning scalar-pseudoscalar pairs, the electroweak production via quark-antiquark annihilation,
pp→qˉq→Z∗→H0A0/h0A0 , can dominate over the QCD production via gluon-gluon fusion [4, 5], even by orders of magnitude. Considerable efforts have been devoted to search for BSM neutral Higgs bosons. Particularly, the exotic decays of heavy scalar (pseudoscalar), such asH0→A0Z0 (A0→H0Z0 ), have attracted attention at the LHC in recent years [6, 7]. The scalar-pseudoscalar pair production is dominated by the Drell-Yan channel; it is an ideal process to investigate the Higgs gauge couplinggH0A0Z0/gh0A0Z0 and should thus be thoroughly invegtigated. The next-to-leading order (NLO) QCD corrections to neutral Higgs-boson pair production at hadron colliders were calculated in Refs. [4, 8], which showed that the QCD corrections can enhance the cross section ofh0A0 production by approximately 30%.Fixed-order perturbative predictions would be unreliable when the exponential enhancement from soft gluon dominates at the edge of the phase space. The large logarithms, such as
αns(M2/p2T)lnm(M2/p2T) at smallpT andαns(1−z)−1lnm(1−z) whenz=M2/ˆs→1 , should be resummed in precision calculations. We extract such logarithms in the partonic matrix element by adopting the Collins-Soper-Sterman resummation technique [9-17] and analyze the threshold resummation effect from parton distribution functions (PDFs) by using the factorization method proposed in Ref. [18]. Generally, the resummation corrections are only considered for fixing the unnatural behaviours in the small-pT and threshold regions, while the fixed-order predictions are suitable for describing the kinematics far away from the edge of the final-state phase space. Thus, the resummation results should be matched with the fixed-order predictions to obtain a reliable description in all kinematical regions.In this study, we thoroughly analyze scalar-pseudoscalar pair production at the
13TeV LHC within the type-I 2HDM at the NLO and next-to-leading logarithmic (NLL) accuracy in QCD. The rest of this paper is organized as follows. In Sec. II, we briefly review the 2HDM. In Sec. III, we present the calculation strategies forϕ0A0 associated production at QCD NLO+NLL accuracy, including the Collins-Soper-Sterman resummation technique and the factorization method for assessing the impact of the threshold-resummation improved PDFs. The numerical results and discussion for both the integrated cross section and the differential distributions with respect to the transverse momentum and invariant mass of the final-stateϕ0A0 system are provided in Sec. IV. Finally, a short summary is given in Sec. V. -
In contrast to the SM, the Higgs sector of the 2HDM consists of two complex scalar
SU(2)L doubletsΦ1,2 with hyperchargeY=+1 . The most general scalar potential, which is invariant under theSU(2)L⊗U(1)Y electroweak gauge symmetry and a discreteZ2 symmetryΦi→(−1)i+1Φi(i=1,2) , is given byV(Φ1,Φ2)=m211Φ†1Φ1+m222Φ†2Φ2−(m212Φ†1Φ2+h.c.)+12λ1(Φ†1Φ1)2+12λ2(Φ†2Φ2)2+λ3(Φ†1Φ1)(Φ†2Φ2)+λ4(Φ†1Φ2)(Φ†2Φ1)+12[λ5(Φ†1Φ2)2+h.c.],
(1) where the dimension-two term
m212 is tolerated because it only breaks theZ2 symmetry softly, andm211,22 ,λ1,2,3,4 are forced to be real owing to the hermiticity of the scalar potential. The two Higgs doublets can be parameterized as [3]Φi=(ϕ+i(vi+ρi+iηi)/√2)(i=1,2),
(2) where
v1 andv2 are the vacuum expectation values (VEVs) of the neutral components ofΦ1 andΦ2 , respectively. In aCP -conserving 2HDM, bothm212 andλ5 are real, and so arev1 andv2 . The eight mass eigenstates of the Higgs sector are given by(H0h0)=(cosαsinα−sinαcosα)(ρ1ρ2),
(3) (G0A0)=(cosβsinβ−sinβcosβ)(η1η2),
(4) (G±H±)=(cosβsinβ−sinβcosβ)(ϕ±1ϕ±2),
(5) where α is the mixing angle in the
CP -even Higgs sector andβ=arctanv2v1 describes the mixing in theCP -odd and charged Higgs sectors. After the spontaneous electroweak symmetry breaking, three out of eight degrees of freedom fromΦ1,2 that correspond to Nambu-Goldstone bosonsG± andG0 are respectively absorbed by weak gauge bosonsW± andZ0 , providing the longitudinal polarizations ofW± andZ0 . The remaining five degrees of freedom become the aforementioned five physical Higgs bosons: twoCP -even Higgs bosonsh0 andH0 , oneCP -odd Higgs bosonA0 , and a pair of charged Higgs bosonsH± . In this study, the seven input parameters for the Higgs sector of aCP -conserving 2HDM are chosen as{mh0,mH0,mA0,mH±,m212,sin(β−α),tanβ},
(6) which are implemented as the “physical basis” in 2HDMC [19]. Then, the Higgs potential in Eq. (1) can be completely determined by the seven Higgs parameters in Eq. (6) and v, where
v≡√v21+v22=(√2GF)−1/2≈246GeV has been classified as an electroweak input parameter.To guarantee the absence of Higgs-mediated flavor changing neutral currents at the tree level, the
Z2 symmetry should be extended to the Yukawa sector. Given that the two Higgs doubletsΦ1,2 have oppositeZ2 charges, each flavor of quark/lepton can only couple to one of the two Higgs doublets. There are four allowed types of Yukawa interaction corresponding to the four independentZ2 charge assignments on the quark and leptonSU(2)L multiplets (Table 1). The Yukawa Lagrangian of the 2HDM can be expressed in terms of Higgs mass eigenstates as2HDM Φ1 
Φ2 
QL 
LL 
uR 
dR 
ℓR 
Type I + − + + − − − Type II + − + + − + + Lepton-specific + − + + − − + Flipped + − + + − + − Table 1. Four types of 2HDMs and the corresponding
Z2 charge assignments on Higgs, quark, and leptonSU(2)L multiplets.L2HDMYukawa=−∑f=u,d,ℓmfv(ξfhˉffh0+ξfHˉffH0−iξfAˉfγ5fA0)−[√2Vudvˉu(muξuAPL+mdξdAPR)dH++√2mℓvξℓAˉνPRℓH++h.c.],
(7) where
ξfh,H,A(f=u,d,ℓ) are the Higgs Yukawa couplings normalized to the SM vertices, and the corresponding values in the type-I, type-II, lepton-specific, and flipped 2HDMs are listed in Table 2.2HDM Type I Type II Lepton-specific Flipped ξuh 
cosα/sinβ 
√ 
√ 
√ 
ξuH 
sinα/sinβ 
ξuA 
cotβ 
ξdh 
cosα/sinβ 
(α,β)→(˜α,˜β) 
(α,β)→(˜α,˜β) 
ξdH 
sinα/sinβ 
ξdA 
−cotβ 
ξℓh 
cosα/sinβ 
(α,β)→(˜α,˜β) 
√ 
ξℓH 
sinα/sinβ 
ξℓA 
−cotβ 
Table 2. Normalized Higgs Yukawa couplings
ξfh,H,A (f= u,d,ℓ) in the type-I, type-II, lepton-specific, and flipped 2HDMs.(˜α,˜β)=(α,β)+π2 .The Higgs gauge interaction is independent of the types of the 2HDM. The couplings of
h0 andH0 to weak gauge boson pair are proportional tosin(β−α) andcos(β−α) , respectively. The 2HDM parameter space is stringently constrained by the requirement that one out of the two neutralCP -even Higgs bosons has physical properties consistent with the125GeV scalar discovered at the CERN LHC. It is well known that if one of the two neutralCP -even Higgs mass eigenstates is approximately aligned in the two-dimensional Higgs field space with the direction of the Higgs VEV vector→v≡(v1,v2) (the so-called alignment limit), the couplings of this Higgs boson are SM-like. The two alignment limits of the 2HDM are listed in Table 3. Given that the SM-like Higgs boson with mass around125GeV seems to be favored by LHC data, we will investigate the scalar-pseudoscalar pair production at the LHC only at the alignment limit.Alignment limit β−α 
h0 
H0 
I π/2 
SM-like II 0 
SM-like Table 3. Two alignment limits of the 2HDM.
-
We adopt the 't Hooft-Feynman gauge and take the five-flavor scheme in our calculations. Apart from the top quark, all other light quarks, including the bottom quark, are treated as massless particles. The UV and IR divergences in the QCD loop and real jet emission corrections are regularized by adopting the dimensional regularization scheme [20]. We employ both the Catani-Seymour dipole subtraction method [21, 22] and the two cutoff phase space slicing method [23] to separate the soft and collinear IR singularities of the real emission correction, and then cross check their correctness.
-
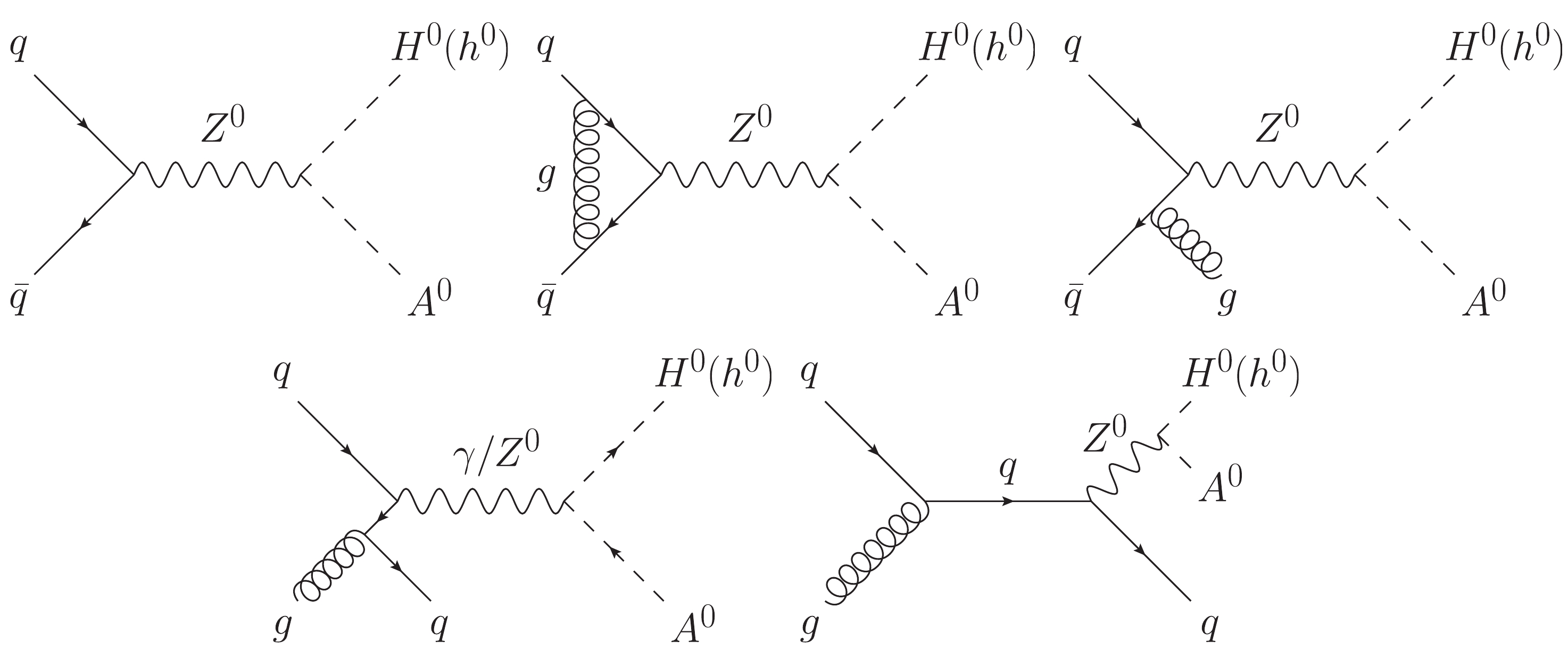
The scalar-pseudoscalar pair can be produced at the LHC via Drell-Yan production mechanism. Some representative LO and QCD NLO Feynman diagrams for
qˉq→H0(h0)A0 are shown in Fig. 1 . In this study, we categorizeqg→H0(h0)A0+q as the real light-quark emission correction to the quark-antiquark-initiated Drell-Yan channel.The
h0A0Z0 andH0A0Z0 gauge interactions in the 2HDM are given bygh0A0Z0=ecos(β−α)sin2θW(ph0−pA0)μ,gH0A0Z0=−esin(β−α)sin2θW(pH0−pA0)μ,
(8) where
θW is the Weinberg weak mixing angle,ph0,H0,A0 are the incoming momenta of the corresponding (pseudo)scalars, and µ is the Lorentz index of the vector bosonZ0 . At the alignment limit, one of the twoCP -even mass eigenstates can be regarded as the SM Higgs bosonh0SM , while the other is a BSMCP -even Higgs boson denoted byϕ0 . We can see from Table 3 that(h0SM,ϕ0)={(h0,H0),(alignmentlimitI:sin(β−α)=1),(H0,h0),(alignmentlimitII:cos(β−α)=1).
(9) Given that the
h0A0Z0 andH0A0Z0 coupling strengths are proportional tocos(β−α) andsin(β−α) , respectively, theh0SMA0 associated production is forbidden up toO(α2αs) at the alignment limit. Thus, we only focus on the Drell-Yan production ofϕ0A0 in the following.The doubly-differential cross section for
pp→ ϕ0A0+X can be perturbatively calculated by means of the QCD factorization theorem:M2d2σdM2dp2T(τ)=∑a,b∫10dxadxbdz[xafa/P(xa,μ2F)]×[xbfb/P(xb,μ2F)]×[zˆσab(z,M2,p2T,μ2F,μ2R)]×δ(τ−xaxbz),
(10) where M and
pT are the invariant mass and transverse momentum of the final-stateϕ0A0 system, respectively. The threshold variables τ andz in Eq. (10) are defined byτ=(M/√s)2,z=(M/√ˆs)2,
(11) where
√s and√ˆs denote the hadronic and partonic center-of-mass energies, respectively. The universal PDFfa/P(x,μ2F) gives the probability to find parton a in proton P at factorization scaleμF as a function of fraction x of the proton's longitudinal momentum carried by the parton. After preforming a Mellin transformation,F(N)=∫10dyyN−1F(y),
(12) on Eq. (10), the hadronic cross section can be written as a simple product of the PDFs and the partonic cross section in the conjugate Mellin N-space as
M2d2σdM2dp2T(N−1)=∑a,bfa/P(N,μ2F)fb/P(N,μ2F)׈σab(N,M2,p2T,μ2F,μ2R).
(13) To be consistent with the CT collaboration [24], we refit the PDF,
fa/P(x,μ2F) , as a polynomial ofx1/2 with eight coefficients,fa/P(x,μ2F)=A0xA1(1−x)A2(1+A3x1/2+A4x+A5x3/2+A6x2+A7x5/2).
(14) Thus, the Mellin moment of the PDF has the form
fa/P(N,μF)=A0[B(A1+N,A2+1)+A3B(A1+N+1/2,A2+1)+A4B(A1+N+1,A2+1)+A5B(A1+N+3/2,A2+1)+A6B(A1+N+2,A2+1)+A7B(A1+N+5/2,A2+1)],
(15) where
B(x,y)≡Γ(x)Γ(y)/Γ(x+y) is the Beta function.According to the factorization scheme presented in Ref. [25], the partonic cross section can be expressed as a product of a process-dependent hard function and a process-independent Sudakov exponential term [13, 14, 26-29]. The higher-order QCD contributions to the partonic cross section contain logarithmic terms of type
αns(M2/p2T)lnm(M2/p2T) , which become large in the small-pT region. These logarithmically-enhanced contributions arising at smallpT spoil the convergence of the fixed-order perturbative expansion and must therefore be resummed to all orders inαs . We adopt the b-space resummation approach, which was fully formulated by Collins, Soper, and Sterman [9-12], to systematically resum the large logarithmic terms at smallpT . In this approach, a Bessel transform is applied to the partonic cross section,ˆσab(N,M2,p2T,μ2F,μ2R)=∫∞0dbb2J0(bpT)׈σab(N,M2,b2,μ2F,μ2R),
(16) where
J0(x) is the zeroth-order Bessel function. Given that impact parameter b is the variable conjugate to transverse momentumpT , the limitM/pT→0 corresponds toMb→∞ . Therefore, the large logarithms ofM/pT arising at smallpT turn into large logarithms of Mb,[(M2/p2T)lnm(M2/p2T)]+⟶lnm+1(M2b2)+⋯
(17) After performing the resummation procedure, the resummed partonic cross section in the conjugate b-space at the NLL accuracy can be expressed as [9-12]
ˆσ(res.)ab(N,M2,b2,μ2F,μ2R)=∑a′,a′′,b′,b′′E(1)a′a(N,1/ˉb2,μ2F)×E(1)b′b(N,1/ˉb2,μ2F)Ca′′a′(N,1/ˉb2)×Cb′′b′(N,1/ˉb2)Ha′′b′′(M2,μ2R)×exp[Ga′′b′′(M2ˉb2,M2,μ2R)],
(18) where
ˉb is the normalized impact parameter defined byˉb=b/b0 withb0=2e−γE [17], and the one-loop QCD evolution operatorE(1)ab is derived from the collinear-improved procedure as recommended in Refs. [30-34]. In the physical resummation scheme, the coefficient functionCab and the Sudakov form factorGab are free from any hard contributions, and the hard functionHab , determined by the finite part of the renormalized virtual contribution, is free from any logarithmic contributions [16]. To transform the resummed partonic cross sectionˆσ(res.)ab(N,M2,b2,μ2F,μ2R) back to the physicalpT -space, we rewrite Eq. (16) as [35]ˆσ(res.)ab(N,M2,p2T,μ2F,μ2R)=∑k=1,2∫Ckdbb4hk(bpT,v)׈σ(res.)ab(N,M2,b2,μ2F,μ2R),
(19) where
hk(x,v)=(−1)kπ∫(−1)kπ+ivπ−ivπdθe−ixsinθ,(k=1,2),
(20) are two auxiliary Hankel-like functions satisfying
h1(x,v)+h2(x,v)=2J0(x) , and the integration contoursCk(k=1,2) in the complex b-plane are defined byCk:b=b(t)≡te(−1)kiφ,t∈[0,+∞)withφ∈(0,π/2).
(21) It is well known that such contours avoid the Landau pole by a deformation into either the upper or lower half complex b-plane.
The invariant mass distribution of the final-state
ϕ0A0 system in the Mellin N-space can be obtained by integrating Eq. (13) over the transverse momentumpT . In the threshold regime, the large logarithmic terms of the typeαns(1−z)−1lnm(1−z) also spoil the convergence of the perturbative series. These singular terms turn into large logarithms of the Mellin variable, N:[(1−z)−1lnm(1−z)]+⟶lnm+1N+⋯.
(22) The corresponding resummed partonic cross section for invariant mass distribution at the NLL accuracy can be expressed as [36, 37]
ˆσ(res.)ab(N,M2,μ2F,μ2R)=∑a′,b′E(1)a′a(N,M2/ˉN2,μ2F)×E(1)b′b(N,M2/ˉN2,μ2F)˜Ha′b′(M2,μ2R)×exp[˜Ga′b′(ˉN,M2,μ2R)],
(23) where
ˉN is the reduced Mellin variable defined byˉN=NeγE .The hard functions,
Hab and˜Hab , do not contain any large logarithms. They can be perturbatively calculated and read at the NLO accuracy:Hab(M2,μ2R)=ˆσ(0)ab(M2)(1+asA0),˜Hab(M2,μ2R)=Hab(M2,μ2R)+asπ26[A(1)a+A(1)b]ˆσ(0)ab(M2),
(24) where
as=αs/(2π) ,A(1)a=2Ca ①,ˆσ(0)ab is the lowest-order partonic cross section, andA0 represents the IR-finite part of the renormalized virtual correction in the dimensional regularization scheme, i.e.,ˆσ(vir.)ab(M2,μ2R)=as(4πμ2RM2)ϵΓ(1−ϵ)Γ(1−2ϵ)(A−2ϵ2+A−1ϵ+A0)ˆσ(0)ab(M2)+O(ϵ).
(25) The Sudakov form factors
Gab and˜Gab collect all the logarithmically-enhanced contributions and take the formGab(ω,M2,μ2R)=LG(1)ab(λ)++∞∑n=0ansG(n+2)ab(λ,M2/μ2R),(G=Gor˜G),
(26) with
λ=asβ0L ,L=lnω , andω=M2ˉb2 andˉN forG=G and˜G , respectively. The functionG(n+1)ab(n=0,1,2,...) on the right side of Eq. (26) resums all theNnLL contributions. In this study, we only consider the LL and NLL terms, i.e.,LG(1)ab andG(2)ab , because the electroweak production ofϕ0A0 is studied at the NLO+NLL accuracy. The analytic expressions forG(1)ab andG(2)ab can be found in Ref. [38]. Finally, theCab function in Eq. (18) at the NLL accuracy can be expressed asCab(N,μ2R)=δab+as[π26Caδab−P′ab(N)],
(27) where
P′ab(N) is theO(ϵ) part of the unregulated Altarelli-Parisi splitting function in the Mellin N-space, i.e.,Pab(z,ϵ)=Pab(z)+ϵP′ab(z),P′ab(N)=∫10dzzN−1P′ab(z).
(28) The resummed partonic cross section
ˆσ(res.)ab gives the dominant contribution in the small-pT and threshold regions, while the fixed-order partonic cross sectionˆσ(f.o.)ab dominates at largepT and smallM/√ˆs . To obtain a reliable theoretical prediction with uniform accuracy in all kinematical regions, the resummed and fixed-order results should be combined consistently by subtracting their overlap,ˆσab=ˆσ(res.)ab+ˆσ(f.o.)ab−ˆσ(o.l.)ab.
(29) This matching procedure guarantees that the combined result
ˆσab contains both the perturbative contributions up to the specific fixed order and the logarithmically-enhanced contributions from higher orders. At the NLO+NLL accuracy,ˆσ(o.l.)ab in Eq. (29) can be obtained by expanding the resummed partonic cross sectionˆσ(res.)ab toO(αs) , i.e.,ˆσ(o.l.)ab=ˆσ(res.)ab(αs=0)+αsdˆσ(res.)abdαs(αs=0).
(30) After multiplying the Mellin moments of the PDFs to the NLO+NLL matched partonic cross section
ˆσab , we obtain the hadronic differential cross section in the Mellin N-space. To get back to the physical space, an inverse Mellin transform,F(τ)=12πi∫CNdNτ−NF(N),
(31) should be applied to the right side of Eq. (13). To achieve this, we must comprehensively estimate the singularities in the Mellin N-space and choose an appropriate integration contour
CN . There are two types of singularities for the hadronic differential cross section in the Mellin N-space: (1) the poles in the Mellin moments of the PDFs (Regge poles), and (2) the Landau pole related to the running of the strong coupling constant. The integration contourCN in the complex N-plane is chosen as [15]CN:N=N(y)≡C+ye±iϕ,y∈[0,+∞)
(32) where
ϕ∈[π/2,π) and the constant C is chosen such that the Regge and Landau poles lie to the left and right ofCN , respectively.In principle, for NLO+NLL calculations, we should employ resummation-improved PDFs for initial-state parton convolution. The threshold-resummation improved PDFs are now available with the NNPDF3.0 set. Compared to the NNPDF3.0 global fit, the threshold-resummation improved PDF fit has to be performed with a reduced data set involving deep-inelastic scattering, Drell-Yan, and top-pair production data, because the threshold resummation calculations are not readily available for all the processes employed in the global analysis. The reduced data set used in the fit of the threshold-resummation improved PDF set would induce a relatively larger PDF error compared to the global PDF set. In this study, we adopt the factorization method proposed in Ref. [18] to combine the smaller PDF error of the global PDF set with the resummation effect from the threshold-resummation improved PDF set. In the factorization method, the NLO+NLL QCD corrected cross section can be approximately calculated by
σNLO+NLL=K×σNLO|(NLOglobal),
(33) where
K=KPDF×KPME,
(34) KPDF=σNLO+NLL|(NLO+NLLreduced)σNLO+NLL|(NLOreduced),KPME=σNLO+NLL|(NLOglobal)σNLO|(NLOglobal)
(35) which describe the impact of the threshold-resummation improved PDFs and the NLL resummation effect from the partonic matrix element, respectively. Subscripts “NLO+NLL reduced ” and “NLO reduced ” appearing in the definition of
KPDF denote the threshold-resummation improved PDF set NNPDF30_nll_disdytop and its fixed-order version NNPDF30_nlo_disdytop [39], respectively. It is well known that the NNPDF cannot be properly transformed to the Mellin space; the refit of the NNPDF replicas in the Mellin space would lead to some convergence issues [40]. Fortunately, however,KPME is expected to be largely independent of the PDF choice because the PDF sets used inKPME are estimated at the same perturbative order [40]. This feature has been verified with the CT18NLO and MSTW2008nlo68cl PDFs, and thus we choose CT18NLO as the “NLO global” PDF set in our calculations. -
Compared to the electroweak production via quark-antiquark annihilation, the gluon-initiated QCD production of the scalar-pseudoscalar pair is a loop-induced production channel. This production mechanism should be taken into consideration at the LHC due to the high luminosity of gluon in proton. In Fig. 2 we depict some representative Feynman diagrams for
gg→ϕ0A0 at the lowest order. Note that the production rate relies not only on the heavy-quark Yukawa couplings, but also on the triple Higgs self-couplings. Unlike the quark-antiquark annihilation channel, the loop-induced gluon-gluon fusion channel is extremely sensitive to the Yukwawa interaction of the 2HDM. Due to the introduction of a soft breakingZ2 symmetry to avoid tree-level FCNCs, each fermion type is only able to couple to one of the two Higgs doublets. There are four allowed types of 2HDMs, type-I, type-II, lepton-specific, and flipped, which correspond to the four different types of Yukawa interaction. In this study, we mainly focused on the type-I 2HDM and calculated the gluon-gluon fusion channel by using the modified FeynArts-3.9, FormCalc-7.3, and LoopTools-2.8 packages [41-43]. -
In this section, we provide some numerical results for
pp→ϕ0A0+X at the13TeV LHC in the type-I 2HDM. The SM input parameters used in this study are set as [44]mW=80.379GeV,mZ=91.1876GeV,mt=172.76GeV,GF=1.1663787×10−5GeV−2,αs(mZ)=0.118.
(36) The input parameters for the Higgs sector of the 2HDM should satisfy the theoretical constraints from perturbative unitarity [45], stability of vacuum [46], and tree-level unitarity [47], which can be checked by 2HDMC [19]. Moreover, the high-energy experiments can also give stringent constraints on the 2HDM input parameters. One of the experimental limits is that the partial width of
Z0→H0A0/h0A0 cannot exceed 2σ uncertainty of the Z-width measurement [44], and others come from the restriction of the physical observables of B meson decays, the measurement of the SM-like Higgs property, and the direct search of Higgs state at the LEP, Tevatron, and LHC, which are integrated in the SuperIso [48], HiggsSignals [49], and Higgsbounds [50] packages, respectively.We use the CT14lo PDF set [24] to perform LO calculation, and employ the CT18NLO PDF [51] to obtain NLO and NLO+NLL QCD corrected cross sections. CT18NLO PDF contains 1 central PDF set and
2×29 Hessian replicas. The PDF uncertainties of a cross section σ calculated with the CT18NLO PDF are given by [52]δ+PDF=1σ0√29∑i=1[max{σi+−σ0,σi−−σ0,0}]2,δ−PDF=1σ0√29∑i=1[max{σ0−σi+,σ0−σi−,0}]2,
(37) where
σ0 is the central value calculated with central set andσi±(i=1,...,29) are the cross sections evaluated with replicas. The factorization scaleμF and the renormalization scaleμR are set to be equal, i.e.,μF=μR=μ , for simplicity. The scale uncertainties of an integrated cross section σ are defined byδ+μ=max{σ(μ)|μ0/2⩽
(38) where
\mu_0 is the central scale. The total theoretical error is defined as the sum in quadrature of the PDF and scale uncertainties. For the quark-initiated Drell-Yan production channel,pp \rightarrow q\bar{q} \rightarrow \phi^0A^0 , the production rate will be calculated at the NLO+NLL accuracy in QCD, and the NLO and NLO+NLL relative corrections are respectively defined as\delta^{\text{NLO}} = \frac{\sigma^{\text{NLO}} - \sigma^{\text{LO}}}{\sigma^{\text{LO}}}, \quad \delta^{\text{NLO+NLL}} = \frac{\sigma^{\text{NLO+NLL}} - \sigma^{\text{LO}}}{\sigma^{\text{LO}}}.
(39) Regarding the gluon-gluon fusion channel,
pp \rightarrow gg \rightarrow \phi^0A^0 , we only consider the lowest-order contribution since it is a loop-induced channel. -
In this subsection, we present the integrated cross sections for
\phi^0A^0 associated production at\sqrt{s} = 13\; \text{TeV} LHC at the alignment limit in the 2HDM. The masses of\phi^0 andA^0 can be alternatively described by the following three parameters,\begin{aligned}[b]& m = \min\left( m_{\phi^0},\, m_{A^0} \right), \qquad \Delta m = \left| m_{\phi^0} - m_{A^0} \right|, \\&\epsilon = \text{sign} \left( m_{\phi^0} - m_{A^0} \right), \end{aligned}
(40) i.e., the minimal mass and mass hierarchy of
\phi^0 andA^0 . The two scenarios in which\epsilon = +1 (m_{\phi^0} > m_{A^0} ) and\epsilon = -1 (m_{\phi^0} < m_{A^0} ) may be referred to as the normal mass hierarchy and inverted mass hierarchy, respectively.The Drell-Yan production channel depends only on the masses of
\phi^0 andA^0 ②. Furthermore, its integrated cross section is independent of\epsilon . In our calculations, we set0 , 50, and100\;\; \text{GeV} as three benchmark values of\Delta m , which correspond, respectively, to the following three\phi^0 -A^0 mass splitting scenarios:● degenerate scenario:
\Delta m = 0 ● hierarchical scenario with small mass splitting:
0< \Delta m < m_Z ● hierarchical scenario with large mass splitting:
\Delta m > m_Z The LO, NLO, NLO+NLL QCD corrected integrated cross sections and the corresponding theoretical relative errors induced by the factorization/renormalization scale and PDFs for
pp \rightarrow q\bar{q} \rightarrow \phi^0A^0 as functions of m for\Delta m = 0 , 50 and100\; \text{GeV} are given in Tables 4, 5, and 6, respectively. The central scale is set as\mu_0 = m_{\phi^0} + m_{A^0} . There is no PDF-induced theoretical error for the LO cross section because the CT14lo PDF used in the LO calculation contains only one central set but no PDF replicas. To study the full NLL resummation effect and the impact of the threshold-resummation improved PDFs in our calculations, we also provide the factorization K-factors K andK_{\text{PDF}} in these tables. The NLO+NLL QCD relative correction\delta^{\text{NLO+NLL}} and the matrix-element-induced factorization K-factorK_{\text{PME}} can be straightforwardly calculated by using\delta^{\text{NLO}} , K, andK_{\text{PDF}} ,m\,\text{[GeV]} 
\sigma^{\text{LO} } \text{[fb]} 
\sigma^{\text{NLO} } \text{[fb]} 
\sigma^{\text{NLO+NLL} } \text{[fb]} 
\delta^{\text{NLO}} [%]
K K_{\text{PDF}} 
50 4923.7_{-9.4{\text{%}}}^{+8.5{\text{%}}} 
6717.8_{-0.4{\text{%}}-3.7{\text{%}}}^{+0.7{\text{%}}+2.8{\text{%}}} 
6731.0_{-0.6{\text{%}}-3.7{\text{%}}}^{+0.0{\text{%}}+2.8{\text{%}}} 
36.4 
1.002 
1.013 
100 
218.7_{-3.2{\text{%}}}^{+2.5{\text{%}}} 
290.2_{-0.4{\text{%}}-3.8{\text{%}}}^{+0.9{\text{%}}+2.9{\text{%}}} 
290.8_{-0.4{\text{%}}-3.8{\text{%}}}^{+0.0{\text{%}}+2.9{\text{%}}} 
32.7 
1.002 
1.011 
150 
49.41_{-0.5{\text{%}}}^{+0.1{\text{%}}} 
63.75_{-0.9{\text{%}}-4.3{\text{%}}}^{+1.4{\text{%}}+3.3{\text{%}}} 
63.94_{-0.4{\text{%}}-4.3{\text{%}}}^{+0.0{\text{%}}+3.3{\text{%}}} 
29.0 
1.003 
1.009 
200 
16.98_{-1.4{\text{%}}}^{+1.2{\text{%}}} 
21.40_{-1.3{\text{%}}-4.7{\text{%}}}^{+1.6{\text{%}}+3.6{\text{%}}} 
21.49_{-0.6{\text{%}}-4.7{\text{%}}}^{+0.1{\text{%}}+3.6{\text{%}}} 
26.0 
1.004 
1.006 
300 
3.504_{-3.3{\text{%}}}^{+3.4{\text{%}}} 
4.249_{-1.8{\text{%}}-5.7{\text{%}}}^{+1.9{\text{%}}+4.3{\text{%}}} 
4.267_{-1.2{\text{%}}-5.7{\text{%}}}^{+0.8{\text{%}}+4.3{\text{%}}} 
21.3 
1.004 
1.001 
400 
1.051_{-4.5{\text{%}}}^{+4.9{\text{%}}} 
1.233_{-2.2{\text{%}}-6.3{\text{%}}}^{+2.2{\text{%}}+5.0{\text{%}}} 
1.237_{-1.7{\text{%}}-6.3{\text{%}}}^{+1.5{\text{%}}+5.0{\text{%}}} 
17.3 
1.003 
0.994 
500 
0.3848_{-5.4{\text{%}}}^{+6.0{\text{%}}} 
0.4387_{-2.5{\text{%}}-7.1{\text{%}}}^{+2.4{\text{%}}+5.8{\text{%}}} 
0.4392_{-2.2{\text{%}}-7.1{\text{%}}}^{+2.1{\text{%}}+5.8{\text{%}}} 
14.0 
1.001 
0.985 
600 
0.1597_{-6.2{\text{%}}}^{+6.9{\text{%}}} 
0.1773_{-2.8{\text{%}}-7.9{\text{%}}}^{+2.6{\text{%}}+6.6{\text{%}}} 
0.1771_{-2.9{\text{%}}-7.9{\text{%}}}^{+2.6{\text{%}}+6.6{\text{%}}} 
11.0 
0.999 
0.977 
700 
0.07213_{-6.9{\text{%}}}^{+7.8{\text{%}}} 
0.07818_{-3.1{\text{%}}-8.8{\text{%}}}^{+2.8{\text{%}}+7.5{\text{%}}} 
0.07770_{-3.5{\text{%}}-8.8{\text{%}}}^{+3.2{\text{%}}+7.5{\text{%}}} 
8.39 
0.994 
0.966 
800 
0.03465_{-7.4{\text{%}}}^{+8.5{\text{%}}} 
0.03670_{-3.3{\text{%}}-9.7{\text{%}}}^{+3.0{\text{%}}+8.4{\text{%}}} 
0.03618_{-4.4{\text{%}}-9.7{\text{%}}}^{+3.7{\text{%}}+8.4{\text{%}}} 
5.92 
0.986 
0.952 
Table 4. LO, NLO, NLO+NLL QCD corrected integrated cross sections, NLO QCD relative corrections, and factorization K-factors (K and
K_{\text{PDF}} ) forpp \rightarrow q\bar{q} \rightarrow \phi^0A^0 at\sqrt{s} = 13\; \text{TeV} LHC within the 2HDM. The cross section central values are folded with the theoretical relative errors estimated from scale variation (first quote) and PDFs (second quote). The mass splitting between\phi^0 andA^0 is fixed to zero (\Delta m = 0 ).m\; \text{[GeV]} 
\sigma^{\text{LO}}\; \text{[fb]} 
\sigma^{\text{NLO}}\; \text{[fb]} 
\sigma^{\text{NLO+NLL}}\; \text{[fb]} 
\delta^{\text{NLO}} [%]
K K_{\text{PDF}} 
50 611.1_{-5.3{\text{%}}}^{+4.5{\text{%}}} 
824.5_{-0.0{\text{%}}-3.7{\text{%}}}^{+0.5{\text{%}}+2.8{\text{%}}} 
825.8_{-0.4{\text{%}}-3.7{\text{%}}}^{+0.0{\text{%}}+2.8{\text{%}}} 
34.9 
1.002 
1.012 
100 
93.88_{-1.6{\text{%}}}^{+1.1{\text{%}}} 
122.7_{-0.7{\text{%}}-4.0{\text{%}}}^{+1.2{\text{%}}+3.1{\text{%}}} 
123.0_{-0.3{\text{%}}-4.0{\text{%}}}^{+0.0{\text{%}}+3.1{\text{%}}} 
30.7 
1.002 
1.010 
150 
27.61_{-0.7{\text{%}}}^{+0.4{\text{%}}} 
35.19_{-1.1{\text{%}}-4.5{\text{%}}}^{+1.5{\text{%}}+3.5{\text{%}}} 
35.31_{-0.5{\text{%}}-4.5{\text{%}}}^{+0.0{\text{%}}+3.5{\text{%}}} 
27.5 
1.003 
1.007 
200 
10.77_{-2.0{\text{%}}}^{+1.9{\text{%}}} 
13.43_{-1.4{\text{%}}-4.9{\text{%}}}^{+1.7{\text{%}}+3.8{\text{%}}} 
13.48_{-0.8{\text{%}}-4.9{\text{%}}}^{+0.3{\text{%}}+3.8{\text{%}}} 
24.7 
1.004 
1.005 
300 
2.517_{-3.6{\text{%}}}^{+3.8{\text{%}}} 
3.026_{-1.9{\text{%}}-5.8{\text{%}}}^{+2.0{\text{%}}+4.5{\text{%}}} 
3.038_{-1.3{\text{%}}-5.8{\text{%}}}^{+1.0{\text{%}}+4.5{\text{%}}} 
20.2 
1.004 
0.999 
400 
0.8032_{-4.8{\text{%}}}^{+5.2{\text{%}}} 
0.9353_{-2.3{\text{%}}-6.5{\text{%}}}^{+2.2{\text{%}}+5.2{\text{%}}} 
0.9388_{-1.9{\text{%}}-6.5{\text{%}}}^{+1.6{\text{%}}+5.2{\text{%}}} 
16.4 
1.004 
0.992 
500 
0.3053_{-5.6{\text{%}}}^{+6.2{\text{%}}} 
0.3457_{-2.6{\text{%}}-7.3{\text{%}}}^{+2.4{\text{%}}+6.0{\text{%}}} 
0.3458_{-2.5{\text{%}}-7.3{\text{%}}}^{+2.2{\text{%}}+6.0{\text{%}}} 
13.2 
1.000 
0.983 
600 
0.1299_{-6.4{\text{%}}}^{+7.2{\text{%}}} 
0.1433_{-2.8{\text{%}}-8.1{\text{%}}}^{+2.7{\text{%}}+6.8{\text{%}}} 
0.1430_{-3.1{\text{%}}-8.1{\text{%}}}^{+2.8{\text{%}}+6.8{\text{%}}} 
10.3 
0.998 
0.974 
700 
0.05969_{-7.0{\text{%}}}^{+7.9{\text{%}}} 
0.06432_{-3.1{\text{%}}-9.0{\text{%}}}^{+2.9{\text{%}}+7.7{\text{%}}} 
0.06361_{-3.3{\text{%}}-9.0{\text{%}}}^{+3.7{\text{%}}+7.7{\text{%}}} 
7.76 
0.989 
0.960 
800 
0.02904_{-7.6{\text{%}}}^{+8.6{\text{%}}} 
0.03059_{-3.4{\text{%}}-9.9{\text{%}}}^{+3.1{\text{%}}+8.7{\text{%}}} 
0.03008_{-4.4{\text{%}}-9.9{\text{%}}}^{+3.9{\text{%}}+8.7{\text{%}}} 
5.34 
0.983 
0.949 
Table 5. Same as Table IV but for
\Delta m = 50\; \text{GeV} .m \text{[GeV]} 
\sigma^{\text{LO} } \text{[fb]} 
\sigma^{\text{NLO} } \text{[fb]} 
\sigma^{\text{NLO+NLL} } \text{[fb]} 
\delta^{\text{NLO}} [%]
K K_{\text{PDF}} 
50 185.0_{-3.0{\text{%}}}^{+2.4{\text{%}}} 
245.3_{-0.4{\text{%}}-3.9{\text{%}}}^{+1.0{\text{%}}+2.9{\text{%}}} 
245.7_{-0.4{\text{%}}-3.9{\text{%}}}^{+0.0{\text{%}}+2.9{\text{%}}} 
32.6 
1.002 
1.011 
100 
45.97_{-0.4{\text{%}}}^{+0.1{\text{%}}} 
59.26_{-1.0{\text{%}}-4.3{\text{%}}}^{+1.4{\text{%}}+3.3{\text{%}}} 
59.43_{-0.4{\text{%}}-4.3{\text{%}}}^{+0.0{\text{%}}+3.3{\text{%}}} 
28.9 
1.003 
1.009 
150 
16.30_{-1.4{\text{%}}}^{+1.2{\text{%}}} 
20.53_{-1.4{\text{%}}-4.8{\text{%}}}^{+1.5{\text{%}}+3.6{\text{%}}} 
20.60_{-0.7{\text{%}}-4.8{\text{%}}}^{+0.1{\text{%}}+3.6{\text{%}}} 
26.0 
1.003 
1.006 
200 
7.033_{-2.5{\text{%}}}^{+2.4{\text{%}}} 
8.683_{-1.6{\text{%}}-5.2{\text{%}}}^{+1.8{\text{%}}+4.0{\text{%}}} 
8.717_{-0.9{\text{%}}-5.2{\text{%}}}^{+0.5{\text{%}}+4.0{\text{%}}} 
23.5 
1.004 
1.004 
300 
1.832_{-3.9{\text{%}}}^{+4.2{\text{%}}} 
2.183_{-2.0{\text{%}}-5.9{\text{%}}}^{+2.1{\text{%}}+4.7{\text{%}}} 
2.192_{-1.5{\text{%}}-5.9{\text{%}}}^{+1.1{\text{%}}+4.7{\text{%}}} 
19.2 
1.004 
0.998 
400 
0.6183_{-5.0{\text{%}}}^{+5.5{\text{%}}} 
0.7146_{-2.3{\text{%}}-6.7{\text{%}}}^{+2.3{\text{%}}+5.4{\text{%}}} 
0.7168_{-2.1{\text{%}}-6.7{\text{%}}}^{+1.8{\text{%}}+5.4{\text{%}}} 
15.6 
1.003 
0.990 
500 
0.2433_{-5.8{\text{%}}}^{+6.5{\text{%}}} 
0.2736_{-2.6{\text{%}}-7.5{\text{%}}}^{+2.5{\text{%}}+6.2{\text{%}}} 
0.2738_{-2.7{\text{%}}-7.5{\text{%}}}^{+2.3{\text{%}}+6.2{\text{%}}} 
12.5 
1.001 
0.982 
600 
0.1059_{-6.5{\text{%}}}^{+7.4{\text{%}}} 
0.1161_{-2.9{\text{%}}-8.4{\text{%}}}^{+2.7{\text{%}}+7.1{\text{%}}} 
0.1157_{-3.2{\text{%}}-8.4{\text{%}}}^{+2.9{\text{%}}+7.1{\text{%}}} 
9.63 
0.997 
0.972 
700 
0.04949_{-7.2{\text{%}}}^{+8.1{\text{%}}} 
0.05301_{-3.2{\text{%}}-9.2{\text{%}}}^{+2.9{\text{%}}+7.9{\text{%}}} 
0.05250_{-3.8{\text{%}}-9.2{\text{%}}}^{+3.4{\text{%}}+7.9{\text{%}}} 
7.11 
0.990 
0.959 
800 
0.02438_{-7.7{\text{%}}}^{+8.8{\text{%}}} 
0.02554_{-3.4{\text{%}}-10.1{\text{%}}}^{+3.1{\text{%}}+9.0{\text{%}}} 
0.02505_{-4.4{\text{%}}-10.1{\text{%}}}^{+3.9{\text{%}}+9.0{\text{%}}} 
4.76 
0.981 
0.945 
Table 6. Same as Table IV but for
\Delta m = 100\; \text{GeV} .\delta^{\text{NLO+NLL}} = \left( K - 1 \right) + K \delta^{\text{NLO}}, \qquad K_{\text{PME}} = \frac{K}{K_{\text{PDF}}}.
(41) As shown in Tables 4, 5, and 6, the QCD correction can significantly enhance the LO production cross section, especially for light scalar-pseudoscalar pair. The NLO QCD relative correction exceeds 30% at
m = 50\; \text{GeV} , and decreases gradually to approximately 5.9%, 5.3%, and 4.8% for\Delta m = 0 , 50, and100\; \text{GeV} , respectively, as m increases to800\; \text{GeV} . The full NLL resummation correction (quantitatively described byK-1 ) slightly enhances the NLO QCD corrected cross section asm < 500\; \text{GeV} , but suppresses it by approximately 2% in the high mass region. Compared to the full NLL resummation correction, the contribution from the threshold-resummation improved PDFs is more sensitive to m. The corresponding relative correction, i.e.,K_{\text{PDF}} - 1 , decreases monotonically as the increase of m, and reaches approximately –5% whenm = 800\; \text{GeV} . Moreover, we can find that the impact of the threshold-resummation improved PDFs becomes increasingly important with the increment of m for heavy scalar-pseudoscalar pair. On the contrary, the NLL QCD relative correction from the partonic matrix element,K_{\text{PME}} - 1 , increases monotonically with the increment of m. It is almost independent of the mass splitting between\phi^0 andA^0 , varying from approximately –1% to 4% as m increases from 50 to800\; \text{GeV} .The QCD production of
\phi^0A^0 via gluon-gluon fusion depends not only onm_{\phi^0} andm_{A^0} , but also onm_{12}^2 and\tan\beta , since the Yukawa couplings and triple Higgs self-couplings are involved in this production channel. We calculate the lowest-order production cross section for this loop-induced channel at the two benchmark points listed in Table 7, which can satisfy both theoretical and experimental constraints. At both benchmark points,H^0 is the BSM{\cal{C}}{\cal{P}} -even Higgs boson, i.e.,H^0 = \phi^0 , and\sin(\beta - \alpha) = 1 at the alignment limit. The other two Higgs parameters of 2HDM,m_{h^0} andm_{H^{\pm}} , are not given in Table 7, because the scalar-pseudoscalar pair production at QCD NLO+NLL accuracy is completely independent from the SM-like and charged Higgs bosons. The integrated cross sections forpp \rightarrow gg \rightarrow \phi^0A^0 at\sqrt{s} = 13\; \text{TeV} LHC in the type-I 2HDM at BP1 and BP2, listed in Table 8, are approximately 1 and0.06\; \text{fb} , respectively. We can see that\sigma_{gg}/\sigma^{\text{NLO+NLL}} , i.e., the ratio of the contribution from gluon-gluon fusion channel to the NLO+NLL QCD corrected cross section of quark-antiquark annihilation channel, is approximately 2.9% at BP1 and can reach 8.0% at BP2. It can be concluded that the scalar-pseudoscalar pair production at the LHC in the type-I 2HDM is predominated by the quark-initiated Drell-Yan production channel, and the gluon-gluon fusion contribution is non-negligible and should be taken into consideration in precision predictions.Benchmark point m_{H^0} \text{/GeV} 
m_{A^0} \text{/GeV} 
m_{12}^2 
\tan\beta 
BP1 150 200 2000 10 BP2 400 500 50000 2 Table 7. Benchmark points BP1 and BP2.
Benchmark point BP1 BP2 \sigma_{gg} \text{/fb} 
1.020_{-19.8{\text{%}}-3.4{\text{%}}}^{+26.4{\text{%}}+3.7{\text{%}}} 
0.05742^{+31.8{\text{%}}+8.0{\text{%}}}_{-22.7{\text{%}}-6.4{\text{%}}} 
Table 8. Lowest-order integrated cross sections for
pp \rightarrow gg \rightarrow \phi^0A^0 at\sqrt{s} = 13\; \text{TeV} LHC in type-I 2HDM at the benchmark points BP1 and BP2. -
Next, we address the transverse momentum distribution of the scalar-pseudoscalar pair produced at the LHC. Since the one-loop-induced gluon-gluon fusion channel does not contribute to the
p_T distribution due to the momentum conservation, we consider only the quark-initiated Drell-Yan production channel. The NLO, NLO+NLL QCD corrected transverse momentum distributions of\phi^0A^0 as well as the overlap between the NLO QCD corrected and NLL QCD resummedp_T distributions (labeled by “NLO”, “NLO+NLL”, and “OVERLAP”) for the Drell-Yan production of\phi^0A^0 at\sqrt{s} = 13\; \text{TeV} LHC in the 2HDM at the benchmark points BP1 and BP2 are shown in Figs. 3(a) and 4(a), respectively. The central scale is\mu_0 = m_{\phi^0} + m_{A^0} . As expected, the NLO QCD correctedp_T distribution and the overlapp_T distribution are in good agreement with each other in the small-p_T region [16] and become divergent asp_T \rightarrow 0 , but the discrepancy between them becomes increasingly evident with the increment ofp_T . The relative discrepancy between the NLO QCD corrected and the overlapp_T distributions, defined as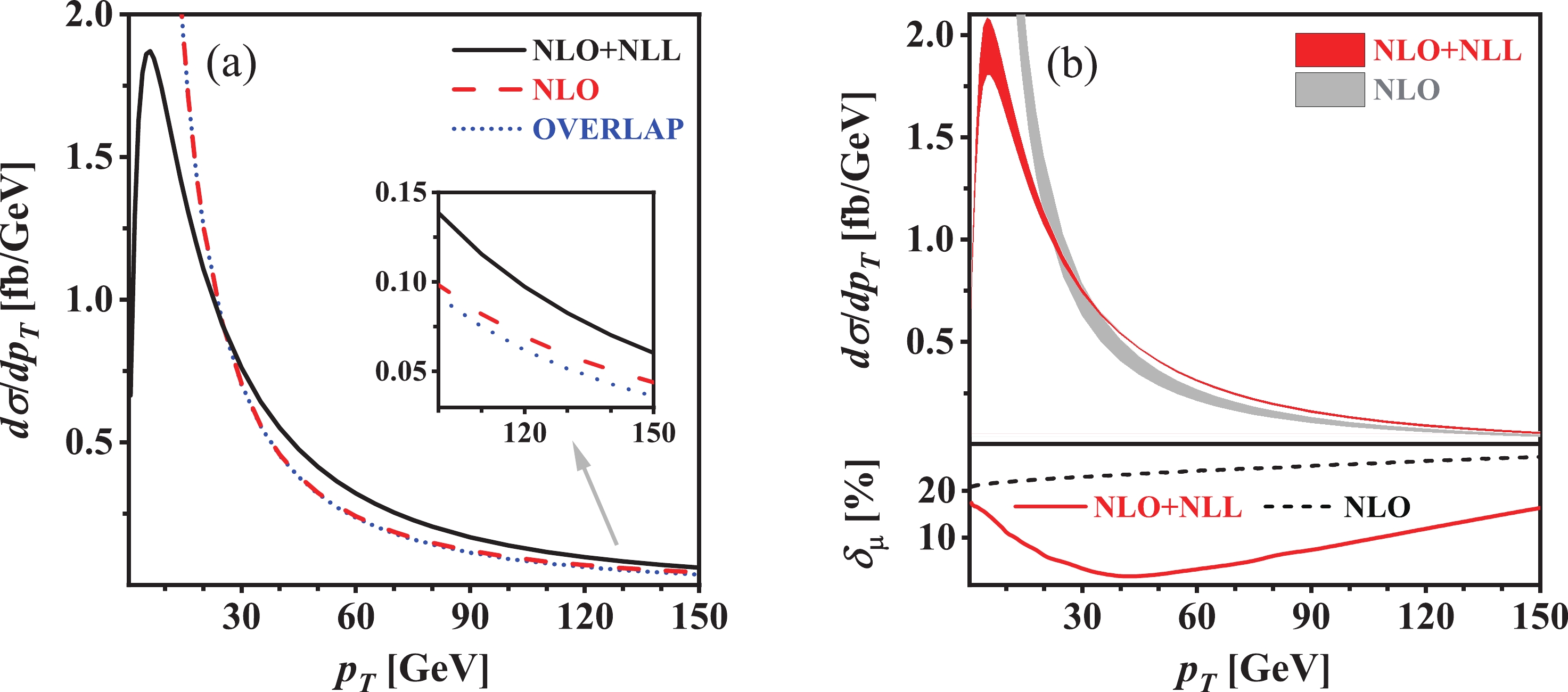
Figure 3. (color online) (a) Transverse momentum distribution of final-state
\phi^0A^0 and (b) its scale uncertainty forpp \rightarrow q\bar{q} \rightarrow \phi^0A^0 at\sqrt{s} = 13\; \text{TeV} LHC within the 2HDM at the benchmark point BP1.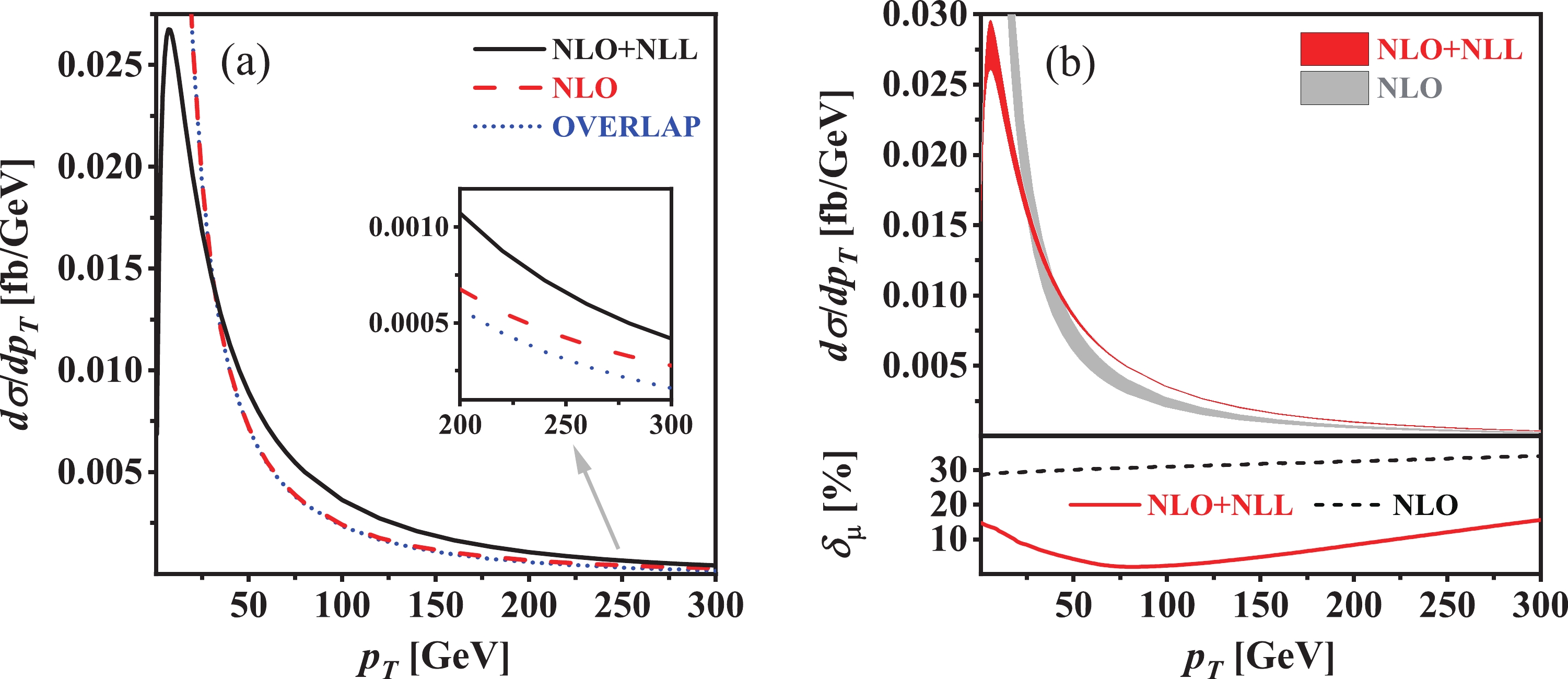
Figure 4. (color online) Same as Fig. 3 but at BP2.
\eta = \left( \frac{{\rm d} \sigma^{\text{NLO}}}{{\rm d} p_T} - \frac{{\rm d} \sigma^{\text{OVERLAP}}}{{\rm d} p_T} \right) \left/ \frac{{\rm d} \sigma^{\text{NLO}}}{{\rm d} p_T} \right.,
(42) can reach about 18.2% and 42.6% when
p_T = 150 and300\; \text{GeV} at BP1 and BP2, respectively. Compared to the NLO QCD correctedp_T distribution, the NLO+NLL QCD correctedp_T distribution is finite and more reliable in the whole final-state phase space. It increases sharply in the small-p_T region, reaches its maximum of around1.9\; \text{fb/GeV} in the vicinity ofp_T \sim 5.5\; \text{GeV} , and then decreases approximately logarithmically with the increment ofp_T at the benchmark point BP1. Concerning the benchmark point BP2, the NLO+NLL QCD correctedp_T distribution peaks atp_T \sim 7.5\; \text{GeV} and its maximum is approximately0.027\; \text{fb/GeV} .The scale uncertainty of a differential distribution with respect to some kinematic variable x can be estimated by
\begin{aligned}[b]& \delta_{\mu}(x) = \max \left\{ \frac{{\rm d} \sigma}{{\rm d} x}(\mu_1) - \frac{{\rm d} \sigma}{{\rm d} x}(\mu_2) \right\} \left/ \frac{{\rm d} \sigma}{{\rm d} x}(\mu_0) \right., \\&\mu_1,\, \mu_2 \in \left[ \mu_0/2,\; 2\mu_0 \right].\end{aligned}
(43) In Figs. 3(b) and 4(b), we plot the scale uncertainties of the NLO and NLO+NLL QCD corrected
p_T distributions, denoted by\delta_{\mu}^{\text{NLO}} and\delta_{\mu}^{\text{NLO+NLL}} , at BP1 and BP2, respectively. As shown in the lower panels of Figs. 3(b) and 4(b), the scale uncertainty of the NLO QCD correctedp_T distribution increases gradually, while the scale uncertainty of the NLO+NLL QCD correctedp_T distribution first decreases consistently before reaching its minimum and then increases monotonically, with the increment ofp_T . Some representative values of\delta_{\mu}^{\text{NLO}} and\delta_{\mu}^{\text{NLO+NLL}} are given in Table 9. This table, as well as Figs. 3(b) and 4(b), clearly shows that\delta_{\mu}^{\text{NLO+NLL}} is much less than\delta_{\mu}^{\text{NLO}} , especially in the intermediate-p_T region. Thus, we conclude that the resummation of higher-order large logarithmic contributions can significantly improve the fixed-order prediction for thep_T distribution; the NLO+NLL QCD correctedp_T distribution is much more reliable in the wholep_T region compared to the NLO QCD correctedp_T distribution.Benchmark point BP1 BP2 p_T = 1\; \text{GeV} 
p_T = 150\; \text{GeV} 
p_T = 2\; \text{GeV} 
p_T = 300\; \text{GeV} 
\delta_{\mu}^{\text{NLO}} 
20.9 %
27.2 %
28.7 %
34.0 %
\delta_{\mu}^{\text{NLO+NLL}} 
17.2 %
16.3 %
16.9 %
15.7 %
\text{min.} \simeq 1.6\%_{\quad \left( @\, p_T \,\sim\, 45\, \text{GeV} \right)} 
\text{min.} \simeq 2.0\%_{\quad \left( @\, p_T \,\sim\, 80\, \text{GeV} \right)} 
Table 9. Scale uncertainties of NLO and NLO+NLL QCD corrected
p_T distributions forpp \rightarrow q\bar{q} \rightarrow \phi^0A^0 at\sqrt{s} = 13\; \text{TeV} LHC within the 2HDM at BP1 and BP2 for some typical values ofp_T . -
In this subsection, we discuss the threshold resummation effect on the invariant mass distribution of the scalar-pseudoscalar pair produced at the
13\; \text{TeV} LHC in the type-I 2HDM. The central scale is set to the invariant mass of the final-state scalar-pseudoscalar pair, i.e.,\mu_0 = M . In the upper panels of Figs. 5(a) and 6(a), we depict the invariant mass distributions of the\phi^0A^0 system for both quark-initiated electroweak Drell-Yan production and gluon-initiated QCD production of\phi^0A^0 at BP1 and BP2, respectively. The corresponding NLO and NLO+NLL QCD relative corrections to the Drell-Yan production channel are provided in the lower panels. The\phi^0A^0 invariant mass distribution of the Drell-Yan channel increases rapidly near the production threshold, and then decreases consistently after reaching its maximum, with the increment of M. It peaks atM \sim 450\; \text{GeV} for BP1 andM \sim 1150\; \text{GeV} for BP2, respectively, at both LO and NLO+NLL accuracies. Compared to the Drell-Yan channel, the\phi^0A^0 invariant mass distribution of the gluon-gluon fusion channel is much smaller, and decreases more quickly with the increment of M. The ratio of the differential cross sections of the two channels,{\rm d}\sigma_{gg}/{\rm d}\sigma^{\text{NLO+NLL}} , is approximately 8.1% atM = 400\; \text{GeV} for BP1 and 24.9% atM = 1000\; \text{GeV} for BP2, respectively, and approaches zero rapidly as the increase of M. It implies that the contribution from the gluon-gluon fusion channel is indispensable near the production threshold, but negligible in the high invariant mass region. The NLO and NLO+NLL QCD relative corrections (\delta^{\text{NLO}} and\delta^{\text{NLO+NLL}} ) to the Drell-Yan channel decrease gradually with the increment of M. They decrease from 29.8% to 1.4% and from 31.0% to −1.3%, respectively, as M increases from400\; \text{GeV} to3\; \text{TeV} at BP1, and vary correspondingly in the range of −7.3%\sim 22.4% and −23.9%\sim 25.9% asM \in [1,\, 4]\; \text{TeV} at BP2.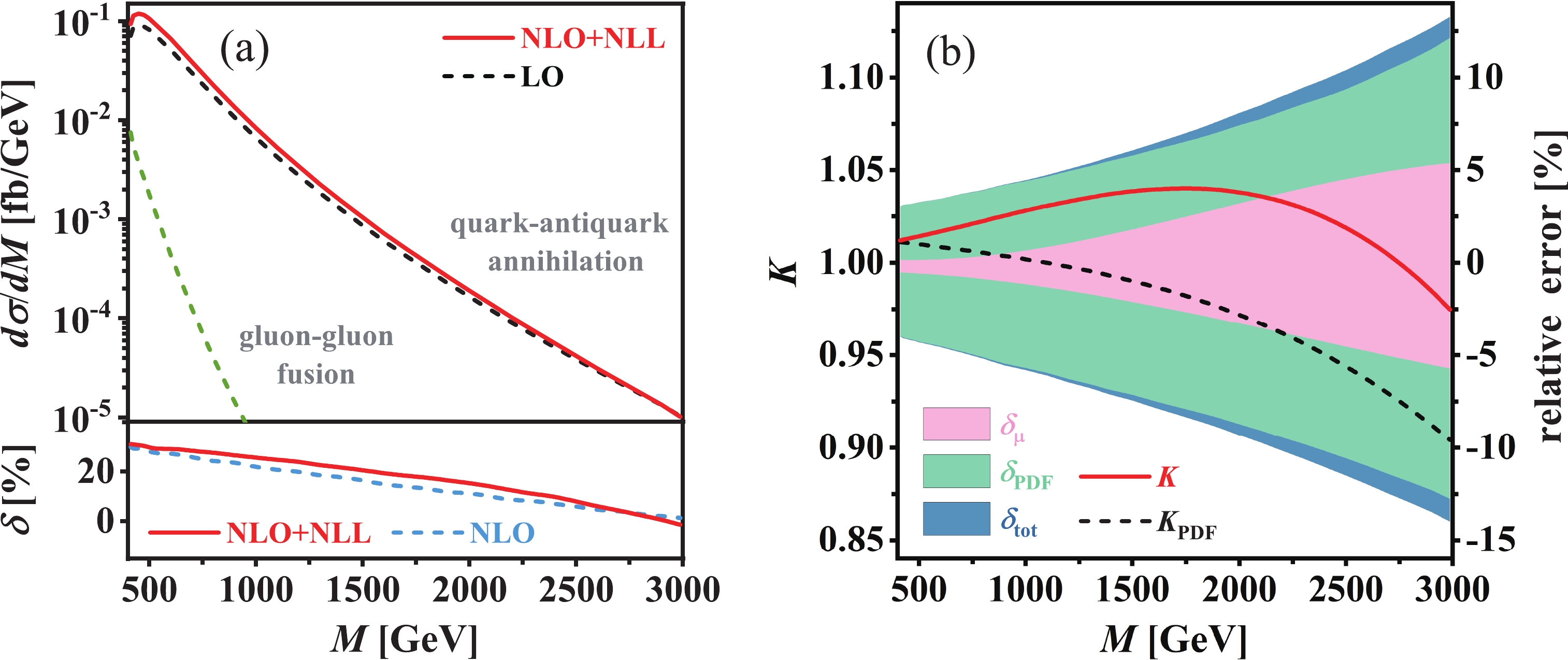
Figure 5. (color online) (a) Invariant mass distribution of final-state
\phi^0A^0 and (b) factorization K-factors (K andK_{\text{PDF}} ) as well as theoretical relative errors (\delta_{\mu} ,\delta_{\text{PDF}} , and\delta_{\text{tot}} ) for\phi^0A^0 associated production at\sqrt{s} = 13\; \text{TeV} LHC in type-I 2HDM at the benchmark point BP1.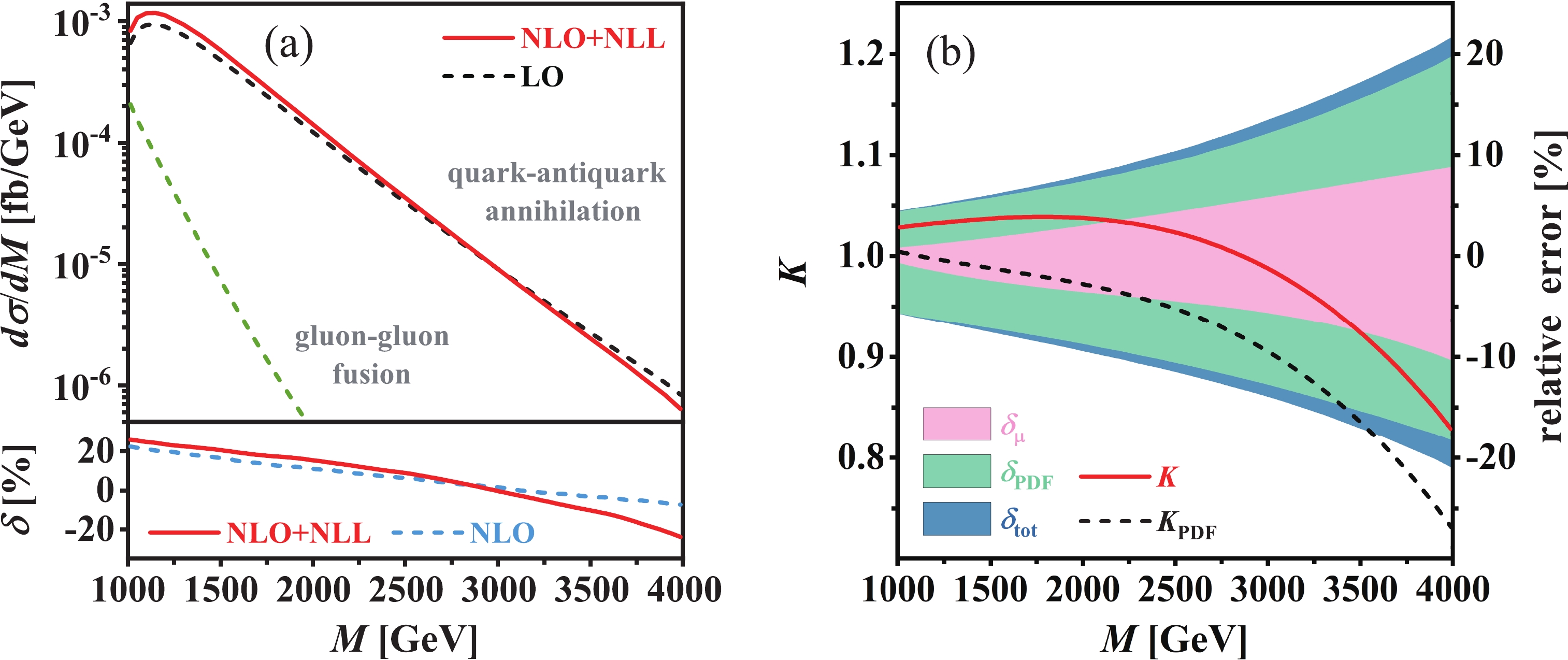
Figure 6. (color online) Same as Fig. 5 but at BP2.
To further demonstrate the full NLL resummation effect and the impact of the threshold-resummation improved PDFs on the
\phi^0A^0 invariant mass distribution of the Drell-Yan channel, we plot the factorization K-factors K andK_{\text{PDF}} as functions of M in Figs. 5(b) and 6(b) for BP1 and BP2, respectively. The theoretical errors from scale variation and PDFs as well as their combination, i.e.,\delta_{\mu} ,\delta_{\text{PDF}} , and\delta_{\text{tot}} , are also displayed in these two figures. At the benchmark point BP1, K increases slowly from 1.01 to 1.04 as the increment of M from400\; \text{GeV} to1.7\; \text{TeV} , and then gradually decreases to 0.97 as M increases to3\; \text{TeV} . The full NLL resummation correction enhances the NLO QCD corrected invariant mass distribution of\phi^0A^0 in the region ofM < 2.7\; \text{TeV} , but it would reduce the invariant mass distribution at sufficiently high invariant mass. However,K_{\text{PDF}} , which quantitatively reflects the impact of the threshold-resummation improved PDFs, decreases consistently from 1.01 to 0.90 as M varies from400\; \text{GeV} to3\; \text{TeV} .K_{\text{PME}} , which describes the NLL resummation effect from the partonic matrix element and is calculated byK/K_{\text{PDF}} , shows the opposite tendency compared toK_{\text{PDF}} : it increases monotonically from1.00 to1.08 with the increment of M. At the benchmark point BP2, K is fairly stable in the range of1\; \text{TeV} < M < 2\; \text{TeV} ; it reaches its maximum of around1.04 atM \sim 1.8\; \text{TeV} and subsequently decreases to0.83 as M increases to4\; \text{TeV} . Simultaneously, a global suppression induced by the threshold-resummation improved PDFs can be clearly observed in the invariant mass distribution. Such suppression effect is very small and could be neglected at relatively low invariant mass, but becomes more and more apparent as the increasing of M. AtM = 4\; \text{TeV} ,K_{\text{PDF}} = 0.73 ; the contribution from the threshold-resummation improved PDFs is more notable at high invariant mass compared to the NLO QCD correction. On the contrary,K_{\text{PME}} increases from 1.02 to 1.13 as M increases from 1 to4\; \text{TeV} . In the high invariant mass region, the contribution from the threshold-resummation improved PDFs is the dominant correction compared to the NLO QCD correction and the NLL resummation correction from the partonic matrix element. For example, atM = 4\; \text{TeV} ,K_{\text{PDF}} - 1 = -27 %,\delta^{\text{NLO}} = -7.3 % andK_{\text{PME}} - 1 = 13 %, respectively. -
Searching for BSM Higgs bosons is an important task at the LHC and future high-energy colliders. In this study, we comprehensively analyze the scalar-pseudoscalar pair production at the
13\; \text{TeV} LHC at the alignment limit in the type-I 2HDM. The Collins-Soper-Sterman resummation approach and the factorization method are employed to resum the NLL contributions and to evaluate the impact of the threshold-resummation improved PDFs, respectively, when addressing the quark-initiated Drell-Yan production channel. Both the integrated cross section and the differential distributions with respect to the transverse momentum and invariant mass of the produced scalar-pseudoscalar pair are provided. For quark-antiquark annihilation channel, the NLO QCD relative correction can exceed 30% in the low Higgs mass region, but decreases rapidly as the increment ofm_{\phi^0} andm_{A^0} . The relative correction induced by the threshold-resummation improved PDFs and the NLL resummation correction from the partonic matrix element,K_{\text{PDF}} - 1 andK_{\text{PME}} - 1 , are insensitive to the mass splitting between\phi^0 andA^0 , and decreases and increases respectively with the increment of Higgs mass. They could be neglected compared to the NLO QCD correction in the low invariant mass region, but become increasingly important with the increment of the invariant mass of\phi^0A^0 , and can even predominate in the high invariant mass region. Moreover, the anomalous behavior of the NLO QCD corrected transverse momentum distribution in the small-p_T region can be resolved, and the scale uncertainty can be heavily reduced, especially in the intermediate-p_T region, by including the NLL resummation correction. Compared to the quark-initiated Drell-Yan channel, the contribution from the gluon-gluon fusion channel is negligible in the high invariant mass region, but indispensable and even comparable to the NLO QCD correction near the production threshold.
Scalar-pseudoscalar pair production at the Large Hadron Collider at NLO+NLL accuracy in QCD
- Received Date: 2021-05-30
- Available Online: 2021-12-15
Abstract: We thoroughly investigate both transverse momentum and threshold resummation effects on scalar-pseudoscalar pair production via quark-antiquark annihilation at the






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





























































 DownLoad:
DownLoad: