-
Astronomic observations of the unexpected dimming of type Ia supernovae (SNe Ia) revealed for the first time that the present universe is in a state of accelerating expansion [1, 2]. To explain the accelerating expansion of the universe, on the one hand, it has been proposed that there is an exotic component of dark energy that is uniformly distributed in the universe. Nevertheless, there are other reasonable mechanisms for the dimming of SNe Ia, for example, the non-conservation of the photon number, which may be caused by scattering and absorption based on some opaque sources. There are many candidates for opaque sources in the universe, such as the dust in the Milky Way and the intermediate galaxy, the intergalactic medium, and their host galaxy [3]. Other plausible mechanisms have been proposed to explain cosmic opacity, for example, scalar fields, which are non-minimally coupled with the electromagnetic Lagrangian [4-7], or the oscillation of photons that become light axions while propagating in extragalactic magnetic fields [8-11]. It has always been controversial whether the extinction effect of SNe Ia has an important influence on the conclusion of the cosmic accelerating expansion [12-15]. Intergalactic opacity may be a possible origin of the dimming of the SNe Ia luminosity [16-21], and the value of intergalactic opacity is constrained to be
$ \lambda_{\rm{V}}\approx0.01- $ $ 0.02 {\rm{Gpc}}^{-1} $ from the quasar continuum objects [19-21]. The reliable reconstruction of the cosmic expansion history is highly dependent on the existence of cosmic opacity, although the present cosmic acceleration has been confirmed independently by baryon acoustic oscillation (BAO) measurements [22], large scale structure observations [23], and cosmic microwave background anisotropy probings [24]. It is therefore necessary to accurately detect cosmic opacity to understand how it affects the reconstruction of the history of the universe in the era of precision cosmology.It has been proposed that cosmic opacity can be tested by employing the cosmic distance-duality relation (CDDR) [25, 26]:
$ {D_{\rm{L}}}{(1+z)}^{-2}/{D_{\rm{A}}} = 1 $ . Here,$ D_{\rm{L}} $ denotes the luminosity distance (LD),$ D_{\rm{A}} $ represents the angular diameter distance (ADD), and z is the cosmological redshift. The CDDR holds in any cosmological model as long as the total photon number is conserved and Riemannian geometry is used to describe the space time [27, 28]. Therefore, any deviation from the CDDR likely indicates the non-conservation of the total number of photons, indicating cosmic opacity [3, 4, 29-31]. Thus far, some studies have been devoted to detecting cosmic opacity by adopting specific cosmological models and SNe Ia observations in a model-dependent way [3, 8, 9, 32]. To probe cosmic opacity in a model-independent way, tests are generally performed using current SNe Ia observations, BAO measurements, Hubble data, galaxy cluster samples, old passive galaxies, the gas mass fraction of galaxy clusters, and strong gravitational lensing [33-41]. However, more recently, Vary$ \check{c} $ uk and Kroupa pointed out that the applicability of the CDDR is strongly limited due to the non-unique interpretation of the LD data in terms of cosmic opacity and the rather low accuracy and deficient extent of the currently available ADD data [42]. As a result, no convincing violation from a transparent universe was obtained in the previous tests using the CDDR. Therefore, new methods and astronomical observations are needed to test cosmic opacity.The detection of gravitational waves (GW) has now opened another window for us to explore the nature of the universe [43], and it has provided another candidate for LD. One can obtain the LD of a GW source by measuring the GW information of the inspiraling binary system, which is called the standard siren [44], analogous to the SNe Ia standard candle. Recently, the GW events GW170817 and GW190521, with their EM counterparts, were detected successively [43-50]. Using the redshift of the EM counterparts of the compact binaries and the LD from the standard siren, the LD-redshift relation can be reconstructed to constrain the cosmological parameters in a cosmological-independent way. Due to the lack of astronomical observation data of GWs with EM counterparts, it is difficult to strictly constrain the cosmological parameters by using the current observational data. Some works have thus advocated for using simulated GW data to explore the potentiality of future GW measurements to constrain the cosmological parameters [51-67], investigate the total mass of the neutrino [68] and the Newton's constant [69], and test cosmic anisotropy [70, 71] and the CDDR [72-74].
The standard sirens can be considered opacity-independent LD indicators because GWs propagate freely in the space-time described by the Friedman-Lemaître-Robertson-Walker metric without any absorption or dissipation [75]. Therefore, the simplest way to detect cosmic opacity is by comparison of the opacity-free LDs with the opacity-dependent LDs at the same redshift. The cosmic opacity can be detected by comparing the LD observed by SNe Ia with that directly measured by GW events. More recently, Wei [76], Qi et al. [77], and Zhou et al. [78] detected cosmic opacity with compilations of Joint Light Analysis (JLA) and the Pantheon SNe Ia compilation and simulated GW data from the ground-based Einstein Telescope (ET). Fu et al. [79] then explored the potentiality of future GW measurements to test cosmic opacity at high redshifts by comparing the mock GWs from future ET measurements with a combination of the current SNe Ia data and gamma-ray burst measurements. Compared with current tests on cosmic opacity, the results indicated that future GW measurements will be important tools for probing cosmic opacity.
It is important to note that most of the tests of cosmic opacity referred to above were conducted by comparing future GW measurements with current EM observations. The quantity of future SNe Ia observations will be approximately three times the current number of observations, and their quality will be greatly improved. For example, the Wide Field Infrared Survey Telescope (WFIRST) [80, 81] is a National Aeronautics and Space Administration (NASA) satellite that will be implemented in the next few decades. Thus, to fully exploit the potentiality of future GW measurements, it is necessary to employ future EM observations to detect the cosmic opacity. By matching the GW measurements with the simulated SNe Ia data at the same redshift, Wei tested cosmic opacity by selecting the nearest SNe Ia data point [76]. The results showed that the constraints on the transparent universe are highly stringent and that the uncertainty of the cosmic opacity parameter ϵ may be reduced to
$ \sigma_{\epsilon}\sim \pm 0.0044 $ at$ 1\sigma $ CL. However, simply using the nearest SNe Ia data point from all available SNe Ia data points that meet the selection criteria leads to larger statistical errors. Compared with a ground-based ET GW detector, the quality of observational data from space-borne GW detectors, such as Deci-Herz Interferometer Gravitational wave Observatory (DECIGO) [71], will be greatly improved in the future. Consequently, the ability of future SNe Ia observations and GW measurements to detect cosmic opacity will also be substantially better. Furthermore, if we assume that the dimming of SNe Ia is mainly caused by intergalactic opacity [19-21], it is necessary to detect and verify intergalactic opacity with future GW and SNe Ia measurements, which is the main motivation of this work.In this work, we first place constraints on the cosmic opacity by using future GW and SNe Ia measurements. To show how the uncertainty of the cosmic opacity constraint depends on the number of simulated GW events, 125, 500, and 1000 data points are simulated from the ground-based ET and space-borne DECIGO, and 2725 data points of future SNe Ia observations are simulated from the WFIRST programme [80, 81]. We employ a binning method with the selection criteria
$ |z_{\rm{GW}}-z_{\rm{SN}}|<0.005 $ to match the GW data to the SNe Ia measurements at the same redshift, and we find that due to improvements in the distribution of SNe Ia data points, most of the GW data can be used to detect cosmic opacity. The results show that the uncertainties of the constraints on cosmic opacity can be reduced to$ \sigma_{\epsilon}\sim 0.0041 $ and 0.0014 at the$ 1\sigma $ confidence level (CL) for 1000 data points from the ET and DECIGO measurements, respectively. Furthermore, to verify cosmic opacity with this method, we compare the value of the constraint on cosmic opacity with the allowable constraint of the intergalactic opacity obtained from current astronomic observations of the quasar continuum. The analyses indicate that future measurements of GWs and SNe Ia have the potentiality to verify intergalactic opacity. -
The WFIRST was planned to be launched in the mid-2020s, and it was the highest ranked large space-based mission of the 2010 New Worlds, New Horizons decadal survey. One of its goals according to NASA's Science Plan is to probe the nature of dark energy, dark matter, and gravity. The uncertainty of the distance and expansion history determined by current cosmological observations is about
$ 1\%-3\% $ , and that of matter clustering is$ 5\%-10\% $ . However, WFIRST is planned to improve the precision of these measurements to$ 0.1\%-0.5\% $ [80, 81]. Therefore, the ability of the WFIRST SNe Ia observations to constrain cosmological parameters will be significantly improved.Following the WFIRST 2015 Report [80, 81], the distribution of SNe Ia measurements from the WFIRST observations is shown in the left panel of Fig. 1. The total number of observations is 2725 in the redshift range
$ 0.1<z<1.7 $ . More than 130 SNe Ia data points are expected from the future observations for each 0.1 redshift bin in the redshift range$ z>0.6 $ . In contrast, the total number of data points in the JLA and Pantheon SNe Ia compilations in this redshift range is 145 and 162, respectively [82, 83]. Therefore, compared with the current SNe Ia observations, the density distribution and the total number of SNe Ia observations in the relatively high redshift range$ 0.6<z<1.7 $ will be significantly improved in the future.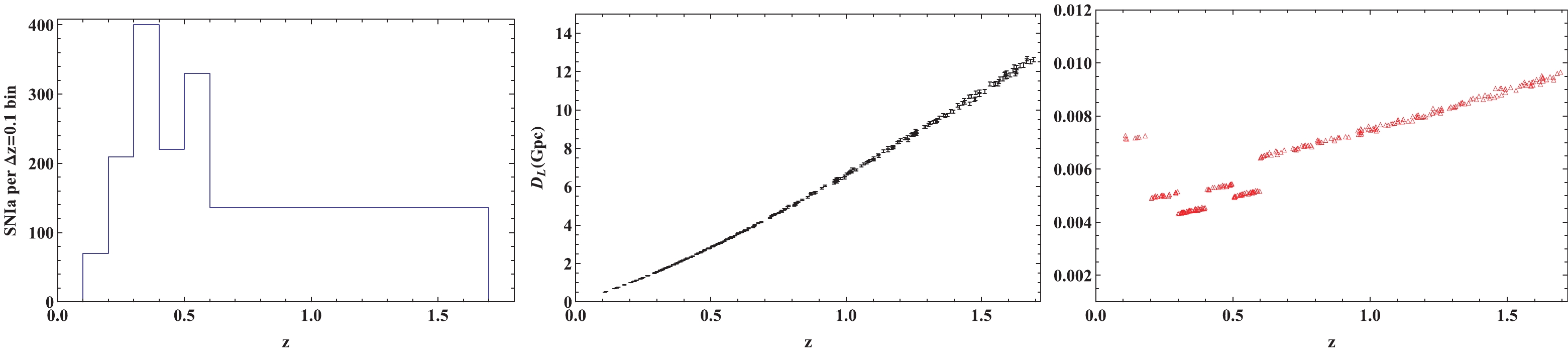
Figure 1. (color online) The redshift distribution (left panel), sample catalogs with one of every ten data points selected (middle panel), and fractional errors in the LD distances per
$ \Delta z=0.1$ bin (right panel) for the forecasted WFRIST measurements.The fiducial LDs (
$ D_{\rm{L}}^{\rm{fid}} $ ) of the SNe Ia observations are obtained from the flat ΛCDM with the constraints from the Planck results [84]:$ h = 0.678,\; \; \; \Omega_{\rm{m}} = 0.308, $

(1) where
$ H_0 = 100 \;h{\rm{km}}{{\rm{s}}^{{\rm{ - 1}}}}{\rm{Mp}}{{\rm{c}}^{{\rm{ - 1}}}} $ denotes the present value of the Hubble constant and$ \Omega_{\rm{m}} $ represents the present cosmic matter density parameter. Then, ($ D_{\rm{L}}^{\rm{fid}} $ ) can be obtained from$ D_{\rm{L}}^{\rm{fid}}(z) = {1+z\over H_0}\int_0^z{{\rm d}z'\over E(z')}\,\,. $

(2) Here,
$ E(z)\equiv H(z)/H_0 $ , and$ H^2(z) = H_0^2[1-\Omega_{\rm{m}}+ \Omega_{\rm{m}}(1+z)^3] $ . The distance modulus can be obtained with$ \mu(z) = 5\log_{10} $ $ (D_{\rm{L}}(z))+ 25 $ . The uncertainty of$ D_{\rm{L}} $ can be written as$ \sigma_{D_{\rm{L}}} = {\log_{10}\over 5}D_{\rm{L}}\sigma_\mu. $

(3) The total uncertainties of the LDs
$ \sigma_{D_{\rm{L,SN}}} $ can be obtained from the following equation:$ \sigma_{D_{\rm{L,SN}}} = \sqrt{(\sigma^{{\rm{stat}}}_{D_{\rm{L, SN}}})^2+(\sigma^{{\rm{sys}}}_{D_{\rm{L,SN}}})^2}\,\,, $

(4) where
$ \sigma^{{\rm{stat}}}_{D_{\rm{L,SN}}} $ denotes the total statistical uncertainty in a$ \Delta z = 0.1 $ redshift bin, and it can be obtained from the following expression:$ \sigma^{{\rm{stat}}}_{D_{\rm{L,SN}}} = {\sqrt{({\sigma^{\rm{meas}}_{D_{\rm{L,SN}}}})^2+({\sigma^{\rm{int}}_{D_{\rm{L, SN}}}})^2+({\sigma^{\rm{lens}}_{D_{\rm{L, SN}}}})^2}\over {\sqrt{ N_{\rm{SN}}}}}\,\,. $

(5) Here,
$ N_{\rm{SN}} $ denotes the number of SNe Ia data points in each bin. The photometric measurement error$ {\sigma^{\rm{meas}}_{D_{\rm{L,SN}}}} $ per SNe Ia data point is assumed to be$ {\sigma^{\rm{meas}}_{D_{\rm{L,SN}}}} = 0.08 $ magnitudes, the intrinsic dispersion is assumed to be$ {\sigma^{\rm{int}}_{D_{\rm{L, SN}}}} = 0.09 $ magnitudes, and the error from gravitational lensing magnification is modeled as$ {\sigma^{\rm{lens}}_{D_{\rm{L, SN}}}} = 0.07z $ magnitudes. The systematic error is assumed to be$ \sigma^{{\rm{sys}}}_{D_{\rm{L,SN}}} = $ $ 0.01(1+z)/1.8 $ magnitudes. We can then obtain the LDs ($ D_{\rm{L}} $ ) of the simulated SNe Ia measurements by using the normal distribution$ D_{\rm{L}} = {\cal{N}}(D_{\rm{L}}^{\rm{fid}},\,\sigma_{D_{\rm{L}}}) $ . The simulated results are shown in the middle and right panels of Fig. 1, where one out of every ten data points is displayed. The average fractional error of the SNe Ia LDs is 0.7%. The average fractional error of the LDs compiled by the Pantheon [82] and JLA [83] are about 6.6% and 8.3%, respectively. Therefore, one can conclude that the uncertainty of the SNe Ia observations will be reduced by an order of magnitude. -
In this subsection, we simulate the future GW measurements from the ground-based ET and space-borne DECIGO. The ET is planned for the third generation of the ground-based GW detector, and it has three 10-km-long arms in an equilateral triangle. It is 10 times more sensitive in detecting GW signals than the advanced ground detector. The frequency range that ET can detect is 1 to
$ 10^4 $ Hz. For the neutron star (NS)-NS or black hole (BH)-NS compact binaries, its redshift range is up to redshift$ z\sim2 $ or$ z \sim5 $ , respectively. The DECIGO is a future space-borne program of the Japanese space mission for GW observations ranging from 0.1 to 10 Hz, and it is composed of four triangle-like units; see Refs. [71, 85] for more details. Following Ref. [65], we briefly summarize the process of simulating the ET and DECIGO GW measurements for simplicity.The ET and DECIGO GW detectors respond to a GW signal, called strain,
$ h(t) $ . In the transverse-traceless gauge, the strain has the form$ h(t) = F_+(\theta,\phi,\psi)h_+ + F_\times(\theta,\phi,\psi)h_\times \,, $

(6) where
$ F_{+,\times} $ presents the beam pattern functions of the two polarizations,$ \psi $ is the polarization angle, and$ \theta,\phi $ denote the angles to the direction of the source in the detector frame. The corresponding pattern functions are given by equations 6 and 7 in Ref. [71] for ET and DECIGO, respectively.The GW signals are from the inspiralling compact binary systems with the total mass
$ M = m_1+m_2 $ [70, 72, 86, 87]. The chirp mass is defined as$ M_{\rm{c}} = M \eta^{3/5} $ , and the symmetric mass ratio η has the form$ \eta = m_1m_2/M^2 $ . The stationary phase approximation is usually applied to compute the Fourier transform of the GW signal:$ {\cal{H}}(f) = {\cal{A}}f^{-7/6}\exp [{\rm i}(2\pi ft_0-\pi/4+2\psi(f/2)-\varphi_{(2.0)})], $

(7) where
$ t_0 $ presents the epoch of the merger,$ \varphi_{(2.0)} $ is the phase parameter, and$ {\cal{A}} $ is the Fourier amplitude with the form$ \begin{aligned}[b] {\cal{A}} =& \frac{1}{D_{\rm{L}}}\sqrt{F_+^2(1+\cos^2(\iota))^2+4F_\times^2\cos^2(\iota)}\\& \times \sqrt{5\pi/96}\pi^{-7/6}{\cal{M}}_{\rm{c}}^{5/6}\,, \end{aligned} $

(8) where ι denotes the inclination angle.
$ {D_{\rm{L}}} $ represents the LD of the GW measurements, and it can be obtained for the simulation estimation from a flat fiducial ΛCDM with the parameters of Eq. (1).Following the process of the advanced LIGO-Virgo network [86, 88], an observational GW event is claimed only when the signal-to-noise ratio (SNR) for the network of the detector is over
$ \rho>8 $ . The SNR from the N independent GW interferometers is given by$ \rho = \sqrt{\sum\limits_{i = 1}^{N}\langle{\cal{H}}^{(i)},{\cal{H}}^{(i)}\rangle}\,, $

(9) where N can be taken as
$ N = 3 $ and$ N = 2 $ for the ET and the DECIGO detectors, respectively. The inner product has the form$ \langle a,b\rangle = 4\int_{f_{\rm{lower}}}^{f_{\rm{upper}}}{\widetilde{a}(f)\widetilde{b}^{\ast}(f)+\widetilde{a}^{\ast}(f)\widetilde{b}(f)\over{2}}{{\rm d}f\over{S_h(f)}}\,, $

(10) where
$ {S_h(f)} $ is the one-side noise power spectral density (PSD). The lower and upper frequencies for ET are fixed to be$ f_{\rm{lower}} = 1 \;{\rm{Hz}} $ and$ f_{\rm{upper}} = 2f_{\rm{LSO}} $ , where$ f_{\rm{LSO}} = 1/ $ $ (6^{3/2}2\pi M_{\rm{obs}}) $ denotes the last stable orbit frequency with$ M_{\rm{obs}} = (1+z)M $ . The lower and upper cutoff frequencies for the DECIGO are given as$ f_{\rm{lower}} = 0.233 (M_{\odot}/M_{\rm{c}})^{5/8} $ $ ({{\rm{yr}}/\tau_{\rm{obs}}})^{3/8}\;{\rm{Hz}} $ and$ f_{\rm{upper}} = 100 \;{\rm{Hz}} $ .$ M_\odot $ denotes the solar mass, and$ \tau_{\rm{obs}} $ corresponds to the observational time, which is set as one year in the mock process. The mass distributions of NS and BH are distributed uniformly on the intervals$ [1,2] M_\odot $ and$ [3,10] M_\odot $ , respectively. The ratio of the observed BH-NS to NS-NS systems is taken to be approximately 0.03 [71, 88]. The observational signals are only considered GW events if the network SNR ρ is$ \rho>8.0 $ and$ \rho>12.0 $ for ET and DECIGO interferometers, respectively [71].Now, using the Fisher information matrix, one can obtain the instrumental uncertainty of the GW LD measurements. It is assumed that
$ {\cal{H}}\propto D_{\rm{L}}^{-1} $ and that the GW LD ($ D_{\rm{L}} $ ) measurements are independent of the remaining GW parameters (the inclination angle$ \iota = 0 $ ). The instrumental uncertainty can be given as$ \sigma_{D_{\rm{L,GW}}}^{\rm{inst}}\simeq{2D_{\rm{L, GW}}/ {\rho}}\, $ . At the same time, the observed GW LD is also influenced by the weak lensing effects. The weak lensing uncertainty for the ET and the DECIGO can be given as$ \sigma_{D_{\rm{L,GW}}}^{\rm{lens}} = $ $ 0.05z D_{\rm{L,GW}} $ [57, 86, 87] and$ D_{\rm{L, GW}}\times0.066[4- 4(1+ $ $ z)^{-0.25}]^{1.8} $ [65], respectively. Therefore, for the ET, the total error bar of GW LD measurements can be written as$ \begin{aligned}[b] \sigma_{D_{\rm{L,GW}}} =& \sqrt{(\sigma_{D_{\rm{L,GW}}}^{\rm{inst}})^2+(\sigma_{D_{\rm{L,GW}}}^{\rm{lens}})^2} \\ =& \sqrt{\bigg({2D_{\rm{L,GW}}\over {\rho}}\bigg)^2+(0.05zD_{\rm{L,GW}})^2}\,. \end{aligned} $

(11) In addition, for the DECIGO measurements, the peculiar velocity error caused by the clustering galaxies and binary barycentric motion is also accounted for:
$ \sigma_{D_{\rm{L, GW}}}^{\rm{pv}}(z) = D_{\rm{L}}(z)\times{\bigg|}1-{(1+z)^2\over{H(z)D_{\rm{L}}}}{\bigg|}\sigma_{\rm{v, gal}}\,. $

(12) $ \sigma_{\rm{v, gal}} $ denotes the one-dimensional velocity dispersion of the clustering galaxies, and the value is set to be$ \sigma_{\rm{v, gal}} = $ $ 300 \;{\rm{km}} {\rm{/s}} $ . Then, the total uncertainty has the form$ \sigma_{D_{\rm{L}}} = \sqrt{(\sigma_{D_{\rm{L,GW}}}^{\rm{inst}})^2+(\sigma_{D_{\rm{L,GW}}}^{\rm{lens}})^2+(\sigma_{D_{\rm{L,GW}}}^{\rm{pv}})^2}. $

(13) It is assumed that the GW source redshift can be found with the accidental events of the EM counterparts in the NS-NS and BH-NS compact binary systems. The distribution of the redshift GW source is taken as the forms of equation 8 and equation 9 in Ref. [71]. It is expected that the rate of the observable NS-NS and BH-NS compact binaries is approximately of the order of
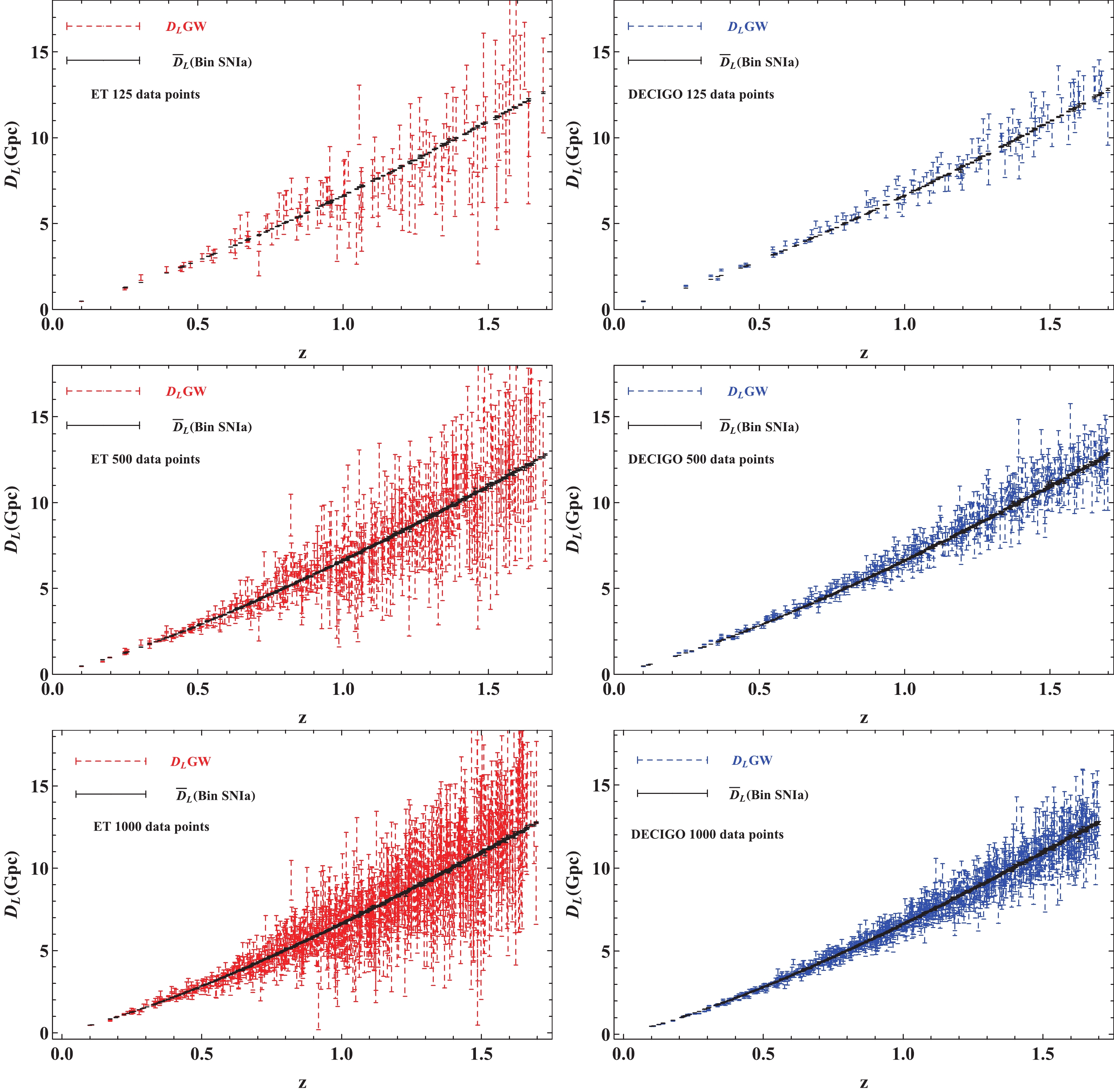
$ 10^3-10^7 $ per year [89]. Assuming that a median detection rate can be obtained$ \sim10^5 $ and that the detection rate of the EM counterpart is about$ 10^{-3} $ of the total number of standard sirens, approximately$ 10^2 $ GW events coupling with EM counterparts are to be detected every year [72, 87]. Over ten years of astronomical observation, we will obtain nearly 1000 GW observation data points with EM counterparts. To see how the uncertainty of the constraint on cosmic opacity depends on the number of mock GW measurements, we simulate 125, 500, and 1000 data points for the ET and DECIGO in the redshift range$ 0.1<z<1.7 $ ; the results are shown in the left and right panels of Fig. 2, respectively. The average fractional errors of the 1000 data points for the ET and DECIGO measurements are 15.98% and 5.15%, respectively. This suggests that the space-borne DECIGO measurements will be more competitive than the ground-based ET measurements when constraining cosmology parameters in the future. -
The LDs obtained from the SNe Ia observations are influenced systematically by cosmic opacity [8], whereas the LDs from the GW standard sirens are considered to be independent of cosmic opacity. Therefore, one can detect cosmic opacity by comparing the LDs obtained from SNe Ia observations with the LDS from GW events at the same redshift. When photons travel from the SNe Ia in the deep universe to our observers, the observed LD can be written as [21, 90, 91]
$ {D_{\rm{L,obs}}}(z) = {D_{\rm{L,true}}}(z){\rm e}^{\tau(z)/2}, $

(14) given that the received photon flux decreases in the form of the function
$ {\rm e}^{-\tau(z)} $ . The true LD can be obtained from the LD of GW measurements. Then the cosmic optical depth$ {\tau(z)} $ , which is related to the scattering and absorption of photons, can be obtained by comparing the LD$ D_{\rm{L}}(z_i) $ of the GW data with that from the SNe Ia observation at the same redshift:$ {\tau(z_i)} = 2\ln {D_{\rm{L,SN}}(z_i) \over{D_{\rm{L, GW}}(z_i)}} . $

(15) The uncertainties of the observational optical depth function,
$ \sigma_{\tau_{\rm{obs}}} $ , can be expressed as$ \sigma_{\tau_{\rm{obs}}} = 2\sqrt{\left({\sigma_{D_{\rm{L,SN}}(z)}\over{D_{\rm{L,SN}}(z)}}\right)^2+\left(\sigma_{D_{\rm{L, GW}}(z)}\over{D_{\rm{L, GW}}(z)}\right)^2}\, . $

(16) Two typical parameterizations are adopted for the optical depth function:
$ \tau(z) = 2\epsilon z $ (P1) and$ \tau(z) = (1+z)^{2\epsilon}-1 $ (P2). -
Note that the cosmic intergalactic opacity was tested by Xie et al. [21], and its value was constrained to be
$ \lambda_{\rm{V}}\approx0.01-0.02 {\rm{Gpc}}^{-1} $ with luminosity and redshifts of the quasar continuum of$ \sim90 000 $ objects in the redshift range$ z < 1.5 $ . Similar results are also obtained in Refs. [19, 20], in which the visual intergalactic attenuation is estimated to be 0.03 mag by correlating the brightness of about 85000 quasars at$ z>1 $ . To test the cosmic opacity resulting from intergalactic dust, the cosmic opacity is also quantified by the redshift-dependent optical depth function$ \lambda_{\rm{B}} $ [92, 93], which has the form$ \tau_{\rm{B}} = \int_0^z\lambda_{\rm{B}}(1+z'){c {\rm d} z'\over{H(z')}}, $

(17) where the parameter
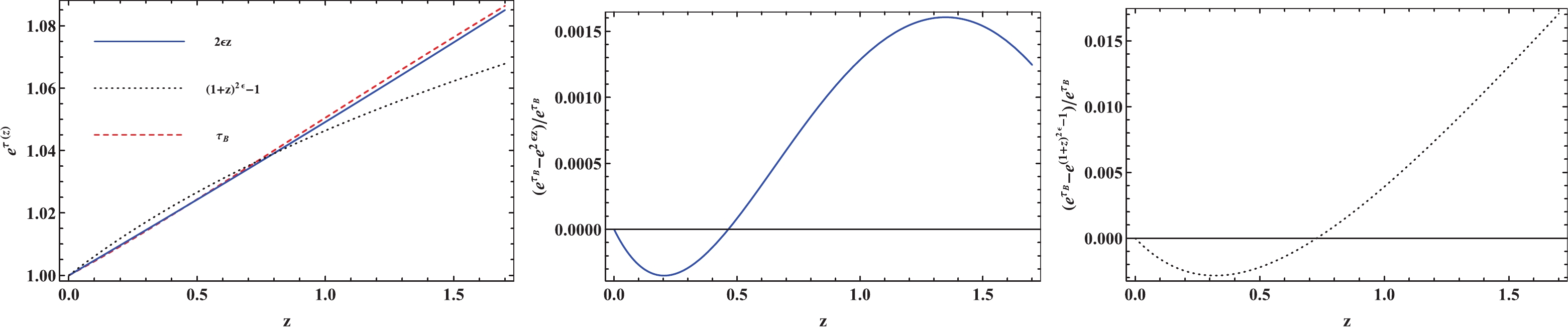
$ \lambda_{\rm{B}} $ denotes the rest-frame B-band attenuation per unit ray path. However, the existence of cosmic opacity given by only one astronomical observation is not sufficient. The GW and SNe Ia measurements can be used to detect cosmic opacity in a different way than the quasar continuum observations. To show how well the parameterizations P1 and P2 for optical depth approximate the cosmic opacity, we fit the intergalactic opacity$ \tau_{\rm{B}} $ with them, where the value of the intergalactic opacity is taken as the minimum value$ \lambda_{\rm{B}}\approx0.01{\rm{Gpc}}^{-1} $ . As shown in Fig. 3, the relative difference between the parameterizations is less than 2%, which is more accurate than most current astronomic observations, when the parameter ϵ is 0.024 and 0.032, respectively. Therefore, these two parameterizations for cosmic intergalactic opacity are valid. Assuming that the dimming of SNe Ia is mainly caused by intergalactic dust, one can verify the cosmic opacity with these two parameterizations. -
In principle, given an LD sample from a GW measurement, the corresponding LD data point of the SNe Ia observation at the same redshift z can be obtained to determine the optical depth
$ \tau{(z_i)} $ . However, in the next few decades, it will be difficult to observe such compact binaries, where gravitational waves and SNe Ia explosions can be detected simultaneously. Some methods have been adopted to achieve this goal [33, 94, 95]. To test cosmic opacity in a cosmological-model-independent method, the nearest SNe Ia data is selected to match a GW measurement [76] with the selection criterion$ \Delta z = |z_{\rm{GW}}-z_{\rm{SN}}|< $ $ 0.005 $ . This matching method is also used to test the CDDR in Refs. [33, 94, 96, 97]. However, when the GW data points do not match SNe Ia data, some available data have to be discarded. In addition, if only one of the available SNe Ia data points that meets the selection criteria is used, there will be a larger statistical error. To avoid these defects, we bin the simulated SNe Ia data that meet the criterion according to the process in Refs. [95, 98].To avoid correlations between the individual astronomical measurements, we select SNe Ia samples with a procedure in which once a data point matches a GW sample, it is not used a second time. We adopt an inverse variance weighted average of all the selected data in this method. If
$ D_{{\rm{L}}i} $ and$ \sigma_{D_{{\rm{L}}i}} $ denote the ith appropriate luminosity distance data point and the corresponding observational uncertainty, respectively, by using the conventional data reduction techniques in Chapter 4 of Ref. [99], one can obtain the weighted mean LD$ \bar{D_{\rm{L}}} $ and its uncertainty$ \sigma_{\bar{D_{\rm{L}}}} $ with the following equations:$ \bar{D_{\rm{L}}} = {\displaystyle\sum(D_{{\rm{L}}i}/\sigma_{D_{{\rm{L}}i}}^2)\over \displaystyle\sum1/\sigma_{D_{{\rm{L}}i}}^2}, $

(18) $ \sigma^2_{\bar{D_{\rm{L}}}} = {1\over \displaystyle\sum1/\sigma_{D_{{\rm{L}}i}}^2}. $

(19) The selection criteria can be met with most of the simulated GW measurements: 125, 499, and 998 data points in the simulated GW compilations can be adopted to probe cosmic opacity. Compared with the tests in Refs. [76, 77], where the selection criterion is also adopted, many more of the available GW measurements can be used to perform the task of testing cosmic opacity in this work. The main reason is that the distribution of SNe Ia observations will be significantly improved in the future, especially in the relative high redshift range
$ z>0.6 $ . Therefore, the potential of future GW measurements can be fully exploited to detect cosmic opacity while matching the SNe Ia observations. The distributions of GW samples and the corresponding SNe Ia LDs obtained with the binning method are shown in Fig. 2.Using the equation
$ P(\epsilon) = A\,{\rm{exp}}[-\chi^2(\epsilon)/2] $ , one can obtain the probability density of ϵ. Here,$ \chi^2(\epsilon) $ can be given by the following expression:$ \chi^{2}(\epsilon) = \sum\frac{{\left[\tau(z,\epsilon)- \tau_{\rm{obs}}\right] }^{2}}{\sigma^2_{\tau_{\rm{obs}}}}\,, $

(20) and A is a normalized coefficient. The results from the observational data are shown in Fig. 4 and Table 1.
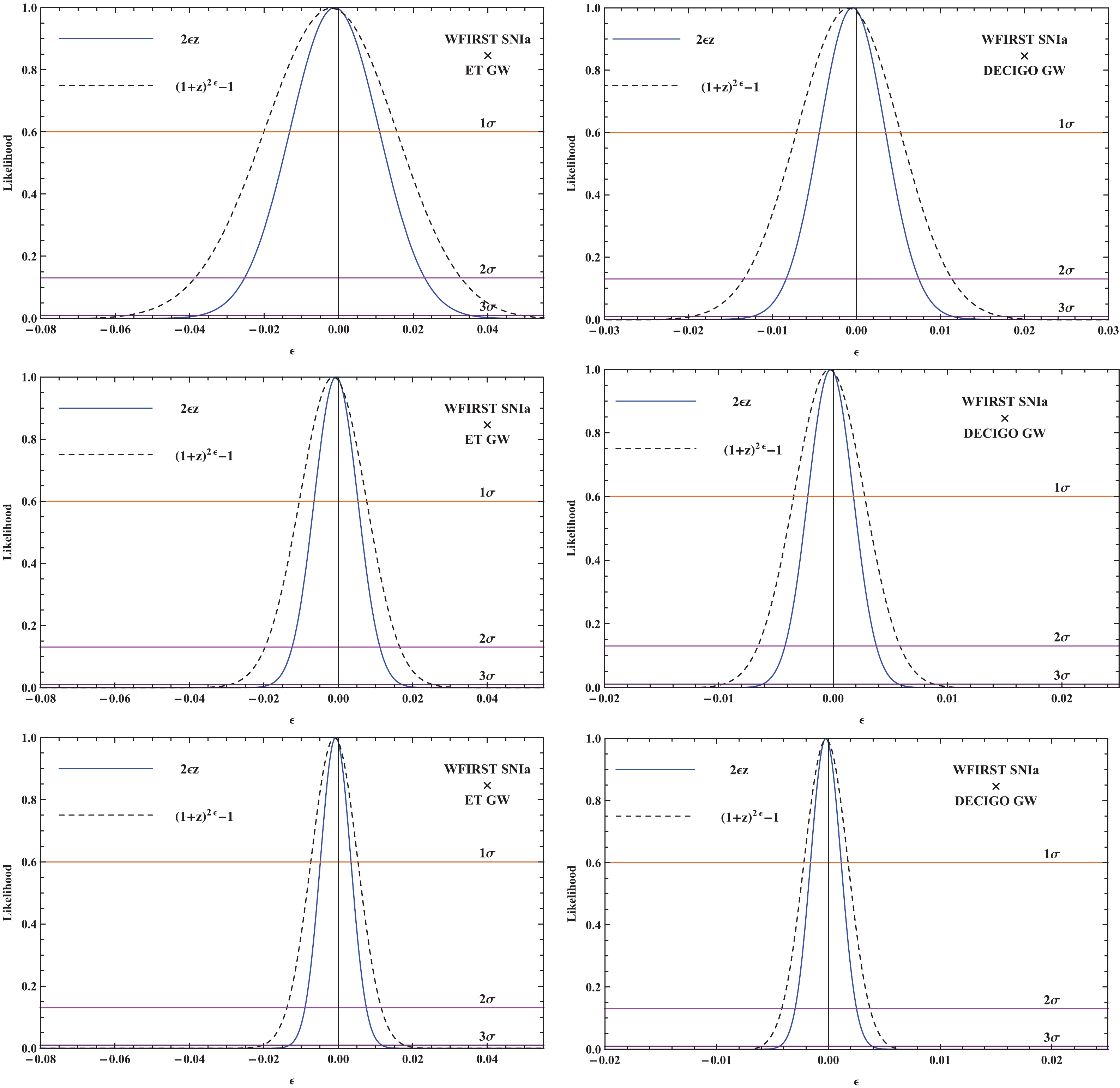
Figure 4. (color online) Likelihood distribution functions obtained from the ET (left panel) and DECIGO (right panel). The top, middle, and bottom panels correspond to the results from 125, 500, and 1000 data points in the catalogs.
Data $\epsilon\,\,( P_1)$ 

$\epsilon \,\,(P_2)$ 

125 ET × 2725 WFIRST (B) ${-0.0011{\pm{0.0120}\pm{0.0241}\pm{0.0362}}}$ 

${-0.0021{\pm{0.0180}\pm{0.0365}\pm{0.0546}}}$ 

500 ET × 2725 WFIRST (B) ${-0.0006{\pm{0.0059}\pm{0.0117}\pm{0.0178}}}$ 

${-0.0013{\pm{0.0093}\pm{0.0185}\pm{0.0276}}}$ 

1000 ET × 2725 WFIRST (B) ${-0.0007{\pm{0.0041}\pm{0.0082}\pm{0.0123}}}$ 

${-0.0010{\pm{0.0064}\pm{0.0128}\pm{0.0195}}}$ 

125 DECIDO × 2725 WFIRST (B) ${-0.0005{\pm{0.0038}\pm{0.0078}\pm{0.0118}}}$ 

${-0.0009{\pm{0.0062}\pm{0.0123}\pm{0.0202}}}$ 

500 DECIDO × 2725 WFIRST(B) ${-0.0003{\pm{0.0019}\pm{0.0039}\pm{0.0059}}}$ 

${-0.0004{\pm{0.0031}\pm{0.0062}\pm{0.0092}}}$ 

1000 DECIDO × 2725 WFIRST(B) ${-0.0002{\pm{0.0014}\pm{0.0028}\pm{0.0041}}}$ 

${-0.0002{\pm{0.0020}\pm{0.0040}\pm{0.0058}}}$ 

ET × 1048 Panthoen (B) [76] ${0.004\pm 0.026}$ 

$\Box$ 

ET × 2000 simulated SNe Ia (B) [76] ${0.0000\pm 0.0044}$ 

$\Box$ 

ET × 740 JLA (B) [77] ${0.002\pm 0.035}$ 

${-0.006\pm 0.053}$ 

ET × 1048 Panthoen (B) [77] ${0.009\pm 0.016}$ 

${0.015\pm 0.025}$ 

SL SNe Ia (LSST) × SNe Ia (B) [39] $\Delta\epsilon=0.027$ 

$\Delta\epsilon=0.082$ 

581 SNe Ia + 19 H(z) × ΛCDM (A) [40] ${0.02\pm0.055}$ 

$\Box$ 

H(z) × Union (A) [8] ${-0.01\pm^{0.08}_{0.09}}$ 

$\Box$ 

H(z)× Union (A) [9] ${-0.04\pm^{0.08}_{0.07}}$ 

$\Box$ 

H(z) × Union2.1 (B) [36] ${-0.01\pm 0.10}$ 

${-0.01\pm 0.12}$ 

Clusters × Union2.1 (B) [38] ${0.009\pm^{ 0.059}_{0.055}}$ 

${0.014\pm^{ 0.071}_{0.069}}$ 

H(z)× JLA (B) [37] ${0.07\pm^{0.107}_{0.121}}$ 

$\Box$ 

ages of old objects × Union2.1 (B) [34] ${0.016\pm^{0.078}_{0.075}}$ 

$\Box$ 

Table 1. Constraints on ϵ with the best fit value at
$ 1\sigma$ ,$ 2\sigma$ , and$ 3\sigma$ CL obtained from each data set. A and B denote the cosmological model-dependent and model-independent methods, respectively. -
The results from the tests on cosmic opacity with the parametrization method are shown in Table 1, where previous results are included for comparison. One can see that the uncertainties of ϵ are gradually reduced with the increase in the number of GW measurements from 125 to 1000 data points. The final constraints on the cosmic opacity are
$ \Delta\epsilon = 0.0041 $ and$ \Delta\epsilon = 0.0014 $ at$ 1\sigma $ CL for the ET and DECIGO measurements, respectively. When using the same number of gravitational wave data points, the ability of the DECIGO detector to constrain the cosmic opacity is about three times that of the ET measurements. The main reason is that the average error bars from the future DECIGO GW data are about one-third of those for the ET data, as shown in Sec. II. This suggests that with improvements in the GW quantity and quality, the ability of space-borne GW measurements to constrain cosmic opacity will be greatly improved in the future. Based on the results of parameterizations for the optical depth, it can be concluded that the parameterization P1 has more stringent constraints on the cosmic opacity than P2.The results show that the constraint on cosmic opacity obtained from 125 GW is
$ \sigma_\epsilon = 0.012 $ at$ 1\sigma $ CL. Comparing the uncertainties of the cosmic opacity with previous tests obtained from other current astronomic measurements, we see that our result is much more stringent than that obtained from the Hubble data [36, 37], galaxy cluster samples [38], and old passive galaxies [34]. In the case of the constraint on cosmic opacity obtained by confronting the simulated GW data with current measurements of SNe Ia data, the constraints from the 1000 simulated GW data points are about 50% less than those of the simulated ET GW data and the JLA SNe Ia data in Refs. [76, 77]. This means that with future improvements in the quality and quantity of SNe Ia observations, the ability of astronomical observation data to constrain cosmic opacity will also be improved. As for the comparison of ET measurements with future SNe Ia observations, our results are similar to those in Ref. [76]. However, the constraints from the space-borne DECIGO are about 70% less than those obtained from Ref. [76]. Therefore, future space-borne GW measurements and SNe Ia observations can serve as powerful tools to detect cosmic opacity.It is now necessary to compare our results with cosmic opacity test results obtained from current astronomical measurements of the quasar continuum for
$ \sim 90000 $ objects [21]. Given that the dimming of SNe Ia is mainly caused by intergalactic opacity, the cosmic opacity parameter ϵ is taken as 0.024, which corresponds to the minimum value$ \lambda_{\rm{B}} = 0.01 $ of the intergalactic opacity parameter. In fact, the value of the cosmic opacity parameter will be larger than the minimum value of intergalactic opacity if other mechanisms also stimulate the cosmic opacity. From Table 1, we see that more than 100 GW events of ET and DECIGO measurements can determine cosmic opacity at$ 2\sigma $ and$ 3\sigma $ CL, respectively. Furthermore, assuming that the cosmic opacity parameter ϵ is far less than the current observation value, i.e., approximately one-fifth of that value or$ \epsilon\sim 0.005 $ , then roughly 1000 GW data points from the space-borne DECIGO will be able to identify the cosmic opacity at$ 3\sigma $ CL. Therefore, the future space-borne and SNe Ia measurements can be considered effective tools for verifying cosmic opacity. -
Cosmic opacity may be caused by the scattering and absorption of opaque sources in the universe or by other specific mechanisms in which the extragalactic magnetic field transforms photons into unobservable particles. However, the extinction effect of SNe Ia caused by cosmic dust and the strange mechanism of cosmic opacity have not fully been understood. The existence of cosmic opacity leads to deviation from the conservation of the total photon number, which makes the observed SNe Ia dimmer than expected. It also affects the reconstruction of the cosmic expansion history when using the SNe Ia observations. It is therefore necessary to accurately test the cosmic opacity with various astronomical observations and methods in the era of precision cosmology.
The LD measurements from the GW sources of standard sirens are not affected by cosmic opacity, which is different from SNe Ia, because they can be directly obtained with the waveform signals. Thus, the measurements of GW and SNe Ia respectively provide the opacity-free and opacity-dependent distances needed to probe cosmic opacity. Recently, to explore the potentiality of future ET GW measurements, tests on cosmic opacity have been done by comparing the LDs of simulated GW measurements with the LDs of the current SNe Ia compilations. However, due to the lack of current SNe Ia data in the observed relatively high redshift range
$ z>0.6 $ , some GW data points have to be discarded when matching the GW data at the same redshift, with the result that the potentiality of future GW measurements is not fully exploited. The quality of SNe Ia data and space-borne GW measurements will be significantly improved in the future. Therefore, it is worth exploiting the potentiality to detect cosmic opacity by using the future SNe Ia and space-borne GW measurements.The Einstein Telescope (ET) is the third-generation ground-based detector. The Deci-Hertz Interferometer Gravitational-wave Observatory (DECIGO) is a space-borne detector proposed by the Japanese, similar to the laser interferometer space antenna (LISA) and the big bang observer (BBO). From the ground-based detector (ET) to the space-based detector (DECIGO), the quality of observation data will also be improved. In this work, we simulate 2725 future data points of SNe Ia observations following the program of the WFIRST-AFTA 2015 Report [80, 81]. The simulation shows that the uncertainty of SNe Ia observations is approximately one order of magnitude smaller than that of the current JLA and Pantheon SNe Ia observations. We then simulate the future GW measurements from the ET and DECIGO in the redshift range
$ 0.1<z<1.7 $ , and we find that the average fractional error of 1000 data points from DECIGO is about one-third of that from the ET. We also simulate 125 and 500 data points for the ET and DECIGO to show how the uncertainty of the constraint on the cosmic opacity depends on the number of simulated GW measurements. To match the GW measurements with the SNe Ia observations at the same redshift, we adopt a binning method with the selection criterion$ \Delta z = |z_{\rm{GW}}-z_{\rm{SN}}|< $ $ 0.005 $ . We find that due to improvements in the SNe Ia distributions, most of the GW data points meet the selection criteria. Thus, the potentiality of the GW measurements is fully exploited to detect cosmic opacity. We also adopt two parameterizations for the optic depth:$ \tau(z) = 2\epsilon z $ (P1) and$ \tau(z) = (1+z)^{2\epsilon}-1 $ (P2). Assuming that dimming of SNe Ia is mainly caused by intergalactic opacity, we find that the parameterizations approximate the intergalactic opacity$ \tau_{\rm{B}} $ well [92, 93]. Therefore, these parameterizations can be used to verify the cosmic opacity with the GW and SNe Ia measurements.First, we see that the uncertainty of the constraints on cosmic opacity decreases with the increase in the number of GW data points from 125 to 1000. The final results are
$ \Delta\epsilon = 0.0041 $ and$ \Delta\epsilon = 0.0014 $ at$ 1\sigma $ CL for 1000 data points from the ET and DECIGO measurements, respectively. We also find that for the same number of gravitational wave data points, due to the improvement of the DECIGO measurement quality, the ability of space-borne DECIGO GW measurements to constrain the cosmic opacity is about three times that of ground-based ET measurements. Second, comparing our results with the previous test results on cosmic opacity obtained from the current astronomic observations, more than 100 GW events can provide much more stringent constraints than those obtained from the Hubble data [36, 37], galaxy cluster samples [38], or old passive galaxies [34]. As for the tests obtained from the current SNe Ia data and mock GW measurements, our results for the 1000 mock DECIGO GW events are at least 50% less than those obtained by comparing the mock data of ET GW measurements with the JLA or Pantheon SNe Ia data in Refs. [76-78]. Lastly, compared with the constraints on intergalactic opacity from current astronomic observations of the quasar continuum, we find that more than 100 GW events of ET and DECIGO measurements can verify cosmic opacity at$ 2\sigma $ and$ 3\sigma $ CL. It can therefore be concluded that given the GW and SNe Ia detectors are indeed set up, future GW and SNe Ia measurements can be considered important and effective tools for probing cosmic opacity.
Exploring the potentiality of future standard candles and standard sirens to detect cosmic opacity
- Received Date: 2021-03-04
- Available Online: 2021-06-15
Abstract: In this work, we explore the potentiality of future gravitational wave (GW) and Type Ia supernovae (SNe Ia) measurements to detect cosmic opacity by comparing the opacity-free luminosity distance (LD) of GW events with the opacity-dependent LD of SNe Ia observations. The GW data are simulated from the future measurements of the ground-based Einstein Telescope (ET) and the space-borne Deci-Herz Interferometer Gravitational wave Observatory (DECIGO). The SNe Ia data are simulated from the observations of the Wide Field Infrared Survey Telescope (WFIRST) that will be collected over the next few decades. A binning method is adopted to match the GW data with the SNe Ia data at the same redshift z with a selection criterion





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: