-
The equation of state (EOS) of dense stellar matter is a mutual problem for nuclear physics and relativistic astrophysics and has been greatly promoted by the detection of gravitational waves from the GW170817 binary neutron star (NS) merger event [1, 2]; see some recent developments reviewed, e.g., in [3-5]. An accurate estimation of the radii of stars (
$ 11.9^{+1.4}_{-1.4} $ km) at 90% credible level [2] was performed using the gravitational wave signal in the late inspiral stage, namely the tidal deformabilities of the stars in a binary, based on a parametrized EOS fulfilling the two-solar-mass constraint from pulsar mass measurements [6-9]. Using X-ray missions, it is also possible to simultaneously measure the masses and radii of the stars in NS low-mass X-ray binaries (LMXBs) and millisecond pulsars [10]. Recently, the NICER mission has obtained the mass ($1.44^{+0.15}_{-0.14} \,{M}_{\odot}$ ) and radius ($ 13.02_{-1.06}^{+1.24}\; \rm km $ ) of PSR J0030+0451 to 68.3% credibility interval [11, 12]. Some possible implications of the measurements have also been studied in combination with gravitational-wave observations [13-15]. These observations are crucial for the detailed study of a matter state with several times the nuclear saturation density,$ \rho_0 $ (with$ \rho_0 = 2.8\times10^{14}\rm g/cm^3 $ ). Among them, the possibility of the existence of strange quark matter (SQM) in the high-density cores of NSs is of particular interest. It could be investigated with future advanced LIGO/Virgo detectors [16-20]. For example, it was shown that the loss of the thermodynamic convexity of an EOS (or the loss of monotonicity of the sound velocity,$ c_s $ ) could have direct effects on both dynamics of the collapse to black hole configurations and resulting gravitational waves [17]. Moreover, the sound velocity behavior is a current pursuit in relativistic heavy-ion collisions, where some interesting findings have already been obtained [21].Model studies on the hadron-quark EOS indicate a likely first-order quark deconfinement phase transition characterized by a decreasing behavior [22] of the adiabatic index,
$\Gamma = (\rho+P)({\rm d}P/{\rm d}\rho)/P$ . The sound velocity,$c_s = \sqrt{{\rm d}P/{\rm d}\rho}$ , should also decrease with the density but exhibits a much uncertain modification [22-31], especially at a density around$ 3 - 5\rho_0 $ . As indicated in Ref. [23], if the two-solar-mass constraint is combined with the knowledge of the hadronic matter EOS below and around the nuclear saturation density,$ c_s $ might first increase, then decrease after reaching a maximum (maybe even up to$ 0.9c $ , with c being the velocity of light), and finally approach from below to the conformal limit,$c/\sqrt{3}$ , which corresponds to that of gases comprising ultra-relativisitc massless particles. The peculiar shape resembles that from the analysis in the case of a crossover EOS [32]. If the deconfinement phase transition is of first-order, under Maxwell construction, there is an energy density jump at the transition pressure [33], leading to$ c_s = 0 $ and sharp peaks in the curve. This is the case if the surface tension of the hadron-quark interface,$ \sigma $ , exceeds some critical value$ \sigma_c $ . Under the Gibbs construction, a mixed-phase consists of point-like hadron matter and quark matter [34]. For a moderate$ \sigma $ (for example,$ \sim \rm 20\; MeV/fm^2 $ as found in the Dyson-Schwinger equation approach [35]), a pasta phase with various shapes is possible [36], and the pressure monotonously increases with the energy density.Nevertheless, although it is known that the degree of freedom is a hadron around the nuclear saturation density, the quantum chromodynamics (QCD) phase state for cold, dense matter having intermediate densities is unfortunately unknown, and a great deal of effort is undergoing in the communities of astrophysics, nuclear physics, and particle physics owing to its crucial importance. One key point is still unclear: does the matter go through a phase transition from hadron matter to quark matter at some intermediate densities, or is quark matter the absolute ground state of strongly interacting matter? (the Bodmer-Witten-Terazawa conjecture [37-39]). Because of the tension of a low tidal deformability (
$ 190^{+390}_{-120} $ [2]) and a high maximum mass ($2.14^{+0.10}_{-0.09} \,{M}_{\odot}$ as the presently heaviest pulsar [40] and$\leqslant 2.35 \,{M}_{\odot}$ based on the numerical simulation studies on NS binary mergers [41-43]) for a certain EOS in the NS model, binary strange quark stars (QSs) have been proposed to be the possible scenario for the GW170817 event [44, 45]. A binary QS merger for some binary configurations could eject a comparable amount of matter (to the binary NS case) [46] to account for the electromagnetic observation in the optical/infrared/UV bands (namely, kilonova). Moreover, a magnetar with a QS EOS is preferred as the post-merger remnant to explain some groups of short gamma-ray burst (SGRB) observations [47, 48].Therefore to understand the phase state of dense matter having intermediate densities relevant to compact stars, the present study aims to be a comprehensive study on the general properties of
$ \Gamma $ and$ c_s $ in the first-order quark confinement phase transition as well as in pure nuclear matter and quark matter. We are also interested in connecting the studies on a mixed-phase and a pure quark phase and establishing some quantitative results for star properties testable against observations. The paper is organized as follows. In Sec. II, we introduce various nuclear many-body approaches employed for the hadron phase and the four effective models employed for the quark phase, including the construction of a hadron-quark mixed-phase under the Maxwell and Gibbs constructions as well as different hadron-quark interface tensions. Sec. III is devoted to discussions, and finally, a short summary is provided in Sec. IV. -
Presently, we have no unified models to deal with the hadron phase and the quark phase because matter is described under different stability conditions. The parameter space for these two states is separated. We use a pure nuclear matter model for the calculations of the NSs and a pure SQM model for the calculations of the QSs. The hadron-quark phase transitions are explored by combining a nuclear matter model with a quark matter model under various equilibrium conditions between the two phases, following which the properties of hybrid stars (HSs, namely NSs whose cores contain deconfined quarks) can be obtained.
-
For the study of nuclear matter, we choose the relativistic mean-field (RMF) model (with the TW99 [49] and DDME2 [50] effective interactions), quark mean-field (QMF) model [51], Brueckner-Hartree-Fock (BHF) approach (with the latest version, BCPM [52]), and variational method (with the standard Akmal-Pandharipande-Ravenhall (APR) formalism [53]). They are among the various microscopic calculations or the most-advanced and widely-employed phenomenological models, without much dependence on the model parameters for the results being as general as possible.
At densities below and around the nuclear saturation density,
$ n_0\approx 0.15 - 0.16\ \mathrm{fm}^{-3} $ , the EOS of nuclear matter is well constrained with terrestrial experiments and nuclear theories, which gives energy per baryon$ E/A\approx 16 $ MeV, incompressibility$ K = 240 \pm 20 $ MeV [54], and symmetry energy$ E_{\rm sym} = 31.7 \pm 3.2 $ MeV and its slope$ L = 58.7 \pm 28.1 $ MeV [55, 56]. Note that the recent PREX-II results [57] on the neutron skin thickness of$ ^{208}\mathrm{Pb} $ may indicate a L value about twice the previous one. The saturation properties of nuclear matter for the employed five EOS models are listed in Table 1 together with the maximum mass of a pure NS and the radius of a typical$ 1.4 \,{M}_{\odot} $ star. We mention that all five NS EOS models fulfill the available robust mass/radius measurements from the gravitational wave signal and the electromagnetic signals [2, 6-9, 11, 12].Model $ n_0 $ /fm−3

$(E/A)$ /MeV

K/MeV $ E_{\rm sym} $ /MeV

L/MeV $ M_{\rm TOV} $ /

${M}_{\odot}$ 

$ R_{\rm 1.4} $ /km

TW99 0.153 16.25 240.27 32.77 55.31 2.09 12.3 DDME2 0.152 16.14 250.92 32.30 51.25 2.50 13.1 QMF18 0.16 16.00 240.00 31.00 40.00 2.07 11.9 BCPM 0.16 16.00 213.75 31.92 52.96 1.98 11.7 APR 0.16 16.00 247.30 33.90 53.80 2.21 11.4 Table 1. The saturation properties of the five nuclear matter EOS models employed, which are consistent with the constraints of terrestrial experiments and nuclear theories, i.e.,
$ K = 240 \pm 20 $ MeV [54],$ E_{\rm sym} = 31.7 \pm 3.2 $ MeV, and$ L = 58.7 \pm 28.1 $ MeV [55, 56]. Also listed are the maximum gravitational mass of the NSs ($ M_{\rm TOV} $ ) and the radius of a typical$1.4 \,{M}_{\odot}$ star. -
SQM is composed of up (u), down (d), and strange (s) quarks, with the charge neutrality maintained by the inclusion of electrons (hereafter, muons as well, if present) as
$ \frac{2}{3}n_u-\frac{1}{3}n_d-\frac{1}{3}n_s-n_e = 0. $

(1) The baryon number conservation,
$ \frac{1}{3}\left(n_u + n_d + n_s\right) = n_{\rm b}, $

(2) is also satisfied, with
$ n_{\rm b} $ being the baryon number density. Owing to the weak interactions between quarks and leptons,$\begin{aligned}& d \rightarrow u + e + \tilde{\nu}_e,\; \; u + e \rightarrow d + \nu_e;\\& s \rightarrow u + e + \tilde{\nu}_e,\; \; u + e \rightarrow s + \nu_e;\quad s + u \leftrightarrow d + u, \end{aligned}$

and the
$ \beta $ -stable conditions$ \mu_s = \mu_d = \mu_u + \mu_e $ should be fulfilled. The energy density and pressure include contributions from both quarks and leptons, and those of leptons can be easily calculated by the model of an ideal Fermi gas. In this section, we mainly introduce the necessary formalism for quarks.In the density regime achieved inside compact stars, it is not possible for dense matter properties to be calculated directly from the first principle lattice QCD or from perturbative QCD. We make use of various phenomenological descriptions of the system, and our studies on SQM and quark stars are based on four effective models. The four quark matter models may include all possible QS models in the market with a high maximum mass (above
$\sim 2 \,{{M}}_{\odot}$ ) and cover approximately the full preferred radius range ($ \sim10 - 14\; \rm km $ ) of a typical$1.4 \,{{M}}_{\odot}$ mass star. In the following, we introduce the four quark matter models, namely the MIT bag model, perturbation model, equivparticle model, and quasiparticle model. -
The most popular approach to obtain the properties of SQM is the MIT bag model [58, 59], with the usual correction of
$ \sim\alpha_\mathrm{s} $ from perturbative QCD. The$ O(\alpha^2_\mathrm{s}) $ pressure was evaluated and approximated [60] in a similar simple form with the original bag model and was used to study hybrid stars and quark stars [15, 48, 61-63]. At a given chemical potential$ \mu_i\; (i = u,d,s) $ , pressure P, particle number density$ n_i $ , and energy density$ \rho $ are determined by$ P = -\Omega_0 - \frac{3\mu^4}{4\pi^{2}}(1-a_4) - B_{\rm eff}, $

(3) $ n_i = \frac{g_i}{6\pi^2} \left(\mu_i^2-m_{i}^2\right)^3 - \frac{\mu^3}{\pi^2}(1-a_4), $

(4) $ \rho = \sum_i \mu_i n_i - P,$

(5) where the average chemical potential is
$ \mu = \sum_i\mu_i/3 $ , and$ g_i $ is the degeneracy factor for particle type i ($ g_u = g_d = $ $ g_s = 6 $ ). The$ a_4 $ parameter is commonly taken to be$ 2\alpha_\mathrm{s}/\pi $ to one loop order [58, 59], with$ \alpha_\mathrm{s} $ being the strong coupling constant. Here, both$ B_{\rm eff} $ and$ a_4 $ are effective parameters including the non-perturbative effects of the strong interactions.$ \Omega_0 $ takes the form of the thermodynamic potential density with non-interacting particles ($ m_{u} = m_{d} = 0, m_{s} = 100 $ MeV are usually used for simplicity), i.e.,$\begin{aligned}[b] \Omega_0 =& -\sum_i\frac{g_i}{24\pi^2} \Bigg[ \mu_i \left(\mu_i^2-\frac{5}{2}m_i^2 \right)\sqrt{{\mu_i}^2-m_i^2} \\&+\frac{3}{2} m_i^4\ln\frac{\mu_i+\sqrt{{\mu_i}^2-m_i^2}}{m_i} \Bigg].\end{aligned} $

(6) -
As mentioned above, the property of quark matter with intermediate densities is not attainable directly by solving QCD. Perturbative QCD can only be applicable at ultra-high densities above
$ \sim40\rho_0 $ [24, 64]. We make use of perturbative calculations in the present perturbation model and introduce additionally non-perturbative corrections through model parameters.We employ the perturbative QCD thermodynamic potential density to the order of
$ \alpha_\mathrm{s} $ [65], i.e.,$ \Omega^\mathrm{pt} = \Omega_0 + \Omega_1 \alpha_\mathrm{s}, $

(7) with
$ \begin{aligned}[b] \Omega_1 =& \sum_{i = u,d,s} \frac{g_i m_i^4}{12\pi^3} \Bigg\{ \left[ 6 \ln\left(\frac{\bar{\Lambda}}{m_i}\right) + 4 \right]\left[u_i v_i - \ln(u_i+v_i)\right] \\& + 3\left[u_i v_i - \ln(u_i+v_i)\right]^2 - 2 v_i^4 \Bigg\}, \end{aligned} $

(8) where
$ u_i \equiv \mu_i/m_i $ and$ v_i \equiv \sqrt{u_i^2-1} $ . Note that the thermodynamic potential density to the zeroth order,$ \Omega_0 $ , is the same as in Eq. (6). Coupling constant$ \alpha_\mathrm{s} $ and quark masses$ m_i $ are running with the energy scale and can be determined by [65]$ \alpha_\mathrm{s}(\bar{\Lambda}) = \frac{1}{\beta_0 L} \left(1- \frac{\beta_1\ln{L}}{\beta_0^2 L}\right), $

(9) $ m_i(\bar{\Lambda}) = \hat{m}_i \alpha_\mathrm{s}^{\frac{\gamma_0}{\beta_0}} \left[ 1 + \left(\frac{\gamma_1}{\beta_0}-\frac{\beta_1\gamma_0}{\beta_0^2}\right) \alpha_\mathrm{s} \right]. $

(10) Here,
$ L\equiv \ln\left( \dfrac{\bar{\Lambda}^2}{\Lambda_{\overline{\mathrm{MS}}}^2}\right) $ , with$ \Lambda $ being the renormalization scale. We take the$ \overline{\mathrm{MS}} $ renormalization point,$ \Lambda_{\overline{\mathrm{MS}}} = 376.9 $ MeV, based on the latest results for a strong coupling constant [66]. Following Eq. (10), the invariant quark masses are$ \hat{m}_u = 3.8 $ MeV,$ \hat{m}_d = 8 $ MeV, and$ \hat{m}_s = 158 $ MeV. The parameters for the$ \beta $ -function and$ \gamma $ -function are$ \beta_0 = \dfrac{1}{4\pi}\left(11-\dfrac{2}{3}N_\mathrm{f}\right) $ ,$\beta_1 = \dfrac{1}{16 \pi^2} \left(102-\dfrac {38}{3} N_\mathrm{f}\right)$ ,$ \gamma_0 = 1/\pi $ , and$ \gamma_1 = \dfrac{1}{16\pi^2} \left(\dfrac{202}{3} - \dfrac{20}{9}N_\mathrm{f}\right) $ [67] (The formulas are for arbitrary$ N_\mathrm{f} $ , and in this study,$ N_\mathrm{f} = 3 $ ). It is not clear how the renormalization scale evolves with the chemical potentials of quarks, and we adopt$ \bar{\Lambda} = \dfrac{C_1}{3} \sum_i\mu_i $ , with$C_1 = 1 \sim 4$ [64].To account for the energy difference between the physical vacuum and perturbative vacuum, we introduce the bag mechanism with a dynamically-scaled bag parameter [68, 69]. The total thermodynamic potential density for SQM can be written as [70]
$ \Omega = \Omega^\mathrm{pt} + B \equiv \Omega^\mathrm{pt} + B_\mathrm{QCD} + (B_0 - B_\mathrm{QCD})\exp{\left[-\left( \frac{\sum_i\mu_i-930}{\Delta\mu}\right)^4\right]}. $

(11) Following [71], we take
$ B_0 = 40,\; 50\; \rm MeV/fm^3 $ for the calculations.$ \Delta\mu = \infty $ indicates there is no medimum effect for the bag parameter. If$ \alpha_\mathrm{s} $ and$ m_{u,d,s} $ are running with the energy scale as reported by the Particle Data Group [66], the maximum mass of a QS does not reach$\sim2 \,{M}_{\odot}$ . In such cases, the dynamical rescaling of the bag constant with a finite$ \Delta \mu $ is essential, which basically originates from the nonperturbative effects, such as chiral symmetry breaking and color superconductivity [72-74].At given chemical potentials
$ \mu_i $ , pressure P, particle number density$ n_i $ , and energy density$ \rho $ are determined by$ P = -\Omega, $

(12) $ \begin{aligned}[b] n_i =& \frac{g_i}{6\pi^2} \left(\mu_i^2-m_i^2\right)^3 -\frac{\partial \Omega_1}{\partial \mu_i} \alpha_\mathrm{s} -\frac{\partial B}{\partial \mu_i} \\ {} & -\frac{C_1}{3}\sum_i \left( \frac{\partial \Omega_0}{\partial m_i} +\frac{\partial \Omega_1}{\partial m_i}\alpha_\mathrm{s}\right) \frac{\rm{d} m_i}{\rm{d} \bar{\Lambda}}\\ & -\frac{C_1}{3} \frac{\partial \Omega_1}{\partial\bar{\Lambda}} \alpha_\mathrm{s} -\frac{C_1}{3} \Omega_1 \frac{\rm{d} \alpha_\mathrm{s}}{\rm{d} \bar{\Lambda}}, \end{aligned} $

(13) $ \rho = \Omega + \sum_i \mu_i n_i. $

(14) -
Besides the bag mechanism, quark confinement can be achieved via density dependence of the mass, as done in the equivparticle model [75, 76]. Taking into account both linear confinement and leading-order perturbative interactions, the quark mass scaling is given by
$ m_i(n_{\mathrm b}) = m_{i0}+Dn_{\mathrm b}^{-1/3}+Cn_{\mathrm b}^{1/3}, $

(15) where
$ m_{i0} $ is the current mass ($ m_{u0} \sim2.3 $ MeV,$ m_{d0} \sim4.8 $ MeV, and$ m_{s0} \sim95 $ MeV) [66], and$ n_{\mathrm b} = (n_u+n_d+n_s)/3 $ is the baryon number density. Parameters D and$ C $ characterize the strengths of the confinement and the leading-order perturbative interactions, respectively, which have been estimated as$ 140 \lesssim \sqrt{D}\lesssim 270 $ MeV [77] and$ C\lesssim 1.2 $ [76].At given particle number densities
$ n_i $ , energy density$ \rho $ , chemical potential$ \mu_i $ , and pressure P are given by$ \rho = \sum_{i} \frac{g_i}{16\pi^{2}} \left[\nu_i(2 \nu_i^2+m_i^2)\sqrt{\nu_i^2+1}-m_i^4 \mathrm{arcsh}\left(\frac{\nu_i}{m_i}\right) \right], $

(16) $ \mu_i = \sqrt{\nu_i^2+m_i^2} + \frac{1}{9}\left(\frac{C}{n_{\mathrm b}^{2/3}}-\frac{D}{n_{\mathrm b}^{4/3}}\right) \sum_in^s_i, $

(17) $ P = \sum_i \mu_i n_i - \rho, $

(18) with the scalar and vector densities being
$\begin{aligned}[b] n^s_i = &\langle \bar{\Psi}_i \Psi_i\rangle = \frac{g_i m_i}{4\pi^{2}} \left[ \nu_i \sqrt{\nu_i^2+1} - m_i^2 \mathrm{arcsh}\left(\frac{\nu_i}{m_i}\right) \right],\\ n_i =& \langle \bar{\Psi}_i \gamma^0 \Psi_i\rangle = \frac{g_i\nu_i^3}{6\pi^2}. \end{aligned} $

(19) Here,
$ \nu_i $ is the Fermi momentum for particle type i. -
Similar to the equivparticle model, in the quasiparticle model, strong interactions are mimicked by effective masses. At zero temperature, by resumming one-loop self energy diagrams in the hard dense loop approximation, the effective mass formula for quarks at finite chemical potentials can be obtained as [78-80]
$ m_i = \frac{m_{i0}}{2}+\sqrt{\frac{m_{i0}^2}{4}+\frac{2 \alpha_\mathrm{s}}{3 \pi} \mu_i^2}. $

(20) Here,
$ m_{i0} $ is the current mass of quark flavor i [66], and$ \alpha_\mathrm{s} $ is the running strong coupling constant given by Eq. (9).At given chemical potentials
$ \mu_i $ , pressure P, particle number density$ n_i $ , and energy density$ \rho $ are determined by$ P = -\Omega = -\Omega_0 - B_0, $

(21) $ n_i = \frac{g_i}{6\pi^2} \left(\mu_i^2-m_i^2\right)^3 - \sum_{j = u,d,s} \frac{\partial \Omega_0}{\partial m_j}\frac{\rm{d} m_j}{\rm{d} \mu_i}, $

(22) $ \rho = \Omega_0 + B_0 + \sum_i \mu_i n_i. $

(23) Again, the bag constant,
$ B_0 $ , represents the vacuum pressure. Based on Eq. (6), the derivative of$ \Omega_0 $ with respect to the effective quark mass,$ m_i $ , is calculated as$ \frac{\partial\Omega_0}{\partial m_i} = \frac{g_im_i}{4\pi^2} \left[ \mu_i \sqrt{\mu_i^2-m_i^2} -m_i^2\ln\frac{\mu_i+\sqrt{\mu_i^2-m_i^2}}{m_i} \right]. $

(24) In the left (right) panel of Fig. 1, we present the energy per baryon (pressure) obtained with the various effective models for representative parameters: the quasiparticle model (labeled as qParticle), equivparticle model (labelled as eParticle), MIT
$ \alpha_\mathrm{s}^2 $ bag model, and perturbation model (labelled as Pertrub.). We notice the opposite effects of$ C_1 $ and$ B_0 $ parameter on the EOS in the perturbation model, namely a large bag constant$ B_0 $ usually results in softening, whereas a large dimensionless parameter$ C_1 $ (namely, a large renormalization scale) results in stiffening. The dynamic scaling of the B parameter with a finite$ \Delta \mu $ brings further repulsion and increases the energy (pressure) evidently from around$ 0.5\; \rm fm^{-3} $ ($ \sim4\rho_0 $ ) in the left (right) panel.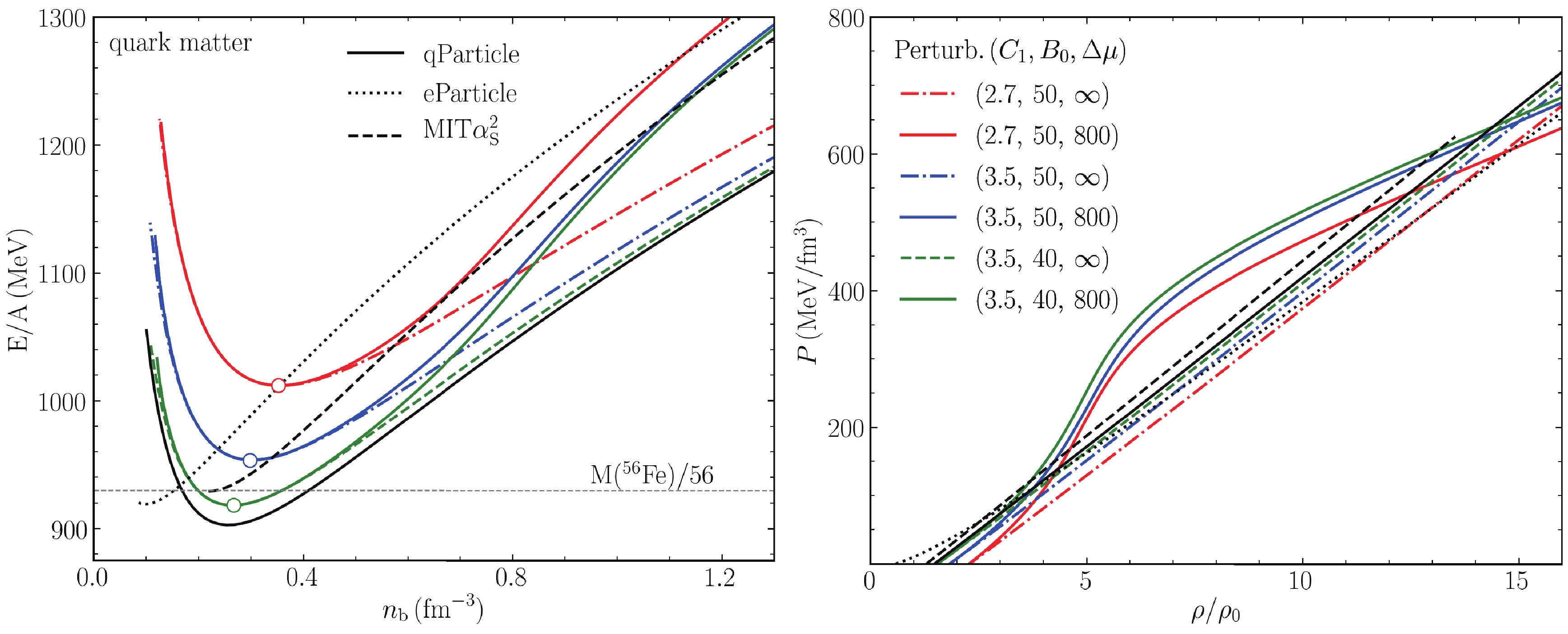
Figure 1. (color online) Energy per baryon
$E/A$ as a function of the baryon number density,$n_{\rm b}$ . The calculations are done with various effective SQM models: the quasiparticle model (black solid curves) with$C_1 = 3.5$ ,$B = 50\; {\rm MeV/fm^3}$ , equivparticle model (black dotted curves) with$C = 0.7,\; \sqrt{D} = 129\; \rm MeV$ , MIT$\alpha_\mathrm{s}^2$ bag model (black dashed curves) with$B_{\rm eff}^{1/4} = 138\; {\rm MeV}$ (namely,$B_{\rm eff}\sim47.2 $ $ {\rm MeV/fm^3}),\; a_4 = 0.61$ , and pertrubation model (colorful curves) with six sets of parameters ($C_1,\; B_0,\; \Delta \mu$ ). The three dots in the left panel represent the mimimum energy points, respectively. The horizontal line corresponds to$E/A = 930\; \rm MeV$ , which is the energy per baryon of the stablest atomic nuclei,$^{56}\rm Fe$ .To estimate whether an SQM is an absolute stable strong-interaction system, we require that at
$ P = 0$ ,$E/A \leqslant M(^{56}\rm Fe)/56 = 930\; MeV $ . The condition is fulfilled under four cases of our calculations:$ \mathrm{qParticle}\; (C_1,B_0) = $ (3.5, 50),$ \mathrm{eParticle}\; (C,\sqrt{D}) = (0.7,\; 129) $ ,$ \mathrm{MIT\alpha_\mathrm{s}^2}\; (B_{\rm eff},a_4) = $ (138, 0.61), and$ \mathrm{Pertrub.}\; (C_1,\;B_0,\; \Delta\mu) = $ $ (3.5,\; 40,\; 800/\infty $ ). These are the cases where a strange QS is possible, and the prediction of the star properties will be presented later in this section. Because zero-pressure density is closely related to the stiffness of the QS EOS (even regarded as the characteristic of stiffness in many previous studies [48, 63]), we mention that the surface density is the lowest in the$ \rm eParticle\; (0.7,\; 129) $ EOS, around$ 0.1\; \rm fm^{-3} $ . Its stiffness will be manifested later in the results of the star properties (Sec. IV C). -
To construct a hadron-quark mixed phase under two extreme scenarios with
$ \sigma\rightarrow 0 $ (the Gibbs construction) and$ \sigma>\sigma_\mathrm{c} $ (the Maxwell construction), we define the fraction of quark matter as$ \chi\equiv V_q/V $ , where$ V_q $ is the volume occupied by quarks, and V is the total volume, i.e.,$ \chi = 0 $ represents the pure nuclear matter, and$ \chi = 1 $ is the quark matter. The total baryon number density is$ n_\mathrm{b} = (1-\chi) (n_p + n_n) +\chi \left(n_u + n_d + n_s\right)/3. $

(25) The total energy density is
$ \rho = (1-\chi) \rho_N +\chi \rho_q +\rho_e, $

(26) where
$ \rho_N $ ,$ \rho_q $ , and$ \rho_e $ are the energy densities of the nuclear matter, quark matter, and electrons, respectively.The constituent particle chemical potentials in the two sectors are linked as follows:
$ \mu_n = \mu_u + 2\mu_d,\; \mu_p = 2\mu_u + \mu_d,\; $ $ \mu_e = \mu_n-\mu_p = \mu_d-\mu_u $ . Two independent chemical potentials,$ (\mu_n, \mu_p) $ or$ (\mu_u, \mu_d) $ , can be determined by solving the charge neutrality equation and the pressure balance equation for a given total baryon number or a given quark fraction [81-84]. The EOS of the mixed phase can be then calculated. We mention that the local charge neutrality condition,$ n_p-n_e = 0,\; \frac{2}{3}n_u-\frac{1}{3}n_d-\frac{1}{3}n_s-n_e = 0,$

(27) is fulfilled within the Maxwell phase transition construction, and the global charge neutrality condition is satisfied within the Gibbs phase transition construction as
$ 0 = (1-\chi)n_p +\chi \left(\frac{2}{3}n_u-\frac{1}{3}n_d-\frac{1}{3}n_s\right)-n_e. $

(28) For the cases with moderate surface tensions (
$ 0<\sigma<\sigma_\mathrm{c} $ ), to construct the geometrical structures of the mixed-phase, we employ a Wigner-Seitz approximation and assume spherical symmetry, i.e., only droplet and bubble phases are considered. The internal structure of the Wigner-Seitz cell is determined by minimizing the energy at a given number density. More formulas can be found in our previous study [70]. -
The results of
$ \Gamma $ and$ c_s $ for NS matter (or betastable nuclear matter) are presented in the left panels of Fig. 2 and Fig. 3, respectively. The corresponding results of quark matter are shown in their right panels.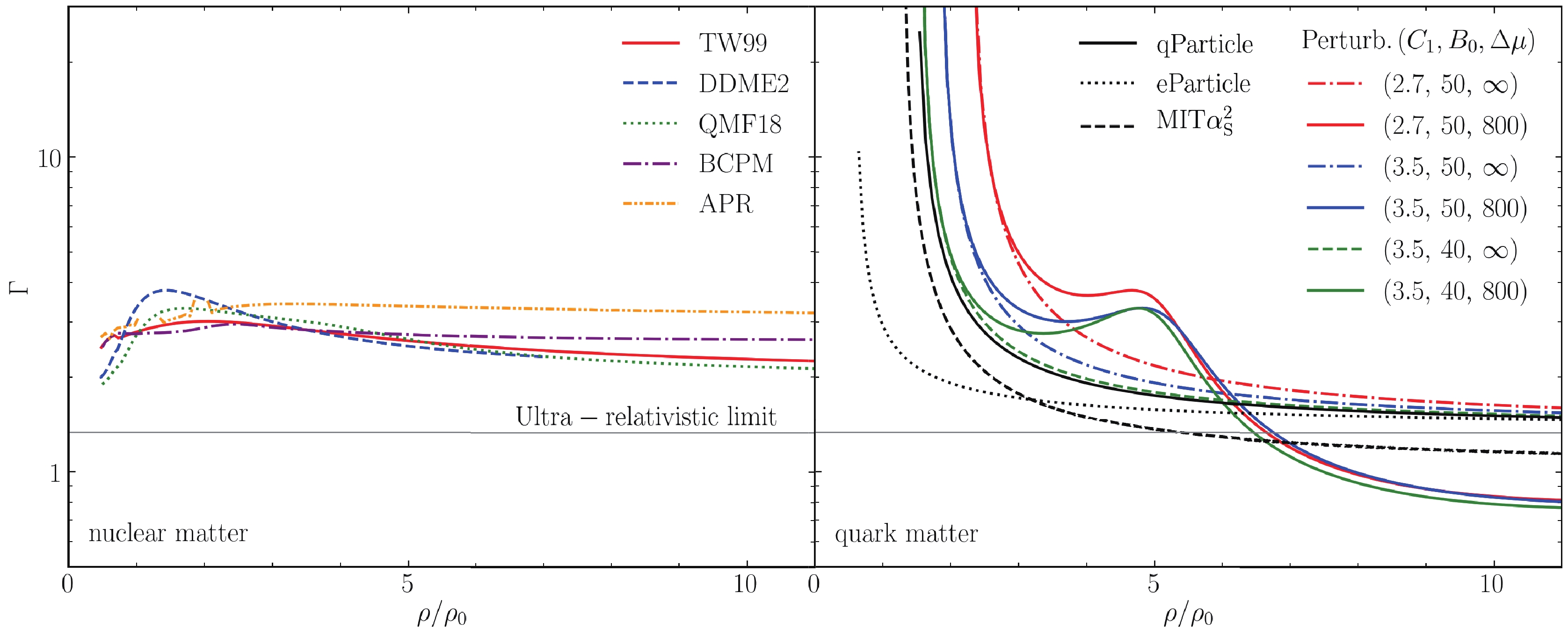
Figure 2. (color online) (Left) Adiabatic index
$\Gamma$ of nuclear matter (left) and SQM (right) as a function of the energy density,$\rho$ (divided by the saturation density,$\rho_0$ ). The results of nuclear matter are obtained with the five various EOS models, namely TW99, DDME2, QMF18, BCPM, and APR. The calculations of SQM are performed with various effective models: quasiParticle, equivparticle, MIT$\alpha_\mathrm{s}^2$ , and perturbation models using six sets of parameters ($C_1,\; B_0,\; \Delta \mu$ ). The horizontal line represents the ultra-relativistic limit.
Figure 3. (color online) Same as Fig. 2 but for the sound speed,
$c_s$ . The horizontal line represents the conformal limit.In Fig. 2 for
$ \Gamma $ , we see that the values mostly lie between$ \sim 2 - 3 $ for nuclear matter and are commonly greater than those of SQM in the intermediate density range. The adiabatic index of SQM matter shows a sharp decrease with the density. In the cases of the quasiparticle model, equivparticle model, and perturbation model (with a fixed bag parameter), they also approach close to the ultra-relativistic limit of$ 4/3 $ at high densities. The lower curves in the high-density range in the MIT$ \alpha_\mathrm{s}^2 $ model and perturbation model (with in-medium bags) indicate that the quark interactions are weak in these cases. In particular, we notice the stiffening of the adiabatic index in the perturbation model from the repulsive contribution brought by the dynamic scaling of the bag parameters.In Fig. 3 of the sound velocity,
$ c_s $ , we see that$ c_s $ increases monotonously from small values with the density using only the nuclear matter EOS, and there is possible a violation of the causality at some high densities, e.g.,$ \sim 6.45\rho_0 $ in the APR case. The model can certainly not be applied for the study of dense matter beyond this density. We mention that the NS central density with a maximum mass of$\sim2.2 \,{M}_{\odot}$ for the APR model is high, reaching up to$ \sim9.75\rho_0 $ , which is beyond the causality violation density. For the SQM EOSs (except the perturbation model with in-medium bags),$ c_s $ also increases monotonously from small values but approaches quickly (around$ \rho_0 $ ) the conformal limit of$c/\sqrt{3}$ from below. However, for the perturbation model with in-medium bags at$ \Delta \mu = $ $ 800\; \rm MeV $ ,$ c_s $ increases and then decreases, resulting in a peak in the curve at$ \sim5\rho_0 $ . This may be what is expected in [25] for NSs, from the analysis based on the two-solar-mass constraint and the empirical evidence below and around nuclear saturation density. The peak can be as high as$ 0.9c $ , similar to the result in [23]. In [24, 27], a relatively lower peak value ($ \sim0.63c $ ) was found. The hadron-quark phase transition can achieve similar$ c_s $ shapes, which we show below. -
We show in Fig. 4 the
$ \Gamma,\; c_s $ results of HS matter under a hadron-quark phase transition. The calculations are performed using the perturbation model for quark matter, in combination with two nuclear matter EOS models (soft TW99 and stiff DDME2) for the study of the stiffness effects. The results of the other three quark matter models should be similar to those of the perturbation model in the cases without the dynamical scaling of the bag parameter, i.e.,$ \Delta\mu = \infty $ . The$ c_s $ results of the pure SQM case of Perturb.(3.5, 40,800) are also shown in the lower panel for comparison. The calculations are performed under various constructions between the two phases: Maxwell construction (with a considerable interface tension and a finite density jump), Gibbs construction (with a zero interface tension), and some proper choices of the hadron-quark interface tension (in the range of$ 1 - 50\; \rm MeV/fm^2 $ ). Varying the surface tension basically indicates that the properties of the quark-hadron mixed-phase interpolate in between the two extremes, i.e., the Gibbs construction scenarios with point-like hadronic matter and quark matter and the Maxwell construction scenarios with bulk separation of the two phases. If we increase the hadron-quark interface tension, the obtained results evolve from the Gibbs case into the Maxwell case, where the density range of the mixed-phase also shrinks.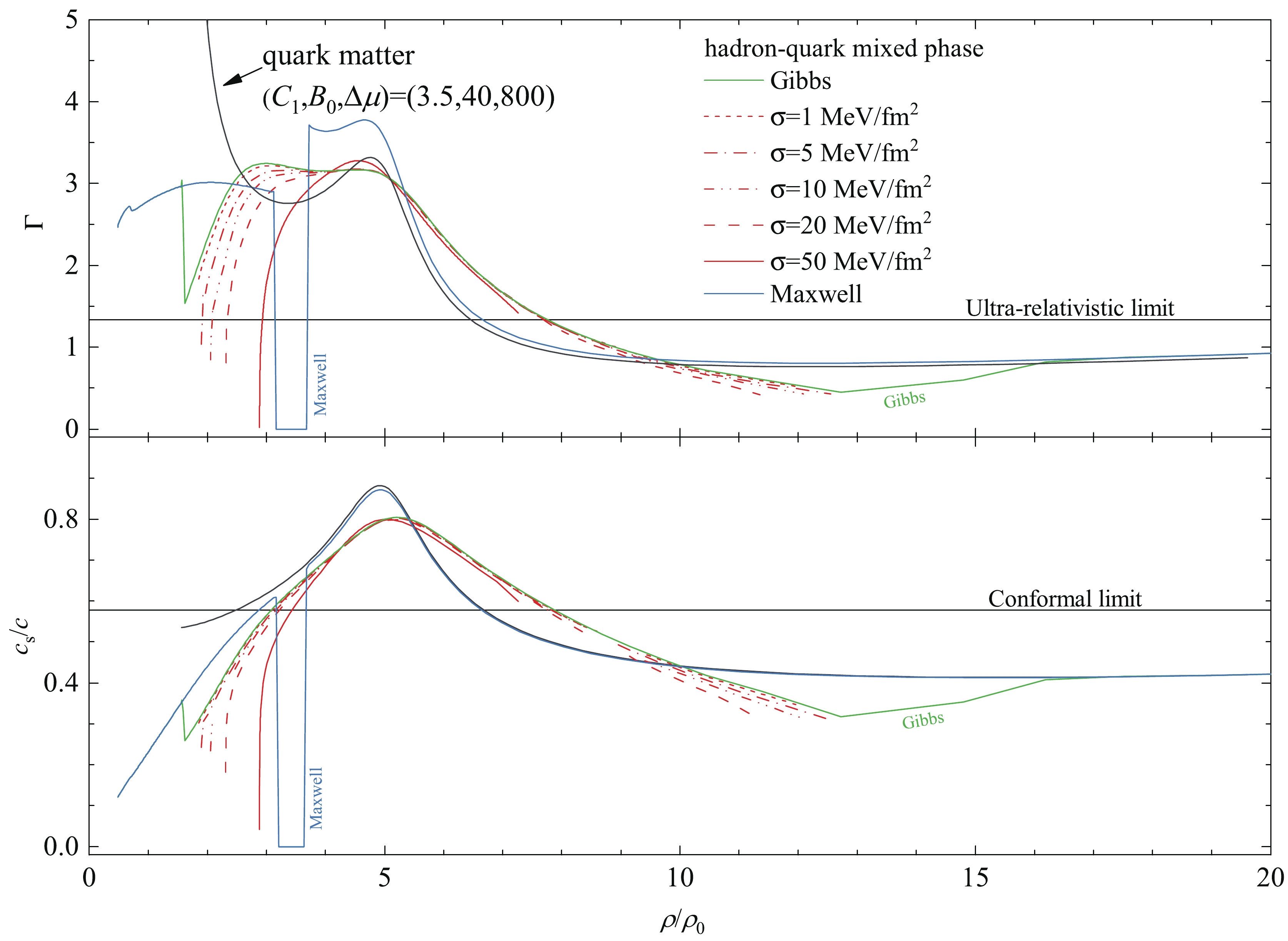
Figure 4. (color online)
$\Gamma$ (Upper) and$c_s$ (lower) for hybrid matter under various constructions between the two phases: Maxwell construction (shadow regions show the finite density jump in this case), Gibbs construction, and some choices of the hadron-quark interface tension ($\sigma = \; 1,\; 5,\; 10,\; 20,\; 50\; \rm MeV/fm^2$ ). For the calculations, the nuclear matter EOS employs the RMF model with the TW99 effective interaction, and the SQM EOS employs the perturbation model with the parameters$C_1 = 2.7,\; B_0 = 50\; \rm MeV/fm^3,\; \Delta \mu = 800\; \rm MeV$ . The$c_s$ results for the pure SQM case of Perturb.(3.5,40,800) are also shown in the lower panel for comparison. The horizontal lines in the upper/lower panel show the ultra-relativisitc limit/conformal limit for$\Gamma$ /$c_s$ .Let us first focus on the Gibbs case with no interface tension. At the quark threshold density, the adiabatic index,
$ \Gamma $ , sharply decreases by almost a factor of two owing to the strong softening of the EOS by an extra degree of freedom. Subsequently, as the density increases,$ \Gamma $ increases because the pressure increases. After reaching a maximum of$ \sim3.2 $ , it starts to decrease rapidly before a small continuous lift due to the repulsion inherent in the SQM modeling. Subsequently, at$ \sim12\rho_0 $ , when it lowers to$ \sim0.5 $ ,$ \Gamma $ increases owing to the change from two phases to a single phase and approaches the pure quark matter result (some value lower than 1)$ \sim16\rho_0 $ . The increase in the hadron-quark interface tension generally lowers the first peak and enhances the second peak simultaneously. Finally, for a large$ \sigma $ such as$ 50\; \rm MeV/fm^2 $ , only the second peak is present, similar to the Maxwell case and the pure quark matter case. The detailed variations for the mixed-phase under various conditions depend mainly on the competition between the softening due to the coexistence of two phases and the stiffening due to the pressure increase.In the systematic study in [22], an evident decrease in the adiabatic index is regarded as a signature of the hadron-quark phase transition. However, the
$ \Gamma $ decrease can be achieved with only one phase of SQM using one of our effective models of quark matter, the perturbation model (with in-medium bags), as one may notice in Fig. 2. The acting of the quark matter as a hadron-quark mixed phase can also be seen in the$ c_s $ study, e.g., in the lower panel of Fig. 4. The behavior of the sound speed of the hadron-quark mixed-phase resembles that of the pure SQM case in the intermediate density region of$ \sim3 - 8\rho_0 $ . A recent Bayesian analysis on HSs adopting the GW170817 and NICER PSR J0030+0451 data found a similar$ c_s $ peak value of$ \sim0.81c $ [14] as presented in the previous section for quark matter. As a consequence, distinguishing between different states of dense matter (including the onset of phase transition) can hardly be achieved by the variations in the sound speed or the adiabatic index, according to the present study. -
In Fig. 5, we show the masses of QSs as functions of the radii (in the left panel) and the central density (in the right panel). The calculations are performed with all four effective quark matter models selected in the present work, i.e., the quasiparticle model
$ (C_1,B_0) = $ (3.5, 50), equivparticle model$ (C,\sqrt{D}) = $ (0.7, 129), and MIT$ \alpha_\mathrm{s}^2 $ $ (B_{\rm eff},a_4) = $ (138, 0.6). In particular, we apply here for the first time the pertrubation model to the self-bound QSs, for two representative cases:$ (C_1,\; B_0,\; \Delta \mu) = $ (3.5, 40, 800) as well as (3.5, 40,$ \infty $ ).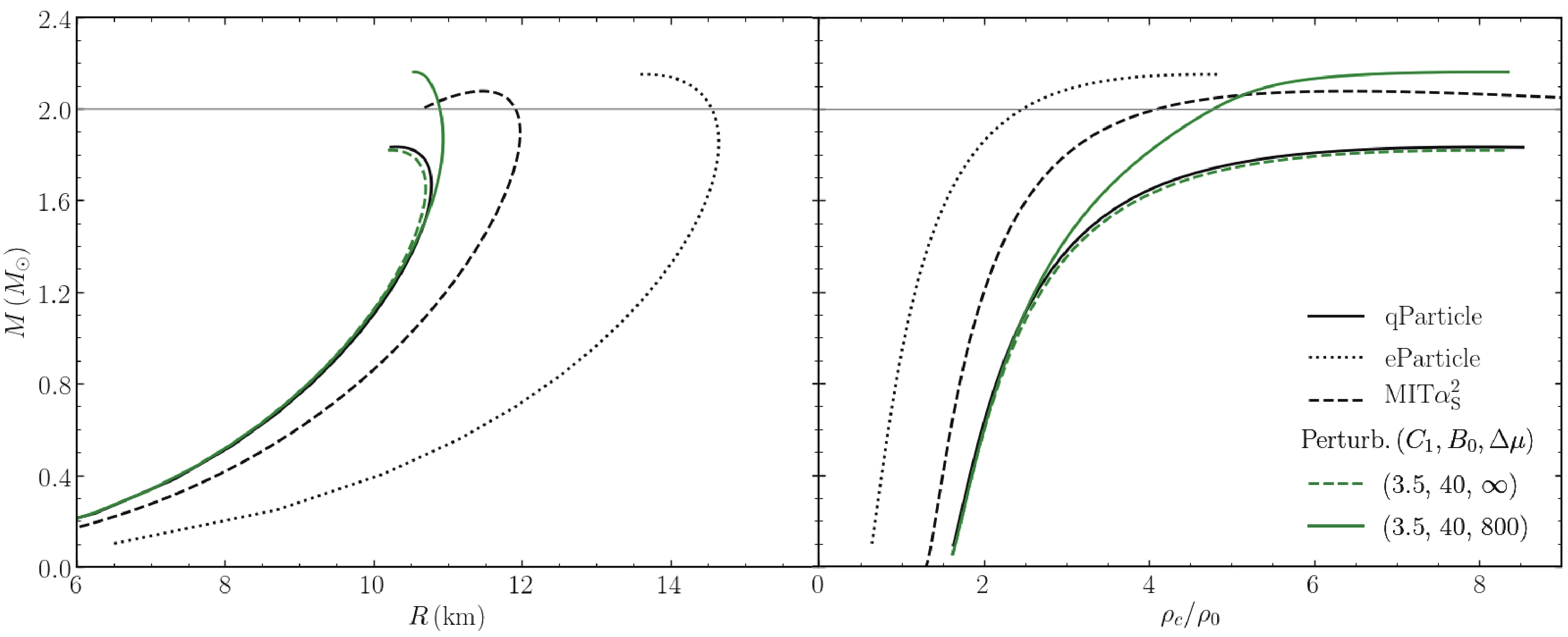
Figure 5. (color online) Masses of QSs as a function of the radii (left panel) and the central density (right panel). The calculations are performed for all four effective quark matter models with typical parameter sets, i.e., the quasiparticle model with
$C_1 = 3.5$ ,$B = 50\; {\rm MeV/fm^3}$ , equivparticle model with$C = 0.7,\; \sqrt{D} = 129\; \rm MeV$ , MIT$\alpha_\mathrm{s}^2$ bag model with$B_{\rm eff}^{1/4} = 138\; {\rm MeV}$ (namely,$B_{\rm eff}\sim47.2 $ $ {\rm MeV/fm^3}),\; a_4 = 0.61$ , and pertrubation model with the parameters$C_1 = 3.5,\; B_0 = 40\; \rm MeV/fm^3,\; \Delta \mu = 800\; \rm MeV$ or$\infty$ . The horizontal lines indicate the two-solar-mass limit.It is seen that the radii of most massive QSs lie between
$ \sim10\; \rm km $ and$ \sim12\; \rm km $ , with one exception in the equivparticle model due to the very low surface density of$ \sim 0.1\; \rm fm^{-3} $ as mentioned before. In the equivparticle model, it is necessary to have a large radius to ensure a large maximum mass above the two-solar mass. Such a high radius ($ \sim 14\; \rm km $ ) may have been excluded by the LIGO/ Virgo observation of NS binary merger GW170817 if one supposes it originates from a binary QS merger. The repulsive contribution from the in-medium bag in the perturbation model demonstrates a new way to achieve a large maximum mass with a small radius, e.g., the mass is increased from$1.8 \,{M}_{\odot}$ (when$ \Delta\mu = \infty $ ) to$2.2 \,{M}_{\odot}$ (when$ \Delta\mu = 800\; \rm MeV $ ) with a similar radius. One more merit of the new perturbation model (with the in-medium bag) is achieving both large maximum mass and large surface density. An extremely low QS surface density (below$ \rho_0 $ ) is not preferred because in such a density realm, it should be confined inside hadrons. Further measurements of a small radius (especially for small pulsars) together with a large maximum mass would help validate this QS EOS model [5] and the effective scaling of the bag parameter used in the model. -
The sound speed,
$c_s = \sqrt{{\rm d}P/{\rm d}\rho}$ , is a fundamental quantity for describing matter state, and the causality limit has been used to set important bounds on dense matter EOS and the maximum masses of NSs [85, 86]. For example, the polytropic form of$ P = (\rho-\rho_0)c^2+P_m $ matching smoothly to a realistic nuclear matter EOS [87] at nuclear saturation density$ \rho_0 $ ($ P_m $ is a constant determined from the matching) gives an upper limit of$\sim4.8 \,{M}_{\odot}$ for the TOV mass. In this study, we explore the possibility of using microphysical quantities (like$ c_s $ ) to shed light on the particle degree of freedom in cold, dense matter in the density region where no first-principle method can be presently applied.We make use of various many-body frameworks for the modeling of pure nuclear matter and quark matter. These employed models cover approximately the full range of NS/QS EOS models regarding their stellar properties. One representative quark matter model, the perturbation model, is used for the study of a hadron-quark deconfinement phase transition, together with two representative EOS models (TW99 and DDME2) for nuclear matter.
We mainly find a dissimilarity in the adiabatic index for pure nuclear matter and quark matter. Moreover, a high sound velocity (i.e., a particular shape) may be necessary for dense matter to fulfill the two-solar-mass constraint:
$ 0.68 c $ for QSs and$ 0.8 c $ for HSs. Correspondingly, both$ \Gamma $ and$ c_s $ cannot effectively signify the composition of matter at intermediate densities relevant to compact stars. The complexity also arises from the additional nonperturbative effects included in the model calculation, which introduce an extra repulsion above$ \sim5\rho_0 $ and affect the predicted structures of QSs. As a result, a more compact QS is possible with a TOV mass as high as$\sim2.2 \,{M}_{\odot}$ . This is a new series of QS EOSs that could lead to interesting observational possibilities for studying the EOS of dense QCD matter and the nonperturbative properties of QCD. Along this line, some studies have pointed out the differences in the dynamical stabilities of one phase stars and multi-phase stars [88]. Further efforts regarding the dynamical properties (such as NS cooling [5, 89] and NS binary merger simulation) of such compact objects may be necessary for identifying the state of QCD matter at intermediate densities. -
The support provided by the China Scholarship Council during a visit of C.-J. X. to JAEA is acknowledged. The computation for this work was supported in part by the HPC Cluster of SKLTP/ITP-CAS and the Supercomputing Center, CNIC, of the CAS.
Sound velocity in dense stellar matter with strangeness and compact stars
- Received Date: 2020-12-31
- Available Online: 2021-05-15
Abstract: The phase state of dense matter in the intermediate density range (





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: