-
The discovery of quark-gluon plasma (QGP), a special state of matter, by ultrarelativistic heavy ion collisions in a ground laboratory has been expected. The initial parton systems produced at the Relativistic Heavy-Ion Collider (RHIC) and Large Hadron Collider (LHC) have an anisotropic momentum distribution and experience a complicated evolution to equilibrium finally. The transport coefficients strongly influence the evolution of the produced hot and dense QCD matter. The relativistic hydrodynamic simulations associated with a small shear viscosity rather successfully explain the flow data and transverse momentum spectra of ultimate hadron from heavy ion collisions; for reviews, please refer to Refs. [1-5]. Soon afterward, the viscous effects on the diverse aspects of the hot QGP, including photon and dilepton production [6,7], heavy quarkonium dissolution [8,9], energy loss suffered by the fast parton traveling through the QGP [10-13] and the induced wakes [14-18], the quark polarization [19] and the chiral magnetic/vortical effects [20-22], the dielectric properties of the QGP medium [23-25], and the dynamical evolution of QCD matter during the first-order phase transition from hadronic matter to quark matter [26], have been addressed in recent years.
At the very early stage of the ultrarelativistic heavy ion collisions [27,28] and in the so-called magnetic scenario for the QGP in the evolution process near the
$ T_c $ region [29,30], there are color-electric flux tubes in the system containing strong color-electric fields. Simultaneously, a significantly strong magnetic field is generated perpendicular to the reaction plane in off-central collisions [31-33]. The study on the electromagnetic properties of the quark-gluon plasma has attracted increasing interest in recent years.Electric conductivity
$ \sigma $ reflects the electromagnetic response of the medium to the applied electric field, which is a transport coefficient describing the charge transport. The electric conductivity enters into the hydrodynamic evolution equations for the QCD plasma produced in heavy ion collisions, dominates the space-time evolution of energy-momentum [28], and influences the quark-gluon chemical equilibration [34]. In off-central ultrarelativistic heavy ion collisions, the electric conductivity determines the duration of the transient strong magnetic field and the strength of the chiral magnetic effect [31,33,35]. As a result, the electric conductivity is responsible for the distribution of the charge-dependent flow of final state hadron sensitive to the chiral magnetic and separation effects in off-central heavy-ion collisions [31,33,35,36]. Moreover, the electric conductivity significantly influences the soft photon and the low mass dilepton yield [34,37-39]. In a word, as shear viscosity, the electric conductivity plays an important role in the matter evolution in ultrarelativistic heavy ion collisions.During the foundation of the QGP kinetic theory in the 1980s-1990s, several scientific groups studied the electric conductivity of the QGP within that theoretical framework [40-46]. Subsequently, with the development of the thermal field theory and the QGP transport theory, this was investigated with the resummation QCD perturbative theory and the effective kinetic theory [47-58]. Recently, the electric conductivity of the QGP has aroused much attention and has been studied with different approaches, including the numerical solution of the Boltzmann equation [59,60], the quasiparticle model [61-63], the Dyson-Schwinger approach [64], and the lattice gauge theory [38,39]. In addition, the study of the electric conductivity in the QGP under magnetic field has attracted increasing interest in the heavy ion community [65-70].
In a thermal plasma system, the temperature gradient in the spatial distribution and the velocity gradient between the adjacent fluid layers will result in heat and momentum transports, respectively. The heat conductivity
$ \lambda $ and the shear viscosity$ \eta $ are the corresponding transport coefficients that dominate the system to approach the heat equilibrium and the momentum isotropy. An applied electric field will induce charge transport, and the electric conductivity$ \sigma $ characterizes the charge transport in the plasma system. Those different transport processes may take place simultaneously in the QGP. In the present paper, we will study the electric conductivity of the QGP in the presence of shear viscosity, which is focused on the mutual impacts between the different transport phenomena in the QGP.The relation between heat transport and charge transport was first addressed in condensed matter systems in history. In a metal, the ratio of the heat conductivity to the electric conductivity multiplied by the system's bulk temperature
${\lambda}/{\sigma T}$ is a constant-Lorentz number, which is known as Wiedemann-Franz law [71]. Some scientific groups have investigated the Wiedemann-Franz law in the QGP and hot dense hadronic systems in Refs. [63,72-75] very recently. In addition, some investigations reported that the ratio of shear viscosity to thermal conductivity$ \dfrac{\eta c_p}{\lambda \rho} $ ($ c_p $ and$ \rho $ are the specific heat at constant pressure and mass density of the system, respectively) is a constant in dilute atomic Fermi gases [76] as well as in the QGP with finite chemical potential [77], which is qualitatively similar to that obtained in a strongly coupled conformal plasma [78]. A constant result for$ \dfrac{\eta c_p}{\lambda \rho} $ is an interesting analogy to the Wiedemann-Franz law.In the context of relativistic heavy ion collisions, the relation between shear viscosity and electric conductivity was focused on in Refs. [61-63,79,80]. In those references, the authors calculated the shear viscosity and electric conductivity separately under the same theoretical framework with the same physical conditions. Then, based on the derived results, the ratio of the shear viscosity to electric conductivity was found to determine which transport process will play a relatively significant role in the evolution of the QGP [61-63,79,80]. In the present work, we study the connection between the electric conductivity and the shear viscosity with an alternative approach. According to Refs. [6,10,81-83], the viscosity modifies the distribution functions of the constituents of the QGP. Based on the chromohydrodynamic equations obtained from the QGP kinetic theory and the distribution function modified by shear viscosity, one can derive the induced color current through which conductivity tensor will be derived. Through the viscous distribution functions, viscous chromohydrodynamic equations, the induced color current, and the conductivity tensor, shear viscosity is embedded into the electric conductivity. Therefore, one can study the viscous effects on the conductivity properties. Quarks carry electric and color charges. The dynamics of quarks are governed by quantum chromodynamics. Thus, we should call the research object the color-electric conductivity.
The paper is organized as follows. In Section II, we briefly review the formalism for the calculation of the electric conductivity. In the next section, by solving the viscous chromohydrodynamic equations formulated from the QGP kinetic theory together with the distribution function modified by the shear viscosity, we derive the induced color current through which the conductivity tensor can be abstracted according to the linear response theory. In Section IV, we evaluate the color-electric conductivity and study the viscous effects on it. Section V presents the summary.
The natural units
$ k_B = \hbar = c = 1 $ , the metric$g_{\mu\nu} = $ $ (+,-,-,-)$ , and the notations$ k^\mu = (\omega,{\bf{k}}) $ and$ K^2 = \omega^2-k^2 $ are used in the paper. -
The electric conductivity can be evaluated from the Kubo formula related to the current-current correlation for a system in thermal equilibrium. It also can be derived by extracting the proportionality coefficient of the induced electric current responding to the applied external electric field according to Ohm's law
${{\mathit{\boldsymbol{j}}}} = \sigma {{\mathit{\boldsymbol{E}}}}$ . Ohm's law can be extended to a covariant form applicable to the non-Abelian plasma [28,40-47]$ j^\mu_a = \sigma^{\mu\nu}_{ab}F^b_{\nu\lambda}u^\lambda, \ \ \ \ \ \ \ a,b = 1,2,...,8, $

(1) where
$ F^b_{\nu\lambda} $ and$ u^\lambda $ are the field strength tensor and the fluid velocity, respectively. The current$ j^\mu_a $ is induced by the color-electric field$ F^b_{\nu\lambda}u^\lambda $ . Therefore, the proportionality coefficient$ \sigma^{\mu\nu}_{ab} $ is the color-electric conductivity tensor through which we can study the conductivity properties.The kinetic equation for partons is given by [41,45,46,48]
$ p^\mu D_\mu Q^i(p,x)+\frac{g}{2}\theta^ip^\mu \{F_{\mu\nu}(x),\partial^\nu_pQ^i(p,x)\} = C, $

(2) $ Q^i(p,x) $ with$ i\in{g,q,\overline{q}} $ denote the distribution functions of gluon, quark, and antiquark, respectively, which are$ (N_c^2-1)\times(N_c^2-1) $ and$ N_c\times N_c $ matrices respectively;$ \theta^{g} = \theta^{q} = 1 $ ,$ \theta^{\bar{q}} = -1 $ , and$ \partial_{\nu}^{(p)} $ denotes the four-momentum derivative.$ D_\mu $ ($ {\cal{D}}_\mu $ ) represents the covariant derivatives$D_\mu = \partial_\mu-{\rm i}g[A_\mu(x),\cdots]$ (${\cal{D}}_\mu = \partial_\mu-{\rm i}g[{\cal{A}}_\mu(x)\cdots]$ ) with the gauge field$ A^{\mu} = A^{\mu}_a \tau^a $ ($ {\cal{A}}^{\mu} = {\cal{A}}^{\mu}_a T^a $ ), where$ \tau^a $ ($ T^a $ ) is the${SU}(N_{c})$ group generators in the fundamental (adjoint) representation with$ {\rm{Tr}}[\tau^a,\tau^b] = \dfrac{1}{2}\delta^{ab} $ (${{\rm Tr}[T^a,T^b]} = N_c\delta^{ab}$ ).$F_{\mu\nu} = \partial_\mu A_\nu-\partial_\nu A_\mu-{\rm i}g[A_\mu,A_\nu]$ represents the strength tensor in the fundamental representation, and$ {\cal{F}}_{\mu\nu} $ is its counterpart in the adjoint representation.$ C $ is the collision term.The transport equations are supplemented by the Yang-Mills equation
$ D_\mu F^{\mu\nu}(x) = j^\nu(x) $ , and the color current$ j^\nu(x) $ is given in the fundamental representation as$ \begin{aligned}[b] j^\nu(x) =& -\frac{g}{2}\int_pp^\nu[Q^q(p,x)-Q^{\bar{q}}(p,x)-\frac{1} {3}{\rm Tr}[Q^q(p,x)\\& -Q^{\bar{q}}(p,x)]+2\tau^a {\rm Tr}[T^aQ^g(p,x)]], \end{aligned}$

(3) where
$\int_p = \int \dfrac{{\rm d}^4p}{(2\pi)^3}2 \Theta(p_0) \delta(p^2).$ In the Vlasov approximation
$ C = 0 $ , by solving the QGP transport equations (2) and (3) associated with Eq. (1) in the linear response approximation, one can obtain the color-electric conductivity of the QGP [40,41,43, 45,46] in the hard thermal loop (HTL) approximation. -
Viscosity will modify the distribution functions of the constituents of a microscopic system [6,10,81-83]. If only shear viscosity is taken into account, the distribution function becomes
$ Q = Q_o+\delta Q = Q_o+\frac{c'}{2T^3}\frac{\eta}{s}Q_o(1\pm Q_o)p^\mu p^\nu\langle \nabla_\mu u_\nu \rangle. $

(4) In Eq. (4), "
$ + $ "("$ - $ ") is for boson (fermion), and$ c' = $ $ \pi^4/90\zeta(5) $ ($ c' = 14 \pi^4/1350\zeta(5) $ ) is for massless boson (fermion) [6,10,82,83].$ \langle \nabla_\mu u_\nu \rangle = \nabla_\mu u_\nu + \nabla_\nu u_\mu - \dfrac{2}{3} \Delta_{\mu\nu}\nabla_{\gamma}u^{\gamma} $ ;$ \nabla_{\mu} = (g_{\mu\nu} - u_{\mu}u_{\nu})\partial^{\nu}$ ;$ \Delta^{\mu\nu} = g^{\mu\nu} - u^{\mu}u^{\nu} $ ; and$ \eta, s $ ,$ T $ , and$ Q_o $ represent the shear viscosity, entropy density, temperature of the system, and equilibrium distribution function of boson or fermion, respectively. This ansatz of the distribution function is widely used in hydrodynamic simulations to study the phenomenology of relativistic heavy ion collisions.Note that only when the system is slightly off-equilibrium, it is possible to evaluate the small deflection of the distribution
$ \delta Q $ from its equilibrium value$ Q_o $ due to non-equilibrium effect [81]. The viscous corrected distribution function used in (4) is much smaller than the equilibrium one$ \delta Q<<Q_o $ , which implies a small value of the velocity gradient. Therefore, the color-electromagnetic fields dominate interaction in QGP system, and the collision terms in transport equations may be neglected. In Refs. [23,24], the authors have extended the ideal chromohydrodynamic equations [46,84,85] to the viscous ones by expanding the collisionless kinetic equation (2) in momentum moments in terms of distribution function modified by shear viscosity (4). It is argued that chromohydrodynamics can describe the polarization effect as the kinetic theory [24,86]. In addition, the fluid equations dealing with conservative equations of the macroscopic physical quantities are much simpler than those of the kinetic theory. Therefore, one can study the connection of the color-electric conductivity and shear viscosity of a quark gluon system with viscous chromohydrodynamics.The constitutive equations for the viscous chromohydrodynamics are [23,24],
$ D_\mu n^\mu = 0, \ \ \ \ \ D_\mu T^{\mu\nu}-\frac{g}{2}\{F^\nu_\mu,n^\mu(x)\} = 0 $

(5) with
$ n^\mu(x) = \int_p p^\mu Q(p,x), \ \ T^{\mu\nu}(x) = \int_p p^\mu p^\nu Q(p,x), $

(6) where
$ Q(p,x) $ is the distribution function modified by shear viscosity (4). For detailed derivation of viscous chromohydrodynamic equations, please refer to Refs. [23,24,85].The four-flow
$ n^\mu $ and energy momentum tensor$ T^{\mu\nu} $ can be expressed in the form [23,24]$ \begin{aligned}[b] n^\mu =& n(x) u^\mu, \\ T^{\mu\nu} =& \frac{1}{2}(\epsilon(x)+p(x)) \{u^\mu,u^\nu\}-p(x)g^{\mu\nu}+\pi^{\mu\nu}, \end{aligned} $

(7) where
$ \begin{aligned}[b] \pi^{\mu\nu} = &\eta \langle \nabla^\mu u^\nu \rangle = \eta \{(g^{\mu\rho}-u^\mu u^\rho)\partial_\rho u^\nu+(g^{\nu\rho}\\&-u^\nu u^\rho)\partial_\rho u^\mu-\frac{2}{3}(g^{\mu\nu}-u^\mu u^\nu)\partial_\sigma u^\sigma\}. \end{aligned} $

(8) If
$ \eta = 0 $ , the distribution function (4) remains the ideal form;$ \pi^{\mu\nu} $ will be absent in (7), and the chromohydrodynamic equations will turn to the ideal ones [84,85].The color current (3) reads
$ j^\mu(x) = -\frac{g}{2}\left(nu^\mu-\frac{1}{3}{\rm Tr} [nu^\mu]\right). $

(9) Eqs. (5), (7) and (9) make up the basic set of equations of viscous chromohydrodynamics. In those equations,
$ n $ ,$ \epsilon $ , and$ p $ represent the particle density, energy density, and pressure, respectively. Usually, hydrodynamic quantities have both colorless and colorful parts; as an example, the particle density can be written as [23,24,85]$ n^\mu_{\alpha\beta} = n_0^\mu I_{\alpha\beta}+\frac{1}{2}n_a^\mu \tau^a_{\alpha\beta} , $

(10) where
$ \alpha,\beta = 1,2,3 $ are color indices, and$ I $ is the identity matrix [85]. -
To perform further analysis, we will linearize the hydrodynamic quantities around the stationary, colorless, and homogeneous state, which is described by
$ \bar{n} $ ,$ \bar{u}^\mu $ ,$ \bar{p} $ , and$ \bar{\epsilon} $ . As an example, the particle density$ n(x) $ can be denoted as$ n(x) = \bar{n}+\delta n(x). $

(11) The covariant derivatives of the hydrodynamic quantities in the stationary, colorless, and homogeneous state vanish, for example,
$ D_\mu\bar{n} = 0 $ . In that state, the color current$ j^\mu(x) = 0 $ . The diagonalized fluctuation quantity should be much smaller than the corresponding stationary one$ \delta n\ll \bar{n} $ [23,24,85]. As in Eq. (10), all fluctuation quantities contain both colorless and colorful components,$ \delta n_{\alpha\beta} = \delta n_0 I_{\alpha\beta}+\frac{1}{2}\delta n_a \tau^a_{\alpha\beta}. $

(12) Substituting the linearized hydrodynamic quantities such as those in Eqs. (11) and (12) into Eq. (7) and their corresponding conservation equations (5), projecting them on
$ \bar{u}^\mu $ and$ (g^{\mu\nu}-\bar{u}^\mu\bar{u}^\nu) $ , considering only the equations for colorful parts of fluctuations, and performing the Fourier transformation, one can obtain equations that can describe color phenomena in the viscous QGP [23,24]$ \bar{n}k_\mu\delta u^\mu_a+ k_\mu\delta n_a\bar{u}^\mu = 0, $

(13) $ \bar{u}^\mu k_\mu\delta\epsilon_a+(\bar{\epsilon}+\bar{p})k_\mu\delta u^\mu_a = 0, $

(14) $ \begin{aligned}[b]& (\bar{\epsilon}+\bar{p})(\bar{u}\cdot K)\delta u^\nu_a+(-k^\nu+\bar{u}^\nu(\bar{u}\cdot K))\delta p_a + \eta\{(K^2 \\&\quad-(K\cdot \bar{u}))\delta u^\nu_a + (k^\mu k^\nu-k^\mu \bar{u}^\nu)\delta u_{\mu,a}+\frac{2}{3}(\bar{u}^\nu (K\cdot \bar{u})\\&\quad -k^\nu)k_\rho\delta u^\rho_a\} = {\rm i} g\bar{n}\bar{u}_\mu F_a^{\mu\nu}(K), \end{aligned} $

(15) with
$ \bar{u}\cdot K = \bar{u}^\mu k_\mu $ .According to Eq. (9), the color current due to the color fluctuations of the hydrodynamic quantities is given by [23,24]
$ j^{\,\mu}_a = -\frac{g}{2}\left(\bar{n}\delta u^\nu_a+ \delta n_a\bar{u}^\mu-\frac{1}{3} {\rm Tr} [\bar{{n}}\delta {u}^\mu_{a}+ \delta {n}_{a}\bar{{u}}^\mu]\right). $

(16) By introducing an EoS,
$ \delta p_a = c_s^2\delta\epsilon_a $ to complete the fluid equations (13), (14), and (15) (the explicit formulism for$ c_s $ will be introduced later), we can solve the color fluctuations of hydrodynamic quantities$ \delta n_a $ ,$ \delta u_{\nu,a} $ , and$ \delta\epsilon_a $ [23,24]:$ \delta n_a = -\frac{\overline{n}k_\mu\delta u_a^\mu}{K\cdot \overline{u}}, \ \ \ \ \ \delta\epsilon_a = -\frac{(\overline{\epsilon}+ \overline{p})k_\mu\delta u_a^\mu}{K\cdot \overline{u}}, $

(17) $ \begin{aligned}[b] \delta u_{\sigma,a} =& \frac{1}{1+D(K^2-(K\cdot \overline{u})^2)}\cdot \frac{g\overline{n}}{(\overline{\epsilon}+\overline{p})(K\cdot\overline{ u})}\{g_{\sigma\nu}\\&+(B+E)(k_\sigma k_\nu-\overline{u}_\sigma k_\nu(K\cdot \overline{u}))\}\cdot \overline{u}_\mu iF_a^{\mu\nu}, \end{aligned} $

(18) with
$ \begin{aligned} B = -\frac{c_s^2} {\omega^2-c_s^2k^2}, \ D = \frac{\eta}{sT\omega}, \ E = -\frac{\dfrac{\eta\omega}{sT} \left(1+4\dfrac{c_s^2k^2} {\omega^2-c_s^2k^2}\right)} {3\omega^2-3c_s^2k^2- 4\dfrac{\eta\omega k^2} {sT}}. \end{aligned} $

(19) Substituting the solved
$ \delta n_a $ and$ \delta u^\mu_a $ into Eq. (16), one can obtain the induced color current due to the color fluctuations of hydrodynamic quantities$ \begin{aligned}[b] j_a^\mu =& -\frac{{\rm i}\omega^2_p}{(K\cdot\overline{ u})}\cdot \frac{1}{1+D(K^2-(K\cdot \overline{u})^2)}\left(g^{\mu\sigma}-\frac{\overline{u}^\mu k^\sigma} {K\cdot \overline{u}}\right) \\& \cdot \{g_{\sigma\nu}+(B+E)(k_\sigma k_\nu-\overline{u}_\sigma k_\nu(K\cdot \overline{u}))\}\overline{u}_\rho F_a^{\rho\nu} , \end{aligned}$

(20) where
$ \omega^2_p = \dfrac{g^2\bar{n}^2}{2(\bar{\epsilon}+\bar{p})} $ is the square of the plasma frequency. For a detailed derivation of$ j_a^\mu $ in chromohydrodynamic approach, please refer to Refs. [23,24]. -
According to Eq. (1), we can extract the conductivity tensor from equation (20)
$ \begin{aligned}[b] \sigma_{ab}^{\mu \nu} =& -\frac{\rm i}{\omega}\frac{\delta^{ab}\omega_p^2}{1-Dk^2}\Bigg\{g^{\mu \nu}+(B+E)(k^\mu k^\nu-\overline{u}^\mu k^\nu (K\cdot \overline{u}) ) \\&-\frac{\overline{u}^\mu k^\nu}{(K\cdot \overline{u})}-(B+E)\left(\frac{K^2\overline{u}^\mu k^\nu}{K\cdot \overline{u}}-\overline{u}^\mu k^\nu (K\cdot \overline{u})\right) \Bigg\}. \end{aligned} $

(21) The diagonalized spatial component of
$ \sigma_{ab}^{\mu \nu} $ in the color space from equation (21) reads$ \sigma^{ij} = -\frac{\rm i}{\omega} \frac{\omega_p^2}{1-Dk^2} \{g^{ij}+(B+E)k^ik^j \}. $

(22) For an isotropic, homogeneous plasma medium,
$ \sigma^{ij} $ reduces to two scalar functions according to project operators [41,58,87]$ \sigma^{ij} = \sigma_L\frac{k^ik^j}{k^2}+\sigma_T\left(\delta^{ij}-\frac{k^ik^j}{k^2}\right). $

(23) $ \sigma_L $ and$ \sigma_T $ are the longitudinal and transverse color-electric conductivities, which are independent response functions and do not mix. From the relation between the dielectric functions and the conductivities, the longitudinal conductivity describes the response of the medium to a scalar potential$ \phi $ , and the transverse one reflects the medium response to a vector potential$ {\bf{A}} $ in electrodynamics; for details, please refer to §3.1 in Ref. [87].According to Eqs. (22) and (23), we can obtain
$ \sigma_L = \sigma^{ij}\frac{k_ik_j}{k^2} = \frac{\rm i}{\omega} \frac{\omega_p^2}{1-Dk^2}\{1-(B+E)k^2 \}, $

(24) and
$ \sigma_T = \frac{1}{2}\left(\delta_{ij}-\frac{k_ik_j}{k^2}\right)\sigma^{ij} = \frac{\rm i}{\omega} \frac{\omega_p^2}{1-Dk^2}. $

(25) Substituting
$ B $ ,$ D $ , and$ E $ mentioned in (19) into (24) and (25) and adopting the effective sound speed [23,24,84,85]$ c_s = \sqrt{\dfrac{1}{3\left(1+\dfrac{1}{2y}\log\dfrac{1-y}{1+y}\right)}+\dfrac{1}{y^2}} \;\; \left(y = \dfrac{k}{\omega}\right), $

one can obtain the scaled longitudinal color-electric conductivity
$ \begin{aligned}[b] \frac{\sigma_L(\omega,k)}{\omega_p} =& -\frac{{\rm i}\omega}{1-\dfrac{\eta k^2} {sT\omega}}\frac{3\omega_p}{k^2}\left(1-\frac{\omega}{2k} \log\frac{\omega+k+{\rm i}\xi}{\omega-k+{\rm i}\xi}\right)\\&+\frac{{\rm i}\omega_p} {1-\dfrac{\eta k^2}{sT\omega}} \frac{\eta}{sT}\frac{1} {1+ 4\dfrac{\eta\omega } {sT}{\left(1-\dfrac{\omega}{2k}\log\dfrac{\omega+k+{\rm i}\xi}{\omega-k+{\rm i}\xi}\right)}}\\& \cdot \Bigg\{3\left(1-\frac{\omega}{2k} \log\frac{\omega+k+{\rm i}\xi}{\omega-k+{\rm i}\xi}\right)\\&+\frac{12\omega^2}{k^2}\left(1-\frac {\omega}{2k} \cdot\log\frac{\omega+k+{\rm i}\xi}{\omega-k+{\rm i}\xi}\right)^2\Bigg\}, \end{aligned} $

(26) and the transverse one
$ \frac{\sigma_T}{\omega_p} = \frac{{\rm i}\omega_p}{\omega} \frac{1}{1-\dfrac{\eta k^2}{s\omega T}}. $

(27) As shown in Eqs. (26) and (27), the longitudinal and transverse conductivities are usually complex functions of
$ \omega,k $ . It is argued that, in electrodynamics, the real part of the conductivity describes a finite dissipation of energy [87]. While the imaginary part of the conductivity defines the phase lag between the applied electric field and the induced electric current, which manifests that the medium response has a time delay with respect to the applied disturbation [87,88]. -
As the collisionless approximations of the QGP transport equations are adopted in the derivation of the chromohydrodynamic equations, we may obtain the conductivities in the level of HTL approximation in the presence of shear viscosity. When
$ \eta/s = 0 $ , (26) turns to$ \sigma_L(\omega,k) = -\frac{3{\rm i}\omega\omega_p^2}{k^2}\left(1-\frac{\omega}{2k} \log\frac{\omega+k+{\rm i}\xi}{\omega-k+{\rm i}\xi}\right). $

(28) One can obtain (28) in terms of the dielectric tensor
$ \varepsilon^{ij} $ in the HTL approximation [41,45,46,58] as well as (23) and (24) associated with the relation between the conductivity tensor and the dielectric tensor (31) [43,45,46,58,87] discussed in the following. Therefore, (28) is the HTL result of the longitudinal color-electric conductivity. According to (28), one can obtain the real part of$ \sigma_L $ $ {\rm Re} \sigma_L(\omega,k) = \frac{3\pi\omega_p^2}{4k}\frac{2\omega^2}{k^2}\Theta(k^2-\omega^2). $

(29) $ \Theta $ is the Heaviside step function, which equals to unity for$ k>\omega $ . There is a discrepancy of the factor$ \dfrac{2\omega^2}{k^2} $ between (29) and (3.36) in Ref. [52] obtained from the transverse polarization self-energy$ \Pi_T(\omega,k) $ within the framework of the Boltzmann equation in the collisionless limit and$ k>>\omega $ .As shown in Eq. (27), the transverse color-electric conductivity
$ \sigma_T $ is a pure imaginary function of$ \omega,k $ . When$ \eta/s = 0 $ , (27) cannot recover the HTL result, which can be derived in terms of the HTL dielectric tensor and Eqs. (31), (23), and (25). The viscous chromohydrodynamics can describe the polarization effect as the kinetic theory, which facilitates us to investigate the viscous effect on the electromagnetic properties of the QGP. However, some dynamical information will be lost during the derivation from the kinetic theory to the chromo hydrodynamics [12,84-86]. Nevertheless, the chromohydrodynamics can describe some dynamical information of the system relevant to the longitudinal dielectric properties of the plasma, which can still capture some interesting physics of the QGP.From the discussion in the last two paragraphs, it is evident that, in the chromohydrodynamic approach, the conductivity properties of the QGP are mainly demonstrated by the longitudinal part of the color-electric conductivity
$ \sigma_L(\omega,k) $ . Note that another study shows that the conductivity properties of the QGP under the magnetic field are also mainly derived from the longitudinal part. To the one-loop order, the transverse (with respect to the magnetic field direction) electric conductivity of the QGP vanishes$ \sigma_\bot = 0 $ [65].In the following, we will apply
$ k = 0.2\omega_p $ and$ T = \omega_p $ to perform numerical analysis to study$ \omega $ -dependent behavior of the color-electric conductivity with different values of shear viscosity. We present the real part of the scaled longitudinal color-electric conductivity with respect to frequency at different shear viscosities in Fig. 1. The black, red, green, and blue curves are the cases of$ \eta/s = 0,0.1,0.2,0.3 $ respectively. Fig. 1 shows that, in the space-like region$ \dfrac{\omega}{k}<1 $ , the real part of the longitudinal color-electric conductivity monotonously increases withfrequency. For low frequencies$ \dfrac{\omega}{k}\leqslant 0.3 $ , the viscous curves of${\rm{Re}} \sigma_{L}/\omega_{p}$ almost superpose each other; shear viscosity has a trivial effect on the conductivity. As the frequency increases, the viscous effects on the color-electric conductivity become appreciable, and${\rm{Re}} \sigma_{L}/\omega_{p}$ reduces with the increase in shear viscosity. While for$ \dfrac{\omega}{k}>0.875 $ , for a fixed frequency,$ {\rm{Re}} \sigma_{\rm{L}}/\omega_{\rm{p}} $ increases with shear viscosity, showing a reversed dependence of the longitudinal color-electric conductivity on shear viscosity compared to the case in the small frequency region. In the time-like region$ \dfrac{\omega}{k}>1 $ , the real part of the longitudinal color-electric conductivity begins to vanish.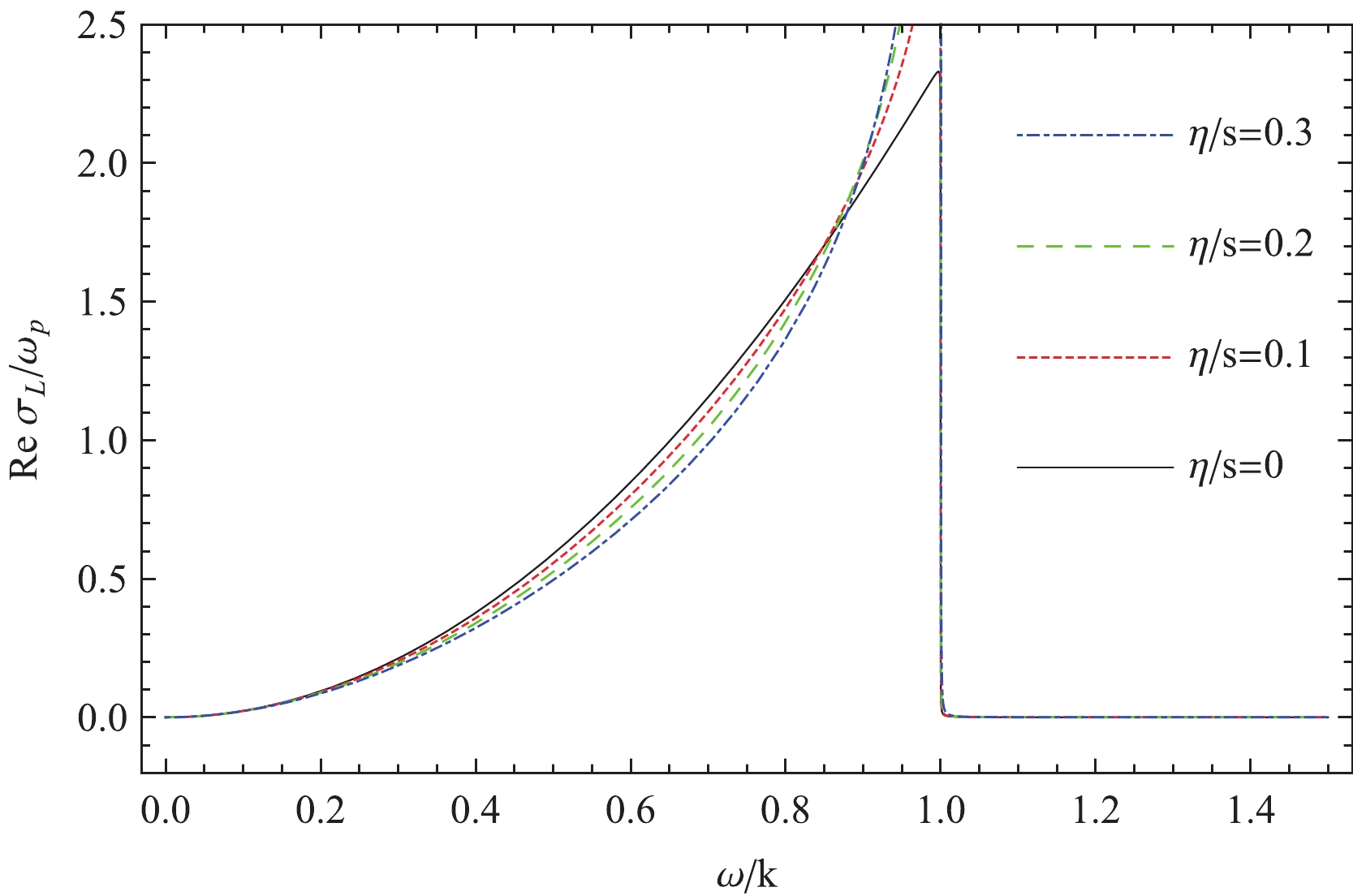
Figure 1. (color online) Real part of the scaled longitudinal color-electric conductivity of the QGP for different ratios of shear viscosity to entropy density
$ \frac{\eta}{s} = 0,0.1,0.2,0.3 $ .The imaginary part of the longitudinal color-electric conductivity is displayed in Fig. 2. In the space-like region, there is a critical frequency which is around
$ \omega_c\sim 0.6k $ ; the imaginary part of the longitudinal color-electric conductivity decreases with frequency for$ \omega\leqslant\omega_c $ . It indicates that shear viscosity has no demonstrable effects on the imaginary part of the conductivity in that frequency region. For$ \omega>\omega_c $ ,${\rm{Im}} \sigma_{L}/\omega_{p}$ rises quickly with increasing frequency. Simultaneously, viscous effects on${\rm{Im}} \sigma_{L}/\omega_{p}$ become remarkable, and${\rm{Im}} \sigma_{L}/\omega_{p}$ diminishes with increasing shear viscosity. In the time-like region,${\rm{Im}} \sigma_{L}/\omega_{p}$ reduces with frequency, while shear viscosity enhances the imaginary part of the longitudinal color-electric conductivity.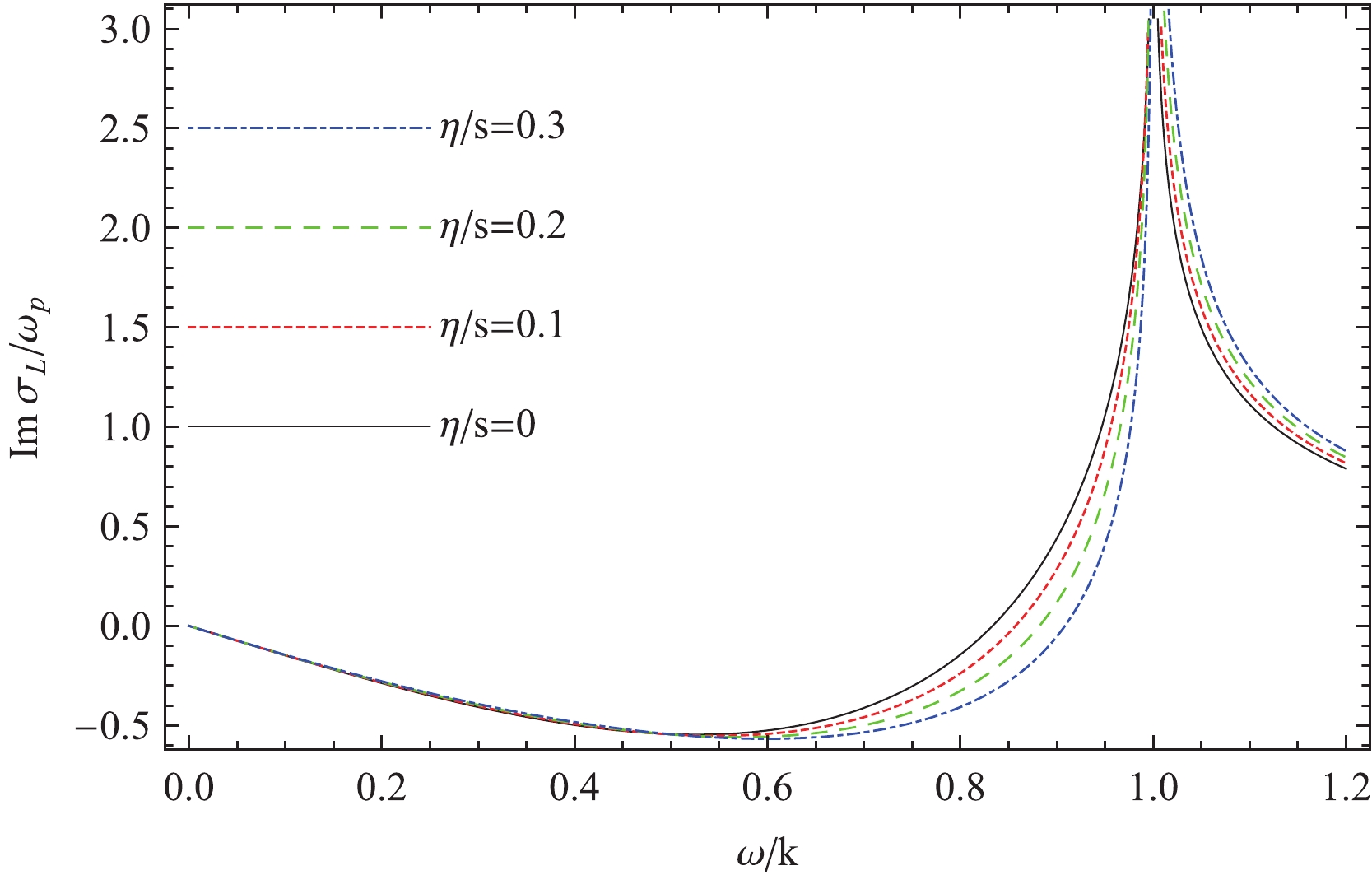
Figure 2. (color online) Imaginary part of the scaled longitudinal color-electric conductivity of the QGP for different ratios of shear viscosity to entropy density
$ \frac{\eta}{s} = 0,0.1,0.2,0.3 $ .From Eq. (26), it is clear that the real part of
$ \sigma_L/\omega_p $ is determined by the imaginary part of the logarithmic function$\log \dfrac{\omega+k+{\rm i}\xi}{\omega-k+{\rm i}\xi}$ , and${\rm Im}\sigma_{L}/\omega_{p}$ is related to the real part of that function correspondingly. The logarithmic function can be expressed by [23,46]$ \log \frac{\omega+k+{\rm i}\xi}{\omega-k+{\rm i}\xi} = \log\mid \frac{\omega+k}{\omega-k}\mid-{\rm i}\pi\Theta(k^2-\omega^2) . $

(30) In the time-like region
$ \omega>k $ ,$ \Theta(k^2-\omega^2) = 0 $ , which results in${\rm{Re}} \sigma_{L}/\omega_{p}$ beginning to vanish in that frequency region, as shown in Fig. 1. There is a singularity located at the position$ \omega = k $ for the real part of the logarithmic function$ \log\mid \dfrac{\omega+k}{\omega-k}\mid $ , which leads to a divergence behavior of${\rm{Im}} \sigma_{L}/\omega_{p}$ at$ \omega/k = 1 $ , as shown in Fig. 2.It is instructive to understand viscous effects on the color-electric conductivity from the viewpoint of dielectric properties. The fields in the medium are different from those in vacuum, and the dielectric functions dominate those differences. Moreover, other electromagnetic properties of the medium can be derived from the latter in principle. Mrowczynski et al. have found that the dielectric tensor and conductivity tensor are related to each other as follows [43,45,46]:
$ \sigma_{ab}^{\alpha\beta}(k) = -{\rm i}\omega[\varepsilon_{ab}^{\alpha\beta}(k)-\delta^{\alpha\beta}\delta_{ab}]. $

(31) If the dielectric tensor and conductivity tensor are expressed according to project operators (23) simultaneously, one can obtain
$ \sigma_L = -{\rm i}\omega\{\varepsilon_L-1 \}. $

(32) In (32),
$ \varepsilon_L $ is the longitudinal dielectric function. Therefore, from (32), the real part of the longitudinal color-electric conductivity relates to the imaginary part of the longitudinal dielectric function. One can obtain the imaginary part of$ \sigma_L $ from the real part of$ \varepsilon_L $ . The longitudinal color-electric conductivity (26) is consistent with the longitudinal dielectric function obtained in Refs. [23,24] in terms of Eq. (32). Furthermore, if the HTL dielectric function$ \varepsilon_L $ [40,41,45,46] is applied to (32), we obtain (28), i.e., the result of the longitudinal conductivity in the HTL approximation.It is argued in Ref. [20] that the electric conductivity arises from competition between "ordered" electric force and "disordered" scatterings. Thus the dissipation involving the disordered scatterings will affect the charge transport. The electric conductivity reflects the medium response to the applied external electric field. The medium properties may be involved in its response to the applied fields. Shear viscosity modifies the distribution functions of the medium constituents, which may play an important role in determining the medium response. Therefore, shear viscosity will have an impact on the charge transport naturally.
It should be stressed that when several different irreversible transport processes (such as heat conductivity, electric conductivity, and shear viscosity) occur simultaneously in a plasma medium, the transport processes may interfere with each other [89]. The driving force due to the gradient of a kind of physical quantity can result in another kind of current [89]. For example, an electric current is produced in a circuit composed of different metals when the junctions are at different temperatures, which is known as the thermoelectric effect or Seebeck effect [71]. Some authors have addressed the Seebeck effect for the hot and dense hadronic matter with a temperature gradient [90] and the QGP in magnetic fields [91] in the context of ultra-relativistic heavy ion collisions. Recently, another study showed that a density gradient of a given charge can generate dissipative currents of another charge [92]. Therefore, it is natural to expect that the velocity gradient might produce an electric current in the system. As a result, shear viscosity could influence the charge transport coefficient, i.e., the electric conductivity.
With the viscous chromohydrodynamic approach, we centered our attention on physics related to the color fluctuation phenomena in QGP at a short time scale where the collision terms of transport equations can be neglected [84,85]. The collisionless kinetic theory is usually applied to study the QGP properties; some important results have been achieved, which coincide with those derived from the diagrammatic approach with hard loop approximation — the HTL approximation. We also applied the collisionless transport equations to derive chromohydrodynamic equations while incorporating dissipative effects. The neglect of the collision terms in transport theory does not imply that there are no dissipative interactions in plasma. It is argued in Ref. [24] that, in addition to the collision terms, the interaction between particles due to the mean field [93] and the turbulent plasma fields [94,95] can induce dissipation in plasma. In addition to the neglect of the collision terms, the derivation from the kinetic theory to chromohydrodynamics results in the loss of some dynamical information [24,84]. Nevertheless, the fluid equations still have rich dynamical content, capturing some correct physics of the QGP. Therefore, we can gain some insight into the physics of the electromagnetic properties of the QGP by applying viscous chromohydrodynamics.
-
In the linear response approximation, we solved the viscous chromohydrodynamic equations, which are derived from the QGP kinetic theory associated with the distribution function modified by shear viscosity. According to the solved color fluctuations of the hydrodynamic quantities, we obtained the induced color current through which the conductivity tensor can be derived. Through the distribution function, viscous chromohydrodynamic equations, and the fluctuating quantities of the fluid, shear viscosity is encoded in the induced color current and the conductivity tensor and gives a corrective contribution to the color current and the color-electric conductivity. In general, the corrective color current due to shear viscosity is much smaller than that induced by the applied external field. Nevertheless, shear viscosity has an appreciable effect on the color-electric conductivity in some frequency regions. Numerical analysis indicates that the conductivity properties of the QGP are mainly demonstrated by the longitudinal part of the color-electric conductivity. In the space-like region, for a small frequency, shear viscosity has a trivial effect on the real and imaginary parts of
$ \sigma_L/\omega_p $ . As the frequency increases, viscous effects become notable, and shear viscosity reduces both the real and imaginary parts of the conductivity in most of the space-like region. In the time-like region, the real part of the longitudinal conductivity begins to vanish, while shear viscosity increases the imaginary part of$ \sigma_L/\omega_p $ .In the early stage of ultrarelativistic heavy ion collisions, the produced strongly interacting matter will have a large temperature gradient between the central and peripheral regions of the fireball and have an anisotropic momentum distribution between longitudinal and transverse expansion. Meanwhile, strong electromagnetic fields will be produced in noncentral collisions. Therefore, several different transport processes will exist simultaneously in the produced parton system in heavy ion collisions, resulting in interferences between different transports in the system. It is argued that the coupling of the bulk viscous pressure to shear-stress tensor (shear-bulk coupling) can give an extra contribution to the bulk viscous pressure. The extra part of the bulk viscous pressure due to shear-bulk coupling can be comparable to the one originating from the Navier-Stokes term, which will remarkably affect the evolution process of the QCD plasma produced in heavy ion collisions [96-99]. Therefore, one can expect that the connection between shear viscosity and electric conductivity may be relevant to some observables in ultrarelativistic heavy-ion collisions, which is an attractive issue and deserves further comprehensive investigations.
-
We thank Yun Guo, Yu-xin Liu, En-ke Wang, and Peng-fei Zhuang for their instructive discussions.
Color-electric conductivity in a viscous quark-gluon plasma
- Received Date: 2020-12-15
- Available Online: 2021-05-15
Abstract: Several different transport processes, such as heat, momentum, and charge transports, may occur simultaneously in a thermal plasma system. The corresponding transport coefficients are heat conductivity, shear viscosity, and electric conductivity. In the present study, we investigate the color-electric conductivity of the quark-gluon plasma (QGP) in the presence of shear viscosity, focusing on the connection between the charge transport and momentum transport. To achieve this goal, we solve the viscous chromohydrodynamic equations obtained from the QGP kinetic theory associated with the distribution function modified by shear viscosity. According to the solved color fluctuations of hydrodynamic quantities, we obtain the induced color current through which the color-electric conductivity is derived. Numerical analysis shows that the conductivity properties of the QGP are mainly demonstrated by the longitudinal part of the color-electric conductivity. Shear viscosity has an appreciable impact on real and imaginary parts of the color-electric conductivity in some frequency regions.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: