Searching for sub-MeV boosted dark matter from xenon electron direct detection

Light dark matter (DM) candidates are well motivated and can be naturally realized when the DM candidate couples feebly to the visible sector [1-5]. In particular, it is difficult for a sub-MeV DM candidate to satisfy the observed relic abundance through the thermal freeze-out mechanism [6-8]; therefore, freeze-in via annihilation of electron-positron pairs is a primary mechanism for DM production [2, 3, 9]. The traditional direct detection of DM-nucleus scattering rapidly loses sensitivity for DM candidates whose mass is below $ \sim{\rm GeV} $, due to the threshold of the recoil energy. An alternative way to search for a light DM candidate is through the scattering off electrons [3, 10, 11], but this is not sensitive to a sub-MeV DM candidate either. It is crucial to develop a new approach to probe for freeze-in DM in this mass range.

A certain fraction of DM candidates in the Galactic halo would be accelerated by energetic cosmic ray (CR) particles as long as the DM candidate interacts with SM particles. The CR-boosted mechanism relaxes the threshold problem and improves the sensitivity for detecting a light DM candidate [12, 13]. It has been extensively discussed in DM-nucleus direct detection experiments, neutrino experiments and CR observations for various DM models [14-22]. In this letter, we investigate the CR-boosted effect on DM-electron direct detection in the freeze-in scenario, and show that the existing data from xenon experiments are able to probe a sub-MeV DM candidate.

For illustration, we consider a typical freeze-in DM model based on the vector-portal, in which the DM candidate is a Dirac fermion ($ \chi $) that couples to the visible sector through an additional gauge boson $ A^\prime_\mu $, named the "dark photon". The Lagrangian is given by

where $ m_{\chi} $ and $ m_{A^\prime} $ denote the mass of the DM candidate and the dark photon, respectively. $ g_\chi $ and $ g_{\rm SM} $ are the coupling strength of $ A^\prime $ to the DM candidate and the electron, respectively. When the DM candidate scatters off an incident CR electron with a given kinetic energy ($ T_{\rm CR} $), the distribution of the DM recoil energy $ T_\chi $ is

where $ \bar{\sigma}_e $ denotes the cross section of DM-free electron scattering for a fixed momentum transfer $ q = \alpha m_e $ [3]. The maximal recoil energy of the DM candidate is [23]

Convoluting the $ T_\chi $ distribution in Eq. (2) with the energy spectrum of incident CR electrons $ {\rm d}\Phi_e/{\rm d}T_{\rm CR} $ yields the recoil flux of the boosted DM candidate [20],

where $ D_{\rm eff}\equiv \int \dfrac{{\rm d}\Omega}{4\pi}\int_{l.o.s}{\rm d}l $ is an effective diffusion distance. See the supplemental materials for details. For a homogeneous CR distribution and NFW DM halo profile [24, 25] (scale radius $ r_s = 20 $ kpc and local DM density $ \rho^{\rm local}_\chi = 0.4\, {{\rm{GeV}}}\,{\rm cm}^{-3} $), integrating along the line-of-sight to 10 kpc yields $ D_{\rm eff} = 8.02\; {\rm kpc} $ [13]. In order to produce a recoil energy $ T_\chi $ after the DM and CR-electron scattering, the minimum kinetic energy ($ T_{\rm CR}^{\rm min} $) of the incident CR electron is given by

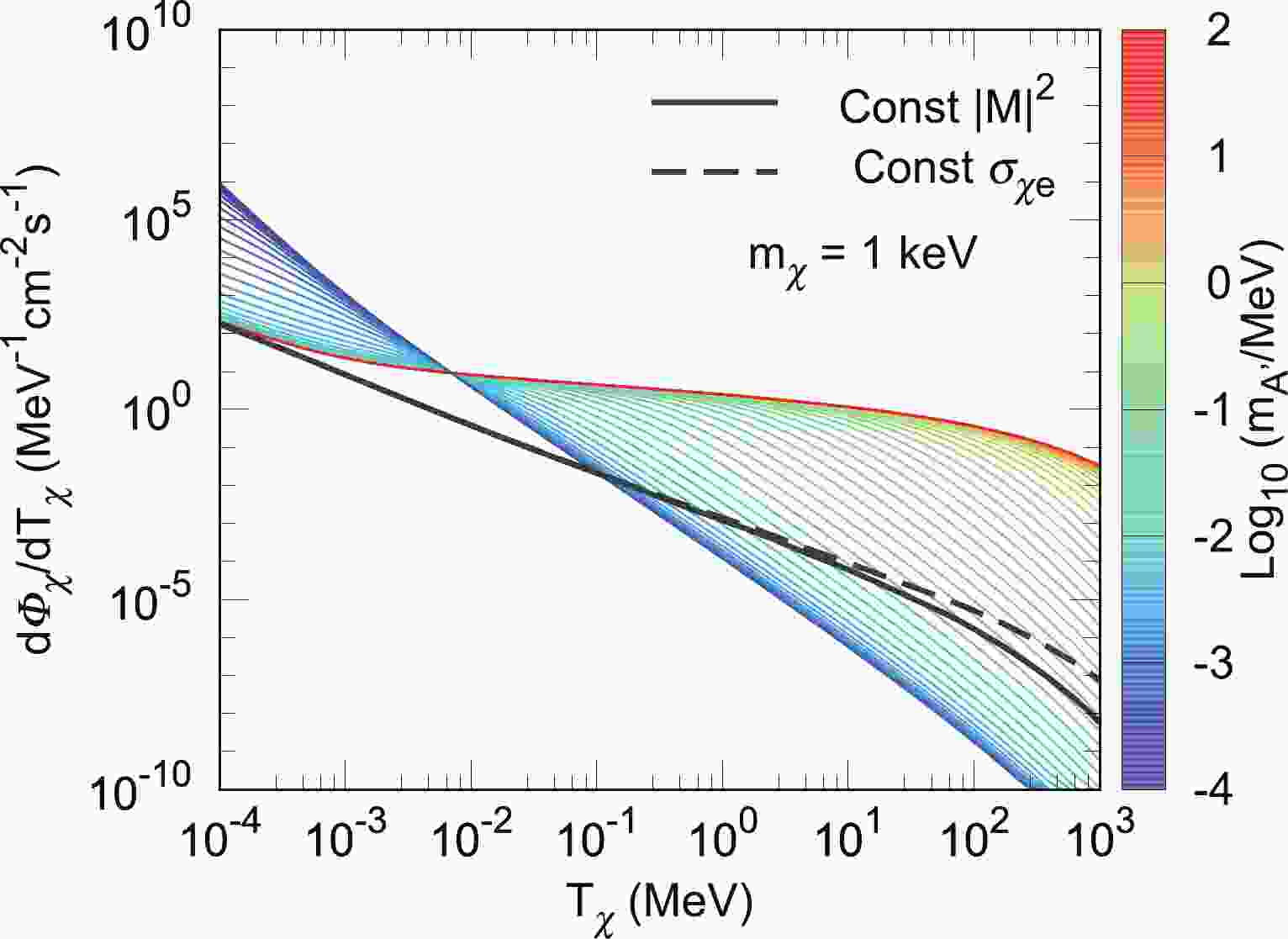
where the plus and minus signs correspond to $ T_\chi > 2m_e $ and $ T_\chi <2m_e $, respectively.

Figure 1 plots the recoil flux $ {\rm d}\Phi_\chi/{\rm d}T_\chi $ distributions as a function of $ T_\chi $ for various $ m_{A^\prime} $'s. Two simplified models are also plotted for comparison. One is the cross section $ \sigma_{\chi e} $ being a constant (black-solid curve), and the other is that the squared matrix element of the DM-electron scattering ($ \overline{|{\cal{M}}|^{2}} $), averaged over initial and summed over final spin states, is a constant (black-dashed curve), i.e.

Figure 1.  (color online) Recoil flux distributions of the DM candidate for varying $m_{A^\prime}$, with $m_\chi=1$ keV and $\bar{\sigma}_e=10^{-30}~{\rm cm}^2$. For comparison, the recoil flux distributions for the approximation of a constant $\sigma_{\chi e}$ (black solid line) and a constant $\overline{|{\cal{M}}|^{2}}$ (black dashed line) are also plotted.

The former case is commonly used in the study of non-relativistic DM candidates, and the latter takes the energy dependence from phase space into account. However, neither treatment is appropriate for an energetically boosted DM candidate whose kinetic energy is much larger than its mass, such that the momentum transfer q cannot be neglected. We consider relativistic kinematics throughout this work. As shown in Fig. 1, the flux distribution exhibits a significant enhancement in the large $ T_\chi $ range with increasing $ m_{A^\prime} $. Note that various recoil flux curves intersect at $ T_\chi = (\alpha m_e)^2/(2m_\chi) $, and the recoil flux distribution of the constant $ \overline{|{\cal{M}}|^{2}} $ slightly deviates from that of the constant $ \sigma_{\chi e} $ when $ 2 m_\chi T_\mathrm{CR} > (m_e + m_\chi)^2 $.

The recoil flux distribution is independent of $ m_{A^\prime} $ when the dark photon is very heavy ($ m_{A^\prime} \gg \sqrt{2 m_{\chi} T_{\chi}} $) or ultralight ($ m_{A^\prime} \ll \alpha m_e $); see the red and blue boundaries of the contour. The recoil flux distributions in the above two limits exhibit distinct dependence on $ T_\chi $; for example, the recoil flux of ultralight dark photons drops rapidly with $ T_\chi $, while the recoil flux of heavy dark photons mildly decreases with $ T_\chi $. The heavy dark photon represents the so-called $ Z^\prime $-portal model, while the ultralight dark photon represents the milli-charged DM model [26].

Equipped with the boosted DM flux, we now discuss DM direct detection through the DM interaction with the electron in xenon atoms. For the ionization process of $ \chi + A \rightarrow \chi + A^+ +e^- $ with the atom A in the $ (n,\,l) $ atomic shell, the velocity-averaged differential cross section with respect to the electron recoil energy $ E_{R} $ is given by [3, 27]

where $ F_{\rm D M} $ is the DM form factor, $ \eta $ denotes the mean inverse speed function and $ \left|f_{\rm ion}^{nl}(k^{\prime}, q)\right|^{2} $ represents the ionization form factor for an electron with initial state $ (n,l) $ and final state with momentum $ k^{\prime} = \sqrt{2 m_e E_R} $. In the case of boosted DM, the DM form factor $ F_{\rm D M} $ is

In the non-relativistic limit, $ T_\chi,E_{R}\ll m_e $, it reproduces the form factor without CR-boost effects, i.e.,

The mean inverse speed function $ \eta $ is replaced by [12]

where $ \Phi_{\rm halo} = n_\chi \bar{v}_\chi $ is the background DM flux in the Galactic halo, with $ \bar{v}_\chi $ being the corresponding average velocity. Here, $ E_{\min} $ is the minimal DM energy to trigger an electron with recoil energy $ E_R $. Similarly, Eq. (10) reproduces the conventional expression

in the non-relativistic limit. The ionization form factor $ \left|f_{\rm ion}^{nl}(k^{\prime}, q)\right|^{2} $ is calculated by using the Roothaan-Hartree-Fock radial wavefunction [28] for the initial electron state and applying a plane wave approximation for the final state. For the initial electron state, we take into account contributions from the $ (5p^6,5s^2,4d^{10},4p^6,4s^2) $ xenon electron shells. The differential ionization rate is obtained by multiplying Eq. (7), summed over different electron shells, by the background DM flux $ \Phi_{\rm halo} $and the number of target atoms $ N_T $,

Figure 2 shows the ionization rate as a function of the electron recoil energy $ E_R $ (in units of $ {\rm tonne}^{-1}\; {\rm year}^{-1} $) for both ultralight (red) and heavy (blue) dark photons, with the choices of $ m_\chi = 1\; {\rm keV} $ and $ \bar{\sigma}_e = 10^{-30}\; \mathrm{cm}^2 $. The vertical band represents the order of magnitude of energy coverage for current xenon experiments. The ultralight dark photon prefers to produce electrons with small recoil energy; however, the heavy dark photon is likely to generate electrons with large recoil energy. The distinct difference follows from the energy dependence in the distribution of $ {\rm d} \sigma_{\chi e}/{\rm d} T_{\chi} $ and the DM form factor $ F_{\rm D M}(q) $. It implies that one might distinguish between dark photons and heavy dark photons from the recoil energy spectrum of the ionized electron when the background is well understood.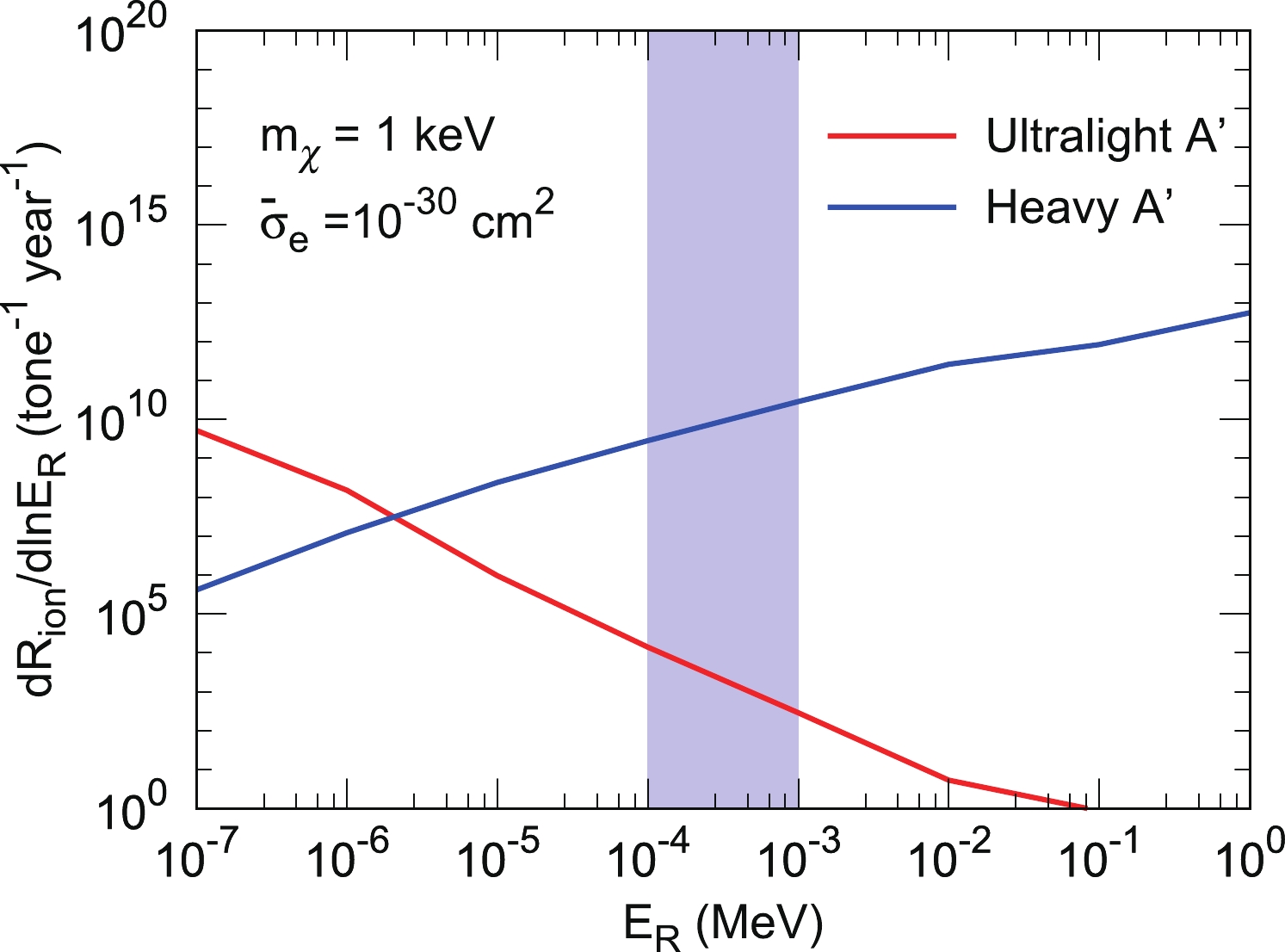

Figure 2.  (color online) Recoil spectra of electrons for benchmark DM mass $m_\chi=1$ keV with scattering cross section $\bar{\sigma}_e=10^{-30}~{\rm cm}^2$. Here we simply consider the recoil electron from the $5s$ state for demonstration.

The recoiling electrons are then converted into scintillation ($ S1 $) and ionization ($ S2 $) signals in liquid xenon experiments, and the observable is the number of photoelectrons (PE). We consider the $ S2 $ signal hereafter, as the XENON100 and XENON1T collaborations release data sets that are based only on the ionization signal [29, 30]. The event spectrum can be schematically written as follows:

where $ T_{\rm exp} $ is the exposure of the detector and $ \varepsilon_{S2} $ is the efficiency of triggering and accepting the $ S2 $ signal. For a given energy deposit $ \Delta E_e = E_R+|E^{nl}_B| $, with $ |E^{nl}_B| $ the binding energy of the $ (n,l) $ shell, the conversion probability of $ S2 $ is $ {\rm pdf}\left(S2|\Delta E_e\right) $, which is modeled as follows [10, 11]. The number of primary quanta produced at the interaction point is $ n^{(1)}_Q = {\rm Floor}(E_R/W) $ with $ W = 13.8 $ eV, and $ n^{(1)}_Q $ is divided into $ n_e $ observable ionized electrons escaping from the interaction point and $ n_\gamma $ unobservable scintillation photons. The fiducial value of the fraction of primary quanta identified as electrons is chosen as $ f_e\simeq 0.83 $. In addition, in the case where the DM candidate ionizes an inner shell electron, secondary quanta are produced by subsequent electron transitions from the outer to inner shell. The number of secondary quanta is $ n^{(2)}_Q = {\rm Floor}((E_i- E_j)/W) $, where $ E_i $ denotes the binding energy of the ith shell. The number of secondary electrons produced follows a binomial distribution with $ n_Q^{(1)}+n_Q^{(2)} $ trials and success probability $ f_e $. Finally, the number of PEs converted from electrons (with total number $ n_e = n^{(1)}_e+n^{(2)}_e $) is described by a Gaussian distribution with mean value $ n_e \mu $ and width $ \sqrt{n_e} \sigma $. The parameters are chosen as $ \mu = 19.7\; (11.4) $ and $ \sigma = 6.9\; (2.8) $ [29, 31].

We derive the limits of $ \bar{\sigma}_e $ imposed by the XENON100 data [29] ($ T_{\rm exp} = 30\; {\rm kg-years} $) and by the XENON1T data [30] (effective $ T_{\rm exp} = 22\; {\rm tonne-days} $), using the same bin steps. We choose the detection efficiency as $ \varepsilon_{S2} = 1 $ for simplicity and obtain the limits by demanding that signal does not exceed the $ 1\sigma $ upper bound (68% C.L.) in each bin. Figure 3 presents benchmark signal spectra versus PE for the ultralight and heavy mediator cases.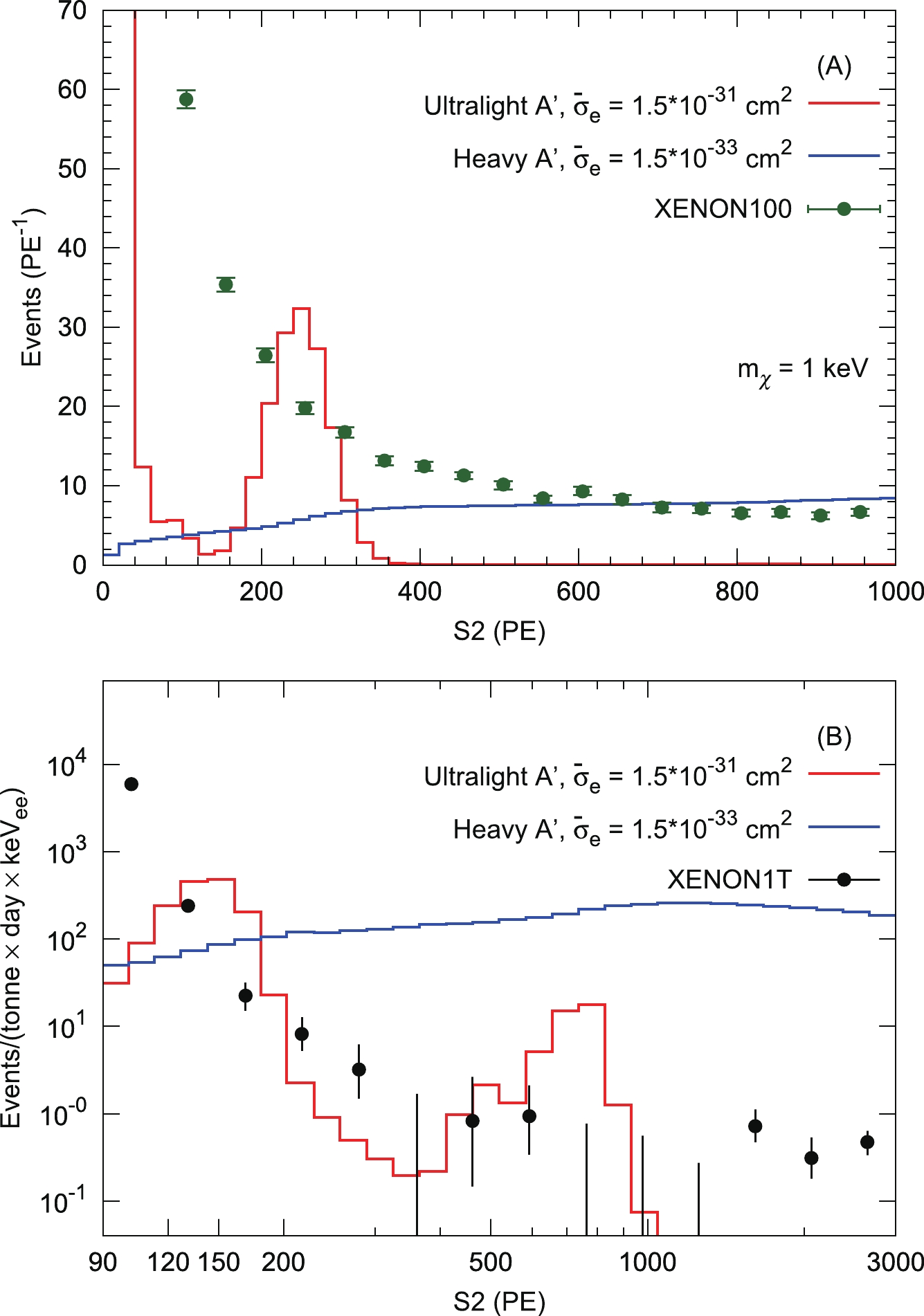

Figure 3.  (color online) Example of expected PE spectra for DM-electron scattering in XENON100 (a) and XENON1T (b) experiments, for both ultralight and heavy mediator cases. Signal spectra are shown for $m_\chi=1$ keV with scattering cross section $\bar{\sigma}_e=1.5\times 10^{-31}~{\rm cm}^2$ ($1.5\times10^{-33}~{\rm cm}^2$) in the ultralight (heavy) mediator case.

Figure 4(a) shows the exclusion limits in the $ m_\chi $-$ \bar{\sigma}_e $ plane for the case of an ultralight mediator, derived from the XENON100 data (red) and the XENON1T data (green). The acceleration mechanism greatly enhances the discovery potential of direct detection experiments for a light DM candidate. For comparison we also plot the parameter region for freeze-in DM (brown curve) [3, 9]. Even though the parameter space of freeze-in DM is well below the current direct detection sensitivity, it can be reached when large experimental exposures are achieved. For example, an experimental exposure of 30 tonne-years can probe the signal region of freeze-in DM with $ m_\chi\sim 1 $ eV when the background is fully controlled. In addition, DM with an ultralight mediator (or equivalent milli-charged DM) can also be constrained by astrophysical observations from supernova cooling and stellar energy loss [32, 33]. The bounds from the direct detection experiments are comparable to those astrophysical constraints.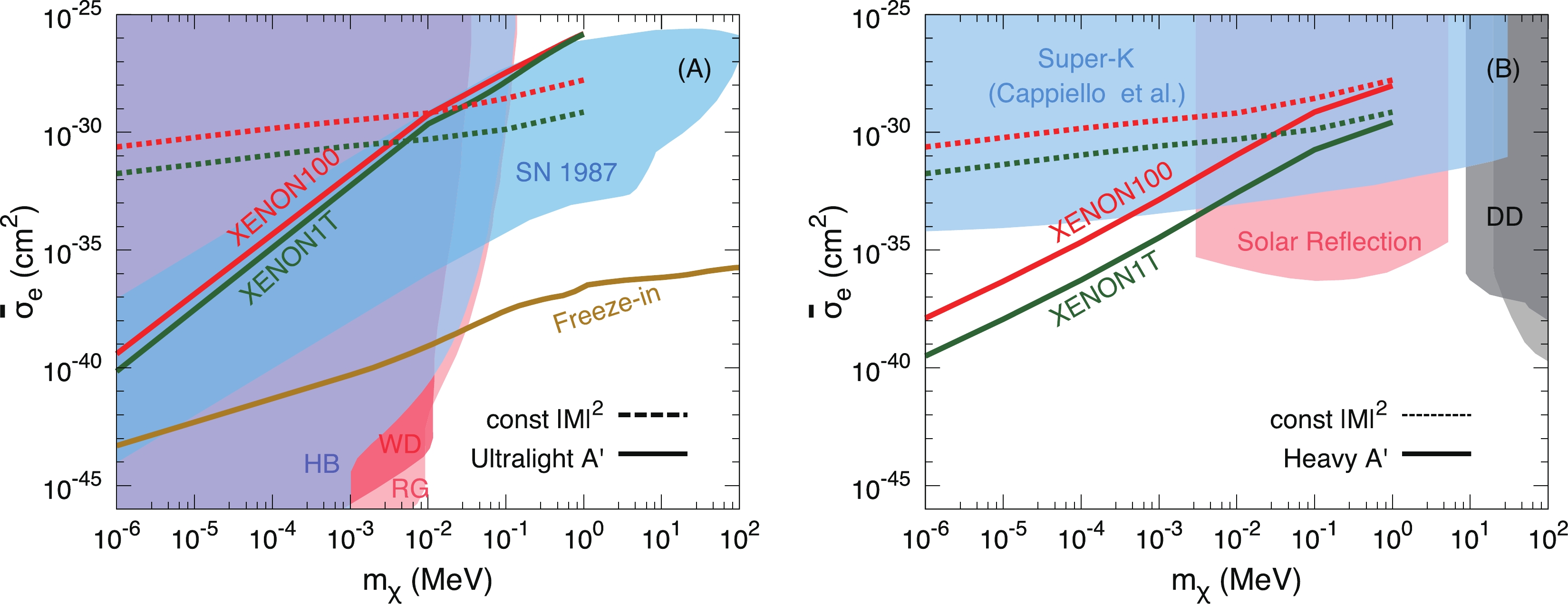

Figure 4.  (color online) (a) Exclusion limits (68% C.L.) in the $ m_\chi $-$ \bar{\sigma}_e $ plane from the XENON100 data (red-solid) and the XENON1T data (green-solid) for the ultralight mediator scenario. For comparison, corresponding limits for constant $ \overline{|{\cal{M}}|^{2}} $ are presented by dashed lines. Also shown are cooling constraints from supernova 1987A (SN 1987) [32], and from the energy loss of red giant (RG) and horizontal branch (HB) stars and white dwarfs (WD) [33]; we also plot the parameter region where DM has the correct relic abundance via the freeze-in mechanism [3, 9]. (b) Exclusion limits (68% C.L.) for the heavy mediator scenario. We also plot constraints from the Super-Kamiokande neutrino experiment (Super-K) [17], solar reflection [12], and previous limits from the XENON10 and the XENON100 direct detection experiments (DD) [10, 11]. Note that the parameter region of DM abundance via the freeze-in mechanism corresponds to the central value of observed relic abundance; other exclusion limits are mostly taken at 90% C.L. In addition, we do not include the limits due to the Earth attenuation effect for boosted DM; see the text for details.

Figure 4(b) displays the exclusion limit of $ \bar{\sigma}_e $ for the case of a heavy mediator. We also plot the limits from the Super-Kamiokande neutrino experiment [17], solar reflection [12], and direct detection experiments without the CR-DM scattering effect [11]. After considering the CR-DM effect, the direct detection experiments have a better sensitivity in the sub-keV mass region. We emphasize that the limits due to the Earth attenuation effect for boosted DM are not included in these figures. DM can scatter with rocks and lose its kinetic energy when passing through the Earth, leading to modification of events and DM energy spectrum in the direct detection experiments, especially for large enough scattering cross section. As a consequence, one expects that the exclusion limits for large cross section should change correspondingly. For DM-nucleon scattering, such an effect has been studied for both non-relativistic DM [34, 35] and boosted DM [36]. However, the situation in DM-electron scattering is much more complicated. In order to estimate the Earth attenuation effect accurately, one needs to know the ionization factor of the atoms contained in each component of the rock. We will leave this issue for future work.

In summary, we have studied the effect of boosted DM on DM-electron direct detection experiments and demonstrate that the current data from liquid noble gas experiments is sensitive to light DM candidates in the sub-MeV range. More importantly, the energy dependence in the cross section plays a crucial role in improving the exclusion limits, e.g., the recoil spectra increase with recoil energy for the heavy mediator case while they decrease with recoil energy for an ultralight mediator. Such opposite energy dependences imply that neutrino experiments such as Super-K are more powerful for heavy mediators due to their much larger acceptance volume and higher energy coverage [37]. On the other hand, direct detection has an advantage for ultralight mediators. These two kinds of experiments are complementary.

The CR-boosted DM mechanism has very rich phenomenologies. For example, it would be interesting to investigate boosted DM flux coming from the Galactic center, which would have high DM density and CR flux. One also expects that the morphology of a signal from the Galactic center would be different from that from a local interstellar source [38]. Moreover, light DM with significant CR acceleration and heavy DM ($ m_\chi \gtrsim 10\; \mathrm{MeV} $) with negligible CR acceleration could potentially produce a degenerate signal; therefore, discriminating these two kinds of scenarios in both model-independent and model-specific way is an intriguing issue [39]. The boosted mechanism might explain or be constrained by the recoil energy spectrum of electrons recently reported by the XENON1T collaboration [40].

We thank Tien-Tien Yu and Su-jie Lin for helpful discussions. We also thank the anonymous referees for careful reading of our manuscript and for valuable comments.

These supplemental materials provide additional details for various results presented in the main text. Some of the results can be applied to other light DM models.

In order to obtain an accurate DM recoil flux, reliable inputs for the electron CR flux are necessary. The observed CR electron spectrum at the Earth extends across many orders of magnitude in energy, ranging from GeV to TeV. Such energetic CR electrons could easily accelerate a fraction of DM particles to relativistic speeds. The flux of CR electrons is obtained by solving the diffusion equation with a widely used galactic CR propagation model. The flux is also modulated periodically according to the solar activity, due to interactions of CR electrons with the heliosphere magnetic field. As a result, the CR spectrum observed at the Earth is different from the interstellar spectrum. Such solar modulation is more important for low energy CR electrons and is negligible for energies above several GeV. The unmodulated local interstellar spectra of CR electrons has been measured by Voyager 1, covering the energy range 2.7-74 MeV [41]. For high energy CR electrons, AMS-02 [42] and DAMPE [43] measurements cover energy ranges from $ 1 $ GeV to $ 4.6 $ TeV. The calculation of boosted DM flux is based on unmodulated CR electron flux. We therefore use GALPROPv54 [44, 45] to obtain the unmodulated best-fit flux for the AMS-02 and DAMPE data sets, and combine the best estimation of Voyager 1 data [46]. The corresponding local interstellar spectrum of CR electrons is shown in Fig. 5, with the measurements.

Figure 5.  (color online) Local interstellar flux of CR electrons as a function of electron kinetic energy T_CR with the data sets from Voyager 1 [41], AMS-02 [42] and DAMPE [43] measurements. For completeness, we also present the Fermi-LAT [47] measurement.

In CR-DM scattering, the initial DM particles are treated as being at rest, since their typical velocities ($ v\sim 10^{-3} $) are negligible compared to the velocities of incoming CR electrons. The recoil energy of DM for a given CR kinetic energy $ T_{\rm CR} $ can be calculated from the standard relativistic kinematics of a 2-body scattering process [23] and are given as:

where $ \theta_{\rm CM} $ is the center-of-mass scattering angle. From the above equation, $ \theta_{\rm CM} $ and $ T_\chi $ are related as

which allows us to translate the variable in the differential cross section from solid angle $ {\rm d} \Omega $ to DM kinetic energy $ {\rm d} T_\chi $ via

where $ \overline{|{\cal{M}}|^{2}} = \frac{1}{4} \sum_{\rm spins}|{\cal{M}}|^{2} $ is the squared DM-electron scattering matrix element, averaged over initial and summed over final spin states. Using Eq. (16) and the Mandelstam variables,

one can derive the formula for $ {\rm d}\sigma_{\chi e}/{\rm d} T_{\chi} $ for a given interaction. Below, we list the expressions for $ {\rm d}\sigma_{\chi e}/{\rm d} T_{\chi} $ for some typical interactions, which are widely used in light DM models:

● Scalar interaction: $ {\cal{L}} \supset g_\chi \overline{\chi} \chi \phi + g_{\rm SM}\overline{f} f \phi $,

● Vector interaction: $ {\cal{L}} \supset g_\chi \overline{\chi} \gamma^\mu \chi A^\prime_\mu + g_{\rm SM}\overline{f} \gamma^{\mu} f A^\prime_\mu $,

● Axial-vector interaction: $ {\cal{L}} \supset g_\chi \overline{\chi} \gamma^\mu \gamma^5 \chi A^\prime_\mu + g_{\rm SM}\overline{f} \gamma^{\mu} \gamma^5 f A^\prime_\mu $,

For the purpose of this paper, we concentrate on the vector interaction, while the limits for other interactions can be obtained in a straightforward way by using our calculation procedures. The DM-electron elastic scattering cross section is conventionally normalized to $ \bar{\sigma}_{e} $ with the following definitions [3]:

where $ \mu_{\chi e} $ is the DM-electron reduced mass, and $ {\cal{M}}_{\rm free}\left(\alpha m_{e}\right) $ is the corresponding matrix element for momentum transfer at reference value $ q = |\boldsymbol{q}| = \alpha m_e $. The DM form factor, $ F_{\rm D M}(q) $, encapsulates all remaining energy dependence of the interaction. With the notation of Eq. (25), the DM-electron reference cross section for benchmark model in Eq. (1) is given by

Combining Eqs. (21) and (27) then gives the expression of $ {\rm d}\sigma_{\chi e}/{\rm d} T_{\chi} $ in Eq. (2)

Finally, from Eqs. (16) and (25), one can easily derive $ {\rm d}\sigma_{\chi e}/{\rm d} T_{\chi} $ corresponding to constant scattering cross section ($ \overline{|{\cal{M}}|^{2}}/(16 \pi s)\equiv \bar{\sigma}_{e} $) and constant matrix element. These are respectively given as:

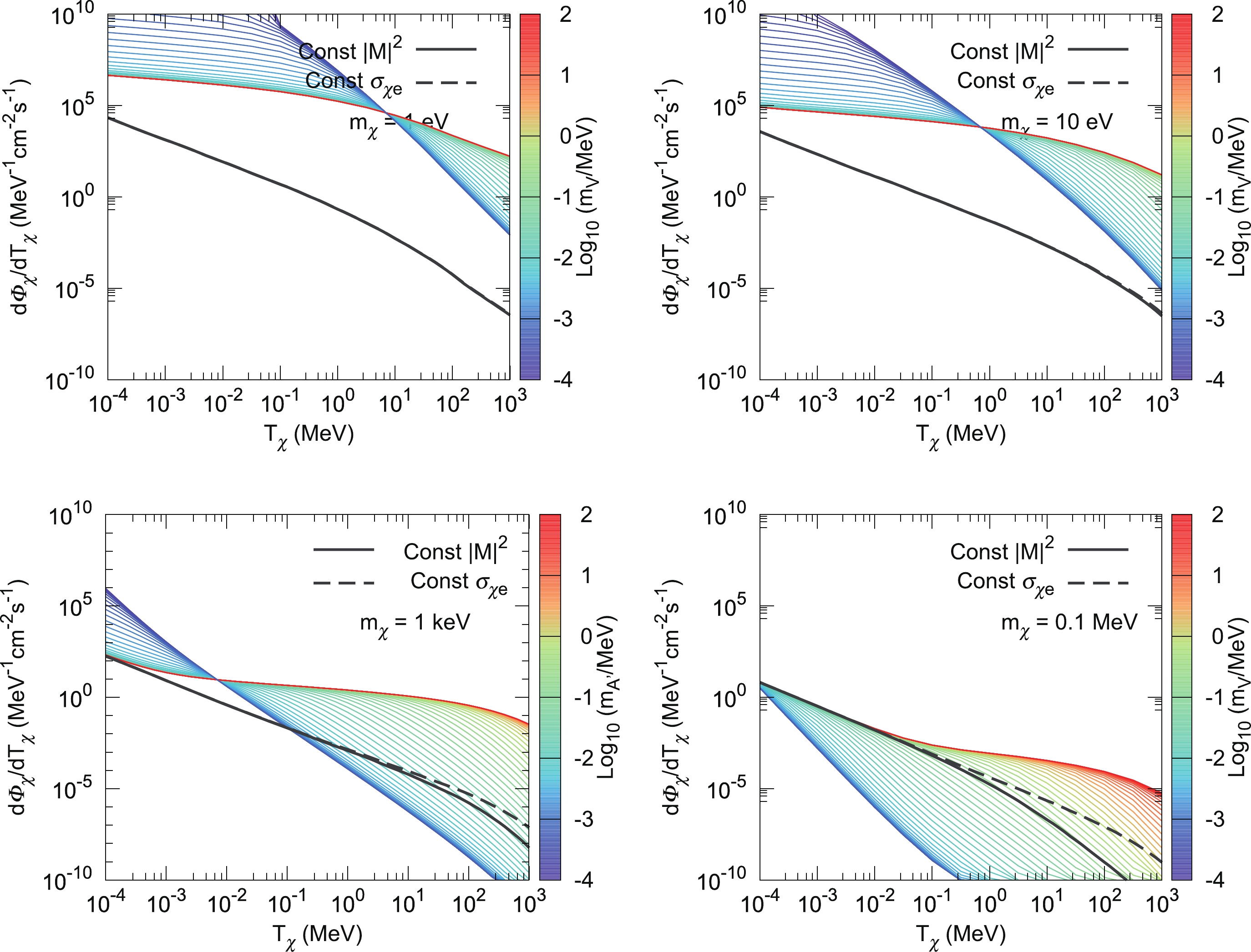
Given the differential cross section in Eqs. (28) and (29), we can calculate the DM recoil flux as a function of DM kinetic energy according to Eq. (4). In Fig. 6, in addition to the $ m_\chi = 1 $ keV recoil flux in the main text, we also present DM recoil fluxes for $ m_\chi = 1 $eV, 10 eV, and 0.1 MeV.

Figure 6.  (color online) DM recoil fluxes for benchmark DM masses $m_\chi=$1 eV, 10 eV, 1 keV and 0.1 MeV with varying mediator mass $m_{A^\prime}$.

The cross section of a DM particle scattering with an electron in a bound state can be derived in a standard way using quantum field theory. In the derivation, one conventionally treats the electron as bounded in a static background potential, which means that the recoil of atoms is neglected. Under such an approximation, the cross section for the elastic $ 2\to 2 $ scattering process $ \chi(p)+e(k) \rightarrow \chi\left(p^{\prime}\right)+e\left(k^{\prime}\right) $ is given by

where $ v_{\chi e} $ is the relative velocity of the incoming DM and electron, and $ \boldsymbol{q} = \boldsymbol{p}-\boldsymbol{p}^{\prime} $ is the momentum transfer from DM to electron. $ \Delta E_\chi $ is the amount of energy lost by the DM in the scattering. Notice that when the initial state is a bounded electron, one just needs to make the replacement $ (2 \pi)^{3} \delta^{3}\left(\boldsymbol{k}-\boldsymbol{k}^\prime+\boldsymbol{q}\right) \rightarrow |f_{i\to \boldsymbol{k}^\prime}(\boldsymbol{q})|^2 $ in Eq. (30). The atomic form factor, $ f_{i\to \boldsymbol{k}^\prime}(\boldsymbol{q}) = \sqrt{V}\int {\rm d}^3 \boldsymbol{r} \psi_i(\boldsymbol{r})\psi^*_{\boldsymbol{k}^\prime}(\boldsymbol{r}){\rm e}^{{\rm i}\boldsymbol{q}\cdot\boldsymbol{r}} $, accounts for the transition from initial to final electron states, and V is the volume for wavefunction normalization. To understand the consistency of such replacement, notice that when both initial and final states are free electrons, this atomic form factor reduces to $ f_{i\to \boldsymbol{k}^\prime}(\boldsymbol{q}) = (2 \pi)^3 \delta^{3}\left(\boldsymbol{k}-\boldsymbol{k}^{\prime}+\boldsymbol{q}\right) $. Here we have included the normalization of the wavefuctions in terms of the volume V, and used the large volume limit $ (2 \pi)^3 \delta^{3}(0)/V\rightarrow 1 $. Then, for the ionization process $ \chi + A \rightarrow \chi + A^+ +e^- $ in the $ (n,\,l) $ atomic shell, Eq. (30) is recast as

Here both initial bounded and recoil electron are non-relativistic, but incoming DM particles could be relativistic in general. The initial bounded electron and recoil electron respectively have energy $ E_e = m_e - |E^{nl}_B| $ and $ E_e^{\prime} = m_e + E_R $, with $ E_R,|E^{nl}_B|\ll m_e $. One can thus make the replacement $ E_eE_e^{\prime}\simeq m_e^2 $ in Eq. (31). The energy deposited in the electron, $ \Delta E_{e} $, is determined by energy conservation, $ \Delta E_{e} = \Delta E_\chi $, with

where $ q = |\boldsymbol{q}| $, $ p = |\boldsymbol{p}| $. Applying the definitions in Eqs. (24) and (25), one can simplify Eq. (31) to

In order to express the differential cross section with respect to electron recoil energy $ E_{R} $, we use the relation $ {\rm d}^{3} \boldsymbol{k}^{\prime} = \frac{1}{2} k^{\prime 3} \,{\rm d} \ln E_{R}\,{\rm d} \Omega_{\boldsymbol{\hat{k}}^{\prime}} $, and rewrite the $ \delta $-function as

Then by taking the derivative of $ \Delta E_\chi $ in Eq. (33) with respect to $ \theta $, Eq. (34) is recast to the expected form,

Integrated with the incoming flux of boosted DM $ {\rm d}{\Phi_\chi}/{{\rm d}T_\chi} $, we finally obtain the velocity-averaged differential ionization cross section,

Here the DM form factor $ F_{\rm DM}(q) $ is evaluated by inverting the matrix element in Eq. (20) by applying Eqs. (24) and (26), giving

It is easy to verify that $ |F_{\rm D M}| $ is reduced to the conventional expression $ |F_{\rm D M}(q)|^{2} = ((\alpha^2 m_e^2 + m_{A^\prime}^{2})/(q^2 + m_{A^\prime}^{2}))^2 $ in the non-relativistic limit, e.g., $ T_\chi,E_{R}\ll m_e $.

The generalized $ \eta $ function is given by

where $ \Phi_{\rm halo}\equiv n_\chi \bar{v} $ is the background DM flux in the Galactic halo. $ E_{\min} $ is the minimum incoming DM energy to produce an electron with recoil energy $ E_R $, which is determined by energy conservation $ \Delta E_\chi = \Delta E_{e} $ when $ \boldsymbol{p} $ and $ \boldsymbol{q} $ are parallel $ (\cos \theta = 1) $, and

Notice that the flux is related to the velocity distribution $ f(\boldsymbol{v}) $ by $ {\rm d}\Phi_\chi(\boldsymbol{v}) = n_\chi |\boldsymbol{v}| f(\boldsymbol{v}){\rm d}^3\boldsymbol{v} $. Equation (39) can be expressed in the standard form,

Similarly, in the non-relativistic limit, one has

Equation (41) reduces to the standard mean inverse speed function $ \eta(v_{\min }) = \int_{v_{\min }} \dfrac{1}{v} f(v) {\rm d}^3 v $.

Finally, the atomic ionization form factor $ \left|f_{\rm ion}^{nl}(k^{\prime}, q)\right|^{2} $ is defined as

where $ f_{n l}(\boldsymbol{q}) $ is the atomic form factor for the $ (n,l) $ electron shell. For the case in which we are interested, the final electron state is always ionized and thus can be taken as a free wavefunction with momentum $ k^{\prime} = \sqrt{2 m_e E_R} $. In this case, $ f_{n l}(\boldsymbol{q}) $ is simplified to

where we have used the definition of momentum space wavefunction of the initial bounded electron $ \psi_{n l m}(\boldsymbol{k}) = \int {\rm d}^{3} \boldsymbol{r} \psi_{n l m}(\boldsymbol{r}) {\rm e}^{-{\rm i} \boldsymbol{k} \cdot \boldsymbol{r}} \equiv \chi_{n l}(k) Y_{l m}(\hat{\boldsymbol{k}}) $, with the normalization $ \int {\rm d}^{3} \boldsymbol{k} \left|\psi_{n l m}(\boldsymbol{k})\right|^2 = (2\pi)^3 $. $ \chi_{n l}(k) $ is the radial wavefunction in momentum space, and $ Y_{l m}(\hat{\boldsymbol{k}}) $ is the spherical harmonic function which accounts for the angular part of the wavefunction. Writing the sum of degenerate states explicitly, we arrive at

where the factor 2 takes account of electron spin. Applying the property of the harmonic function,

and changing the integration variable to initial electron momentum k by using $ \sin \theta {\rm d} \theta = k {\rm d} k/(k^\prime q) $, we obtain the expression for atomic ionization form factor in Ref. [3],

Here we give the detailed computation of the momentum space radial wave function $ \chi_{n l}(p) $ for DM-electron elastic scattering, which is used to calculate the atomic ionization form factor. $ \chi_{n l}(p) $ is obtained by splitting the coordinate space wavefunction $ \psi_{n l m}(x) $ into its radial part $ R_{nl}(r) $ and its angular part $ Y_{l m}(\boldsymbol{\theta},\; \boldsymbol{\phi}) $. The exact expression is given by [48]

Here, $ \boldsymbol{p} $ is a momentum space vector with arbitrary orientation $ (\theta_p, \phi_p) $, and $ p = |\boldsymbol{p}| $. $ P_l(\cos \theta) $ is a Legendre polynomial. To obtain the above result, we have used the orthogonality of the spherical harmonics,

and the Gegenbauer formula,

which expresses the spherical Bessel function $ j_{l}(x) $ with Fourier type integration over the Legendre polynomial. In the RHF method, the radial wavefunctions $ R_{nl}(r) $ are approximated by a linear combination of Slater-type orbitals [28]:

where $ a_{0} $ is the Bohr radius, and the values of coefficients $ C_{n l k} $, $ Z_{l k} $ and $ n_{l k} $ are provided in Ref. [28]. Then $ \chi_{n l}(p) $ can be expressed as

Applying the Hankel transform formula [49],

with $ \,_{2} F_{1}\left(a,\,b,\,c,\, x\right) $ being the hypergeometric function, $ J_{\nu}(x) $ the Bessel function of the first kind and $ j_l(x) = \sqrt{\dfrac{\pi}{2x}}J_{\nu+\frac{1}{2}}(x) $, we can evaluate Eq. (49) analytically, which yields

We notice that Eq. (55) has a slightly different expression from Eq. (C3) in Ref. [48], which leads to a small difference in the value of $ \chi_{n l}(p) $, especially for high l. As a crosscheck, we have performed full numerical integration of Eq. (53) for sample points and found good agreement with our analytical result.

We provide additional details to convert the recoiling electron's recoil energy into a specific number of electrons. Our modeling procedure closely follows Refs. [10, 11]. A primary electron with deposited energy $ \Delta E_e = E_R+|E^{nl}_B| $ can produce $ n_e $ observable electrons, $ n_\gamma $ unobservable scintillation photons, and heat. The relevant quantities satisfy the following relations:

Here $ W = 13.8 $ eV is the average energy required to produce a single quantum (photon or electron), and $ N_{i} $ and $ N_{\rm ex} $ are the corresponding numbers of ions and excited atoms created by $ E_R $ and follow $ N_{\rm ex}/N_i\simeq 0.2 $ [50] at energies above a keV. $ f_R $ is the fraction of ions that can recombine, and we assume $ f_R = 0 $ at low energy [51]. This then implies that $ n_e = N_i $ and $ n_\gamma = N_{\rm ex} $, and the fraction of initial quanta observed as electrons is given by [52]

Furthermore, we assume that the photons associated with the de-excitation of the next-to-outer shells can photoionize to create an additional $ n^{(2)}_Q $ quanta, which are listed in Table 1 for full xenon electron shells. In the calculation, we only consider contributions from the $ (5p^6,5s^2,4d^{10},4p^6,4s^2) $ shells. The total number of electrons is given by $ n_e = n^{(1)}_e+n^{(2)}_e $, where $ n^{(1)}_e $ is the primary electron and $ n^{(2)} $ are the secondary electrons produced. $ n^{(1)} $ equals 0 or 1 with probability $ f_R $ and $ 1-f_R $ respectively, and $ n^{(2)}_e $ follows a binomial distribution with $ n^{(1)}_Q+n^{(2)}_Q $ trials and success probability $ f_e $. As an example, in Fig. 7 we plot the differential rate $ {\rm d}N/{\rm d}n_e $ as a function of number of electrons $ n_e $ for both ultralight and heavy mediator cases.

Shell	$5p^6$	$5s^2$	$4d^{10}$	$4p^6$	$4s^2$	$3d^{10}$	$3p^6$	$3s^2$	$2p^6$	$2s^2$	$1s^2$
$|E^{nl}_B|$/eV	12.4	25.7	75.6	163.5	213.8	710.7	958.4	1093.2	4837.7	5152.2	33317.6
$n^{(2)}_Q$	0	0	4	6-9	3-14	36-50	17-68	9-78	271-349	22-372	2040-2431

Table 1.  Binding energy and number of additional quanta for full xenon electron shells.

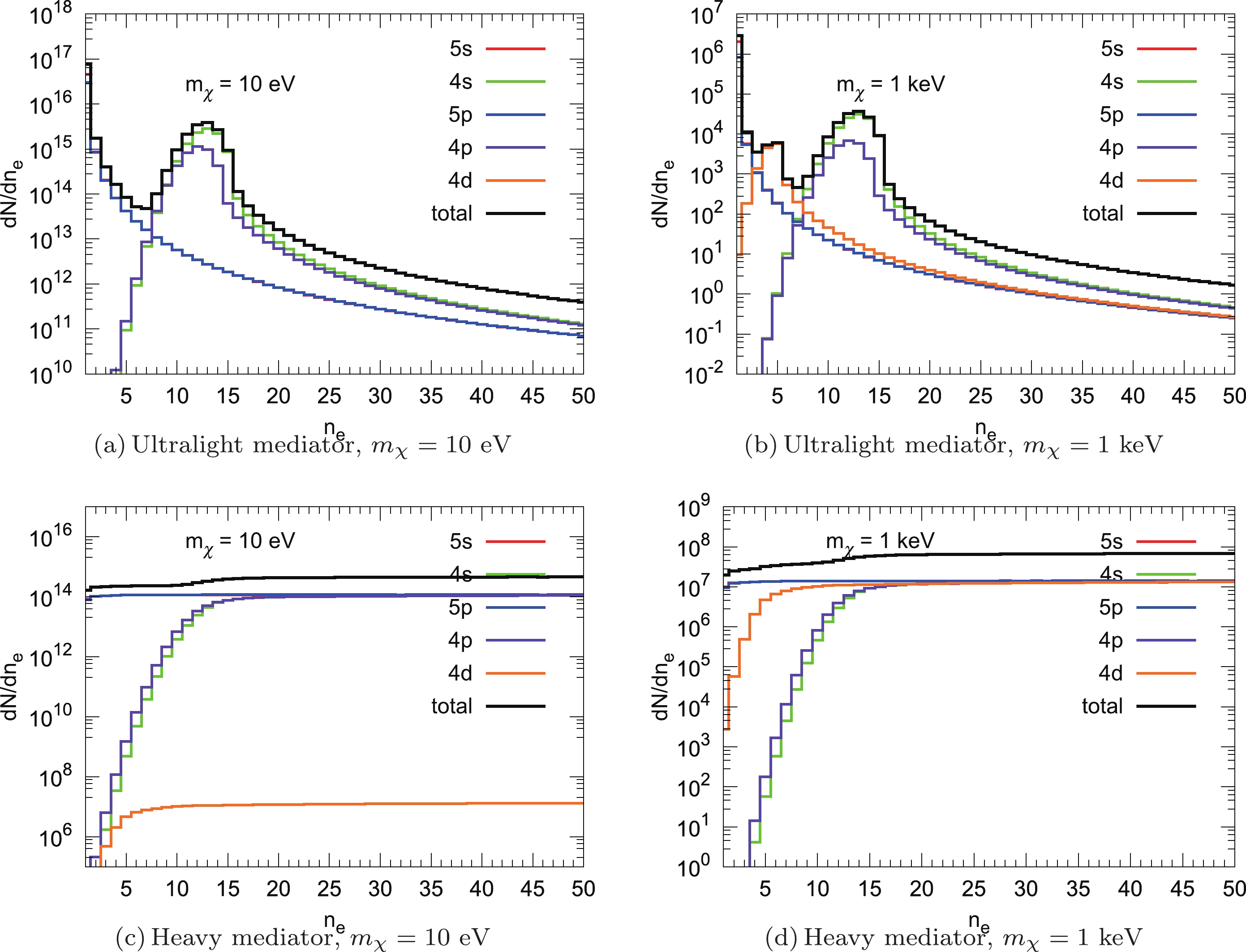
Figure 7.  (color online) Differential rate ${\rm d}N/{\rm d}n_e$ versus number of electrons $n_e$ for $m_\chi=10$ eV and 1 keV, where the top (bottom) panel corresponds to the ultralight (heavy) mediator cases. The colored lines show the contributions from various xenon shells and the black lines show total contributions.