-
The nuclear Drell-Yan production of leptons provides an ideal tool to study parton dynamics and nuclear effects in cold nuclear matter. The observed suppression of the nuclear Drell-Yan production ratios (
$ R_{A_{1}/A_{2}} $ ) is generally believed to be induced by the nuclear effects incorporated in nuclear parton distribution functions (nPDFs) and the initial-state parton energy loss [1-3]. Studying the Drell-Yan nuclear modification is conducive to revealing the properties of the radiative energy loss when partons propagate through the nuclear medium, and moreover, may help to better understand the energy loss effect which causes the jet quenching phenomenon observed at RHIC and the LHC [4, 5].In the past three decades and more, NA3 [6], NA10 [7], E772 [8], E866 [9] and E906 [10] measurements have provided sufficient experimental data to study the suppression of the Drell-Yan differential cross section ratios. Several groups have interpreted the nuclear attenuation in the Drell-Yan process by means of phenomenological models based on energy loss and the nuclear effects of nPDFs [1-3, 11-14]. In Ref. [1], data from E772 and E866 were analyzed, using a very different reference frame and prescription for calculating the shadowing. By disentangling energy loss and shadowing when analyzing experimental data, they extracted the mean quark energy loss per unit path length
$ {\rm d}E/{\rm d}z = 2.73 \pm 0.37 \pm 0.5 $ GeV/fm, which is consistent with theoretical expectations including the effects of the inelastic interaction of the incident proton at the surface of the nucleus. Reference [12] analyzed data from E866 and NA3, and extracted the transport coefficient to be$ \hat{q} = 0.24\pm0.18 $ GeV/fm$ ^{2} $ by means of EKS98 nPDFs [15] and the energy loss distribution based on the BDMPS approach, which corresponds to a mean energy loss per unit length$ {\rm d}E/{\rm d}z = 0.20 \pm 0.15 $ GeV/fm for$ L = 5 $ fm and$ A\approx 200 $ . By means of EPS08 nPDFs [16], Ref. [14] analyzed data from E866 with the transport coefficient$ \hat{q} = 0.024 $ GeV$ ^{2} $ /fm (corresponding to a mean energy loss per unit length$ {\rm d}E/{\rm d}z = 0.20 $ GeV/fm for$ L = 5 $ fm) determined from the nuclear modification of single-inclusive DIS hadron spectra as measured by the HERMES experiment [17]. Because the EKS98 nPDFs [15] and EPS08 nPDFs [16] determine the nuclear shadowing of sea quarks from E866 and E772 nuclear Drell-Yan data, which may be substantially contaminated by energy loss, the initial state energy loss in the Drell-Yan process constrained by the EKS98 or EPS08 nPDFs is underestimated due to an overestimation of the nuclear shadowing correction to the sea quark distribution. So, the conclusions derived from the above two articles (Ref. [12] and Ref. [14]) are analogous.From the above comments, it can be seen that conclusions about the role of the initial-state energy loss effect on Drell-Yan suppression are dependent on the nPDF sets used in the calculations of the Drell-Yan differential cross section ratios. Like the energy loss effect, the shadowing effect incorporated in nPDFs can also induce the suppression of Drell-Yan ratios. Since the underlying mechanisms driving the in-medium corrections of the nucleon substructure have not been completely understood, the shadowing effect has not been determined reliably. Several sets of nPDFs, such as EKS98 [15], EPS08 [16], EPS09 [18], HKN07 [19] and nDS [20], determine the distributions of the valence quarks at larger momentum fraction and the sea quarks at smaller momentum fraction, by fitting the nuclear Drell-Yan data. This may lead to overestimating the nuclear modification in the sea quark distribution, in view of the role of energy loss in Drell-Yan suppression. Hence, by means of these sets of nPDFs, studies of the nuclear effects of nPDFs and the initial-state energy loss effect in the Drell-Yan process cannot reach a reliable conclusion. Lately, by including data constraints from the new LHC experiments, neutrino DIS measurements and low-mass Drell-Yan data (NA3 [6], NA10 [7] and E615 [21]), the EPPS16 nPDF set [22] has been produced. This significantly extends the kinematic reach of the data constraints and leads to a more reliable modification of the nuclear effects of nPDFs.
The initial-state parton energy loss in the nuclear Drell-Yan process is sensitive to the Landau-Pomeranchuk-Migdal (LPM) regime [23], due to the gluon formation time
$ t_{f} $ ($ t_{f}\propto 1/q_{T}^{2} $ as expressed in Ref. [14]) being much smaller than the medium length$ L_{A} $ for large values of$ q_{T} $ , which is different from the fully coherent energy loss (FCEL) [24]. Like initial-state (final-state) parton energy loss, FCEL can also induce a significant hadron suppression in hadron-nucleus collisions. In some hadron-nucleus collisions, these two kinds of energy loss effect both exist and it is difficult to distinguish them, such as in the suppression of$ J/\psi $ production. Since FCEL is absent in the nuclear Drell-Yan process, we can clearly probe the initial-state energy loss and constrain the transport coefficient in the cold nuclear medium by means of Drell-Yan measurements. This may help to disentangle the relative contributions of the initial-state (final-state) energy loss and coherent energy loss, when they both exist in some hadron-nucleus collisions.Up to now, the mechanism of medium-induced parton energy loss has not been understood completely. Due to the lack of reliable determination of the nuclear PDFs and of global analysis for precision data at different incident energies, there is no consensus about the role and the transport coefficient of the initial-state parton energy loss in the nuclear Drell-Yan process. In this work, by means of the new EPPS16 nPDFs [22] and the analytic parametrizations of quenching weights derived from the Baier-Dokshitzer-Mueller-Peign
$ \acute{e} $ -Schiff (BDMPS) formalism based on the LPM regime [25-27], the Drell-Yan nuclear modification due to the nuclear effects of nPDFs and initial-state quark energy loss will be investigated. To accurately extract the value of the transport coefficient, a global fit will be carried out by including all the incident energy data from the new E906 (120 GeV) to E866 (800 GeV). Furthermore, at next-to-leading order (NLO), the initial-state gluon energy loss rooted in the primary NLO subprocess (Compton scattering) will also be investigated. The theoretical framework is presented in Section II, results and discussion are presented in Section III, and a summary is given in Section IV. -
In the nuclear Drell-Yan process, the incident parton undergoes multiple soft collisions accompanied by gluon emission when traveling through the nuclear medium. These radiated gluons carry away some energy
$ \epsilon $ of the incident parton with the probability distribution$ D(\epsilon) $ . In nuclear Drell-Yan hadron production, as the gluon formation time$ t_{f} $ is much smaller than the medium length$ L_{A} $ , the parton energy loss is in the LPM regime [23],$ \langle\epsilon\rangle_{\rm LPM}\propto\hat{q}L^{2}, $

(1) where
$ \hat{q} $ represents the transport coefficient and L is the length of traversed nuclear matter, which is different from the FCEL regime [24], where$ \langle\epsilon\rangle_{\rm FCEL}\propto\frac{\sqrt{\hat{q}L}}{M}\cdot E, $

(2) where M and E represent the mass and energy of the parton respectively. A formalism suitable for describing the LPM energy loss has been presented by Baier, Dokshitzer, Mueller, Peign
$ \acute{e} $ and Schiff (BDMPS) [25, 26]. Based on the BDMPS energy loss framework, an analytic parametrization of the probability distribution$ D(\epsilon) $ for LPM initial-state energy loss has been derived by F. Arleo [27]:$ D(\epsilon) = \frac{1}{\sqrt{2\pi}\sigma(\epsilon/\omega_{c})}\exp\left[-\frac{(\log(\epsilon/\omega_{c})-\mu)^{2}}{2\sigma^{2}}\right], $

(3) where
$ \omega_{c} = \dfrac{1}{2}\hat{q}L^{2} $ ,$ \mu = -2.55 $ and$ \sigma = 0.57 $ .The energy
$ \epsilon $ carried away by radiated gluons results in a change in the incident parton momentum fraction prior to the hard QCD process:$ x_{1}\rightarrow x'_{1} = x_{1}+\epsilon/E_{\rm beam}, $

(4) where
$ x_{1} $ represents the momentum fraction of the partons in the beam hadron. The model for LPM initial-state energy loss can be expressed as:$ \frac{{\rm d}^{2}\sigma'_{h-A}}{{\rm d}x_{\rm F}{\rm d}M^{2}} = \int_{0}^{(1-x_{1})E_{\rm beam}}{\rm d}\epsilon D(\epsilon)\frac{{\rm d}^{2}\sigma_{h-A}}{{\rm d}x_{\rm F}{\rm d}M^{2}}(x'_{1},x_{2},Q^{2}). $

(5) Here
$ x_{2} $ denotes the momentum fraction of the partons in the target,$ x_{\rm F} = x_{1}-x_{2} $ , and the invariant mass of a lepton pair$ Q^{2} = M^{2} = sx_{1}x_{2} $ ($ \sqrt{s} $ is the center of mass energy of the hadronic collision).The NLO Drell-Yan differential cross section consists of the partonic cross section
$ \dfrac{{\rm d}^{2}\sigma^{\rm DY}_{h-A}}{{\rm d}x_{\rm F}{\rm d}M^{2}} $ from the process of the Born diagram$ q\bar{q}\rightarrow \gamma^{*} $ ,$ \dfrac{{\rm d}^{2}\sigma^{\rm C}_{h-A}}{{\rm d}x_{\rm F}{\rm d}M^{2}} $ from the Compton scattering$ qg\rightarrow q\gamma^{*} $ , and$ \dfrac{{\rm d}^{2}\sigma^{\rm Ann}_{h-A}}{{\rm d}x_{\rm F}{\rm d}M^{2}} $ from the annihilation process$ q\bar{q}\rightarrow g\gamma^{*} $ , and hence can be given as:$ \frac{{\rm d}^{2}\sigma_{h-A}}{{\rm d}x_{\rm F}{\rm d}M^{2}} = \frac{{\rm d}^{2}\sigma^{\rm DY}_{h-A}}{{\rm d}x_{\rm F}{\rm d}M^{2}}+\frac{{\rm d}^{2}\sigma^{\rm C}_{h-A}}{{\rm d}x_{\rm F}{\rm d}M^{2}}+\frac{{\rm d}^{2}\sigma^{\rm Ann}_{h-A}}{{\rm d}x_{\rm F}{\rm d}M^{2}}, $

(6) where
$ \frac{{\rm d}^{2}\sigma^{\rm DY(C,Ann)}_{h-A}}{{\rm d}x_{\rm F}{\rm d}M^{2}} = \int_{x_{1}}^{1}{\rm d}t_{1}\int_{x_{2}}^{1}\frac{{\rm d}^{2}\hat{\sigma}^{\rm DY(C,Ann)}}{{\rm d}x_{\rm F}{\rm d}M^{2}}\hat{Q}^{\rm DY(C,Ann)}(t_{1},t_{2}){\rm d}t_{2}. $

(7) Here
$ t_{1} $ and$ t_{2} $ are the fractions of hadron momenta taken by quarks or gluons. For the process of the Born diagram$ q\bar{q}\rightarrow \gamma^{*} $ :$ \frac{{\rm d}^{2}\hat{\sigma}^{\rm DY}}{{\rm d}x_{\rm F}{\rm d}M^{2}} = \frac{4\pi\alpha^{2}}{9M^{2}s}\frac{1}{x_{1}+x_{2}}\delta(t_{1}-x_{1})\delta(t_{2}-x_{2}), $

(8) $ \begin{aligned}[b] \hat{Q}^{\rm DY}(t_{1},t_{2}) =& \sum\limits_{f}e_{f}^{2}[q_{f}^{h}(t_{1},Q^{2})\bar{q}_{f}^{A}(t_{2},Q^{2})\\&+\bar{q}_{f}^{h}(t_{1},Q^{2})q_{f}^{A}(t_{2},Q^{2})], \end{aligned}$

(9) for the Compton scattering
$ qg\rightarrow q\gamma^{*} $ :$ \frac{{\rm d}^{2}\hat{\sigma}^{\rm C}}{{\rm d}x_{\rm F}{\rm d}M^{2}} = \frac{3}{16}\times\frac{16\alpha^{2}\alpha_{s}(Q^{2})}{27M^{2}s}\frac{1}{x_{1}+x_{2}}C(x_{1},x_{2},t_{1},t_{2}), $

(10) $\begin{aligned}[b] \hat{Q}^{\rm C}(t_{1},t_{2}) =& \sum\limits_{f}e_{f}^{2}\{g^{h}(t_{1},Q^{2})[q_{f}^{A}(t_{2},Q^{2})+\bar{q}_{f}^{A}(t_{2},Q^{2})] \\&+g^{A}(t_{2},Q^{2})[q_{f}^{h}(t_{1},Q^{2})+\bar{q}_{f}^{A}(t_{1},Q^{2})]\},\end{aligned} $

(11) and for the annihilation process
$ q\bar{q}\rightarrow g\gamma^{*} $ :$\begin{aligned}[b]\frac{{\rm d}^{2}\hat{\sigma}^{\rm Ann}}{{\rm d}x_{\rm F}{\rm d}M^{2}} = \frac{1}{2}\times\frac{16\alpha^{2}\alpha_{s}(Q^{2})}{27M^{2}s}\frac{1}{x_{1}+x_{2}} Ann(x_{1},x_{2},t_{1},t_{2}), \end{aligned}$

(12) $ \begin{aligned}[b] \hat{Q}^{\rm Ann}(t_{1},t_{2}) =& \sum\limits_{f}e_{f}^{2}[q_{f}^{h}(t_{1},Q^{2})\bar{q}_{f}^{A}(t_{2},Q^{2})\\&+\bar{q}_{f}^{h}(t_{1},Q^{2})q_{f}^{A}(t_{2},Q^{2})].\end{aligned}$

(13) In the above formulas,
$ q^{h(A)}_{f}(x_{1(2)},Q^{2}) $ refers to the parton distribution function with flavor f in the hadron (nucleus A),$ e_{f} $ denotes the charge of the quark with flavor f,$ \alpha $ represents the fine structure constant,$ \alpha_{s}(Q^{2}) $ is the specific expression of the function, and the complex expressions of functions$ C(x_{1},x_{2},t_{1},t_{2}) $ and$ Ann(x_{1},x_{2},t_{1},t_{2}) $ are shown in Ref. [28]. The partonic density of nucleus A is different from that of a free proton due to the complex nuclear environment, with effects such as EMC suppression, shadowing and anti-shadowing. In this paper, the Drell-Yan nuclear modification due to the nuclear effects of nPDFs is computed with the latest EPPS16 set [22].In the above energy loss correction model for interpreting the nuclear Drell-Yan suppression, the transport coefficient
$ \hat{q} $ is the only parameter. It measures the properties of the initial-state energy loss effect in a cold medium and can be constrained from$ \chi^{2} $ analysis of the fit of the experimental data by calculating the Drell-Yan differential cross section ratio:$ R_{A_{1}/A_{2}}(x_{\rm F}) = \frac{A_{2}}{A_{1}}\left(\frac{{\rm d}^{2}\sigma'_{h-A1}}{{\rm d}x_{\rm F}{\rm d}M}\bigg/\frac{{\rm d}^{2}\sigma'_{h-A2}}{{\rm d}x_{\rm F}{\rm d}M}\right). $

(14) -
Firstly, we investigate the nuclear effects of nPDFs on the nuclear Drell-Yan ratio using the EPPS16 nPDFs [22] together with the nCTEQ15 parton density of the proton [29] or the parton distributions of the negative pion [30]. It should be noted that in our calculation the corrections from isospin effects are neglected due to their small influence on the Drell-Yan ratios [2]. The solid lines in Figs. 1, 2, 3, 4, 5 show the next-to-leading order Drell-Yan ratios
$ R_{A_{1}/A_{2}} $ , and the dashed lines correspond to the leading order calculations ($ q\bar{q}\rightarrow \gamma^{*} $ ). They are both modified only by the nPDF corrections. It is found that the theoretical results at next-to-leading order and leading order are almost identical for the E906, NA3 and NA10 experiments, and there is a small difference between the two results for the E866 experiments. From the above expressions of$ \dfrac{{\rm d}^{2}\sigma^{\rm DY}_{h-A}}{{\rm d}x_{\rm F}{\rm d}M^{2}} $ (see Eq. (9)),$ \dfrac{{\rm d}^{2}\sigma^{\rm C}_{h-A}}{{\rm d}x_{\rm F}{\rm d}M^{2}} $ (see Eq. (11)) and$ \dfrac{{\rm d}^{2}\sigma^{\rm Ann}_{h-A}}{{\rm d}x_{\rm F}{\rm d}M^{2}} $ (see Eq. (13)) in Section II, we can calculate and derive that:
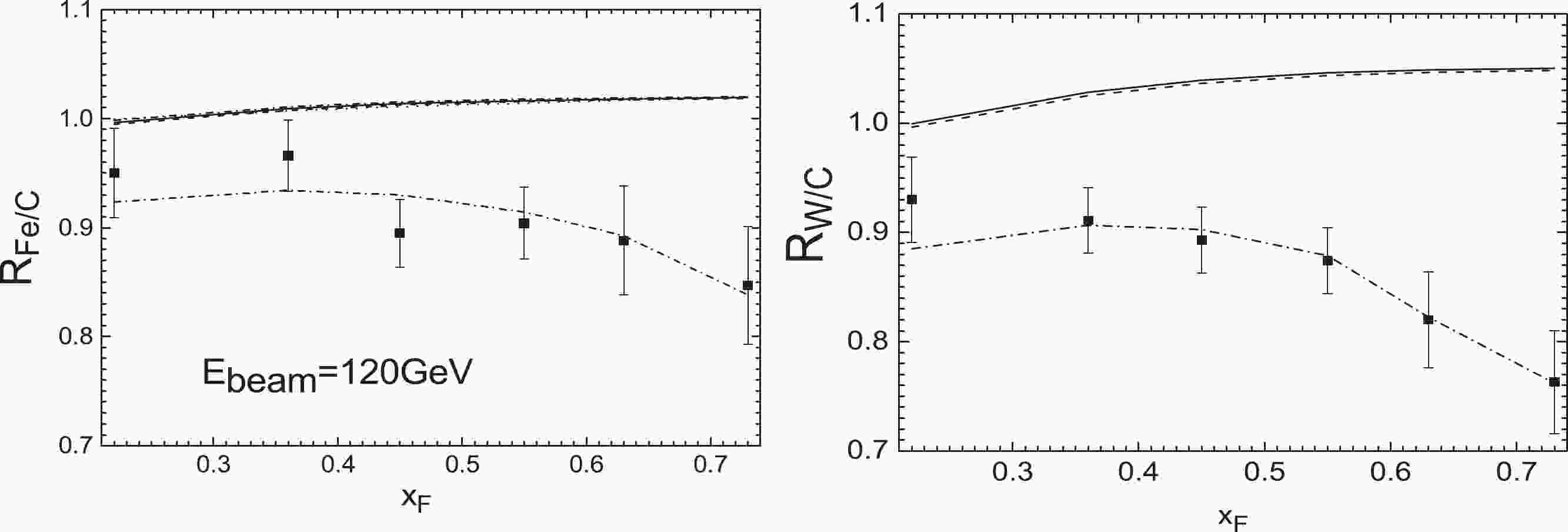
Figure 1. E906 nuclear Drell-Yan ratios
$ R_{\rm Fe/C}(x_{\rm F}) $ (left) and$ R_{\rm W/C}(x_{\rm F}) $ (right) compared to the theoretical results with EPPS16 nPDFs at next-to-leading order (solid lines), leading order calculation (dashed lines), and considering initial-state quark energy loss from the process of the Born diagram$ q\bar{q}\rightarrow \gamma^{*} $ (dashed-dotted lines).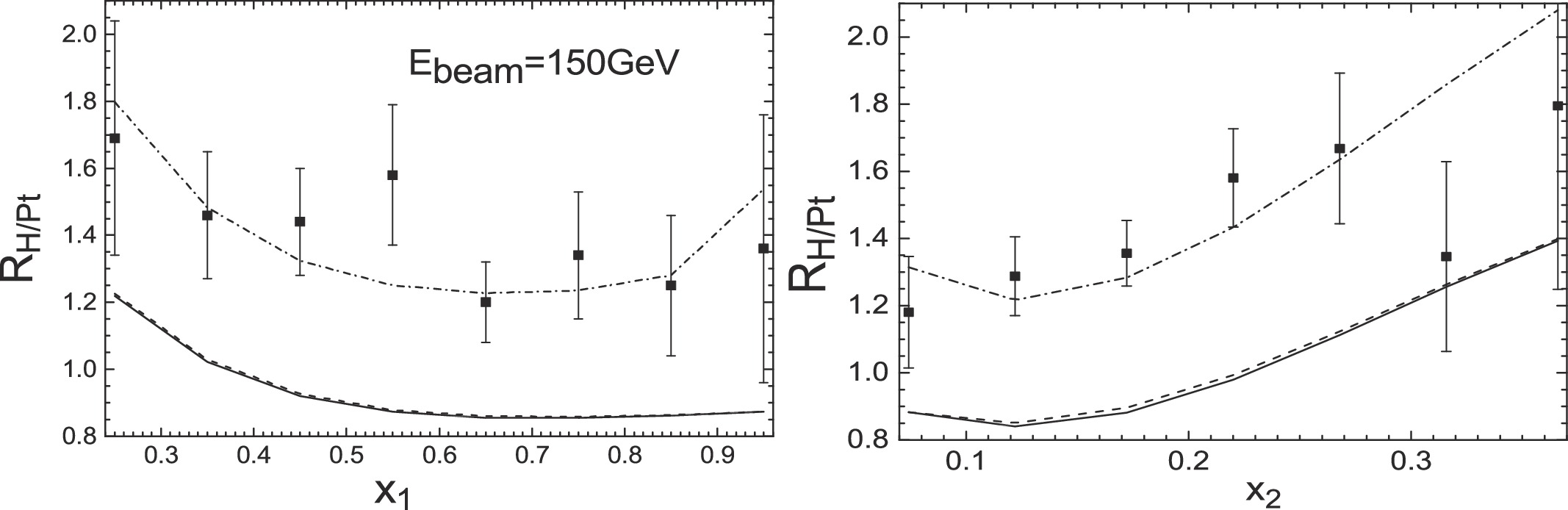
Figure 2. NA3 nuclear Drell-Yan ratios
$ R_{\rm H/Pt}(x_{1}) $ (left) and$ R_{\rm H/Pt}(x_{2}) $ (right) compared to the theoretical results with EPPS16 nPDFs at next-to-leading order (solid lines), leading order calculation (dashed lines), and considering initial-state quark energy loss from the process of the Born diagram$ q\bar{q}\rightarrow \gamma^{*} $ (dashed-dotted lines).
Figure 3. NA10(140 GeV) nuclear Drell-Yan ratios
$ R_{\rm W/D}(x_{1}) $ (left) and$ R_{\rm W/D}(x_{2}) $ (right) compared to the theoretical results with EPPS16 nPDFs at next-to-leading order (solid lines), leading order calculation (dashed lines), and considering initial-state quark energy loss from the process of the Born diagram$ q\bar{q}\rightarrow \gamma^{*} $ (dashed-dotted lines).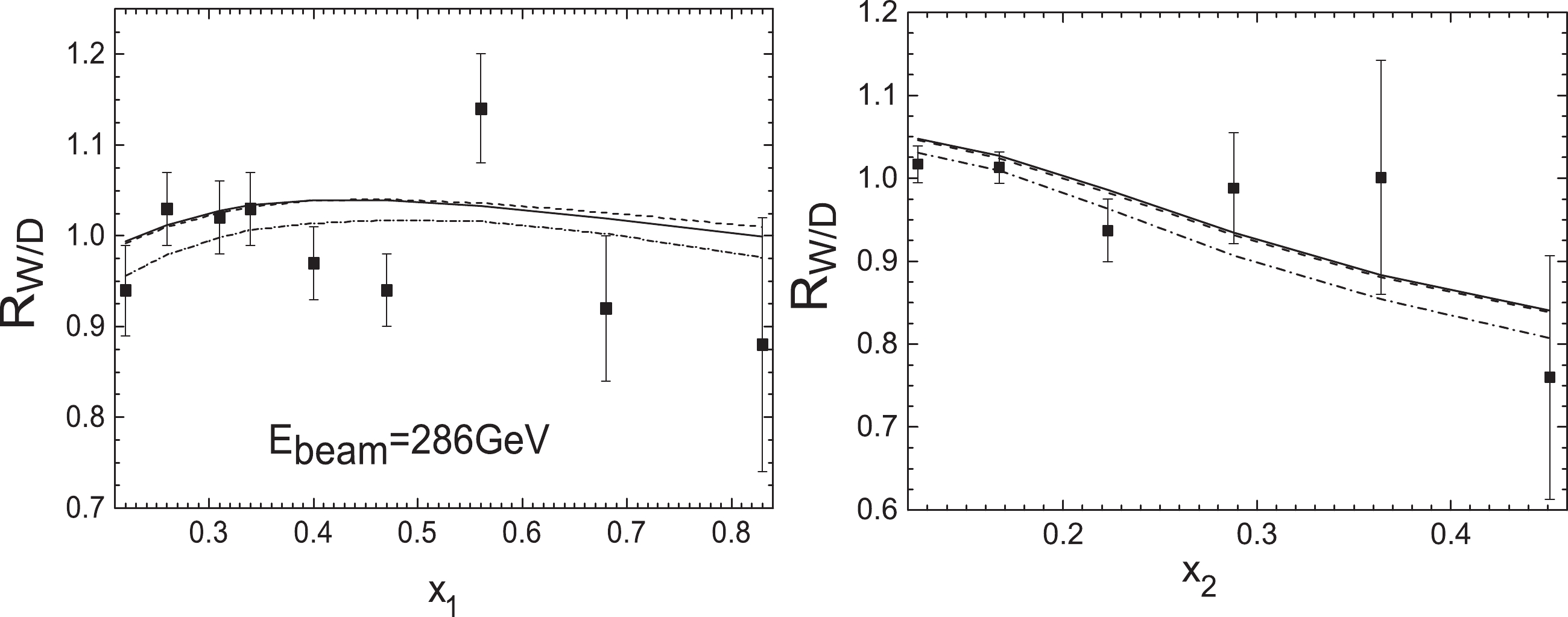
Figure 4. NA10(286 GeV) nuclear Drell-Yan ratios
$ R_{\rm W/D}(x_{1}) $ (left) and$ R_{\rm W/D}(x_{2}) $ (right) compared to the theoretical results with EPPS16 nPDFs at next-to-leading order (solid lines), leading order calculation (dashed lines), and considering initial-state quark energy loss from the process of the Born diagram$ q\bar{q}\rightarrow \gamma^{*} $ (dashed-dotted lines).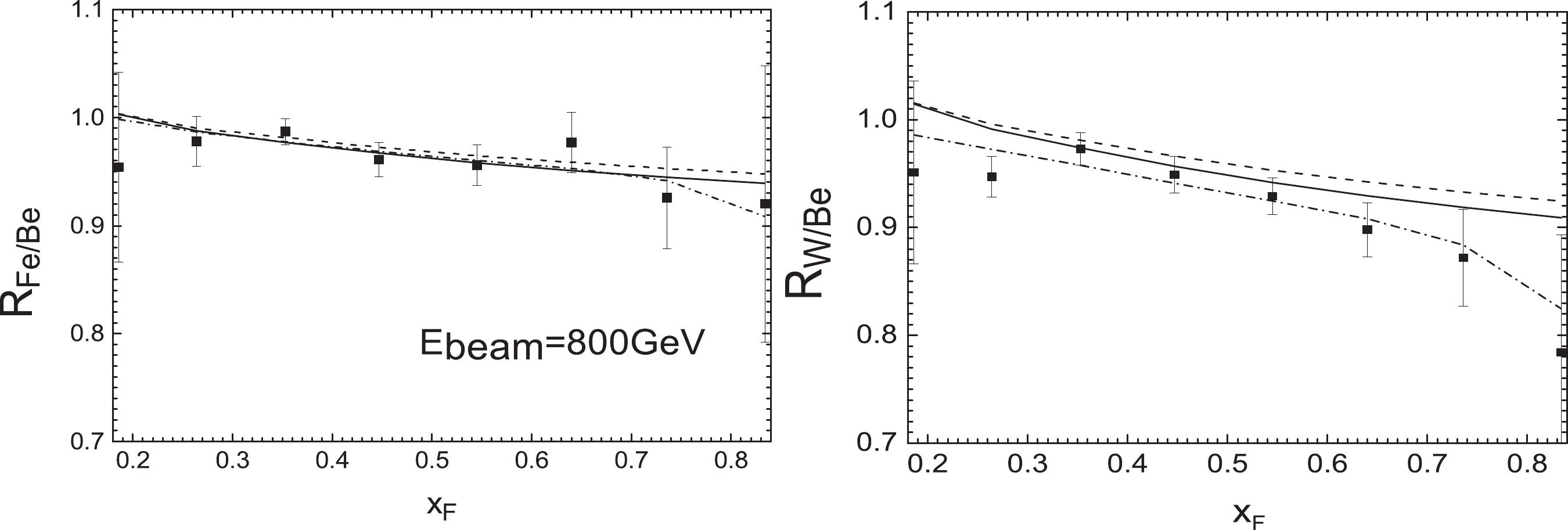
Figure 5. E866 nuclear Drell-Yan ratios
$ R_{\rm Fe/Be}(x_{\rm F}) $ (left) and$ R_{\rm W/Be}(x_{\rm F}) $ (right) compared to the theoretical results with EPPS16 nPDFs at next-to-leading order (solid lines), leading order calculation (dashed lines), and considering initial-state quark energy loss from the process of the Born diagram$ q\bar{q}\rightarrow \gamma^{*} $ (dashed-dotted lines).$ \begin{aligned}[b]\frac{{\rm d}^{2}\sigma^{\rm DY}_{h-A_{1}}}{{\rm d}x_{\rm F}{\rm d}M^{2}}\bigg/\frac{{\rm d}^{2}\sigma^{\rm DY}_{h-A_{2}}}{{\rm d}x_{\rm F}{\rm d}M^{2}}\approx\frac{{\rm d}^{2}\sigma^{\rm Ann}_{h-A_{1}}}{{\rm d}x_{\rm F}{\rm d}M^{2}}\bigg/\frac{{\rm d}^{2}\sigma^{\rm Ann}_{h-A_{2}}}{{\rm d}x_{\rm F}{\rm d}M^{2}} \approx \frac{{\rm d}^{2}\sigma^{\rm C}_{h-A_{1}}}{{\rm d}x_{\rm F}{\rm d}M^{2}}\bigg/\frac{{\rm d}^{2}\sigma^{\rm C}_{h-A_{2}}}{{\rm d}x_{\rm F}{\rm d}M^{2}}, \end{aligned} $

(15) in the momentum fraction range where the nuclear effects of gluon distributions are not gigantic. Therefore, the form of the differential cross section ratio given by the nuclear Drell-Yan data actually diminishes the QCD next-to-leading order correction. From Figs. 1, 2, 3, 4, 5 we can also see that there is an obvious deviation between the calculations obtained by only including the EPPS16 nPDFs corrections and the measurements of the E906 (120 GeV), NA3 (150 GeV) and NA10 (140 GeV) experiments at lower incident energies. However, a good fit can be seen between the results and the E866 (800 GeV) and NA10 (286 GeV) measurements with higher beam energies. Further, in Table 1, we compute the
$ \chi^{2}/N $ (N is the number of data points) at leading order calculation. Table 1 also shows that the nuclear effects of nPDFs play a more important role in the Drell-Yan nuclear modification with the increase of beam energy.Exp.data Data points Beam/GeV $\chi^{2}/ndf$ 

E906( $x_{\rm F}$ )

12 120 15.07 NA3( $x_{1(2)}$ )

15 150 7.31 NA10( $x_{1(2)}$ )

9 140 6.55 NA10( $x_{1(2)}$ )

15 286 1.43 E866( $x_{\rm F}$ )

16 800 1.22 Table 1.
$\chi^{2}/N$ values obtained only with EPPS16 nPDFs [22].Secondly, we consider the initial-state quark energy loss in nuclear Drell-Yan production. In view of the correction model for initial-state energy loss and the above discussion, the energy loss effect in the Compton scattering and annihilation processes can also be diminished due to the form of the differential cross section ratio given by the nuclear Drell-Yan data. Therefore, in a leading order calculation, only the quark energy loss from the process of the Born diagram
$ q\bar{q}\rightarrow \gamma^{*} $ is considered. We calculate the Drell-Yan ratios$ R_{A_{1}/A_{2}} $ using the EPPS16 nPDFs [22] together with the analytic parametrization of quenching weights based on the BDMPS formalism [27] (Eq. (3)). The values of transport coefficient$ \hat{q} $ and$ \chi^{2}/ndf $ extracted from the corresponding experimental data are shown in Table 2. Comparing Table 2 and Table 1 shows that, when considering the initial-state quark energy loss effect, the fitting degree of the calculation results with the experimental data is greatly improved, especially for low incident energy data (E906-120 GeV, NA3-150 GeV and NA10-140 GeV).Exp.data Data points Momentum fraction $\hat{q}$ /(GeV

$^{2}$ /fm)

$\chi^{2}/ndf$ 

E906( $R_{\rm Fe/C}(x_{\rm F})$ )

6 $0.22<x_{\rm F}<0.73$ 

$0.45\pm0.06$ 

0.46 E906( $R_{\rm W/C}(x_{\rm F})$ )

6 $0.22<x_{\rm F}<0.73$ 

$0.25\pm0.02$ 

0.25 Glob fit E906-120 GeV 12 $0.25\pm0.02$ 

0.91 NA3( $R_{\rm H/Pt}(x_{1})$ )

8 $0.25<x_{1}<0.95$ 

$0.24\pm0.11$ 

0.46 NA3( $R_{\rm H/Pt}(x_{2})$ )

7 $0.074<x_{2}<0.366$ 

$0.24\pm0.11$ 

0.88 Glob fit NA3-150 GeV 15 $0.24\pm0.10$ 

0.65 NA10-140 GeV( $R_{\rm W/D}(x_{1})$ )

5 $0.39<x_{1}<0.82$ 

$0.35\pm0.02$ 

1.13 NA10-140 GeV( $R_{\rm W/D}(x_{2})$ )

4 $0.163<x_{2}<0.360$ 

$0.27\pm0.04$ 

0.31 Glob fit NA10-140 GeV 9 $0.30\pm0.05$ 

0.99 NA10-286 GeV( $R_{\rm W/D}(x_{1})$ )

9 $0.22<x_{1}<0.83$ 

$0.19\pm0.11$ 

1.45 NA10-286 GeV( $R_{\rm W/D}(x_{2})$ )

6 $0.125<x_{2}<0.451$ 

$0.10\pm0.07$ 

0.59 Glob fit NA10-286 GeV 15 $0.14\pm0.05$ 

1.14 E866( $R_{\rm Fe/Be}(x_{\rm F})$ )

8 $0.186<x_{\rm F}<0.834$ 

$0.17\pm0.17$ 

0.27 E866( $R_{\rm W/Be}(x_{\rm F})$ )

8 $0.186<x_{\rm F}<0.834$ 

$0.39\pm0.10$ 

0.46 Glob fit E866-800 GeV 16 $0.36\pm0.10$ 

0.41 Global fit 67 $0.26\pm0.04$ 

0.82 Table 2.
$\hat{q}$ and$\chi^{2}/ndf$ values obtained with EPPS16 nPDFs [22] and initial-state quark energy loss.A plot of
$ \chi^2 $ as a function of$ \hat{q} $ for the global fit of all data is given in Fig. 6. From Fig. 6, we can easily and clearly see that the global fit shows the best value is$ \hat{q} = 0.26\pm0.04 $ GeV2/fm ($ \chi^{2}/ndf = 0.82 $ ), which is a little smaller than the result$ \hat{q} = 0.32\pm0.04 $ GeV2/fm obtained using the HKM nPDFs [31] in our previous work [3]. Since the HKM nPDFs [31] are obtained using only the experimental data for nuclear structure functions, the shadowing effect of the nPDFs on the suppression of Drell-Yan ratios has been reduced in the$ 0.01 < x < 0.3 $ region. In addition, as discussed in Ref. [12], the mean BDMPS energy loss$ \langle\epsilon\rangle $ experienced by the fast parton in the medium is given by:$ \langle\epsilon\rangle\equiv \int D(\epsilon){\rm d}\epsilon = \frac{1}{2}\alpha C_{R}\omega_{c}, $

(16) where
$ \alpha = \frac{1}{2}, \;C_{R} = \frac{4}{3} $ , and the mean quark energy loss per unit path length$ {\rm d}E/{\rm d}z $ is:$ \frac{{\rm d}E}{{\rm d}Z}\equiv\frac{\langle\epsilon\rangle}{L} = \delta\times\left(\frac{L}{10\;{\rm fm}}\right), $

(17) where
$ \delta $ is a parameter simply related to the transport coefficient$ \hat{q} $ and means the mean BDMPS energy loss per unit path length with$ L = 10 $ fm. It can be derived that the mean BDMPS energy loss per unit path length$ {\rm d}E/{\rm d}z = \dfrac{1}{6}\hat{q}L $ . Here the transport coefficient$ \hat{q} = 0.26\pm 0.04 $ GeV$ ^{2} $ /fm corresponds to$ \dfrac{{\rm d}E}{{\rm d}Z}\approx1.10\pm0.17 $ GeV/fm for$ L = 5 $ fm, which is much bigger than the result$ \dfrac{{\rm d}E}{{\rm d}Z} = 0.20\pm0.15 $ GeV/fm obtained by using EKS98 nPDFs in Ref. [12], the result$ \dfrac{{\rm d}E}{{\rm d}Z} = 0.20 $ GeV/fm obtained by EPS08 nPDFs in Ref. [14], or the result$ \dfrac{{\rm d}E}{{\rm d}Z} = 0.23\pm0.09 $ GeV/fm obtained by EPS09 nPDFs in Ref. [13]. For$ L = 10 $ fm, the transport coefficient$ \hat{q} = 0.26\pm0.04 $ GeV$ ^{2} $ /fm corresponds to$ \dfrac{{\rm d}E}{{\rm d}Z}\approx2.20\pm0.34 $ GeV/fm, which is approximately identical to the result$ \dfrac{{\rm d}E}{{\rm d}Z} = 2.73\pm0.37\pm0.5 $ GeV/fm obtained by unambiguously separating shadowing and energy loss in Ref. [1]. This indicates that with the EPPS16 nPDFs, the value of quark energy loss can actually be better constrained from the nuclear Drell-Yan data by avoiding overestimation of the shadowing correction. The reason is that although the fit of the EPPS16 nPDFs includes the nuclear Drell-Yan data, the new data (NA3 [6], NA10 [7] and E615 [21]) increase the variety of the momentum fraction of the target parton from 0.074 to 0.451 with respect to EPS09 and efficiently avoid overestimating the nuclear modification of the sea quark distribution. Furthermore, the fit of the EPPS16 nPDFs includes the data from higher energy LHC proton-lead collisions, which can completely disregard energy loss and provide better constraints for the A dependence of the parton nuclear modifications. For large beam energy nuclear Drell-Yan experiments such as E866 and E772, a large portion of the data is in the range$ x_{2} < 0.05 $ , which falls in the region of significant nuclear shadowing. For low beam energy measurements such as NA3, NA10 and E906, a large portion of the data is in the range$ 0.1 <x_{2} < 0.45 $ , which falls in the region of only tiny (anti-)shadowing. The nuclear modification of the Drell-Yan process is sensitive to nPDFs mainly due to some kinds of nPDF (such as EPS09, EPS08 and EKS98) determining nuclear shadowing of sea quarks from E866 and E772 nuclear Drell-Yan data, which may be substantially contaminated by energy loss. To minimize the dependence on nPDFs, the nuclear Drell-Yan measurements at lower beam energy should provide better constraints for the initial-state parton energy loss.With the value of the transport coefficient
$ \hat{q} $ displayed in Table 2, the results considering the energy loss effect from the process of the Born diagram$ q\bar{q}\rightarrow \gamma^{*} $ are showed as the dashed-dotted lines in Figs. 1, 2, 3, 4, 5. It is found that the calculations using the EPPS16 nPDFs together with the initial-state quark energy loss effect are in good agreement with the Drell-Yan data, especially for low-mass Drell-Yan measurements (E906-120 GeV, NA3-150 GeV and NA10-140 GeV), and the fitting degree is better than the results acquired using the EPPS16 nPDF and the fully coherent regime$ \hat{q} = 0.07-0.09 $ GeV2/fm extracted from$ J/\psi $ measurements [2]. The role of the incident quark energy loss effect in the suppression of Drell-Yan ratios reduces with increasing beam energy, and becomes more important with increasing nuclear mass number A.Thirdly, we appraise the role of the initial-state gluon energy loss by means of the primary NLO subprocess (Compton scattering) in Drell-Yan production. At next-to-leading order, the differential cross section of Compton scattering
$ qg\rightarrow q\gamma^{*} $ involves the gluon distributions of the incident hadron and the target nucleus, as seen in Eq. (11). This provides an opportunity to explore the initial-state gluon energy loss effect. In order to avoid diminishing the QCD NLO correction to the data form of Drell-Yan ratios and better investigate the gluon energy loss in Compton scattering$ qg\rightarrow q\gamma^{*} $ , we separately calculate the Compton differential cross section ratios$ R_{\rm Fe(W)/C}(x_{\rm F}) $ at 120 GeV. The results can be seen in Fig. 7. The dotted lines represent the results without nuclear modification of the gluon distribution of the target nucleus, the solid lines include the gluon nuclear effects, the dashed-dotted lines correspond to the calculations including the initial-state energy loss of the gluon, and the dashed lines include both quark and gluon energy loss. From Fig. 7, it can be seen that the deviation between the dotted lines and the solid lines increases to approximately 2% for$ R_{\rm Fe/C}(x_{\rm F}) $ and 3.5% for$ R_{\rm W/C}(x_{\rm F}) $ at$ x_{\rm F}\approx0.73 $ , which indicates that the role of the nuclear effects of gluon distributions in Compton scattering is apparent and becomes more important with the increase of$ x_{\rm F} $ as well as the nuclear mass number A. The deviation between the solid and the dashed-dotted lines is approximately from 1% to 0 with$ x_{\rm F} $ from 0.22 to 0.73, which illustrates that the role of the initial-state gluon energy loss effect in the suppression of Compton scattering ratios is not very important, and reduces with increasing$ x_{\rm F} $ . The deviation between the dashed-dotted lines and the dashed lines is approximately from 5% to 19% for$ R_{\rm Fe/C}(x_{\rm F}) $ and from 8% to 29% for$ R_{\rm W/C}(x_{\rm F}) $ with$ x_{\rm F} $ from 0.22 to 0.73, which illustrates that the initial-state quark energy loss effect in Compton scattering becomes more significant with the increase of$ x_{\rm F} $ and nuclear mass number A. It is clear that in the range$ 0.22<x_{\rm F}<0.73 $ at$ E_{\rm beam} = 120 $ GeV, the initial-state quark energy loss is the dominant effect which induces the suppression of Compton scattering ratios, the nuclear effects of the gluon leading to the rise of Compton scattering ratios are obvious, and the initial-state gluon energy loss has an influence on the suppression at small$ x_{\rm F} $ . This means that it may be feasible to investigate the initial-state gluon energy loss from a separate calculation of the primary NLO subprocess (Compton scattering) in Drell-Yan production in the small$ x_{\rm F} $ range and at lower incident energy.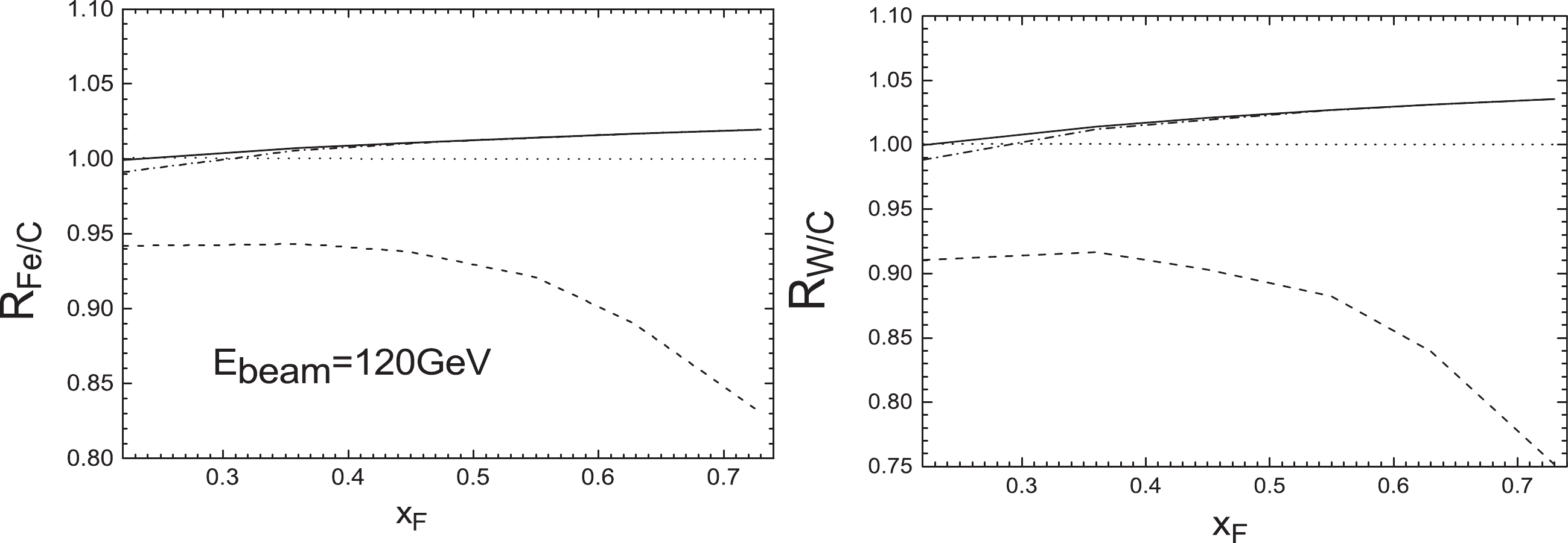
Figure 7. Differential cross section ratios
$ R_{\rm Fe/C}(x_{\rm F}) $ (left) and$ R_{\rm W/C}(x_{\rm F}) $ (right) from the Compton scattering$ qg\rightarrow q\gamma^{*} $ . The dotted (solid) lines represent the results without (with) the nuclear modification of the gluon distribution, and the dashed-dotted (dashed) lines correspond to the calculations including the initial-state energy loss of the gluon (quark and gluon). -
By means of the new EPPS16 nPDFs [22] and the analytic parametrizations of quenching weights derived from the BDMPS formalism based on the LPM regime [25-27], the Drell-Yan nuclear modification due to the nuclear effects of nPDFs and initial-state parton energy loss has been investigated, by globally analyzing all the incident energy experimental data (67 points) including E906-120 GeV [10], NA3-150 GeV [6], NA10-140 GeV [7], NA10-286 GeV [7], and E866-800 GeV [9]. It is found that the calculations with the EPPS16 nPDF together with the initial-state energy loss effect are in good agreement with the Drell-Yan data, and that the role of the energy loss effect in the suppression of Drell-Yan ratios is prominent, especially for low-mass Drell-Yan measurements. The nuclear effects of nPDFs become more obvious with increasing nuclear mass number A, the same as the energy loss effect. The value of the transport coefficient extracted by a global fit is
$ \hat{q} = 0.26\pm0.04 $ GeV$ ^{2} $ /fm ($ \chi^{2}/ndf = 0.82 $ ).In addition, to avoid diminishing the QCD NLO correction to the data form of Drell-Yan ratios and better investigate the gluon energy loss in Compton scattering
$ qg\rightarrow q\gamma^{*} $ , we separately calculate the Compton differential cross section ratios$ R_{\rm Fe(W)/C}(x_{\rm F}) $ at 120 GeV. The calculations indicate that the nuclear effects of gluon distributions leading to the rise of Compton scattering rations are obvious and become more important with the increase of$ x_{\rm F} $ and nuclear mass number A. The role of the initial-state gluon energy loss in the suppression of Compton scattering ratios is not very important and disappears with the increase of$ x_{\rm F} $ and nuclear mass number A. The initial-state quark energy loss effect is the dominant effect which induces the suppression of Compton scattering ratios and becomes more significant with the increase of$ x_{\rm F} $ . This mean that it may be feasible to investigate the energy loss of the gluon from a separate calculation of the primary NLO subprocess (Compton scattering) in Drell-Yan production in the small$ x_{\rm F} $ range and at lower incident energy.
Drell-Yan nuclear modification due to nuclear effects of nPDFs and initial-state parton energy loss
- Received Date: 2020-10-26
- Available Online: 2021-04-15
Abstract: By globally analyzing nuclear Drell-Yan data including all incident energies, the nuclear effects of nuclear parton distribution functions (nPDFs) and initial-state parton energy loss are investigated. Based on the Landau-Pomeranchuk-Migdal (LPM) regime, the calculations are carried out by means of analytic parametrizations of quenching weights derived from the Baier-Dokshitzer-Mueller-Peign






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: