Systematic study of two-proton radioactivity within a Gamow-like model

I. INTRODUCTION

• I. INTRODUCTION
• II. THEORETICAL FRAMEWORK
•      A Gamow-like model
•      B Two different empirical formulas
• III. RESULTS AND DISCUSSION
• IV. SUMMARY
• ACKNOWLEDGEMENTS

Two-proton ($2p$) radioactivity, i.e., the spontaneous emission of two protons from the ground state or isomer state of a radioactive nucleus, has become a significant tool in the last decades to shed new light on the nuclear structure information of rich-proton nuclei near or beyond the proton drip line [1-8]. This new decay mode was predicted for the first time in 1960s by Zel’dovich and Goldansky [1-3]. Subsequently, the not true $2p$ radioactivity (i.e., the $2p$ radioactivity released energy $Q_{2p} > 0$ and proton radioactivity released energy $Q_p > 0$) produced by short-lived nuclear resonances was reported [9-14]. With the development of theoretical studies and the improvement of experimental techniques, in 2002, true $2p$ radioactivity ($Q_{2p} > 0$ and $Q_p < 0$) was reported for the first time with the observation of $^{45}$Fe $\to$ $^{43}$Cr +p+p in two independent experiments at GANIL and GSI, respectively [15, 16]. Later on, the $2p$ radioactivity of $^{19}$Mg, $^{48}$Ni, and $^{54}$Zn were also reported in different experiments [17-19]. Recently, in an experiment conducted with the BigRIPS separator at the RIKEN Nishina Center, the $2p$ radioactivity of $^{67}$Kr was observed [20], showing a good agreement with the predictions of possible $2p$ radioactivity candidates by theoretical mass models [21-25]. Moreover, the $2p$ radioactivity of the long-lived isomer $^{94}$Ag$^{\rm m}$, whose parent nucleus has a very large deformation, was observed by Mukha $et\ al$. in an experiment at GSI [26].

Concerning $2{p}$ radioactivity process, owing to the pairing interactions of nucleons, a sequential emission of two protons is impossible. The two protons of this process may be an isotropic emission with no angular correlation or a correlated emission forming $^2$He-like cluster with strongly correlation from the parent nuclei [15, 27-29]. In theory, many models were proposed to study $2p$ radioactivity. These models successfully reproduced the half-lives of $2p$ radioactive nuclei or predicted the possible $2p$ radioactivity candidates, such as the direct decay model [30-34], the simultaneous versus sequential decay model [2, 35], the diproton model [3, 4], and the three-body model, among others [5, 36-39]. Especially, the three-body model treats $2p$ radioactivity process as a three-body problem in which the parent nucleus is composed by two protons and a remnant core. Furthermore, empirical formulas constitute an effective tool to investigate $2p$ radioactivity. These formulas were proposed on the basis of the distinguished Geiger and Nuttal (G-N) law [40], including a four-parameter empirical formula proposed by Sreeja $et\ al.$ [41] and a two-parameter empirical formula proposed by Liu $et\ al.$ [42]. In 2013, based on the Gamow theory, Zdeb $et\ al$. proposed a simple phenomenological model named Gamow-like model that contains a single effective nuclear radius parameter, i.e., $r_{0}$, to investigate $\alpha$ decay and cluster radioactivity [43, 44]. Using this model, the calculated half-lives were found to agree reasonably well with the experimental data. Recently, the Gamow-like model was successfully extended to study proton radioactivity [45]. Essentially, the physical processes of $\alpha$ decay, cluster, and proton radioactivity are similar. They can be easily described as a quantum mechanical tunneling effect in which the emitted particles are different [46-52]. Considering a $2p$ radioactivity process that shares the same theory with $\alpha$ decay, cluster, and proton radioactivity processes, whether the Gamow-like model can be extended to study 2p radioactivity or not is an interesting question. To this end, in this study, we systematically analyzed the half-lives of $2p$ radioactive nuclei with 4 $<$ Z $<$ 36 using the Gamow-like model.

This article is organized as follows. In the next section, the theoretical framework of the Gamow-like model and two different empirical formulas are briefly presented. In Section III, the results are presented and discussed. Finally, a summary is given in Section IV.

II. THEORETICAL FRAMEWORK

• I. INTRODUCTION
• II. THEORETICAL FRAMEWORK
•      A Gamow-like model
•      B Two different empirical formulas
• III. RESULTS AND DISCUSSION
• IV. SUMMARY
• ACKNOWLEDGEMENTS

A Gamow-like model

• I. INTRODUCTION
• II. THEORETICAL FRAMEWORK
•      A Gamow-like model
•      B Two different empirical formulas
• III. RESULTS AND DISCUSSION
• IV. SUMMARY
• ACKNOWLEDGEMENTS

In the framework of the Gamow-like model, the $2p$ radioactivity half-life is evaluated as

where $\lambda$ is a decay constant that can be obtained from

where $S_{2p}$ = $G^2[A/ (A -2)]^{2n}\chi ^2$ is the spectroscopic factor of the $2p$ radioactivity obtained by the cluster overlap approximation [4] with $G^2 = (2n)! / [2^{2n}(n!)^2]$ [53]; $n \approx (3Z)^{1/3}$$-$1 is the average principal proton oscillator quantum number [54]. In this study, $\chi ^2$ is set as 0.0143, according to a previous study by Cui $et\ al.$ [55]. $\nu$, i.e., the frequency of assaults on the barrier, can be given by the harmonic oscillator frequency present in the Nilsson potential [56],

where h, $\hbar$, $\omega$, and A are the Planck constant, the reduced Planck constant, the angular frequency, and mass number of parent nucleus, respectively.

P, i.e., the Gamow penetrability factor through the barrier, is calculated by the semi-classical Wentzel-Kramers-Brillouin (WKB) approximation and expressed as [57]

where $\mu = m_{2p}m_{d} / (m_{2p} + m_{d}) \simeq 938.3 \times 2 \times A_{d} /A\,{\rm{MeV}}/{\rm{c}}^2$ represents the reduced mass with $m_{2p}$, $m_{d}$, and $A_{d}$ being the mass of the emitted two protons, the residual daughter nucleus, and the mass number of daughter nucleus, respectively. In addition, $E_{k} = Q_{2p}{(A - 2)} / {A}$ denotes the kinetic energy of emitted protons, and $V(r)$ is the total interaction potential between the paired two protons and the daughter nucleus (see Fig. 1), which is written as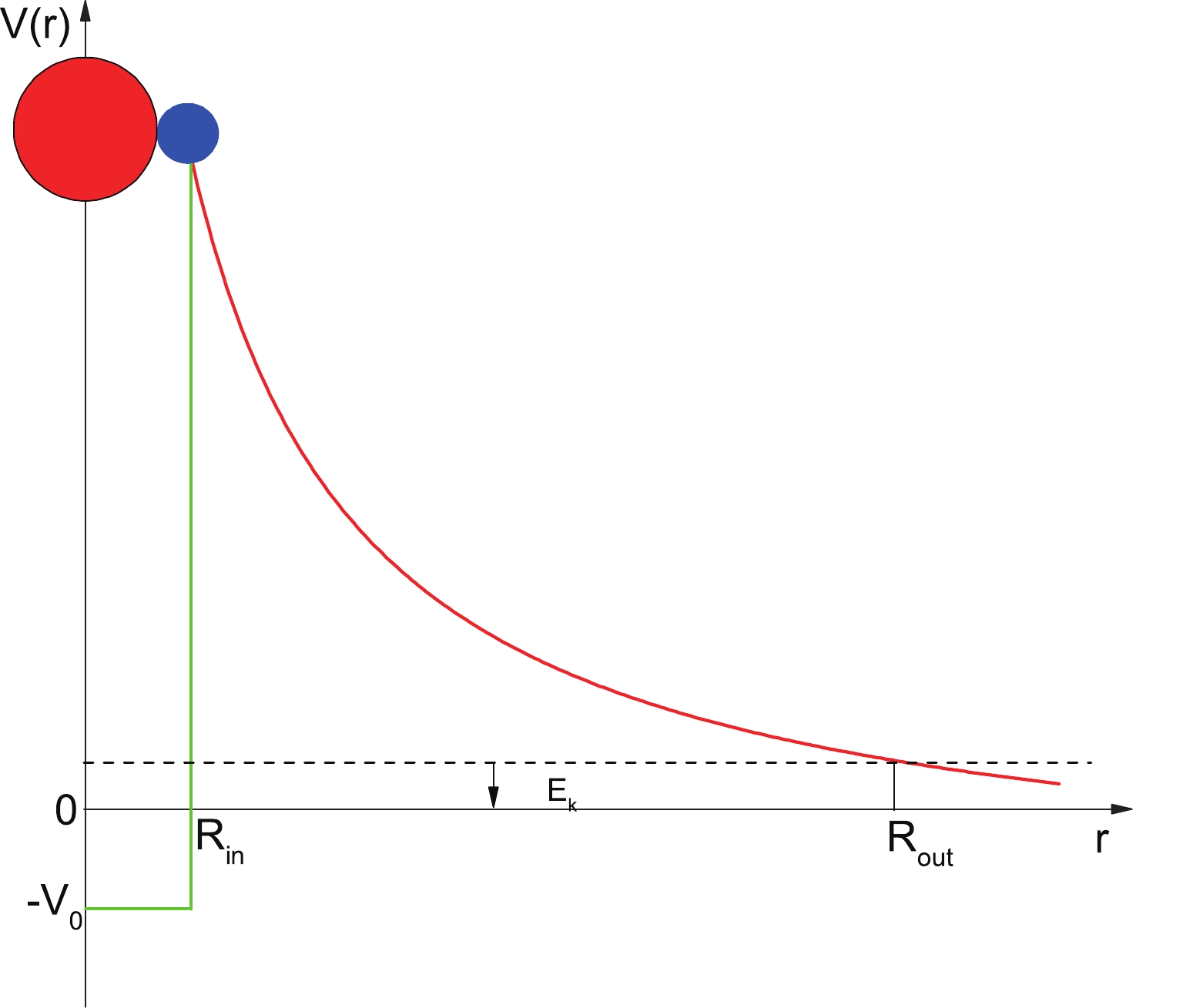

Figure 1

Figure 1.  (color online) Sketch map of interaction potential $V(r)$ versus the distance between the preformed paired two-proton (blue sphere) and the daughter nucleus (red sphere) centers for $2p$ radioactivity.

DownLoad: Full-Size Img PowerPoint

$R_{\rm{out}}$ is the outer turning point from the potential barrier determined by the condition $V( R_{\rm{out}})$ = $E_{k}$; $R_{\rm{in}}$ represents the spherical square well radius, which can be obtained by the sum of the half-width of radial distribution of the proton pair and the radius of the daughter nucleus. It can be expressed as

where $A_{2p} = 2$ is the mass number of the emitted two protons, and $r_{0}$ denotes the effective nuclear radius parameter, which is determined by fitting the experimental data.

In this framework, $V_{0}$ is the depth of the potential well. Moreover, $V_{\rm C}(r) = {2 Z_{d}e^2} / {r}$, which can be obtained under the assumption of a uniformly charged sphere with radius R; r denotes the center-of-mass distance between the paired two protons and the daughter nucleus. Finally, $V_{l}(r) = {\hbar}^2\left(l\,+\, \dfrac{1}{2}\right)^2/{2 \mu r^2}$ is adopted as the Langer modified centrifugal barrier because $l(l + 1)\rightarrow\left(l + \dfrac{1}{2}\right)^2$ , which is a necessary correction for one-dimensional problems [58]; l is the orbital angular momentum taken away by the emitted two-proton.

B Two different empirical formulas

• I. INTRODUCTION
• II. THEORETICAL FRAMEWORK
•      A Gamow-like model
•      B Two different empirical formulas
• III. RESULTS AND DISCUSSION
• IV. SUMMARY
• ACKNOWLEDGEMENTS

1   Sreeja formula

Based on the calculated $2p$ radioactivity half-lives $T_{1/2}$ of 33 nuclei extracted from a study by Goncalves $et\ al.$ [27], Sreeja and Balasubramaniama analyzed the relationship between ${\rm{log_{10}}}T_{1/2}$ and the inverse square root of the $2p$ radioactivity released energy $Q_{2p}^{-1/2}$ corresponding to different angular momenta, l = 0, 2, and 4. Fitting the slopes and intercepts obtained for l = 0, 2, and 4, a unified four-parameter empirical formula was proposed to investigate $2p$ radioactivity, expressed as [41]

where $\xi = Z_{ d}^{\;0.8} / Q_{2p}^{-1/2}$, with $Z_d$ being the charge of daughter nucleus; $a = 0.1578$, $b = 1.9474$, $c = -1.8795$, and $d = -24.847$ are adjustable parameters.

2   Liu formula

In a previous study of ours, based on experimental data and partial calculated results extracted from the aforementioned study by Goncalves $et\ al.$ [27] and considering the contributions of the charge of the daughter nucleus $Z_d$ and the angular momentum l to $2p$ radioactivity half-lives, we proposed a two-parameter empirical formula to study $2p$ radioactivity that can be expressed as [42]

where the adjustable parameters a and b are 2.032 and $-26.832$, respectively. The value of $\beta$ is 0.25, which reflects the effect of different l-values on the 2p radioactivity half-lives.

III. RESULTS AND DISCUSSION

• I. INTRODUCTION
• II. THEORETICAL FRAMEWORK
•      A Gamow-like model
•      B Two different empirical formulas
• III. RESULTS AND DISCUSSION
• IV. SUMMARY
• ACKNOWLEDGEMENTS

In this study, the value of the only one adjustable parameter in Gamow-like model, $r_{0}$, is equal to 1.28 fm as a result of fitting the experimental data of $^{19}$Mg, $^{45}$Fe, $^{48}$Ni, $^{54}$Zn, and $^{67}$Kr. This value is close to that obtained for $\alpha$ decay, cluster radioactivity ($r_{0}$ = 1.20 fm) [43, 44], and proton radioactivity (1.21 fm) [45]. This confirms the rationality of such a value. Below, we systematically calculate the $2p$ radioactivity half-lives of nuclei having experimental data within the Gamow-like model. For comparison, the experimental $2p$ radioactivity half-lives as well as the calculated ones using the effective liquid drop model (ELDM), the generalized liquid drop model (GLDM), and two different empirical formulas are also provided. All the detailed numerical results are presented in Table 1. In this table, the first three columns represent the $2p$ radioactive parent nuclei, the $2p$ radioactivity released energy $Q_{2p}$, and the logarithmical experimental $2p$ radioactivity half-life ${\rm{log}}_{10}T_{1/2}^{\,{\rm expt}}$, respectively. The last five columns represent the logarithmical $2p$ radioactivity half-life calculated by three different theoretical models and two empirical formulas, which are denoted as Gamow-like, ELDM, GLDM, Sreeja, and Liu, respectively. More intuitively, Fig. 2 shows the differences between the calculated $2p$ radioactivity half-lives using the different theoretical models, i.e., Gamow-like, ELDM, and GLDM, empirical formulas of Sreeja and Liu, and the experimental data ${\rm{log}}_{10}T_{1/2}^{\,{\rm calc}} - {\rm{log}}_{10}T_{1/2}^{\,{\rm expt}}$. Note that all the differences for the true $2p$ radioactive nuclei ($^{19}$Mg, $^{45}$Fe, $^{48}$Ni, $^{54}$Zn, and $^{67}$Kr) are basically within $\pm$1, which means that the calculated $2p$ radioactivity half-lives using the Gamow-like model can reproduce the experimental ones for the true $2p$ radioactivity nuclei well.

Table 1

Table 1.  Comparisons between the calculated $2p$ radioactivity half-lives using three different theoretical models, two empirical formulas, and the experimental values. The experimental $2p$ radioactivity half-lives ${\rm{log}}_{10}{{T}}_{1/2}^{\rm{expt}}$ and experimental $2p$ radioactivity released energy $Q_{2p}$ are extracted from the corresponding references.

Nuclei	$Q_{2p}$/MeV	${\rm{log}}_{10}{{T}}_{1/2}$/s
		Expt	Gamow-like	ELDM [27]	GLDM [55]	Sreeja [41]	Liu [42]
$^{6}$Be	1.371 [9]	$-20.30$ [9]	$-19.70$	$-19.97$	$-19.37$	$-21.95$	$-23.81$
$^{12}$O	1.638 [14]	$>-20.20$ [14]	$-18.04$	$-18.27$	$-19.71$	$-18.47$	$-20.17$
	1.820 [2]	$-20.94$ [2]	$-18.30$	$-$	$-19.46$	$-18.79$	$-20.52$
	1.790 [12]	$-20.10$ [12]	$-18.26$	$-$	$-19.43$	$-18.74$	$-20.46$
	1.800 [13]	$-20.12$ [13]	$-18.27$	$-$	$-19.44$	$-18.76$	$-20.48$
$^{16}$Ne	1.330 [2]	$-20.64$ [2]	$-16.23$	$-$	$-16.45$	$-15.94$	$-17.53$
	1.400 [11]	$-20.38$ [11]	$-16.43$	$-16.60$	$-16.63$	$-16.16$	$-17.77$
$^{19}$Mg	0.750 [19]	$-11.40$ [19]	$-11.46$	$-11.72$	$-11.79$	$-10.66$	$-12.03$
$^{45}$Fe	1.100 [16]	$-2.40$ [16]	$-2.09$	$-$	$-2.23$	$-1.25$	$-2.21$
	1.140 [15]	$-2.07$ [15]	$-2.58$	$-$	$-2.71$	$-1.66$	$-2.64$
	1.154 [18]	$-2.55$ [18]	$-2.74$	$-2.43$	$-2.87$	$-1.80$	$-2.79$
	1.210 [59]	$-2.42$ [59]	$-3.37$		$-3.50$	$-2.34$	$-3.35$
$^{48}$Ni	1.290 [60]	$-2.52$ [60]	$-2.59$	$-$	$-2.62$	$-1.61$	$-2.59$
	1.350 [18]	$-2.08$ [18]	$-3.21$	$-$	$-3.24$	$-2.13$	$-3.13$
$^{54}$Zn	1.280 [61]	$-2.79$ [61]	$-0.93$	$-$	$-0.87$	$-0.10$	$-1.01$
	1.480 [17]	$-2.43$ [17]	$-3.01$	$-2.52$	$-2.95$	$-1.83$	$-2.81$
$^{67}$Kr	1.690 [20]	$-1.70$ [20]	$-0.76$	$-0.06$	$-1.25$	$0.31$	$-0.58$

DownLoad: CSV

Show Table

Figure 2

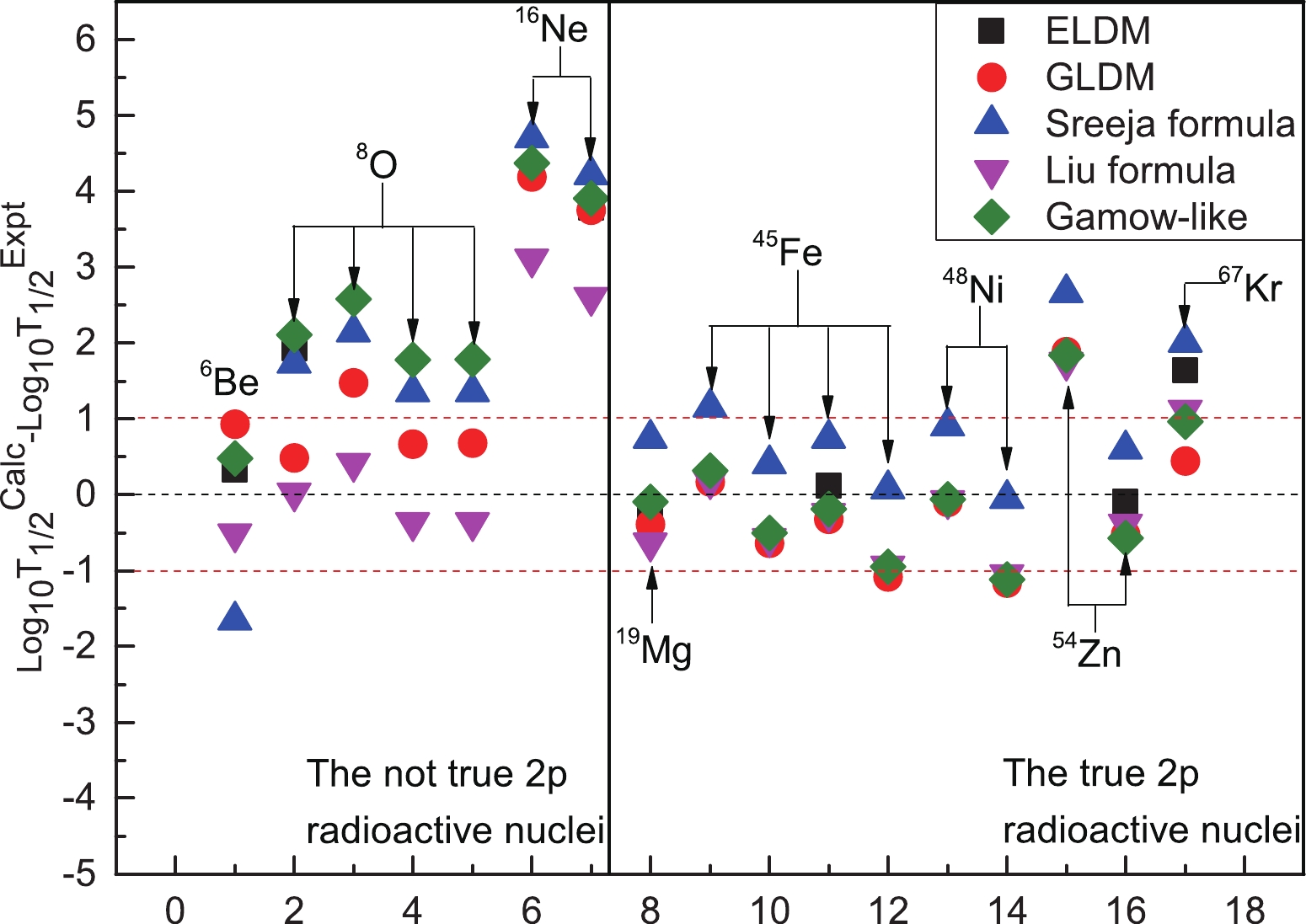
Figure 2.  (color online) Deviations between the calculated $2p$ radioactivity half-lives and the experimental ones for the true $2p$ radioactive nuclei and not true $2p$ radioactive nuclei.

DownLoad: Full-Size Img PowerPoint

To further demonstrate the good agreement between the $2p$ radioactivity half-lives calculated by the Gamow-like model and the experimental data, the standard deviation $\sigma$ was used, which is defined by

Here, ${\rm{log}}_{10}T_{1/2}^{\rm{expt}.}i$ and ${\rm{log}}_{10}T_{1/2}^{\rm{calc.}}i$ represent the logarithmic forms of experimental and calculated $2p$ radioactivity half-life for the i-th nucleus, respectively. The $\sigma$ values resulting from the experimental data are also compared with the calculations using ELDM, GLDM, and two different empirical formulas, according to Eq. (9). All the calculated results are listed in Table 2. From this table, we can clearly see that the $\sigma$ value between the experimental data and the values calculated using the Gamow-like model is smaller than those resulting from using GLDM and the two different empirical formulas. This means that the calculated $2p$ radioactivity half-lives obtained by the Gamow-like model can better reproduce the experimental data of true $2p$ radioactive nuclei. Nevertheless, regarding the short-lived $2p$ radioactive nuclei ($^{6}$Be, $^{12}$O and $^{10}$Ne), the experimental data cannot be reproduced properly, especially for $^{10}$Ne, with a reported $Q_{2p}$ = 1.33 MeV and 1.40 MeV. Note that the differences between the experimental $2p$ radioactivity half-lives and the calculated ones exceed two orders of magnitude. Considering the imperfection of detection technologies and radioactive beam facilities in early experiments, the experimental data may not be accurate enough. Moreover, it is worth noting that several studies have indicated that the nuclear deformation effect or collective mechanisms will affect the $2p$ radioactivity half-lives to some extent. The above factors should be considered in the context of the Gamow-like model, GLDM, and ELDM in future studies [62, 63]. In general, the Gamow-like model can be treated as a new and effective tool to study $2p$ radioactivity.

Table 2

Table 2.  Standard deviation $\sigma$ between the experimental data and the calculated values using different theoretical models and empirical formulas for the true $2p$ radioactive nuclei.

Modelquantity	Gamow-like	ELDM	GLDM	Sreeja	Liu
$\sigma$	0.844	0.531	0.852	1.222	0.967
cases	10	4	10	10	10

DownLoad: CSV

Show Table

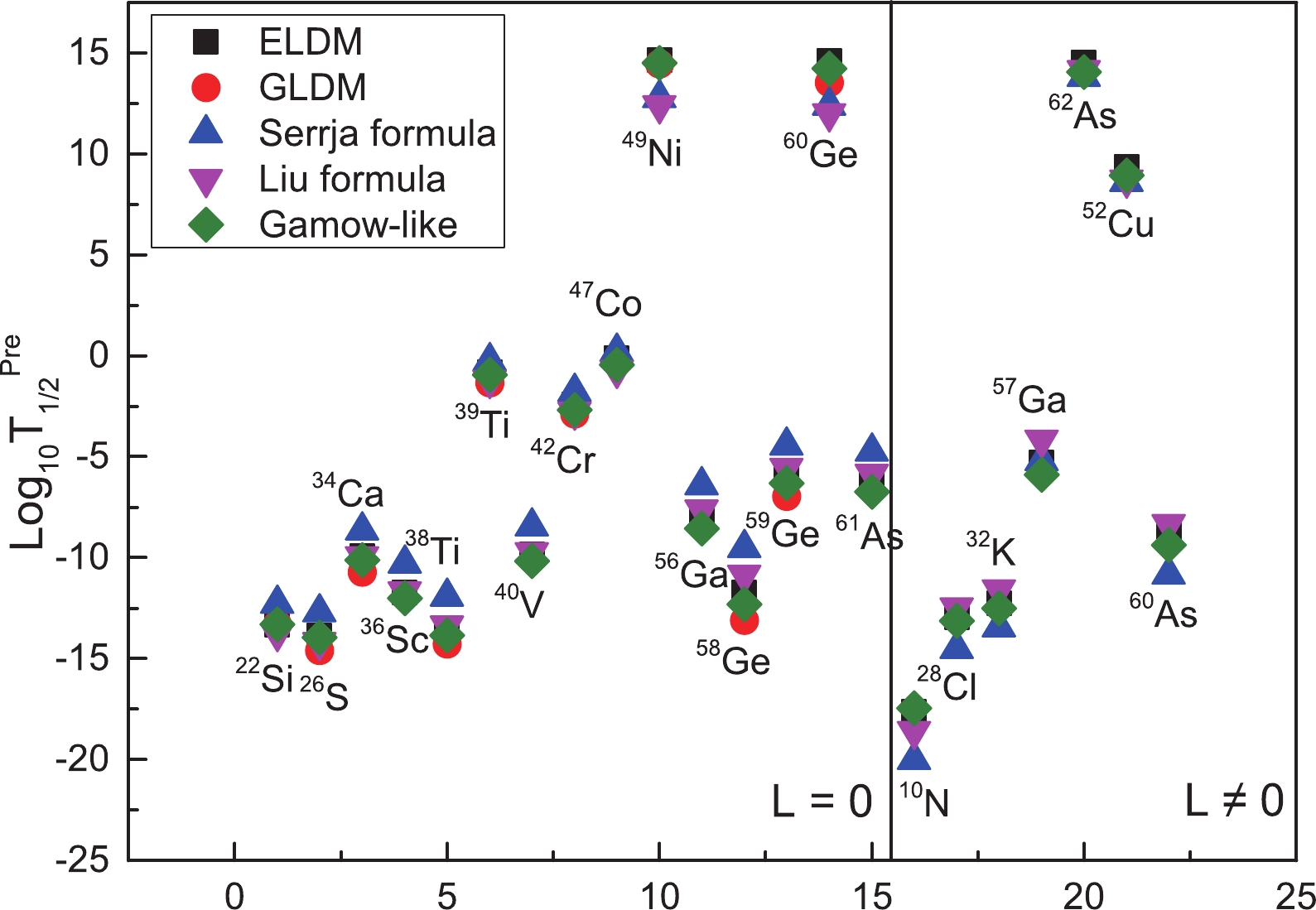
Given the good agreement between the calculated results with the Gamow-like model and the experimental data, as well as other theoretical calculated values, we used this model to predict the half-lives of possible $2p$ radioactivity candidates with $2p$ radioactivity released energy $Q_{2p} > 0$, extracted from the latest evaluated atomic mass table AME2016 [64, 65]. The detailed results are presented in Table 3. For comparison, the predicted results using ELDM, GLDM, and the two different empirical formulas are also presented in Table 3, in which the first three columns denote the possible $2p$ radioactivity candidate, the angular momentum taken away by the emitted two-proton, and the $2p$ radioactivity released energy; they were extracted from a previous study by Gonalves $et\ al.$ [27]. The last five columns represent the predicted $2p$ radioactivity half-lives using the Gamow-like model, ELDM, GLDM, Sreeja formula, and Liu formula, respectively. Note from this table that the predicted results using these models and formulas basically have the same magnitude. Taking $^{22}$Si as an example, the predicted results are $-13.31$, $-13.32$, $-13.30$, $-12.30$, and $-13.73$, respectively. More intuitively, to illustrate the consistency of the predicted results using different models and formulas, we plot the logarithmic predicted half-lives of possible $2p$ radioactivity candidates in Fig. 3. In this figure, the black square, red circle, blue upward triangle, magenta downward triangle, and olive diamond represent the logarithmic form of predicted half-lives of possible $2p$ radioactivity candidates using ELDM, GLDM, Sreeja formula, Liu formula, and Gamow-like model, respectively. Note from this figure that the $2p$ radioactivity half-lives predicted using the Gamow-like model show better agreement with the ones predicted using ELDM in most cases, compared to others models. This further confirms the rationality of the Gamow-like model as a useful tool to study $2p$ radioactivity. Furthermore, the predicted possible $2p$ radioactivity candidates can provide theoretical direction for future experiments.

Table 3

Table 3.  Comparison of the predicted half-lives for possible $2p$ radioactivity candidates whose $2p$ radioactivity is energetically allowed or observed but not yet quantified in NUBASE2016 [66].

Nuclei	$Q_{2p}$/MeV	l	${\rm{log}}_{10}{{T}}_{1/2}^{\rm{Pre}}$/s
			Gamow-like	ELDM [27]	GLDM [55]	Sreeja [41]	Liu [42]
$^{22}$Si	1.283	0	$-13.25$	$-13.32$	$-13.30$	$-12.30$	$-13.74$
$^{26}$S	1.755	0	$-13.92$	$-13.86$	$-14.59$	$-12.71$	$-14.16$
$^{34}$Ca	1.474	0	$-10.10$	$-9.91$	$-10.71$	$-8.65$	$-9.93$
$^{36}$Sc	1.993	0	$-12.00$	$-11.74$		$-10.30$	$-11.66$
$^{38}$Ti	2.743	0	$-13.84$	$-13.56$	$-14.27$	$-11.93$	$-13.35$
$^{39}$Ti	0.758	0	$-0.91$	$-0.81$	$-1.34$	$-0.28$	$-1.19$
$^{40}$V	1.842	0	$-10.15$	$-9.85$		$-8.46$	$-9.73$
$^{42}$Cr	1.002	0	$-2.65$	$-2.43$	$-2.88$	$-1.78$	$-2.76$
$^{47}$Co	1.042	0	$-0.42$	$-0.11$		$0.21$	$-0.69$
$^{49}$Ni	0.492	0	$14.54$	$14.64$	$14.46$	$12.78$	$12.43$
$^{56}$Ga	2.443	0	$-8.57$	$-8.00$		$-6.42$	$-7.61$
$^{58}$Ge	3.732	0	$-12.32$	$-11.74$	$-13.10$	$-9.53$	$-10.85$
$^{59}$Ge	2.102	0	$-6.31$	$-5.71$	$-6.97$	$-4.44$	$-5.54$
$^{60}$Ge	0.631	0	$14.24$	$14.62$	$13.55$	$12.40$	$12.04$
$^{61}$As	2.282	0	$-6.76$	$-6.12$		$-4.74$	$-5.85$
$^{10}$N	1.300	1	$-17.36$	$-17.64$		$-20.04$	$-18.59$
$^{28}$Cl	1.965	2	$-13.11$	$-12.95$		$-14.52$	$-12.46$
$^{32}$K	2.077	2	$-12.49$	$-12.25$		$-13.46$	$-11.55$
$^{57}$Ga	2.047	2	$-5.91$	$-5.30$		$-5.22$	$-4.14$
$^{62}$As	0.692	2	$14.06$	$14.52$		$13.83$	$14.18$
$^{52}$Cu	0.772	4	$8.94$	$9.36$		$8.62$	$8.74$
$^{60}$As	3.492	4	$-9.40$	$-8.68$		$-10.84$	$-8.33$

DownLoad: CSV

Show Table

Figure 3

Figure 3.  (color online) Comparison of the predicted $2p$ radioactivity half-lives using the Gamow-like, ELDM, GLDM, and two different empirical formulas.

DownLoad: Full-Size Img PowerPoint

IV. SUMMARY

• I. INTRODUCTION
• II. THEORETICAL FRAMEWORK
•      A Gamow-like model
•      B Two different empirical formulas
• III. RESULTS AND DISCUSSION
• IV. SUMMARY
• ACKNOWLEDGEMENTS

In the present study, based on the Gamow-like model, the half-lives of two-proton ($2p$) radioactivity nuclei with 4 $<$ Z $<$ 36 were systematically investigated. The only parameter in this model, i.e., the effective nuclear radius, was found to be $r_0$ = 1.28 fm, obtained by fitting the experimental data of $^{19}$Mg, $^{45}$Fe, $^{48}$Ni, $^{54}$Zn, and $^{67}$Kr. This value is close to those for $\alpha$ decay, cluster, and proton radioactivity processes. The calculated results are in good agreement with the experimental data and values calculated using other theoretical models and empirical formulas. In addition, the half-lives of possible $2p$ radioactivity candidates were predicted, with reasonable agreement with other predictions. This study provides a theoretical reference for future experimental studies.

ACKNOWLEDGEMENTS

• I. INTRODUCTION
• II. THEORETICAL FRAMEWORK
•      A Gamow-like model
•      B Two different empirical formulas
• III. RESULTS AND DISCUSSION
• IV. SUMMARY
• ACKNOWLEDGEMENTS

We would like to thank Prof. K. Pomorski, Dr. X. -D. Sun, and J. -G. Deng for useful discussions.

References