New Geiger-Nuttall law for two-proton radioactivity

I. INTRODUCTION

• I. INTRODUCTION
• II. THEORETICAL FRAMEWORK
• III. RESULTS AND DISCUSSION
• IV. SUMMARY
• ACKNOWLEDGEMENTS

In recent years, there has been much work focused on nuclei beyond the proton drip line, due to the fact that they show new phenomena that cannot be found in stable nuclei [1-3]. This includes the two-proton ($2p$) radioactivity phenomenon, which was predicted by Zel'dovich [4] and Goldansky [5, 6] in the 1960s. From the perspective of pairing energy, the two protons emitted in a $2p$ radioactivity process should be simultaneous emission from the ground state of a radioactive nucleus beyond the drip line. However, there is no agreement on whether the two protons are simultaneously emitted as two indepedent protons or as a "diproton emission" similar to the emission of a ²He-like cluster from the mother nucleus. Obviously, for odd-proton-number (odd-Z) nuclei, proton radioactivity is the predominant decay mode. For even-proton-number (even-Z) nuclei lying near the proton drip line, the $2p$ radioactivity phenomenon may occur due to the effect of proton pairing [7]. Experimentally, the probability of the $2p$ decay width of ¹⁶Ne and ¹²O was reported in 1978 [8]. Later, the ground-state true $2p$ radioactivity of ⁴⁵Fe was observed at the Grand Acc$\acute{\rm{e}}$$\rm{l}$$\acute{\rm{e}}$rateur National d'Ions Lourds (GANIL) [9] and Gesellschaft f$\ddot{\rm{u}}$r Schwerionenforschung (GSI) [10], respectively. In 2005, the $2p$ radioactivity of ⁵⁴Zn was detected at GANIL [11], followed by the $2p$ radioactivity of ⁴⁸Ni [12]. In 2007, the $2p$ radioactivity of ¹⁹Mg was revealed by tracking the decay products [13]. Recently, the $2p$ emission of ⁶⁷Kr was observed in an experiment with the BigRIPS separator [14].

Theoretically, various models have been proposed to investigate 2p radioactivity, including the direct decay model [15-21], the simultaneous versus sequential decay model [22], the diproton model [23, 24], and the three-body model [25-28]. Using an R-matrix formula, B. A. Brown et al. reproduced the $2p$ radioactivity half-lives of ⁴⁵Fe [29]. Following this, using the continuum shell model, J. Rotureau et al. microcosmically described the $2p$ radioactivity in ⁴⁵Fe, ⁴⁸Ni and ⁵⁴Zn [30]. In 2017, M. Goncalves et al. used the effective liquid drop model (ELDM) to calculate the half-lives of $2p$ radioactive nuclei [31]. Their calculated results can reproduce the experimental data well [32, 33]. Furthermore, based on the ELDM, they predicted the $2p$ radioactivity half-lives of 33 nuclei with $2p$ radioactivity released energy $Q_{2p} > 0$, obtained from the latest evaluated atomic mass table AME2016 [34, 35]. In 2019, Sreeja et al. proposed a four-parameter empirical formula to study the $2p$ radioactivity half-lives [36]. These parameters were obtained by fitting the predicted results from Goncalves et al. [33]. Their calculated results agree well with the known experimental data. Recently, Cui et al. studied the $2p$ radioactivity of the ground state of nuclei based on a generalized liquid drop model (GLDM) [37], in which the $2p$ radioactivity process is described as a pair particle preformed near the surface of the parent nucleus penetrating the barrier between the cluster and daughter nucleus. In this view, $2p$ radioactivity shares a similar theory to barrier penetration with different kinds of charged particle radioactivity, such as $\alpha$ decay, cluster radioactivity, proton radioactivity and so on [38-43]. In our previous work [44], based on the Geiger-Nuttall (G-N) law [45], we proposed a two-parameter empirical formula for a new G-N law for proton radioactivity, which can be treated as an effective tool to study proton radioactivity. Therefore, whether the G-N law can be extended to study $2p$ radioactivity or not is an interesting topic. In this work, a two-parameter analytic formula, which is related to the $2p$ radioactivity half-life $T_{1/2}$, $2p$ radioactivity released energy $Q_{2p}$, the charge of the daughter nucleus $Z_d$, and the orbital angular momentum l taken away by the two emitted protons, is proposed to study $2p$ radioactivity.

This article is organized as follows. In the next section, the theoretical framework for the new G-N law is described in detail. In Section III, the detailed calculations, discussion and predictions are provided. In Section IV, a brief summary is given.

II. THEORETICAL FRAMEWORK

• I. INTRODUCTION
• II. THEORETICAL FRAMEWORK
• III. RESULTS AND DISCUSSION
• IV. SUMMARY
• ACKNOWLEDGEMENTS

In 1911, Geiger and Nuttall found there is a phenomenological relationship between the $\alpha$ decay half-life $T_{1/2}$ and the decay energy $Q_{\alpha}$. This relationship is the so-called Geiger-Nuttall (G-N) law. It is expressed as:

where a and b represent the two isotopic chain–dependent parameters of this formula. Later, the G-N law was widely applied to study the half-lives of $\alpha$ decay [38, 46-48], cluster radioactivity [49-51] and proton radioactivity [52-54]. However, relative to $\alpha$ decay and cluster radioactivity, the proton radioactivity half-life is more sensitive to the centrifugal barrier. This means that the linear relationship between the half-life of the proton radioactivity and the released energy $Q_p$ only exists for proton-radioactive isotopes with the same orbital angular momentum l taken away by the emitted proton [44, 52, 54]. Similarly, the $2p$ radioactivity half-life may also depend strongly on the $2p$ radioactivity released energy $Q_{2p}$ and the orbital angular momentum l taken away by the two emitted protons. Recently, considering the contributions of $Q_{2p}$ and the orbital angular momentum l to the $2p$ radioactivity half-life, Sreeja et al. put forward a four-parameter empirical formula to study the $2p$ radioactivity half-lives, which is expressed as [36]

where a = 0.1578, b = 1.9474, $c = -1.8795$, and $d = -24.847$ denote the adjustable parameters, which are obtained by fitting the calculated results of the ELDM [33]. Their calculated results can reproduce the known experimental data well.

In our previous work [44], considering the contributions of the daughter nuclear charge $Z_d$ and the orbital angular momentum l taken away by the emitted proton to the proton radioactivity half-life, we proposed a two-parameter empirical formula for a new G-N law for proton radioactivity. This formula is written as:

where $a_{\beta} = 0.843$ and $b_{\beta} = -27.194$ are the fitted parameters. The exponent on the orbital angular momentum l taken away by the emitted proton, $\beta$ , is 1, which is obtained by fitting 44 experimental data points of proton radioactivity in the ground state and isomeric state. Combined with the work from Sreeja et al. [36, 54] and our previous work [44], it is interesting to examine whether or not a two-parameter form of the empirical formula is suitable to investigate $2p$ radioactivity. In this work, because there are no experimental data for $2p$ radioactive nuclei with orbital angular momentum $l \ne 0$, we choose the experimental data for true $2p$ radioactive nuclei (¹⁹Mg, ⁴⁵Fe, ⁴⁸Ni, ⁵⁴Zn and ⁶⁷Kr) with l = 0, and the predicted $2p$ radioactivity half-lives of 7 nuclei with $l \ne 0$ (1 case with l = 1, 4 cases with l = 2 and 2 cases with l = 4) are extracted from Goncalves et al. [33].

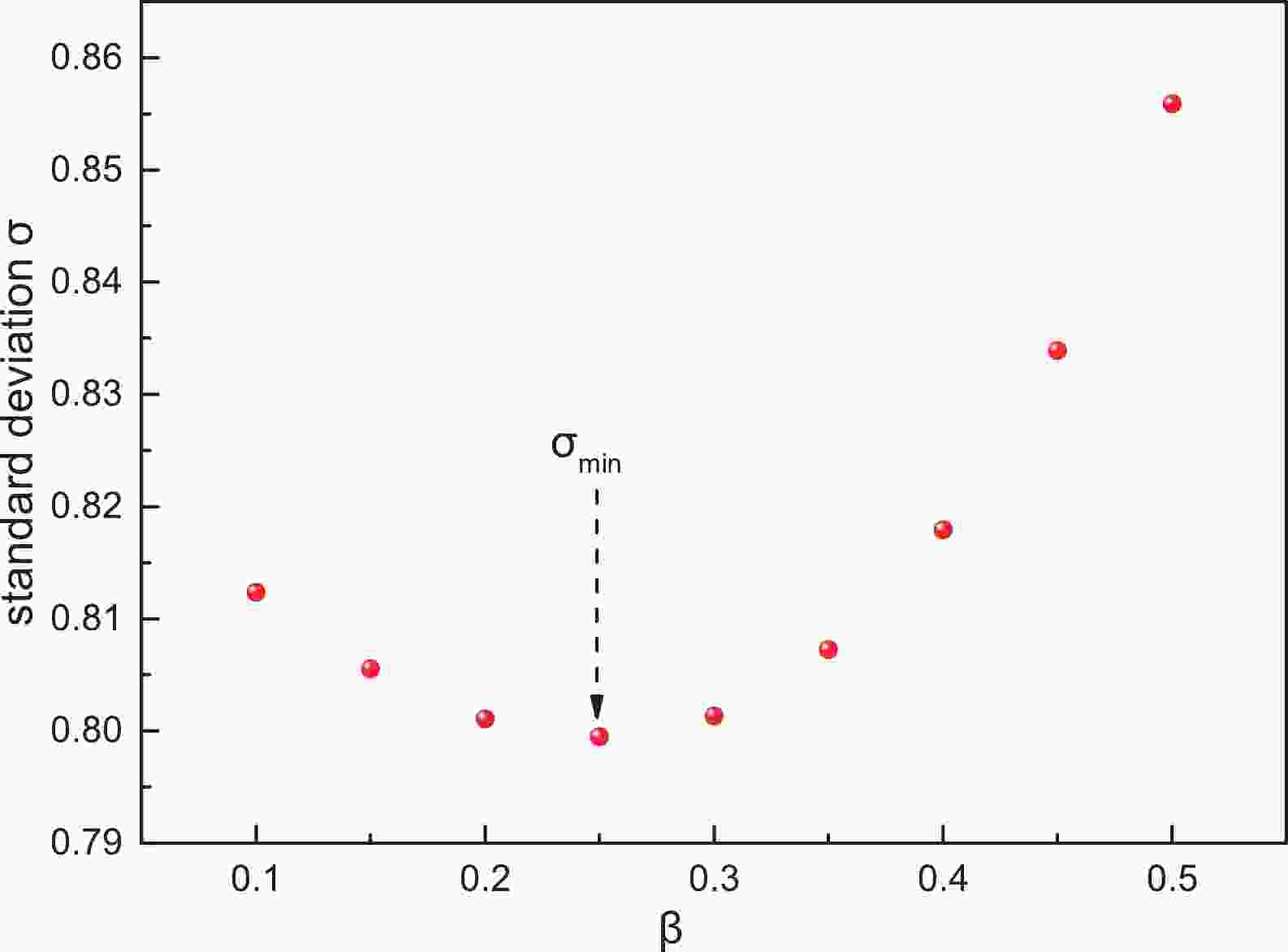
First, for the $\beta$ value describing the effect of l on the $2p$ radioactivity half-life, we choose the $\beta$ value corresponding to the smallest standard deviation $\sigma$ between the database and the calculated $2p$ radioactivity half-lives as the optimal value, with $\beta$ varying from 0.1 to 0.5. The relationship between the $\sigma$ and $\beta$ values is shown in Fig. 1. It is clear that $\sigma$ is smallest when $\beta$ is equal to 0.25. Comparing with the $\beta$ value of Eq. (3) reflecting the effect of l on the proton radioactivity half-life, this $\beta$ value is smaller. The reason may be that the reduced mass $\mu$ of a proton-radioactive nucleus is smaller than that of a $2p$-radioactive nucleus, leading to the contribution of the centrifugal barrier to the half-life of the $2p$-radioactive nucleus being smaller. Correspondingly, the values of parameters a and b are given as:

Figure 1

Figure 1.  (color online) Relationship between the standard deviation $\sigma$ and the value of β.

DownLoad: Full-Size Img PowerPoint

Then, we can obtain a final formula, which can be written as:

III. RESULTS AND DISCUSSION

• I. INTRODUCTION
• II. THEORETICAL FRAMEWORK
• III. RESULTS AND DISCUSSION
• IV. SUMMARY
• ACKNOWLEDGEMENTS

The primary aim of this work is to verify the feasibility of using Eq. (5) to investigate $2p$ radioactivity. The calculated logarithmic half-lives of $2p$-radioactive nuclei are listed in the seventh column of Table 1. Meanwhile, for comparison, the calculated results using GLDM, ELDM and a four-parameter empirical formula are shown in the fourth to sixth column of this table, respectively. In Table 1, the first three columns denote the $2p$-radioactive nucleus, the experimental $2p$ radioactivity released energy $Q_{2p}$ and the logarithmic experimental $2p$ radioactivity half-life ${\rm{log}}_{10}T_{1/2}^{\rm{exp}}$, respectively. For quantitative comparisons between the calculated $2p$ radioactivity half-lives using our empirical formula and the experimental results, the last column gives the logarithm of errors between the experimental $2p$ radioactivity half-lives and those calculated using our empirical formula ${\rm{log_{10}}}HF = {\rm{log}}_{10}{{T}_{1/2}^{\,\rm{exp}}} -{\rm{log}}_{10}{{T}_{1/2}^{\,\rm{cal}}}$. From this table, it can be seen that for the true $2p$-radioactive nuclei ¹⁹Mg, ⁴⁵Fe, ⁴⁸Ni, ⁵⁴Zn and ⁶⁷Kr ($Q_p < 0$, $Q_{2p} > 0$), most values of ${\rm{log_{10}}}HF$ are between -1 and 1. Particularly, for the cases of ⁴⁸Ni, with $Q_{2p}$ = 1.290, and ⁴⁵Fe, with $Q_{2p}$ = 1.154, the values of ${\rm{log_{10}}}HF$ are 0.07 and 0.24, indicating our calculated results can reproduce the experimental data well. As for the sequential or pseudo-$2p$-radioactive nuclei ⁶Be, ¹²O and ¹⁶Ne ($Q_p > 0$, $Q_{2p} > 0$), the values of ${\rm{log_{10}}}HF$ for ⁶Be and ¹⁶Ne are relatively large. Likewise, the differences between the experimental data and the calculated $2p$ radioactivity half-lives using GLDM, ELDM and the four-parameter empirical formula are more than three orders of magnitude. This may be due to the limitations of the early experimental equipment, resulting in the measured decay widths of these $2p$ radioactivity nuclei not being accurate enough. It would be helpful to measure the experimental $2p$ half-lives of these nuclei again in the future. In the case of ¹²O, the values of ${\rm{log_{10}}}HF$ are small, implying that our formula may also be suitable for studying pseudo-$2p$-radioactive nuclei which have relatively accurate experimental data.

Table 1

Table 1.  Comparison of the experimental data for $2p$-radioactive nuclei with different theoretical models (GLDM, ELDM, the four-parameter empirical formula of Ref. [36] and our empirical formula. Experimental data are taken from the corresponding references.

Nucleus	$Q_{2p}^{\rm{\,exp}}$/MeV	${\rm{log_{10}}}{T}_{1/2}^{\exp}$/s	${\rm{log_{10}}}{T}_{1/2}^{{\rm{GLDM}}}$/s [37]	${\rm{log_{10}}}{T}_{1/2}^{{\rm{ELDM}}}$/s [33]	${\rm{log_{10}}}{T}_{1/2}$/s [36]	${\rm{log_{10}}}{T}_{1/2}^{{\rm{This}}\;{\rm{work}}}$/s	${\rm{log_{10}}}$HF
6Be	1.371 [55]	$-20.30$ [55]	$-19.37$	$-19.97$	$-21.95$	$-23.81$	3.51
12O	1.638 [56]	$>-20.20$ [56]	$-19.17$	$-18.27$	$-18.47$	$-20.17$	$>-0.03$
	1.820 [8]	$-20.94$ [8]	$-20.94$	–	$-18.79$	$-20.52$	$-0.42$
	1.790 [57]	$-20.10$ [57]	$-20.10$	–	$-18.74$	$-20.46$	$0.36$
	1.800 [58]	$-20.12$ [58]	$-20.12$	–	$-18.76$	$-20.48$	$0.36$
16Ne	1.33 [8]	$-20.64$ [8]	$-16.45$	–	$-15.94$	$-17.53$	$-3.11$
	1.400 [59]	$-20.38$ [59]	$-16.63$	$-16.60$	$-16.16$	$-17.77$	$-2.61$
19Mg	0.750 [13]	$-11.40$ [13]	$-11.79$	$-11.72$	$-10.66$	$-12.03$	$0.63$
45Fe	1.100 [10]	$-2.40$ [10]	$-2.23$	–	$-1.25$	$-2.21$	$-0.19$
	1.140 [9]	$-2.07$ [9]	$-2.71$	–	$-1.66$	$-2.64$	$0.57$
	1.210 [60]	$-2.42$ [60]	$-3.50$	–	$-2.34$	$-3.35$	$0.93$
	1.154 [12]	$-2.55$ [12]	$-2.87$	$-2.43$	$-1.81$	$-2.79$	$0.24$
48Ni	1.350 [12]	$-2.08$ [12]	$-3.24$	–	$-2.13$	$-3.13$	$1.05$
	1.290 [61]	$-2.52$ [61]	$-2.62$	–	$-1.61$	$-2.59$	$0.07$
54Zn	1.480 [11]	$-2.43$ [11]	$-2.95$	$-2.52$	$-1.83$	$-2.81$	$0.38$
	1.280 [62]	$-2.76$ [62]	$-0.87$	–	$-0.10$	$-1.01$	$-1.75$
67Kr	1.690 [14]	$-1.70$ [14]	$-1.25$	$-0.06$	0.31	$-0.58$	$-1.12$

DownLoad: CSV

Show Table

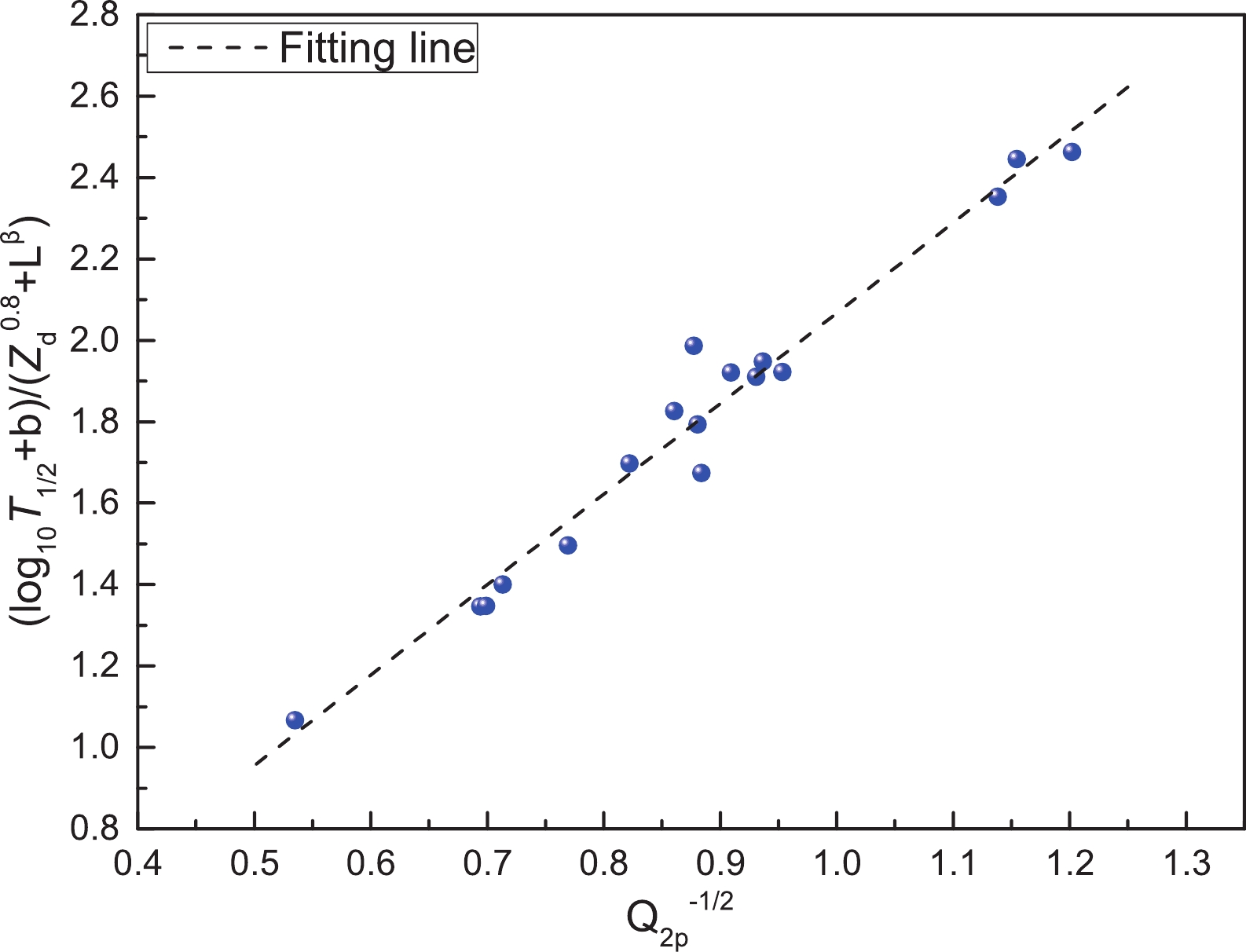
To further test the feasibility of our empirical formula, we also use Eq. (5) to predict the $2p$ radioactivity half-lives of 22 nuclei with $2p$ radioactivity released energy $Q_{2p} > 0$. The $Q_{2p}$ values are taken from the latest evaluated atomic mass table AME2016 and shown in the second column of Table 2. In this table, the first and third columns give the $2p$ radioactivity candidates and the angular momentum l taken away by the two emitted protons, respectively. For a benchmark, the predicted results using GLDM, ELDM and the four-parameter empirical formula, extracted from Refs. [37], [33] and [36] respectively, are also listed in this table. We can clearly see that for $l\ne 0$, the predicted results using our empirical formula are closer to those predicted using ELDM than those predicted using the four-parameter empirical formula. Most of the predicted results are of the same order of magnitude. As an example, in the cases of ²⁸Cl (⁶⁰As), the predicted $2p$ radioactivity half-lives using ELDM, the four-parameter empirical formula and our empirical formula are $-12.95$ ($-8.68$), $-14.52$ ($-10.84$) and $-12.46$ ($-8.33$), respectively. This implies that our empirical formula is also suitable for studying nuclei with orbital angular momentum $l\neq0$. In the case of $l = 0$, the predicted $2p$ radioactivity half-lives using our empirical formula are in good agreement with those from GLDM and ELDM. To further demonstrate the significant correlation between the $2p$ radioactivity half-lives $T_{1/2}$ and the $2p$ radioactivity released energies $Q_{2p}$, based on Eq. (5), we plot the quantity $[{\rm{log_{10}}}{T}_{1/2} + 26.832]/(Z_{d}^{0.8}+l^{\,0.25})$ as a function of $Q_{2p}^{-1/2}$ in Fig. 2. In this figure, there is an obvious linear dependence of ${\rm{log}}_{10}T_{1/2}$ on $Q_{2p}$$^{-1/2}$, while the contributions of charge number $Z_{d}$ and orbital angular momentum l on the $2p$ radioactivity half-lives are removed.

Table 2

Table 2.  Comparison of calculated $2p$ radioactivity half-lives using GLDM, ELDM, the four-parameter empirical formula from Ref. [36] and our empirical formula. The $2p$ radioactivity released energy $Q_{2p}$ and orbital angular momentum l taken away by the two emitted protons are taken from Ref. [33].

Nucleus	$Q_{2p}$/MeV	l	${\rm{log_{10}}}{T}_{1/2}^{{\rm{GLDM}}}$/s [37]	${\rm{log_{10}}}{T}_{1/2}^{{\rm{ELDM}}}$/s [33]	${\rm{log_{10}}}{T}_{1/2}$/s [36]	${\rm{log_{10}}}{T}_{1/2}^{{\rm{This}}\;{\rm{work}}}$/s
22Si	1.283	0	$-13.30$	$-13.32$	$-12.30$	$-13.74$
26S	1.755	0	$-14.59$	$-13.86$	$-12.71$	$-14.16$
34Ca	1.474	0	$-10.71$	$-9.91$	$-8.65$	$-9.93$
36Sc	1.993	0		$-11.74$	$-10.30$	$-11.66$
38Ti	2.743	0	$-14.27$	$-13.56$	$-11.93$	$-13.35$
39Ti	0.758	0	$-1.34$	$-0.81$	$-0.28$	$-1.19$
40V	1.842	0		$-9.85$	$-8.46$	$-9.73$
42Cr	1.002	0	$-2.88$	$-2.43$	$-1.78$	$-2.76$
47Co	1.042	0		$-0.11$	$0.21$	$-0.69$
49Ni	0.492	0	$14.46$	$14.64$	$12.78$	$12.43$
56Ga	2.443	0		$-8.00$	$-6.42$	$-7.61$
58Ge	3.732	0	$-13.10$	$-11.74$	$-9.53$	$-10.85$
59Ge	2.102	0	$-6.97$	$-5.71$	$-4.44$	$-5.54$
60Ge	0.631	0	$13.55$	$14.62$	$12.40$	$12.04$
61As	2.282	0		$-6.12$	$-4.74$	$-5.85$
10N	1.3	1		$-17.64$	$-20.04$	$-18.59$
28Cl	1.965	2		$-12.95$	$-14.52$	$-12.46$
32K	2.077	2		$-12.25$	$-13.46$	$-11.55$
57Ga	2.047	2		$-5.30$	$-5.22$	$-4.14$
62As	0.692	2		$14.52$	$13.83$	14.18
52Cu	0.772	4		$9.36$	$8.62$	8.74
60As	3.492	4		$-8.68$	$-10.84$	$-8.33$

DownLoad: CSV

Show Table

Figure 2

Figure 2.  (color online) The linear relationship between the quantity $[{\rm{log_{10}}}{T}_{1/2} + 26.832]/(Z_{d}^{0.8}+l^{\,0.25})$ and $Q_{2p}$ for the database used to fit the parameters of Eq. (5).

DownLoad: Full-Size Img PowerPoint

IV. SUMMARY

• I. INTRODUCTION
• II. THEORETICAL FRAMEWORK
• III. RESULTS AND DISCUSSION
• IV. SUMMARY
• ACKNOWLEDGEMENTS

In this work, considering the contributions of the charge of the daughter nucleus $Z_{d}$ and the orbital angular momentum l taken away by the two emitted protons, a two-parameter empirical formula of a new Geiger-Nuttall law is proposed for studying $2p$ radioactivity. Using this formula, the experimental data of the true $2p$-radioactive nuclei can be reproduced well. Meanwhile, it is found that the calculated results using our empirical formula are agreement with those from GLDM, ELDM and the four-parameter empirical formula. Moreover, using our formula, the half-lives of possible $2p$ radioactivity candidates are predicted. These predicted results may provide theoretical help for future experiments.

ACKNOWLEDGEMENTS

• I. INTRODUCTION
• II. THEORETICAL FRAMEWORK
• III. RESULTS AND DISCUSSION
• IV. SUMMARY
• ACKNOWLEDGEMENTS

We would like to thank X. -D. Sun, J. -G. Deng, and J. -H. Cheng for useful discussions.

References