-
The widely accepted physical framework, the Standard Model (SM), can explain the fundamental properties of and force between leptons and baryons. It was substantially confirmed after the discovery of the Higgs boson, which breaks the weak isospin symmetry of the electroweak interaction [1]. A theoretical complement of SM extensions [2] has been used to explain the astrophysical observations of evidence for dark matter [3-6], thought to account for a quarter of the universe's total energy density and composed of subatomic particles. A new proposed gauge vector boson is the force mediator of Weakly Interacting Massive Particle (WIMP) annihilations [6]. This boson is expected to be a light neutral spin-1 boson with a small gauge coupling in the MeV/c
$ ^{2} $ to hundred MeV/c$ ^{2} $ mass range via allowed decays into leptons and hadrons [7].The differential cross section for electron Deep Inelastic Scattering (DIS) can be expressed as
$ \frac{{\rm d}\sigma}{{\rm d}\Omega {\rm d}E'} = \sigma_{\rm Mott}[W_{2}(Q^{2},\nu)+2W_{1}(Q^{2},\nu){\rm tan}^{2}(\theta/2)], $

(1) $ \sigma_{\rm Mott} = \frac{\alpha^{2}{\rm cos}^{2}(\theta/2)}{4E^{2}{\rm sin}^{4}(\theta/2)}, $

(2) where
$ \alpha $ is the fine-structure constant, E and$ \theta $ are the incident electron energy and the scattering angle, respectively, and$ W_{1} $ and$ W_{2} $ are form factors. Under the limit of high energy and momentum transfer, the structure function has been found to scale with the form factors of$ F_{1}(x) = mW_{1}(x) $ and$ F_{2}(x) = \nu W_{2}(x) $ , where m and$ \nu $ are the free nucleon mass and the transfer energy in the electron DIS reaction, respectively. The two structure functions are connected to each other by the CallanGross relation [8],$ F_{2}(x) = 2xF_{1}(x) $ . Therefore, the ratio of differential cross-sections depending on x is proportional to that of the structure function$ F_{2}(x) $ . The ratio of the per-nucleon lepton DIS cross section of heavier nuclei to that of deuterium is less than one, known as the EMC effect [9-13], indicates a quenching of nuclear structure functions with respect to those of the isolated nucleon. Structure functions are interpreted as a linear combination of quark distribution functions. The quark distribution corresponding to the EMC effect is essentially altered accordingly. Do the properties of the EMC-effect tagged nucleon, such as its mass, also change remarkably? This is an attractive topic for both the experimental and theoretical sides of nuclear and particle physics. Only a few experimental studies have been carried out because of the extreme difficulty of producing the proper nuclear in-medium state and using an indirect method to deduce the dependent nucleon mass information. It is thus quite interesting to probe the mass of the nucleon and its dependence on the EMC effect in the nucleus via a phenomenological framework based on the quark distribution functions.We mine the world-wide experimental EMC effect data to extract the nucleon mass in light and heavy nuclei using the Bjorken re-scaling method. A reducing trend of the mass of the EMC-effect tagged nucleon with A is clearly exhibited; this can be understood using the model of the release of non-nucleonic components from the nucleon under a configuration with a strong nucleon-nucleon interaction. The detailed description of the analysis process and results are shown in the following sections.
-
The momentum fraction of the quark in the free nucleon is
$ x = Q^{2}/2m\nu $ , where$ Q^{2} = \overrightarrow{q}^{2}-\nu^{2} $ ;$ \overrightarrow{q} $ is the 3-vector momentum transfer in the ($ e, e' $ ) reaction. The nucleon structure functions ($ F_{2}(x) $ ) in the nucleus detected by the charged lepton DIS reaction differ significantly from those measured for the free nucleon, i.e., the EMC effect, which probably indicates the essential modification of the quark distribution in bound nucleons. Therefore, the momentum fraction of quarks in the nucleon in the nucleus is formed as$ x' = Q^{2}/2m^{\ast}\nu $ , resulting from the altered quantity of the nucleon mass in the nucleus, especially the EMC-effect tagged nucleon. An x-rescaling was modeled as$ x' = xm/m^{\ast} = x\eta $ , reflecting the modification of the bound nucleon mass inside the nuclei [14], even though experiments have detected only a momentum-averaged$ m^{\ast} $ for the EMC-effect. The ratio of differential cross sections of the DIS reaction for nuclei and deuterium is approximately equal to their nuclear structure function ratio. The x dependence of$ R(A) = 2F_{2}^{(A)}(x)/AF_{2}^{(D)}(x) $ for different targets was measured previously using the electron DIS reaction [15]. Although$ m^{\ast}/m $ was extracted based on the electron DIS measurements using x-rescaling with the parton model [14],$ F_{2}(x) $ of nuclei were roughly expressed by x parameterizations for the valence quark distribution without gluon and anti-quark considerations [14]. We utilized the modern parton distribution function to analyze the new measured EMC-effect data and obtained a different function for$ m^{\ast}/m $ that depends on$ A^{-1/3} $ . Remarkably, a quantized-mass relationship for the reduced mass of an EMC-effect tagged nucleon and the mass of well-known mesons are observed.To extract
$ m^{\ast}/m $ , the ratio of the nuclear structure function is expressed as [16]$ \begin{aligned}[b] R(x,Q^{2}) =& \frac{F_{2}^{A}(x,Q^{2})}{F_{2}^{D}(x,Q^{2})} = \frac{5(u^{A}+\overline{u}^{A}+d^{A}+\overline{d}^{A})+4s^{A}}{5(u+\overline{u}+d+\overline{d})+4s}\\ &+\frac{3\left(\dfrac{2Z}{A}-1\right)(u^{A}+\overline{u}^{A}-d^{A}-\overline{d}^{A})}{5(u+\overline{u}+d+\overline{d})+4s}, \end{aligned} $

(3) where
$ u, \;\overline{u},\;d,\;\overline{d} $ and s are the parton distributions of the free proton [17], and$ u^{A},\;\overline{u}^{A},\;d^{A},\;\overline{d}^{A} $ and$ s^{A} $ are the nuclear parton distributions [18],$ \begin{aligned}[b] u_{v}^{A}(x) =& w_{u_{v}}(x,A,Z)\frac{Zu_{v}(x)+Nd_{v}(x)}{A},\\ d_{v}^{A}(x) =& w_{d_{v}}(x,A,Z)\frac{Zd_{v}(x)+Nu_{v}(x)}{A},\\ \overline{u}^{A}(x) =& w_{\overline{q}}(x,A,Z)\frac{Z\overline{u}(x)+N\overline{d}(x)}{A},\\ \overline{d}^{A}(x) =& w_{\overline{q}}(x,A,Z)\frac{Z\overline{d}(x)+N\overline{u}(x)}{A},\\ s^{A}(x) =& w_{\overline{q}}(x,A,Z)s(x), \end{aligned} $

(4) where
$ w_{i} $ is a weight function that indicates nuclear modification for type-i parton distribution. Because$ w_{i} $ are x-dependent functions, we let$ w_{i} = 1 $ and utilize$ \eta x $ to replace$ x' $ to describe the nuclear modification.Recently,
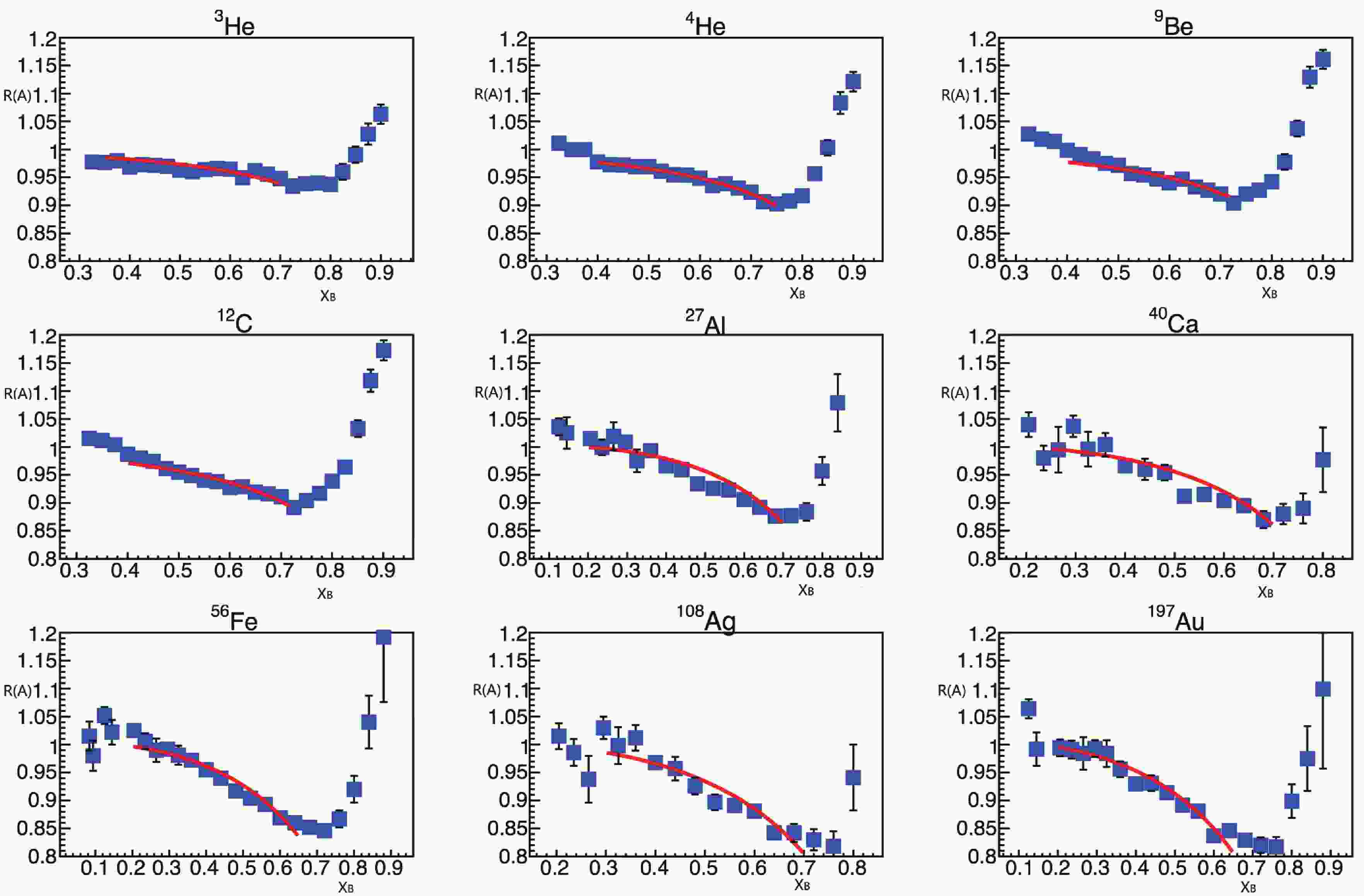
$ R(A) $ of several nuclei were precisely re-measured in the J-Lab [13], and the data were corrected for isoscalar, nuclear Coulomb field, inelastic scattering, and Short Range Correlation (SRC) center-of-mass motion. We carried out the x-rescaling for the new measured$ R(A) $ as$ 2F_{2}^{(A)}(\eta x)/AF_{2}^{(D)}(\eta x) $ and adopted the new parameterization of nuclear parton distributions [18], including valence-, anti-, and sea-quark descriptions for nuclear structure functions [16, 17]; we then performed a fit (Fig. 1) to deduce the only parameter$ \eta $ , i.e.,$ m/m^{\ast} $ . The new$ m^{\ast}/m $ depending on$ A^{-1/3} $ are plotted and fitted with a function of$ m^{\ast}/m = 0.994-0.069{\rm e}^{-4.488A^{-1/3}} $ , as shown in Fig. 2, which differs from the linear function given in Ref. [14]. The nucleon mass reduction is related to the density distributions of the nucleus, which are usually described by a Woods-Saxon type distribution as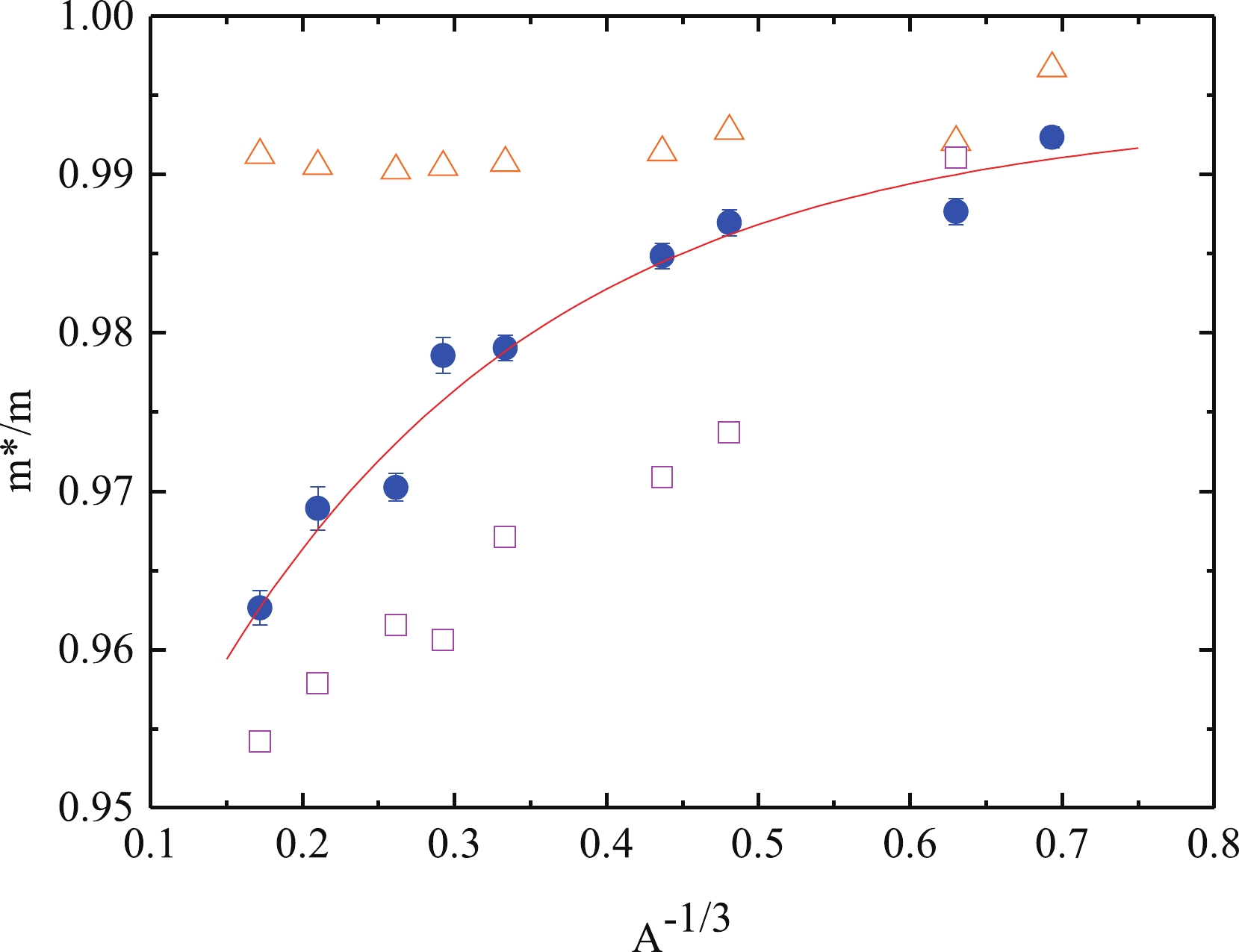
Figure 2. (color online) Ratio of
$ m^{\ast}/m $ depending on$ A^{-1/3} $ : triangles denote the ratio of average per nucleon mass calculated from mean field theory [19] to the free nucleon mass, and solid circles indicate$ m^{\ast}/m $ extracted from$ 2\sigma_{A}/A\sigma_{2} $ experimental data in the range of$ 0.35\leq x \leq0.7 $ to the free nucleon mass [13, 15]. Squares indicate the previous$ m^{\ast}/m $ value [14]. The solid curve is the fitting by the function$ m^{\ast}/m = 0.994- 0.069{\rm e}^{-4.488A^{-1/3}} $ .$ \rho_{\rm ws}(r) = \rho_{0}\left [1+{\rm exp}\left (\frac{r-R}{a}\right )\right ]^{-1}, $

(5) with diffuseness parameter
$ a\sim $ 0.53 fm, where$ \rho_{0}\sim $ 0.17 fm$ ^{-1} $ is the density at the center of the nucleus. The radius parameter R is formed by mass number A as$ R\sim1.10A^{1/3} $ (fm). Therefore, an exponential function was utilized for fitting$ m^{\ast}/m $ depending on$ A^{-1/3} $ .The
$ R(A) $ data after the isospin correction are shown in Fig. 1. The directly measured EMC effect of$ R(A) $ of$ ^{3} $ He is larger than one, and those of the isospin symmetry and neutron rich nuclei are less than one, which indicates an enhancement of the structure function for the proton-excess nucleus and a shrinkage of the structure function for the isospin symmetry and neutron rich nuclei compared with that of the free nucleon.$ R(A) $ is the ratio of the structure function averaged by atomic number A; it reflects the characteristics of the major nucleons. Conversely, the main mass of the nucleon comes from the dynamic motion of quarks and gluon. The variation of the structure function corresponds to the changed mass of the nucleon in the EMC-effect region. Therefore, it is expected that the isospin splitting of the nucleon is$ m^{\ast}_{p}>m^{\ast}_{n} $ for the proton-excess nuclei and the isospin symmetry and neutron rich nuclei in the EMC-effect range of$ 0.35< x < 0.7 $ . -
The existence of a light boson with mass
$ m_{B}c^{2}<20 $ MeV, coupling to baryons of the Higgs boson or the proposed scalar partners of the graviton, would give rise to a force with relatively long-range$ \hbar c/m_{B}c^{2}>10 $ fm [20]. This light boson is possibly produced from a color-singlet cluster formed by sea quarks and gluons in the bound nucleon. The color-singlet cluster might be released from the bound nucleons, rather than the valence quarks that represent the quantum number of nucleons and are confined by the QCD potential. The released color-singlet clusters can exchange momentum within the nucleus. Those clusters are proposed to be the origin of the non-nucleonic components in the nucleus and significantly influence the nuclear effect on the structure function [21]. If the non-nucleonic degree of freedom is combined with the x-rescaling model, a perfect description of the structure function ratio for the isospin scalar nucleus in the region$ x < 0.7 $ can be realized [21].The formation of the color-singlet clusters is only connected with the color distribution and should not be related to the momentum distribution [21]. The parton momentum distribution in the color-singlet clusters can be expressed as
$ P_{i}'(x,Q^{2}) = c_{i}(Q^{2})P_{i}(x,Q^{2}) $ , where$ i = s,g $ indicate sea quarks or gluons, and$ P_{i}(x,Q^{2}) $ are their momentum distribution in the nucleon.$ c_{i} (Q^{2}) $ is the fraction of momentum distribution$ P_{i}(x,Q^{2}) $ in the released cluster. Assuming$ \beta = c_{s}(Q^{2})S+c_{g}(Q^{2})G $ , where$ G = \int_{0}^{\infty} P_{G}(x){\rm d}x $ and$ S = \int_{0}^{\infty}P_{S}(x){\rm d}x $ ,$ \beta $ is$ Q^{2} $ independent. It is easier for the nucleons at the center of the nucleus to produce color-singlet clusters because there are more surrounding nucleons than those on the nuclear surface to supply the nuclear medium environment. Hence,$ c_{i}(Q^{2}) $ is an averaged value, and$ \beta $ becomes larger with increasing A. According to the uncertainty principle, the longitudinal size of a parton would extend over more than one nucleon and participate in the reaction with the neighbor nucleon if x is very small, which results in the shadowing region of$ R(A) $ . The momentum of the nucleus is therefore$ P_{A} = A(1+\beta-\alpha)P_{N} $ , where$ \alpha $ is the fraction of the common parton in the nucleus and$ P_{N} $ is the nucleon momentum distribution. The fraction of parton momentum in the nucleon is$ x' = \frac{P_{\rm parton}}{P_{N}} = \frac{P_{\rm parton}}{P_{A}}\left(\frac{P_{N}}{P_{A}}\right)^{-1}= \frac{Q^{2}}{2M_{A}\omega}A(1+\beta-\alpha) = \eta x, $

(6) $ \eta = (1+\beta-\alpha)Am/M_{A} $ , where$ M_{A} $ is the mass of a nucleus. Hence, the total fraction of the non-nucleonic color-singlet cluster$ (\beta-\alpha) $ in nuclei can be obtained, and its$ A^{-1/3} $ dependence is shown in Fig. 3. The corresponding fitting function is$ 0.0032+0.0901{\rm e}^{-7.1428A^{-1/3}} $ . -
Two nucleons located in a SRC pair imply that their distance r is smaller than that of two normal nucleons inside a nucleus. The range of the relative momentum of the dominant neutron-proton pair is from 1.5 to 5.0 fm
$ ^{-1} $ [9]. Under this condition, the two SRC nucleons are strongly overlapped, and their interaction potential is positive and has a force mediated by$ \omega $ mesons. The effective nucleon mass shows a dip at the relative momentum exactly over the Fermi surface [22]. This minimum mass may result from releasing the color-singlet cluster from the very close SRC nucleons with high local density.The slope of the EMC effect
$ -{\rm d}R_{\rm EMC}/{\rm d}x $ and the scaling factor$ a_{2} $ of SRC have a linear correlation for light and medium nuclei, which implies that both stem from the high local density and large nucleon virtuality ($ \nu = P^{2}-m^{2} $ , where P is the four-momentum). The difference in the free nucleon mass and the EMC-effect tagged nucleon mass ($ \delta_{m} = m-m^{\ast} $ ) is a linear function that depends on the average proton number$ N_{p} $ in the high-momentum region above 2 fm$ ^{-1} $ , as shown in Fig. 4. We calculated the average SRC-proton number for$ ^{3} $ He,$ ^{4} $ He,$ ^{9} $ Be,$ ^{12} $ C, and$ ^{40} $ Ca, with their single nucleon momentum distributions [23], which are obtained from many-body variational Monte Carlo calculations (VMC) using the phenomenological AV18 two-nucleon and Urbana-X three-nucleon potentials (AV18+UX). We also calculated the average SRC-proton number for$ ^{56} $ Fe with Ciofi and Simula's parameterization of momentum distribution [24]. The probability of SRC$ np $ pairs is 20 times that of$ nn $ pairs or$ pp $ pairs above the Fermi momentum. For the isospin symmetry nuclei, the average SRC-proton number$ N_{p} $ is approximately equal to the average SRC-neutron number$ N_{n} $ over 2 fm$ ^{-1} $ . In the case of isospin asymmetry nuclei, especially neutron rich nuclei,$ N_{n} $ is slightly larger than$ N_{p} $ because of the occupation of$ nn $ pairs. Here, we adopt$ N_{p} $ dependence to show the mass of the color-singlet cluster released by the high-momentum SRC proton. As shown in Fig. 4, a linear function$ \delta_{m} = 6.141N_{p}+10.749 $ for fitting, except for$ ^{3} $ He,was found, and the value of 16.890$ \pm $ 0.016 MeV/c$ ^{2} $ was found when$ N_{p} $ is equal to one. This mass quantity is surprisingly consistent with the measurement showing the possible indication of a light neutral boson in$ ^{8} $ Be [25]. The high consistency implies the existence of a light neutral boson with a mass of approximately 16.89 MeV/c$ ^{2} $ , which may be produced by the two close touching correlated nucleon pair and re-absorbed by the two flying away correlated nucleons.
Figure 4. (color online) Mass (
$ \delta_{m} $ ) of the color-singlet cluster depending on the short-range-correlated proton number$ N_{p} $ .The masses of non-nucleonic color-singlet clusters leaked from bound nucleons might be mass-quantized by multiples of the unit 17.35 MeV/c
$ ^{2} $ . A connection is found between Mac Gregor's Constituent Quark mass model and Nambu's empirical mass formula$ M = nm_{\rm e}/4\alpha $ , where n is a positive integer,$ m_{\rm e} $ is the electron mass, and$ \alpha $ is the fine-structure constant [26]. All particles except stable leptons with masses below 1 GeV/c$ ^{2} $ obey this empirical mass criterion, as shown in Fig. 5. If$ n = 1 $ ,$ M = 17.35 $ MeV/c$ ^{2} $ , which is very close to the mass (16.89 MeV/c$ ^{2} $ ) of the color singlet component released by the correlated nucleon pair. As long as$ n = 8 $ , the value of M is similar to the mass of the pion meson. The meson cloud around a nucleon probably consists of the pion meson and the new proposed light neutral boson. The mass quantity in the present study (close to 17.35 MeV/c$ ^{2} $ ) implies that it might be one of the elementary building blocks in nature and probably is a new light vector gauge boson generated in SRC nucleon-nucleon interactions.
Figure 5. (color online) Particle masses M (MeV/c
$ ^{2} $ ) depending on quantum number n: star indicates the present deduced mass of a color-singlet cluster released per proton in the momentum region greater than 2 fm$ ^{-1} $ ; solid circle denotes a particle mass less than 1 GeV/c$ ^{2} $ depending on the quantum number n; the line is the fitting with a linear function for M and n. -
In summary, the mass ratio
$ m^{\ast}/m $ , deduced from the x-rescaling of the ratio of the nuclear structure function in the EMC effect region with the parton model, is interpreted by configuration of the non-nucleonic color-singlet cluster released from the short-distance correlated nucleons inside the nuclei. The mass of the color-singlet cluster is derived from the fitting of the mass difference between the mass$ m^{\ast} $ and free nucleon mass depending on the SRC-proton number$ N_{p} $ . This mass quantity is determined to be 16.890$ \pm $ 0.016 MeV/c$ ^{2} $ , which evidences the possibility of a light neutral boson and quantized mass of matter. -
The authors are grateful for financial support from the China Scholarship Council.
Possible light neutral boson and particle mass quantization
- Received Date: 2020-04-10
- Available Online: 2021-01-15
Abstract: Qualities of nucleons, such as the fundamental parameter mass, might be modified in extreme conditions relative to those of isolated nucleons. We show the ratio of the EMC-effect tagged nucleon mass to that of the free one (





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: