-
Among the fundamental properties of nuclei are the clustering phenomena, i.e., the effects that present themselves with a certain degree of separation of a nucleus into two or more multi-nucleon substructures. These phenomena are exhibited in the internal properties of nuclei and intimately connected with the properties of nuclear reactions with composite particles in entrance and/or exit channels as well as with characteristics of nuclear resonance decay.
The elaboration of a microscopic theoretical method, i.e., starting from a certain NN-potential and considering a nucleus or a two-fragment collision channel as an A-nucleon or an (A1 + A2)-nucleon system, has resulted in the emergence of the resonating group model (RGM) [1, 2]. In succeeding years, a variety of additional theoretical techniques have been developed to study nuclear clustering, such as the generator coordinate method (GCM) [3, 4], microscopic cluster model [5, 6], THSR approach [7-9], antisymmetrized molecular dynamics (AMD) [10], algebraic version of the RGM [11, 12], and cluster-nucleon configuration interaction model [13-16]. In these models, various aspects of clustering phenomena are studied. These methods are adapted for studying cluster effects in light nuclei. It should be noted that most of these methods are based on effective NN-potentials and used for calculation of specific highly clustered states.
Modern high-precision methods for describing both the properties of light nuclei and the characteristics of reactions induced by light nuclei collisions have seen much progress. Such approaches, called ab initio, are based on new possibilities provided by modern high-performance supercomputers. An important role among the methods describing the structure of light nuclei belong to various ab initio methods, such as different versions of the no-core shell model (NCSM) [17-21], Gamov shell model (GSM) [22-24], Green functions Monte Carlo method [25-27], coupled cluster method [28], and lattice effective field theory for multi-nucleon systems [29-31]. These methods are all based on realistic NN-potentials, NNN-potentials, etc. These potentials can be derived from chiral effective field theory [32-34] or from nucleon scattering data using the J-matrix inverse scattering method [35].
In the current work, a new method of this type is developed. It is based on one of the versions of NCSM and a special projecting technique of its wave functions (WFs). The Daejeon16 NN-potential [32], which is built using the N3LO limitation of chiral effective field theory [36] softened by similarity renormalization group (SRG) transformation [37] and the JISP16 NN-potential, based on the inverse scattering method [35], are used. These potentials were tested in large-scale calculations of different properties of nuclei with mass
$ A \leqslant 16 $ , and the results indicated their reliability. Naturally, the more recently reported Daejeon16 potential gives results of higher quality in this mass region because of the more accurate fit of its parameters and a better convergence of the variational procedure. We carry out computations of the eigenvalues and the eigenvectors of discussed Hamiltonians using NCSM. This approach is one of the most advanced and reliable among various ab initio methods. This model is based on solving the A-nucleon Schr${\rm {\ddot o}} $ dinger equation using realistic NN-potentials on the complete basis of totally antisymmetric A-nucleon WFs up to the maximal total number of oscillator quanta$ N^{\rm max}_{\rm tot} $ . The size of this basis, for example, in the widely met M-scheme can sometimes reach values of approximately 109 – 1010 in cases where a modern supercomputer is employed. This method has been used for calculation of the binding and excitation energies characterizing the ground and excited states of nuclei and unstable resonances as well as the nuclear sizes and their electromagnetic observables in several studies.The NCSM model and methods similar to it are, however, not adapted to describe clustering effects, nuclear reactions, and asymptotic properties of nuclei resonances directly. For these purposes, different methods have been proposed. For systems with
$ A \leqslant 5 $ , ab initio description of continuum spectrum states could be based on Faddeev and Faddeev-Yakubovsky equations [38, 39]. Ab initio approaches focused on the discussed problem have also been presented in literature. Among them, the methods that combine the NCSM and RGM, namely the no-core shell model / resonating group model (NCSM/RGM) [40] and no-core shell model with continuum (NCSMC) [41-44], seem to be the most versatile. Examples of a good description of the asymptotic characteristics of the decay channels of the spectra of 7Be and 7Li are presented in [44]. Regarding the NCSMC, fermionic molecular dynamics (FMD) [45-47] offers an ab initio approach focused on the unified description of both bound and continuum states. Another approach – the cluster channel orthogonal functions method (CCOFM) – also employs a basis combining NCSM and orthogonalized cluster-channel WFs [48, 49].Alpha clustering is undoubtedly the most common and important cluster phenomenon. Alpha decay of nuclear resonances is, together with nucleon emission, the most popular decay process in experimental nuclear spectroscopy. Nevertheless, ab initio theoretical calculations of the process are presented in literature by a fairly small number of works. In Ref. [49] the alpha-cluster properties of the rotational band of the 8Be nucleus was studied. The alpha-particle spectroscopic factors (SFs) were presented but not alpha-decay widths. The alpha decay of states of the same band was the subject of Refs. [50-52]. Another version of RGM based on realistic NN-potentials, including the JISP16 (in Ref. [52]), was utilized for calculations involving a basis limited by the maximum total number of oscillator quanta
$N ^{\rm max}_{\rm tot} $ = 12 [50] or 10 [51, 52]. NCSM calculations were also performed, but their results were used for the computation of the decay widths indirectly – as a control method for the results of RGM calculations of the excitation energies and the SFs.In the current study, the binding and excitation energies, as well as the alpha-decay properties of all positive parity states, both clustered and non-clustered, located in a wide range of 8Be nucleus excitation energies, are investigated in a unified scheme. The scheme is based on computation of the Hamiltonian eigenvalues and eigenvectors in the framework of the conventional NCSM involving the complete basis with the cut-off parameter
$N_{\rm max}^{\rm tot} $ = 14 and projection of the resulting eigenvectors onto the WFs of the cluster channels obtained in the framework of the CCOFM. The values obtained in the framework of the projecting procedure, namely the alpha-particle form factors, allow calculation of the decay widths of the states under study. The binding and excitation energies of the states under study, as well as the statistical weights of the components with the isospin T = 1, which are also basic characteristics of the nucleus spectrum, constitute an integral part of the complex of studied objects, together with the alpha-decay widths. -
Let us demonstrate how translationally invariant A-nucleon WFs of an arbitrary two-fragment decay channel with separation A = A1 + A2 are built in the CCOFM. A useful feature of the procedure is that each function of this basis can be represented as a superposition of Slater determinants (SDs). To do so, the technique of so-called cluster coefficients (CCs) is exploited.
The oscillator-basis terms of the cluster channel
$ c_\kappa $ are expressed in the following form:$ \Psi^{c_\kappa} _{{A\,},nl} = \hat A\{\Psi^{\{k_1\}} _{A\,_1 } \Psi^{\{k_2\}} _{A\,_2 } \varphi _{nl} (\vec \rho )\} _{J_cJM_JT} , $

(1) where
$ \hat A $ is the antisymmetrizer;$ \Psi^{\{k_i\}} _{A\,_i} $ is a translationally invariant internal WF of the fragment labelled by a set of quantum numbers$ \{k_i\} $ ; and$ \varphi _{nlm} (\vec \rho ) $ is the WF of the relative motion. The channel WF is labelled by the set of quantum numbers$ c_\kappa \,$ that includes$ \{k_1\},\{k_2\},n,l,J_c,J,M_J,T $ , where J is the total momentum, and$ J_c $ is the channel spin. As mentioned above, the function should be represented as a linear combination of the SDs containing the one-nucleon WFs of the oscillator basis. For this purpose, the two-fragment WF in another representation$ \Psi^{\{k_1,k_2\}} _{{A\,},nlm} = \hat A\{\Psi^{\{k_1\}} _{A\,_1} \Psi^{\{k_2\}} _{A\,_2} \varphi _{nlm} (\vec \rho )\} _{J_c,M_{J_c},M_JT} $

(2) is multiplied by a function of the zero center of mass (CM) vibrations
$ \Phi _{000} (\vec R) $ . Then, the transformation of WFs caused by changing from$ \vec R, \vec \rho $ to$ \vec R_1 ,\vec R_2 $ coordinates – the Talmi-Moshinsky-Smirnov transformation – is performed [53], and WF (2) takes the form$ {{\Phi _{000}}(\vec R)\Psi _{A{\kern 1pt} ,nlm}^{\{ {k_1},{k_2}\} } = \sum\limits_{{N_i},{L_i},{M_i}} {\left\langle {\begin{array}{*{20}{c}} {000}\\ {nlm} \end{array}\left| {\begin{array}{*{20}{c}} {{N_1},{L_1},{M_1}}\\ {{N_2},{L_2},{M_2}} \end{array}} \right.} \right\rangle } } {\hat A{{\Big\{ \Phi _{{N_1},{L_1},{M_1}}^{{A_1}}({{\vec R}_1})\Psi _{A{{\kern 1pt} _1}}^{\{ {k_1}\} }\Phi _{{N_2},{L_2},{M_2}}^{{A_2}}({{\vec R}_2})\Psi _{A{{\kern 1pt} _2}}^{\{ {k_2}\} }\Big\} }_{{J_c},{M_{{J_c}}},{M_J}T}}.} $

(3) The main procedure of this method is the transformation of internal WFs corresponding to each fragment multiplied by non-zero CM vibrations into a superposition of SDs
$ \Phi _{N_i ,L_i ,M_i }^{A_i } (\vec R_i )\Psi^{\{k_i\}}_{A\,_i } = \sum\limits_k {X_{N_i ,L_i ,M_i }^{A_i (k)} \Psi _{A\,_i (k)}^{SD} }. $

(4) Quantity
$ X_{N_i ,L_i ,M_i }^{A_i (k)} $ is called a cluster coefficient (CC). The technique using these objects is presented in detail in [54]. There is a large number of methods elaborated for the calculation of CCs. The most general scheme is based on the method of the second quantization of the oscillator quanta. In this scheme, the WF of the CM motion is presented as$ \Phi _{N_i ,L_i ,M_i }^{A_i } (\vec R_i ) = N_{N_i ,L_i } (\hat{ \vec \mu^{\dagger}})^{N_i - L_i } Y_{N_i ,L_i } (\hat{ \vec \mu^{\dagger}})\Phi_{000}^{A_i} (\vec R_i ), $

(5) where
$ \hat{ \vec \mu^{\dagger}} $ is the creation operator of the oscillator quantum, and$ N_{N_i ,L_i } $ is the norm constant. The creation operator of the oscillator quanta of the CM vibrations is represented as follows:$ \hat{\vec \mu^{\dagger}} = \frac{1}{\sqrt{A}} \sum\limits_{i = 1}^{A} \vec a_{i}^{+}. $

(6) Thus, the CC turns out to be reduced to a matrix element of the tensor operator expressed in terms of
$ \hat{ \vec \mu^{\dagger}} $ :$ < \Psi _{A_i (k)}^{SD} |\Phi _{N_i ,L_i ,M_i }^{A_i } (\vec R_i ) \Psi^{\{k_i\}}_{A_i } > = N_{N_i ,L_i } \left\langle {\Psi _{A\,_i (k)}^{SD} } \right| (\hat \mu ^\dagger )^{N_i - L_i } Y_{N_i ,L_i } (\hat{ \vec \mu^{\dagger}}) \left| {\Phi _{000}^{A_i } (\vec R_i )\Psi^{\{k_i\}}_{A\,_i } } \right\rangle . $

(7) A conventional relationship between the translationally invariant and ordinary shell-model WFs
$ \Psi _{A\,_i }^{\rm shell} = \Psi^{\{k_i\}}_{A\,_i } * \Phi _{000}^{A_i } (\vec R_i ) $

(8) is used as a definition of the former one. The NCSM WFs of the fragments
$ \Psi _{A\,_i }^{\rm shell} $ are involved in the calculations.For the calculations of
$ \Phi _{N_i ,L_i ,M_i }^{A_i } (\vec R_i )\Psi^{\{k_i\}}_{A\,_i } $ WFs with N+1 oscillator quanta along the CM coordinate, the total set of WFs$ \Phi _{N_i ,L_i ,M_i }^{A_i } (\vec R_i )\Psi^{\{k_i\}}_{A\,_i } $ with N oscillator quanta is used in the following set of equations:$ \begin{split} \hat{\mu^{\dagger}_q}| \Phi^{A_i}_{N_iL_iM_i}(\vec R_i) \Psi^{\{k_i\}}_{A\,_i } \rangle =& \frac{1}{\sqrt{A}} \sum \limits_{i = 1}^{A} a^{\dagger}_{iq} \sum \limits_{k} X_{N_i ,L_i ,M_i }^{A_i (k)} \Psi _{A\,_i (k)}^{SD} \\ =&\frac{1}{\sqrt{2L_i+3}} C^{L_iM_i1q}_{(L_i+1)(M_i+q)} < N_i L_i+1\left\Vert \mu^{\dagger} \right\Vert N_i L_i > | \Phi^{A_i}_{N_i(L_i+1)(M_i+q)}(\vec R_i) \Psi^{\{k_i\}}_{A\,_i } \rangle \\&+\frac{1}{\sqrt{2L_i-1}} C^{L_iM_i1q}_{(L_i-1)(M_i+q)} < N_i+1 L_i-1\left\Vert \mu^{\dagger} \right\Vert N_i L_i > | \Phi^{A_i}_{(N_i+1)(L_i-1)(M_i+q)}(\vec R_i) \Psi^{\{k_i\}}_{A\,_i } \rangle. \end{split} $

(9) Using this set of equations and the set of Talmi-Moshinsky-Smirnov coefficients, one can construct WFs
$ \Phi _{000} (\vec R)\Psi^{c_\kappa} _{{A\,},nlm} $ (3). The last step is to construct$ \Psi^{c_\kappa} _{{A\,},n} $ basis WFs for each channel$ c_\kappa $ (2) from a basis of$ \Psi^{\{k_1,k_2\}} _{{A\,},nlm} $ using Clebsch-Gordan coefficients.It should be noted that WFs of terms (1) of one and the same channel
$ c_\kappa $ characterized by the pair of internal functions$ \Psi^{\{k_1\}}_{A_1} $ ,$ \Psi^{\{k_2\}}_{A_2} $ and extra quantum numbers$ l,J_c,J,M_J,T $ are non-orthogonal. Creation of orthonormalized basis functions of channel$ c_\kappa $ is performed by diagonalization of the exchange kernel$ \begin{split} ||N_{nn'} || =& < \Psi^{c_\kappa} _{{A\,},n'}|\Psi^{c_\kappa} _{{A\,},n} > \\ =&< \Psi^{\{k_1\}} _{A_1} \,\Psi^{\{k_2\}} _{A_2} \,\varphi _{nl} (\rho ) |\hat A^2 |\Psi^{\{k_1\}} _{A_1} \,\Psi^{\{k_2\}} _{A_2} \,\varphi _{n'l} (\rho ) > . \end{split} $

(10) The eigenvalues and eigenvectors of this exchange kernel are given by the expressions
$ \varepsilon _{\kappa,k} = < \hat A\{ \Psi^{\{k_1\}} _{A_1} \,\Psi^{\{k_2\}} _{A_2} \,f_l^k (\rho ) \} |\hat 1|\hat A\{ \Psi^{\{k_1\}} _{A_1} \,\Psi^{\{k_2\}}_{A_2} \} \,f_l^k (\rho ) > , $

(11) $ f_l^k (\rho ) = \sum\limits_n {B_{nl}^k \varphi _{nl} (\rho )}. $

(12) As a result, the WF of the orthonormalized basis channel basis
$ c_\kappa $ is represented in the form$ \Psi^{SD,c_\kappa} _{{A\,},kl} = \varepsilon^{-1/2} _{\kappa,k}|\hat A\{ \Psi^{\{k_1\}} _{A_1} \,\Psi^{\{k_2\}}_{A_2} \,f_l^k (\rho ) \} >. $

(13) The statistical weight of the WFs obtained in such a way is a measure of clustering in a certain nuclear state described by WF
$ \Psi_A $ . This value is called the SF or, following the definition proposed in [55], the amount of clustering. It has the form$ S_l^{c_\kappa} = \sum\limits_k<\Psi_A|\Psi^{SD,c_\kappa} _{{A\,},kl}>^2. $

(14) The NCSM basis is complete and therefore contains the discussed clustered components in the form of superpositions of the NCSM WFs. Therefore, the NCSM calculations allow one to determine the cluster SFs and the statistical weights of all other components, which are considered non-clustered.
The cluster form factor (CFF) is a projection of the function of an initial A-nucleon state
$ \Psi_{A} $ onto the WFs of a particular channel$ c_\kappa $ characterized by an arbitrary value of k. It describes the relative motion of subsystems and has the form$ \begin{aligned}[b] \Phi^{c_\kappa}_A(\rho) =& \sum\limits_k\varepsilon^{-1/2} _{\kappa,k}<\Psi _{A}|\hat A\{ \Psi^{\{k_1\}} _{A_1} \,\Psi^{\{k_2\}}_{A_2} \,f_l^k (\rho ) \}>f_l^k (\rho ) \\ = &\sum\limits_k\varepsilon^{-1/2} _{\kappa,k}\sum\limits_{n, n'}B_{nl}^k B_{n'l}^{k} C_{AA_1A_2}^{n'l}\varphi _{nl} (\rho ), \end{aligned} $

(15) where the mathematical object
$ \begin{aligned}[b] C_{AA_1A_2}^{nl} =& < \hat A\{\Psi^{\{k_1\}} _{A_1} \Psi^{\{k_2\}} _{A_2} \varphi _{nl} (\rho ) \} | \Psi _{A} > \\ =&<\Psi^{SD,c_\kappa} _{A, nl}|\Phi _{000} (R)| \Psi _{A} > = <\Psi^{SD,c_\kappa} _{A, nl}|\Psi^{SM} _{A} >, \end{aligned} $

(16) is called the spectroscopic amplitude. Various calculation methods, depending on the masses of the initial nuclei and fragments, are described in [54, 56-58]. The amplitude of the CFF is determined as
$ K_{AA_1A_2}^{nl} = \sum\limits_{k, n'}\varepsilon^{-1/2} _{\kappa,k}B_{nl}^k B_{n'l}^{k} C_{AA_1A_2}^{n'l} . $

(17) The values of the SF and the CFF of channel
$ c_\kappa $ are related by the following relationship$ S_l^{c_\kappa} = \int {|\Phi^{c_\kappa}_A(\rho)|^2 } \rho ^2 {\rm d}\rho , $

(18) and thus,
$ S_l^{c_\kappa} = \sum\limits_k {\varepsilon _k^{ - 1} \sum\limits_{nn'} {C_{AA_1A_2}^{nl} } C_{AA_1A_2}^{n'l} B_{nl}^k } \;B_{n'l}^k . $

(19) The definitions of the CFF (15) and SF (18) are completely equivalent to those proposed in [59] (the so-called "new" SF and CFF). In contrast to the traditional definition, the new SF characterizes the total contribution of orthonormalized cluster components to the WF that is a solution of the Schr
$ {\rm {\ddot o}} $ dinger equation for A nucleons. Reasons for the necessity of its use to describe decays and reactions can be found in [55, 60]. In [14-16], it was demonstrated that the correct definition eliminates a sharp contradiction between theoretical calculations of the cross-sections for knock-out and transfer reactions of$ \alpha $ clusters and experimental data.Compared with the SF, the CFF is a more informative characteristic because it allows matching with the asymptotic WF of the relative motion in the range of validity of the shell-model solution and thus determines the amplitude of the WF in the asymptotic region.
It is convenient to use the CFF for computing the widths of resonances and the asymptotic normalization coefficients of bound states, which in turn are used to calculate the cross-sections of resonant and peripheral reactions, respectively. The CFF in its new definition allows matching with the asymptotic WF at relatively small distances, where the nuclear interaction is negligibly weak, but exchange effects generated by the antisymmetry of the total channel WF are still not negligibly small. This property is very important for dealing with NCSM WFs.
In the proposed approach, a direct matching procedure is applied to calculate the widths of narrow resonances. For such resonances or, more precisely, for those resonances whose small width is due to the low penetrability of the potential barrier, we used a very compact procedure proposed in [61]. This procedure is applicable because for such resonances, there is a sufficiently wide range of distances in which the nuclear attraction is already switched off and, at the same time, the potential barrier is sufficiently high. At any inner point
$ \rho_{\rm in} $ of this area, the relationship between the regular and irregular solutions$ F_l (\eta,k\rho_{\rm in} ) $ and$ G_l (\eta,k\rho_{\rm in} ) $ of the two-body Schr$ {\rm {\ddot o}} $ dinger equation in the WKB approximation has the form$ F_l (\eta,k\rho_{\rm in} )/ G_l (\eta,k\rho_{\rm in} ) = P_l (\rho_{\rm in} ) \ll 1 , $

(20) where
$ P_l (\rho_{\rm in} ) $ is the penetrability of the part of the potential barrier located between the point$ \rho_{\rm in} $ and the outer turning point. The smallness of this penetrability is the condition of applicability of the approximation, where the contribution of the regular solution can be neglected. To determine the position of the matching point of the CFF and irregular WF in this range, we use the condition of equality of the logarithmic derivatives$ \frac{{\rm d}\Phi _A^{c_\kappa } (\rho)/{\rm d}\rho}{\Phi _A^{c_\kappa } (\rho )} = \frac{{\rm d}G_l (\eta,k\rho)/{\rm d}\rho}{{G_l (\eta,k\rho )}}, $

(21) which determines the matching point
$ \rho_{m} $ . Comparison of the values of the CFF and function$ G_l (\eta,k\rho) $ at the matching point allows one to determine the amplitude of the channel WF in the asymptotic region, which takes the form$ \beta G_l (\eta,k\rho) $ , where$ \beta = \Phi _A^{c_\kappa } (\rho _{m})/G_l (\eta,k\rho _{m}). $

(22) As a result, the decay width is given by the expression
$ \Gamma = \frac{{\hbar ^2 }}{{\mu k}}\left [ \frac{{\Phi _A^{c_\kappa } (\rho _{m})}}{{G_l (\eta,k\rho _{m})}}\right ]^2. $

(23) To make the list of the states of a certain nucleus accessible for studies on the discussed scheme wider, large-width resonances are considered in the following way. In the case where a resonance is wide and the penetrability
$ P_l (\rho_{\rm in} ) $ (20) is therefore not small, the width of this resonance is calculated using the simple version of the conventional R-matrix theory, in which the decay width takes the form$ \Gamma = \frac{\hbar^2}{\mu k} (F^2_l (\eta,k\rho_{m} ) + G^2_l (\eta,k \rho_{m} ))^{-1} (\Phi _A^{c_\kappa} (\rho_{m} ))^2. $

(24) Naturally, the use of this version leads to a reduction in the accuracy of the calculated results, but it should be noted that the accuracy of the the data extracted from various experiments, concerning large-width resonances, is also quite limited. That is why the simplified version of the approach turns out to be workable. Thus, the proposed method, together with habitual calculations using the NCSM, allow one to calculate simultaneously nearly all properties of the ground and excited states of light nuclei.
The critical point of the approach is a correct representation of the form of the CFF at distances at which, first, the nuclear interaction is negligible and, second, the "memory" of the exchange effects remains exclusively in the exchange kernel matrix
$ ||N_{nn'} || $ . -
As declared above, the goal of the current study is to simultaneously describe the energies and alpha-decay widths of a large list of positive parity states of the 8Be nucleus. It is important to present special features of the application of the proposed general approach to the stated problem and to justify their need.
First, even large-scale high-precision calculations cannot completely reproduce the data of the spectroscopic tables concerning a certain nucleus. On the one hand, many unknown levels appear in these calculations. Moreover, some well-known states turn out to be "lost", or their energies are significantly shifted, depending on the choice of the NN-potential and/or the size of the basis. To make the pattern of theoretical results more understandable, in the current study, we perform the computations using two well-tested potentials, Daejeon16 [32] and JISP16 [35]. The NCSM calculations of the energies and WFs were carried out using the Bigstick code [62], which is convenient for use on multiprocessor computing clusters.
Second, it is well known that the 0
$ _1^+ $ , 2$ _1^+ $ , and 4$ _1^+ $ states of the 8Be nucleus are strongly clustered. The SFs of the$ \alpha+\alpha $ channel in these states determining the contribution of the channel WFs to the total WFs are found below in Tables 4 and 5. Nevertheless, in our previous work [49], it was demonstrated that the relatively small contribution of non-clustered configurations in the WFs of the clustered states is crucially important for calculating the total binding energies of these states. The ground state of the discussed nucleus was considered as an example. A more detailed illustration of this fact is represented in Tables 1 and 2, where the total binding energies of the 0$ _1^+ $ , 2$ _1^+ $ , and 4$ _1^+ $ states using the NCSM and the cluster basis are shown. For the Daejeon16 NN-potential, the contribution of the$ \alpha+\alpha $ (RGM-like) components of the basis with realistic WFs of 4He clusters to the total binding energy is dominant only for a very short basis. An increase in the basis cut-off parameter results in fast growth of the contribution of the components of different nature (non-clustered ones). For the JISP16 NN-potential, the contribution of the non-clustered components of the basis to the total binding energy is rather large, even with a short basis. The reason for this is that the Daejeon16 interaction is "softer" in the sense of SRG-transformation. This tendency is confirmed by previous results [50], in which a very soft potential with the parameter$ \lambda $ = 1.4 fm$ ^{-1} $ was used, and the difference in the total binding energy of the NCSM and the RGM calculations was found to be not large. Nevertheless, the problem of the total binding energy computation using realistic but not effective NN-potentials cannot be solved in the framework of a pure cluster model. For the excitation energies of the clustered states of nuclei, the situation is somewhat better, but even in such cases, it is difficult to conclude that these results are trustworthy. Obviously, the RGM-like bases, instead of the complete NCSM one, are unusable for investigations of non-clustered and slightly clustered states. That is why we use the full-size NCSM basis for calculation of all values under study: the binding and excitation energies, the CFFs, and the SFs.$J^\pi$ 

model ${{N}}_{\rm max}^{\rm tot} = 4$ 

${{N}}_{\rm max}^{\rm tot} = 6$ 

${{N}}_{\rm max}^{\rm tot} = 8$ 

${{N}}_{\rm max}^{\rm tot} = 10$ 

${{N}}_{\rm max}^{\rm tot} = 12$ 

$0^+$ 

NCSM 22.207 34.930 44.624 49.679 52.247 RGM-like 21.765 23.622 29.755 33.191 − $2^+$ 

NCSM 18.230 30.539 40.650 45.849 48.479 RGM-like − 13.894 21.407 26.258 − $4^+$ 

NCSM 10.160 21.008 31.470 36.723 39.450 RGM-like − − 8.911 13.966 − Table 1. Total binding energies of lower states of 8Be nucleus obtained using the JISP16 potential with
$ \hbar \omega $ = 22.5 MeV.$J^\pi$ 

model ${{N}}_{\rm max}^{\rm tot} = 4$ 

${{N}}_{\rm max}^{\rm tot} = 6$ 

${{N}}_{\rm max}^{\rm tot} = 8$ 

${{N}}_{\rm max}^{\rm tot} = 10$ 

${{N}}_{\rm max}^{\rm tot} = 12$ 

$0^+$ 

NCSM 36.204 46.467 52.169 54.618 55.721 RGM-like 33.999 38.662 44.151 45.723 − $2^+$ 

NCSM 32.901 42.818 48.531 51.071 52.246 RGM-like − 32.311 38.673 41.031 − $4^+$ 

NCSM 25.462 34.085 39.774 42.417 43.784 RGM-like − − 27.913 31.142 − Table 2. Same data as in Table 1 obtained using the Daejeon16 potential with
$ \hbar \omega $ = 15 MeV.Third, various computations performed in the framework of the NCSM demonstrate that a large basis is necessary to reach a convergency of the values of the total binding energies and the excitation energies of light nuclei in the case where the Daejeon16 and JISP16 interactions are studied. That is why the basis cut-off parameter
$ N_{\rm max}^{\rm tot} $ = 14 is exploited in the calculations of the energies and the WFs of the 8Be nucleus. The size of the Slater determinant basis corresponding to$ N_{\rm max}^{\rm tot} $ = 14 is approximately$ 2 \cdot 10^8 $ . The requirements of the basis necessary for an accurate computation of the cluster SFs and CFFs are studied in the current work. Some results of this study concerning the lowest 0$ ^+ $ state of 8Be are illustrated in Table 3. The coefficients (amplitudes)$ K^{nl = 0}_{AA_1A_2} $ of CFF expansion onto oscillator functions are presented in the table. These values indicate that the dominant amplitudes of the CFF mostly converge for the basis cut-off parameter$ N^{\rm max}_{\rm tot} = 12 $ , and the choice of the cut-off parameter$ N_{\rm cl}^{\rm max} $ of the bases of the cluster WFs weakly affects these quantities. Therefore, the channel form factor and channel SF do not noticeably depend on the accuracy of the subsystems description, and amplitudes with a relatively small cluster cut-off parameter$ N_{\rm cl}^{\rm max} $ and large quantum number of relative motion can be used for a better description of the CFF asymptotic range. The use of the large basis cut-off parameter$N_{\rm max}^{\rm tot} $ = 14 to obtain 8Be nucleus WFs is, nevertheless, preferable in the framework of calculations of the decay widths because the matching procedure of the CFF and the asymptotic WF determining a certain decay width requires a realistic description of the former value in the peripheral region. We illustrate this issue below.$N_{\rm tot}^{\rm max}$ 

$N_{\rm cl}^{\rm max}$ 

n=0 n=2 n=4 n=6 n=8 n=10 n=12 n=14 12 0 0.0 0.0 0.785 -0.285 0.195 -0.095 0.040 − 2 -0.113 -0.258 0.819 -0.284 0.210 − − − 4 -0.078 -0.135 0.878 − − − − − 14 0 0.0 0.0 0.761 -0.302 0.223 -0.128 0.071 -0.029 2 -0.107 -0.249 0.795 -0.306 0.243 -0.139 − − 4 -0.0063 -0.237 0.805 -0.322 − − − − Table 3. Amplitudes of the
$ \alpha $ -cluster form factor$ K_{AA_1A_2}^{nl = 0} $ for the ground state of the 8Be nucleus in various bases.Fourth, in the present work, we focus primarily on calculation of the asymptotic properties of 8Be states, namely the alpha-decay widths. For sub-barrier processes, these values are strongly dependent on the decay energy. As demonstrated above, the experimental total binding energies of the 8Be nucleus states are well reproduced for nearly all states (see Tables 4, 5, and 6). However, the decay energy, being a differential quantity, is evidently reproduced with a lower relative precision. Therefore, there is a question of whether the accuracy of NCSM computations achieved so far for the level energy over the decay threshold is satisfactory to determine such decay widths. The
$ \alpha+\alpha $ -decay of the ground state of 8Be is a good subject for analysis. In calculation using the Daejeon16 potential, the total binding energy of$ ^4 $ He is equal to 28.372 MeV, whereas the experimental value is 28.296 MeV. This leads to a difference between the theoretical and experimental resonance energy values for the lowest 0$ ^+ $ state$ \Delta E $ = 335 keV. Such a difference is typical for high-precision calculations of the total binding energy of lower levels of nuclei from the discussed mass region. However, the absolute values of the resonance energy are very different, i.e., 92 keV (value from data tables) and 427 keV (value calculated using the Daejeon16 interaction). Let us consider the effect of the substitution of both quantities into the formulas of the decay width. This effect is illustrated in Fig. 1, showing the behavior of the irregular Coulomb WF$ G_0 (\eta,k\rho_{in} ) $ at the discussed energies. As seen, the substitution of the calculated energy value will result in overestimation of the decay width of the 0$ ^+ $ state by more than two orders of magnitude compared with substitution of the proper experimental value. This effect is not drastic, but it is significant for the 2$ ^+ $ state and negligible for higher excited states. A clear illustration of this is given in Fig. 2, showing the behavior of regular and irregular Coulomb WFs$ F_4 (\eta,k\rho_{\rm in} ) $ and$ G_4 (\eta,k\rho_{\rm in} ) $ at the calculated and experimental energies characterizing the 4$ ^+ $ state ($ \Delta E $ = 270 keV). In fact, the effect is poorly visible, in spite of the fact that the discussed level is placed near the top of the potential barrier. Nevertheless, in the current study, the experimental resonance energies are used where possible. Conversely, Fig. 2 shows that for states with such energies, the regular solutions cannot be neglected.$ J^\pi,\bar T $ 

$ E_{\rm bind} /{\rm{MeV}}$ 

$ E^*_{\rm dae}/{\rm{MeV}} $ 

$ E^*_{\rm exp} /{\rm{MeV}} (T)$ 

SF $ \Gamma_{\rm th} /{\rm{MeV}}$ 

$ \Gamma_{\rm exp}/{\rm{MeV}} $ 

0 $ _1^+,0 $ 

56.25 0.0 0.0 (0) 0.879 7.29 eV 5.57 (6.8)* eV 2 $ _1^+,0 $ 

52.85 3.40 3.03 $ \pm $ 0.01 (0)

0.849 1.17 1.513 4 $ _1^+,0 $ 

44.63 11.62 11.35 $ \pm $ 0.15 (0)

0.792 2.41 3.5 0 $ _2^+,0 $ 

44.54 11.71 − 0.813 8.86 − 2 $ _2^+,0.001 $ 

42.09 14.16 − 0.715 3.57 − 2 $ _3^+,0.971 $ 

39.65 16.59 16.626 $ \pm $ 0.003 (0+1)

0.0025 0.019 0.108 2 $ _4^+,0.078 $ 

39.05 17.19 16.922 $ \pm $ 0.003 (0+1)

0.354 0.416 0.074 4 $ _2^+,0.001 $ 

37.48 18.76 − 0.288 3.39 − 2 $ _5^+,0.065 $ 

35.02 21.22 20.1 $ \pm $ 0.01 (0)

0.0459 0.434 0.8 (1.1) 0 $ _3^+,0.852 $ 

35.01 21.23 20.2 $ \pm $ 0.01 (0)

0.0208 0.056 0.7 ( $ \le $ 1)

0 $ _4^+,0.315 $ 

34.44 21.80 − 0.0610 0.092 − 2 $ _6^+,0.966 $ 

34.27 21.97 − 0.0039 0.002 − 4 $ _3^+,0.007 $ 

34.24 22.00 19.86 $ \pm $ 0.05 (0)

0.441 5.13 0.7 2 $ _7^+,0.028 $ 

33.57 22.70 22.2 (0) 0.059 0.135 0.8 2 $ _8^+,0.996 $ 

33.22 23.02 − 0.001 0.004 − 0 $ _5^+,0.017 $ 

32.91 23.33 − 0.215 1.71 − 4 $ _4^+,0 $ .997

32.69 23.55 − 0.0009 0.009 − $ J^\pi,\bar T $ 

$ E_{\rm bind}/{\rm{MeV}} $ 

$ E^*_{\rm jisp}/{\rm{MeV}} $ 

$ E^*_{\rm exp} /{\rm{MeV}}(T) $ 

SF $ \Gamma_{\rm th} /{\rm{MeV}}$ 

$ \Gamma_{\rm exp}/{\rm{MeV}} $ 

0 $ _1^+,0 $ 

53.77 0.0 0.0 (0) 0.841 6.72 eV 5.57 (6.8)* eV 2 $ _1^+,0 $ 

50.11 3.66 3.03 $ \pm $ 0.01 (0)

0.803 1.08 1.513 4 $ _1^+,0 $ 

41.28 12.50 11.35 $ \pm $ 0.15 (0)

0.729 1.65 3.5 2 $ _2^+,0.987 $ 

37.11 16.66 16.626 $ \pm $ 0.003 (0+1)

0.0003 0.005 0.108 2 $ _3^+,0.038 $ 

36.45 17.33 16.922 $ \pm $ 0.003 (0+1)

0.018 0.305 0.074 0 $ _2^+,0.002 $ 

34.80 18.98 − 0.698 10.45 − 4 $ _2^+,0.002 $ 

33.87 19.91 19.86 $ \pm $ 0.05 (0)

0.022 0.249 0.7 2 $ _4^+,0.008 $ 

33.06 20.72 20.1 $ \pm $ 0.01 (0)

0.166 2.91 0.8 (1.1)* 2 $ _5^+,0.995 $ 

31.87 21.90 − 0.0045 0.079 − 0 $ _3^+,0.986 $ 

31.55 22.23 20.2 $ \pm $ 0.01 (0)

0.0086 0.110 0.7 ( $ \le $ 1)*

2 $ _6^+,0.005 $ 

31.45 22.33 22.2 (0) 0.354 5.53 0.8 2 $ _7^+,0.999 $ 

30.16 23.62 − 0.0008 0.0011 − 0 $ _4^+,0.039 $ 

30.17 23.64 − 0.317 2.48 − 4 $ _3^+,0.999 $ 

29.42 24.36 − 0.00015 0.0026 − 2 $ _8^+,0.004 $ 

28.72 25.06 − 0.270 3.67 − 4 $ _4^+,0.001 $ 

27.58 26,20 − 0.216 3.74 − Table 5. Same data as in Table 4 for the JISP16 potential with
$ \hbar\omega $ = 22.5 MeV.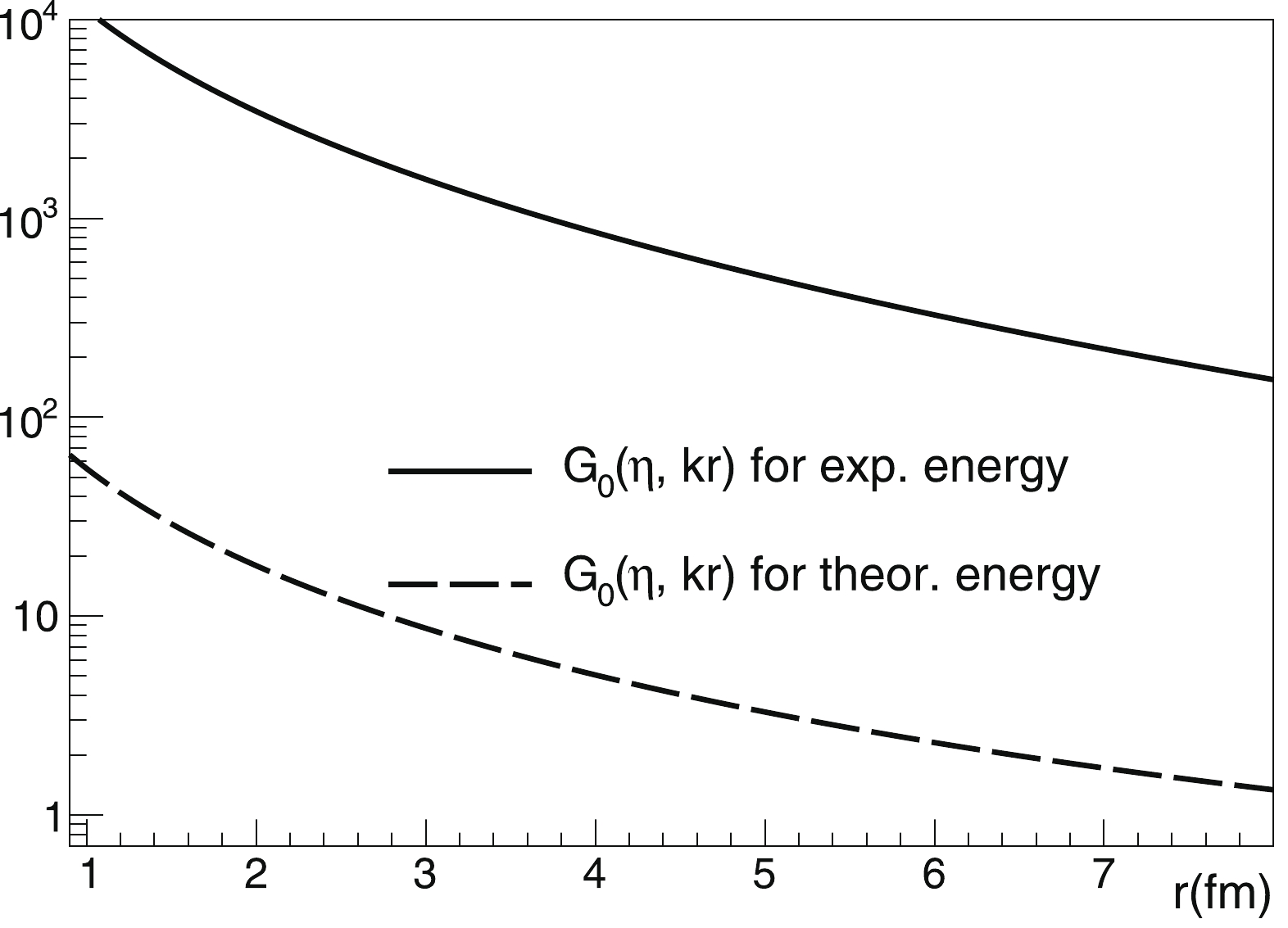
Figure 1. Asymptotic irregular WFs of the
$\alpha+\alpha$ channel for experimental and theoretical decay energies of the 0$_1^+$ state of the 8Be nucleus.
Figure 2. (color online) Asymptotic regular and irregular WFs of the
$\alpha+\alpha$ channel for the 4$_1^+$ state of the 8Be nucleus.$J^\pi$ 

$\bar T_{\rm dae}$ 

$\bar T_{\rm jisp}$ 

$E^*_{\rm dae}/{\rm{MeV}}$ 

$E^*_{\rm jisp}/{\rm{MeV}}$ 

$E^*_{\rm exp}/{\rm{MeV}}(T)$ 

1 $_1^+$ 

0.994 0.996 18.01 18.43 17.640 $\pm$ 0.010 (1)

3 $_1^+$ 

0.993 0.998 18.89 19.36 19.07 $\pm$ 0.03 (1)

1 $_2^+$ 

0.036 0.020 19.14 19.72 18.150 $\pm$ 0.004 (0)

3 $_2^+$ 

0.023 0.007 19.72 20.46 19.235 $\pm$ 0.010 (0)

1 $_3^+$ 

0.992 0.997 21.13 22.46 − 1 $_4^+$ 

0.020 0.008 21.33 21.64 − 3 $_3^+$ 

− 0.007 − 23.82 − 1 $_5^+$ 

0.994 0.997 23.31 24.36 24.038 Table 6. Values of the isospin and the excitation energy for the states with abnormal parity for the Daejeon16 and JISP16 potentials.
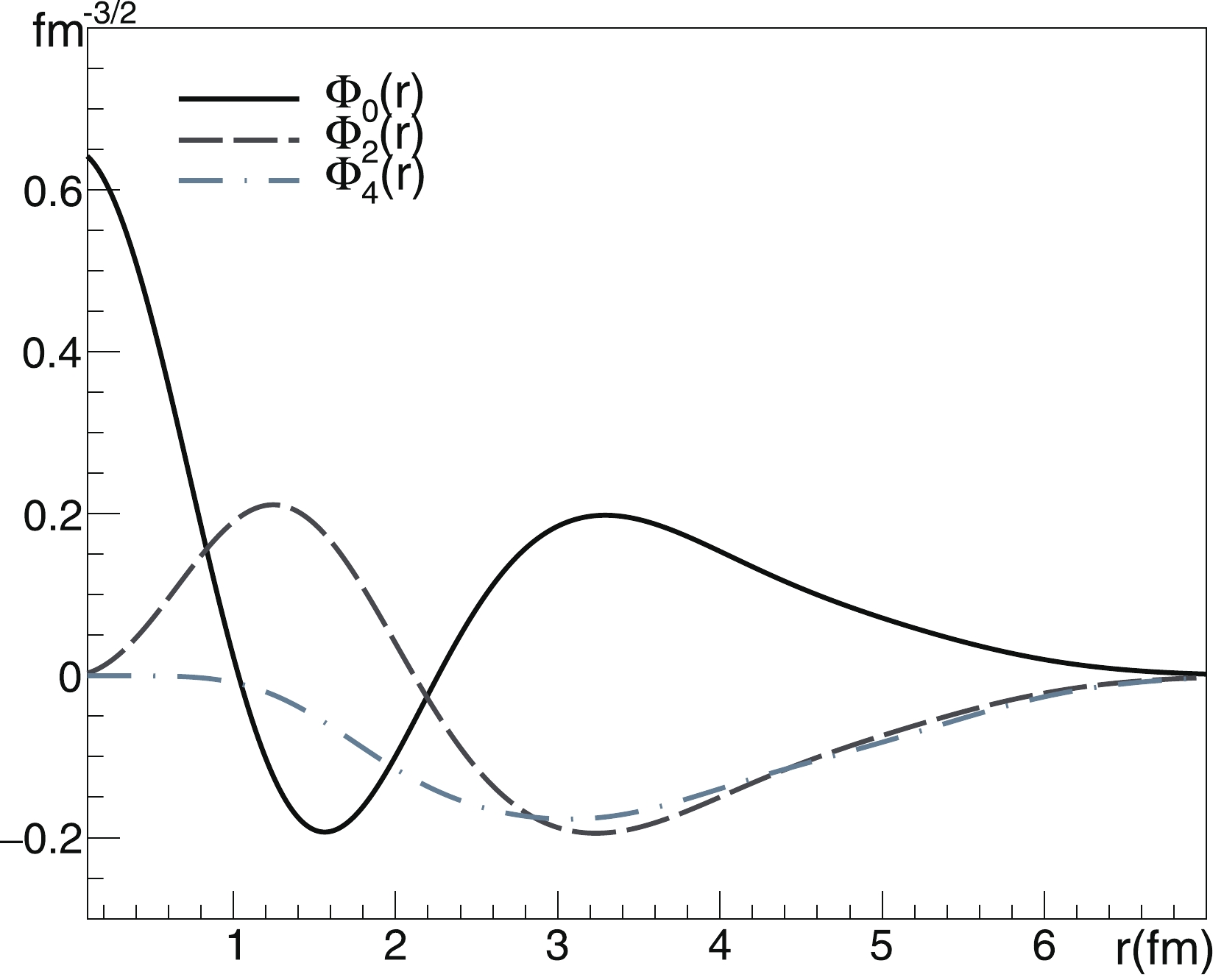
It would be beneficial to present some peculiarities of the matching procedure in use. The CFFs as functions of distance between the CMs of the
$ \alpha $ clusters for the states 0$ _1^+ $ , 2$ _1^+ $ , and 4$ _1^+ $ of the 8Be nucleus computed using the Daejeon16 NN-potential are presented in Fig. 3. The outer maxima of all these functions are located in the range 3.0$ \div $ 3.4 fm. To determine the decay widths, these functions should be matched with the asymptotic solution. For the first two, the conditions (20) and (23) are valid. For the third one, the width is determined by expression (24).The procedure for calculation of the decay channel asymptotic properties was discussed above (see Eqs. (20) – (24)). The matching of the asymptotic solution with the CFF is performed in the coordinate space, so the CFF as a function of relative motion is defined. An example demonstrating the difference in the form of the CFFs obtained using the Daejeon16 and JISP16 NN-interactions is presented in Fig. 4. The ground state of the 8Be nucleus is considered. The outer maxima of the curves differ by approximately 0.4 fm. As we demonstrate below, such a noticeable difference in the shape of the functions does not necessarily result in a significant difference in the decay widths.
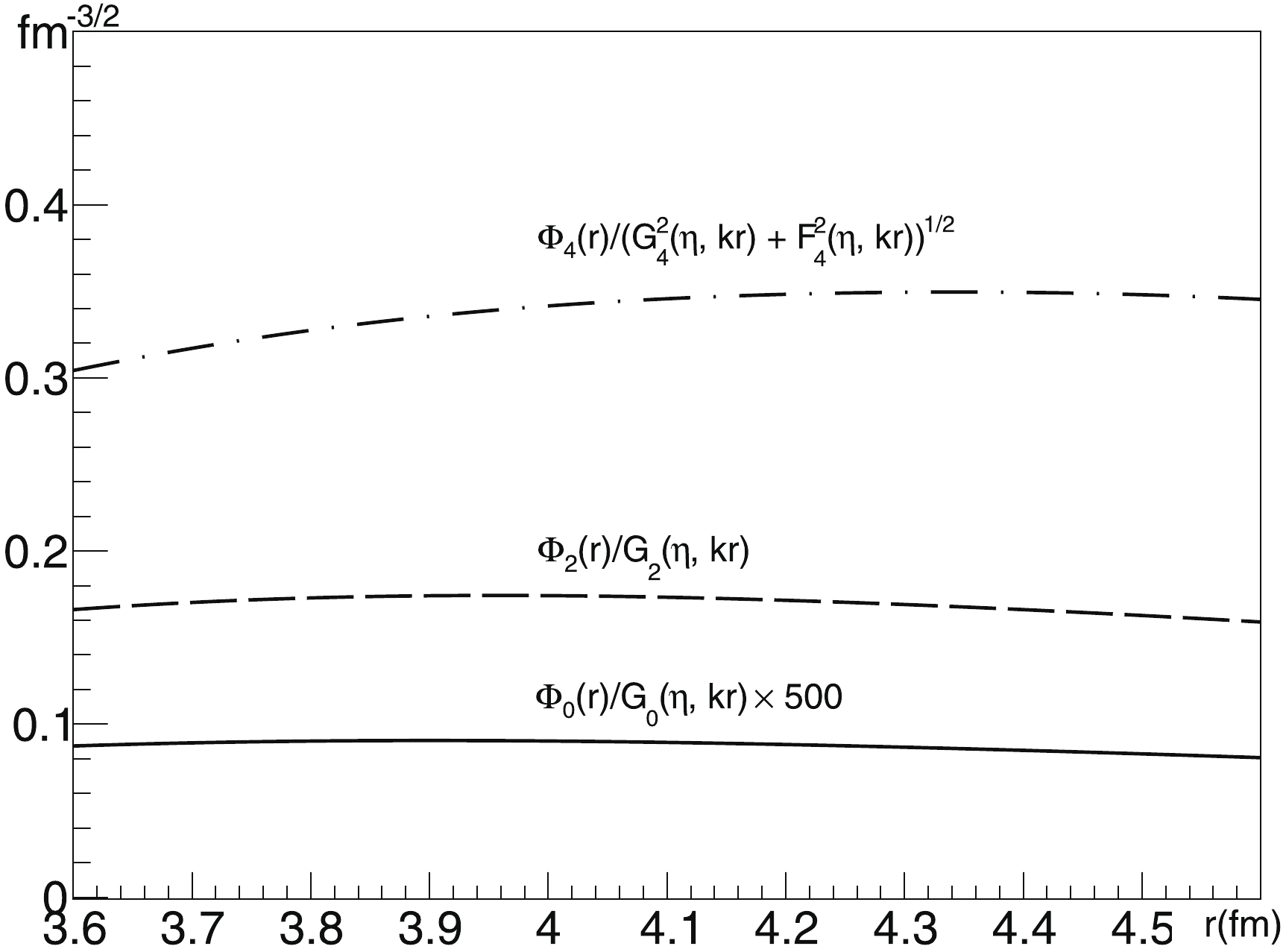
The reliability of the matching procedure may be tested by analysis of the behavior of the ratio of the CFF to the asymptotic WF
$ \Phi _A^{c_\kappa } (\rho_{m})/G_l (\eta,k\rho _{m}) $ or the corresponding ratio from Exp. (23) near the matching point. In Fig. 5, the discussed behavior for the lowest 0$ ^+ $ , 2$ ^+ $ and 4$ ^+ $ states is depicted. The matching points characterizing the decay process of these states turn out to be located at the distances 3.92, 3.96, and 4.34 fm, respectively. As evident from the figure, all of these ratios vary only slightly near their matching points. The behavior shown here provides reason enough to conclude that the CFF computed in the framework of the chosen NCSM basis takes the form of the asymptotic WF in the presented range of distances. In other words, the required asymptotic WF is achieved. Minor variations in the asymptotic WFs with a change in the decay energy$ \Delta E $ = 270 keV (see Fig. 2), together with the stability of the discussed ratio in the vicinity of the matching point, properly confirm the reliability of the procedure used in the current work to calculate the alpha-decay widths. -
In the framework of the presented scheme, the computations of the total binding and excitation energies, statistical weights of the components with the isospin
$ T = 1 $ , and alpha-decay widths of the positive parity states of the 8Be nucleus with excitation energies ranging up to approximately 25 MeV were carried out. Thus, it seems reasonable to qualify the current work as an effort to describe an almost complete set of spectroscopic data related to the discussed states theoretically. The results of the computations are presented in Tables 4, 5, and 6. The experimental data for all levels whose spin and parity are determined are also shown.As the data in Table 4 suggest, the calculations based on the Daejeon16 NN-potential reproduce the experimental value of the total binding energy of the ground state of the discussed nucleus
$ E_{\rm b} = 56.50 $ MeV with high precision. Regarding the total binding energy of the ground state of the 8Be nucleus calculated using the JISP16 NN-potential (see Table 5), this value is 2.73 MeV less than the experimental one. It is known that the values of the total binding energies of nuclei from the the mass region A$ \sim 8 $ more or less close to the experimental ones may also be achieved in the calculations with the second mentioned potential. However, for that, it is necessary to, first, exploit a supercomputer and, second, extrapolate the values obtained for a number of different values of$ \hbar\omega $ to higher values of the basis cut-off parameter N$ _{\rm max}^{\rm tot} $ using a special technique. Therefore, the Daejeon16 potential has the advantage of more rapid convergence of the total binding energy.Consideration of the excitation energies of the 8Be nucleus states themselves indicates very good agreement of the results obtained using the Daejeon16 potential (
$ E^*_{\rm dae} $ ) and the JISP16 interaction ($ E^*_{\rm jisp} $ ) with each other as well as agreement of those with the tabulated experimental data$ E^*_{\rm exp} $ . For levels of abnormal parity 1$ ^+ $ and 3$ ^+ $ , this is evident from Table 6. Just two quantities obtained using the JISP16 potential$ E^*_{\rm jisp} $ differ by more than 1 MeV from the experimental ones. There is no example of such a difference among the results of the Daejeon16-based calculations. In general, a moderate advantage of the latter approach is seen in the smaller root-mean square deviation from the experiment. The discussed table shows that the excitation energies of the predicted states with abnormal parity for the two exploited interactions differ by approximately 1 MeV or less. Only one state of this parity predicted by JISP16-based computations (3$ _3^+ $ ) is not reproduced by Daejeon16-based ones.The excitation energies of normal-parity states of the 8Be nucleus contained in various nuclear data tables are presented in the fifth columns of Tables 4 and 5. At first glance, it is easy to establish one-to-one correspondence between each of these states and any state obtained in the framework of the computations performed using the Daejeon16 NN-potential or the JISP16 interaction, as presented in Tables 4 and 5. Moreover, both these interaction models result in a good quantitative agreement between the theoretical and experimental data. There are three examples of significant but not critical discrepancies of the energy values for Daejeon16-based investigations: approximately 1 MeV, for levels 0
$ _3^+ $ and 2$ _5^+ $ , and more than 2 MeV, for level 4$ _3^+ $ . A similar pattern characterizes JISP16-based investigations: a difference of approximately 1 MeV is observed for level 4$ _1^+ $ and more than 2 MeV for level 0$ _3^+ $ . As is the case in consideration of the abnormal parity states, a modest advantage for the Daejeon16-based approach is seen. Some levels predicted in each of the discussed approaches allow one-to-one correspondence to be established among them. Indeed, a good correlation of the excitation energies of the levels with identical quantum numbers predicted by the Daejeon16-based and JISP16-based approaches is respectively exhibited for four examples: 2$ _6^+ \leftrightarrow 2_5^+ $ , 2$ _8^+ \leftrightarrow 2_7^+ $ , 0$ _5^+ \leftrightarrow 0_4^+ $ , and 4$ _4^+ \leftrightarrow 4_3^+ $ .Naturally, the isospin quantum number is a good identifier of nuclear states. Because of that, the statistical weights of the components of WFs with isospin
$ T = 1 $ are also calculated. They are presented in Tables 4, 5, and 6. In the current work, we prefer to demonstrate the values of multipliers of these components (they are denoted by symbol$ \bar T $ ) but not their squares. All these values are concentrated near zero or unity; therefore, they provide an additional and, as can be seen from Tables 4 and 5, important means to classify the states in a complicated spectrum and establish the correspondence between calculated and measured levels. The information regarding the weights of the components with a certain isospin play an independent role in studies of the Coulomb effect and other exotic effects in nuclei.The duplicated prediction of the states of both normal and abnormal parity in two different approaches (see above), together with a good description of many known levels, gives ground to propose experiments aimed at searching for the predicted states. This proposal appears promising because detection of levels predicted theoretically (perhaps a part of them) would be a verification of the capability of high-precision theoretical approaches in spectroscopic studies of light nuclei. This seems to be especially important in studies of exotic light nuclei.
A major novelty of the presented work is represented by the computations of the alpha-decay widths of all decaying (i.e., normal parity) states of the 8Be nucleus. The values of the alpha-decay widths of various nuclides being measured or calculated are of fundamental importance in low-energy nuclear physics, nuclear spectroscopy in particular. They determine the branching ratios of resonance nuclear reactions with alpha-particles in the entrance or exit channels. The quantities directly connected to them, namely the SFs and asymptotic normalization coefficients on the alpha-cluster channels, play a significant role in the analysis of nuclear fusion and direct nuclear reactions.
Knowledge of the discussed widths helps to determine the quantum numbers of decaying states and thus to build nuclear spectra. In the present section, we demonstrate the capabilities of the approach based on computation of the alpha-decay widths in studies of nuclear spectra, with respect to the example of the 8Be nucleus. The experimental data for the total decay widths are contained in the last columns of Tables 4 and 5. The thresholds of proton and neutron decay of the 8Be nucleus are located at the energies
$ S_p = 17.26 $ and$ 18.90 $ MeV, respectively. Thus, the alpha-decay width of a lower level coincides with the total width. For higher levels, the total widths presented in the spectroscopic tables may serve as upper limits of the corresponding alpha-decay widths.The question arises of whether the accuracy of the decay width computations is sufficient to consider a calculated width as reliable and therefore able to serve as an identifier of state characteristics. The tables under discussion demonstrate that sometimes the discrepancy between the values extracted from experiments and the ones obtained theoretically turns out to be several multiples. This discrepancy appears probably as a result of, first, application of the potentials that are not specifically adopted for calculations of the CFFs and, second, the necessity to use the simple version of the R-matrix theory for highly excited states. To answer the question, it is reasonable to take a second look at the range of variation of the widths presented in Tables 4 and 5, both experimental and theoretical. For the calculated values, this range is more than 500 times, even if the cases of the decay of levels with isospin
$ \bar T \sim 1 $ and the special case of the ground state are excluded. The same range is a characteristic of the number of alpha-decay widths extracted from the experiments. Thus, occasional coincidences of the values of the decay widths obtained in calculations and measurements are unlikely. This fact gives reliable grounds to use a procedure for comparison of the theoretically obtained and experimentally extracted decay widths to search for a correspondence between certain states. It is interesting to note that sometimes even the SF (these values are presented in the fifth columns of Tables 4 and 5) turns out to be a satisfactory identifier of a state because the SF values and decay widths are rather strongly correlated.This comparison offers complementary possibilities for analyzing various nuclear spectra, the 8Be nucleus spectrum in particular. The analysis of the data obtained in the Daejeon16-based calculations leads to the following conclusions. The great decay width of the state 4
$ _3^+ $ (5.13 MeV), which is much greater than the total decay width of the known 19.96 MeV state, in addition to the rather large discrepancy in the excitation energy, is evidence that the identification of this state is most likely incorrect. Therefore, the 4$ _3^+ $ state presented in the spectroscopic tables is not reproduced in the Daejeon16-based calculations, in contrast to the JISP16-based ones. A modest disadvantage of the discussed potential manifests itself in overestimation of the alpha decay width of the 2$ _4^+ $ level and underestimation of the width of the 2$ _3^+ $ state. The decay-width test confirms good reproduction of the properties of all other known levels. The same analysis of the results of the JISP16-based calculations sheds light on the following problems. Two states, 2$ _4^+ $ and 2$ _6^+ $ , have large calculated widths. As is the case for the just-discussed 4$ _2^+ $ level obtained in the Daejeon16-based calculations, one cannot exclude the possibility that these two levels exist in reality and have not been detected yet because of their large widths. At the same time, the large widths of these levels show that the levels known from experiments that were identified with the discussed ones, because of the energy marker, turn out to be non-reproduced. These circumstances do not violate the good general description of the 8Be nucleus spectrum.Let us return to the analysis of the predicted levels of normal parity. The triple 0
$ _2^+ $ , 2$ _2^+ $ , 4$ _2^+ $ states with large alpha-decay widths presented in Table 4 attract major attention. This appears like a typical rotational band with the rotational quantum$ \hbar^2/2\mu r^2 \sim 0.38 $ MeV. The SFs and the alpha-decay widths of these states confirm that they are strongly clustered. Surprisingly, a similar rotational band may be found in the spectrum obtained in the JISP16-based computations. It corresponds to the triple 0$ _2^+ $ , 2$ _4^+ $ , 4$ _4^+ $ states characterized by the rotational quantum$ \sim 0.33 $ MeV. At the same time, a large difference in the location of these bands in the 8Be nucleus spectrum occurs. It is important to note that this band cannot be found in the absence of the data on the alpha-decay widths. This duplicated prediction makes the situation intriguing. In our opinion, it would be interesting to detect such a new band of alpha-clustered states and to determine the real excitation energies of its members.There are a number of other states possessing noticeable cluster properties, as predicted in both interaction models (0
$ _5^+ \leftrightarrow 0_4^+ $ ) and as found in one of the two approaches, i.e., 4$ _3^+ $ , for the Daejeon16-bases studies, and 2$ _4^+ $ , 2$ _6^+ $ , 2$ _8^+ $ , for JISP16-based ones. Experimental studies of the 8Be nucleus spectrum in the excitation energy area in which all mentioned states are located and, in principle, the spectrum as a whole, are of interest as they contribute to the spectroscopic information array and physics of nuclear clustering. These investigations may also present a test to check the quality of various NN-potentials exploited in ab initio calculations.Perhaps a popular experimental approach aimed to measure the cross-sections of elastic scattering of alpha-particles from various light nuclei – the so-called thick target inverse kinematics technique proposed in Refs. [65, 66] (a detailed description can be found in Ref. [13]) – adapted for the discussed purposes would be convenient for the proposed measurements.
In conclusion, we list the basic results obtained in this study.
1. A method allowing simultaneous ab initio calculations of the total binding and excitation energies, statistical weights of the components that are characterized by a certain value of the isospin, together with the quantities that determine the degree of the alpha-clustering, i.e., SFs, CFFs, and alpha-decay widths, is developed.
2. The ab initio theoretical studies of the properties of 8Be nucleus states located in a wide range of the excitation energies, both clustered and non-clustered, are carried out for the first time.
3. For the lowest rotational band 0
$ ^+_1 $ , 2$ ^+_1 $ , and 4$ ^+_1 $ states of the 8Be nucleus, it is demonstrated that non-clustered components of the WFs of these states make a large contribution to the total binding energy, in spite of the small statistical weight of these components in each of the WFs.4. In the majority of instances, the results of the computations of the listed characteristics turn out to be in a good agreement with the tabulated spectroscopic data.
5. The alpha-decay width is a good characteristic to identify various nuclear states and to establish a correspondence between observed and calculated nuclear levels.
6. A number of levels, both manifesting strongly and not showing noticeable alpha-clustering properties, which have not been found experimentally, are predicted. The most interesting is two-way prediction of the second rotational band of the 8Be nucleus, which is strongly clustered. A corresponding verification experiment is proposed.
Finally, good prospects for ab initio approaches in the studies of several characteristics of light nuclei spectra, interpretation of the properties of known nuclear states, and prediction of levels that are not observed to date and their characteristics are shown.
The authors are grateful to A. M. Shirokov, A. I. Mazur, and I. A. Mazur for the realistic JISP16 and Daejeon16 NN-potentials matrixes provided by them and to Calvin W. Johnson for his high-performance shell model code Bigstick and assistance with NCSM calculations.
Description of alpha-clustering of 8Be nucleus states in high-precision theoretical approach
- Received Date: 2020-06-26
- Available Online: 2020-12-01
Abstract: Scrupulous theoretical study of 8Be nucleus states, both clustered and non-clustered, is performed over a wide range of excitation energies. The quantities that characterize the degree of the alpha-clustering of these states, i.e., spectroscopic factors, cluster form factors, and alpha-decay widths, are computed in the framework of the developed accurate ab initio approach. Other basic properties of the 8Be spectrum, including the binding and excitation energies and the mean values of the isospin, are calculated simultaneously. In the majority of instances, the results of the computation turn out to be in good agreement with the spectroscopic data. A number of predictions are made, and corresponding verification experiments are proposed. Prospects of the developed approach for nuclear spectroscopy are demonstrated.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: