Scotogenic dark symmetry as a residual subgroup of Standard Model symmetries

The Standard Model of particle physics is a highly successful theory with an enormous predictive power. Thus far, many of its predictions have been experimentally verified. In addition, the discovery of the scalar Boson in 2012 at the Large Hadron Collider [1,2], if confirmed, will be the final verification of the Standard Model. With hundreds of precise observables and dozens of predicted particles, the model is without a doubt one of the most accurate theories in the history of human science. Despite its success, however, the Standard Model also has some serious drawbacks that need to be addressed to obtain a more complete fundamental theory. Two of the main issues it faces, although not the only ones, are neutrino masses and dark matter.

Although direct detection experiments on dark matter have thus far shown only negative results [3,4], the cosmological evidence for its existence are abundant. Observations ranging from galaxy rotation curves to galaxy clusters or gravitational lensing, all point to the existence of dark matter, a hitherto unknown type of matter that interacts gravitationally but has little to no electromagnetic interaction [5]. From a particle-physics point of view, a completely stable, or sufficiently long lived, and electrically neutral but weakly interacting massive particle (WIMP) is one of the most popular dark matter candidates. The Standard Model unfortunately has no such candidate. This has created the need to extend the matter content and possibly the symmetry inventory to explain the cosmological observations pointing toward the existence of dark matter. In this letter, we show that the global $ U(1)_{B-L} $ already present in the Standard Model is sufficient to ensure the stability of dark matter. Furthermore, such a dark matter candidate can be intimately related with the other major experimental shortcoming of the Standard Model, namely, the lack of a neutrino mass generation mechanism.

The neutrinos are predicted to be massless in the Standard Model. However, owing to data from various oscillation experiments, we can confidently state that neutrinos are massive particles [6-11]. Consequently, the Standard Model has to be extended to accommodate the existence of massive neutrinos [12,13]. During the past several decades, various extensions of the Standard Model have been proposed to understand massive neutrinos. Most of the initial studies on neutrino mass models assumed that neutrinos are Majorana, and several seesaw [14-19] and loop mass mechanisms [20-22] have been proposed to explain their small yet non-zero masses. Majorana neutrino mass models still remain the popular choice for the Standard Model extensions that try to explain the existence of massive neutrinos [23-32].

Typically, Majorana mass models break the global Lepton number $ U(1)_L $ symmetry (or equivalently, the anomaly-free $ U(1)_{B-L} $ symmetry) of the Standard Model to a residual $ {\cal{Z}}_2 $ subgroup. However, breaking $ U(1)_{B-L} $ to higher $ {\cal{Z}}_m $ subgroups is also feasible, where $ m\in \mathbb{Z}^+ $ and $ m \geqslant 2 $, with $ \mathbb{Z}^+ $ being the set of all positive integers. In fact, in absence of any other conserved symmetries beyond the Standard Model, the Dirac or Majorana nature of neutrinos depends on the $ U(1)_{B-L} $ breaking pattern, as argued in [33] and [34]. If $ U(1)_{B-L} $ remains conserved, then neutrinos have to be Dirac because the Majorana mass term is forbidden. When $ U(1)_{B-L} $ breaks to a residual $ {\cal{Z}}_m $ subgroup with the Standard Model lepton doublets $ L_i = (\nu_{L_i}, l_{L_i})^T $, with $ i = 1,2,3 $ transforming non-trivially under such condition, then [33,34]

When $ U(1)_{B-L} $ is broken down to an even $ {\cal{Z}}_{2n} $ residual subgroup, a further classification can be made depending on how $ L_i $ transforms under $ {\cal{Z}}_{2n} $,

where $ \omega = {\rm e}^{\frac{2\pi i}{2n}} $ is the $ \rm{2n}^{\rm{th}} $ root of unity with $ \omega^{2n} = 1 $. Thus, Majorana neutrinos can also be obtained when $ U(1)_{B-L} $ is broken to any even $ {\cal{Z}}_{2n} $ residual subgroup beyond $ {\cal{Z}}_2 $. Despite an extremely large number of studies on mass mechanisms for Majorana neutrinos, to the best of our knowledge, the option of $ U(1)_{B-L} \to {\cal{Z}}_{2n} $, $ n \geqslant 2 $ leading to Majorana neutrinos in congruence with (2) has yet to be explored.

In this letter, we show that for Majorana neutrinos with $ U(1)_{B-L} \to {\cal{Z}}_{2n} $, the residual $ {\cal{Z}}_{2n} $ subgroup can also be used to obtain a stable candidate for dark matter without adding any new symmetry to the Standard Model. We further show that such a dark matter candidate can also be intimately connected with the neutrino mass generation mechanism, being the lightest of the loop mediators leading to Majorana masses for the neutrinos through a scotogenic approach [22]. Thus, the residual $ {\cal{Z}}_{2n} $ subgroup provides scotogenic dark symmetry, which in a original scotogenic model had to be imposed as an extra ad hoc condition^① [26].

We start our discussion in Section 2 highlighting the general conditions required to have a loop mass generation mechanism for neutrinos with the residual $ {\cal{Z}}_{2n} $ symmetry providing a scotogenic dark symmetry. After illustrating the general applicability of the framework, we discuss a class of simple one-loop models that can be constructed using our general criterion. In Section 3, we will take one of these models as an explicit example and discuss it in further detail. Finally, we conclude our discussion and summarize the main results in Section 4.

As pointed out in (1) and (2), to have Majorana neutrinos, the $ U(1)_{B-L} $ symmetry must be broken into an even subgroup $ {\cal{Z}}_{2n} $. In addition, the lepton doublets $ L_i $ should also belong to the subgroup $ {\cal{Z}}_2 \subset {\cal{Z}}_{2n} $, i.e., $ L_i $ either transforms trivially or as $ \omega^n $ with $ \omega^{2n} = 1 $. A connection between these symmetries and the stability of the dark matter can be found, as first stated in [34] for Dirac neutrinos. In this letter, we follow an analogous approach linking the generation of naturally small Majorana neutrino masses with the stability of dark matter providing the appropriate symmetry breaking pattern $ U(1)_{B-L}\rightarrow{\cal{Z}}_{2n} $. This further implies that neutrino masses arise at the loop level because the tree-level Majorana and Dirac masses are forbidden by the symmetry.

To achieve this, new fields with exotic $ B-L $ charges are required^① [34]. Since in the Standard Model lepton doublets $ L_i $ have a $ B-L $ charge of $ -1 $, to avoid all possible tree-level Dirac mass terms, no new fermion can carry $ \pm 1 $ charges under $ U(1)_{B-L} $ symmetry. Furthermore, the lowest order Majorana mass term, i.e., the Weinberg operator $ \bar{L}^cLHH $, is not invariant under $ U(1)_{B-L} $, and thus is automatically absent. To generate neutrino masses, we should go to higher dimensional operators,

where $ \chi_i $; $ i = 1, ... k $ are scalar fields transforming non-trivially under $ U(1)_{B-L} $. The operator in (3) should be invariant under Standard Model symmetries including $ U(1)_{B-L} $. This means that the $ B-L $ charges of the fields $ \chi_i $ must sum to $ 2 $. Although in principle some of them can also have non-trivial transformations under $ SU(2)_L \otimes U(1)_Y $, for the sake of simplicity we will take all $ \chi_i $ to be Standard Model gauge singlets. Because $ \chi_i $ are charged under $ U(1)_{B-L} $, once they acquire a vacuum expectation value (vev), the $ U(1)_{B-L} $ symmetry will break down to a residual $ {\cal{Z}}_{2n} $ subgroup, with $ n $ depending on the charges of the particles in the model.

As pointed out previously in [13], [34], and [35], the stability of dark matter can be achieved automatically if $ U(1)_{B-L} $ is broken to an even $ {\cal{Z}}_{2n} $ provided that all Standard Model particles transform as even under $ {\cal{Z}}_{2n} $, whereas the dark matter candidate is odd. Here, by even (odd) we mean fields, which transform as even (odd) powers of $ \omega $ under $ {\cal{Z}}_{2n} $ with $ \omega^{2n} = 1 $. Thus, the necessity of $ U(1)_{B-L} $ breaking to an even $ {\cal{Z}}_{2n} $ does not only come from the Majorana nature of neutrinos but also from the requirement of a stable dark matter in this setup. An even residual $ {\cal{Z}}_{2n} $ symmetry ensures that if the Standard Model belongs to the $ {\cal{Z}}_n $ subgroup, then a dark sector with all the fields transforming as odd under $ {\cal{Z}}_{2n} $ is separated from it. The interplay between both sectors and the stability of dark matter can be seen graphically in Fig. 1. Note that any odd particle under residual $ {\cal{Z}}_{2n} $ symmetry can only decay into the Standard Model particles plus another odd particle. This implies that the lightest of the odd particles will be automatically stable (see [34] for more details).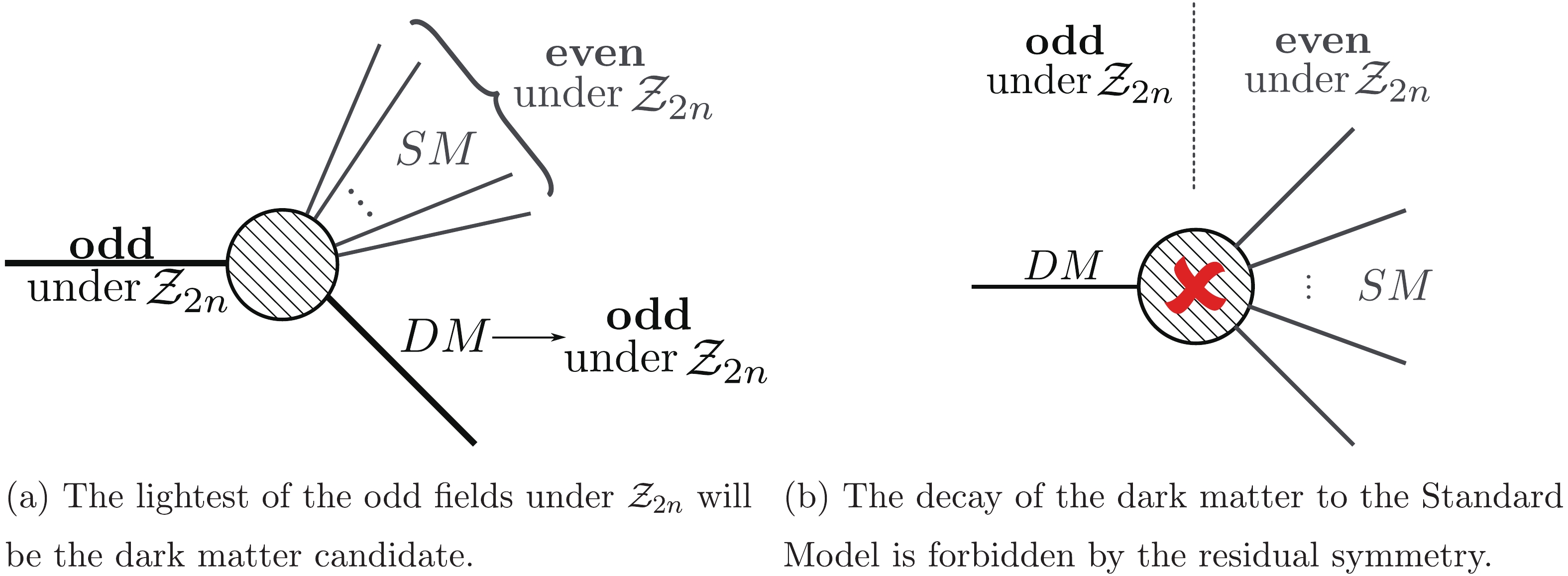

Figure 1.  (color online) There are two distinct sectors transforming as odd or even under the residual $ {\cal{Z}}_{2n} $ symmetry. In our setup, all internal fields are odd, whereas SM is even. Owing to the $ {\cal{Z}}_{2n} $ symmetry, an odd particle can only decay to the SM plus another odd particle. Thus, the lightest of the odd particles is stable and a good dark matter candidate.

Following this framework, in the simplest scenario, one can realize the operator (3) at the one-loop level with only one field $ \chi $ with $ B-L $ charge $ 2 $, i.e., the 6-dimension operator $ \bar{L}^c LHH \chi $. The possible one-loop realizations of the operator can be classified, following the philosophy of [23, 25, 28, 30, 31], into three renormalizable genuine topologies, which lead to ten different diagrams, as can be seen in Fig. 2. We associate the topology with graphs or Feynman diagrams where no Lorentz nature is considered. We refer to diagrams if fermion and scalar lines are specified. The concept of genuineness is then attributed to those models for which the main contribution to neutrino masses comes from the one-loop level realization of the operator $ \bar{L}^c LHH \chi $. We call topologies or diagrams that generate at least one of these models genuine by inference. For example, diagrams that unavoidably contain the vertices ($ L H$ + fermion) or ($ \bar{L}^c L $ + scalar) are not genuine because they will generate a dominant type-I/III or type-II seesaw contribution, respectively.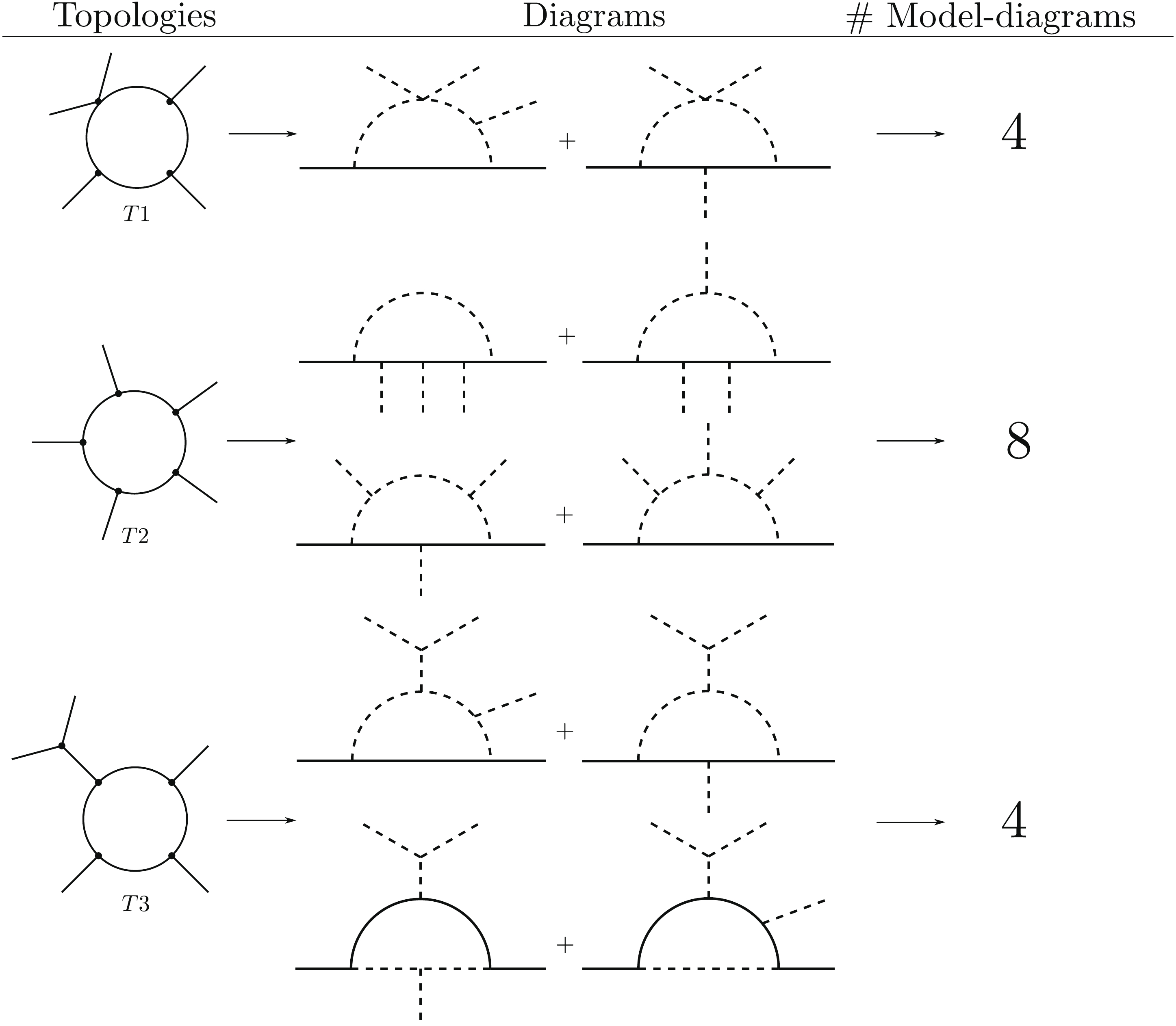

Figure 2.  Renormalizable genuine topologies that generate the operator $ \bar{L}^c LHH \chi $. For each topology, all diagrams are given along with the number of model-diagrams. Each model-diagram can be generated by arranging in all possible ways $ \chi $ and two instances of $ H $ in the external scalar legs.

The ten different diagrams depicted in Fig. 2 generate 16 model diagrams. Each model diagram is generated from a given diagram by the different arrangements of the two Higgs doublets and the Higgs singlet $ \chi $ of $ \bar{L}^c LHH \chi $ in the external scalar lines. For instance, taking topology $ T1 $, each of its diagrams generates two model diagrams inserting $ \chi $, i.e., in the quartic scalar coupling or in the trilinear coupling with scalars or fermions. In the case of $ T3 $ , the arrangement of $ \chi $ and both Higgs particles is unique, as a trilinear vertex with two instance of $ H $ is not allowed because it would generate a dominant type-II seesaw contribution. Note that, for each model-diagram, there is an infinite series of possible models because there is always a free set of charges running in the loop.

The intention of this letter is not to provide an exhaustive classification, but to show in a systematic way the wide range of possibilities, yet unexplored, of the simplest realizations of the framework given in this section. We will now choose one of the simplest diagrams to build a particular, consistent, and complete model as an example of how this general method works.

In this section, we construct a complete explicit ultra-violet (UV) model realization of the 6-dimension operator $ \bar{L}^c LHH \chi $ to further describe the formalism described in Section 2. We add a new vector-like fermion pair $ F_L $ and $ F_R $ with charge $ 1/2 $ under $ U(1)_{B-L} $ but a singlet under the Standard Model gauge symmetries. Because the field breaking the $ U(1)_{B-L} $ symmetry, $ \chi $, transforms into $ 2 $, the fractional charges of the new fields will imply the breaking pattern is $ U(1)_{B-L} \rightarrow {\cal{Z}}_4 $. Note that, given the fractional charges of $ F_L $ and $ F_R $, there will be no tree-level Dirac mass term for the neutrinos. Thus, additional scalars $ \eta_i $; $ i = 1,2,3 $ are also needed to generate a one-loop contribution to the neutrino masses. The relevant matter fields and their transformation under $ SU(2)_L \otimes U(1)_Y\otimes U(1)_{B-L} $ are given in Table 1, as well as the charges under the residual $ {\cal{Z}}_4 $ subgroup that survives after spontaneously breaking the symmetry.

	Fields	$ SU(2)_L \otimes U(1)_Y $	$ U(1)_{B-L} $	$ {\cal{Z}}_{4} $
Fermions	$ L_i $	($ {\bf{2}}, {-1/2} $)	$ -1 $	$ \omega^2 $
	$ e_{R_i} $	($ {\bf{1}}, {-1} $)	$ -1 $	$ \omega^2 $
	$ F_{R} $	($ {\bf{1}}, {0} $)	$ 1/2 $	$ \omega $
	$ F_{L} $	($ {\bf{1}}, {0} $)	$ 1/2 $	$ \omega $
Scalars	$ H $	($ {\bf{2}}, {1/2} $)	$ 0 $	$ 1 $
	$ \chi $	($ {\bf{1}}, {0} $)	$ 2 $	$ 1 $
	$ \eta_1 $	($ {\bf{2}}, {-1/2} $)	$ {-3/2} $	$ \omega $
	$ \eta_2 $	($ {\bf{2}}, {-1/2} $)	$ {-1/2} $	$ \omega^3 $
	$ \eta_3 $	($ {\bf{2}}, {-1/2} $)	$ {3/2} $	$ \omega^3 $

Table 1.  Particle content of the model with $ i\in\{e, \mu, \tau\} $. All fields listed in the table are $ SU(3)_C $ singlets. The field $ \chi $ acquires a vev consequently breaking the $ U(1)_{B-L} $ symmetry into its $ {\cal{Z}}_4 $ subgroup given the half-integer charges running in the loop (see the text for details).

It is clear that the $ U(1)_{B-L} $ symmetry given in Table 1 is anomalous. The canonical solution to make $ U(1)_{B-L} $ anomaly free is to add three right-handed fermions $ N_R $ with $ (-1,-1,-1) $ charges under $ B-L $ symmetry. However, as noted previously in Section 2, these charges are not allowed because they lead to tree-level Dirac coupling between the Standard Model lepton doublets $ L_i $. Instead, to cancel the anomalies, one can simply add three new neutral right-handed fermions $ N_R $ with charges $ (-4,-4,5) $ under $ U(1)_{B-L} $. This charge assignment also leads to anomaly free $ U(1)_{B-L} $ symmetry [36-39]. Other anomaly free solutions with several additional chiral fermions carrying exotic $ B-L $ charges, can also be found, as discussed in [40-47]. However, the (−4, −4,5) solution seems to be minimal [48-54]. These right-handed neutrinos can be given Majorana masses through the vev of singlet Higgses with charges 8 and 10 under $ B-L $^②. The $ N_R $ will not play a role in the light neutrino mass generation, but they could be relevant in colliders, particularly if one gauges the $ U(1)_{B-L} $ symmetry. The dark matter phenomenology will also be influenced by the addition of these neutral fields. Note that the residual charges of these fields are $ (1, 1, \omega^2) $, i.e., they are even fermions and therefore there are effective decay operators allowed by the symmetry. However, because they will be disconnected from the rest of the model they will be accidentally stable. This implies that the dark matter will be multi-component. Another option is to extend the model in such a way that these neutral fermions decay. The minimal content we found is the addition of a doublet $ H_6 $ with charge $ 6 $ under $ B-L $ and with a small induced vev through $ H_6 H^\dagger \chi_2 \chi_8^\dagger $, along with a singlet scalar with charge 1. Moreover, note that the residual transformation of the third right-handed neutrino is $ \omega^2 $. Therefore, there should be non-renormalizable operators allowed by $ B-L $ that can mix the left-and right-handed neutrinos. However, because these new fields will be disconnected from the rest of the model, these operators will not be realized in our model. In other words, our Lagrangian has an accidental $ U(1)_{N_3} $ that prevents this mixing from occurring.

With this setup, the anomaly free $ B-L $ will forbid the tree-level mass term for the neutrinos, but the new field content can accommodate the one-loop neutrino mass diagram of Fig. 3 in a scotogenic manner, thus explaining the smallness of the neutrino masses and dark matter stability in a natural way.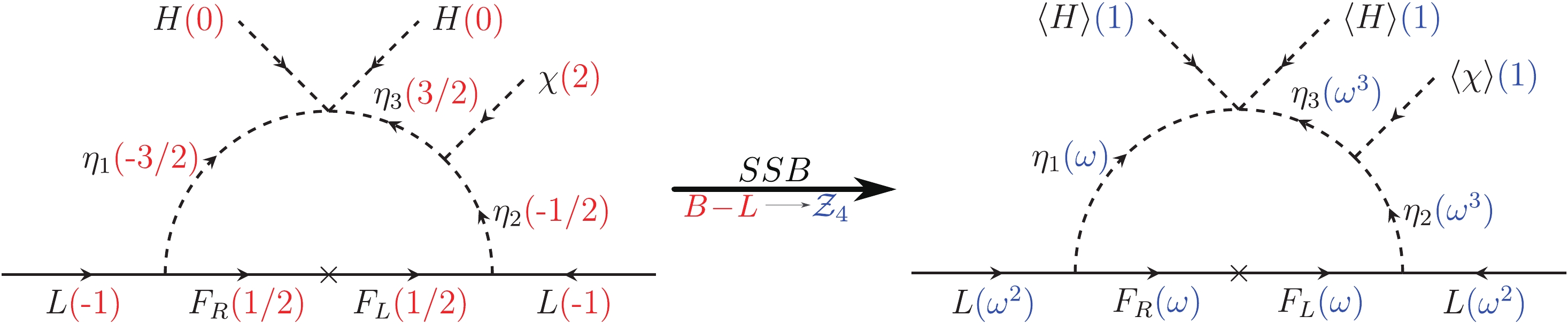

Figure 3.  (color online) Leading order neutrino mass diagram with $ B-L $ charges (left). After spontaneous symmetry breaking (SSB), as $ \chi $ has charge $ 2 $ under $ B-L $ and there are half-integer charged fields, $ U(1)_{B-L} $ is broken to its subgroup $ {\cal{Z}}_4 $ (right).

If $ U(1)_{B-L} $ maintains a globally anomalous symmetry without adding new extra fermions, a Goldstone boson will appear, typically called Majoron in the literature. There have been extensive studies of Majoron phenomenology and it is well-established that Majoron models are viable with respect to phenomenological and experimental constraints, both from cosmology and colliders^② [55-61].

The complete Lagrangian is divided into several pieces for a better understanding. The Lagrangian of the model consist of the following parts:

1. The charged lepton mass Lagrangian is exactly identical to that of the Standard Model:

where $ Y_l $ is a $ 3 \times 3 $ Yukawa matrix and $ L $ and $ l_R $ are 3-vectors. After spontaneous symmetry breaking, $ Y_l/{\rm{v}} $ will be the mass matrix for the charged lepton, where v is the vaccum expectation value of the Standard Model Higgs $ H $.

2. The mass of the vector-like pair $ F_{L} $ and $ F_{R} $ will simply be given by the following:

where $ M $ is a general mass matrix whose entries are expected to be much larger than the electroweak scale, and therefore $ F $ will be a heavy Dirac fermion. We will use $ m_F $ for the eigenvalues of $ M .$

3. There are also other Yukawa interaction terms that will not contribute to the tree-level fermion masses but appear in the one-loop level:

4. The scalar terms relevant for neutrino masses are given by the following:

Apart from the standard kinetic and gauge terms, the scalar potential consists of 37 extra terms that we omitted for simplicity. Moreover, $ SU(2) $ contractions have been suppressed for brevity. However, let us briefly discuss the scalar Lagrangian involving fields with non-zero vev. This Lagrangian is extremely simple because it is just a minimal extension of the standard model by a new singlet. In particular, the Lagrangian is given by the following:

We can now trivially obtain the tadpole equations as follows:

where the mass of the CP-even states is extracted. In the approximation where $ u \ll v $, we have

We can conclude that this light singlet will be invisible to all current experiments [58]. As a benchmark point, we can take $ u \sim 10 $ GeV, leading to a singlet mass of similar order.

Regarding the neutrino masses, as we pointed out earlier, there is no tree-level mass term for the neutrinos because the exotic charges of the new fermions forbid a Standard Model-like coupling with a Higgs particle. Moreover, note that the Weinberg operator $ \bar{L}^c L H H $ is also forbidden by the same $ U(1)_{B-L} $ charges. The leading contribution to the neutrino masses will arise at the radiative level coming from the allowed operator $ \bar{L}^c LHH \chi $ , as shown in Fig. 3.

The neutrino mass matrix can be directly computed in the mass insertion approximation from Fig. 3 along with the Lagrangian as follows:

where we have considered that the mass matrix $ M_{\sigma} $ of the vector-like fermions $ F_{L/R} $ is diagonal. Here, $ U_{ai} $ is the rotation matrix of the scalars to the mass basis, which is defined as $ \eta^0_i = U_{ij} \eta^0_{m_i} $, with eigenvalues $ m_i $, whereas $ B_0 $ is a one-loop function defined in the Passarino-Veltman notation [62]. Considering the leading order in vevs, we can estimate the scale of neutrino masses by the following:

where u is the vev of $ \chi $, and $ \Lambda $ is the characteristic scale of the loop, i.e., the dominant mass scale in the loop. The mass of the dark matter candidate will necessarily be lower than this scale. Note that to have two massive neutrinos only one generation of $ F $ is needed, whereas two generations of $ F $ can generate three non-zero neutrino masses. This is due to, as usual, the sum of two contributions: one coming from the diagram shown in Fig. 3 and another coming from its transpose. An estimate of the neutrino mass scale can be obtained if one considers that $ {\rm{u}} \sim {\cal{O}}(10) $ GeV. With $ \kappa $ order $ 1 $ GeV, $ Y \sim {\cal{O}}(0.1) $ and $ \lambda \sim {\cal{O}}(1) $, the atmospheric scale of 0.05 eV can be fit with masses on the order of 10 TeV.

Moreover, as can be seen from Fig. 3, all particles running in the neutrino mass loop are odd under the residual $ {\cal{Z}}_4 $ symmetry. Thus, they all belong to the dark sector with the lightest among them, i.e., the lightest out of $ \eta_i $ and $ F_{L/R} $, being a good candidate for stable dark matter. As mentioned before, the stability of the dark matter is due to the fact that all dark sector particles have charges that are odd under the residual $ {\cal{Z}}_4 $ symmetry. However, all Standard Model particles are even under $ {\cal{Z}}_4 $. Hence, for the lightest dark sector particle, there is no possible effective decay operator at any order allowed by the remnant $ {\cal{Z}}_4 $, as shown in Fig. 1.

To summarize, the neutrino mass and dark matter remain two of the most important shortcomings of the Standard Model. Scotogenic models where the dark sector particles run in the neutrino mass loop provide a particularly attractive scenario to address both of these shortcomings in a Standard Model extension. In this study, we showed that a scotogenic symmetry responsible for the dark matter stability can be obtained as a residual $ {\cal{Z}}_{2n} $ subgroup of the $ U(1)_{B-L} $ symmetry already present in the Standard Model. We then briefly listed the general conditions required for our formalism to work for any even residual $ {\cal{Z}}_{2n} $ subgroup, as previously applied for the case of Dirac neutrinos [34]. We showed that our framework can be applied broadly to many different cases, but remains unexplored. Particularizing to a simple case with just one extra scalar Higgs singlet, we discussed all possible realizations at a one-loop level. Finally, one simple realistic example with a remnant $ {\cal{Z}}_{4} $ symmetry was explained in more detail to illustrate how the spontaneous symmetry breaking of $ U(1)_{B-L} $ to an even $ {\cal{Z}}_{2n} $ can be easily accommodated, granting the stability of dark matter.

We would like to remark that, although we only fleshed out the case for one-loop models in this study, our formalism can be implemented at higher loops and for any even $ {\cal{Z}}_{2n} $ symmetry. Finally, because in our formalism the global $ U(1)_{B-L} $ symmetry is maintained as anomaly free, all models based on our formalism can be gauged in a straightforward manner. Such gauged models will lead to an even richer phenomenology.

EP would like to thank the group AHEP (IFIC) for their hospitality during his visits. RS would also like to thank IFUNAM for the warm hospitality provided during his visit.