-
Due to the expansion of the universe there are several ways to define the distance in cosmology, among which the luminosity distance and angular diameter distance are two important definitions. The former is based on the fact that for an object with fixed luminosity, the measured flux is inversely proportional to the square of the distance to the source, while the latter is defined as the ratio of the physical transverse size and the angular size of an object. The cosmic distance duality relation (DDR) correlates the luminosity distance to the angular diameter distance by
DL(z)=(1+z)2DA(z) [1, 2]. The standard DDR holds in any metric theory of gravity such as the general relativity, as long as photons travel along null geodesics, and the photon number is conserved during propagation [3, 4]. The violation of DDR may be caused e.g. by the extinction of photons by intergalactic dust [5], coupling of photons to other particles [ 6], or variation of fundamental constants [7]. DDR is a fundamental relation in the standard cosmological model. Any violation of DDR would imply that there is new physics beyond the standard cosmological model. Therefore, testing the validity of DDR is of great importance. In fact, several works have been devoted to testing DDR [8-18].The method to test DDR is simple: just measure the angular diameter distance (
DA ) and luminosity distance (DL ) to the same redshift, then compare these two distances to see if DDR is valid or not. However, in practice this is not trivial. AlthoughDA andDL can be measured independently in several ways, it is difficult to simultaneously measureDA andDL from the same object. The usual way is to measureDA andDL from different objects located at different positions. For example, the luminosity distance can be measured from the type-Ia supernovae standard candles [19, 20], or the gravitational waves standard sirens [21, 22]. The angular diameter distance can be measured e.g. from the BAO signals in the galaxy spectrum [23, 24], using the Sunyaev-Zel'dovich effect of galaxy clusters [25, 26], angular size of ultra-compact radio sources [27], or strong gravitational lensing system [28].One of the main problems of the above methods is that
DA andDL are measured from different objects located at different redshifts and sky positions. To test DDR, one must apply special techniques such as interpolations and Gaussian processes so thatDL andDA can be compared at the same redshift. Although the standard DDR only involves distances and not directions in the sky, if the universe is anisotropic (caused e.g. by the inhomogeneous and anisotropic distribution of matter) it is unreasonable to test DDR usingDA andDL measured from objects located in different directions [29]. Of course, the ideal way to avoid this problem is to measureDA andDL from the same object, and then to directly compare these two distances. Hence, is there any way to measureDA andDL from the same source? We show in the following that the strongly lensed gravitational waves can satisfy this requirement.In this paper, we propose a new method to test DDR using the strongly lensed gravitational waves. The spectroscopic observation of the redshifts of the lens and the source, the photometric observation of the lens galaxy together with the observations of the GW image positions and the relative time delay between images, give the angular diameter distance and the luminosity distance to the GW source. Thus, the strongly lensed GWs provide a unique way to test DDR using a single source. The structure of the paper is as follows: the method is described in Sec. 2, and the related discussion in Sec. 3. A short summary is given in Sec. 4.
-
We consider the situation where a GW event originates from the coalescence of a compact binary system (e.g. NS-NS binary and NS-BH binary) and is strongly gravitationally lensed by a foreground galaxy. We also assume that the lens galaxy is modelled as a singular isothermal sphere. With this configuration, two images appear at the angular positions
θ1 andθ2 with respect to the lens position. The Einstein radiusθE=|θ1−θ2|/2 is given by [30]θE=4πσ2SISDA(zl,zs)c2DA(zs),
(1) where
σSIS is the velocity dispersion of the lens galaxy,DA(zs) andDA(zl,zs) are the angular diameter distances from the observer to the source and from the lens to the source, respectively. If the angular resolution of the GW detector is suficiently high so that the angular positions of the two images can be well measured and the Einstein radius precisely determined, and if the velocity dispersion of the lens galaxy is measured independently, then we can obtain the distance ratioRA≡DA(zl,zs)DA(zs)=c2θE4πσ2SIS.
(2) On the other hand, two images of GW propagating along different paths have a relative time delay which is given by [30]
Δt=(1+zl)DΔtcΔϕ,
(3) where
DΔt≡DA(zl)DA(zs)DA(zl,zs)=c1+zlΔtΔϕ
(4) is the so-called time-delay distance, and
Δϕ=(θ1−β)22−Ψ(θ1)−(θ2−β)22+Ψ(θ2)
(5) is the difference of the Fermat potential of the lens galaxy calculated at the image positions, and
Ψ(θ) is the rescaled projected gravitational potential of the lens galaxy. For the singular isothermal spherical lens,Ψ(θ)=θE|θ| . If the gravitational potential of the lens galaxy can be well measured from the photometric and dynamical observations such that the Fermat potential can be calculated, and if the spectroscopic redshift of the lens galaxy is precisely known, then the time-delay distance can be determined from the observed time delay between two GW images.In a spatially flat universe, the comoving distance is related to the angular diameter distance by
r(zs)= (1+zs)DA(zs) ,r(zl)=(1+zl)DA(zl) ,r(zl,zs)=(1+zs) DA(zl,zs) , where the comoving distance from the lens to the source is simply given byr(zl,zs)=r(zs)−r(zl) . Therefore, the angular diameter distance from the lens to the source readsDA(zl,zs)=DA(zs)−1+zl1+zsDA(zl).
(6) Eqs. (2), (4), (6) can be uniquely solved for
DA(zl) ,DA(zs) andDA(zl,zs) .What we are interested in is the distance from the observer to the source, which reads
DA(zs)=1+zl1+zsRADΔt1−RA,
(7) where
RA andDΔt are given by Eqs. (2) and (4), respectively. Using the error propagation formulae, we obtain the uncertainty ofDA(zs) ,δDA(zs)DA(zs)=√(δRARA(1−RA))2+(δDΔtDΔt)2,
(8) where
δRARA=√(δθEθE)2+4(δσSISσSIS)2,
(9) and
δDΔtDΔt=√(δΔtΔt)2+(δΔϕΔϕ)2.
(10) If the observables (
zl ,zs ,Δt ,Δϕ ,θE ,σSIS ) are measured, thenDA(zs) and its uncertainty can be obtained using Eqs. (7)-(10).The luminosity distance to the source
DL(zs) can be inferred directly from the GW signals [21, 22]. As standard sirens, GWs can provide luminosity distance independent of the model, and are thus widely used as cosmological probes [31-34].DL(zs) is inversely proportional to the amplitude of the spacetime strain in the Fourier space,DL(zs)∝1/A . Due to the degeneracy betweenDL(zs) and the inclination angle of the orbital plane of the binary, the uncertainty ofDL(zs) may be very large. However, if the GW event is accompanied by a short gamma-ray burst (GRB), then due to the beaming of GRB outflow we can assume that the inclination angle is small, hence the degeneracy breaks. In this case, the uncertainty ofDL(zs) can be estimated as [35, 36]δDL(zs)DL(zs)=√(2ρ)2+(0.05zs)2,
(11) where
ρ is the signal-to-noise ratio (SNR) of the detector response to the GW signal, and the term0.05zs represents the uncertainty of the weak lensing effect caused by the matter distribution along the line-of-sight.Note that
DL(zs) directly inferred from GW signals is not the true luminosity distance. This is becauseDL(zs) is inversely proportional to the amplitude of the GW strain, while the latter is magnified by the lensing effect. For the singular isothermal spherical lens, the magnification is given byμ±=1±θE/β , whereβ is the actual position of the source, and "± " represent the first and second images, respectively. The actual position of the sourceβ can be determined from deep photometric imaging,β/θE= (F+−F−)/(F++F−) , whereF± are the photometric fluxes of the two images. Given the magnification factor determined from the photometric observations, the true distance can be obtained fromDtrueL=√μ±DobsL . The uncertainty ofμ± propagates toDL . Therefore, the final uncertainty ofDL(zs) is given byδDL(zs)DL(zs)=√(2ρ)2+(0.05zs)2+14(δμ±μ±)2.
(12) Since the magnification is derived directly from the photometric fluxes of the two images, the uncertainty of
DL(zs) is uncorrelated with that ofDA(zs) . If two GW images are observed, the distance inferred from different images can be used for a cross-check, and the uncertainty ofDL(zs) can be further reduced.Given that the angular diameter distance and the luminosity distance are measured, DDR can be directly tested. We define the possible deviation from the standard DDR as
Δ=DL−(1+z)2DADL.
(13) If the uncertainty of the luminosity distance is uncorrelated with that of the angular diameter distance, then the uncertainty of
Δ is given byδΔ=(1+z)2√(δDA)2D2L+D2A(δDL)2D4L=√(δDADA)2+(δDLDL)2,
(14) where we assumed in the last equality that the violation of DDR, if it exists, is very small. If DDR is valid,
Δ should be consistent with zero. Any deviation of Eq. (13) from zero would imply the violation of DDR.In summary,
DA(zs) withDL(zs) can be measured from a strongly lensed GW system. This provides a unique way to simultaneously measure the angular diameter distance and the luminosity distance from the same object. This method is independent of the cosmological models, except for the assumption that the universe is spatially flat. Therefore, the strongly lensed GW provides a model-independent tool to test DDR. -
Although the idea proposed here seems theoretically promising, in practice there are many challenges. The biggest challenge is the identification of the lensed GW signal. For a typical lensing system, the angular separation between two images is of the order of arc seconds. This is far beyond the angular resolution of the running GW detectors such as LIGO and Virgo. Even for the planned third generation GW detectors such as the Einstein Telescope and Cosmic Explorer, the situation is not more optimistic. However, the localization capability of a network of third generation GW detectors is expected to be precise enough to identify the host galaxy [37]. If the host galaxy can be identified and the electromagnetic counterparts can be observed, then different images can be distinguished with photometric observations. If we assume that light and GW propagate along the same null geodesics, then the positions of photometry images overlap with GW images. GW is a transient event which lasts at most several seconds, while the time delay between different images is typically of the order of several months or even several years. This makes the observation of GW lensing much more difficult than the observation of regular lensing, such as the lensing of a quasar or supernova. The GW detectors must keep running to ensure that both images can be recorded.
More than one hundred strong gravitational lensing systems in which a quasar acts as the source have been found up to now, see e.g. the catalog compiled in [38]. The redshift of the source is usually in the range from
zs∼0.5 tozs∼3.5 . If we assume that the lensed GW sources fall into a similar redshift range as the quasars, they would be far beyond the effective detection range of LIGO and Virgo. However, this distance is reachable by the planned Einstein Telescope, which is designed to detect GW events up toz∼5 . It is expected that about103∼107 GW events can be detected by the Einstein Telescope per year [39], among which several may be strongly lensed by a foreground galaxy. It is optimistically estimated that about50−100 strongly lensed GW events can be observed by the Einstein Telescope per year [40]. With the space-based detectors such as the Big Bang Observer [41], the detection rate is expected to be much higher. Among these lensed GW events, several are expected to be produced by the coalescence of NS-NS binary or NS-BH binary, which may be accompanied by electromagnetic counterparts, hence the redshift can be measured independently. In addition, the redshift range also falls into the effective detection range of some existing gamma-ray burst detectors such as the Fermi satellite, so that joint observations of GWs and electromagnetic counterparts are possible. Thus, despite big challenges, there is still a significant possibility of detecting strongly lensed GW events in the near future.The uncertainty of
DA(zs) mainly comes from the measurements ofΔϕ ,θE andσSIS . It was shown in [42] that the accuracy ofΔϕ in the strongly lensed GW systems can be improved by a factor of five compared to the strongly lensed quasar systems, because the GW signals do not suffer from the bright AGN contamination from the lens galaxy. We follow [42] and assume a 0.6% uncertainty ofΔϕ . The accuracy ofθE is expected to be at the ~1% level in the future LSST survey [43]. According to the quasar lensing systems compiled in [38], the measured uncertainty of the velocity dispersion of the lens galaxy is of the order of ~10%, with the best accuracy ~3%. Due to the improvements of observational techniques, it is expected that the uncertainty can be further reduced in the future. We follow [43] and assume the uncertainty ofσSIS at the level of 5%. If the host galaxy is identified, the redshifts of the lens and the source can be measured precisely by the spectroscopic method, so that their uncertainties are negligible. Due to the transient nature of a GW event, the time delay between two GW images can also be precisely measured with a negligible uncertainty. It was shown that the redshift of the strongly lensed GW source has a sharp peak nearzs∼2 [44], and the median value of the redshift of the lens iszl∼0.8 [43]. With the expected accuracy, for a typical lens system atzl∼0.8 andzs∼2 , the uncertainty ofDA(zs) is estimated from Eq. (8) asδDA/DA∼ 20%. In fact, the uncertainty mainly arises from the error ofσSIS . To reduce the uncertainty, a more precise measurement ofσSIS is needed.The uncertainty of
DL(zs) mainly comes from three aspects: SNR of the GW signal recorded by the detector, the week lensing effect caused by the matter along the light path, and the uncertainty of the magnification factor. To ensure the significance, we require that SNR is at leastρ≳16 , compared to the usual criterionρ≳8 . For a GW source located atzs∼2 , the uncertainty caused by the weak lensing effect is about 10%. Hence, the uncertainty ofDL(zs) from Eq. (11) is at the level of 16%. For a source located at a redshift higher than 2, the uncertainty of the luminosity distance is dominated by the weak lensing term, and the accuracy may be worse than our rough estimate. However, if two GW images are observed, both can be used to determine the luminosity distance, and the accuracy can be improved by a factor of√2 . Therefore, it is still possible to measureDL(zs) with an accuracy better than 16% for high redshift events. The determination of the magnification factorμ± could be highly uncertain due to the contamination of the image flux by the foreground lensing galaxy. We follow [43] and assume a ~20% uncertainty ofμ± . Taking this uncertainty into consideration, the final uncertainty ofDL(zs) is at the ~20% level.Based on the above discussion, we expect that, although challenging, it will be possible in the future to measure
DA andDL to the GW source with an accuracy better than ~20%. With this accuracy, a single strongly lensed GW event could, according to Eq. (14), constrain DDR at the level of ~28%. If∼100 events with a similar accuracy are detected, DDR could be constrained at the ~3% level. Although the accuracy of this method with the present techniques may be not as competitive as the methods mentioned in the introduction, this is a unique way to test DDR using a single source.We use here the singular isothermal spherical (SIS) model as an example of how our method works. In the actual case, the lens model is generally more complex than the simple SIS model. If the matter distribution of the lens deviates from the simple SIS model, as for example in the more general power law model, most of our formulae still work, except for the change of the Einstein radius Eq. (1), and the form of the Fermi potential Eq. (5). Besides, some other uncertainties arise from the lens parameters, e.g. the index of the power law model. What is needed is to accurately model the mass distribution of the lens galaxy, regardless of its concrete form. It was shown that the redshift of the lens galaxy in strongly lensed GW systems is usually below
z∼1 [14, 43], which is a similar redshift range as of the lens galaxies in quasar lensing systems. In this redshift range, the dispersion velocity and mass distribution of the lens galaxy is expected to be measured with an acceptable accuracy by the future LSST survey using the photometric and spectroscopic data.The method proposed here does not depend on the cosmological model, but we assume that the universe is spatially flat. This assumption is reasonable because the observations of the cosmic microwave background radiation by the Planck satellite show that the data are consistent with a flat universe [45, 46]. If the universe is non-flat, the space curvature must be known in order to calculate the distance from the lens to the source, and Eqs. (6) and (7), which depend on the curvature, need to be modified. Very recently, some works found a moderate evidence of a closed universe [47, 48]. Even if the universe is non-flat, the distance measured in the local universe, where the strongly lensed GW events can be detected (
z≲5 ), is not strongly affected since the space curvature is small. Besides, the uncertainties of lens modelling and of the GW signal are much larger than the uncertainty due to the possible non-flatness of the universe. Therefore, our analysis does not strongly depend on the specific value of the space curvature.It should be noted that our calculations are based on the framework of general relativity. The violation of general relativity may, although not necessarily, cause a violation of DDR. If the future data show strong evidence of DDR violation, there may still be feasible interpretations. The violation of DDR may be caused, for example, by the dust extinction, coupling of photons or gravitons to some unknown particles, photons or gravitons which are massive, etc. The method proposed here can only test if DDR is valid or not. Interpreting the reason for DDR violation, however, requires further investigations.
-
In this paper, we proposed a new method to test DDR using the strongly lensed GW events. The photometric and spectroscopic observations of the source and lens galaxies, combined with the GW observation, provides a unique way to measure the angular diameter distance and the luminosity distance to the GW source. This is to our knowledge the first time a method is proposed to measure the angular diameter distance and the luminosity distance from the same object up to high redshifts. Although this method is beyond the present-day observational technology, we cannot exclude the possibility that it will be put into practice with the construction of the third generation GW detectors in the near future.
A new method to test the cosmic distance duality relation using the strongly lensed gravitational waves
- Received Date: 2020-01-17
- Available Online: 2020-07-01
Abstract: We propose a new method to test the cosmic distance duality relation using the strongly lensed gravitational waves. The simultaneous observation of the image positions, relative time delay between different images, redshift measurements of the lens and the source, together with the mass modelling of the lens galaxy, provide the angular diameter distance to the gravitational wave source. On the other hand, the luminosity distance to the source can be obtained from the observation of the gravitational wave signals. To our knowledge this is the first time a method is proposed to simultaneously measure the angular diameter distance and the luminosity distance from the same source. Hence, the strongly lensed gravitational waves provide a unique method to test the cosmic distance duality relation. With the construction of the third generation gravitational detectors such as the Einstein Telescope, it will be possible to test the cosmic distance duality relation with an accuracy of a few percent.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF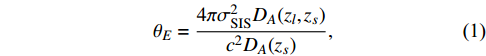
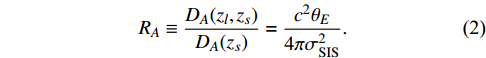
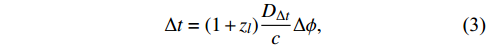
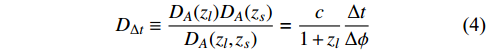
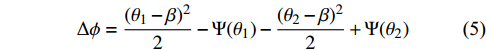
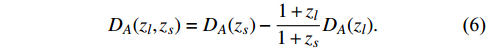
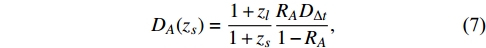
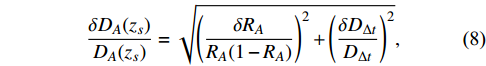
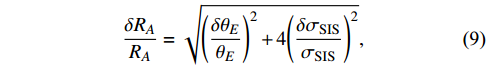
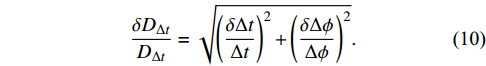
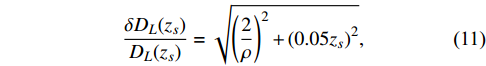
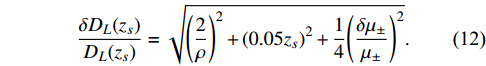
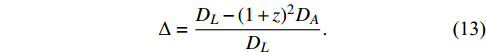
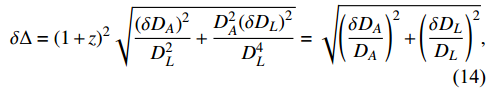

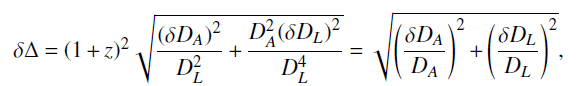



























 DownLoad:
DownLoad: