-
The
$ \alpha $ decay is among the most important decay modes for heavy and superheavy nuclei, and it has long been a useful tool in nuclear physics and astrophysics [1-6]. Measurements on$ \alpha $ decays have long been employed for investigations on the nuclear structure [7-12]. Various theoretical models based on the shell model, fission-like model, and cluster model are applied in such studies [13-18].During past decades, there has been an increasing desire to investigate the nuclear properties achieved by considering the influences of the neutron skin thickness (NST) on the alpha and cluster decay processes [19-22], where NST is defined by the difference between neutron and proton root mean square (RMS) radii,
$ \Delta{r_{np}}\equiv R_{n}-R_{p} $ , and it can be related to the difference in nuclear asymmetric equation states inside and on the surface of the nucleus [23-25]. It is expected that heavy nuclei have a neutron skin structure, and that most of them are alpha emitters [26]. The NST consideration can impact the alpha core potential, reducing the calculated half-life against$ \alpha $ decay [20, 22]. Microscopically, due to the 120Sn (p, p$ \alpha $ ) 116Cd, 12C (6Li, d) 16O, and 16O (6Li, d) 20Ni reactions, the$ \alpha $ clustering on the nuclear surface and surface peak position of the wave function are investigated [27-29]. Furthermore, by investigating the absolute decay width within shell models, cluster-like shell models, and Bardeen-Cooper-Schrieffer approaches, the essential prerequisite for a realistic model of the mother nucleus indicated that it should correctly describe the cluster correlation in the surface region [1]. Therefore, studies on the surface of the nuclei, where the alpha cluster forms, have become critical.Various studies have explored neutron and proton distributions and the measurement on RMS radii [19, 21, 23, 30, 31]. Although the RMS charge radii are accurately measurable by electron scattering, muonic atom X-rays, and the isotope shift [32], the neutron RMS radii of heavy nuclei are significantly less known. Furthermore, uncertainties of extracted neutron RMS radii are more than ten times larger than those of the charge radii [33]. Consequently, various theoretical and experimental studies have been employed for skin thickness of neutron and proton determinations [34-36]. Typically, the 208Pb is a nucleus with the double magic closed-shell, with its NST being widely investigated for decades [23, 37]. Experimentally, the measured neutron skin thickness of 208Pb ranges from 0.13 to 0.49 fm obtained by hadron scattering experiments involving pions, protons, and antiprotons, parity violation in electron scattering, measurements electric dipole polarizabilities of nuclei, and isospin diffusion in heavy-ion collisions [30, 33-37]. The uncertainty may originate from limitations in the measurements.
Numerous approaches are employed to study the ground-state properties of nuclei, such as symmetry energies, binding energies, RMS radius, and nucleon density distributions. The Hartree-Fock model based on Skyrme forces is a successful approach for examining the ground-state properties of nuclei that includes several microscopic and phenomenological models, such as the relativistic Dirac-Brueckner-Hartree-Fock, nonrelativistic Brueckner-Hartree-Fock, and the nonrelativistic mean-field model based on Skyrme-like interactions [38-47]. Generally, the
$ \alpha $ decay process occurs at low energy levels, typically$ (_{84}^{212}{\rm Po} = \,_{82}^{208}{\rm Pb} \otimes \alpha) $ , and this level of energy cannot cause sensible deviations in the ground-state and nuclear matter properties of an alpha emitter, suggesting that such investigations within the Hartree-Fock model and Skyrme forces are a good selection [48, 49]. Therefore, we carry out our studies by considering the same and constant mean-field, which simultaneously describing the ground-state properties of parent and daughter nuclei. In this work, by applying several Skyrme forces with their corresponding density distributions calculated from the Hartree-Fock model, we intend to examine the NST of the 208Pb and properties of the$ \alpha $ decay process for 212Po.This paper is organized as follows: the formalism of potential, half-life calculations, and the cluster formation model are illustrated in Sec. 2. Our results and discussion are presented in Sec. 3. The main results and conclusions are provided in Sec. 4.
-
The total potential
$ V(r) $ is written by$ V(r) = V_{\rm C}(r)+ V_{N}(r) + V_{\ell}(r), $

(1) where
$ V_{\rm C}, V_{N} $ , and$ V_{\ell} $ are the Coulomb potential, nuclear potential, and centrifugal potential, respectively. In this study, we investigated the$ \alpha $ decay of 212Po that the transferred angular momentum for this decay process is zero. Therefore, the total potential is$ V(r) = V_{\rm C}(r)+ \lambda V_{F}(r). $

(2) The nuclear part is obtained by the double-folding model within folding the densities of the
$ \alpha $ and the daughter nuclei with the effective M3Y interaction,$ V_{N} = \lambda V_{F}(r) = \lambda \iint{\rho_{\alpha}(r_{\alpha})\, V_{\rm eff}\, \rho_{d}(r_{d})\, {\rm d}^{3}r_{\alpha}\,{\rm d}^{3}r_{d}}, $

(3) where
$ \rho_{d} $ and$ V_{\rm eff} $ are the density of the daughter nucleus and the effective nucleon-nucleon interaction [50, 51], respectively. In this study, the$ \rho_{d} $ is calculated by Hartree-Fock formalism based on the Skyrme forces [38]. The density distribution function of the$ \alpha $ particle,$ \rho_{\alpha} $ , as used in the folding calculations, has the Gaussian form [52]$ \rho(r) = 0.4229\,{\rm e}^{-0.7024r^2}. $

(4) Here, we used the M3Y Reid-NN forces with a zero-range approximation for nucleon-nucleon interaction [53]. The parameter
$ \lambda $ in Eq. (2) changes the folded potential strength that is known as the strength parameter that is determined using the Bohr-Sommerfeld quantization condition [54-56]:$ \int_{r_{1}}^{r_{2}}\sqrt{\frac{2\mu}{\hbar^{2}}|V(r)-Q|}\,{\rm d}r = (2n + 1)\frac{\pi}{2} = (G-\ell+1)\frac{\pi}{2}, $

(5) where
$ r_{1} $ ,$ r_{2} $ (and$ r_{3} $ later) are classical turning points are obtained by$ V (r) = Q $ (the$ \alpha $ decay energy). The global quantum number G of a cluster state can be obtained by the Wildermuth condition [57]:$ G = 2N + \ell = \sum\limits_{i = 1}^{4}g_{i}, $

(6) where N is the number of nodes of the
$ \alpha $ -core wave function;$ \ell $ is the relative angular momentum of the cluster motion, and,$ g_{i} $ ; is the oscillator quantum number of a cluster nucleon. For$ \alpha $ decay, we can take G as$ G = 2N + \ell = \left\{ {\begin{array}{*{20}{l}} {18,}&{N \leqslant 82,}\\ {20,}&{82 < N \leqslant 126,}\\ {22.}&{N > 126.} \end{array}} \right. $

(7) The half-life of the
$ \alpha $ decay is$ T_{1/2} = \hbar \ln2/\Gamma_{\alpha} $ . In this relation,$ \Gamma_{\alpha} $ is the$ \alpha $ decay width of the cluster state within the Gurtviz and Kälbermann method, determined as [58]$ \Gamma_{\alpha} = P_{\alpha} F \frac{\hbar^{2}}{4\mu}{\rm exp}\left( -2\int_{r_{2}}^{r_{3}} k(r)\,{\rm d}r \right), $

(8) where F is normalization factor can be defined as below
$ F\int_{r_1}^{r_2}\frac{{\rm d}r}{k(r)}\, = 1, $

(9) and the wave number
$ k(r) $ is$ k(r) = \sqrt{\frac{2\mu}{\hbar^2}|V(r)-Q|}\,. $

(10) Finally,
$ P_{\alpha} $ is the spectroscopic or preformation factor, calculated by$ T_{1/2}^{\rm theo}/T_{1/2}^{\rm exp} $ . -
In the cluster formation model (CFM), it is assumed that the parent nucleus is a compilation of different cluster states [17]. For each preformation, there is a different wave function and a different Hamiltonian. Therefore, we assume that for each preformation or clusterization, there is a clusterization state represented by a wave function. If the parent nucleus has N different clusterization states with total energy E, the Hamiltonian
$ H_{i} $ belongs to the ith clusterization defined with an ith wave function, therefore$ H_{i}\Psi_{i} = E\Psi_{i} \qquad i = 1,2,\dots,N. $

(11) Therefore, this nucleus is described by a total time-independent wave function that is a linear combination of these clusterization orthonormalized wave functions
$ {\Psi _i} = \sum\limits_{i = 1}^N {{a_i}} {\Psi _i},$

(12) where
$ a_{i} $ are the amplitudes for the clusterization states of the complete set and within the orthogonality condition,$ \sum\limits_{i}^{N}|a_{i}|^{2} = 1. $

(13) Each cluster has specific formation energy
$ E_{fi} $ that$ E_{fi} = |a_{i}|^{2}E. $

(14) The probability of the
$ \alpha $ clusterization state$ P_{\alpha} $ is equivalent to$ a_{\alpha}^{2} $ . It can be calculated as:$ P_{\alpha} = |a_{\alpha}|^{2} = \frac{E_{f\alpha}}{E}. $

(15) Here,
$ a_{\alpha} $ and$ E_{f\alpha} $ denote the coefficient of the$ \alpha $ clusterization and the formation energy of an$ \alpha $ cluster, respectively. E is composed of the$ E_{f\alpha} $ and the interaction energy between$ \alpha $ cluster and daughter nuclei. The detailed illustrations are provided in Ref. [17]. In the framework of CFM, the$ \alpha $ cluster formation energy$ E_{f\alpha} $ and total energy E of a considered system can be expressed as:$ \begin{split} E_{f\alpha} =& 3B(A,Z)+B(A-4,Z-2)\\ &-2B(A-1,Z-1)-2B(A-1,Z), \end{split}$

(16) $ E = B(A,Z)-B(A-4,Z-2), $

(17) $ B(A, Z) $ is the binding energy of the nucleus with mass number A and proton number Z. These defined energies in Eq. (16) and Eq. (17) belong to even-even nuclei, and for an odd atomic number or odd neutron number, the formation energies are calculated differently [59, 60].Moreover, the formation probability of each cluster state calculates by the CFM can efficiently reproduce a more realistic formation probability, which follows the calculation of Varga et al. [13, 14].
-
To investigate the NST of 208Pb, we employed the density distributions that are self-consistently determined by Hartree-Fock calculations, based on different parameterizations of the Skyrme energy density functional. The Hamiltonian density functional used in this study and a more detailed discussion is presented in Ref. [61].
The energy per nucleon of an infinite asymmetric nuclear matter (ANM) with a proton fraction
$ \eta = Z/A $ in terms of the Skyrme energy density function is written as,$ \begin{split} E_{A} =& \frac{3\hbar^{2}}{10m}k^{2}_{F}H_{5/3}+\frac{t_{0}}{4}\rho\left[(x_{0}+2)-\left(x_{0}+\frac{1}{2}\right)H_{2}\right]\\ &+\frac{t_{3}\rho^{\sigma+1}}{24}\left[(x_{3}+2)-\left(x_{3}+\frac{1}{3}\right)H_{2}\right]\\ &+\frac{3k^{2}_{F}}{40}\bigg\{ (2t_{1}+2t_{2}+ t_{1}x_{1}+ t_{2}x_{2}) \rho H_{5/3} \\ &+\left(\frac{t_{2}}{2}-\frac{t_{1}}{2} + t_{2}x_{2}-t_{1}x_{1}\right)\rho H_{8/3}\bigg\}, \end{split} $

(18) where
$ k_{F} = (3\pi^{2}\rho/2)^{1/3} $ and$ H_{n}(\eta) = 2^{n-1}[\eta^{n}+(1-\eta)^{n}] $ . The parameters$ x_{0} - x_{3} $ ,$ t_0 - t_3 $ ,$ W_0 $ , and$ \sigma $ are obtained by fitting different properties of nuclei, m is the nucleon mass, and$ \rho = \rho_{\pi} + \rho_{\nu} $ is the nuclear density. The symmetry energy$ E_{\rm sym} $ is defined by expanding Eq. (18) as a function of$ \eta $ and$ \rho $ that measures the isospin dependence of the nucleon-nucleon (NN) interaction as,$ \begin{split} E_{\rm sym}(\rho) =& \frac{1}{8}\frac{\partial^{2}E_{A}(\rho,\eta)}{\partial \eta^{2}}\bigg|_{\eta = \frac{1}{2}} = \frac{\hbar^{2}k^{2}_{F}}{6m}\\ &-\frac{t_{0}}{4}\left(x_{0}+\frac{1}{2}\right)\rho-\frac{t_{3}}{24}\left(x_{3}+\frac{1}{2}\right)\rho^{\sigma+1}\\ &+\frac{k^{2}_{F}}{24}\{(4t_{2}-3t_{1}x_{1}+5t_{2}x_{2})\rho\}. \end{split} $

(19) The symmetry energy coefficient
$ a_{\rm sym} = E_{\rm sym}(\rho_{0}) $ is defined at the normal saturation density$ \rho_{0} $ . Further, another important quantity associated with the symmetry energy is the slope L of its density dependence. It can be written in the form$ \begin{split} L =& 3\rho_{0}\frac{\partial E_{\rm sym}(\rho)}{\partial \rho}\bigg|_{\rho_{0}} = \frac{\hbar^{2}k^{2}_{F0}}{3m}\\ &-\frac{3t_{0}}{4}\left( x_{0}+\frac{1}{2} \right)\rho_{0}-\frac{t_{3}}{8}\left(x_{3}+\frac{1}{2}\right)(\sigma+1)\rho_{0}^{\sigma+1}\\ &+\frac{k^{2}_{F0}}{24}[5(4t_{2}-3t_{1}x_{1}+5t_{2}x_{2})\rho], \end{split} $

(20) with
$ k_{F0} = (3\pi^{2}\rho_{0}/2)^{1/3} $ .The volume incompressibility of ANM at saturation density is calculated as the derivative of pressure
$ P = \rho^{2} \frac{\partial(E_{A})}{\partial \rho} $ with respect to the number density$ \rho $ :$ K = 9\frac{\partial P}{\rho} = 9\rho^{2}\bigg(\frac{\partial^{2}E_{A}}{\partial \rho^{2}}\bigg). $

(21) To achieve an evaluation about the NST of nuclei, we calculated the neutron and proton RMS radii within nucleon density distributions, estimated by various Skyrme forces that they are expressed as
$ R^{\rm rms}_{n(p)} = <R^{2}_{n(p)}>^{1/2} = \, \left(\frac{\int r^{2}_{n(p)}\rho_{n(p)}({{r}}){\rm d}{{r}}} {\int \rho_{n(p)}({{r}}){\rm d}{{r}}} \right)^{1/2}. $

(22) To calculate the NST value within RMS radii that are obtained by Eq. (22), we used the nucleon density distributions that are being estimated by the Hartree-Fock based on the Skyrme forces. We assumed that the mean-fields and the Skyrme forces that describe the nuclear matter and ground-state properties of parent and daughter would not be affected by the
$ \alpha $ decay process, as the$ \alpha $ decay process is a low energy phenomenon, and the amount of required energy for the transition from initial interior alpha clusterization state bound with daughter nucleus to free alpha particle and the daughter nucleus is not as significant, as it can actually cause a sensible variation in the ground-state properties of alpha emitters [17]. Therefore, from this viewpoint, we selected the same mean-field and Skyrme forces that can simultaneously describe the ground-state properties of 212Po and 208Pb.We investigated the NST value of 208Pb and its effects on the
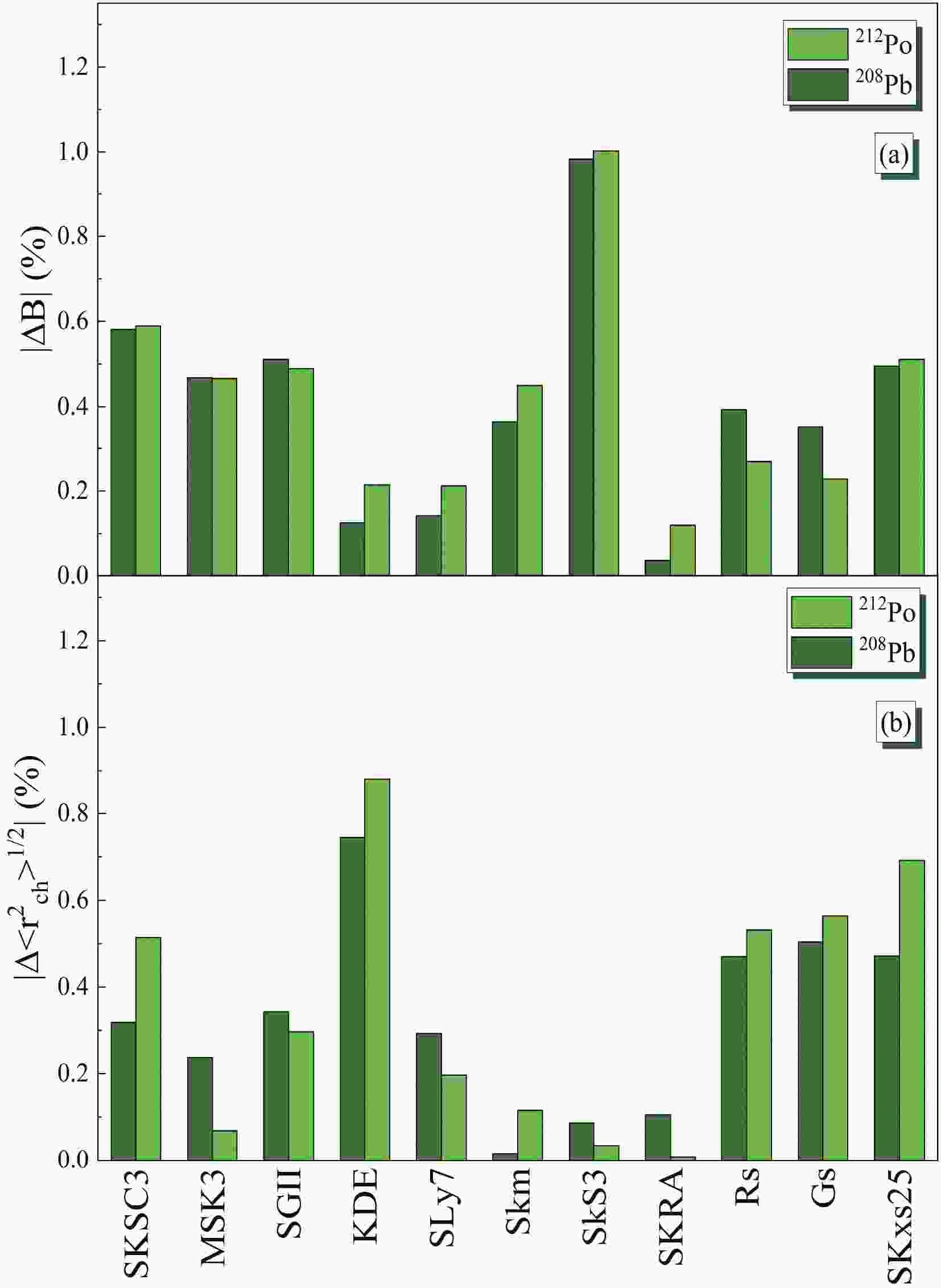
$ \alpha $ decay process of 212Po by employing various Skyrme NN interactions, associated with an extensive slope of the symmetry energy range from$ -49.7 $ to$ 100.1 $ MeV and with different nuclear matter incompressibility range from$ 200 $ MeV to$ 370 $ MeV, yielding different equations of state, binding energies, and RMS radii. The percentage of relative deviations for the calculated binding energies and the RMS radii for 212Po and 208Pb from their corresponding empirical values are presented in Fig. 1. The selected mutual forces SKxs25 ($ L = 100.10 $ MeV) [62], SGII ($ L = 37.63 $ MeV) [63], SKRA ($ L = 53.04 $ MeV) [64], Skm ($ L = 49.34 $ MeV) [65], KDE ($ L = 41.42 $ MeV) [66], SkS$ 3 $ ($ L = 51.74 $ MeV) [67], SLy7 ($ L = 46.94 $ MeV) [68], SKSC$ 3 $ ($ L = 0.81 $ MeV) [69], MSK$ 3 $ ($ L = 7.04 $ MeV) [70], Gs ($ L = 93.31 $ MeV) [47], and Rs ($ L = 86.39 $ MeV) [47] are presented, which can simultaneously estimate the binding energies and RMS radii of parent and daughter nuclei with relative deviations of less than one percent. The experimental binding energies for 212Po and its daughter 208Pb are$ 1655.771 $ MeV and$ 1636.430 $ MeV, respectively. The experimental RMS radius of the daughter nucleus is$ 5.5012 $ fm [32]. Since the experimental RMS value for 212Po has not been reported yet, the relation,$ R_{\rm ch}^{\rm RMS} = (r_{0}+r_{1} A^{-2/3}+r_{2} A^{-4/3}) A^{1/3} $ with$ r_{0} = 0.9071(13) $ fm,$ r_{1} = 1.105(25) $ fm, and$ r_{2} = -0.548(34) $ fm, is adopted for determining RMS radius 212Po. This relation is obtained by fitting to the experimental data of the ground-state RMS radii for a wide range of the nuclei [32].
Figure 1. (color online) Percentage of relative deviations of theoretical binding energies and root-mean-square charge radii from their experimental data for 212Po and 208Pb nuclei in (a) and (b), respectively.
The calculated NST values of 208Pb within Eq. (22) and the neutron and proton density distributions associated with the selected Skyrme forces as a function of the symmetry energy (L) are presented in Fig. 2. The results indicate an increasing trend for NST values as a function of the L. This tend could be owing to the density dependence of the nuclear symmetry energy. In principle, it can be obtained from the NST in heavy nuclei, since it is strongly correlated with the slope parameter L of the nuclear matter symmetry energy at saturation density [24, 71-74]. Hence, the Skyrme forces that have a different estimation regarding the nucleon distributions, yielding different NST, it is possible that the NST to be affected by different symmetry energies corresponding to each Skyrme force. It can be expected that by increasing the nuclear symmetry energy, the differences between proton and neutron density distributions in the considered nucleus becomes more apparent [49, 75]. As shown in Fig. 2, the slope of the nuclear symmetry energy can be higher, where the neutron distribution is more different than the proton density distribution.
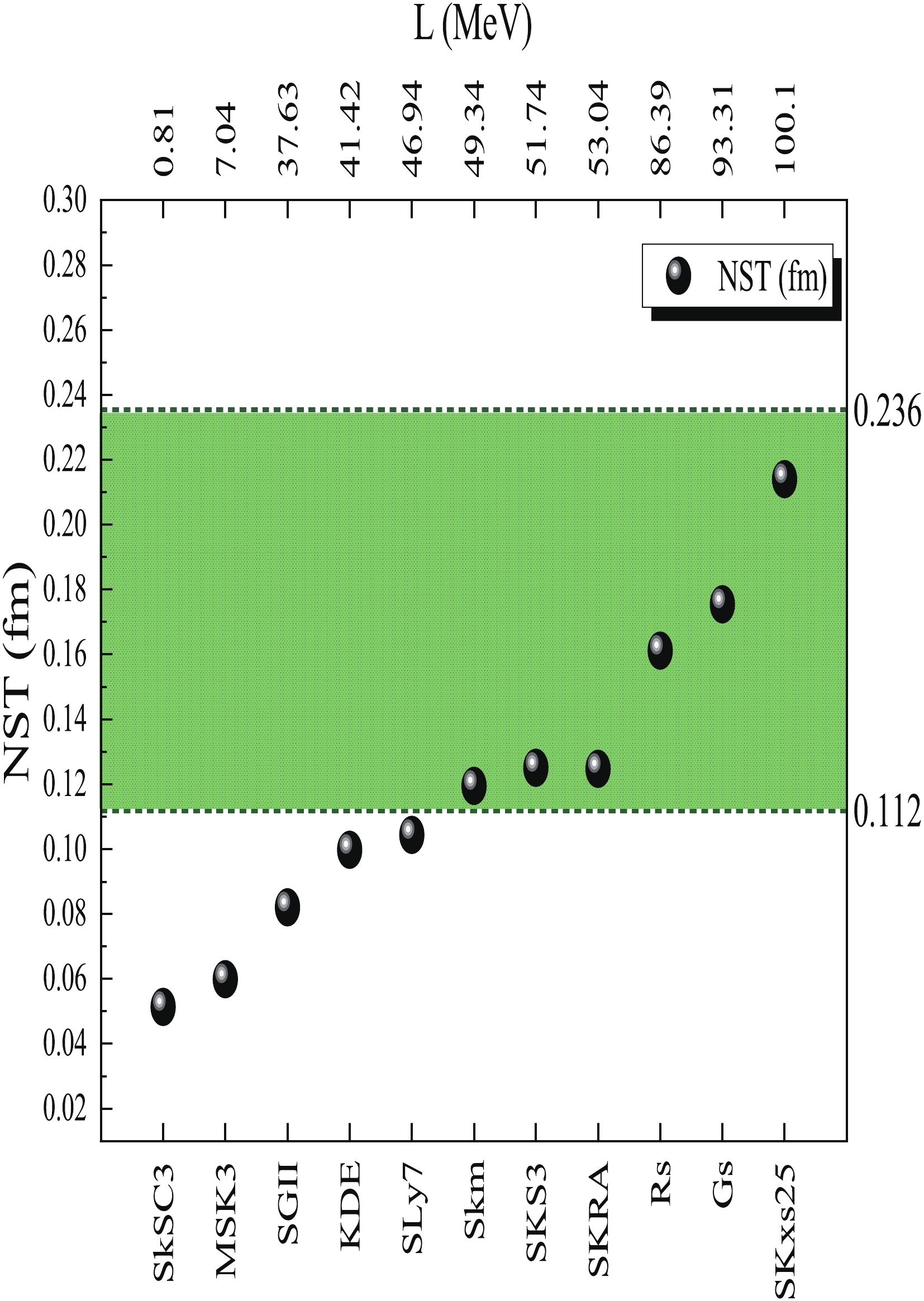
Figure 2. (color online) Calculated NST for selected Skyrme forces, colored region indicates NST values calculated by linear relationship presented in Ref. [34].
Since the neutron RMS radii of nuclei are less known in comparison with proton RMS radii, two extreme modes are usually employed to investigate the NST of the nuclei. The "neutron skin type" distribution is defined as
$ r_{n}>r_{p} $ and$ a_{n} = a_{p} = 0.54 $ fm and the "neutron halo type" distribution is understood as$ r_{n} = r_{p} $ and$ a_{n}>a_{p} $ [34]. Consequently, depending on which type is being considered for nuclei, the extracted NST contains uncertainty. Different experimental and theoretical investigations have been performed to evaluate NST to keep away from these extreme modes, especially for 208Pb. For instance, the neutron skin thickness of 208Pb was extracted as$ \Delta R_{np} = 0.15\pm $ $0.03(\rm stat.)^{+0.01}_{-0.03}(\rm sys.) $ fm from coherent pion photo production cross-sections, and the lead radius experiment (PREX) collaboration of JLab measured it as$ \Delta R_{np} = 0.33^{+0.16}_{-0.18} $ fm through parity-violating electron scattering [76, 77]. Further, a linear relationship between$ \Delta R_{np} $ with the isospin asymmetry$ \delta = (N-Z)/A $ is found by antiprotonic atom X-ray data, which is expressed as [34]$ \Delta R_{np} = (-0.04\pm0.03)+(1.01\pm0.15)\delta. $

(23) This relationship yields a value of
$ \Delta R_{np} = 0.174(62) $ fm for 208Pb, which is consistent with both the empirical values and theoretical predictions. The NST range of the 208Pb extracted by this relationship is in the range from 0.112 to 0.236 fm, as indicated by the green band in Fig. 2. The Skyrme forces Skm, SKS3 , SKRA, Rs, Gs, and SKxs25 are located within this green band.The effect of the NST consideration on the total potential calculation is shown in Fig. 3(a), typically for the Skyrme force
$ {\rm Rs} $ . The non-zero NST can cause a reduction in the total potential calculation. As illustrated in Fig. 2, the symmetry energy can affect the neutron skin thickness and nucleon density distributions. Hence, to investigate the effects of these nucleon density distributions that are theoretically suggested for 208Pb on the total potential, we calculated the total potential by the double-folding model and those neutron and proton density distributions that are corresponding to selected Skyrme forces. These influences on the calculated total potentials for sets of Skyrme forces SKxs25, SKRA, Skm, SkS3, Gs, and Rs that their NST values located in the range of experimental data, the green band in Fig. 2, are shown in Fig. 3(b), especially from the first turning point to the distance$ r = 11 $ fm. Differently calculated total potentials Fig. 3(b) represent that the choice of each characteristic nucleon density distribution can cause sensible variation in the calculation of the total potential.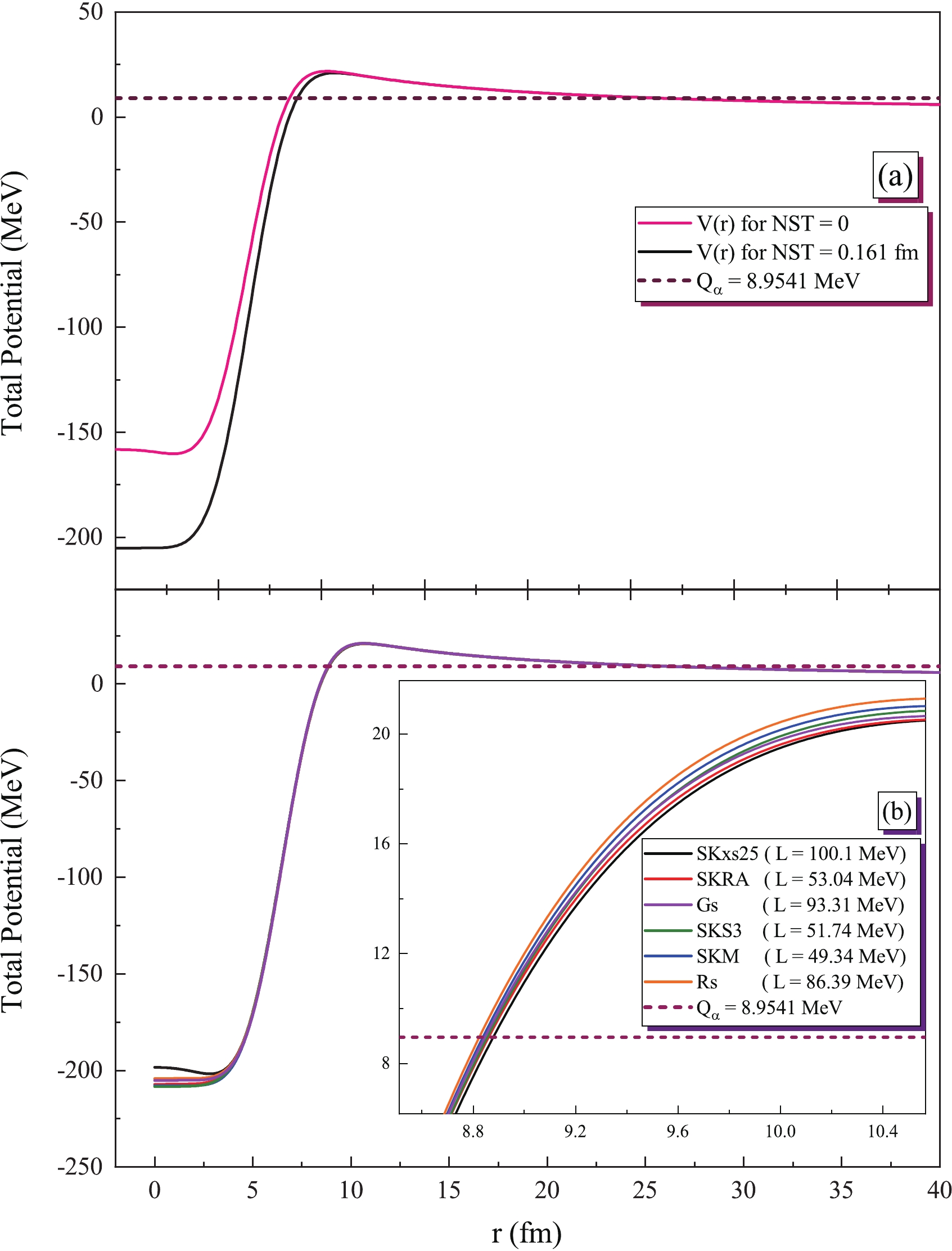
Figure 3. (color online) (a) Calculated total potential for
$\Delta{r_{np}} = 0 $ and$\Delta{r_{np}} = 0.161$ fm for Rs Skyrme force and (b) calculated total potential within different nucleon density distributions showing NST values in the range of the experimental data.By employing these total potentials, we calculated
$ \alpha $ decay half-lives and$ \alpha $ formation probabilities that were obtained by$ T_{1/2}^{\rm theo}/T_{1/2}^{\rm exp} $ presented in Fig. 4 and Fig. 5, respectively. To simultaneously satisfy the predictions of different theoretical models and experimental data, the evaluation of our estimated formation probabilities with the prediction of CFM would be beneficial, since the 212Po has a high cluster-like structure.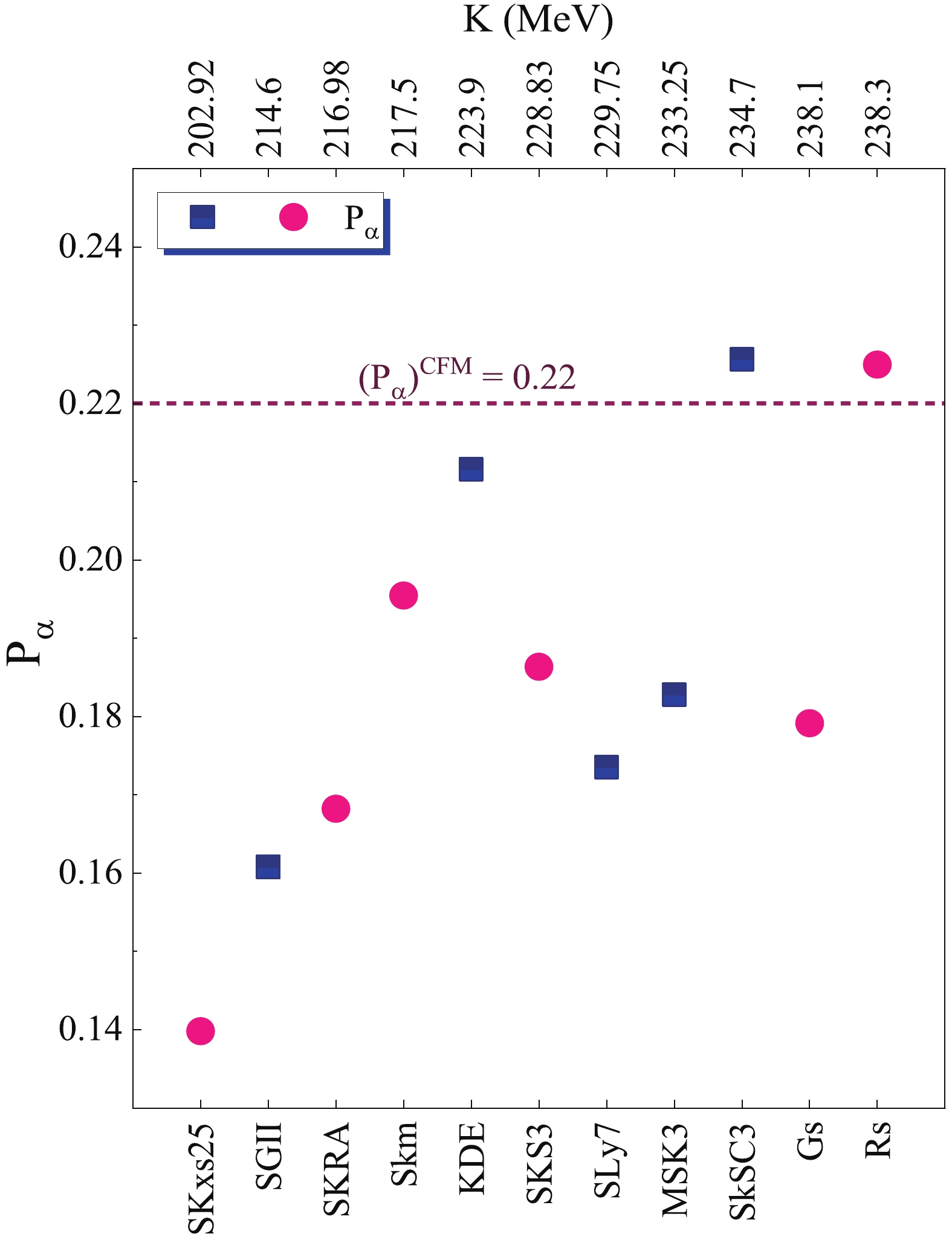
Figure 5. (color online) Calculated alpha formation probabilities for each Skyrme force. Dashed line depicts alpha formation probability within cluster model framework. Circles depict forces showing that their NST values are in the range predicted by Eq. (23) located within green band in Fig. 2.
The CFM illustrates each possible cluster formation probability in parent nuclei, such that its estimations will be more accurate for the nuclei with cluster-like structures, especially. This cluster-like structure supports the alpha clustering occurrence at the surface of alpha emitters [1, 14, 57]. The estimated
$ \alpha $ cluster formation probability within CFM by the use of experimental binding energies in$ \alpha $ decay for 212Po is 0.22, indicated by the dashed line in Fig. 5. Further, from all Skyrme forces presented in Fig. 5, the estimated$ \alpha $ formation probabilities of the SKxs$ 25 $ , SKRA, Skm, SkS$ 3 $ , Gs, and Rs indicate formation probabilities that correspond to the forces that their NST values satisfy in the experimental data. Therefore, the estimated$ \alpha $ formation probabilities associated with these mentioned forces can be acceptable. The obtained results in Fig. 4 and Fig. 5 indicate that, although the$ \alpha $ decay process is not capable of changing nuclear matter properties, different nucleon density distributions associated with the different symmetry energies can affect the$ \alpha $ decay investigations, theoretically. The presented result in Fig. 4 indicates that the estimated half-lives within the SKxs$ 25 $ , SKRA, Skm, SkS$ 3 $ , Gs, and Rs Skyrme forces that their NST values are consistent with the experimental data, and they vary from$ 42 $ ns for SKxs$ 25 $ (with$ L = 100.1 $ MeV) to$ 68 $ ns for Rs (with$ L = 86.39 $ MeV) following with the NST variation.Moreover, from those estimated
$ \alpha $ formation probabilities within SKxs$ 25 $ , SKRA, Skm, SkS$ 3 $ , Gs, and Rs indicated by circlular shapes in Fig. 5, the Skyrme force$ {\rm Rs} $ can efficiently reproduce the formation probability calculated within CFM characterized by dashed line Fig. 5. Therefore, one can expect that$ {\rm Rs} $ is one of the appropriate forces for studying the nuclear properties of 208Pb within$ \alpha $ decay of 212Po. The obtained results indicate that the$ \alpha $ decay half-life and its preformation probability can be affected by 10% for 212Po by assuming the$ \alpha $ emitter in the different nuclear matter incompressibilities and symmetry energies. Such influences may imply that the theoretical studies for$ \alpha $ decay can be affected by each nuclear matter property that is being considered for the nuclei in their ground-states. Although KDE and SKSC3 satisfy the alpha formation probability of the CFM, their NST values are not consistent with experimental data. Furthermore, the most common approaches are estimating the NST value of 208Pb, which ranges from$ 0.14 $ to$ 0.18 $ fm [23, 34, 35, 63, 70, 78]. Our estimated NST value of 208Pb is consistent with these measured values.The values of the slope of the symmetry energy, L, corresponding to each Skyrme force, are shown in the upper axis of Fig. 2. The predicted values of NST increase with increasing L, and this increasing trend can be attributed to the variation of the symmetry energy. Because the symmetry energy correlates with the isospin asymmetry of the nuclei, one can expect that any variation in symmetry energy can cause variation in the nucleon density distributions. Therefore, the higher symmetry energy can cause the differences between neutron and proton density distributions to become more apparent. As presented in Fig. 2, the slope of the symmetry energy for 208Pb is estimated to be
$ 75\pm25 $ MeV, characterized by the sets of Skyrme forces SKxs$ 25 $ , SKRA, Skm, SkS$ 3 $ , Gs, and Rs, with their NST values located in the range of the experimental data. In contrast, due to the coherent pion photoproduction and PREX experiments on the measuring the NST value of the 208Pb, and strong correlation between NST and the slope of the symmetry energy through the various cluster radio-activities, the estimated L values of the 208Pb attributed to these experiments are$ L(\rho_{0}) = $ $85\pm10 $ MeV, and$ L(\rho_{0}) = 80-170 $ MeV, respectively [19]. Therefore, a good agreement can be seen between these reported values and our estimated slope of the symmetry energy for 208Pb. However, the sets of Skyrme forces SKxs$ 25 $ , SKRA, Skm, SkS3, Gs, and Rs can theoretically be acceptable forces. According to the obtained results, the Rs force ($ \Delta{r_{np}} = 0.161 $ fm,$ L = 86.39 $ MeV,$ K = 238.30 $ MeV, and$ a_{\rm sym} = 29.20 $ MeV can efficiently and simultaneously satisfy the experimental NST value, alpha formation probability estimates by CFM, and obtained slope of the symmetry energy for 208Pb.Typically, the half-height radius and diffuseness of proton density distribution, which are determined by fitted two-parameter Fermi distribution function to the density associated with Skyrme force Rs, are
$ 6.5961 $ fm and$ 0.4865 $ fm, respectively, while these values for neutron density distribution are$ 6.8192 $ fm and$ 0.5496 $ fm, respectively. These estimated parameters indicate remarkable differences between half-height radii and diffuseness of proton and neutron density distributions, whereas they are not observed in the neutron skin type and neutron halo type. Thus, one can expect that some extreme states are being avoided by more detailed information on the nuclei properties. -
We investigated the NST value of 208Pb and the nuclear properties of the
$ \alpha $ decay process for 212Po. For evaluating the ground-state properties of 212Po and 208Pb, we used various Skyrme forces associated with an extensive slope of the symmetry energy. We conducted our investigations with the viewpoint that the employed mean-field and Skyrme forces remained constant throughout the$ \alpha $ decay process of 212Po. The influences of the selected neutron skin thickness on the$ \alpha $ decay half-lives and formation probabilities are determined. To consider the experimental NST values and CFM in our calculation, since the 212Po has a high cluster-like structure, the Skyrme forces that could simultaneously reproduce the experimental NST values and cluster properties of the 212Po were selected. The slope of the symmetry energy of the 208Pb is estimated to be$ 75\pm25 $ MeV by employing the sets of Skyrme forces SKxs$ 25 $ , SKRA, Skm, SkS$ 3 $ , Gs, and Rs, such that their NST values are consistent with the experimental data, where the$ {\rm Rs} $ Skyrme force with an NST value$ 0.161 $ fm can efficiently satisfy the experimental and theoretical approaches. Furthermore, the estimated$ \alpha $ formation probability by the$ {\rm Rs} $ force corresponded to values calculated by the cluster model approach.
Constraints on neutron skin thickness and symmetry energy of 208Pb through Skyrme forces and cluster model
- Received Date: 2019-12-02
- Available Online: 2020-05-01
Abstract: We used the cluster structure properties of the 212Po to estimate the neutron skin thickness of 208Pb. For this purpose, we considered two important components: (a) alpha decay is a low energy phenomenon; therefore, one can expect that the mean-field, which can explain the ground state properties of 212Po, does not change during the alpha decay process. (b) 212Po has a high alpha cluster-like structure, two protons and two neutrons outside its core nucleus with a double magic closed-shell, and the cluster model is a powerful formalism for the estimation of alpha decay preformation factor of such nuclei. The slope of the symmetry energy of 208Pb is estimated to be





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: