-
One of the astonishing discoveries of the heavy-ion collision program at the relativistic heavy-ion collider (RHIC) and at the Large Hadron Collider (LHC) is that the medium thus created acts like near-perfect fluid [1-5]. Offering low viscosity and high opacity, this fluid is called the strongly coupled quark-gluon plasma (QGP) [6]. Penetrating and well calibrated probes are needed for quantitative deduction of the properties of QGP. Heavy quarks (HQs) especially charm quarks, which are produced in primordial hard collisions and behave like an impurity in QGP, have been used as probes of the properties of QGP [7, 8]. The diffusion of HQs in QGP is similar to the Brownian motion of gas molecules with multiple collisions with other molecules [9]. Delayed by a factor of ~
$\frac{{{m_Q}}}{T} = 6 - 20$ , thermal relaxation time of HQs (with the charm quark mass~1.5 GeV and the bottom quark mass~4.8 GeV) is much larger than the rest of the bulk medium. Therefore, HQs are not fully equilibrated with the surrounding medium as they diffuse in it. Yet HQs undergo multiple collisions with medium constituents and lose their energy and momentum as they approach thermal equilibrium. As a result, HQs develop significant momentum anisotropies through collisions with the medium in non-central heavy-ion collisions [10-12]. The p+p and p+A collisions provide the baseline results to study the full heavy-ion (Au+Au or Pb+Pb) collision spectra.Many theoretical approaches [13-17] (and references therein) have been applied to explain the single HQ diffusion in QGP, especially the Fokker-Planck and Boltzmann transport approaches. In these approaches, two important constituents are required for quantitative calculations of the HQ transport; one is an excellent understanding of microscopic interactions of HQs in QGP, which are characterized by their transport (diffusion and drag) coefficients (in particular at low and intermediate momenta). The second is a realistic description of the expanding medium through which HQs propagate [18]. Traditional observables include the elliptic flow (v2) and the nuclear modification factor (RAA), which describe the consequences of single HQ propagation in the deconfined phase of strongly coupled QGP in realistic simulations. The elliptic flow implies active anisotropic collective motion of heavy quarks in the expanding hot and dense fireball. The nuclear modification factor describes the suppression at high transverse momentum (pT) because of substantial energy loss of fast moving HQs while traversing the medium. However, more detailed characterization of the QGP properties requires new observables beyond the traditional ones, such as the heavy quark-antiquark (
$Q\bar Q$ ) pair azimuthal correlation, which has gained special attention in recent studies [19, 20]. Previously, the fireball+Langevin model has been used to calculate the traditional observables of single heavy quark diffusion in QGP [6, 18]. We generalize this model to investigate the azimuthal correlations among the charm-anticharm ($c\bar c$ ) pairs. Azimuthal correlations dN/dϕ among$c\bar c$ pairs and the changes in these correlations during their diffusion in QGP is a matter of interest. In this work, we limit our study to the leading order (LO) (production of heavy quarks in the initial hard scatterings)$Q\bar Q$ azimuthal back-to-back (Δϕ=π) correlations [19]. Because of multiple collisions and energy losses of the$Q\bar Q$ pair with the medium constituents, these initial correlations are broadened [21-23]. At low pT, the initial correlations are largely washed out, indicating the presence of a locally thermalized partonic plasma. The$c\bar c$ pairs with minimal initial momentum are expected to lose not only their initial back-to-back correlations but also to be pushed into the same direction by the outward collective flow of the medium, thus obtaining a final correlation around (Δϕ$\simeq 0$ ). This effect is called the “partonic wind” effect [24]. At high pT, the back-to-back correlations are expected to largely survive the evolution of the medium. The purpose of the present work is to establish a quantitative framework for the diffusion of charm-anticharm quark pairs in the deconfined and strongly coupled medium, which are used to probe the properties of QGP. Non-perturbative elastic diffusion of HQs in the QGP medium and the modification of azimuthal correlations between the$c\bar c$ pairs are simulated by the fireball+Langevin dynamics, from which single charm quark diffusion (RAA and v2) and azimuthal angle correlations dN/dϕ of${c\bar c}$ pairs, at different thermal relaxation rates and different transverse momenta, are investigated.The rest of the paper is organized as follows. In Section 2, the fireball model [18] is described briefly. In Section 3, the Langevin process based on the Fokker-Plank equations [10] is elaborated. In Section 4, a brief introduction of the thermal relaxation rate is given. In Section 5, the simulation results are presented and discussed, including the single HQ and correlated
$c\bar c$ observables. Finally, in Section 6, a summary and conclusions are given. -
Considering the elliptic fireball model [18] for the medium expansion and its evolution, the expansion parameters of the created fireball are given as
${a_t} = {a_0} + {v_0}\left[ {t - \frac{{1 - {e^{ - {K_1}t}}}}{{{K_1}}}} \right] - \Delta v\left[ {t - \frac{{1 - {e^{{K_2}t}}}}{{{K_2}}}} \right] \tag{1a}, $

(1a) ${b_t} = {b_0} + {v_0}\left[ {t - \frac{{1 - {e^{ - {K_1}t}}}}{{{K_1}}}} \right] - \Delta v\left[ {t - \frac{{1 - {e^{{K_2}t}}}}{{{K_2}}}} \right]\tag{1b},$

(1b) where a0=5.563 fm, b0=4.451 fm, v0=0.519c, Δv=0.1229c, K1=0.552 c/fm, K2=1.31 c/fm. The volume of the fireball as a function of time is written as follows
${V_{fb}}(t) = \pi {a_t}{b_t}z$

(2) where
$z = {z_0} + ct$ . z0 and z are the initial and final positions of the fireball along the$z - $ axis, c is the speed of light and t is time. The transverse flow v(t, x) is parametrized by the elliptical coordinates in the transverse plane (x, y).$(x,y) = r = [{a_0}\sinh ({\rm{\mu}} )\cos ({\rm{\nu}} ),{a_0}\cosh ({\rm{\mu}} )\sin ({\rm{\nu}} )],$

${r_{{K_2}}} = [{b_t}\cos ({\rm{\nu}} ),{a_t}\sin ({\rm{\nu}} )],$

(3) ${v_a}(t) = \frac{{{\rm d}{a_t}}}{{{\rm d}t}},{v_b}(t) = \frac{{{\rm d}{b_t}}}{{{\rm d}t}},$

$v = \left[ {\frac{r}{{{r_{{K_2}}}}}{v_b}\cos ({\rm{\nu}} ),\frac{r}{{{r_{{K_2}}}}}{v_a}\sin ({\rm{\nu}} )} \right].$

(4) We assume an isentropic expansion of the fireball medium created in Pb+Pb collisions at 2.76 TeV. We use the massless ideal gas equation of state (EoS) for QGP to gauge the temperature evolution of the fireball. The energy density (
${\varepsilon _{\rm QGP}}$ ) and the pressure density (${P_{\rm QGP}}$ ) of QGP are related by the following relation:${\varepsilon _{\rm QGP}} = T{s_T} - {P_{\rm QGP}},$

(5) where sT is the entropy density and T represents the temperature of the medium. The energy density and pressure density are given by
$ {{\rm{\varepsilon}} _{\rm QGP}} = \frac{\pi }{{30}}[16 + 10.5{N_F}]{T^4} + {B_{\rm QGP}}, $

(6) $ {P_{\rm QGP}} = \frac{{{{\rm{\varepsilon}} _{\rm QGP}}}}{3} = \frac{\pi }{{90}}[16 + 10.5{N_F}]{T^4} - {B_{\rm QGP}}, $

(7) with the bag constant
${B_{\rm QGP}} = \frac{{2.04N}}{{\begin{array}{*{20}{c}}{4\pi {R^4}}\end{array}}} = 356\frac{{\rm MeV}}{{{\rm f}{{\rm m}^3}}}$ in a first order phase transition scenario [18]. The entropy density then reads${s_T} = \frac{S}{{{V_{fb}}(t)}} = \frac{{4{\pi ^2}}}{{90}}g{T^3},$

(8) where g is the combined degeneracy of quarks and gluons, with g=16+10.5NF. NF is the number of quark flavors equal to 2.5 (taking into account the larger mass of strange quarks). For semi-central 2.76 TeV Pb+Pb collisions with an impact parameter b=7 fm, the total entropy S of the system
$ S = {s_T}{V_{fb}}(t) \approx 9000 $

(9) is determined by fitting the multiplicity of the charged particles per unit pseudo-rapidity
$\left({\frac{{{\rm d}{N_{ch}}}}{{{\rm d}\eta }}\sim 720} \right)$ produced in such a collision. Eq. (8) can also be re-arranged for the temperature of the medium, which is time dependent:$T(t) = {\left[ {\frac{{90}}{{4{\pi ^2}}}\frac{S}{{g{V_{fb}}(t)}}} \right]^{1/3}}.$

(10) The variation of temperature with respect to the lifetime of the QGP phase is shown in Fig. 1. The initial QGP temperature is taken as T
$ \simeq 340$ MeV, which decreases to the phase transition (first order) temperature Tc$ \simeq 180 $ MeV after 4.341 fm/c. During the mixed phase, the temperature remains constant at Tc$ \simeq 180$ MeV, and the curve becomes flat. In the fireball+Langevin simulations, the medium evolution lasts until the end of the mixed phase. The temperature-time evolution of the QGP fireball starts at τ0=0.6 fm/c (the longitudinal proper time τ is the same as the laboratory time t at mid-rapidity) and stops at almost τ =7.6 fm/c, corresponding to the decoupling energy density of edec=0.4435 GeV/fm3. The dominant shape of the fireball is elliptic (almond-shaped). Pressure gradients are created by the interactions between particles in the fireball so that the initial spatial asymmetry is converted into particle momentum anisotropy between px and py, described by the coefficient of the second harmonic (elliptic flow) of the azimuthal angle distributions [25, 26].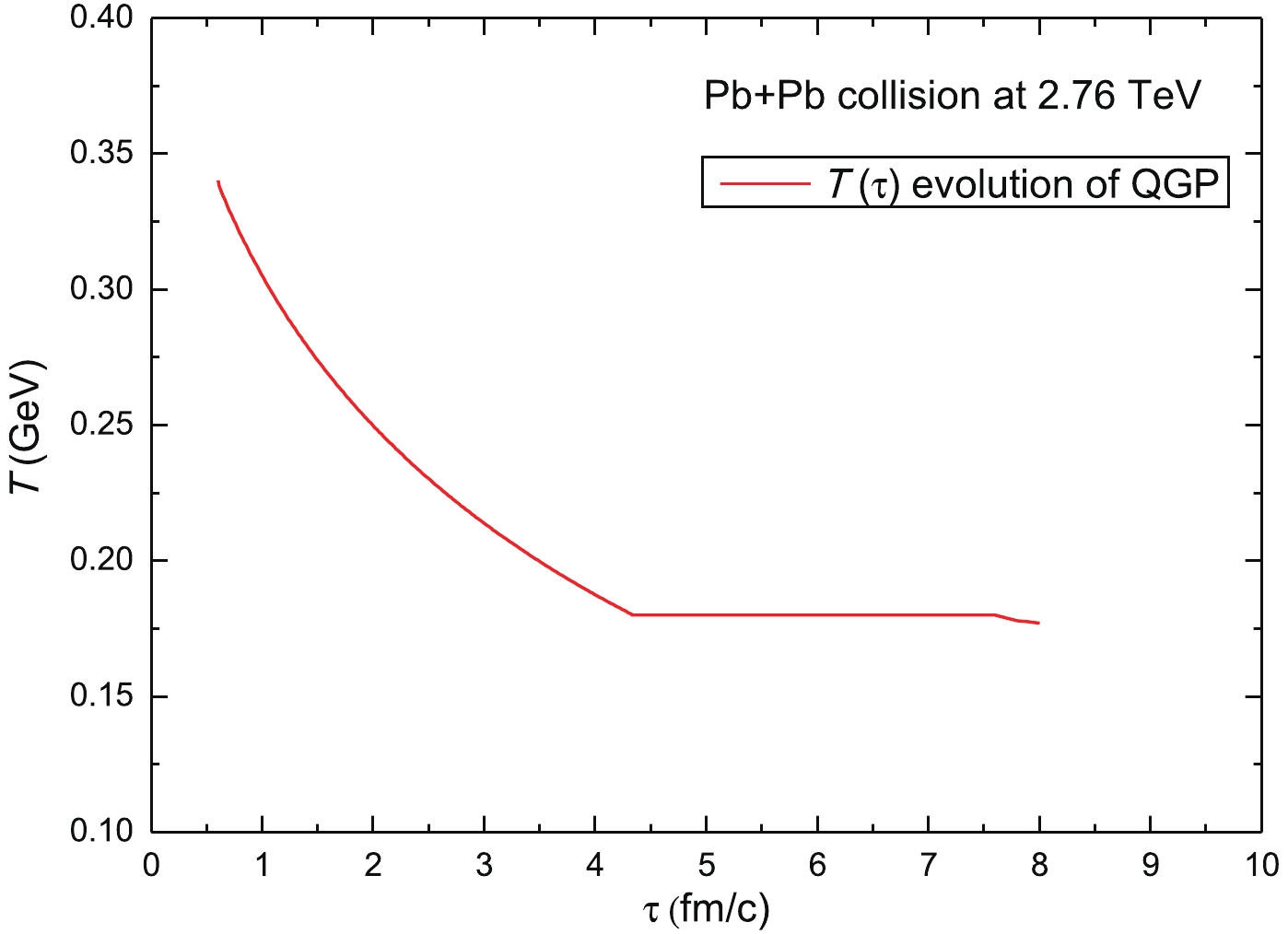
Figure 1. (color online) Temperature-time profile for the elliptic fireball evolution in Pb+Pb collisions at 2.76 TeV. Different lifetimes of QGP and mixed phases can be observed.
Transverse momentum of the particles is
${p_T} = \sqrt {p_x^2 + p_y^{2}} $ .$\frac{{{\rm d}N}}{{{p_T}{\rm d}{p_T}{\rm d}{\phi _p}}} = \frac{{{\rm d}N}}{{2\pi {p_T}{\rm d}{p_T}}}\left[ {1 + 2{v_2}\left( {{p_T}} \right){\rm{cos}}\left( {2{\phi _p}} \right) + \ldots } \right].$

(11) -
The Langevin equations [6] are given as
${\rm d}{x_i} = \frac{{{p_i}}}{E}{\rm d}t,$

(12) $ {\rm d}{p_i} = - \Gamma (T,p){p_i}{\rm d}t + \sqrt {{\rm d}t} {G_{ij}}(T,p + \chi {\rm d}p){{\rm{\rho}} _j}, $

(13) which specify the rules to update the position (x) and momentum (p) of HQ in a time step dt. The friction force is
${\rm{\Gamma }}$ (T, p) p , and ρj is the independent Gaussian noise which follows the normal distribution.$ \in (p) = \frac{{\exp \left( { - {{{\rho ^2}} / 2}} \right)}}{{{{\left( {2\pi } \right)}^{{3 / 2}}}}}$

(14) $E\left(p \right) = \sqrt {m_Q^2 + {p^{2}}} $ is the relativistic on-shell energy of the Brownian particle and mQ is the mass of the heavy quark. The matrix of coefficients Gij describes the stochastically fluctuating force.${\rm{\Gamma }}\left(p \right)$ is the drag coefficient and T is the equilibrium temperature of the medium.The Fokker-Planck equation for the phase-space distribution function “f” of the Brownian particle is
$\frac{{\partial f(t,p)}}{{\partial t}} = \frac{\partial }{{\partial {p_k}}}\left[ {{U_k}(p)f(t,p) + \frac{\partial }{{\partial {p_l}}}\left\{ {{W_{kl}}(p)f(t,p)} \right\}} \right],$

(15) where
$k,l \in \left\{ {1,2,3} \right\}$ .${U_k}\left(p \right)$ is the drag and${W_{kl}}\left(p \right)$ is the diffusion coefficient. HQ is expected to approach the equilibrium distribution of the medium constituents, given by the relativistic Boltzmann-Jϋttner distribution [27].${f_{\rm equi}}(x,p) = g{e^{ - \frac{{E(p)}}{T}}}$

(16) When HQ has the same distribution as the medium, the drag and diffusion coefficients are related by the following dissipation-fluctuation relation [6].
${U_k}(p,T) = {W_{ij}}(p,T)\frac{1}{T}\frac{{\partial E(p)}}{{\partial {p_k}}} - \frac{{\partial {W_{ij}}(p,T)}}{{\partial {p_k}}}.$

(17) Eqs. (12) and (13) satisfy the Fokker-Plank equation, found from the average change of an arbitrary phase-space function with time [28]:
$ \begin{split} \frac{{\partial f(t,p)}}{{\partial t}} =& \frac{\partial }{{\partial {p_k}}}\left[ {\left( {\Gamma (p){p_k} - \chi {G_{lj}}(p)\frac{{\partial {G_{ij}}}}{{\partial {p_l}}}} \right)f(t,p)} \right]\\ &+ \frac{1}{2}\frac{{{\partial ^2}}}{{\partial {p_k}\partial {p_j}}}\left[ {{G_{kl}}(p){G_{jl}}(p)f(t,p)} \right], \end{split}$

(18) Comparing Eqs. (15) and (18), we get
$U(p) = \Gamma (p){p_k} - \chi {G_{ij}}(p)\frac{{\partial {G_{ij}}}}{{\partial {p_l}}}.$

(19) As shown in Ref. [6], comparing Eqs. (17) and (19) and using the diagonal approximation of the diffusion coefficient (which is a controlled approximation at low and intermediate pT), and putting
${W_{kl}}\left(p \right) = D\left(p \right)$ and${G_{ij}}\left(p \right) = \sqrt {2D\left(p \right)} {\delta _{ij}}$ , Eq. (17) reduces to$U(p) = \frac{1}{{E(p)}}\left( {\frac{{D\left[ {E\left( p \right)} \right]}}{T} - \frac{{\partial D\left[ {E(p)} \right]}}{{\partial E}}} \right),$

(20) which converts to the drag coefficient Γ(p)
$\Gamma (p) = \frac{1}{{E(p)}}\left\{ {\frac{{D[E(p)]}}{T} - (1 - \chi )\frac{{\partial D[E(p)]}}{{\partial E}}} \right\},$

(21) where χ=0 or 1, corresponding to the pre-point or post-point numerical scheme. For the post-point scheme, the equilibrium condition (relativistic fluctuation dissipation relation) is then given by [10]:
$D(p) = \Gamma (p)E(p)T.$

(22) In the non-relativistic limit, we neglect the momentum dependence and have
$D = m\gamma T$ , which is the classical Einstein relation. In terms of the diagonal diffusion coefficient D(p), the Langevin updating rules become$ {\rm d}{x_i} = \frac{{{p_i}}}{E}{\rm d}t, $

(23) $ {\rm d}{p_i} = - \Gamma (T,p){p_i}{\rm d}t + \sqrt {2D(p + \chi {\rm d}p){\rm d}t} {\rho _i}. $

(24) The Fokker-Planck and Langevin equations are not Lorentz invariant. Thus, the momentum of test particle is first updated in the fluid rest frame, followed by a boost back to the laboratory frame with a fluid four velocity
${u^\mu } = \gamma (1,{{v}})$ . The equilibrium condition Eq. (22) should be satisfied in the long time limit so that the test particle distribution converges to the Boltzmann-Jϋttner distribution Eq. (16). In practice, we use the post-point Langevin scheme with χ=1. -
The transport coefficient calculated from the microscopic interactions of HQs with the bulk medium is known as the thermal relaxation rate U(p,T). In the post-point Langevin scheme, using the transport coefficients from the heavy-light quark T matrix [29]:
$\Gamma (p,T) = U(p,T) + \frac{1}{E}\frac{{\partial D(p,T)}}{{\partial E}}.$

(25) By using the equilibrium condition Eq. (22) and the above Eq. (25), the thermal relaxation rate in terms of the drag coefficient Γ(p, T) can be written as,
$\Gamma (p) = U(p) + O(\frac{T}{{{m_Q}}}) +...,$

(26) where the terms of higher order can be neglected. We use the relaxation rate from Refs. [29, 30], where the interaction of HQs with thermal light quarks and gluons was calculated using the non-perturbative thermodynamic T matrix approach. The charm quark thermal relaxation rate as a function of the three-momentum for different critical temperatures is displayed in Fig. 2.
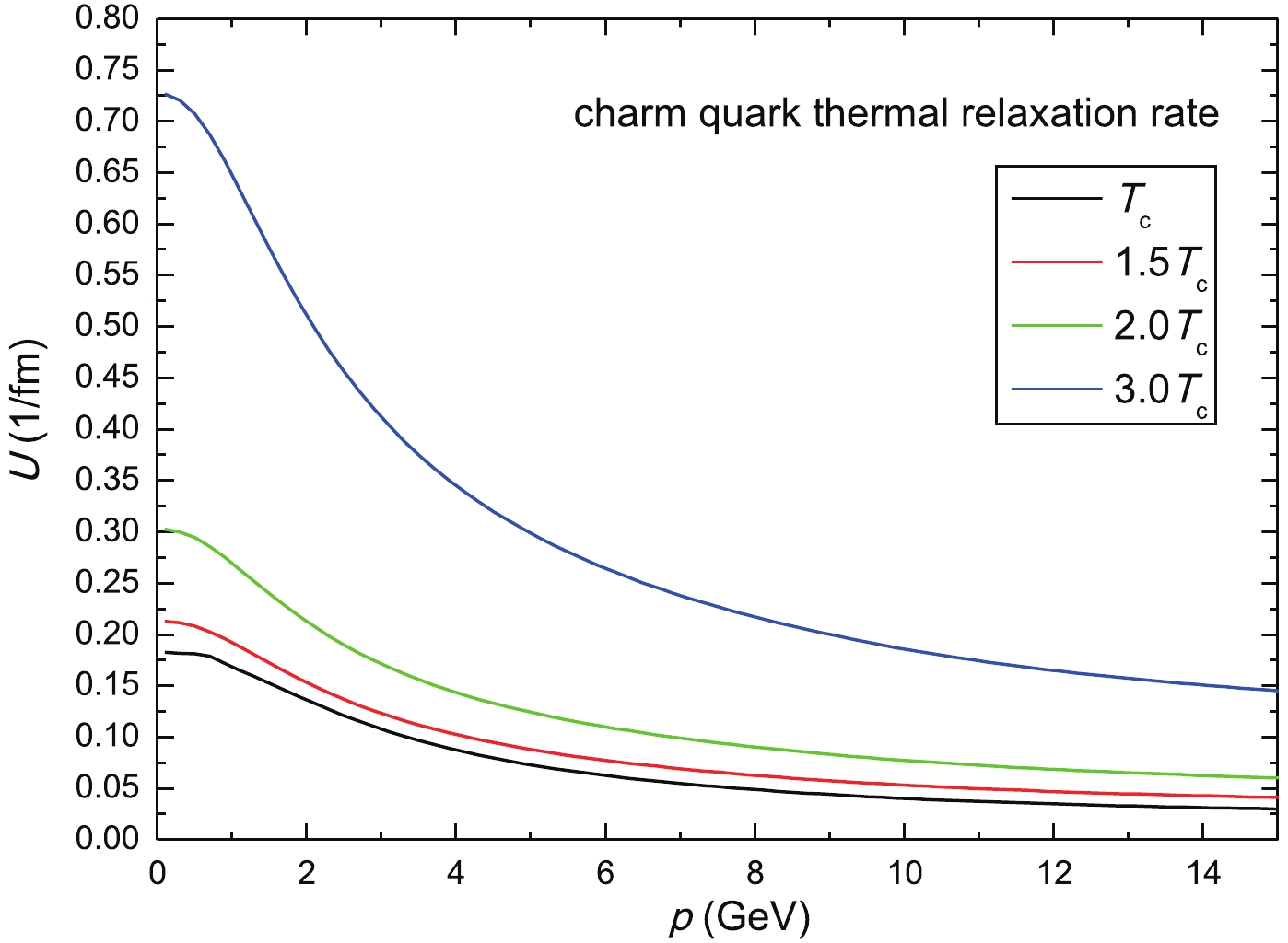
Figure 2. (color online) Charm quark thermal relaxation rate as a function of the three-momentum for different values of the critical temperature Tc obtained using the heavy-light quark T matrix.
The non-perturbative thermal relaxation rates [29] show a substantial enhancement relative to the usual perturbative QCD (pQCD) calculations at low momenta and for 1-2 Tc, where the remnant confining force survives color screening. Moreover, at very high momenta or temperatures, the non-perturbative calculations converge to the pQCD results as dictated by the asymptotic freedom. Taken as a whole, a unique momentum dependence of the charm thermal relaxation rate appears, which manifests in the heavy quark observables, in particular in v2.
-
The fireball+Langevin simulations were used to evaluate heavy quark diffusion in QGP created in Pb+Pb collisions at 2.76 TeV and the impact parameter b=7 fm. The phase transition temperature was taken as Tc=180 MeV, and the temperature dependent heavy quark masses were used [6]. Post-point Langevin scenario was implemented in these simulations. The traditional observables (nuclear modification factor RAA and elliptic flow v2) of the single charm quark were first calculated for various thermal relaxation rates. The back-to-back (Δϕ=π) charm-anticharm (
${c\bar c}$ ) pairs, created using the leading order (LO) pQCD production scheme, were then propagated in the QGP medium. The azimuthal angle between the${c\bar c}$ pairs changed during the propagation due to multiple collisions with the medium partons. A substantial change in the${c\bar c}$ angle difference was observed at the end of the diffusion process. The azimuthal correlations dN/dϕ were calculated for different thermal relaxation rates and transverse momenta. The results are compiled and discussed in the following sections. -
The number of heavy quarks produced in heavy-ion collisions is related to the binary nucleon-nucleon collisions (we assume that there is no charm quark production in the thermal processes in QGP). Hence, their initial distribution follows the binary collision density. For the initial distribution of the single charm-quark transverse momentum (pT), we use the following parametrization of the FONLL result [26]
$\frac{{{\rm d}N}}{{{\rm d}{p_T}}} = \frac{{C.{p_T}}}{{{{(p_T^a + b)}^d}}},$

(27) where a=2.169, b=11.93811, d=2.73886, and C is a normalization constant (in the present work, no charm shadowing is introduced). After Langevin diffusion with the T matrix thermal relaxation rate, the charm quark pT spectrum at the decoupling point (i.e. at the end of the mixed phase at Tc=180 MeV) is obtained for semi-central Pb+Pb collision at 2.76 TeV. Fig. 3 shows the distribution of the number of charm quarks with respect to the transverse momentum pT. A comparison of the initial charm quark pT spectrum and the Langevin pT spectrum is shown. The Langevin pT spectrum decreases below the initial pT spectrum for high pT as a result of the energy loss of charm quarks that diffuse in QGP, whereas at (very) low pT the former surpasses the latter, indicating that there is an accumulation of charm quarks at (very) low pT due to thermalization. The single HQ diffusion in the QGP medium is quantified by the suppression factor (nuclear modification factor) RAA and the elliptic flow v2
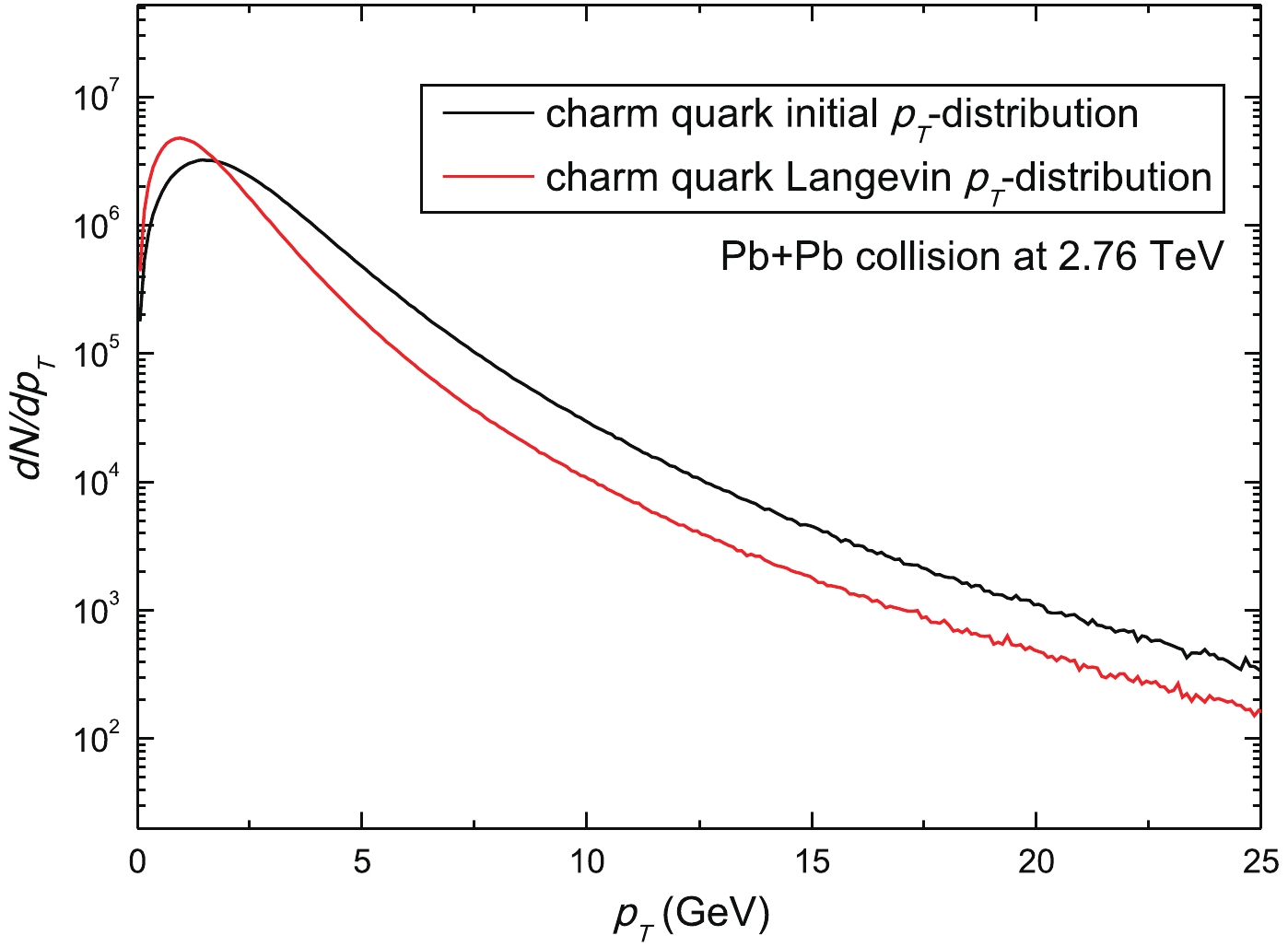
Figure 3. (color online) Charm quark initial pT spectrum and the spectrum obtained from the fireball+Langevin simulations of Pb+Pb collisions at 2.76 TeV. Heavy quarks diffuse in the fireball with temperatures Ti=340 MeV and Tf=180 MeV.
${R_{AA}}({p_T}) = \frac{{{{{\rm d}{N_{AA}}} / {{\rm d}{p_T}}}}}{{{N_{\rm col}}({{{\rm d}{N_{pp}}} / {{\rm d}{p_T}}})}},$

(28) ${v_2}({p_T}) = \frac{{\int {\left( {{{{\rm d}{N_{AA}}} / {{\rm d}{p_T}{\rm d}\phi }}} \right)\cos \left( {2\phi } \right){\rm d}\phi } }}{{\int {\left( {{{{\rm d}{N_{AA}}} / {{\rm d}{p_T}{\rm d}\phi }}} \right){\rm d}\phi } }} \approx \left\langle {\cos \left( {2\phi } \right)} \right\rangle, $

(29) where Ncol is the number of binary nucleon-nucleon collisions.
The single charm quark nuclear modification factor for semi-central (b=7 fm) Pb+Pb collision at 2.76 TeV obtained with the fireball+Langevin simulations and using different thermal relaxation rates is plotted in Fig. 4. It can be seen that with the increase of the thermal relaxation rate, the suppression at higher pT becomes stronger, while the accumulation of charm quarks at low pT becomes more pronounced. This is due to the substantial energy loss of fast-moving HQs in hard scatterings while diffusing in the QGP medium.

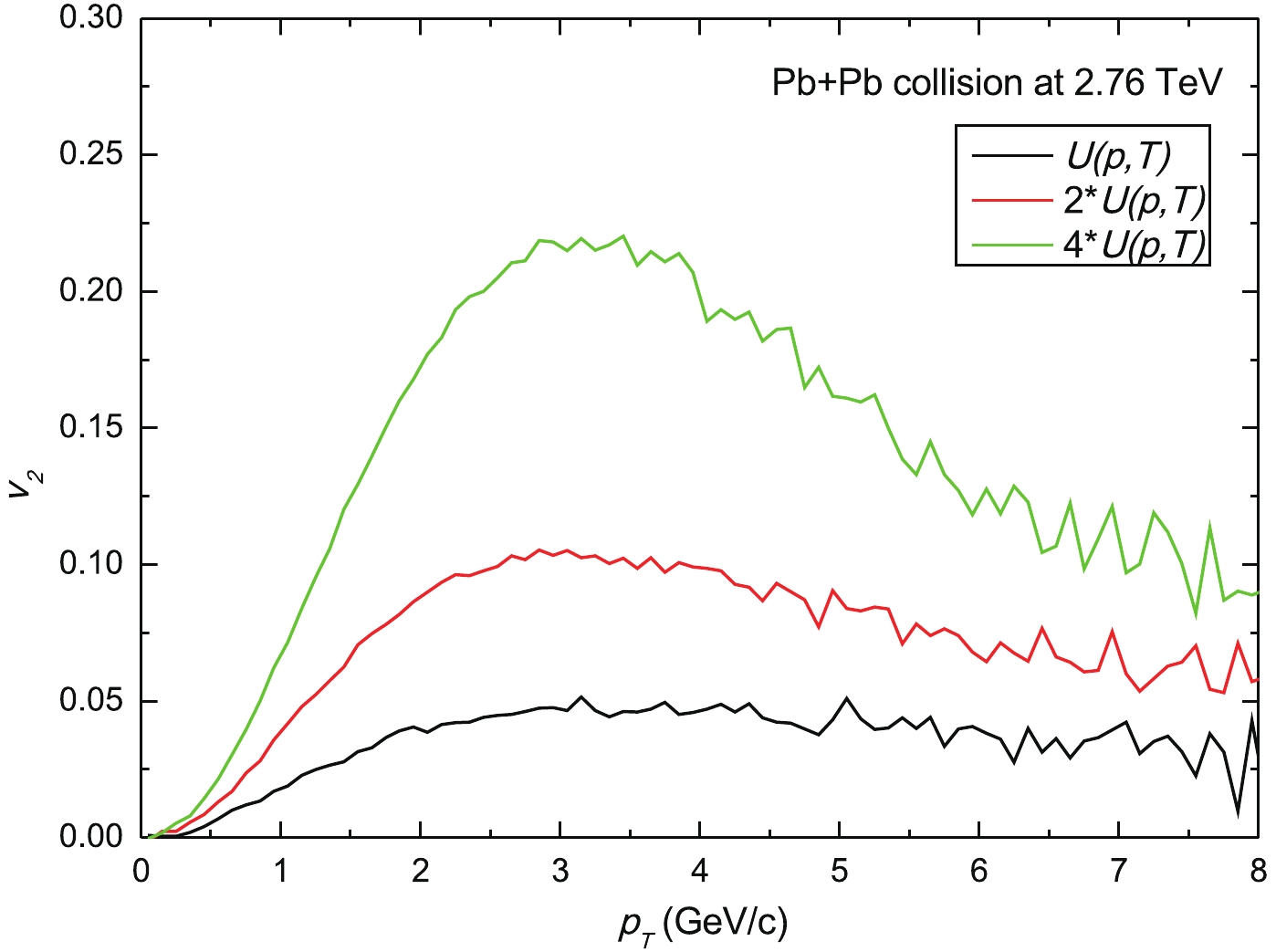
Figure 4. (color online) Nuclear modification factor RAA of charm quarks in Pb+Pb collisions at the LHC energy obtained with the fireball+Langevin simulations, for three values of the thermal relaxation rate U(p,T).
Fig. 5 shows the variation of the elliptic flow (v2) of HQs with increasing thermal relaxation rate. At low pT, v2 increases until it reaches the maximum, followed by a decrease for high pT. Partonic wind effect plays a vital role in the increase of the elliptic flow at low transverse momenta. The increase in thermal relaxation rate allows HQs to diffuse more slowly in the QGP medium, and thus to collide with the medium partons more frequently, so that they flow almost in the direction of the medium flow and acquire substantial v2. Due to high partonic wind effect the peak of v2 increases with increasing thermal relaxation rate. As a result, the elliptic flow roughly scales with the thermal relaxation rate.
-
Here, we discuss the HQs (
${c\bar c}$ ) pair diffusion in the QGP medium produced in Pb+Pb collisions at the LHC energy. Azimuthal correlations of the${c\bar c}$ pairs for different thermal relaxation rates and transverse momenta are studied. We assumed the LO approximation for the initial azimuthal correlation of the${c\bar c}$ pairs. Therefore, charm and anticharm quarks in a correlated pair move back-to-back in the transverse direction with Δϕ=π and${p_{T,c}} = {p_{T,\bar c}}$ . The pairs are produced at the same spatial point following the binding collision number density scaling. After initialization, the charm-anticharm quarks propagate in QGP, which is modeled by the fireball+Langevin simulations. The evolution of charm and anticharm quarks is tracked until they leave QGP, and at this pont we record the difference of the azimuthal angle Δϕ of the${c\bar c}$ pair. Fig. 6 shows the distribution of${c\bar c}$ pairs with respect to the angle difference between the charm and anticharm quarks in a correlated pair. pT is integrated, but the effects of different thermal relaxation rates are compared. We observe that in general the initial back-to-back correlation (which would be represented by a delta-function at Δϕ=π in Fig. 6.) is smeared out after the Langevin diffusion of charm and anticharm quarks in QGP. With increasing thermal relaxation rate, this smearing becomes more and more pronounced. For three times the default T matrix relaxation rate, the distribution becomes almost flat, implying that the initial back-to-back correlation is completely smeared out. This is qualitatively consistent with the observations in Fig. 5 that with such a large relaxation rate, charm (or anticharm) quarks have acquired a large v2, reaching up to ~0.20.
Figure 6. (color online) Azimuthal correlations of initially correlated
${c\bar c}$ pairs at the transition temperature. The azimuthal distribution dN/dϕ of${c\bar c}$ pairs is plotted as a function of the angle difference Δϕ for different values of the thermal relaxation rate U(p, T).In order to study the change of the
${c\bar c}$ pair correlation further, we present the distribution dN/dϕ in different pT classes. Fig. 7 displays the broadening of the azimuthal correlation of${c\bar c}$ pairs in three pT classes: pT = 0-2 GeV, 2-4 GeV, and above 4 GeV, with the default T matrix thermal relaxation rate. For the${c\bar c}$ pairs with lowest transverse momenta, the initial correlations are almost washed out, as the low momentum charm (anticharm) quarks have the largest relaxation rate, implying that they could be largely thermalized within a relatively short time. Furthermore, the low momentum charm and anticharm quarks largely participate in the radial flow of the system and tend to travel in almost the same direction towards the region of Δϕ=0. With increasing pT, e.g. in the pT class of 2-4 GeV, the pertinent smearing becomes less pronounced and there is more of a residual of the initial back-to-back azimuthal correlations. Finally, pairs having pT>4GeV exhibit a rather high peak around (Δϕ=π), which means that the initial back-to-back correlations of these pairs suffer little change since they escape the system at an early time without significant re-scattering. It should be kept in mind that these features were obtained from the simulations with LO (back-to-back) initial correlations. Including the NLO initial correlations, such as${c\bar c}$ pairs produced from gluon splitting, would change the quantitative results shown here. However, the pattern of variation of the correlations with respect to the pT class and the magnitude of thermal relaxation rate should remain the same. -
In this work, we have performed a study of the single HQ diffusion and the correlated
${c\bar c}$ pair azimuthal correlations in QGP created in heavy-ion collisions. The transport of HQs in dense nuclear matter is simulated using the Langevin equations and considering elastic collisions and Brownian motion scenario. The space-time evolution of QGP produced in Pb+Pb collisions at the LHC energy is simulated with the (2+1) dimensional fireball model. Apart from the traditional observables (RAA and v2) and their variation with thermal relaxation rates, we have explored a new observable, the${c\bar c}$ azimuthal correlation. One of the advantages of this observable is that it provides an opportunity to probe different properties of the QGP fireball and is able to quantify the energy loss of HQs with the broadening of their angular distribution. For a better estimate of the influence of the medium on the azimuthal correlations of heavy quark pairs, we have calculated the angular correlations as a function of both the thermal relaxation rate and the transverse momentum. Variations of the azimuthal correlations for different pT classes were also inspected and analyzed. A suppression of HQs increases when the thermal relaxation rate increases. The elliptic flow of HQs increases in the low pT class until it reaches a maximum at the intermediate pT , and then decreases for high pT. At the same time, less and less initial back-to-back correlations survive, in particular for low pT. For high pT, a large part of${c\bar c}$ azimuthal correlations survive the diffusion process.The smearing of the correlations is expected to have major ramifications on the dilepton invariant spectrum in the intermediate mass range, complementing the thermal dilepton production in QGP in this mass range. We plan to generalize the calculations presented here to include hadronization (coalescence and fragmentation) and initial next-to-leading order (NLO)
${c\bar c}$ correlations. Also, a more realistic modeling of the medium evolution will be used in a future work.
Modification of the spectra of correlated charm-anticharm quark pairs in the quark-gluon plasma
- Received Date: 2019-10-23
- Accepted Date: 2019-12-26
- Available Online: 2020-05-01
Abstract: Heavy quarks play an important role in probing the properties of strongly interacting quark-gluon plasma (QGP) created in ultra-relativistic heavy-ion collisions. We study the interactions of single heavy (charm) quarks and correlated charm and anticharm (





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: