-
Neutron-antineutron (
$ n-\bar n $ ) oscillations involve a change of the baryon number (B) by two units ($ |\Delta B| = 2 $ ). An experimental observation would allow a glimpse on physics beyond the standard model, see e.g. [1]. Since in such oscillations B is violated the process satisfies one of the Sakharov conditions [2] that have been formulated in order to explain the observation that there is more matter than anti-matter in the universe. Given such important and far-reaching consequences it is not surprising that there is a vast amount of literature on this topic [3]. Indeed, even within the past two years a wealth of papers have been published that deal with various and quite different aspects of$ n-\bar n $ oscillations [4-11].The key quanitity in this subject is the free
$ n-\bar n $ oscillation time,$ \tau_{ n-\bar n} $ . The presently best experimental limit on it is$ \tau_{ n-\bar n} > 0.86 \times 10^8 \ {\rm s} \approx 2.7 $ yr (with 90% C.L.) [12]. Additional information can be gained by studying$ n-\bar n $ oscillations in a nuclear environment. Corresponding experiments have been performed, e.g., for 56Fe [13], 16O [14], and for the deuteron (2H) [15], while others are planned [16]. In such a case the oscillation process is suppressed as compared to the free situation. The pertinent lifetime$ \tau_{\rm nuc} $ is commonly expressed in terms of the one in free space as [3]$ \tau_{\rm nuc} = R\, \tau^2_{ n-\bar n} \ , $

(1) where R is an intranuclear suppression factor, also called reduced lifetime, that depends on the specific nucleus. It can be calculated from nuclear theory and then can be used to relate the measured lifetimes of those nuclei with the free
$ n-\bar n $ oscillation time [3], see, e.g., Refs. [17-21].For a long time the suppression factors published in Ref. [18] have been used as standard by experimentalists in the interpretation of their measurements [13,15]. For example, in case of the deuteron the corresponding value is
$ R \sim (2.40-2.56) \times 10^{22} $ s−1, a prediction based on the phenomenological antinucleon-nucleon ($ \bar NN $ ) potentials by Dover and Richard [22,23]. Recently, however, those values have been called into question in a work by Oosterhof et al. [7]. In that study an effective field theory for the$ |\Delta B| = 2 $ interaction is constructed and the quantity R is evaluated within the power counting scheme proposed by Kaplan, Savage, and Wise (KSW) [24,25] for the nucleon-nucleon ($ NN $ ) and$ \bar NN $ interactions. The value of R for the deuteron obtained in that approach is with$ (1.1\pm 0.3) \times 10^{22} $ s−1 about a factor 2 smaller than the one by Dover et al. [18].In the present paper we report on a calculation of the deuteron annihilation lifetime, considering neutron-antineutron oscillations. The main motivation comes, of course, from the aforementioned discrepancy and the work aims at providing if possible a plausible explanation for the difference. In our study we follow closely the benchmark calculations of Sandars [17] and Dover et al. [18]. The essential new aspect is that we employ modern interactions for the involved
$ NN $ and the$ \bar NN $ systems. Modern means that these interactions have been derived in a consistent and systematic framework, namely chiral effective field theory (EFT) [26]. And it means that these potentials are in line with present-day empirical information. This concerns specifically the$ \bar NN $ system where a wealth of data on$ \bar pp $ scattering and the charge-exchange reaction$ \bar pp \to \bar n n $ has accumulated in the years after the publication of Ref. [18], notably due to measurements at the LEAR facility at CERN [27]. That fact is accounted for by utilizing$ \bar NN $ potentials which have been fitted to up-to-date phase shifts and inelasticities provided by a recently published phase-shift analysis of available$ \bar pp $ scattering data [28].The
$ \bar NN $ interactions used in the present study are taken from two works [29,30]. In the first reference,$ \bar NN $ potentials up to next-to-next-to-leading order (N2LO) were constructed, based on a modified Weinberg power counting, in close analogy to pertinent studies of the$ NN $ interaction [31]. In the second, the study was extended to next-to-next-to-next-to-leading order (N3LO) and, in addition, a new regularization scheme was implemented that had been introduced in the$ NN $ study of Ref. [32]. In the actual calculations we rely mostly on the recent more refined potential of higher order [30] that describes$ \bar NN $ phase shifts and scattering observables up to laboratory energies of$ T_{\rm lab}\sim 250 $ MeV. However, additional calculations with the other potential are performed in order to estimate possible uncertainties that arise, e.g., from the employed regularization scheme.The paper is structured in the following way: In Sec. 2 a basic description of the employed formalism is provided. Our results are presented and discussed in Sec. 3. We compare also with the works of [18] and [7]. The paper closes with a brief summary.
-
In our treatment of
$ n-\bar n $ oscillations in the deuteron we follow very closely the formalism outlined in Refs. [17,18]. However, contrary to those works our calculation is performed in momentum space and, therefore, we provide details about the main steps below. The starting point is the eigenvalue (Schrödinger) equation [17]$ \left( {\begin{array}{*{20}{l}} {{H_0} + {V_{np}}}&{{V_{n - \bar n}}}\\ {{V_{n - \bar n}}}&{{H_0} + {V_{\bar np}}} \end{array}} \right)\left( {\begin{array}{*{20}{l}} {|{\psi _{np}}\rangle }\\ {|{\psi _{\bar np}}\rangle } \end{array}} \right) = (E - i\Gamma /2)\left( {\begin{array}{*{20}{l}} {|{\psi _{np}}\rangle }\\ {|{\psi _{\bar np}}\rangle } \end{array}} \right)\;. $

(2) Here,
$ V_{np} $ and$ V_{ \bar np} $ are the potentials in the$ np $ and$ \bar n p $ systems and$ |\psi_{np} \rangle $ and$ |\psi_{ \bar np} \rangle $ are the corresponding wave functions. The systems are coupled via$ V_{ n-\bar n} $ which is given by the$ { n-\bar n} $ transition matrix element$ \delta m_{ n-\bar n} $ where the latter is proportional to the inverse of the$ n-\bar n $ oscillation time, i.e.$ V_{ n-\bar n} = \delta m_{ n-\bar n} = \hbar / \tau_{ n-\bar n} $ [3].To leading order the
$ \bar np $ component$ |\psi_{ \bar np} \rangle $ obeys the equation$ (H_0 + V_{ \bar n p} - E_d) |\psi_{ \bar np} \rangle = -V_{ n-\bar n} |\psi_{d} \rangle \ , $

(3) where
$ E_d $ is the unperturbed energy of the deuteron and$ |\psi_{d} \rangle $ is the corresponding deuteron wave function. The decay width of the deuteron,$ \Gamma_d $ , is then [17]$ \Gamma_d = -2\, V_{ n-\bar n}\, {\rm Im} \langle \psi_{d} |\psi_{ \bar np} \rangle \ . $

(4) We solve Eq. (3) in momentum space. Performing a partial wave decomposition and taking into account the coupling of the
$ ^3S_1 $ and$ ^3D_1 $ channels, the above integral equation reads$ \begin{split} (2 E_p - E_d)\,\psi^{L}_{ \bar np} (p) &+ \sum_{L'}\int \frac{{\rm d}q\,q^2}{(2\pi)^3} V^{L,L'}_{ \bar n p}(p,q)\, \psi^{L'}_{ \bar np} (q) \\ =& -V_{n- \bar n}\, \psi^L_{d}(p) \ , \end{split} $

(5) with
$ L,\,L' = 0,\,2 $ . Note that$ E_d $ is the total energy corresponding to the deuteron, i.e.$ E_d - 2 m_N =2 \sqrt{ m_N^2 - \kappa^2} - $ $2 m_N = -B_d $ where$ B_d $ is the standard binding energy of$ 2.225 $ MeV and$ \kappa = \sqrt{m_N B_d} \simeq 45.7 $ MeV is the binding momentum. The deuteron wave function is normalized by$ \int {\rm d}p p^2\, \left[(\psi^0_{d}(p))^2 + \psi^2_{d}(p))^2\right] = 1 \, $

(6) and the width is provided by
$ \Gamma_d = -2\, V_{n- \bar n}\, {\rm Im} \sum_L \int {\rm d}p p^2\, \psi^L_{d}(p) \, \psi^L_{ \bar np}(p) \ . $

(7) The deuteron lifetime
$ \tau_d $ is given by$ \tau_d = \hbar /\Gamma_d $ . The interesting quantity is the so-called reduced lifetime R [17,18,21] which relates the free$ n-\bar n $ oscillation lifetime with that of the deuteron,$ \tau_d = R\, \tau^2_{ n-\bar n} \quad {\rm i.e.} \quad R = \frac{\hbar} {\Gamma_d \tau^2_{ n-\bar n} } \ . $

(8) -
As already stated in the Introduction, we use the
$ \bar NN $ interactions from Refs. [29,30] derived within chiral EFT and the deuteron wave functions from the corresponding$ NN $ potentials [31,32], derived in the same framework. We consider the two$ \bar NN $ interactions because they are based on rather different regularization schemes. In the earlier potential [29] a non-local exponential exponential regulator was employed for the whole potential while in the recent work [30] a local regulator was adopted for the evaluation of the one- and two-pion contributions, see Refs. [30,32] for details. Comparing the pertinent results will allow us to shed light on the question in how far the choice of the regulator influences the predictions. For exploring further the sensitivity of the results to the deuteron wave function we employ also those of two meson-exchange potentials [33,34].Our results are summarized in Table 1. They are based on our N3LO interaction with cutoff
$ R_0 = 0.9 $ fm from Ref. [30] and the N2LO interaction with cutoff$ \{\Lambda,\tilde\Lambda\} = \{450,500\} $ MeV from Ref. [29]. For details on those interactions we refer the reader to the corresponding publications. Besides the predictions for R based on the chiral$ \bar NN $ interactions we list also the values given in Ref. [18] where the$ \bar NN $ potentials DR1 and DR2 by Dover-Richard [22,23] have been utilized. Furthermore we include results from the calculation of Oosterhof et al. performed directly within EFT on the basis of the KSW approach. In this case R can be represented in a compact analytical form which reads up to NLO [7]$\chi$ EFT N2LO [29]

$\chi$ EFT N3LO [30]

DR $_1$ [18]

DR $_2$ [18]

R ( $s^{-1}$ )

$2.49\times 10^{22}$ 

$2.56\times 10^{22}$ 

$2.56\times 10^{22}$ 

$2.40\times 10^{22}$ 

(Eq. (9)) $(1.1\pm 0.3)\times 10^{22}$ 

$(1.2\pm 0.3)\times 10^{22}$ 

$(1.4\pm 0.4)\times 10^{22}$ 

$(1.3\pm 0.3)\times 10^{22}$ 

${a_{^3S_1}}$ (fm)

$0.44-{\rm i}\,0.91$ 

$0.44-{\rm i}\,0.96$ 

$0.87-{\rm i}\,0.66$ 

$0.89-{\rm i}\,0.71$ 

Table 1. Reduced lifetime
$ {R} $ calculated for the$ \chi $ EFT$ \bar NN $ potentials from Refs. [29,30], together with information on the pertinent$ \bar n p $ $ ^3S_1 $ scattering length. Results for the Dover-Richard potentials DR$ _1 $ and DR$ _2 $ are taken from Ref. [18]. The corresponding scattering lengths are from Ref. [35]. Predictions based on Eq. (9), i.e. on the KSW approach applied in Ref. [7], are indicated too.$ R = -\frac{\kappa}{m_N}\, \frac{1}{{\rm Im}\,a_{ \bar np}}\, \frac{1} {1+ 0.4+2 \kappa\, {\rm Re}\,a_{ \bar np}-0.13\pm 0.4} \ . $

(9) Obviously, the only parameter here is the
$ \bar n p $ $ ^3S_1 $ scattering length. All other quantities that enter are well established$ NN $ observables, cf. Ref. [7] for details. Note that in that paper, the scattering length$ {\rm Re}\,a_{ \bar np} $ was taken from Ref. [30].As can be seen from Table 1 the values for R predicted by the chiral
$ \bar NN $ interactions are fairly similar to those obtained for the DR potentials in the past. The results based on the framework employed by Oosterhof et al. [7], utilizing the scattering length from the N3LO chiral$ \bar NN $ interaction [30], on the other hand, are rather different. This suggests that the large discrepancy observed in Ref. [7] is certainly not due to differences in Im$ a_{ \bar n p} $ but primarily a consequence of the different approaches.For illustration we present in Fig. 1 the wave functions of the
$ ^3S_1 $ component of the deuteron and of the corresponding$ \bar n p $ state with arbitrary normalizations. In case of the latter the imaginary part is shown which is relevant for the determination of the width, cf. Eq. (7). The impact of the different regularization schemes used in Refs. [29,31] and [30,32], respectively, can be clearly seen from the different behavior of the wave functions for large momenta. Note, however, that the bulk contribution to the integral in Eq. (7) comes from momenta$ p\leqslant 300 $ MeV/c. Contributions from larger momenta to$ \Gamma_d $ are only in the order of 5% as revealed by test calculations.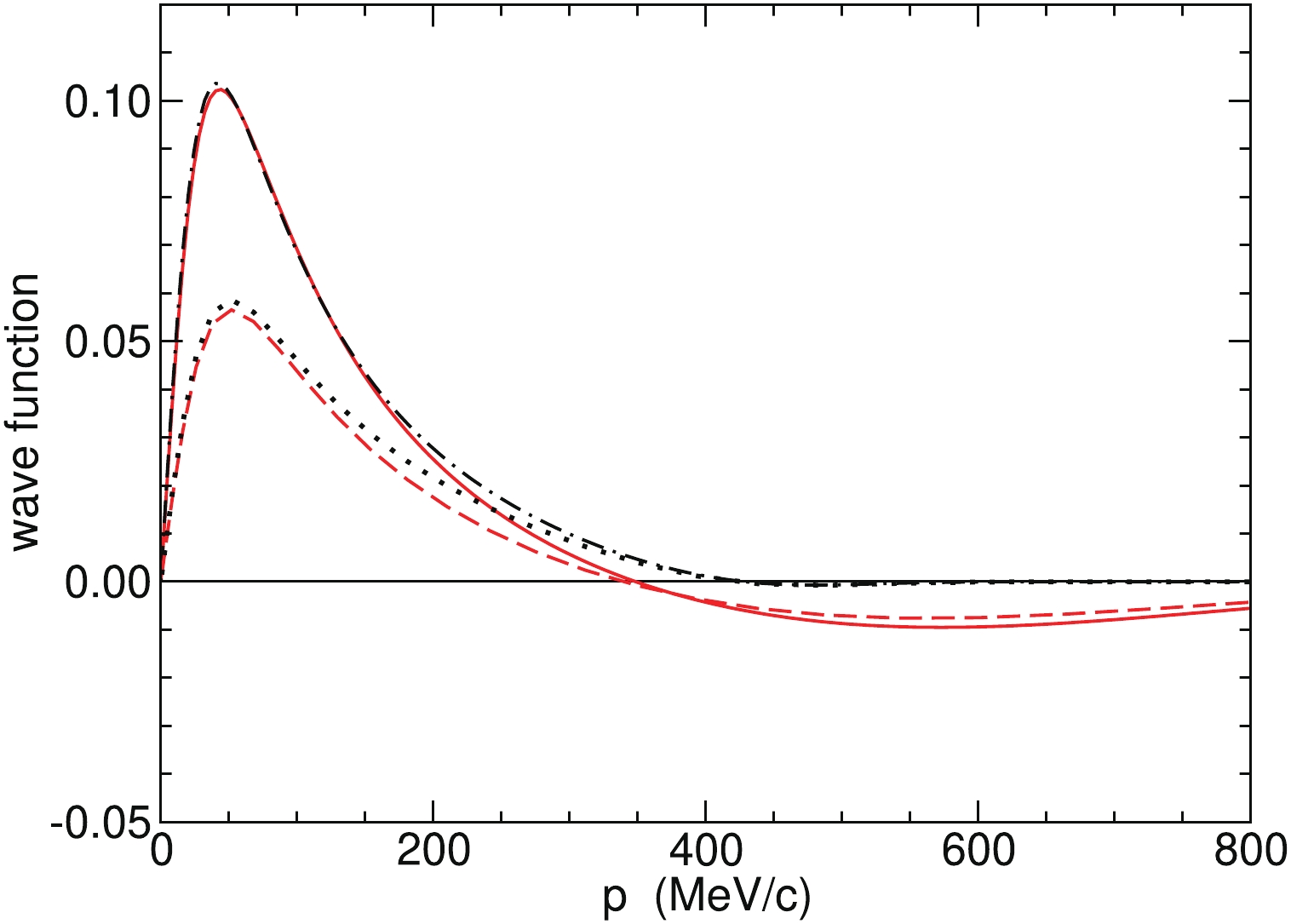
Figure 1. (color online) Wave functions of the deuteron (
$ \psi_d $ ; upper curves) and of the$ \bar n p $ state in the$ ^3S_1 $ partial wave (imaginary part of$ \psi_{\bar n p} $ ; lower curves), multiplied by the momentum p and with arbitrary normalization. Solid and dashed (red) curves are for the N3LO$ \bar NN $ interaction [30] with cutoff$ R_0 = 0.9 $ fm and dash-dotted and dotted (black) curves for the N2LO$ \bar NN $ interacton [29] with cutoff$ \{\Lambda,\tilde\Lambda\} = \{450,500\} $ MeV.In order to investigate the sensitivity of our results to the utilized input we performed various exploratory calculations. First of all, we employed the NLO and N2LO variants of the considered
$ \bar NN $ (and$ NN $ ) interactions. The corresponding predictions for R were found to lie within a range of$ (2.48 - 2.65)\times 10^{22} $ s−1. Taking this variation as measure for the uncertainty due to the nuclear structure, i.e. the$ NN $ and$ \bar NN $ interactions (wave functions), leads to a value of roughly$ R = (2.6\pm 0.1)\times 10^{22} $ s−1. Applying the method proposed in Ref. [32] for estimating the uncertainty to the calculation based on the$ \bar NN $ interaction from 2017 [30], say, would actually lead to a slightly smaller uncertainty. We have also varied the deuteron wave functions alone. As an extreme case we even took wave functions from phenomenological NN potentials derived in an entirely different framework, namely in the meson-exchange picture [33,34]. Also here the obtained values for R stayed within the range given above. Finally, omitting the D-wave component of the deuteron wave function, which is kept in our calculation and in the one by Dover et al. [18] causes a 5% variation. But it leads to an increase of the value of R and, thus, does not bring it closer to the values presented by Oosterhof et al. Overall, we confirm the observation by Dover et al. that the predictions for R are fairly insensitive to the details of the employed$ \bar NN $ potentials [18], provided that these potentials describe the$ \bar pp $ data at low energies.Since in Ref. [7] the
$ \bar NN $ interaction is represented by the leading-order term, i.e. the scattering length alone, we have evaluated the effective range parameter for our$ \bar NN $ interactions and used it to extrapolate the$ \bar NN $ amplitude to the deuteron pole. The found variations are in the order of$ 10 $ % and can certainly not explain the large difference documented in Table 1.We do not have a clear explanation for the difference of our results (and those of Ref. [18]) to the ones of Oosterhof et al. [7]. However, we believe that it is due to the fact that in the latter work the width
$ \Gamma_d $ is evaluated following the perturbative scheme developed by Kaplan, Savage, and Wise [25]. In that scheme there is no proper deuteron wave function. Rather one works with an effectively constructed wave function that is represented in terms of an irreducible two-point function [7,25]. This seems to work well for some electromagnetic form factors of the deuteron, at least at low momentum transfer [25,36]. On the other hand, the quadrupole moment of the deuteron is overestimated by 40% [25], which hints that the properties of the wave function at large distances (small momenta) are not that well represented in this scheme. Clearly, this should have an impact on the quantity studied in the present work as well. Note that a comparable agreement (mismatch) with regard to the KSW scheme has been also observed in studies of the electric dipole moment (magnetic quadrupole moment) of the deuteron [37-39]. In any case, one should not forget that there is convergence problem of the KSW approach for$ NN $ partial waves where the tensor force from pion exchange is present [40]. It affects specifically the$ ^3S_1 $ -$ ^3D_1 $ channel where difficulties appear already for momenta around$ 100 $ MeV/c, see [40] and also the discussions in Refs. [26,41]. Interestingly enough, this is the momentum region where the dominant contributions in our calculation come from, see Fig. 1.In contrast to [7] in our study the
$ \bar NN $ ($ NN $ ) and$ |\Delta B| = 2 $ interactions are not treated at the same order. Guided by the success of the work by Epelbaum et al. [31,32] based on the Weinberg counting the non-perturbative effects due to the$ NN $ and$ \bar NN $ interactions are fully take into account from the very beginning. It is worth mentioning that in this approach the quadrupole moment of the deuteron is very close to its empirical value already for interactions at NLO [31,32].Finally, note that in the present work we have only considered the contribution from actual
$ n-\bar n $ oscillations to the deuteron decay rate. In principle, there can be also contributions from a direct annihilation of the$ NN $ system. Moreover, there can be a$ NN\to \bar NN $ transition involving both nucleons and the$ \bar NN $ state. The latter gives rise to a$ |\Delta B| = 2 $ four-baryon contact term involving an unknown complex low-energy constant, which has been discussed and considered in the work by Oosterhof et al. [7]. We refrain from introducing such a contribution in the present study which, anyway, is of higher order in the employed counting scheme. In this context, we would like to mention that for most$ |\Delta B| = 2 $ sources considered in Ref. [7] the deuteron decay rate was found to be dominated by free$ n-\bar n $ oscillations. Nonetheless, an uncertainty in the order of$ \pm 0.3 \times 10^{22} $ s−1 for the reduced lifetime R due to additional$ |\Delta B| = 2 $ mechanisms, as suggested in that work, has to be certainly expected. Note that additional decay mechanisms should always increase the decay width of the deuteron and, thus, lead to smaller values of the reduced lifetime R. -
In the present work we have considered neutron-antineutron oscillations in the deuteron. In particular, we have calculated the deuteron lifetime in terms of the free-space
$ n-\bar n $ oscillation time based on$ \bar NN $ [29,30] and$ NN $ [31,32] interactions derived within chiral effective field theory. The value obtained for the so-called reduced lifetime R which relates the free-space$ n-\bar n $ oscillation time$ \tau_{ n-\bar n} $ with the deuteron lifetime is found to be$ R = (2.6\pm 0.1) \times 10^{22} $ s−1, where the quoted uncertainty is due to the$ NN $ and$ \bar NN $ interactions (wave functions).Our result for R is close to the value obtained by Dover and collaborators more than three decades ago [18] but disagrees with recent EFT calculations, performed within the perturbative scheme proposed by Kaplan, Savage, and Wise [7], by about a factor of 2. We believe that the difference is due to the fact that in the perturbative KSW scheme there is no proper deuteron wave function. Rather this ingredient is represented effectively in terms of an irreducible two-point function. It is known from past studies that the KSW approach fails to describe quantities that depend more sensitively on the wave function like, for example, the quadrupole moment of the deuteron [25].
We acknowledge stimulating discussions with Jordy de Vries, Andreas Nogga and Tom Luu.
Neutron-antineutron oscillations in the deuteron studied with NN and ${{\bar NN}}$ interactions based on chiral effective field theory
- Received Date: 2019-11-06
- Available Online: 2020-03-01
Abstract: Neutron-antineutron (







 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: