Abstract
HTML
Reference
Related
PDF
-
The quark model [1,2] predicts the existence of multiplets of baryon and meson states. Baryons containing two charm quarks and a light quark provide a unique system for testing the low-energy limit of quantum chromodynamics (QCD). The production of doubly charmed baryons at hadron colliders can be treated as two independent processes: production of a
cc diquark followed by the hadronisation of the diquark into a baryon [3-9]. The production cross-section of doubly charmed baryons in proton-proton collisions at a centre-of-mass energy√s=13TeV is predicted to be in the range 60–1800 nb [3-9], which is between10−4 and10−3 times that of the total charm production [4].A doubly charmed baryon was first reported by the SELEX collaboration [10,11]. They found that 20% of their
Λ+c yield originated fromΞ+cc decays, which is several orders of magnitude higher than theoretical prediction [4]. However, this signal has not been confirmed by searches performed at the FOCUS [12], BaBar [13], Belle [14], and LHCb [15,16] experiments. Recently, the LHCb collaboration observed a peak in theΛ+cK−π+π+ mass spectrum at a mass of3621.40±0.78MeV/c2 [17], consistent with expectations for theΞ++cc baryon. TheΞ++cc lifetime was measured to be0.256+0.024−0.022(stat)±0.014 (syst)ps [18], indicating that it decays through the weak interaction. A new decay mode,Ξ++cc→Ξ+cπ+ , was observed by the LHCb collaboration [19], and the measuredΞ++cc mass was found to be consistent with that measured usingΞ++cc→Λ+cK−π+π+ decays. TheΞ++cc→D+pK−π+ decay has been searched for, but no signal was found [20].This paper presents a measurement of
Ξ++cc production inpp collisions at a centre-of-mass energy of√s=13TeV , following the same analysis strategy as that used in Refs. [15,17,18]. TheΞ++cc production cross-section,σ(Ξ++cc) , times the branching fraction of theΞ++cc→Λ+cK−π+π+ decay, is measured relative to the promptΛ+c production cross-section,σ(Λ+c) , in the transverse momentum range4<pT<15GeV/c and the rapidity range2.0<y<4.5 . The data used correspond to an integrated luminosity of1.7fb−1 collected by the LHCb experiment in 2016. TheΛ+c baryon is reconstructed via theΛ+c→pK−π+ decay. The inclusion of the charge-conjugate decay processes is implied throughout this paper. The production rate ratio is defined as,R≡σ(Ξ++cc)×B(Ξ++cc→Λ+cK−π+π+)σ(Λ+c)=NsigNnormεnormεsig,
(1) where “sig” and “norm” refer to the signal (
Ξ++cc ) and normalisation(Λ+c) modes, N is the signal yield andε is the total efficiency to reconstruct and select these decays. -
The LHCb detector [21,22] is a single-arm forward spectrometer covering the pseudorapidity range
2<η<5 , designed for the study of particles containing b or c quarks. The detector includes a high-precision tracking system consisting of a silicon-strip vertex detector surrounding thepp interaction region [23], a large-area silicon-strip detector located upstream of a dipole magnet with a bending power of about 4 Tm, and three stations of silicon-strip detectors and straw drift tubes [24] placed downstream of the magnet. The tracking system provides a measurement of the momentum, p, of charged particles with a relative uncertainty that varies from 0.5% at low momentum to 1.0% at200GeV/c . The minimum distance of a track to a primary vertex, the impact parameter, is measured with a resolution of(15+29/pT) µm, wherepT is expressed inGeV/c . Different types of charged hadrons are distinguished using information from two ring-imaging Cherenkov detectors [25]. Photons, electrons and hadrons are identified by a calorimeter system consisting of scintillating-pad (SPD) and preshower detectors, an electromagnetic and a hadronic calorimeter. Muons are identified by a system composed of alternating layers of iron and multiwire proportional chambers [26]. The online event selection is performed by a trigger [27], which consists of a hardware stage, based on information from the calorimeters and muon systems [28,29], followed by a software stage, which applies a full event reconstruction incorporating near-real-time alignment and calibration of the detector [30]. The output of the reconstruction performed in the software trigger [31] is used as input to the present analysis.Simulated samples are required to develop the candidate selection and to estimate the efficiency of the detector acceptance and the imposed selection requirements. Simulated
pp collisions are generated using Pythia [32] with a specific LHCb configuration [33]. A dedicated package, GenXicc2.0 [34], is used to simulate theΞ++cc baryon production. Decays of unstable particles are described by EvtGen [35], in which final-state radiation is generated using Photos [36]. The interaction of the generated particles with the detector, and its response, are simulated using the Geant4 toolkit [37] as described in Ref. [38]. -
The
Λ+c→pK−π+ candidate is reconstructed through three charged particles identified as p,K− andπ+ hadrons, which form a common vertex and do not originate from any primary vertex (PV) in the event. The decay vertex of theΛ+c candidate is required to be displaced from any PV by requiring its proper decay time to be greater than 0.15 ps, corresponding to about 1.5 times theΛ+c decay time resolution [39]. EachΛ+c candidate with mass in the range 2270-2306MeV/c2 is then combined with three additional particles to form aΞ++cc candidate. The three particles must form a common vertex with theΛ+c candidate and have hadron-identification information consistent with them being twoπ+ mesons and oneK− meson. TheΛ+c decay vertex is required to be downstream of theΞ++cc vertex. Additionally, theΞ++cc candidates must havepT>4GeV/c and originate from a PV.The combinatorial background is suppressed using two multivariate classifiers based on a boosted decision tree algorithm [40]. One classifier is optimised to select
Λ+c candidates irrespective of their origin, and the other is optimised to selectΞ++cc candidates. While both classifiers are applied to the signal channel, only the first is applied to the normalisation decay channel. The first classifier is trained withΛ+c signal in the simulatedΞ++cc sample and background candidates in theΛ+c mass sideband. The second classifier is trained using data candidates in theΛ+c andΞ++cc signal mass region, where wrong-sign (WS)Λ+cK−π+π− combinations are used as proxy for the background. The first multivariate classifier is trained with the following variables: theχ2 of theΛ+c vertex fit; the largest distance of closest approach among the decay products; the scalar sum of thepT and the smallestpT of the three decay products of theΛ+c candidate; the smallest and largestχ2IP of the decay products of theΛ+c candidate with respect to its PV. Here,χ2IP is defined as the difference inχ2 of the PV fit with and without the particle in question. The PV of any single particle is defined to be that with respect to which the particle has the smallestχ2IP . The second multivariate classifier is trained with the following variables: theχ2IP of theΞ++cc candidate to its PV; the angle between theΞ++cc momentum and the direction from the PV to theΞ++cc decay vertex; the logarithm of theχ2 of theΞ++cc flight distance between theΞ++cc decay vertex and the PV; the vertex fitχ2 of theΞ++cc candidate; theχ2 of a kinematic refit [41] that requires theΞ++cc candidate to originate from a PV; the scalar sum of thepT and the smallestpT of the six final state tracks of theΞ++cc candidate. Here the flight distanceχ2 is defined as the change inχ2 of theΞ++cc decay vertex if it is constrained to coincide with the PV. Candidates retained for analysis must have two classifier responses exceeding thresholds chosen by performing a two-dimensional maximisation of the figure of meritε/(5/2+√B) [42]. Hereε and B are the estimated signal efficiency determined from signal simulation and background yield under the signal peak, respectively. The background is estimated from the WS sample. The same threshold of the first classifier, optimised for the signal mode, is applied to the normalisation mode.Finally, the
Ξ++cc andΛ+c candidates are required to have their transverse momentum and rapidity in the fiducial ranges of 4-15GeV/c and 2.0-4.5, respectively. After the multivariate selection is applied, events may still contain more than oneΞ++cc candidate in the signal region. Candidates made of duplicate tracks are removed by requiring all pairs of tracks with the same charge to have an opening angle larger than0.5mrad . Duplicate candidates, which are due to the interchange between identical particles from theΛ+c decay or directly from theΞ++cc decay (e.g., theK− particle from theΞ++cc decay and theK− particle from theΛ+c decay), can cause peaking structures in theΞ++cc invariant mass distribution. In this case, one of the candidates is chosen at random to be retained and the others are discarded. The systematic uncertainty associated with this procedure is negligible. -
After the full selection is applied, the data sets are further filtered into two disjoint subsamples using information from the hardware trigger. The first contains candidates that are triggered by at least one of the
Λ+c decay products with high transverse energy deposited in the calorimeters, referred to as Triggered On Signal (TOS). The second consists of the events that are exclusively triggered by particles unrelated to the signal decay products; these events can, for example, be triggered by the decay products of the charmed hadrons produced together with the signal baryon, referred to as exclusively Triggered Independently of Signal (exTIS).To determine the
Ξ++cc baryon signal yields, an unbinned extended maximum-likelihood fit is performed simultaneously to theΛ+cK−π+π+ invariant-mass spectra in the interval 3470-3770MeV/c2 of the two trigger categories. The mass distribution of the signal is described by the sum of a Gaussian function and a modified Gaussian function with power-law tails on both sides of the function [43] with a common peak position. The tail parameters and the relative fraction of the two Gaussian functions for the signal model are determined from simulation, while the common peak position and the mass resolution are allowed to vary in the fit. The background is described by a second-order Chebyshev polynomial. Fig. 1 shows theΛ+cK−π+π+ invariant-mass distribution in data together with the fit results for the two trigger categories. The fit returns a mass of3621.34±0.74MeV/c2 , and a mass resolution of7.1±1.3MeV/c2 , where the uncertainties are statistical only.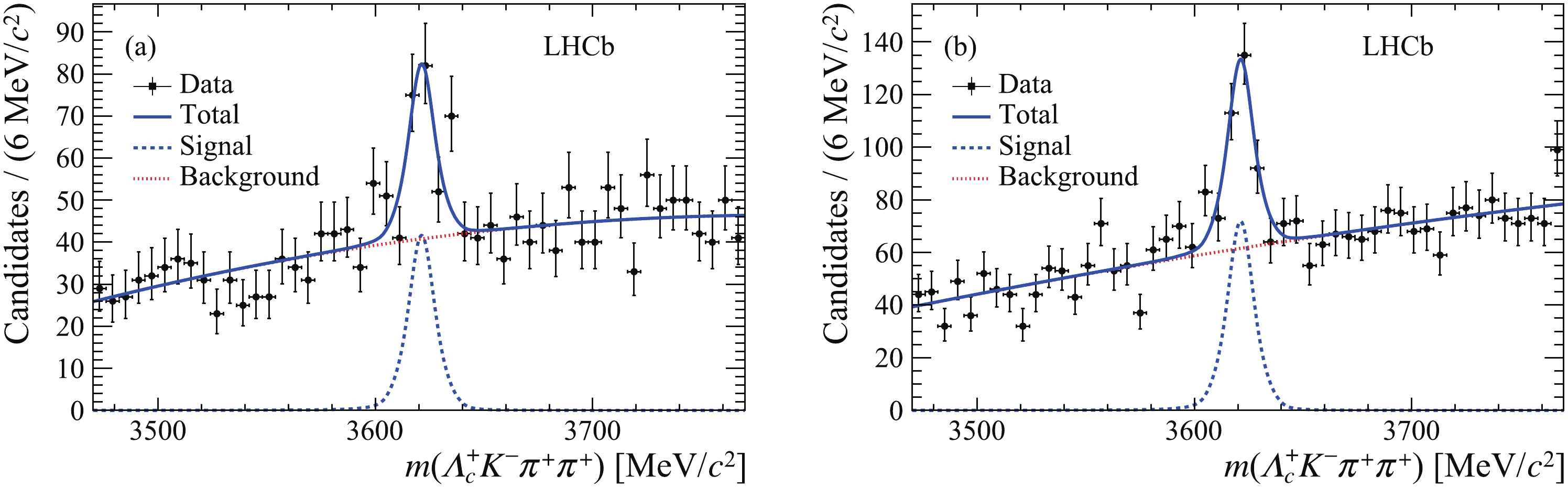
Figure 1. (color online) Invariant-mass distributions of
Ξ++cc candidates (a) triggered by TOS and (b) triggered by exTIS, with fit results shown.The determination of the prompt
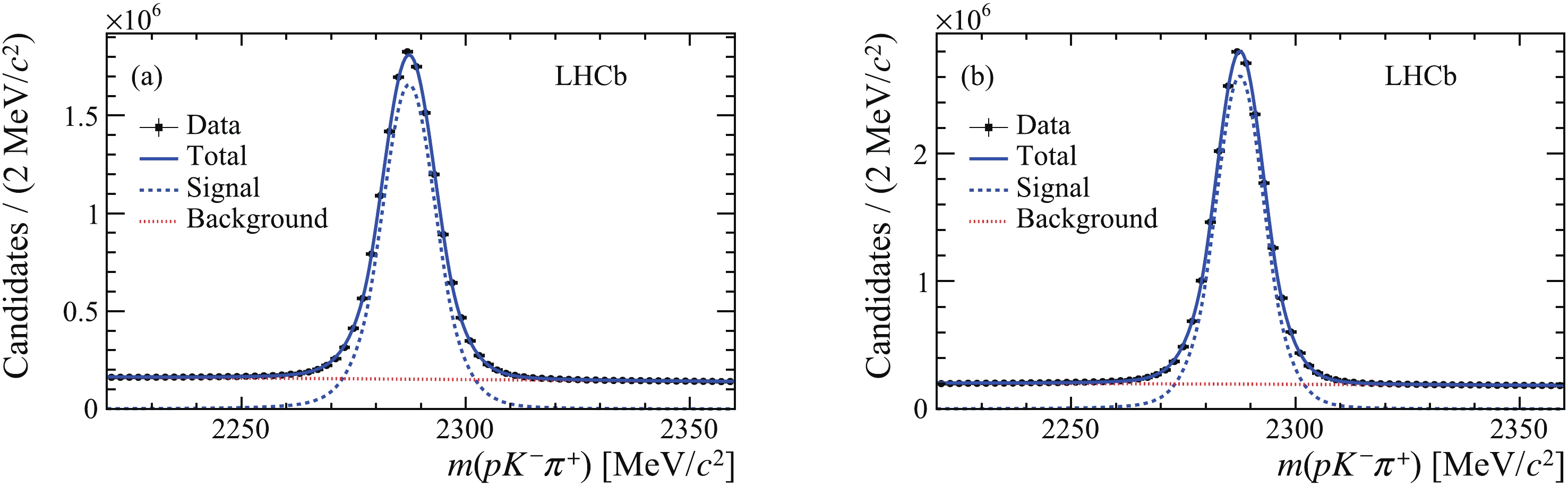
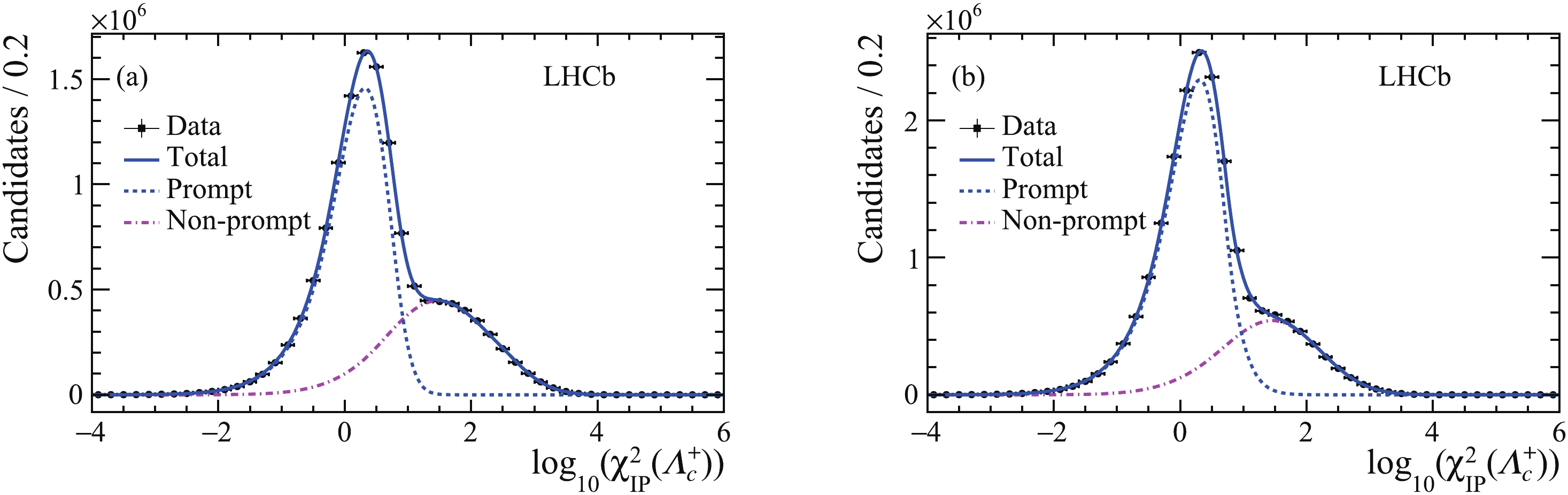
Λ+c baryon yields, which are contaminated byΛ+c candidates produced in b-hadron decays, is done in two steps [44]. First, a binned extended maximum-likelihood fit to them(pK−π+) invariant-mass distribution in the interval 2220-2360MeV/c2 is performed to determine the total number ofΛ+c candidates. Then a binned extended maximum-likelihood fit to the background-subtractedlog10(χ2IP(Λ+c)) distribution is performed to separate the promptΛ+c component from that originated in b-hadron decays. The mass distribution ofΛ+c candidates is described by a sum of a Gaussian function and a modified Gaussian function with power-law tails on both sides with a common peak position. The background mass distribution is described by a first-order Chebyshev polynomial. Thelog10(χ2IP(Λ+c)) distribution, after subtracting the combinatorial background using the sPlot technique [45], is described by two Bukin functions [46]. All the parameters except the peak position and resolution of the functions are derived from a fit to simulated signal. Figs. 2 and 3 show thepK−π+ invariant-mass distribution andlog10(χ2IP(Λ+c)) distributions in data together with the fit results for the two trigger categories. The signal yields for both the signal and the normalisation modes are presented in Table 1.Category Nsig 
Nnorm[103] 
TOS 116±23 
8764±6 
exTIS 210±29 
13889±8 
Table 1. Yields of the signal and normalisation modes.
Figure 2. (color online) Invariant-mass distributions of
Λ+c candidates (a) triggered by TOS and (b) triggered by exTIS, with fit results shown.
Figure 3. (color online) Distributions of
log10(χ2IP(Λ+c)) for background-subtracted candidates (a) triggered by TOS and (b) triggered by exTIS, with fit results shown. -
For each trigger category and for both the signal and the normalisation channels, the total efficiencies are computed as products of the detector geometrical acceptance and of the efficiencies related to particle reconstruction, event selection, particle identification and trigger. All the efficiencies are calculated using simulation that is corrected using data. For both the signal and the normalisation modes, the kinematic distributions in simulation samples, including the transverse momentum and rapidity of the
Ξ++cc andΛ+c baryons and the event multiplicity, are weighted to match those in the corresponding data. The efficiencies are calculated under three lifetime(τΞ++cc) hypotheses: the central value of the measured lifetime, and the lifetime increased or decreased by its measured uncertainty [18]. The dependence of the efficiency on theΞ++cc baryon lifetime is almost linear, with the efficiency ratio varying by 25% from the lower lifetime to the higher one. The resonant structures of theΛ+c→pK−π+ decay are also weighted based on the background-subtracted data, as the simulation samples do not model well the structure seen in the data. The tracking efficiency is corrected with control data samples, as described in Ref. [47]. The particle-identification efficiency is corrected in bins of particle momentum, pseudorapidity and event multiplicity, using the results of a tag-and-probe method applied to calibration samples [48]. The efficiency ratios of the normalisation mode to the signal mode are presented in Table 2.Category εnorm/εsig 
τΞ++cc=0.230ps 
τΞ++cc=0.256ps 
τΞ++cc=0.284ps 
TOS 22.00±1.09 
19.50±1.71 
17.50±1.50 
exTIS 16.64±1.30 
14.56±1.06 
12.95±0.80 
Table 2. Ratios of the normalisation and signal efficiencies.
-
The sources of systematic uncertainties affecting the measurement of the production ratio include the choice of the fit model and the evaluation of the total efficiency. The uncertainties are summarised in Table 3.
Source TOS [%] exTIS [%] Simulation sample size 8.8 7.3 Fit model 5.4 5.3 Hardware trigger 9.0 6.3 Tracking 3.4 3.4 Particle identification 5.5 5.4 Kinematic correction 7.3 6.0 Sum in quadrature 16.8 14.1 Table 3. Relative systematic uncertainties on the production ratio measurement for the two trigger categories.
For both the signal and normalisation modes, the uncertainties due to the choice of the particular fit model are estimated by using alternative functions where the signal is described by a sum of two Gaussian functions with a common peak position and the background is described by a second-order polynomial function. The difference in the ratio of signal yields between the two fits is assigned as systematic uncertainty. Additional effects coming from the
log10(χ2IP(Λ+c)) fit are tested with alternative functions where the parameters used to describe the nonprompt signal are determined from aΛ0b baryon data sample. The effect from the background subtraction is studied using the shape determined with the candidates in theΛ+c baryon mass sidebands.The limited size of the simulation samples leads to systematic uncertainties on the efficiencies. The systematic uncertainty due to the trigger selection efficiency is estimated with a tag-and-probe method exploiting a sample of events that are also triggered by particles unrelated to the signal candidate [27]. Due to the small sample size of the signal channel in data, two different control samples are used. The first sample comprises
Λ0b→Λ+cπ−π+π− decays, which are topologically similar to theΞ++cc→Λ+cK−π+π+ decay. The second sample comprisesB+c→J/ψπ+ decays. This decay does not have the same topology but shares another feature with the signal: there should be at least two other heavy-flavour particles (b- or c-hadrons) produced in the same event that can be responsible for the trigger decision. The hardware trigger efficiencies of theΛ0b ,B+c decay channels and promptΛ+c channel, are measured using the tag-and-probe method. Similar selections to those applied to the signal channel are applied to both the data and simulation for the control samples. The efficiency ratio of theΛ0b ,B+c decays to theΛ+c decays is estimated and the difference of the ratio in data and in simulation is assigned as a systematic uncertainty. The transverse-energy threshold in the calorimeter hardware trigger varied during data taking, and this variation is not fully described by the simulation. The threshold used in the simulated samples is higher than that applied to some data. To investigate the influence of this difference, the same hardware trigger requirement used in the simulation is applied to the data. The measurement is repeated and the change in the measured production ratio is taken as a systematic uncertainty.The systematic uncertainty related to the tracking efficiency includes three effects. First, the tracking efficiency depends on the detector occupancy, which is not well described by simulation. The distribution of the number of SPD hits in simulated samples is weighted to match that in data and an uncertainty of 0.8% per track is assigned to account for remaining difference in multiplicity between data and simulation [47]. Secondly, the uncertainty due to the finite size of the control samples is propagated to the final systematic uncertainty using a large number of pseudoexperiments. Finally, an uncertainty is assigned to the track reconstruction efficiency due to uncertainties on the material budget of the detector and on the modelling of hadronic interaction with the detector material.
The systematic uncertainty related to the particle-identification efficiency includes three effects. The effect from the limited size of calibration samples is evaluated with a large number of pseudoexperiments. Effects of binning in momentum, pseudorapidity and event multiplicity is evaluated by increasing or decreasing the bin sizes by a factor of two. In this estimation, the effects of the correlations between tracks on the particle identification performance are taken into account using simulated samples.
The uncertainties on the weights used for the correction of the kinematic distributions of the simulation samples are propagated as a systematic uncertainty on the production ratio.
-
The production-rate ratio is calculated for the TOS and the exTIS categories of events for three different
Ξ++cc lifetime scenarios using Eq. (1). The separate ratios in the TOS and exTIS categories are presented in Table 4 and are found to be consistent. The combination of the trigger categories, using the Best Linear Unbiased Estimate method [49] is also reported. In the combination, the systematic uncertainties coming from the simulation sample size and hardware trigger are assumed to be uncorrelated, while the other systematic uncertainties are considered to be 100% correlated.Category R[10−4] 
τΞ++cc=0.230ps 
τΞ++cc=0.256ps 
τΞ++cc=0.284ps 
TOS 2.90±0.57±0.49 
2.57±0.51±0.43 
2.31±0.46±0.39 
exTIS 2.41±0.35±0.34 
2.11±0.31±0.30 
1.88±0.27±0.27 
Combined 2.53±0.30±0.33 
2.22±0.27±0.29 
1.98±0.23±0.26 
Table 4. Production rate ratio results for three different
Ξ++cc lifetime hypotheses. The first uncertainty is statistical and the second is systematic. -
A first measurement of the
Ξ++cc production cross-section relative to that ofΛ+c baryons is presented. The ratio ofΞ++cc production cross-section times the branching fraction of theΞ++cc→Λ+cK−π+π+ decay relative to the promptΛ+c production cross-section in the kinematic region4<pT<15GeV/c and2.0<y<4.5 is measured to be(2.22±0.27±0.29)×10−4 , assuming the central value of theΞ++cc lifetime measured in Ref. [18], where the first uncertainty is statistical and the second systematic. This is the first measurement of the production of the doubly charmed baryons inpp collisions and will deepen our understanding on their production mechanism.We thank Chao-Hsi Chang, Cai-Dian Lü, Xing-Gang Wu, and Fu-Sheng Yu for the discussions on the production and decays of double-heavy-flavour baryons. We express our gratitude to our colleagues in the CERN accelerator departments for the excellent performance of the LHC. We thank the technical and administrative staff at the LHCb institutes.
Measurement of Ξ++cc production in pp collisions at √s=13 TeV
- Received Date: 2019-10-25
- Available Online: 2020-02-01
Abstract: The production of
DownLoad: