Effective field theory of the Majorana dark matter

1. Introduction

• 1. Introduction
• 2. Relic density
• 3. Direct detection
• 4. Applications
•      4.1 Singlet-doublet dark matter
•      4.2 MSSM
• 5. Conclusion

From the viewpoint of standard cosmology, cold dark matter (DM) is a neutral particle beyond the Standard Model (SM), which has not been observed in either particle astrophysics or collider experiments. Due to its electrically neutral property, it is natural to consider DM as a Majorana fermion. The Majorana DM appears in a number of well known models, such as the neutralino [1], singlet-doublet [2-9], Higgs-portal [10-13] and Z-portal [14-19] DM.

For the Majorana DM, the effective Lagrangian at the weak scale is described by,

where the SM Lagrangian ${\cal{L}}_{\rm{SM}}$ contains the interactions between DM mediators h and Z and SM particles,

with

Here, the weak scale $\upsilon _{\rm{EW}}$=246 GeV, $g\simeq 0.65$ is the gauge coupling of the $SU(2)_{L}$ group, $\theta_{W}$ denotes the weak mixing angle, and $Q_{f}$ is the electric charge, with $T_{3f}=+(-)\displaystyle\frac{1}{2}$ for the up (down)-type SM fermion, respectively.

Moreover, ${\cal{L}}_{\rm{dark}}$ in Eq. (1) generally contains the interactions between Majorana DM (in 4-component notation) and SM mediators^①,

The $c_h$ and $c_z$ interaction terms constitute the minimal framework from the perspective of the effective field theory, where higher-dimensional operators [20] , responsible for the obvious gauge invariance of Eq. (4), should be taken into account. We refer to ${\cal{L}}_{\rm{dark}}$ in Eq. (4) as the “minimal” effective field theory.

New physical particles beyond the minimal effective field theory impose diverse effects. If they are decoupled, their net effects are recorded in parameters $c_{h}$ and $c_{z}$ in Eq. (4). Conversely, if they are not, they should be included in Eq. (2) or Eq. (4), which either play the role of the new mediator between DM and SM sectors, or contribute to new DM annihilation final states if they are kinetically allowed. In the former case, the Lagrangians in Eq. (2) and Eq. (4) contain all possible contributions to DM annihilation and DM scattering cross sections. In the latter case, new particles with a mass of the order of the weak scale yield a small number of new Feynman diagrams for these cross sections. When the number of new particles is large, the numerical treatment is more viable than an analytical one. Nevertheless, it is only the analytical treatment that can clearly show the ingredients required for recognizing the future signatures of DM direct detection, which is the main motivation for this study.

The rest of the paper is organized as follows. Section 2 is devoted to an analytical derivation of DM annihilation into the SM final states in the minimal framework. We will compare our results with numerical calculations. In Section 3, we show the parameter space subject to the latest DM direct detection limits in a model-independent way. In Section 4, we apply our method to the singlet-doublet and the minimal supersymmetric standard model (MSSM). Finally, we conclude in Section 5.

2. Relic density

• 1. Introduction
• 2. Relic density
• 3. Direct detection
• 4. Applications
•      4.1 Singlet-doublet dark matter
•      4.2 MSSM
• 5. Conclusion

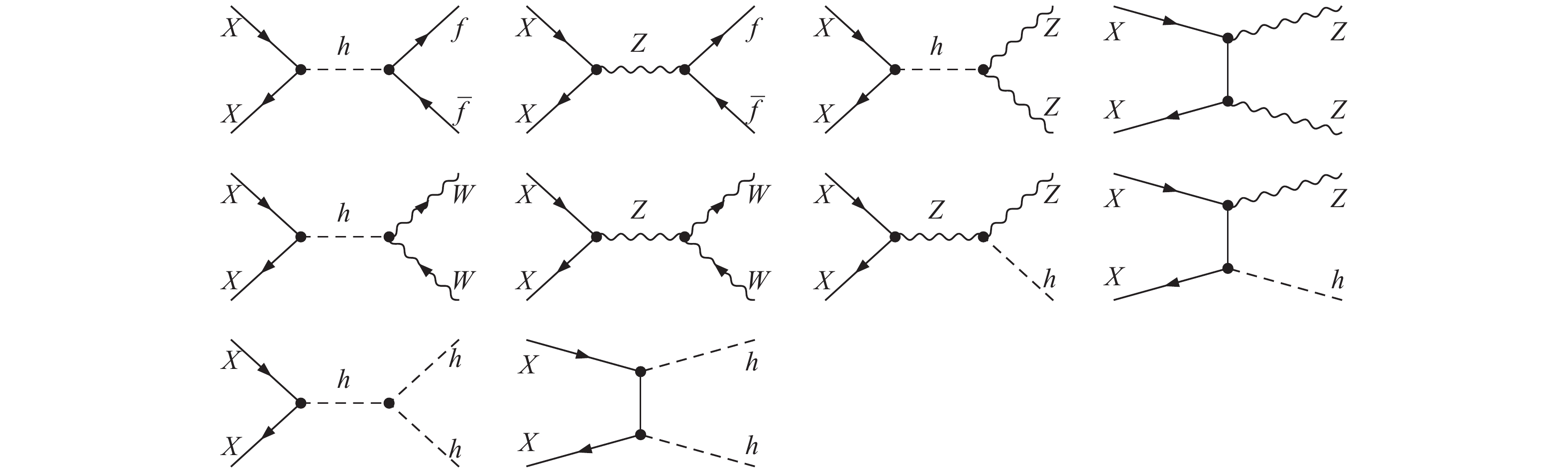
According to the effective Lagrangian in Eq. (1), DM can annihilate into the SM final states such as $f\bar{f}$, ZZ, WW, Zh and hh through the SM mediators h and/or Z. In order to calculate the DM relic density, we first derive the thermally averaged cross section $\left<\sigma v_{\chi}\right>$. The Feynman diagrams responsible are shown in Fig. 1. Although the Feynman diagrams similar to Fig. 1 have already been discussed in a more complicated context such as the neutralino DM [21], a concrete analytical expression for the DM annihilation cross section is only viable in some simplified situations, such as the minimal framework discussed here.

Figure 1

Figure 1.  Feynman diagrams for DM annihilation into the SM final states.

DownLoad: Full-Size Img PowerPoint

As is well known, the DM annihilation cross section times the DM relative velocity $v_{\chi}$ can be expanded in the standard way,

In Table 1 , we introduce the coefficients a and b for the various SM final states of Fig. 1. Direct evaluation yields

Table 1

Table 1.  Coefficients of the $\sigma v_{\chi}$ expansion into the individual SM final states.

channel	a	b
$f\bar{f}$	$a_{ff}$	$b_{ff}$
ZZ	$a_{zz}$	$b_{zz}$
$W^{+}W^{-}$	−	$b_{\rm{ww}}$
$hh$	−	$b_{hh}$
Zh	$a_{zh}$	$b_{zh}$

DownLoad: CSV

Show Table

and

where $N_{c}=1(3)$ for the SM lepton (quark), and $m_{\chi}$ refers to the DM mass. Functionals $r_{ij}$ and $r_{\chi ij}$ are defined respectively as

A few comments are in order regarding our results. First, in the case $c_{h}\rightarrow 0$, both $a_{ff}$ and $a_{zz}$ in Eq. (6)-Eq. (7) coincide with the results for the Z portal [15, 19], but $b_{ff}$ and $b_{zz}$ in [19] are both two times that in Eq. (9) and Eq. (11), respectively. Second, in the case $c_{z}\rightarrow 0$ , all coefficients a in Eq. (6)-Eq. (8) disappear, the same as in the Higgs portal, and our $b_{ff}$ in Eq. (9) and $b_{zz}$ and $b_{hh}$ (the $c^{2}_{h}$-term) are in agreement with the results of [13] and [10], respectively. Third, when both $c_{z}$ and $c_{h}$ are non-zero, interference effects occur in $b_{zz}$ and $b_{zh}$, which are explicitly shown. These interference effects can be neglected except in some particular DM mass range between $m_z$ and $m_h$, where it is not small relative to the other contributions. Finally, we have also included the SM Higgs self-interaction contribution to $b_{hh}$ in Eq. (12). We verified that our results agree with the numerical calculations obtained using the code MicrOMEGAs [22], with a deviation of at most 10%-15% in the estimate of the DM relic density.

3. Direct detection

• 1. Introduction
• 2. Relic density
• 3. Direct detection
• 4. Applications
•      4.1 Singlet-doublet dark matter
•      4.2 MSSM
• 5. Conclusion

The interactions in Eq. (4) yield both spin-dependent (SD) and spin-independent (SI) effective couplings between DM and SM nucleons. In particular, the Yukawa coupling constants $c_{h}$ and $c_{z}$ control the SI and SD scattering cross sections, respectively, which are given by [1, 23],

Here, the nuclear form factors have been chosen as in [24]. The approximations for $\sigma_{\rm{SI}}$ and $\sigma_{\rm{SD}}$ are always valid for the DM mass $m_{\chi}$ above a few times $m_{p, n}$.

In Fig. 2 , we show the parameter space of the DM relic density $\Omega_{\rm{DM}}h^{2}=0.1199\pm 0.0027$ [25] in the two-parameter plane $c_{h}$ and $c_{z}$, with the contours referring to DM masses in units of GeV. We also draw contours from the latest PandaX-II [26], Xenon-1T [27] and LUX 2016 [28] limits. Parameter regions above the color lines, or on the right-hand side of the blue line, are excluded, from which we find that model-independent exclusion limit for the DM mass is about ~155 GeV. Only a small region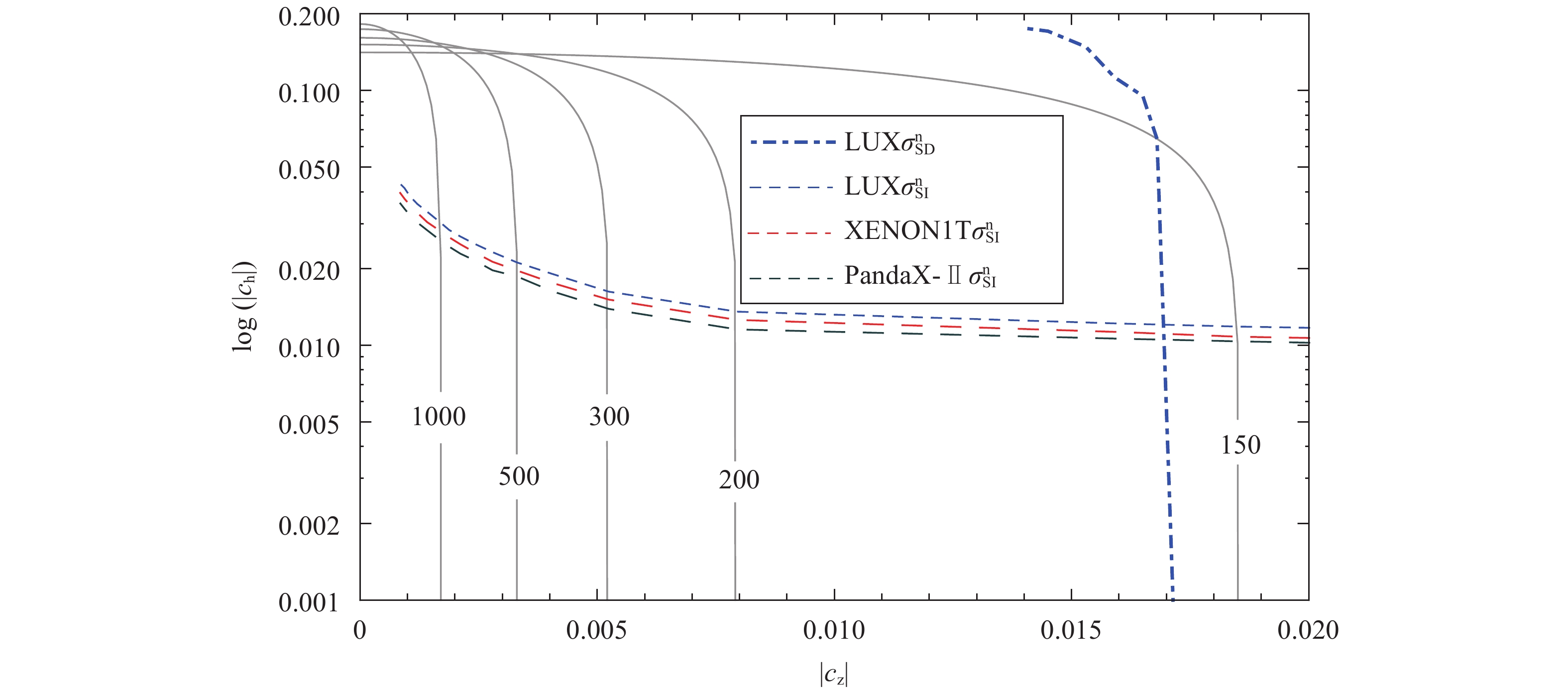

Figure 2

Figure 2.  (color online) Parameter space of the DM relic density in the two-parameter plane $c_{h}$ and $c_{z}$ subject to the latest PandaX-II [26] (green), Xenon-1T [27] (red), and LUX 2016 [28] (blue) limits. The DM masses (in units of GeV) referring to each contour are drawn for clarity, which implies that the model-independent exclusion limit for the DM mass is about ~155 GeV.

DownLoad: Full-Size Img PowerPoint

is left for future tests. If this region is excluded by future experimental limits, we can draw the conclusion that either a new particle(s) is required at the weak scale, or that the simplified Majorana DM models are disfavored. In what follows, we will discuss the implication of our results on a few simplified models.

The parameter space for the coupling of $c_z$ and $c_h$ (alternatively the DM mass range), as given by Eq. (15), is not affected by other constraints such as the mono-jet limit [29-31] at the LHC, or the constraint on the DM annihilation cross section $\sigma(\chi\chi\rightarrow \gamma\gamma)$ at Fermi-LAT [32-34]. The mono-jet constraint is sensitive to parameter $c_z$ only for a DM mass $m_{\chi} < M_{Z}/2$ in our situation, which excludes a DM mass below ~50 GeV for $c_{z}=1.0$, see e.g. [31]. This implies that the surviving DM mass range referred to in Eq. (15), is not sensitive to the present mono-jet limit. On the other hand, the Fermi-LAT constraint on the $\gamma$ spectrum is sensitive to both $c_z$ and $c_h$ for a DM mass below ~500 GeV, where the Feynman diagram for $\sigma\left(\chi\chi\rightarrow h/Z \rightarrow\gamma\gamma\right)$ is dominated by the top, bottom fermion loop and W boson loop. As expected, there is a peak in the $\gamma$ spectrum that appears for a DM mass close to half of the mediator mass, i.e, $M_{h}/2$ or $M_{Z}/2$ in our case. When the DM mass, such as that corresponding to Eq. (15), obviously deviates from the pole masses above, the Fermi-LAT constraint is weak as well.

4. Applications

• 1. Introduction
• 2. Relic density
• 3. Direct detection
• 4. Applications
•      4.1 Singlet-doublet dark matter
•      4.2 MSSM
• 5. Conclusion

4.1 Singlet-doublet dark matter

• 1. Introduction
• 2. Relic density
• 3. Direct detection
• 4. Applications
•      4.1 Singlet-doublet dark matter
•      4.2 MSSM
• 5. Conclusion

This model contains two fermion doublets $L'=(l'^{0},$$l^{-})^{T}$, $L=(l^{+}, l^{0})^{T}$ and a fermion singlet $\psi_{s}$. The dark sector Lagrangian ${\cal{L}}_{\rm{dark}}$ reads as [2-4],

where $m_{s}$, $m_{D}$ and $y_{1, 2}$ are the mass and Yukawa coupling parameters, respectively. H denotes the SM Higgs doublet. In the basis $(\psi_{s}, l'^{0}, l^{0})$ the symmetric mass matrix for neutral fermions is given by,

This model is similar to the neutralino sector of the next-to-minimal supersymmetric model (NMSSM) where bino and wino components are both decoupled. Imposing the decoupling limit $m_{D}>> m_{s}, \upsilon_{\rm{EW}}$ on the dark sector yields only a light singlet-like DM with mass $m_{\chi}\simeq m_{s}$. With this limit, the effective couplings $c_{h\bar{\chi}\chi}$ and $c_{z\bar{\chi}\chi}$ reduce to, respectively [7],

Note that $\mid c_{z} \mid$ and $\mid c_{h}\mid$ are both unchanged under the exchange $y_{1}\leftrightarrow y_{2}$. Since the parameter ranges in Eq. (15) favor a larger value of $\mid c_{h} \mid$ relative to $\mid c_{z}\mid$, this implies that the product $y_{1}y_{2}$ in Eq. (18) should be at most of the order of $m_{\chi}/m_{D}$. Otherwise, $\mid c_{h}\mid$ at the crossing points with the contours of the DM relic density would be too large with respect to the direct detection limits, as shown in Fig. 2.

In Fig. 3 , we show the contours of the DM mass projected on the plane $c_{h}-c_{z}$ for $y_{1}=-3$ and $y_{2}=0.1$, where the condition that the DM mass $m_{\chi}\simeq m_{s}$ should be at least an order of magnitude smaller than $m_{D}$ has been imposed. The crossing points with the contours of the DM relic density are indeed beneath the DM direct detection limits for the DM mass range between 200 GeV and 600 GeV. When the magnitude of $y_{1}$ is tuned to be smaller than 2, these viable crossing points disappear.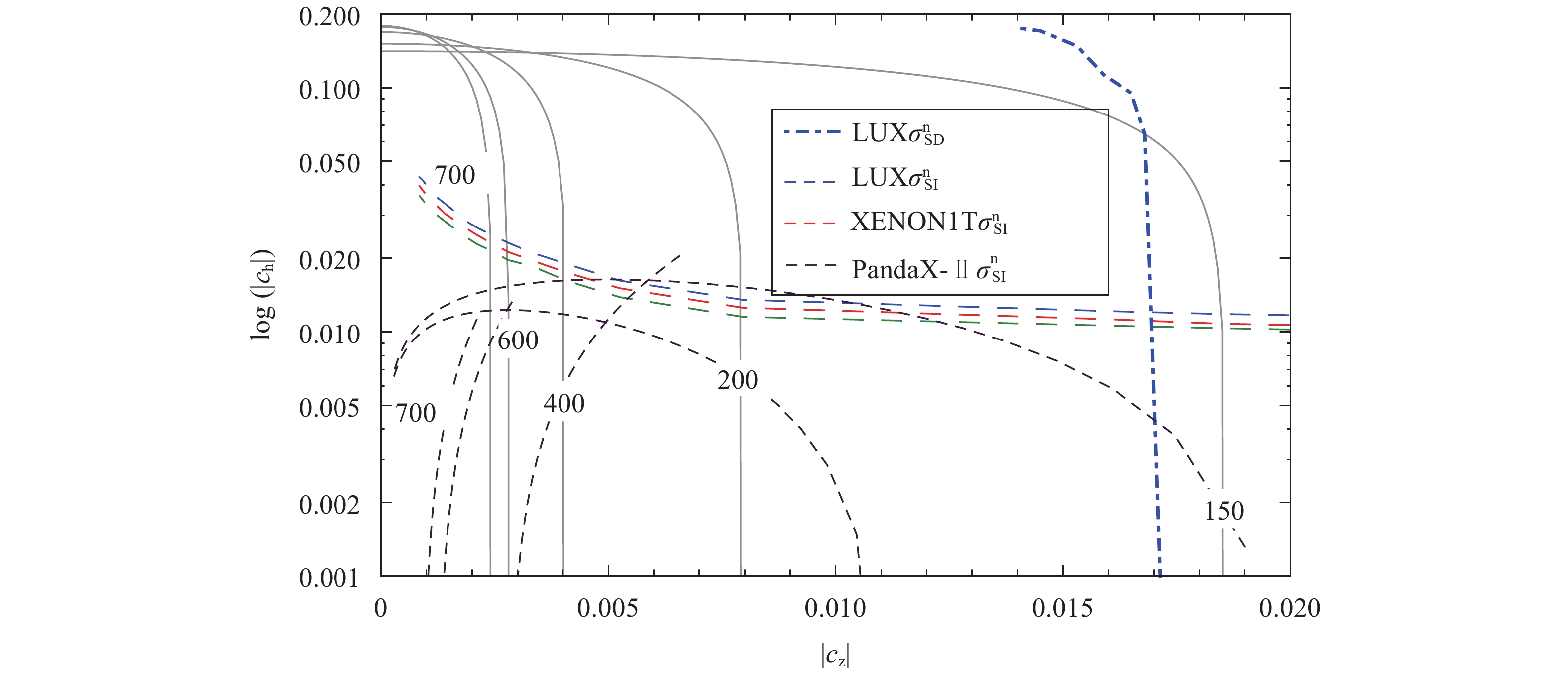

Figure 3

Figure 3.  (color online) Contours of the DM mass in dotted lines projected on the plane $c_{h}-c_{z}$ for $y_{1}=-3$ and $y_{2}=0.1$. Contours of the DM relic density and color lines are the same as in Fig. 2. We have imposed the condition that the DM mass $m_{\chi}$ should be at least an order of magnitude smaller than $m_{D}$.

DownLoad: Full-Size Img PowerPoint

4.2 MSSM

• 1. Introduction
• 2. Relic density
• 3. Direct detection
• 4. Applications
•      4.1 Singlet-doublet dark matter
•      4.2 MSSM
• 5. Conclusion

We now discuss the application to MSSM with decoupling mass spectrum, in which all supersymmetric particles, except the lightest neutralino, are decoupled from the weak scale. The symmetric neutralino mass matrix $M_{\chi}$ under the gauge eigenstates $(\tilde{B}^{0}, \tilde{W}^{0}, \tilde{H}^{0}_{d}, \tilde{H^{0}_{u}})$ is given by,

Imposing the decoupling limit on the Higgs sector and the neutralino sector by $\mid\mu\mid, M_{1}>> M_{2}, m_{Z}$ simultaneously, leads to a wino-like DM with mass $m_{\chi^{0}_{1}}\simeq M_{2}$ and reduced effective coupling coefficients $c_{h}$ and $c_{z}$ [35-37],

respectively. On the other hand, imposing a different decoupling limit $\mid\mu\mid, M_{2}>>M_{1}, m_{Z}$ , we obtain a bino-like DM with mass $m_{\chi^{0}_{1}}\simeq M_{1}$ and

Both decoupling limits yield a light chargino $\tilde{\chi}^{\pm}$ with a mass slightly larger than DM mass. For the bino-like DM, the modification to the DM annihilation cross section can be ignored, whereas for the wino-like DM, the correction due to chargino-exchanging DM annihilation into $W^{+}W^{-}$ is small^&#9313;, apart from a large contribution of co-annihilation, which occurs in the DM mass range above ~1 TeV [38]. For the decoupling limit, $\mid c_{z} \mid < 1.0\times 10^{-3}$ in Eq. (20)-Eq. (21), given $\mid m_{\chi^{0}_{1}}/\mu \mid \leqslant 0.1$ and $m_{Z}/\mid \mu \mid \leqslant 0.1$. From the contours of the DM relic density in Fig. 2, one finds that the wino-like DM with DM mass below 1 TeV is excluded, which is consistent with the concrete estimate of the wino-like DM mass in Ref. [38].

5. Conclusion

• 1. Introduction
• 2. Relic density
• 3. Direct detection
• 4. Applications
•      4.1 Singlet-doublet dark matter
•      4.2 MSSM
• 5. Conclusion

In this paper, we have revisited the Majorana DM, a weakly interacting massive particle, from the viewpoint of the minimal effective field theory. Unlike the Dirac-type analogy, there is no vector coupling between the Majorana DM and Z boson. In this framework, there are only three parameters, i.e., the DM mass and the Yukawa coupling constants $c_{h}$ and $c_{Z}$. Accordingly, it is sufficient to constrain the parameter space in a relatively model-independent way. In order to achieve this, an analytical derivation of DM annihilation into all possible SM final states was performed, which included contributions such as the interference effects and the SM Higgs self-interaction. The fit to the latest LUX, PandaX-II and Xenon-1T limits points to a DM mass lower bound of about ~155 GeV. Also, preliminary applications to the singlet-doublet and MSSM have been addressed. In the singlet-doublet model, we found that the singlet-like DM with a mass range between 200 GeV and 600 GeV still survives the latest DM direct detection limits. In the MSSM with decoupled mass spectrum, we recovered the exclusion limits for the neutralino DM mass, such as the wino-like DM.

References