-
The timelike electromagnetic form factors (FFs) provide a key for understanding the strong interactions and inner structure of hadrons. They have been measured via the process
$ e^+e^-\rightarrow B\bar{B} $ [1-5] (where$ B $ stands for a spin-1/2 ground baryon state), and a non-vanishing cross-section in the near-threshold region was observed [6-9]. The unusual behavior near the threshold implies a more complicated underlying physics scenario, which has driven many theoretical interpretations, including the$ B\bar{B} $ bound states or meson-like resonances [10-17], final-state interactions [18,19] and an attractive Coulomb interaction [20,21].Very recently, the BESIII collaboration studied the process
$ e^+e^-\rightarrow \Lambda\bar{\Lambda} $ with improved precision [22]. The Born cross-section at$ \sqrt{s} = 2.2324 $ GeV, which is 1.0 MeV above the$ \Lambda\bar{\Lambda} $ mass threshold, was measured as$ 305\pm45^{+66}_{-36} $ pb. Could it be that this unexpected feature in the near-threshold region is due to an unobserved strangeonium meson resonance? In the present work, we try to answer this question.We calculate the spectrum of the
$ s\bar{s} $ system in the framework of the Godfrey-Isgur (GI) model [23], which gives a good description of the known mesons and baryons [23-25]. After obtaining the masses of the higher excited strangeonium states, we estimate the electronic decay width of the$ J^{PC} = 1^{–} $ states$ \phi(2D,\; 3D,\; 4D,\; 5D) $ and$ \phi(3S,\; 4S,\; 5S,\; 6S) $ with the Van Royen-Weisskopf formula [26]. We use the extended quark-pair creation model [27,28] to calculate the partial decay widths of the vector states$ \Lambda\bar{\Lambda} $ ,$ \Xi^{-(*)}\bar{\Xi}^+ $ , and$ \Sigma^{+(*)}\bar{\Sigma}^{-(*)} $ with the obtained spatial wave functions. Considering the theoretical calculations of the two-body strong decays of the$ s\bar{s} $ system in literature [29-34], we emphasize in the present work the baryon-antibaryon decay mode and electronic decay properties.According to the theoretical predictions of various models, the masses of
$ \phi(3^3S_1) $ and$ \phi(2^3D_1) $ mesons are about 2.2 GeV (see Table 1). Therefore, we calculate the$ e^+e^- $ and$ \Lambda\bar{\Lambda} $ partial decay widths of the excited vector states$ \phi(3^3S_1) $ and$ \phi(2^3D_1) $ . We find that the electronic decay width of$ \phi(3^3S_1) $ is about 3 times smaller than of$ \phi(2^3D_1) $ . However, around 2232 MeV, the partial decay width of the$ \Lambda\bar{\Lambda} $ mode can be up to several MeV for$ \phi(3^3S_1) $ , while the partial$ \Lambda\bar{\Lambda} $ decay width of the state$ \phi(2^3D_1) $ has a very small value$ {\cal{O}}(10^{-3}) $ keV. The threshold enhancement in the process$ e^+e^-\rightarrow \Lambda\bar{\Lambda} $ observed by the BESIII collaboration [22] may be caused by$ \phi(3^3S_1) $ . We also note that the$ \Lambda\bar{\Lambda} $ and$ \Sigma^{+}\bar{\Sigma}^{-} $ partial decay widths of the states$ \phi(3^3D_1) $ and$ \phi(4^3S_1) $ are several MeV. These two states have a good potential to be observed in future experiments via their main baryon-antibaryon decay channels.state this work mass MGI [29] GI [23] RQM [35] COQM [36] exp. [37] $ \phi(1^3S_1) $ 

1009 1030 1020 1038 1020 1020 $ \phi(2^3S_1) $ 

1688 1687 1690 1698 1740 1680 $ \phi(3^3S_1) $ 

2204 2149 $ \cdot\cdot\cdot $ 

2119 2250 – $ \phi(4^3S_1) $ 

2627 2498 $ \cdot\cdot\cdot $ 

2472 2540 – $ \phi(5^3S_1) $ 

2996 $ \cdot\cdot\cdot $ 

$ \cdot\cdot\cdot $ 

2782 $ \cdot\cdot\cdot $ 

– $ \phi(6^3S_1) $ 

3327 $ \cdot\cdot\cdot $ 

$ \cdot\cdot\cdot $ 

$ \cdot\cdot\cdot $ 

$ \cdot\cdot\cdot $ 

– $ \phi(1^3D_1) $ 

1883 1869 $ \cdot\cdot\cdot $ 

1845 1750 – $ \phi(2^3D_1) $ 

2342 2276 $ \cdot\cdot\cdot $ 

2258 2260 – $ \phi(3^3D_1) $ 

2732 2593 $ \cdot\cdot\cdot $ 

2607 $ \cdot\cdot\cdot $ 

– $ \phi(4^3D_1) $ 

3079 $ \cdot\cdot\cdot $ 

$ \cdot\cdot\cdot $ 

$ \cdot\cdot\cdot $ 

$ \cdot\cdot\cdot $ 

– $ \phi(5^3D_1) $ 

3395 $ \cdot\cdot\cdot $ 

$ \cdot\cdot\cdot $ 

$ \cdot\cdot\cdot $ 

$ \cdot\cdot\cdot $ 

– Table 1. Predicted masses (MeV) of the higher
$ \phi $ mesons with$ J^{PC} = 1^{–} $ given by various models.This paper is organized as follows. In Sec. 2, we give a brief introduction to the GI model and calculate the spectrum of the
$ s\bar{s} $ system. We then present the Van Royen-Weisskopf formula and give the electronic decay properties in Sec. 3. In Sec. 4, we discuss the extended quark-pair creation model and the results of baryon-antibaryon decay. We give a short summary in Sec. 5. -
In this work, we employ the GI model to calculate the mass spectrum of the higher excited strangeonium. According to the GI model [23], the Hamiltonian for the quark and antiquark reads
$ \tilde{H} = \left({{p}}^2+m_1^2\right)^{1/2} +\left({{p}}^2+m_2^2\right)^{1/2} +V_{\rm{eff}}({{p}},{{r}}), $

(1) where
$ m_i $ and$ {{p}} $ are the quark mass and momentum in the center-of-mass frame.$ V_{\rm{eff}}({{p}},{{r}}) $ is the potential between the quark and antiquark, which can be obtained from the on-shell scattering amplitude between the quark and antiquark in the center-of-mass frame. This Hamiltonian contains the short-range$ \gamma^{\mu}\otimes\gamma_{\mu} $ one-gluon-exchange (OGE) interaction, and the$ 1\otimes1 $ linear confining interaction suggested by lattice QCD. In the nonrelativistic limit, it can be reduced to the familiar Breit-Fermi interaction$ V_{\rm{eff}}({{p}},{{r}}) = {H}_{12}^{\rm{conf}}+{H}_{12}^{\rm{hyp}}+{H}_{12}^{\rm{so}}. $

(2) Here,
$ {H}_{12}^{\rm{conf}} $ is the spin-independent linear confinement and Coulomb-type interaction;$ {H}_{12}^{\rm{hyp}} $ is the color-hyperfine interaction and$ {H}_{12}^{\rm{so}} $ is the spin-orbit interaction.In order to include relativistic effects, Godfrey and Isgur built a semiquantitative model [23]. Introducing the smearing function for a meson
$ q_i\bar{q}_j $ $ \rho_{ij}({{r}}-{{r}}') = \frac{\sigma_{ij}^3}{\pi^{3/2}}\mathrm{e}^{-\sigma_{ij}^2({{r}}-{{r}}')^2}, $

(3) the OGE potential
$ G(r) = -4\alpha(r)/3r $ and the confining potential$ S(r) = br+c $ are smeared into$ \tilde{G}(r) $ and$ \tilde{S}(r) $ via$ \tilde{f}(r) = \int\mathrm{d}^3{{r}}'\rho_{ij}({{r}}-{{r}}')f(r'). $

(4) Introducing the momentum-dependent factors, the Coulomb term is modified according to
$ \tilde{G}(r) {\to} \left(1+\frac{p^2}{E_1E_2}\right)^{1/2} \tilde{G}(r) \left(1+\frac{p^2}{E_1E_2}\right)^{1/2}, $

(5) and the contact, tensor, vector spin-orbit, and scalar spin-orbit potentials are modified according to
$ \frac{\tilde{V}_{i}(r)}{m_1m_2} {\to} \left(\frac{m_1m_2}{E_1E_2}\right)^{1/2+\epsilon_i} \frac{\tilde{V}_{i}(r)}{m_1m_2} \left(\frac{m_1m_2}{E_1E_2}\right)^{1/2+\epsilon_i} $

(6) where
$ \epsilon_{i} $ corresponds to the contact (c), tensor (t), vector spin-orbit [so(v)], and scalar spin-orbit [so(s)].With the notation
$ f_{\alpha\beta}^{i}(r) = \left(\frac{m_{\alpha}m_{\beta}}{E_{\alpha}E_{\beta}}\right)^{1/2+\epsilon_{i}} f(r) \left(\frac{m_{\alpha}m_{\beta}}{E_{\alpha}E_{\beta}}\right)^{1/2+\epsilon_{i}} $

(7) we have
$ V_{\rm{eff}}({{p}},{{r}}) = \tilde{H}_{12}^{\rm{conf}}+\tilde{H}_{12}^{\rm{hyp}}+\tilde{H}_{12}^{\rm{so}}, $

(8) where
$ \tilde{H}_{12}^{\rm{conf}} = \left(1+\frac{p^2}{E_1E_2}\right)^{1/2} \tilde{G}(r) \left(1+\frac{p^2}{E_1E_2}\right)^{1/2} +\tilde{S}(r), $

(9) $ \begin{split} \tilde{H}_{12}^{\rm{so}} = \frac{{{S}}_1\cdot{{L}}}{2m_1^2}\frac{1}{r}\frac{\partial\tilde{G}_{11}^{{\rm{so}}({\rm v})}}{\partial{r}} +\frac{{{S}}_2\cdot{{L}}}{2m_2^2}\frac{1}{r}\frac{\partial\tilde{G}_{22}^{{\rm{so}}({\rm v})}}{\partial{r}} \end{split}$

$ \begin{split}&+\frac{\left({{S}}_1+{{S}}_2\right)\cdot{{L}}}{m_1m_2}\frac{1}{r}\frac{\partial\tilde{G}_{12}^{{\rm{so}}({\rm v})}}{\partial{r}} -\frac{{{S}}_1\cdot{{L}}}{2m_1^2}\frac{1}{r}\frac{\partial\tilde{S}_{11}^{{\rm{so}}({\rm s})}}{\partial{r}}\\& -\frac{{{S}}_2\cdot{{L}}}{2m_2^2}\frac{1}{r}\frac{\partial\tilde{S}_{22}^{{\rm{so}}({\rm s})}}{\partial{r}}, \end{split}$

(10) and
$ \begin{split} \tilde{H}_{12}^{\rm{hyp}} =& \frac{2{{S}}_{i}\cdot{{S}}_{j}}{3m_1m_2}\nabla^2\tilde{G}_{12}^{\rm{c}} -\left(\frac{{{S}}_{1}\cdot{\hat{r}}{{S}}_{2}\cdot\hat{r}-\frac{1}{3}{{S}}_{1}\cdot{{S}}_{2}}{m_1m_2}\right) \\&\times\left(\frac{\partial^2}{\partial{r}^2}-\frac{1}{r}\frac{\partial}{\partial{r}}\right)\tilde{G}_{12}^{\rm{t}}. \end{split}$

(11) The spin-orbit term
$ \tilde{H}_{12}^{\rm{so}} $ can be decomposed into a symmetric part$ \tilde{H}_{(12)}^{\rm{so}} $ and an antisymmetric part$ \tilde{H}_{[12]}^{\rm{so}} $ , while the$ \tilde{H}_{[12]}^{\rm{so}} $ vanishes when$ m_1 = m_2 $ .We adopt the free parameters in the original GI model [23], and diagonalize the Hamiltonian in the simple harmonic oscillator bases
$ |n ^{2S+1}L_{J}\rangle $ . The resulting mass spectrum of the strangeonium is shown in Fig. 1. The predicted masses of the higher vector$ \phi $ mesons in various models are listed in Table 1. -
With the Van Royen-Weisskopf formula [26,38], the electronic decay width of the excited vector strangeonium states is given by
$ \Gamma[\phi(nS)\rightarrow e^+e^-]\propto \frac{4\alpha^2e^2_s}{M^2_{nS}}|R_{nS}(0)|^2, $

(12) $ \Gamma[\phi(nD)\rightarrow e^+e^-]\propto \frac{25\alpha^2e^2_s}{2M^2_{nD}m^4_s}|R{''}_{nD}(0)|^2. $

(13) Here,
$ \alpha = \frac{1}{137} $ denotes the fine structure constant.$ m_s = 450 $ MeV and$ e_s = -\frac{1}{3} $ are the strange quark constituent mass and charge in units of electron charge.$ M_{nS}(M_{nD}) $ is the mass of$ \phi(nS)(\phi(nD)) $ .$ R_{nS}(0) $ represents the radial$ S $ -wave function at the origin, and$ R{''}_{nD}(0) $ represents the second derivative of the radial$ D $ -wave function at the origin.In our calculations, we adopt the simple harmonic oscillator (SHO) wave functions for the space wave functions of the initial meson. With the wave functions obtained in calculations of the mass spectrum, we get the root mean square radius of the vector states. We can then determine the harmonic oscillator strength
$ \beta_{th} $ for the two strange quarks in the initial meson (as listed in Table 2).state sass $ \beta_{th} $ 

$ R $ 

$ \Gamma[e^+e^-] $ /keV

$ \phi(3^3S_1) $ 

2204 368 0.17 0.21 $ \phi(4^3S_1) $ 

2627 351 0.12 0.15 $ \phi(5^3S_1) $ 

2996 341 0.09 0.11 $ \phi(6^3S_1) $ 

3327 334 0.08 0.10 $ \phi(2^3D_1) $ 

2342 375 0.47 0.59 $ \phi(3^3D_1) $ 

2732 355 0.54 0.68 $ \phi(4^3D_1) $ 

3079 344 0.61 0.77 $ \phi(5^3D_1) $ 

3395 336 0.70 0.88 Table 2. Predicted electronic decay widths of the higher
$ \phi $ mesons with$ J^{PC}=1^{–} $ . The units are MeV for the mass and harmonic oscillator strength$ \beta_{th} $ , and keV for the$ e^+e^- $ decay width.$ R $ is the electronic decay width ratio of the higher excited state and the state$ \phi(1S) $ .$ \Gamma[e^+e^-]=R\times\Gamma[\phi(1S)\rightarrow e^+e^-] $ denotes the electronic decay width for each state.According to PDG [37], the electronic decay branching ratio for
$ \phi(1S) $ is$ {\cal{B}}[\phi(1S)\rightarrow e^+e^-] = (2.973\pm0.034)\times10^{-4}. $

(14) Combining this ratio with the total decay width (
$ \Gamma = 4.249\pm0.013 $ MeV), the central value of the electronic decay width is$ \Gamma[\phi(1S)\rightarrow e^+e^-] = 1.26 $ keV. From Eqs. (12) and (13), we can obtain the ratio of electronic decay width of the higher excited vector strangeonium states and the state$ \phi(1S) $ . Thus, we get the electronic decay widths of these states, as shown in Table 2.From Table 2, the ratio
$ R $ is smaller than one. The electronic decay widths of the excited vector strangeonium states$ \phi(3S,\; 4S,\; 5S,\; 6S) $ and$ \phi(2D,\; 3D,\; 4D,\; 5D) $ are smaller than of the state$ \phi(1S) $ . On the other hand, the electronic decay width of the$ D $ -wave vector strangeonium is about$ 3\sim 8 $ times larger than of the$ S $ -wave vector strangeonium. For the$ S $ -wave states, our predictions are in accordance with Ref. [39], while for the$ D $ -wave states, our predictions are about 3 times larger than in Ref. [39].Considering the uncertainties of the predicted mass and harmonic oscillator strength
$ \beta_{th} $ , we plot the variation of the electronic decay width ratio$ R $ as a function of the mass with the values of$ \beta $ =$ \beta_{th}+20 $ MeV,$ \beta_{th} $ , and$ \beta_{th}-20 $ MeV, in Fig. 2. It is obvious that the ratio$ R $ decreases with mass for the same value of$ \beta $ . -
The quark-pair creation (
$ ^3P_0 $ ) model was first proposed by Micu [40], Carlitz and Kislinger [41], and further developed by the Orsay group [42-44], and has been widely used in studies of the OZI-allowed two-body strong decay of hadrons. Very recently, the$ ^3P_0 $ model was extended to some OZI-allowed three-body strong decays [28] as well. In the framework of this model, the interaction Hamiltonian for one quark-pair creation is described as [45-47]$ H_{q\bar{q}} = \gamma\sum_f2m_f\int {\rm d}^3x\bar{\psi}_f\psi_f. $

(15) Here,
$ \gamma $ is a dimensionless parameter usually determined by fitting the experimental data.$ m_f $ denotes the constituent quark mass of flavor$ f $ , and$ \psi_f $ stands for the Dirac quark field.In our previous work [27], we extended the
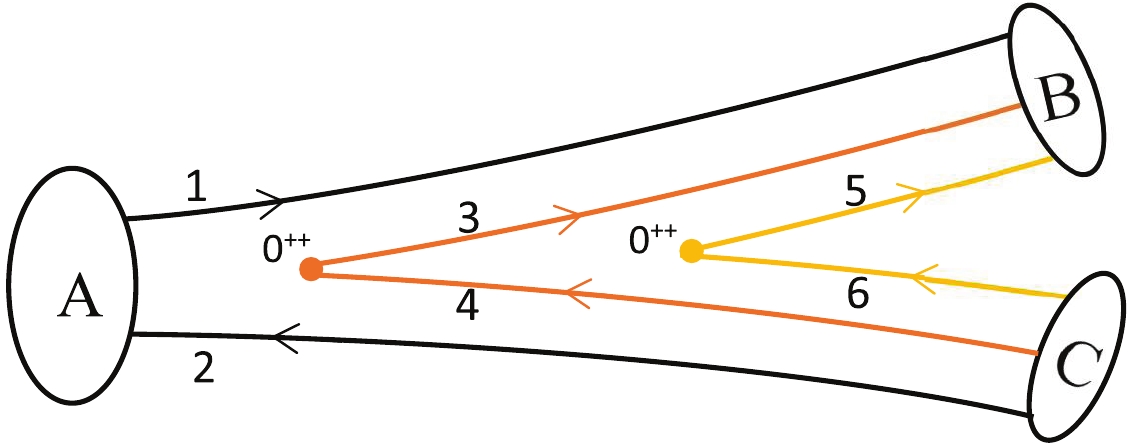
$ ^3P_0 $ model to study the partial decay width of the$ \Lambda_c\bar{\Lambda}_c $ mode for the charmonium system. In this work, we use this model to study the process$ \phi^*(A)\rightarrow B(B)+\bar{B}(C) $ , where$ \phi^* $ denotes the excited strangeonium state. As pointed out in Ref. [27], two light quark pairs should be created in this type of reaction (as shown in Fig. 3), and the helicity amplitude$ M^{M_{J_A}M_{J_B}M_{J_B}} $ reads$\delta^3({{p}}_A-{{p}}_B-{{p}}_C)M^{M_{J_A}M_{J_B}M_{J_B}} \\ = \sum_k\frac{\langle BC|H_{q\bar{q}}|k\rangle\langle k|H_{q\bar{q}}|A\rangle}{E_k-E_A}. $

(16) Here,
$ {{p}}_I(I = A,\; B,\; C) $ denotes the momentum of the hadron.$ E_{A(k)} $ represents the energy of the initial (intermediate) state$ A(k) $ . Considering the quark-hadron duality [48], we simplify the calculations by taking$ E_k-E_A $ as a constant, namely$ E_k-E_A\approx2m_{q} $ . Here,$ m_q $ is the constituent quark mass of the created quark. We adopt this crude approximation since the intermediate state differs from the initial state by two additional quarks at the quark level [27,28]. Thus, we can rewrite Eq. (16) as$ \delta^3({{p}}_A-{{p}}_B-{{p}}_C)M^{M_{J_A}M_{J_B}M_{J_B}}\approx\frac{\langle BC|H_{q\bar{q}}H_{q\bar{q}}|A\rangle}{2m_{q}}. $

(17) The transition operator for the creation of two quark pairs in the nonrelativistic limit reads
$ \begin{split}T =& \frac{9\gamma^2}{2m_{q}} \sum_{m,m'}\langle1m;1-m|00\rangle\langle1m';1-m'|00\rangle\\ &\times\int {\rm d}^3{{p}}_3{\rm d}^3{{p}}_4{\rm d}^3{{p}}_5{\rm d}^3{{p}}_6\delta^3({{p}}_3+{{p}}_4)\delta^3({{p}}_5+{{p}}_6)\\ &\times\varphi^{34}_0\omega^{34}_0\chi^{34}_{1,-m} {\cal{Y}}_1^m(\frac{{{p}}_3-{{p}}_4}{2})a^{\dagger}_{3i}b^{\dagger}_{4j}\\ &\times\varphi^{56}_0\omega^{56}_0\chi^{56}_{1,-m'} {\cal{Y}}_1^{m'}(\frac{{{p}}_5-{{p}}_6}{2})a^{\dagger}_{5i}b^{\dagger}_{6j}, \end{split}$

(18) where
$ {{p}}_i $ ($ i $ = 3, 4, 5, 6) stands for the three-vector momentum of the$ i $ th quark.$ \varphi_0 = (u\bar{u}+d\bar{d}+s\bar{s})/\sqrt{3} $ corresponds to the flavor function, and$ \omega_0 = \delta_{ij} $ represents the color singlet of the quark pairs created in vacuum.$ \chi_{1,-m(m')} $ are the spin triplet states for the created quark pairs. The solid harmonic polynomial$ {\cal{Y}}_1^{m(m')}({{p}})\equiv|{{p}}|Y^{m(m')}_1(\theta_p,\phi_p) $ denotes the$ P $ -wave quark pairs.$ a^{\dagger}_{i}b^{\dagger}_{j} $ is the creation operator representing the quark-pair creation in vacuum.Finally, the hadronic decay width
$ \Gamma $ in the relativistic phase space reads$ \Gamma[A\rightarrow BC] = \pi^2\frac{|{{p}}|}{M_A^2}\frac{1}{2J_A+1}\sum_{M_{J_A},M_{J_B},M_{J_C}}|{\cal{M}}^{M_{J_A}M_{J_B}M_{J_C}}|^2. $

(19) Here,
$ {{p}} $ represents the momentum of the daughter baryon.$ M_A $ and$ J_A $ are the mass and total angular quantum number of the parent baryon$ A $ . In the center-of-mass frame of the parent baryon$ A $ ,$ {{p}} $ reads$ |{{p}}| = \frac{\sqrt{[M_A^2-(M_B-M_C)^2][M_A^2-(M_B+M_C)^2]}}{2M_A}. $

(20) In our calculations, we take the standard constituent quark masses, namely
$ m_u $ =$ m_d $ = 330 MeV and$ m_s $ = 450 MeV. The masses of the final baryons are taken from PDG [37], as listed in Table 3. We adopt the simple harmonic oscillator (SHO) wave functions for the space-wave functions of the hadrons. The harmonic oscillator strength$ \beta_{th} $ for the two strange quarks in the initial mesons is determined by the spatial wave functions obtained in the calculations of the mass spectrum (as listed in Table 1). The harmonic oscillator strength for the two light quarks in the final baryons is taken as$ \alpha = 400 $ MeV. As for the strength of the quark-pair creation in vacuum, we adopt the same value as in Ref. [49],$ \gamma = 6.95 $ . The uncertainty of the strength$ \gamma $ is about 30% [47, 50-52], and the partial decay widths are proportional to$ \gamma^4 $ . Thus, our predictions may bare quite a large uncertainty.parameter value mass of the final baryon $ \Lambda $ 

1115.68 $ \bar{\Lambda} $ 

1115.68 $ \Sigma^+ $ 

1189.37 $ \bar{\Sigma}^- $ 

1189.37 $ \Xi^- $ 

1321.71 $ \bar{\Xi}^+ $ 

1321.71 $ \Sigma^{+*} $ 

1382.80 $ \bar{\Sigma}^{-*} $ 

1382.80 $ \Xi^{-*} $ 

1535.0 constituent quark mass $ m_u $ 

330 $ m_d $ 

330 $ m_s $ 

450 harmonic oscillator parameter $ \alpha $ 

400 strength of the quark pair $ \gamma $ 

6.95 creation from the vacuum -
In 2007, the BABAR collaboration measured the cross-section of
$ e^+e^-\rightarrow \Lambda\bar{\Lambda} $ from threshold up to 3 GeV [9], and observed a possible nonvanishing cross-section at threshold. Recently, the BESIII collaboration published a measurement of the process$ e^+e^-\rightarrow \Lambda\bar{\Lambda} $ [22] with improved precision. The Born cross-section at$ \sqrt{s} = 2232.4 $ MeV, which is 1.0 MeV above the$ \Lambda\bar{\Lambda} $ mass threshold, was measured as$ 305\pm45^{+66}_{-36} $ pb, which indicates an obvious threshold enhancement.According to various predictions (see Table 1), there are two strangeonium meson resonances
$ \phi(3^3S_1) $ and$ \phi(2^3D_1) $ , both with masses around 2.2 GeV and$ J^P = 1^{–} $ . As a possible source of the observed threshold enhancement, it is crucial to study the decay properties of the states$ \phi(3^3S_1) $ and$ \phi(2^3D_1) $ .We first explore the
$ \Lambda\bar{\Lambda} $ partial decay width of the state$ \phi(3^3S_1) $ and obtain$ \Gamma[\phi(3^3S_1){\to}\Lambda\bar{\Lambda}] \sim 5.84\;\rm{ MeV} $

(21) with a mass of
$ M = 2232 $ MeV (see Table 4). This partial decay width is large enough to be observed in experiments, and indicates that the observed threshold enhancement may arise from this state. Although the phase space is considerably suppressed around the threshold, the transition amplitude for this decay mode is quite large. Hence, the partial decay width of the$ \Lambda\bar{\Lambda} $ mode for the state$ \phi(3^3S_1) $ reaches several MeV. Considering the uncertainties of the predicted mass, we studied the variation of the$ \Lambda\bar{\Lambda} $ decay width as a function of the mass of the state$ \phi(3^3S_1) $ . The decay width increases rapidly with the mass in the range of (2233−2300) MeV.state $ \beta_{th} $ /MeV

$ \Gamma_{\Lambda\bar{\Lambda}} $ /MeV

$ \psi(3^3S_1) $ 

368 5.84 $ \psi(2^3D_1) $ 

375 $ 3.90\times10^{-6} $ 

Table 4. Partial decay widths of the vector strangonium with a mass of
$ M=2232 $ MeV.We investigate now the decay properties of the state
$ \phi(2^3D_1) $ . Fixing the mass at$ M = 2232 $ MeV, we get$ \Gamma[\phi(2^3D_1){\to}\Lambda\bar{\Lambda}] \sim 3.90\times10^{-6}\;\rm{ MeV}. $

(22) This width seems to be too small to be observed in experiments. Combining the predicted partial decay width of
$ \phi(3^3S_1) $ , we obtain$ \frac{\Gamma[\phi(3^3S_1){\to}\Lambda\bar{\Lambda}]}{\Gamma[\phi(2^3D_1){\to}\Lambda\bar{\Lambda}]}\sim 1.50\times10^{6}. $

(23) The decay ratio of
$ \phi(3^3S_1) $ into the$ \Lambda\bar{\Lambda} $ channel is about$ {\cal{O}}(10^6) $ larger than of$ \phi(2^3D_1) $ into the$ \Lambda\bar{\Lambda} $ channel. Combining their electronic decay widths calculated in Sec. 3, we conclude that if the threshold enhancement reported by the BESIII collaboration in the process$ e^+e^-\rightarrow \Lambda\bar{\Lambda} $ is related to an unobserved strangeonium meson resonance then this state should most likely be$ \phi(3^3S_1) $ .Besides the uncertainties coming from the predicted mass and harmonic oscillator strength
$ \beta_{th} $ , the results of$ \phi(3^3S_1) $ and$ \phi(2^3D_1) $ may have large uncertainties due to their lower masses. At the hadron level, the energy of the intermediate states with spin parity$ J^{PC} = 1^{–} $ , such as molecular states$ KK_1(1270) $ ,$ K*(892)K^*_0(700) $ ,$ K*(892)K_1(1270) $ and$ \phi(1020)a_0(980) $ , is about 1.7~2.1 GeV. Thus,$ E_k-E_A $ is small and sensitive to the masses of intermediates states. In this case, taking$ E_k-E_A $ = 2$ m_q $ will introduce a large uncertainty in the calculations. -
Besides
$ \phi(3^3S_1) $ and$ \phi(2^3D_1) $ , we also analyzed the decay properties of the S-wave states$ \phi(4^3S_1,\; 5^3S_1,\; 6^3S_1) $ and the D-wave states$ \phi(3^3D_1,\; 4^3D_1,\; 5^3D_1) $ . The decay properties are shown in Table 5. From the table, we see that the$ \Lambda\bar{\Lambda} $ partial decay width of$ \phi(3^3D_1) $ can be up to$ \Gamma\sim3.5 $ MeV, which is larger than the other five vector states considered in this work. This considerable width indicates that this state has a good potential to be observed in the$ \Lambda\bar{\Lambda} $ decay channel.state mass $ \beta_{th} $ 

$ \Gamma_{\Lambda\bar{\Lambda}} $ 

$ \phi(4^3S_1) $ 

2627 351 1.81 $ \phi(5^3S_1) $ 

2996 341 0.08 $ \phi(6^3S_1) $ 

3327 334 0.84 $ \phi(3^3D_1) $ 

2732 355 3.40 $ \phi(4^3D_1) $ 

3079 344 0.27 $ \phi(5^3D_1) $ 

3395 336 0.10 Table 5. Predicted partial decay widths of the higher
$ \phi $ mesons with$ J^{PC}=1^{–} $ , in units of MeV.Similarly, taking into account the uncertainties of the theoretical masses and harmonic oscillator strength
$ \beta_{th} $ , we plot the$ \Lambda\bar{\Lambda} $ partial decay widths of these states as function of the mass in Fig. 4 with the values of$ \beta $ =$ \beta_{th} $ +20 MeV,$ \beta_{th} $ , and$ \beta_{th} $ -20 MeV. According to Fig. 4, the curve for the state$ \phi(3^3D_1) $ has a bowl structure in the mass range of 2550 MeV to 2850 MeV, and the partial width reaches$ \Gamma\sim3.7 $ MeV for$ \beta = \beta_{th} $ . The$ \Lambda\bar{\Lambda} $ partial decay width for$ \phi(5^3D_1) $ is the smallest and is less than$ \Gamma<0.4 $ MeV in the mass range of$ M = (3150-3450) $ MeV. As to$ \phi(4^3S_1) $ , its$ \Lambda\bar{\Lambda} $ decay width is very sensitive to the mass (see Fig. 4). For$ \beta = \beta_{th} $ , its width varies in the range of$ \Gamma\sim(0.0-4.8) $ MeV for masses in the range of$ M = (2450-2750) $ MeV. If the mass of$ \phi(4^3S_1) $ is in the range (2496-2590) MeV, the decay width of the$ \Lambda\bar{\Lambda} $ mode is less than one MeV. Most of the$ \Lambda\bar{\Lambda} $ partial decay widths for the other three states,$ \phi(4^3D_1) $ ,$ \phi(5^3S_1) $ and$ \phi(6^3S_1) $ , are also less than one MeV (see Fig. 4).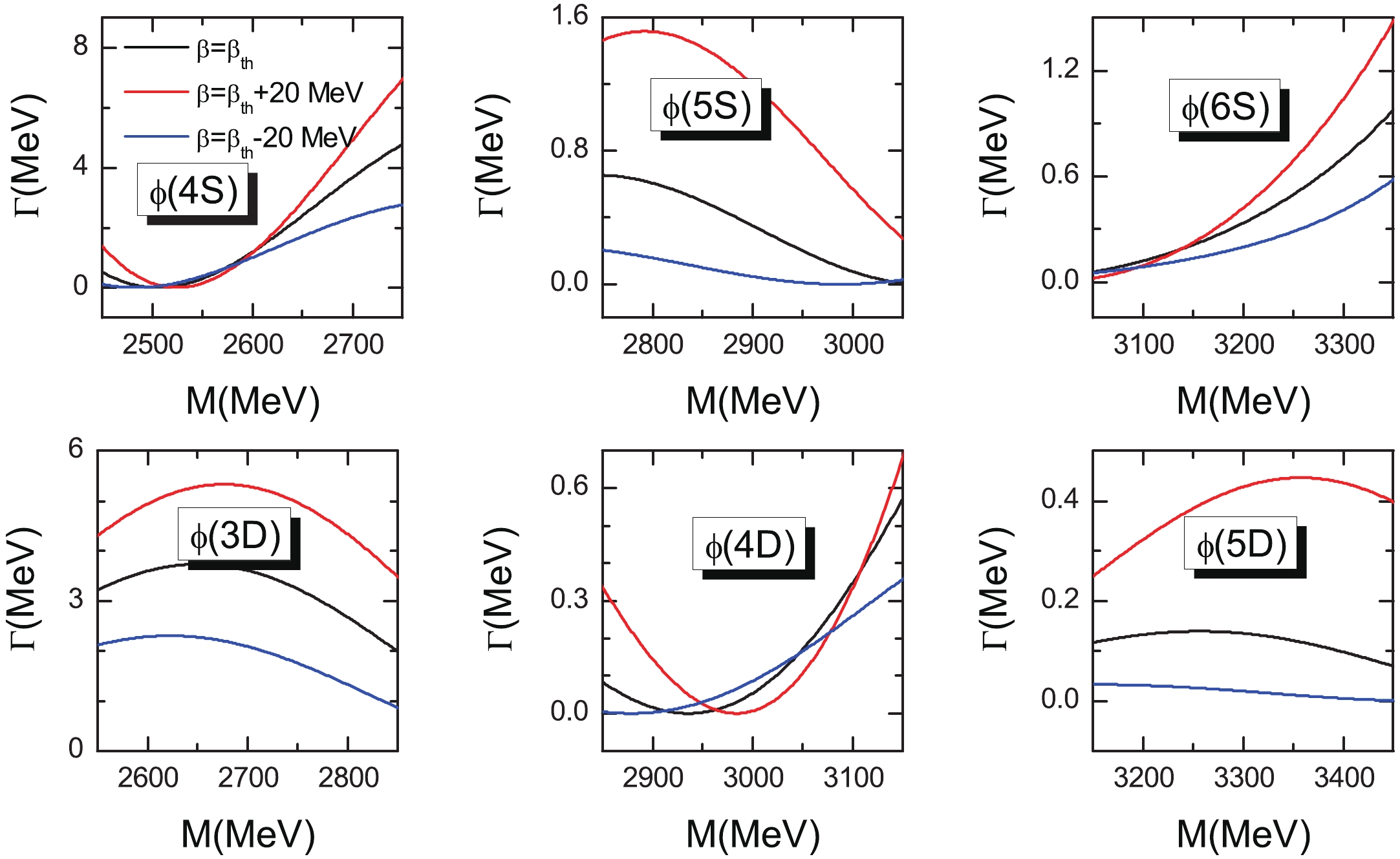
Figure 4. (color online) Variation of the
$ \Lambda\bar{\Lambda} $ decay width with the mass of the S- and D-wave vector strangeonium. The red, black, and blue lines correspond to the predictions with the values of$ \beta $ =$ \beta_{th}+20 $ MeV,$ \beta_{th} $ , and$ \beta_{th}-20 $ MeV, respectively. -
Besides the
$ \Lambda\bar{\Lambda} $ decay mode, we also investigated the$ \Xi^{-(*)}\bar{\Xi}^+ $ and$ \Sigma^{+(*)}\bar{\Sigma}^{-(*)} $ decay modes for the excited vector strangeonium. According to the predicted masses listed in Table 1, the masses of the states$ \phi(3S) $ and$ \phi(2D) $ are below the threshold of$ \Xi^{-(*)}\bar{\Xi}^+ $ and$ \Sigma^{+(*)}\bar{\Sigma}^{-(*)} $ . Thus, we focus in this section on the partial decay properties of the vector strangeonium states$ \phi(4S,\; 5S,\; 6S) $ and$ \phi(3D,\; 4D,\; 5D) $ . Our predictions are shown in Table 6.state mass $ \beta $ 

$ \Gamma[\Xi^-\bar{\Xi}^+] $ 

$ \Gamma[\Sigma^+\bar{\Sigma}^-] $ 

$ \Gamma[\Sigma^{+*}\bar{\Sigma}^-] $ 

$ \Gamma[\Sigma^{+*}\bar{\Sigma}^{-*}] $ 

$ \Gamma[\Xi^{-*}\bar{\Xi}^+] $ 

$ \phi(4^3S_1) $ 

2627 351 $ \cdot\cdot\cdot $ 

2.86 0.91 $ \cdot\cdot\cdot $ 

$ \cdot\cdot\cdot $ 

$ \phi(5^3S_1) $ 

2996 341 1.28 0.05 0.62 1.69 0.03 $ \phi(6^3S_1) $ 

3327 334 $ 2.26\times 10^{-3} $ 

0.08 0.06 $ 5.67\times 10^{-3} $ 

$ 7.63\times 10^{-4} $ 

$ \phi(3^3D_1) $ 

2732 355 0.16 1.49 0.41 $ \cdot\cdot\cdot $ 

$ \cdot\cdot\cdot $ 

$ \phi(4^3D_1) $ 

3079 344 0.11 0.02 0.07 0.86 0.01 $ \phi(5^3D_1) $ 

3395 336 0.02 0.08 0.03 0.58 $ 9.55\times 10^{-5} $ 

Table 6. Partial decay widths of the higher
$ \phi $ mesons with$ J^{PC} = 1^{–} $ , in units of MeV.From Table 6, we note that the
$ \Sigma^{+}\bar{\Sigma}^{-} $ partial decay width of$ \phi(4^3S_1) $ and$ \phi(3^3D_1) $ can be up to$ \Gamma\sim2.9 $ MeV and$ \Gamma\sim1.5 $ MeV, respectively, which is large enough to be observed in future experiments. On the other hand, the$ \Xi^{-}\bar{\Xi}^+ $ and$ \Sigma^{+*}\bar{\Sigma}^{-*} $ partial decay widths of the state$ \phi(5^3S_1) $ are both larger than one MeV.In addition, we also plot the decay properties of the states
$ \phi(4S,\; 5S,\; 6S) $ and$ \phi(3D,\; 4D,\; 5D) $ as a function of the mass in Fig. 5.
Figure 5. (color online) Variation of the partial decay widths with the mass of the S- and D-wave vector strangeonium.
To investigate the uncertainties of the parameter
$ \beta_{th} $ , we considered the partial decay properties for different$ \beta_{th} $ values. The theoretical results are not shown in the present work. According to our calculations, our main predictions hold in a reasonable range of the parameter$ \beta_{th} $ . -
In the present work, we have studied the mass spectrum of the strangeonium system with the GI model, investigated the electronic decay width, and the
$ \Lambda\bar{\Lambda} $ ,$ \Xi^{-(*)}\bar{\Xi}^+ $ , and$ \Sigma^{+(*)}\bar{\Sigma}^{-(*)} $ double baryons decay widths of the excited vector strangeonium states$ \phi(3S,\; 4S,\; 5S,\; 6S) $ and$ \phi(2D,\; 3D,\; 4D,\; 5D) $ .We concluded that the electronic decay widths of the excited vector strangeonium states
$ \phi(3S,\; 4S,\; 5S,\; 6S) $ and$ \phi(2D,\; 3D,\; 4D,\; 5D) $ are smaller than of the state$ \phi(1S) $ . On the other hand, the electronic decay width of the$ D $ -wave vector strangeonium is about$ 3\sim8 $ times larger than of the$ S $ -wave vector strangeonium.The partial decay width of the
$ \Lambda\bar{\Lambda} $ mode can be up to$ \sim5.84 $ MeV for$ \phi(3S) $ , while the partial$ \Lambda\bar{\Lambda} $ decay width of the state$ \phi(2D) $ is about$ {\cal{O}}(10^{-3}) $ keV. Thus, the ratio of the$ \Lambda\bar{\Lambda} $ decay width of the states$ \phi(3^3S_1) $ and$ \phi(2^3D_1) $ is$ {\cal{O}}(10^6) $ . If the threshold enhancement reported by the BESIII collaboration in the process$ e^+e^-\rightarrow \Lambda\bar{\Lambda} $ does arise from an unobserved strangeonium meson, the resonance is most likely the strangeonium state$ \phi(3S) $ . We also noted that the$ \Lambda\bar{\Lambda} $ and$ \Sigma^{+}\bar{\Sigma}^{-} $ partial decay widths of the states$ \phi(3^3D_1) $ and$ \phi(4^3S_1) $ are several MeV, which is sufficient to be observed in future experiments. The double baryons decay modes provide a unique probe of the excited vector strangeonium resonances, which may be produced and investigated at BESIII and BelleII.We would like to thank Xiao-Lin Chen and Wei-Zhen Deng for very helpful suggestions. We also thank Guang-Juan Wang and Lu Meng for very useful discussions.
A possible explanation of the threshold enhancement in the process $ {{e^+e^-\rightarrow \Lambda\bar{\Lambda} }}$
- Received Date: 2019-06-27
- Available Online: 2019-11-01
Abstract: Inspired by the recent measurement of the process







 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















































 DownLoad:
DownLoad: